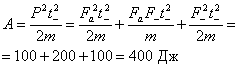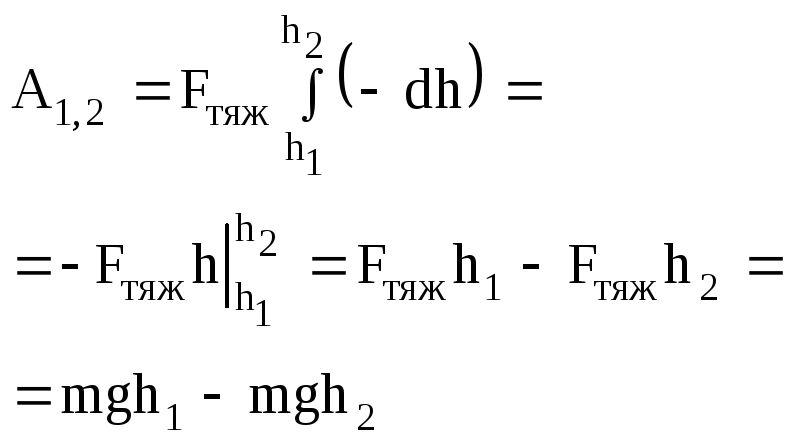- Подробности
- Обновлено 30.05.2018 20:11
- Просмотров: 706
Задачи по физике – это просто!
Вспомним
Формулы, по которым можно вычислить работу силы:
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Типовые задачи из курса школьной физики по динамике на расчет работы, совершаемой силой тяжести.
Задача 1
Автомобиль массой 500 кг движется вверх по наклонной плоскости, расположенной под угломм 30o к горизонту. Найти работу силы тяжести на пути в 200 метров.
Задача 2
Какую работу совершит сила тяжести при падении мяча массой 0,5 кг на землю из состояния покоя с высоты 5 метров?
Задача 3
Какую работу совершает сила тяжести при отскоке мяча от земли, если он поднимается на высоту 2-х метров? Масса мяча составляет 0,4 кг.
Задача 4
Скорость падающего кирпича массой 2 кг на некотором отрезке пути изменилась от 3 м/с до 6 м/с. Определить работу, совершенную силой тяжести.
- Авторы
- Резюме
- Файлы
Иванов Е.М.
Работа силы тяжести при падении тел зависит от силы сопротивления среды. Чем больше сила сопротивления, тем больше время падения и больше импульс силы тяжести. Работа, совершаемая силой, пропорциональна квадрату импульса: A=I2/2m.
В курсах физики утверждается, что если тело массы равномерно поднимать вверх на высоту
с помощью силы
, то сила совершает работу
, равную потенциальной энергии
, а сила тяжести отрицательную работу
[1]. Автором [2] было показано, что работа подъема тела на высоту
всегда больше
. Чтобы поднимать тело вверх, необходимо приложить силу
. Работа подъема будет равна
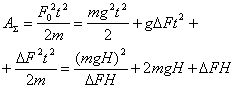
Время подъема найдется из соотношения:
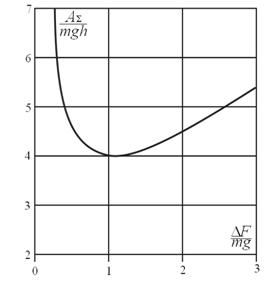
. На графике (рис. 1) показана зависимость работы
, выраженной в долях
, от величины соотношения
. Работа имеет минимум, равный
при
. При свободном падении тела с высоты
потенциальная энергия переходит в кинетическую
, где
.
Рисунок 1. Зависимость работы , выраженной в долях
, от величины соотношения
Таким образом, потенциальная энергия соответствует только работе, совершаемой силой тяжести при СВОБОДНОМ падении тела. Работа при свободном падении:
(a)
(b) (2)
Т.к. , а
,
-импульс силы тяжести.
Рассмотрим работу, совершаемую силой тяжести, при других случаях падения тел.
СЛУЧАЙ I. Падение происходит при действии постоянной силы , направленной вертикально. Если сила направлена вниз (
), как сила тяжести, то это движение можно рассматривать как свободное падение под действием силы
, как в гравитационном поле напряженности
. Примем следующие числовые значения:
кг,
м,
м/с2,
Н. Получаем: время падения
с2, скорость
(м/с)2,
Дж, работа
Дж.
Таким образом, работа падения не равна потенциальной энергии Дж (при обычном свободном падении
с2,
(м/с)2,
Дж).
Если сила направлена вертикально вверх (), то она является силой сопротивления (трения). В этом случае падение происходит под действием результирующей силы:
Н
с ускорением: м/с2.
Время падения: с2, скорость
(м/с)2,
Дж. Используя обычную формулу (2a) для расчета работы, получаем:
Дж. Используя формулу (2b), имеем
Дж.
Автором в работах [3, 4,5] показано, что работа силы (производство энергии) пропорциональна квадрату импульса силы:
Это говорит о том, что в общем случае работа зависит от времени действия силы, а не от пути, т.к. один и тот же путь (в данном случае м) может быть пройден за разное время в зависимости от величины силы сопротивления. Время падения:
, работа
. Из этих выражений могут быть составлены безразмерные комплексы
(а)
(b) (3)
Где может изменяться от 0 до 1. Случай
соответствует условию левитации тела, когда оно неподвижно зависает под действием двух одинаковых, но противоположно направленных сил
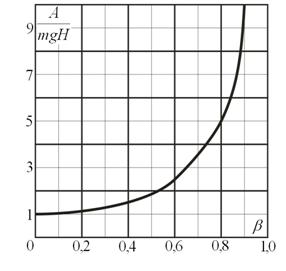
. На графике (рис. 2) показана зависимость комплекса
в зависимости от величины
.
Рисунок 2. Показана зависимость комплекса в зависимости от величины
Таким образом, в случае действия постоянной силы сопротивления (трения), работа, совершаемая силой тяжести , возрастает и в пределе
при
. Случай
соответствует статической задаче, когда груз удерживается подвесом на неизменной высоте
.
СЛУЧАЙ II. Падение происходит при действии силы сопротивления, пропорциональной скорости падения:
(4)
Решение этого дифференциального уравнения при нулевых начальных условиях имеет вид:
(а)
(b) (5)
(6)
Если использовать общепринятую формулу , то получаем
Дж. Примем
Н·с/м. Расчет по формуле
при
с (время определяется из трансцендентного уравнения (6) при
) дает численное значение работы
Дж. Силу
можно представить в виде суммы двух сил:
, где
– сила, вызывающая ускоренное движение тела вниз в соответствии со II законом Ньютона, ускорение определяется выражением (5b), а сила
– сила сопротивления, скорость определяется выражением (5a).
Используя импульсы сил , работу, совершаемую силой тяжести, можно расписать более подробно
(7)
Импульс силы, вызывающей ускоренное движение тела:
(8)
При с
Н·с;
Дж.
Импульс силы трения:
(9)
При с
Н·с;
Дж.
Работа, связанная с трением при УСКОРЕННОМ движении:
Дж
Суммарная работа Дж
Таким образом, работа совершаемая силой тяжести при падении тел, зависит от силы сопротивления среды. Чем больше сила сопротивления, тем больше время падения и больше импульс силы тяжести, а работа, совершаемая силой, пропорциональна квадрату импульса силы: 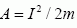
СПИСОК ЛИТЕРАТУРЫ
1. Кикоин И.К., Кикоин А.К. Физика: Учебн. для 9 кл. средн. шк. – М.: Просвещение, 1990.
2. Иванов Е.М. Работа и энергия в классической механике и первый закон термодинамики. Димитровград: ДИТУД УлГТУ, 2005.
3. Иванов Е.М. Определение работы и работа силы трения. //Успехи современного естествознания. 2005. №8. С.10
4. Иванов Е.М. Работа при движении тел с трением. //Фундаментальные исследования. 2005. №6. С.10
5. Иванов Е.М. Работа в классической механике. //Современные наукоемкие технологии. 2005. №5 С. 12.
Библиографическая ссылка
Иванов Е.М. РАБОТА ПАДЕНИЯ ТЕЛА В ОДНОРОДНОМ ПОЛЕ ТЯЖЕСТИ // Современные проблемы науки и образования. – 2006. – № 4.
;
URL: https://science-education.ru/ru/article/view?id=369 (дата обращения: 20.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
у
Найдем работу, которую совершает сила
тяжести
,
действующая на падающее тело массойm,
при его перемещении из точки 1 в точку
2 по произвольному пути (рис.4.6).
Полная работа:
.
Силу тяжести при
можно считать постоянной, тогда
.
Так как
направление вектора
противоположно возрастанию высотыh(α = 180), то
.
Работа силы тяжести равна убыли
потенциальной энергии, зависит от
начального и конечного положений тела
над Землей и не зависит от формы траектории
его движения. Следовательно, сила тяжести
есть консервативная сила.
3.6.3. Потенциальная энергия пружины
Внешняя сила, сжимая или растягивая
пружину, совершает работу. Освобожденная
от внешнего воздействия, пружина
восстанавливает свою форму, а потенциальная
энергия, запасенная пружиной в процессе
деформации, превращается в другие виды
энергии. Мерой энергии превратившейся
в другие виды, является величина работы,
совершенная упругой силой.
Работа упругой силы
на участкеdx
dA = Fхdx = – kxdx,
Полная
работа при изменении длины пружины на
Δх = х2 – х1

Потенциальная энергия деформированной
пружины
(3.26)
где
С = 0, так как потенциальная энергия
недеформированной пружины равна нулю.
Р
упругой силы не зависит от того, как
произошло изменение длины пружины.
Поэтому упругая сила так же как и сила
гравитационного притяжения консервативна.
3.6.4. Потенциальный барьер и яма
Потенциальная энергия может быть
представлена графически. График,
выражающий зависимость потенциальной
энергии от соответствующей координаты,
называется потенциальной кривой. По
характеру потенциальной кривой
определяется величина и направление
силы, действующей на тело вдоль
соответствующего направления.
Проанализируем одну из возможных
потенциальных кривых. Возьмем кривую
изменения потенциальной энергии Епсистемы тел, когда в системе одно тело
перемещается вдоль оси х (рис. 3.12). Сила
действующая на тело
.
где
– угол наклона к оси касательной
проведенной в соответствующей точке
кривой Еп=f(x)
.
B точке х1(,
поэтому)cила противоположна
направлению х и препятствует удалению
тела из системы. В точке х2(tgα < 0,
силаFх > 0)
силаFхсовпадает
с направлением оси х, и способствует
движению тела в данном направлении. В
точке х0(tgα = 0) сила на
тело не действует. Величину силы можно
определить по крутизне потенциальной
кривой: чем круче кривая, тем больше
численное значениеtgα,
например, величина силы в точке 2 больше,
чем в точке 1.
Резкое возрастание потенциальной кривой
вдоль направления движения тела
определяет потенциальный барьер, который
характеризуется высотой и шириной. Так,
для тела, находящейся в точке с координатой
х1, высота потенциального барьера
ΔЕп, ширина Δх = (х2– x1).
Если потенциальный барьер встречается
на пути движения тела, как в положительном,
так и в отрицательном направлении оси,
то, оно находится в потенциальной яме.
Форма и глубина потенциальной ямы
зависят от природы сил взаимодействия
и конфигурации системы тел.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
17.05.20158.11 Mб14курс лекций новый.doc
- #
- #
- #
- #
задача на работу силы тяжести. мы знаем массу и знаем время и ускорение свободного падения как найти работу силы тяжести
Человек Пурген
Ученик
(204),
закрыт
12 лет назад
Лучший ответ
А.УМАРОВ
Оракул
(70014)
12 лет назад
Работа A=mgh; высота h=gt^2/2
Остальные ответы
Валентина Вавилова(Серкова)
Гений
(62183)
12 лет назад
Работа силы тяжести равна произведению силы тяжести ( mg) на рассотяния от нулевнго уровня
( поверхности Земли или другого небесного тела) A=mgh . или по времени найти высоту ( h)
h=gt^/2 и подставит в 1 формулу.
Похожие вопросы
Совсем недавно, мы
изучили работу силы. Напомним, что работа силы равна произведению модуля силы,
модуля перемещения и косинуса угла между направлениями силы и перемещения:
Рассмотрим теперь частный
случай — работу силы тяжести при перемещении тела с высоты h1
на высоту h2.
Первый случай — это
падение тела вертикально вниз.
В этом случае,
перемещение, конечно же, будет равно
Сила тяжести, как мы
знаем, равна
.
Поскольку сила тяжести
направлена вертикально вниз, как и перемещение, косинус угла между
направлениями этих векторов равен единице. Таким образом, мы получим, что
работа силы тяжести равна:
Второй случай — это когда
тело, наоборот, подбрасывают вертикально вверх с высоты h1
на высоту h2.
В этом случае, угол между
направлением силы тяжести и направлением перемещения составит 180о.
Это приводит нас к тому, что работа силы тяжести опять-таки равна:
Наконец, рассмотрим
случай, когда между направлением силы тяжести и перемещением существует
произвольный угол α.
Обозначим модуль
перемещения за s. В этом случае,
работа силы тяжести равна:
Но, исходя из определения
косинуса:
Таким образом, мы в
третий раз получили одинаковый результат.
Более того, если даже мы
рассмотрим криволинейную траекторию, то убедимся, что результат будет тем же.
Любую кривую мы можем
представить в виде ломаной линии, состоящей из очень маленьких горизонтальных и
вертикальных отрезков. На горизонтальных отрезках работа силы тяжести будет
равна нулю, поскольку в этом случае направление перемещения перпендикулярно
направлению силы тяжести. На вертикальных участках работа будет равна: A
= mg(s1
+ … + sn).
Очевидно, что эта сумма будет равна (h1
– h2):
Таким образом, мы
убедились, что работа силы тяжести не зависит от траектории движения тела.
Имеет значение лишь то, насколько начальное положение тела отличается от
конечного. Это плавно подводит нас к понятию потенциальной энергии, которое
мы рассмотрим немного позже.
Из приведенных примеров
вытекает еще один важный вывод: при движении тела по замкнутой траектории
работа силы тяжести равна нулю. Для начала рассмотрим контур, имеющий форму
прямоугольника. Как мы уже убедились, при движении тела в горизонтальном
направлении, работа силы тяжести равна нулю. Вектор перемещения направлен
перпендикулярно вектору силы тяжести. При перемещении же по противолежащим
вертикальным сторонам контура, сила тяжести совершает работу, равную по
абсолютной величине, но противоположную по знаку.
В одном случае вектор
перемещения направлен так же, как вектор силы тяжести, а в другом — направлен в
противоположную сторону. Это довольно логично, поскольку при движении тела
вниз, сила тяжести ему «помогает», а при движении вверх — наоборот, мешает.
Мы можем сколь угодно
усложнить эту траекторию, получив совершенно произвольный замкнутый контур.
Но опять же, разбив все
кривые на ломаные линии с горизонтальными и вертикальными участками, мы
убедимся, что суммарная работа будет равна нулю.
Силы, обладающие такими
свойствами, называются консервативными. То есть, консервативная сила — это
такая сила, работа которой в замкнутом контуре равна нулю.
Примеры решения задач.
Задача 1. Охотник
стреляет со скалы под углом 40° к горизонту. За время падения пули работа силы
тяжести составила 5 Дж. Если пуля вошла в землю на расстоянии 250 м от скалы,
то какова её масса?
Задача 2. Находясь
на Нептуне, тело совершило перемещение так, как показано на рисунке. При этом
перемещении работа силы тяжести составила 840 Дж. Если масса данного тела равна
5 кг, то каково ускорение свободного падения на Нептуне?