Продолжаем предыдущий урок на тему “Применение криволинейных интегралов 2 рода”.
Готовые ответы задач на работу силового поля помогут студентам выучить тему, и научат быстро находить нужные интегралы.
Пример 4.2 Найти работу силы F (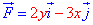 ) при перемещении точки вдоль кривой C:
) при перемещении точки вдоль кривой C:
x2/4+y2/9=1 от точки A(- 2;0) к точке B(0;3).
Решение: Запишем уравнение заданного эллипса в параметрическом виде: x=2*cos(t), y=3*sin(t).
Наведем графически траекторию материальной точки вдоль эллипса.
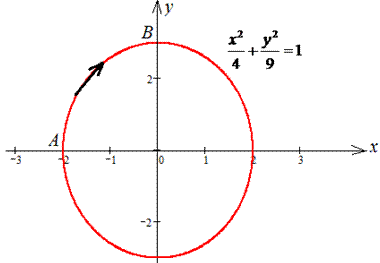
Тогда дифференциал переменных по параметру будет равен dx=-2*sin(t)dt, dy=3*cos(t)dt .
При этом пределы интегрирования ограничатся точками Pi и Pi/2.
Найдем работу силы F по кривой C через криволинейный интеграл ІІ рода : 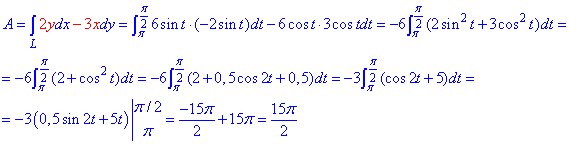
Пересмотрите внимательно формулы интегрирования синуса и косинуса, и понижения степени для таких функций.
Пример 4.4 Найти работу силы 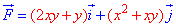 по перемещению точки вдоль кривой C:
по перемещению точки вдоль кривой C:
y=4-2x^2 от точки 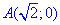 к точке
к точке 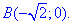
Решение: Построим траекторию движения материальной точки вдоль параболы L: y=4-2x2.
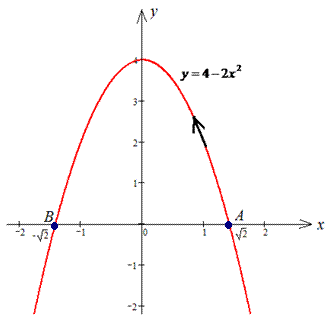
Вычисляем дифференциал дуги y=4-2x2, dy=-4x*dx и из условия выписиваем пределы интегрирования 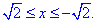
Работа силы F находим с помощью криволинейного интеграла второго рода
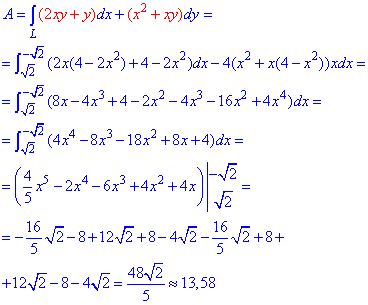
Интегрирование занимает не мало времени и при превращениях можно допустить ошибку, поэтому будьте внимательные в этих местах.
Пример 4.11 Найти работу силы 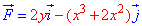 при перемещении вдоль кривой C:
при перемещении вдоль кривой C:
y=ln(x) от точки A(1;0) к точке B(e;1).
Решение: Траектория материальной точки вдоль логарифма имеет вид 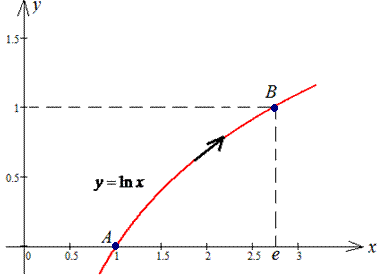
Находим дифференциал логарифма y=ln (x), dy=dx/x.
Пределы интегрирования изменяются от единицы к экспоненте.
Работа силы F с помощью криволинейного интеграла ІІ рода примет значение:
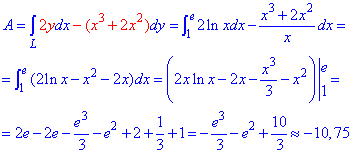
Здесь для логарифма применили правило интегрирования частями (u*dv).
Пример 4.13 Найти работу силы F при перемещении вдоль кривой C:
x2+y2=9 от точки A (0;-3) к точке 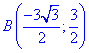 , где F задана формулой
, где F задана формулой
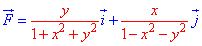
Решение: Построим траекторию движения материальной точки вдоль круга радиусом 3.
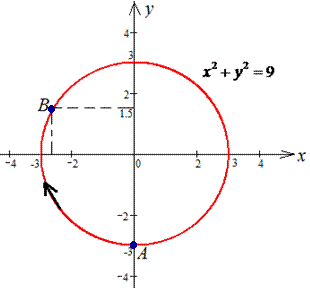
Чтобы не выражать две функции (верхняя и нижняя кривая круга) запишем зависимость x(y) и вычислим дифференциал дуги
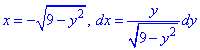
При этом ордината изменяется от – 3 до 3/2.
Применяя криволинейный интеграл ІІ рода находим роботу силы F при перемещении вдоль круга:
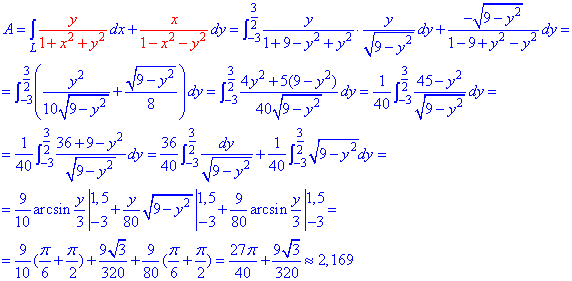
Бороться с корнями во время интегрирования непросто, о чем свидетельствует приведенные вычисления.
Намного проще вычислять интеграл при переходе к полярной системе координат.
Дальше наведем методику интегрирования:
ІІ – способ:
Параметризуэм заданный круг:
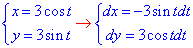
Учитывая, что во время движения от точки A(0;-3) к точке 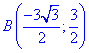 угол изменяется от
угол изменяется от 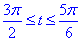
Вычисляем искомый криволинейный интеграл ІІ рода : 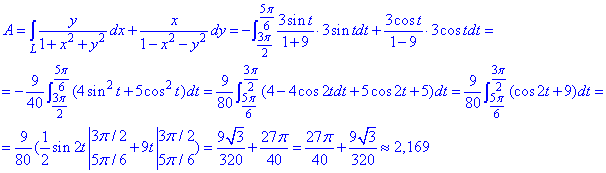
В плане вычислений второй метод более легкий, поэтому для круговых и эллиптических форм кривой при симметричном вхождении x, y в уравнение силы рекомендуем переходить к полярной системе координат.
Пример 4.15 Найти работу силы 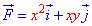 при перемещении вдоль кривой C:
при перемещении вдоль кривой C:
4x2+y2=4 от точки A(0;2) к точке B (-1;0).
Решение: Траектория движения материальной точки по эллипсу приведена ниже
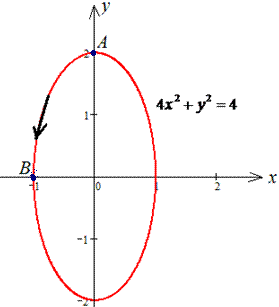
Записываем верхнюю дугу эллипса и ее производную.
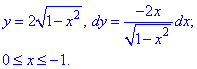
Пределы интегрирования изменяются от 0 к -1
Работа силы F через криволинейный интеграл второга рода выражается зависимостью:
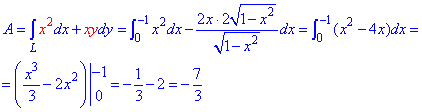
Пример 4.18 Найти работу силы 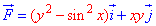 по перемещению материальной точки вдоль кривой C:
по перемещению материальной точки вдоль кривой C:
y=cos(x) от точки A(Pi/2;0) к точке B(-Pi/2;0).
Решение: Изобразим траекторию материальной точки вдоль косинуса
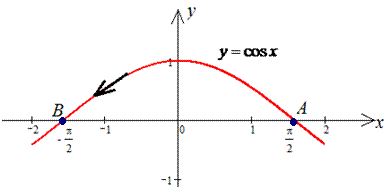
Построим дифференциал кривой y=cos(x), dy=-sin(x)*dx.
Он нужен для возведения криволинейного интегралу ІІ рода к определенному.
Находим работу силы F по перемещении вдоль контура интегрированием
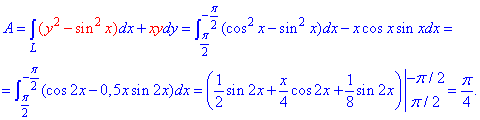
Для понижения под интегралом степеней косинуса и синуса применили известные тригонометрические формулы.
Пример 4.21 Найти работу силы 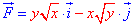 при перемещении вдоль кривой C:
при перемещении вдоль кривой C:
y=x3 от точки A(0;0) к точке B(2;8).
Решение: Построим траекторию материальной точки вдоль кривой y=x3.
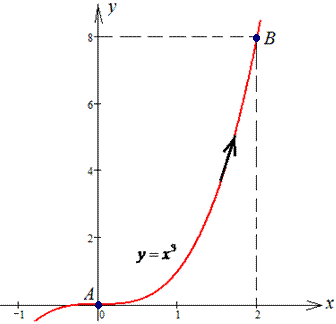
Вычисляем дифференциал дуги dy=3x2dx.
Пределы интегрирования приведены на рисунку и в условии.
Работа силы F находим с помощью криволинейного интегралу ІІ рода:
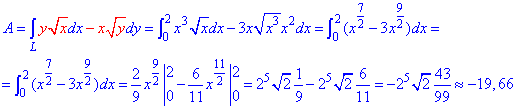
Превращаем все к показательной форме и интегрируем.
Пример 4.23 Найти работу силы 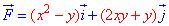 при перемещении вдоль кривой C: x2+2y2=2 от точки
при перемещении вдоль кривой C: x2+2y2=2 от точки 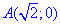 к точке
к точке 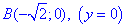
Решение: За инструкцией строим траекторию материальной точки вдоль эллипса: x2+2y2=2.
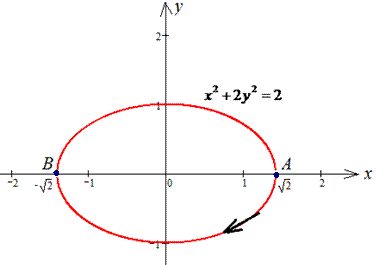
Для простоты вычислений криволинейного интеграла ІІ рода параметризуэм эллипс:
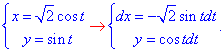
Учитывая, что от точки 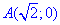 к точке
к точке 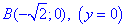 угол изменяется в пределах
угол изменяется в пределах 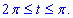 переходим к интегрированию
переходим к интегрированию
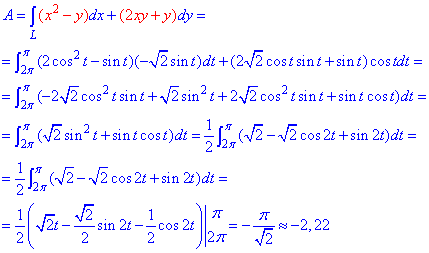
Понижаем степени и интегрируем.
Пример 4.24 Найти работу силы 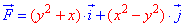 при перемещении вдоль кривой C:
при перемещении вдоль кривой C:
y=1-|x| от точки A(-1;0) к точке B(2;- 1).
Решение: Наведем траекторию материальной точки вдоль модуль функции.
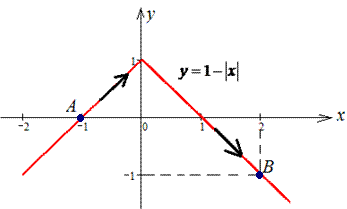
Как ни хотелось встретить задания с разбитием кривой на два интервала, однако одно Пример содержит такое условие. Разделим на две части: y=1+x, тогда пределы равны [-1;0] и дифференциал dy=dx;
На втором участке y=1-x имеем [0;2] и dy=-dx.
Вычисляем работу силы F, потраченную на перемещении точки вдоль модуль функции:
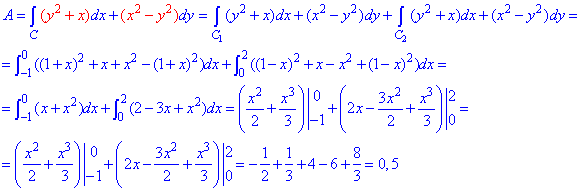
На этом ознакомление из такого сорта примерами завершено.
Больше готовых ответов из курса высшей математики ищите на страницах сайта.
На материальную точку $Tleft(x,yright)$ действует переменная сила $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$. Под действием этой силы материальная точка перемещается на отрезке $left[6;15right]$ от точки $M$ до точки $N$ вдоль синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$. Найти работу переменной силы $overline{F}$ на криволинейном пути от точки $M$ до точки $N$. Построить графическое изображение пути от точки $M$ до точки $N$, а также векторы переменной сили $overline{F}$ в этих точках.
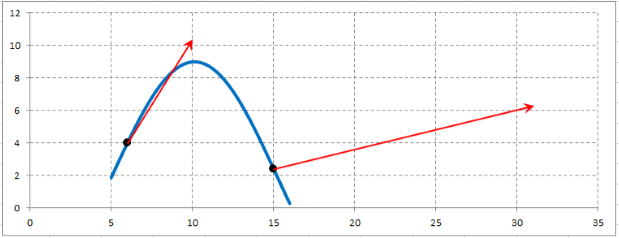
Выполняем графическое изображение синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$ на отрезке $left[6;15right]$.
Находим значения синусоиды в точках $x_{M} =6$ и $x_{N} =15$:
- $y_{M} =7cdot sin left(0,31cdot 6-1,57right)+2approx 4$;
- $y_{N} =7cdot sin left(0,31cdot 15-1,57right)+2approx 2,43$.
Выполняем графические изображения векторов переменной силы $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$, значения которого в точках $M$ и $N$ соответственно равны $overline{F}_{M} =left(3cdot 6-2cdot 4right)cdot overline{i}+4cdot 4cdot overline{j}=10cdot overline{i}+16cdot overline{j}$ и $bar{F}_{N} =left(3cdot 15-2cdot 2,43right)cdot overline{i}+4cdot 2,43cdot overline{j}=40,14cdot overline{i}+9,72cdot overline{j}$.
Работу данной силы на данном участке кривой $MN$ вычисляем по формуле $A=int limits _{a}^{b}Pleft(x,yleft(xright)right)cdot dx +int limits _{a}^{b}Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
Здесь участок кривой $MN$ задан на отрезке $left[x_{M} ,; x_{N} right]$, поэтому формула для работы приобретает вид: $A=int limits _{x_{M} }^{x_{N} }Pleft(x,yleft(xright)right)cdot dx +int limits _{x_{M} }^{x_{N} }Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
В этой формуле первый интеграл дает значение работы силы $F$ вдоль оси $Ox$, второй интеграл — вдоль оси $Oy$.
Находим работу силы вдоль оси $Ox$: $A_{x} =int limits _{6}^{15}Pleft(x,yleft(xright)right)cdot dx $.
Согласно условию задачи имеем:
[Pleft(x,yright)=3cdot x-2cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2.]
Поэтому:
[Pleft(x,yleft(xright)right)=3cdot x-2cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=]
[=3cdot x-14cdot sin left(0,31cdot x-1,57right)-4.]
Далее получаем:
[A_{x} =int limits _{6}^{15}left(3cdot x-14cdot sin left(0,31cdot x-1,57right)-4right)cdot dx =]
[=int limits _{6}^{15}3cdot xcdot dx +int limits _{6}^{15}left(-14cdot sin left(0,31cdot x-1,57right)right)cdot dx +int limits _{6}^{15}left(-4right)cdot dx =]
[=3cdot int limits _{6}^{15}xcdot dx -14cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dx -4cdot int limits _{6}^{15}dx =]
[=3cdot left[frac{x^{2} }{2} right]_{6}^{15} -14cdot left[-frac{1}{0,31} cdot cos left(0,31cdot x-1,57right)right]_{6}^{15} -4cdot left[xright]_{6}^{15} =]
[=1,5cdot left(15^{2} -6^{2} right)+frac{14}{0,31} cdot left(cos left(0,31cdot 15-1,57right)-cos left(0,31cdot 6-1,57right)right)-]
[-4cdot left(15-6right)=135,15.]
Находим работу силы вдоль оси $Oy$: $A_{y} =int limits _{6}^{15}Qleft(x,yleft(xright)right)cdot y’cdot dx $.
Согласно условию задачи имеем:
[Qleft(x,yright)=4cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2. ]
Поэтому:
[Qleft(x,yleft(xright)right)=4cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=28cdot sin left(0,31cdot x-1,57right)+8;]
[y’=7cdot 0,31cdot cos left(0,31cdot x-1,57right)=2,17cdot cos left(0,31cdot x-1,57right).]
Далее получаем:
[A_{y} =int limits _{6}^{15}left(28cdot sin left(0,31cdot x-1,57right)+8right)cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}28cdot 2,17cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}8cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}60,76cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}17,36cdot cos left(0,31cdot x-1,57right)cdot dx .]
Вычисляем первый интеграл $I_{1} $:
[I_{1} =60,76cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=60,76cdot frac{1}{0,31} cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dleft(sin left(0,31cdot x-1,57right)right) =]
[=196cdot left[frac{sin ^{2} left(0,31cdot x-1,57right)}{2} right]_{6}^{15} =]
[=98cdot left(sin ^{2} left(0,31cdot 15-1,57right)-sin ^{2} left(0,31cdot 6-1,57right)right)approx -7,64.]
Вычисляем второй интеграл $I_{2} $:
[I_{2} =17,36cdot int limits _{6}^{15}cos left(0,31cdot x-1,57right)cdot dx =]
[=17,36cdot frac{1}{0,31} cdot left[sin left(0,31cdot x-1,57right)right]_{6}^{15} =]
[=56cdot left(sin left(0,31cdot 15-1,57right)-sin left(0,31cdot 6-1,57right)right)approx -12,57.]
Работа силы вдоль оси $Oy$:
[A_{y} =I_{1} +I_{2} =-7,64-12,57=-20,21.]
Общая работа силы при перемещении вдоль кривой:
[A=A_{x} +A_{y} =135,15-20,21=114,94.]
Назначение. Онлайн калькулятор предназначен для нахождения работы силы F при перемещении вдоль дуги линии L.
- Решение онлайн
- Видеоинструкция
Криволинейные и поверхностные интегралы второго рода
Рассмотрим многообразие σ. Пусть τ(x,y,z)– единичный вектор касательной к σ, если σ – кривая, а n(x,y,z)– единичный вектор нормали к σ, если σ – поверхность в R3. Введём векторы dl=τ·dl и dS=n·dS, где dl и dS – длина и площадь соответствующего участка кривой или поверхности. Будем считать, что dσ=dl, если σ – кривая, и dσ=dS, если σ – поверхность. Назовём dσ ориентированной мерой соответствующего участка кривой или поверхности.
Определение. Пусть заданы ориентированное непрерывное кусочно-гладкое многообразие σ и на σ – вектор-функция F(x,y,z)=P(x,y,z)i+Q(x,y,z)+R(x,y,z). Разобьем многообразие на части многообразиями меньшей размерности (кривую – точками, поверхность –кривыми), внутри каждого полученного элементарного многообразия выберем по точке M0(x0,y0,z0), M1(x1,y1,z1), … ,Mn(xn,yn,zn). Посчитаем значения F(xi,yi,zi), i=1,2,…,n вектор-функции в этих точках,умножим скалярно эти значения на ориентированную меру dσi данного элементарного многообразия (ориентированные длину или площадь соответствующего участка многообразия) и просуммируем. Предел полученных сумм ![]() если онсуществует, не зависит от способа разбиения многообразия на части и выбора точек внутри каждого элементарного многообразия, при условии, что диаметр элементарного участка стремится к нулю, называется интегралом по многообразию (криволинейным интегралом, если σ -кривая и поверхностным, если σ – поверхность) второго рода, интеграломвдоль ориентированного многообразия, или интегралом от вектора F вдоль σ, и обозначается в общем случае
если онсуществует, не зависит от способа разбиения многообразия на части и выбора точек внутри каждого элементарного многообразия, при условии, что диаметр элементарного участка стремится к нулю, называется интегралом по многообразию (криволинейным интегралом, если σ -кривая и поверхностным, если σ – поверхность) второго рода, интеграломвдоль ориентированного многообразия, или интегралом от вектора F вдоль σ, и обозначается в общем случае![]() , в случаях криволинейного и поверхностного интегралов
, в случаях криволинейного и поверхностного интегралов ![]()
![]() соответственно.
соответственно.
Заметим, что если F(x,y,z) – сила, то ![]() – работа этой силы по перемещению материальной точки вдоль кривой, если F(x,y,z) – стационарное (не зависящее от времени) поле скоростей текущей жидкости, то
– работа этой силы по перемещению материальной точки вдоль кривой, если F(x,y,z) – стационарное (не зависящее от времени) поле скоростей текущей жидкости, то ![]() – количество жидкости, протекающей через поверхность S в единицу времени (поток вектора через поверхность).
– количество жидкости, протекающей через поверхность S в единицу времени (поток вектора через поверхность).
Если кривая задана параметрически  или, что то же самое, в векторной форме,
или, что то же самое, в векторной форме,

то

![]()
и для криволинейного интеграла второго рода имеем

Так как dS=n·dS=(cosα, cosβ, cosγ), где cosα, cosβ, cosγ – направляющие косинусы единичного вектора нормали n и cosαdS=dydz, cosβdS=dxdz, cosγdS=dxdy, то для поверхностного интеграла второго рода получаем
![]()
![]()
Если поверхность задана параметрически  или, что тоже самое, в векторной форме
или, что тоже самое, в векторной форме
r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k, (u,v)∈D
то
![]()



где  – якобианы (определители матриц Якоби, или, что то же самое, матриц производных) вектор-функций
– якобианы (определители матриц Якоби, или, что то же самое, матриц производных) вектор-функций ![]()
![]() соответственно.
соответственно.
Если поверхность S может быть задана одновременно уравнениями ![]() то поверхностный интеграл второго рода вычисляется по формуле
то поверхностный интеграл второго рода вычисляется по формуле
![]()
![]()
![]()
где D1, D2, D3 – проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно и знак “+” берётся, если угол между вектором нормали и осью, вдоль которой ведётся проектирование, острый, а знак “–“, если этот угол тупой.
Свойства криволинейного и поверхностного интегралов второго рода
Отметим некоторые свойства криволинейного и поверхностного интегралов второго рода.
Теорема 1. Криволинейный и поверхностный интегралы 2-го рода зависят от ориентации кривой и поверхности, точнее
![]() .
.
Теорема 2. Пусть σ=σ1∪σ2 и размерность пересечения dlim(σ1∩σ2)=n-1. Тогда
![]()
Доказательство. Включив в число многообразий разбиения в определении интеграла по многообразию второго рода общую границу σ1 с σ2 получаем требуемое.
Пример №1. Найти работу силы F при перемещении вдоль дуги линии L от точки M0 до точки M1.
F=x2yi+yj;, L: отрезок M0M1
M0(-1;3), M0(0;1)
Решение.
Находим уравнение прямой вдоль отрезка M0M1.
![]() или
или y=-2x+1
dy=-2dx

Пределы изменения x: [-1; 0]

Пример №2. Вычислить ![]() вдоль кривой
вдоль кривой ![]() , если t∈[0;π]
, если t∈[0;π]
Имеем

Пример №3. Вычислить поток вектора f(x,y,z)=(yz,xz,xy)T через часть плоскости x+y+z=a лежащую в первом октанте.
Поток вектора через поверхность равен поверхностному интегралу второго рода ![]() Поверхность однозначно проектируется на все три координатные плоскости. Поэтому интеграл может быть вычислен с помощью проектирования на них. Тогда
Поверхность однозначно проектируется на все три координатные плоскости. Поэтому интеграл может быть вычислен с помощью проектирования на них. Тогда
![]()
![]()
![]()
где S1, S2, S3 – проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно. Посчитаем первый из них. Имеем 
 Остальные два интеграла считаются аналогично и также равны
Остальные два интеграла считаются аналогично и также равны ![]() Поэтому поток вектора через поверхность равен
Поэтому поток вектора через поверхность равен ![]() Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями. Поэтому поток вектора через поверхность равен
Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями. Поэтому поток вектора через поверхность равен ![]() Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями.
Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями.

Работа переменной силы
Пусть материальная точка 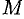 перемещается под действием силы
перемещается под действием силы 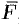 , направленной вдоль оси
, направленной вдоль оси 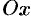 и имеющей переменную величину
и имеющей переменную величину 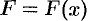 , где
, где 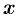 — абсцисса движущейся точки
— абсцисса движущейся точки 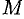 .
.
Найдем работу 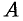 силы
силы 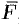 по перемещению точки
по перемещению точки 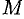 вдоль оси
вдоль оси 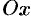 из точки
из точки 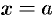 в точку
в точку 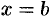 (
(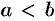 ). Для этого отрезок
). Для этого отрезок  точками
точками 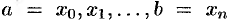
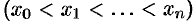 разобьем на
разобьем на  частичных отрезков
частичных отрезков 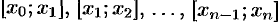 . Сила, действующая на отрезке
. Сила, действующая на отрезке 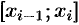 , меняется от точки к точке. Но если длина отрезка
, меняется от точки к точке. Но если длина отрезка 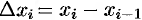 достаточно мала, то сила
достаточно мала, то сила 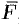 на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции
на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции 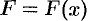 в произвольно выбранной точке
в произвольно выбранной точке 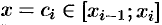 . Поэтому работа, совершенная этой силой на отрезке
. Поэтому работа, совершенная этой силой на отрезке 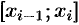 , равна произведению
, равна произведению 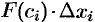 . (Как работа постоянной силы
. (Как работа постоянной силы 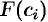 на участке
на участке 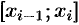 .)
.)
Приближенное значение работы 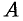 силы
силы 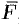 на всем отрезке
на всем отрезке  есть
есть
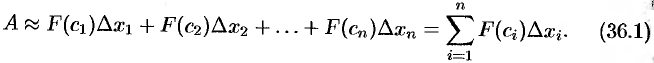
Это приближенное равенство тем точнее, чем меньше длина 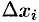 . Поэтому за точное значение работы
. Поэтому за точное значение работы 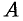 принимается предел суммы (36.1). при условии, что наибольшая длина
принимается предел суммы (36.1). при условии, что наибольшая длина 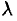 частичных отрезков стремится к нулю:
частичных отрезков стремится к нулю:
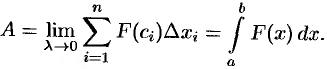
Итак, работа переменной силы 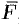 , величина которой есть непрерывная функция
, величина которой есть непрерывная функция 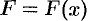 , действующей на отрезке
, действующей на отрезке  , равна определенному интегралу от величины
, равна определенному интегралу от величины 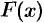 силы, взятому по отрезку
силы, взятому по отрезку  .
.
В этом состоит физический смысл определенного интеграла.
Аналогично можно показать, что путь 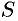 , пройденный точкой за промежуток времени от
, пройденный точкой за промежуток времени от 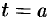 до
до 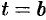 , равен определенному интегралу от скорости
, равен определенному интегралу от скорости 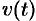 :
:
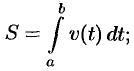
масса 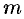 неоднородного стержня па отрезке
неоднородного стержня па отрезке  равна определенному интегралу от плотности
равна определенному интегралу от плотности 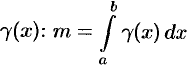 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:

Вычисление работы сил
![]()
![]()
или
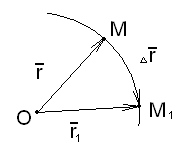
Элементарная
работа силы равна:
![]()
![]()
Полная работа силы
вычисляется через интеграл
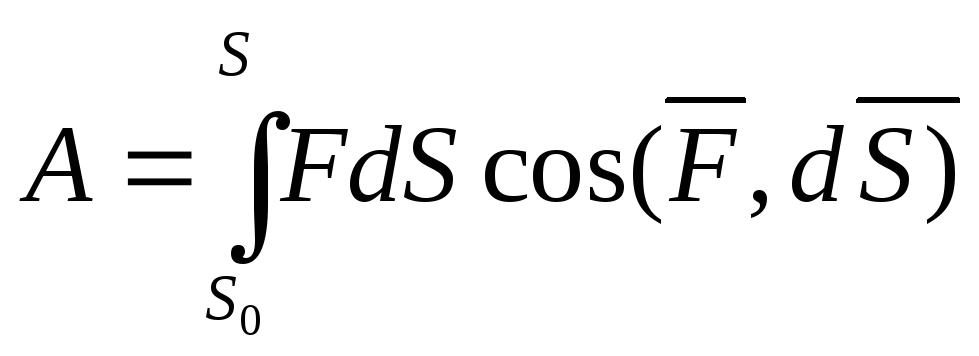
и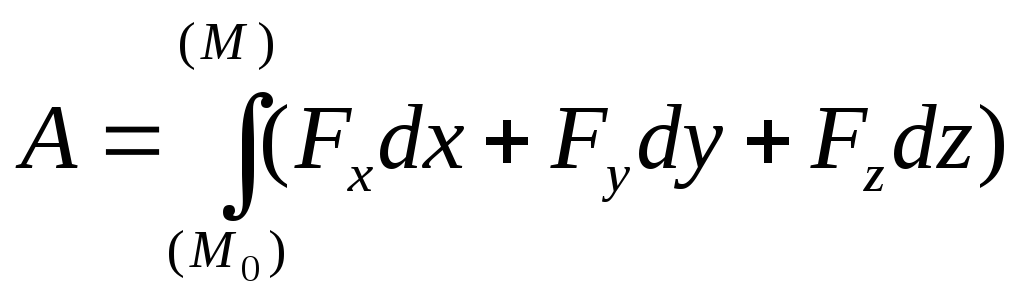 ли
ли
Работа силы в некоторых случаях
-
Сила постоянна
по величине. Точка или тело движется
прямолинейно.
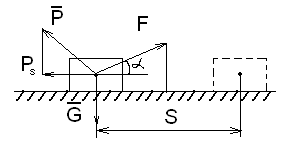
![]()
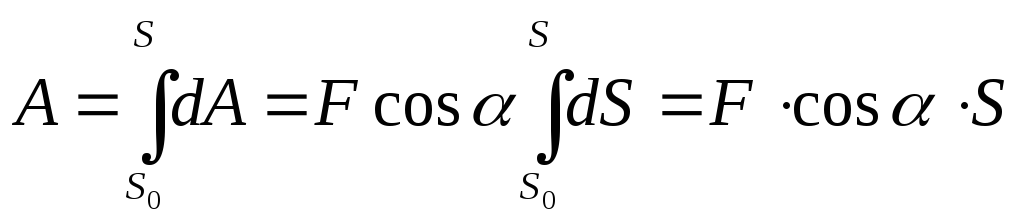
Знаки работы:
при α < 90°; A
> 0
при α = 90°; A
= 0
при 90°
< α <
180°; A
<
0
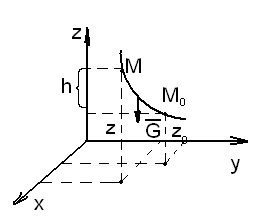
-
Р
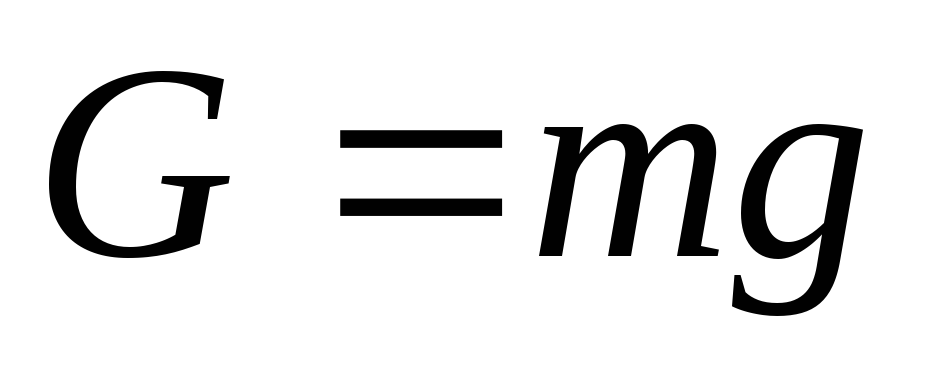 абота
абота
силы тяжести.
![]()
![]()
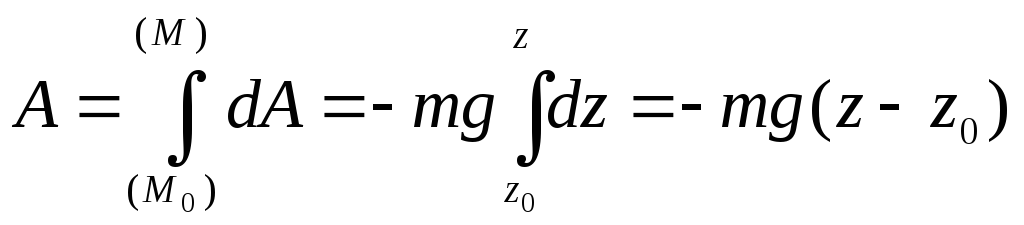
![]()
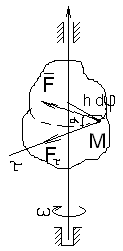
-
Работа силы при
вращательном движении тела вокруг
неподвижной оси.
![]()
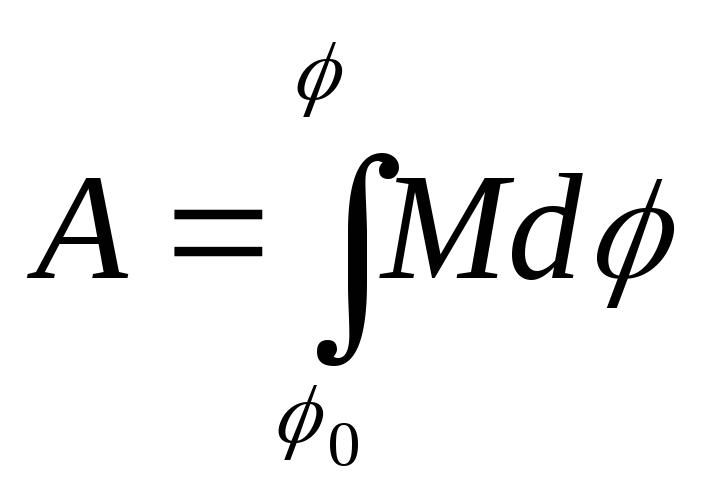
Е![]() сли
сли
М =
const, то
-
Работа силы
упругости пружины.
![]()
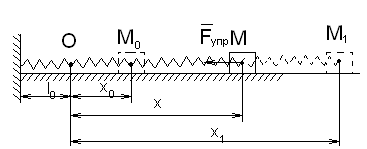
![]()
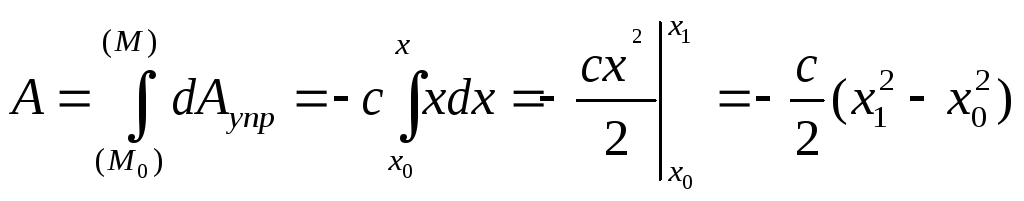
![]()
Если x0
= 0, то
Единицей измерения работыв СИ
является –![]()
Установим зависимость между моментами
инерции относительно параллельных
осей, одна из которых проходит через
центр масс.
Теорема о моментах инерции относительно
параллельных осей. (Теорема Штейнера)
Момент инерции системы относительно
какой-либо оси равен моменту инерции
относительно параллельной оси, проходящей
через центр масс, плюс произведение
массы системы на квадрат расстояния
между этими осями.
![]()
Доказательство: Пусть имеется две
декартовы системы координат
![]() и
и![]() ,
,
оси которых параллельны. Начало системы![]() находится в центре масс системы. Докажем
находится в центре масс системы. Докажем
теорему для осей![]() и
и![]() .
.
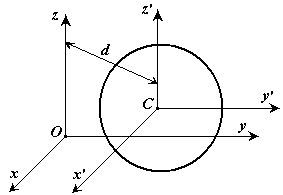
![]()
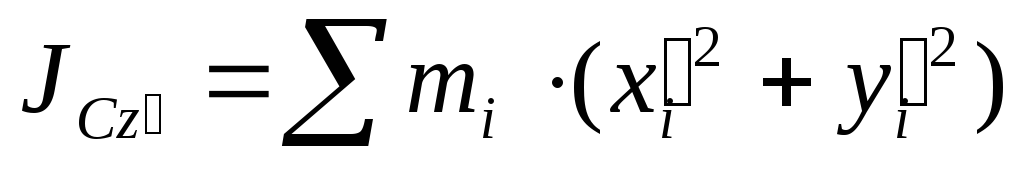
Координаты связаны между собой
соотношениями:
![]() ,
,![]() ,
,![]()
Работа силы. Мощность.
Одна из основных характеристик силы,
оценивающих действие силы на тело при
некотором его перемещении.
Э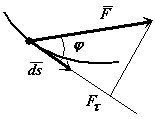 лементарная
лементарная
работа силыскалярная величина
равная произведению элементарного
перемещения на проекцию силы на это
перемещение.
![]() .
.![]() ,
,
![]()
Элементарная работа силыравна
скалярному произведению силы на
элементарное перемещение или на
дифференциал радиуса вектора точки
приложения силы.
![]()
Элементарная работа силыравна
скалярному произведению элементарного
импульса силы на скорость точки.
![]()
Мощностью силыназывается
величина, определяющая работу, совершаемую
силой в единицу времени. В общем случае
мощность равна первой производной по
времени от работы.
![]() ,
,![]()
Мощностьравна скалярному
произведению силы на скорость.
Единицей измерения мощности в СИ является
–
![]()
В технике за единицу силы принимается
![]() .
.
Теорема об изменении кинетической энергии системы.
Эта теорема существует в двух формах.
Теорема.Дифференциал кинетической
энергии системы равен сумме элементарных
работ всех внешних и внутренних сил,
действующих на систему.
![]()
Теорема.Изменение кинетической
энергии системы при ее перемещении из
одного положения в другое равно сумме
работ всех внешних и внутренних сил,
действующих на систему, на соответствующих
перемещениях точек системы при том же
перемещении системы..
![]()
Теорема Кенига.Кинетическая энергия
системы в абсолютном движении складывается
из кинетической энергии центра масс,
если в нем сосредоточить всю массу
системы, и кинетической энергии системы
при ее движении относительно центра
масс.
![]()
Вычисление обобщённых сил
Если система имеет
n
степеней свободы, то у неё n
обобщённых координат, независимых друг
от друга (q1,
q2,
…, qn)
и n
возможных перемещений (δq1,
δq2,
…, δqn).
Сумма элементарных работ, приложенных
к системе сил, на возможные перемещения
системы равна
![]() .
.
Обобщёнными силами
называются коэффициенты, стоящие перед
соответственными возможными перемещениями.
Так как обобщённые координаты не зависят
друг от друга, то для определения
обобщённой силы системе необходимо
сообщить возможные перемещения,
соответствующие координатам, а все
остальные возможные перемещения принять
за нуль, то есть для определения Q1
необходимо, чтобы δq1
≠ 0, δq2
= 0, δq3
= 0, …, δqn
= 0, тогда
![]()
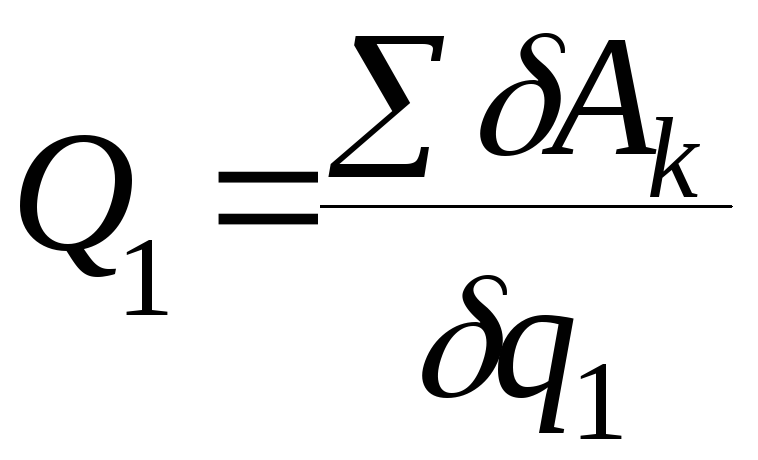 .
.
Размерность
обобщённых сил зависит от размерности
обобщённых координат: если qj
= x
(м), то Qj
– сила (Н);
если qj
= φ
(рад), то Qj
– момент (Н∙м).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
