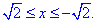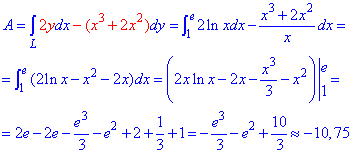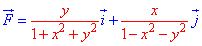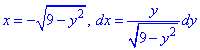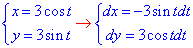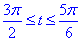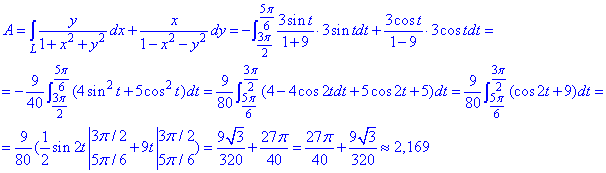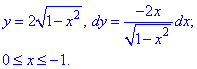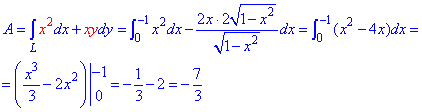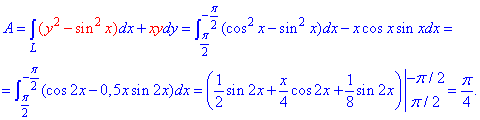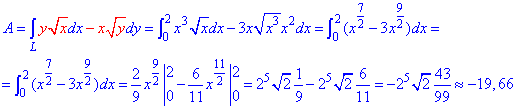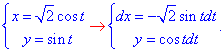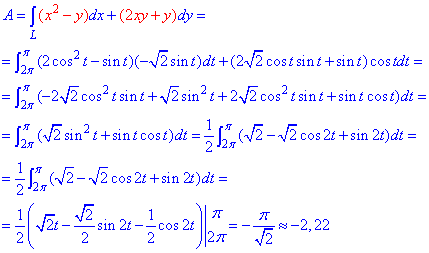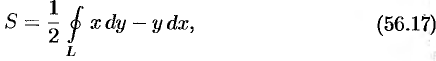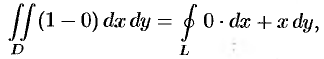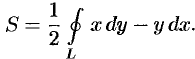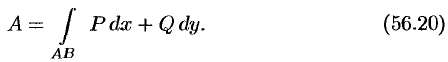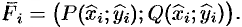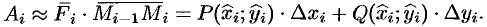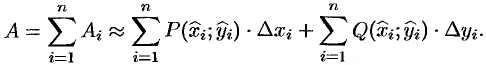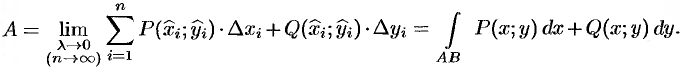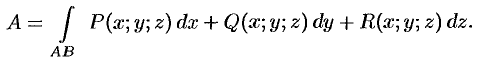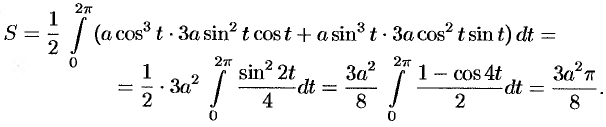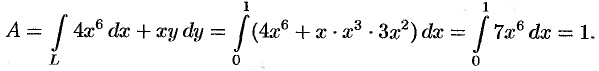Продолжаем предыдущий урок на тему “Применение криволинейных интегралов 2 рода”.
Готовые ответы задач на работу силового поля помогут студентам выучить тему, и научат быстро находить нужные интегралы.
Пример 4.2 Найти работу силы F (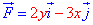
x2/4+y2/9=1 от точки A(- 2;0) к точке B(0;3).
Решение: Запишем уравнение заданного эллипса в параметрическом виде: x=2*cos(t), y=3*sin(t).
Наведем графически траекторию материальной точки вдоль эллипса.
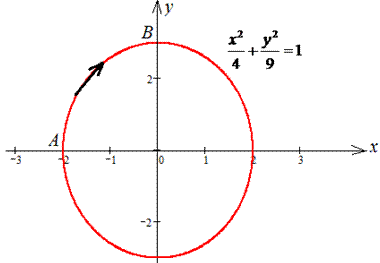
Тогда дифференциал переменных по параметру будет равен dx=-2*sin(t)dt, dy=3*cos(t)dt .
При этом пределы интегрирования ограничатся точками Pi и Pi/2.
Найдем работу силы F по кривой C через криволинейный интеграл ІІ рода : 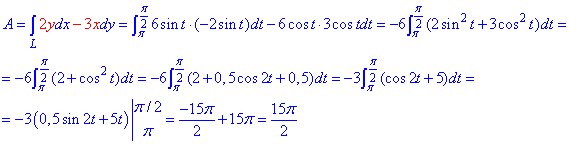
Пересмотрите внимательно формулы интегрирования синуса и косинуса, и понижения степени для таких функций.
Пример 4.4 Найти работу силы 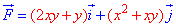
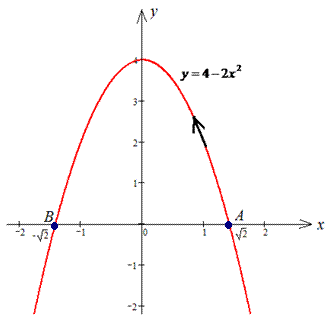
y=4-2x^2 от точки 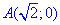
Решение: Построим траекторию движения материальной точки вдоль параболы L: y=4-2x2.
Вычисляем дифференциал дуги y=4-2x2, dy=-4x*dx и из условия выписиваем пределы интегрирования
Работа силы F находим с помощью криволинейного интеграла второго рода
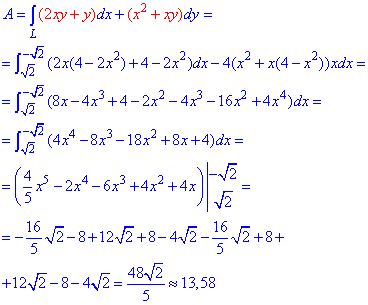
Интегрирование занимает не мало времени и при превращениях можно допустить ошибку, поэтому будьте внимательные в этих местах.
Пример 4.11 Найти работу силы 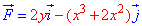
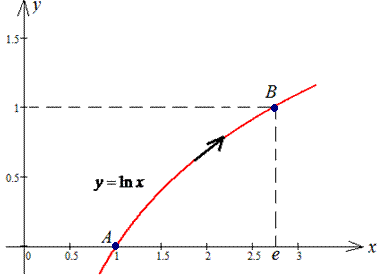
y=ln(x) от точки A(1;0) к точке B(e;1).
Решение: Траектория материальной точки вдоль логарифма имеет вид
Находим дифференциал логарифма y=ln (x), dy=dx/x.
Пределы интегрирования изменяются от единицы к экспоненте.
Работа силы F с помощью криволинейного интеграла ІІ рода примет значение:
Здесь для логарифма применили правило интегрирования частями (u*dv).
Пример 4.13 Найти работу силы F при перемещении вдоль кривой C:
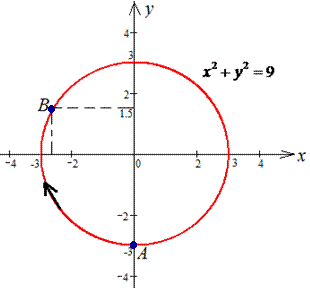
x2+y2=9 от точки A (0;-3) к точке 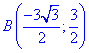
Решение: Построим траекторию движения материальной точки вдоль круга радиусом 3.
Чтобы не выражать две функции (верхняя и нижняя кривая круга) запишем зависимость x(y) и вычислим дифференциал дуги
При этом ордината изменяется от – 3 до 3/2.
Применяя криволинейный интеграл ІІ рода находим роботу силы F при перемещении вдоль круга:
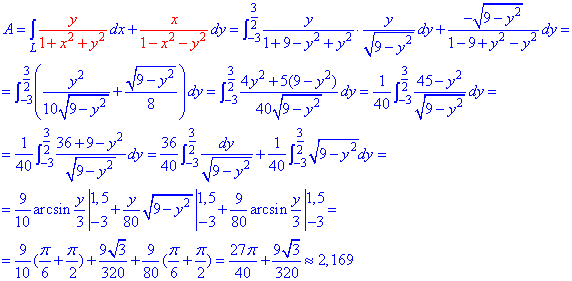
Бороться с корнями во время интегрирования непросто, о чем свидетельствует приведенные вычисления.
Намного проще вычислять интеграл при переходе к полярной системе координат.
Дальше наведем методику интегрирования:
ІІ – способ:
Параметризуэм заданный круг:
Учитывая, что во время движения от точки A(0;-3) к точке 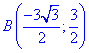
Вычисляем искомый криволинейный интеграл ІІ рода :
В плане вычислений второй метод более легкий, поэтому для круговых и эллиптических форм кривой при симметричном вхождении x, y в уравнение силы рекомендуем переходить к полярной системе координат.
Пример 4.15 Найти работу силы 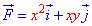
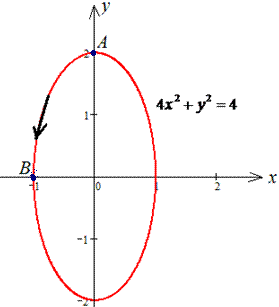
4x2+y2=4 от точки A(0;2) к точке B (-1;0).
Решение: Траектория движения материальной точки по эллипсу приведена ниже
Записываем верхнюю дугу эллипса и ее производную.
Пределы интегрирования изменяются от 0 к -1
Работа силы F через криволинейный интеграл второга рода выражается зависимостью:
Пример 4.18 Найти работу силы 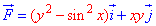
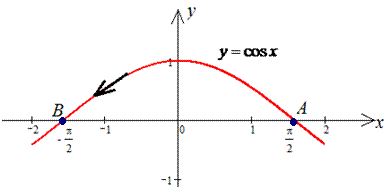
y=cos(x) от точки A(Pi/2;0) к точке B(-Pi/2;0).
Решение: Изобразим траекторию материальной точки вдоль косинуса
Построим дифференциал кривой y=cos(x), dy=-sin(x)*dx.
Он нужен для возведения криволинейного интегралу ІІ рода к определенному.
Находим работу силы F по перемещении вдоль контура интегрированием
Для понижения под интегралом степеней косинуса и синуса применили известные тригонометрические формулы.
Пример 4.21 Найти работу силы 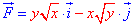
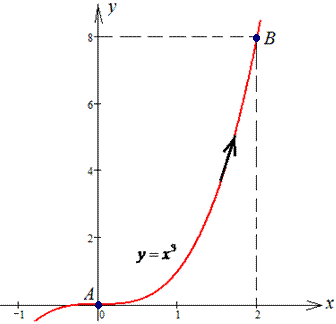
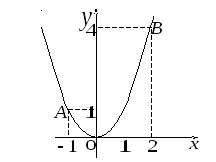
y=x3 от точки A(0;0) к точке B(2;8).
Решение: Построим траекторию материальной точки вдоль кривой y=x3.
Вычисляем дифференциал дуги dy=3x2dx.
Пределы интегрирования приведены на рисунку и в условии.
Работа силы F находим с помощью криволинейного интегралу ІІ рода:
Превращаем все к показательной форме и интегрируем.
Пример 4.23 Найти работу силы 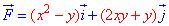
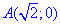
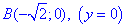
Решение: За инструкцией строим траекторию материальной точки вдоль эллипса: x2+2y2=2.
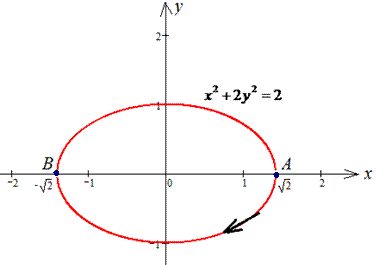
Для простоты вычислений криволинейного интеграла ІІ рода параметризуэм эллипс:
Учитывая, что от точки 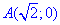
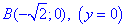
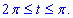
Понижаем степени и интегрируем.
Пример 4.24 Найти работу силы 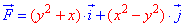
y=1-|x| от точки A(-1;0) к точке B(2;- 1).
Решение: Наведем траекторию материальной точки вдоль модуль функции.
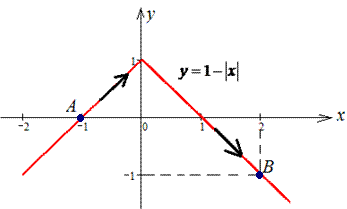
Как ни хотелось встретить задания с разбитием кривой на два интервала, однако одно Пример содержит такое условие. Разделим на две части: y=1+x, тогда пределы равны [-1;0] и дифференциал dy=dx;
На втором участке y=1-x имеем [0;2] и dy=-dx.
Вычисляем работу силы F, потраченную на перемещении точки вдоль модуль функции:
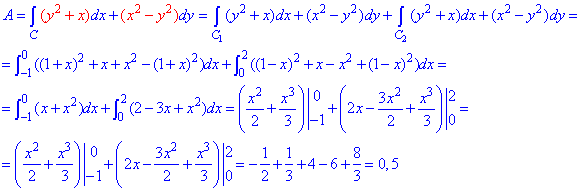
На этом ознакомление из такого сорта примерами завершено.
Больше готовых ответов из курса высшей математики ищите на страницах сайта.
Назначение. Онлайн калькулятор предназначен для нахождения работы силы F при перемещении вдоль дуги линии L.
- Решение онлайн
- Видеоинструкция
Криволинейные и поверхностные интегралы второго рода
Рассмотрим многообразие σ. Пусть τ(x,y,z)– единичный вектор касательной к σ, если σ – кривая, а n(x,y,z)– единичный вектор нормали к σ, если σ – поверхность в R3. Введём векторы dl=τ·dl и dS=n·dS, где dl и dS – длина и площадь соответствующего участка кривой или поверхности. Будем считать, что dσ=dl, если σ – кривая, и dσ=dS, если σ – поверхность. Назовём dσ ориентированной мерой соответствующего участка кривой или поверхности.
Определение. Пусть заданы ориентированное непрерывное кусочно-гладкое многообразие σ и на σ – вектор-функция F(x,y,z)=P(x,y,z)i+Q(x,y,z)+R(x,y,z). Разобьем многообразие на части многообразиями меньшей размерности (кривую – точками, поверхность –кривыми), внутри каждого полученного элементарного многообразия выберем по точке M0(x0,y0,z0), M1(x1,y1,z1), … ,Mn(xn,yn,zn). Посчитаем значения F(xi,yi,zi), i=1,2,…,n вектор-функции в этих точках,умножим скалярно эти значения на ориентированную меру dσi данного элементарного многообразия (ориентированные длину или площадь соответствующего участка многообразия) и просуммируем. Предел полученных сумм если онсуществует, не зависит от способа разбиения многообразия на части и выбора точек внутри каждого элементарного многообразия, при условии, что диаметр элементарного участка стремится к нулю, называется интегралом по многообразию (криволинейным интегралом, если σ -кривая и поверхностным, если σ – поверхность) второго рода, интеграломвдоль ориентированного многообразия, или интегралом от вектора F вдоль σ, и обозначается в общем случае
, в случаях криволинейного и поверхностного интегралов
соответственно.
Заметим, что если F(x,y,z) – сила, то – работа этой силы по перемещению материальной точки вдоль кривой, если F(x,y,z) – стационарное (не зависящее от времени) поле скоростей текущей жидкости, то
– количество жидкости, протекающей через поверхность S в единицу времени (поток вектора через поверхность).
Если кривая задана параметрически 
то
и для криволинейного интеграла второго рода имеем
Так как dS=n·dS=(cosα, cosβ, cosγ), где cosα, cosβ, cosγ – направляющие косинусы единичного вектора нормали n и cosαdS=dydz, cosβdS=dxdz, cosγdS=dxdy, то для поверхностного интеграла второго рода получаем
Если поверхность задана параметрически 
r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k, (u,v)∈D
то
где 
соответственно.
Если поверхность S может быть задана одновременно уравнениями то поверхностный интеграл второго рода вычисляется по формуле
где D1, D2, D3 – проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно и знак “+” берётся, если угол между вектором нормали и осью, вдоль которой ведётся проектирование, острый, а знак “–“, если этот угол тупой.
Свойства криволинейного и поверхностного интегралов второго рода
Отметим некоторые свойства криволинейного и поверхностного интегралов второго рода.
Теорема 1. Криволинейный и поверхностный интегралы 2-го рода зависят от ориентации кривой и поверхности, точнее
.
Теорема 2. Пусть σ=σ1∪σ2 и размерность пересечения dlim(σ1∩σ2)=n-1. Тогда
Доказательство. Включив в число многообразий разбиения в определении интеграла по многообразию второго рода общую границу σ1 с σ2 получаем требуемое.
Пример №1. Найти работу силы F при перемещении вдоль дуги линии L от точки M0 до точки M1.
F=x2yi+yj;, L: отрезок M0M1
M0(-1;3), M0(0;1)
Решение.
Находим уравнение прямой вдоль отрезка M0M1.
или
y=-2x+1
dy=-2dx
Пределы изменения x: [-1; 0]
Пример №2. Вычислить вдоль кривой
, если t∈[0;π]
Имеем
Пример №3. Вычислить поток вектора f(x,y,z)=(yz,xz,xy)T через часть плоскости x+y+z=a лежащую в первом октанте.
Поток вектора через поверхность равен поверхностному интегралу второго рода Поверхность однозначно проектируется на все три координатные плоскости. Поэтому интеграл может быть вычислен с помощью проектирования на них. Тогда
где S1, S2, S3 – проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно. Посчитаем первый из них. Имеем 
Поэтому поток вектора через поверхность равен
Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями. Поэтому поток вектора через поверхность равен
Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями.
Криволинейные интегралы второго рода Задача о вычислении работы переменной силы. Определение криволинейного интеграла второго рода
Напомним, что если сила
постоянна (по величине и по направлению),
а путь
прямолинеен, то работа этой силы на
заданном пути равна скалярному
произведению векторови
:
.
Пусть переменная сила
действует вдоль кривой
,
меняясь при этом в каждой точке приложения
как по модулю, так и по направлению, т.е.,
где,
,
― непрерывные вдоль данной кривой
функции. При перемещении материальной
точки вдоль данной кривойсила
совершает некоторую работу
.
Чтобы найти эту работу разобьем
произвольным образом кривую начастей
,
длиной
.В каждой части
выберем произвольным образом точку
,
лежащую на кривой.
Пусть― единичный вектор касательной к кривой
в точке
.
Тогда вместо участкаможно приближенно рассматривать вектор
,
равный ему по длине и приблизительно
по направлению, учитывая направление
вдоль кривой.
Следовательно, ( если считать силу
(
)
постоянной на участке)
элементарная работасилы
на участке
приближенно равна скалярному произведению:
.
Вся работа силы
на криволинейном пути
приближенно выражается формулой
.
Переходя к пределу при
,
где― длина наибольшей из элементарных дуг
,
получаем точное значение работы
.
Если данная интегральная сумма имеет
предел при
,
то он называется криволинейным интегралом
второго рода от вектор – функциипо кривой
и
обозначается
.
Таким образом, с механической точки
зрения криволинейный интеграл второго
рода есть работа переменной силы вдоль
некоторой линии перемещения.
.
Отметим также, что определение
криволинейного интеграла второго рода
остается в силе и когда кривая
замкнутая. В этом случае начальная и
конечная точки совпадают. Криволинейный
интеграл второго рода по замкнутому
контуруобозначается следующим образом:
.
Отметим два свойства криволинейного
интеграла.
Свойство 1.Криволинейный интеграл
определяется подынтегральным выражением,
формой кривой интегрирования и указанием
направления интегрирования. При изменении
направления интегрирования криволинейный
интеграл меняет знак на противоположный.
Свойство 2.Разобьем кривую
интегрирования
точкой
на части
и,
тогда
.
Криволинейный интеграл второго рода в координатной форме
При определении криволинейного интеграла
второго рода элементарная работа
силы
на участке
находилась как скалярное произведение
вектораи вектора, приближенно равного по длине
и направлению участку.
Вместо вектора,
в качестве вектора, близкого кможно взять вектор
, начало и конец которого совпадают с
началом и концом участка.
Найдем скалярное произведение векторов
и
в координатной форме как сумму произведений
соответствующих координат:
Переходя к пределу при
,
где― длина наибольшей из элементарных дуг
,
получаем точное значение работы
.
Следовательно, криволинейный интеграл
второго рода в скалярной координатной
форме имеет вид:
или, в более краткой форме
.
Вычисление криволинейных интегралов второго рода
Пусть линия
задана параметрически
:
.
Тогда по определению дифференциала
Отметим начало дуги
точкой
,
конец — точкой.
В этом случае говорят, что задано
направление перемещения по кривой от
точкик точке
и тем самым указано направление
ориентирующего вектора.
Покажем, что вычисление криволинейного
интеграла второго рода по линии
заданной параметрически, сводится к
вычислению однократного определенного
интеграла по параметру:
А в случае плоской кривой, когда
,
последняя формула примет вид:
Замечание.Для плоской кривой,
заданной уравнением,
криволинейный интеграл второго рода в
координатной скалярной форме сводится
к определенному интегралу по переменной
(Выбрана ориентация
,
при которой,
соответствуют началу и окончанию пути
интегрирования.)
Если кривая
задана уравнением
,
,
то при соответствующей ориентации
интегрирование по переменнойбудет осуществляться от
до
:
.
Пример. Вычислить,
где—
отрезок прямой с началом в точкеи концом в точке
.
Решение. Изобразим на рисунке линию
интегрирования.
Воспользуемся формулами параметрических
уравнений прямой с направляющим
вектором
,
проходящей через начальную точку с
координатами:
Запишем параметрические уравнения
прямой, которой принадлежит отрезок
,
приняв за направляющий вектор прямойвектор
.
.
Начальной точкой отрезка
является
точка.
Следовательно, параметрические уравнения
этой прямой:
Из полученных уравнений находим, что
точке
соответствует значение параметра
,
а точкезначение
.
По определению дифференциала
Подставляя в интеграл значения
и
,
а также учитывая значения параметраи
,
соответствующие началу и концу дуги,
получим:
.
Пример. Вычислить,
где—
отрезок прямой с началом в точкеи концом в точке
.
Решение. Изобразим на рисунке линию
интегрирования.
Воспользуемся формулами параметрических
уравнений прямой с направляющим
вектором
,
проходящей через начальную точку с
координатами:
Запишем параметрические уравнения
прямой, которой принадлежит отрезок
,
приняв за направляющий вектор прямойвектор
,
т. е..
Начальной точкой отрезка
является
точка.
Следовательно, параметрические уравнения
этой прямой:
Из полученных уравнений находим, что
точке
соответствует значение параметра
,
а точкезначение
.
По определению дифференциала
Учитывая, что
и
,
подставляем в интеграл только значенияи
,
а также значения параметраи
,
соответствующие началу и концу дуги
.
Пример. Вычислить,
где—плоская
кривая, являющаяся частью параболыот точки
до точки
.
Решение. Изобразим на рисунке линию
интегрирования.
Воспользуемся формулой:
В данном случае
соответствуют началу и окончанию пути
интегрирования,,
следовательно:
.
Соседние файлы в предмете Высшая математика
- #
- #
- #
- #
- #
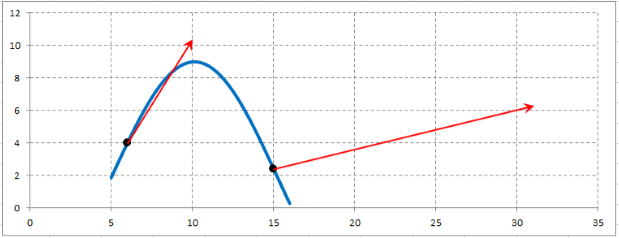
На материальную точку $Tleft(x,yright)$ действует переменная сила $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$. Под действием этой силы материальная точка перемещается на отрезке $left[6;15right]$ от точки $M$ до точки $N$ вдоль синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$. Найти работу переменной силы $overline{F}$ на криволинейном пути от точки $M$ до точки $N$. Построить графическое изображение пути от точки $M$ до точки $N$, а также векторы переменной сили $overline{F}$ в этих точках.
Выполняем графическое изображение синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$ на отрезке $left[6;15right]$.
Находим значения синусоиды в точках $x_{M} =6$ и $x_{N} =15$:
- $y_{M} =7cdot sin left(0,31cdot 6-1,57right)+2approx 4$;
- $y_{N} =7cdot sin left(0,31cdot 15-1,57right)+2approx 2,43$.
Выполняем графические изображения векторов переменной силы $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$, значения которого в точках $M$ и $N$ соответственно равны $overline{F}_{M} =left(3cdot 6-2cdot 4right)cdot overline{i}+4cdot 4cdot overline{j}=10cdot overline{i}+16cdot overline{j}$ и $bar{F}_{N} =left(3cdot 15-2cdot 2,43right)cdot overline{i}+4cdot 2,43cdot overline{j}=40,14cdot overline{i}+9,72cdot overline{j}$.
Работу данной силы на данном участке кривой $MN$ вычисляем по формуле $A=int limits _{a}^{b}Pleft(x,yleft(xright)right)cdot dx +int limits _{a}^{b}Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
Здесь участок кривой $MN$ задан на отрезке $left[x_{M} ,; x_{N} right]$, поэтому формула для работы приобретает вид: $A=int limits _{x_{M} }^{x_{N} }Pleft(x,yleft(xright)right)cdot dx +int limits _{x_{M} }^{x_{N} }Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
В этой формуле первый интеграл дает значение работы силы $F$ вдоль оси $Ox$, второй интеграл — вдоль оси $Oy$.
Находим работу силы вдоль оси $Ox$: $A_{x} =int limits _{6}^{15}Pleft(x,yleft(xright)right)cdot dx $.
Согласно условию задачи имеем:
[Pleft(x,yright)=3cdot x-2cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2.]
Поэтому:
[Pleft(x,yleft(xright)right)=3cdot x-2cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=]
[=3cdot x-14cdot sin left(0,31cdot x-1,57right)-4.]
Далее получаем:
[A_{x} =int limits _{6}^{15}left(3cdot x-14cdot sin left(0,31cdot x-1,57right)-4right)cdot dx =]
[=int limits _{6}^{15}3cdot xcdot dx +int limits _{6}^{15}left(-14cdot sin left(0,31cdot x-1,57right)right)cdot dx +int limits _{6}^{15}left(-4right)cdot dx =]
[=3cdot int limits _{6}^{15}xcdot dx -14cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dx -4cdot int limits _{6}^{15}dx =]
[=3cdot left[frac{x^{2} }{2} right]_{6}^{15} -14cdot left[-frac{1}{0,31} cdot cos left(0,31cdot x-1,57right)right]_{6}^{15} -4cdot left[xright]_{6}^{15} =]
[=1,5cdot left(15^{2} -6^{2} right)+frac{14}{0,31} cdot left(cos left(0,31cdot 15-1,57right)-cos left(0,31cdot 6-1,57right)right)-]
[-4cdot left(15-6right)=135,15.]
Находим работу силы вдоль оси $Oy$: $A_{y} =int limits _{6}^{15}Qleft(x,yleft(xright)right)cdot y’cdot dx $.
Согласно условию задачи имеем:
[Qleft(x,yright)=4cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2. ]
Поэтому:
[Qleft(x,yleft(xright)right)=4cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=28cdot sin left(0,31cdot x-1,57right)+8;]
[y’=7cdot 0,31cdot cos left(0,31cdot x-1,57right)=2,17cdot cos left(0,31cdot x-1,57right).]
Далее получаем:
[A_{y} =int limits _{6}^{15}left(28cdot sin left(0,31cdot x-1,57right)+8right)cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}28cdot 2,17cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}8cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}60,76cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}17,36cdot cos left(0,31cdot x-1,57right)cdot dx .]
Вычисляем первый интеграл $I_{1} $:
[I_{1} =60,76cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=60,76cdot frac{1}{0,31} cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dleft(sin left(0,31cdot x-1,57right)right) =]
[=196cdot left[frac{sin ^{2} left(0,31cdot x-1,57right)}{2} right]_{6}^{15} =]
[=98cdot left(sin ^{2} left(0,31cdot 15-1,57right)-sin ^{2} left(0,31cdot 6-1,57right)right)approx -7,64.]
Вычисляем второй интеграл $I_{2} $:
[I_{2} =17,36cdot int limits _{6}^{15}cos left(0,31cdot x-1,57right)cdot dx =]
[=17,36cdot frac{1}{0,31} cdot left[sin left(0,31cdot x-1,57right)right]_{6}^{15} =]
[=56cdot left(sin left(0,31cdot 15-1,57right)-sin left(0,31cdot 6-1,57right)right)approx -12,57.]
Работа силы вдоль оси $Oy$:
[A_{y} =I_{1} +I_{2} =-7,64-12,57=-20,21.]
Общая работа силы при перемещении вдоль кривой:
[A=A_{x} +A_{y} =135,15-20,21=114,94.]
Некоторые приложения криволинейного интеграла II рода
Площадь плоской фигуры
Площадь 
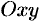

при этом кривая 
Действительно, положив в формуле Остроградского-Грина (56.8) 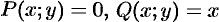
или
Аналогично, полагая 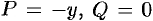
Сложив почленно равенства (56.18) и (56.19) и разделив на два, получим:
Формула (56.17) используется чаще, чем формулы (56.18) и (56.19).
Работа переменной силы
Переменная сила 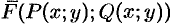

Действительно, пусть материальная точка 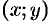
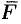
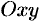

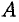
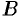
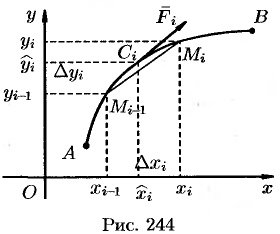
Разобьем кривую 
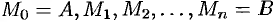

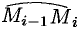
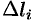
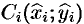
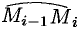
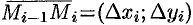
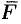
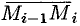
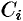
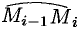
Тогда скалярное произведение 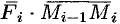
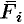
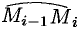
Приближенное значение работы 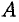
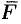
величину
За точное значение работы 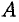
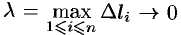
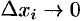
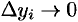
Замечание. В случае пространственной кривой 
Пример №56.6.
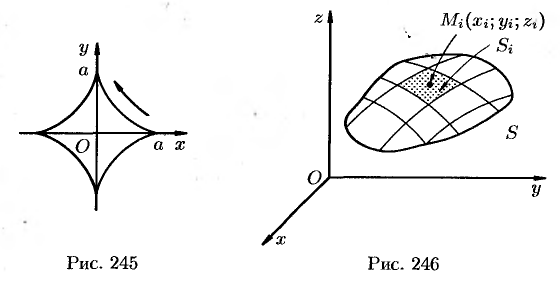
Найти площадь фигуры, ограниченной астроидой 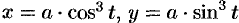
Решение:
При обхождении астроиды в положительном направлении параметр 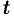
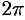
Применяя формулы (56.17) и (56.4), получим:
Пример №56.7.
Найти работу силы 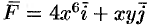
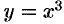
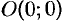
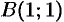
Решение:
По формуле (56.20) находим:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны: