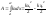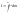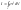Usually, a dancing person is considered to be more energetic compared to a sitting person. A security guard who has been standing at his place the whole day has been working for hours. In real life, this seems obvious, but these terms and definitions work differently when it comes to physics. In physics, work has been defined as the product of force and displacement. This means, that if there is no displacement, work done is zero, no matter how much force or time was spent. This definition builds up concepts like the work-energy theorem. Let’s see this in detail.
Work
Consider a block of mass M sitting on a surface. Now, Aman comes and starts applying a force F, on the block. Only applying the force for some time, he is able to shift the block by 4 meters on the surface. The block and the force are shown in the figure below. Now, since displacement is there. According to physics terminology, the work is done.
For a constant force
and the displacement
. The work done is defined by,
This is the dot product between two vectors, so if the Force makes an angle with the displacement. Then the work done will be given by,
W = |F||r|cos()
Work done by a Variable Force
The above equations are cases of calculating work done with the assumption that the force that is being applied to the body is constant. Often, this is not the case. Forces vary in direction and magnitude with time and sometimes with distance too. So, calculating the work done with this assumption is not right and is not perfectly generalizable.
Let’s consider a force that changes its magnitude. Consider the case of a spring and Hooke’s law. According to Hooke’s law, the restoring force of a perfectly elastic spring is proportional to its extension. The direction of this force is opposite to the extension. There the force acting is given by,
F = -kx
Here, k is the spring constant.
This is an example of a variable Force. For calculating the work done by a variable force, we should add all the infinitely small work done in all the infinitesimally small intervals. Let’s denote the infinitesimally small interval by “dt”. So, to add to the work done in such a scenario, an integral must be used.
The interval “dt” can be used to calculate the change in the extension of spring.
dx = vdt
Using the relations of force from the Hooke’s law.
This work is done by a force applied on the spring for an extension of
For a force which is varying and is given by
and produces a displacement given by the vector
. The work done is given by,
Force-Displacement Plot
The above concept can be understood more clearly using the force-displacement plot. The plot below shows a variable force with the displacement it is producing. It is known that the integrals represent the area under the curve. So, in this case, the area under the curve gives the work done by the force on the body. The area under the curve is divided into many rectangles which represent the displacement.
The area of a single rectangle is . This represents the work done by the force for an infinitesimally small displacement. The total sum of the area of all the rectangles gives the total work done.
W =
⇒ W = ∫Fdx
Sample Problems
Question 1: Find the work done when a force of 20N acting in the direction of displacement produces a displacement of 5 m.
Solution:
The work done by a constant force is given by,
W = |F||r|cos(
)
Here,
W = |F||r|cos(
)
⇒ W = (20)(5)(cos(0))
⇒ W= 100
Question 2: Find the work done when a force of F = 30i + 5j produces a displacement r = 5i + 2j.
Solution:
The work done by a constant force is given by,
W =
and
Calculating the dot product.
W =
⇒ W = (30i + 5j). (5i + 2j)
⇒ W= (30)(5) + (5)(2)
⇒W = 150 + 10
⇒W = 160 J
Question 3: Find the work done when a force of F = x produces a displacement of 4m.
Solution:
The work done by a variable force is given by,
W = ∫Fdx
F(x) = x
Calculating the work done.
W =
Here, the displacement is x = 4
W =
⇒ W =
⇒ W = 8J
Question 4: Find the work done when a force of F = x2 produces a displacement of 3 m.
Solution:
The work done by a variable force is given by,
W = ∫Fdx
F(x) = x2
Calculating the work done.
W =
Here, the displacement is x = 3
W =
⇒ W =
⇒ W = 4.5 J
Question 5: Find the work done when a force of F = x + 4 produces a displacement of 2 m.
Solution:
The work done by a variable force is given by,
W = ∫Fdx
F(x) = x + 4
Calculating the work done.
W =
Here, the displacement is x = 2
W =
⇒ W =
⇒ W = 10 J
Question 6: Find the work done when a force of F = sin(x) produces a displacement from -1 to 1.
Solution:
The work done by a variable force is given by,
W = ∫Fdx
F(x) = sin(x)
Calculating the work done.
W =
Last Updated :
30 Jun, 2021
Like Article
Save Article
Работа,
совершаемая постоянной силой F
при перемещении тела M
на прямолинейном участке пути s
равна A=Fs=Fscos().
Работа – скалярная величина. Если
cos()>0,
то работа – положительна.
Консервативная
(потенциальная) сила – сила,
работа которой определяется только
начальным и конечным положениями тела
и не зависит от формы пути.
Примером
работы, совершаемой переменной силой,
может служить работа упругой или
квазиупругой силы F=-kx,
где k – упругость, x
– смещение тела, на которое действует
упругая сила F
относительно положения равновесия
(x=0).
Мощность
– величина,
характеризующая скорость выполнения
работы. N=dA/dt.
Консервативные силы и потенциальные поля.
Поле,
в котором работа силы не зависит от
формы пути, а зависит лишь от положения
начальной и конечной точек траектории,
называют потенциальными,
а силы, действующие в нём, – консервативными.
В
потенциальном поле работа сил по любому
замкнутому контуру равна нулю.
7.Кинетическая энергия и её связь с работой внешних и внутренних сил.
Кинетической
энергией называют
энергию, зависящую от скорости движения
тела.
Всякое
движущее тело может производить работу.
Кинетическая энергия определяется
работой, которую может совершать тело
вследствие того, что оно обладает
определённой скоростью.
А=
–m(d/dt).
Элементарная работа, совершаемая
движущимся телом против силы F
на пути dx
равна A=-Fdx=-m(d/dx)=-md.
Если
скорость тела уменьшается от 1
до 2,
то A=m12/2-
m22/2,
т.е. работа равна убыли кинетической
энергии тела, т.к. работа совершается
против внешних сил. Если внешние силы,
действуя на тело, совершают работу, то
кинетическая энергия тела, движущегося
со скоростью
равна Eк=m2/2.
При
изменении скорости тела на d
кинетическая энергия изменяется на
dEк=d(m2/2)=md.
8. Закон сохранения механической энергии.
E=Eк+U=const.
Для
консервативных систем, в которых не
происходит преобразование механической
энергии в другие формы энергии (нет
трений и других сил, зависящих от
скорости), полная энергия системы при
ей движении остаётся неизменной.
9.
Момент силы.
Пусть
некоторое тело под действием силы F,
приложенной в точке А, приходит во
вращение вокруг оси ОО’.
Сила
действует в плоскости, перпендикулярной
оси. Перпендикуляр р, опущенный из точки
О (лежащей на оси) на направление силы,
называют плечом
силы.
Произведение силы на плечо определяет
модуль момента
силы
относительно точки О: M=Fp=Frsin(rF).
Момент
силы есть
вектор, определяемый векторным
произведением радиус-вектора точки
приложения силы и вектора силы. M=[rF].
Момент
импульса материальной точки.
Момент
импульса –
вектор, совпадающий по направлению с
вектором угловой скорости.
Момент
импульса материальной точки равен
L=I.
Связь
между моментом силы и моментом импульса.
Основное
уравнение динамики вращательного
движения.
Рассмотрим
вначале материальную точку А массой
m,
движущуюся по окружности радиусом r.
Пусть на неё действует постоянная сила
F,
направленная по касательной к окружности.
Согласно второму закону Ньютона, эта
сила вызывает тангенциальное ускорение.
a=F/m
или F=
am.
a=r
=> F=rm;
Fr=mr2;
M=Fr;
I=
mr2
=> M=I
или =
M/I.
Угловое
ускорение точки при её вращении вокруг
неподвижной оси пропорционально
вращающему моменту и обратно
пропорционально моменту инерции.
10.Момент
инерции.
Инертность
тел при вращательном движении зависит
не только от массы, но и от её распределения
в пространстве относительно оси
вращения. Мерой инертности при
вращательном движении служит величина,
называемая моментом
инерции тела
относительно оси вращения.
Если
тело однородно и его плотность =m/V,
то
Момент
инерции тела зависит от того, относительно
какой оси оно вращается и как распределена
масса тела по объёму.
|
Тонкий |
Перп. |
ml2/12 |
|
Перп. |
ml2/3 |
|
|
Кольцо, |
Перп. |
mR2 |
|
Диск |
mR2/2 |
|
|
Шар |
Центр |
2mR2/5 |
Момент
импульса вращающегося тела
равен сумме моментов импульсов отдельных
его частей L=sum(miri2)=I.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
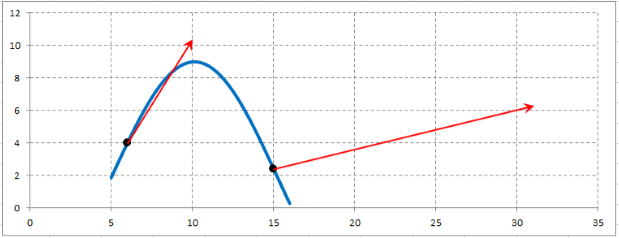
На материальную точку $Tleft(x,yright)$ действует переменная сила $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$. Под действием этой силы материальная точка перемещается на отрезке $left[6;15right]$ от точки $M$ до точки $N$ вдоль синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$. Найти работу переменной силы $overline{F}$ на криволинейном пути от точки $M$ до точки $N$. Построить графическое изображение пути от точки $M$ до точки $N$, а также векторы переменной сили $overline{F}$ в этих точках.
Выполняем графическое изображение синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$ на отрезке $left[6;15right]$.
Находим значения синусоиды в точках $x_{M} =6$ и $x_{N} =15$:
- $y_{M} =7cdot sin left(0,31cdot 6-1,57right)+2approx 4$;
- $y_{N} =7cdot sin left(0,31cdot 15-1,57right)+2approx 2,43$.
Выполняем графические изображения векторов переменной силы $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$, значения которого в точках $M$ и $N$ соответственно равны $overline{F}_{M} =left(3cdot 6-2cdot 4right)cdot overline{i}+4cdot 4cdot overline{j}=10cdot overline{i}+16cdot overline{j}$ и $bar{F}_{N} =left(3cdot 15-2cdot 2,43right)cdot overline{i}+4cdot 2,43cdot overline{j}=40,14cdot overline{i}+9,72cdot overline{j}$.
Работу данной силы на данном участке кривой $MN$ вычисляем по формуле $A=int limits _{a}^{b}Pleft(x,yleft(xright)right)cdot dx +int limits _{a}^{b}Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
Здесь участок кривой $MN$ задан на отрезке $left[x_{M} ,; x_{N} right]$, поэтому формула для работы приобретает вид: $A=int limits _{x_{M} }^{x_{N} }Pleft(x,yleft(xright)right)cdot dx +int limits _{x_{M} }^{x_{N} }Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
В этой формуле первый интеграл дает значение работы силы $F$ вдоль оси $Ox$, второй интеграл — вдоль оси $Oy$.
Находим работу силы вдоль оси $Ox$: $A_{x} =int limits _{6}^{15}Pleft(x,yleft(xright)right)cdot dx $.
Согласно условию задачи имеем:
[Pleft(x,yright)=3cdot x-2cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2.]
Поэтому:
[Pleft(x,yleft(xright)right)=3cdot x-2cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=]
[=3cdot x-14cdot sin left(0,31cdot x-1,57right)-4.]
Далее получаем:
[A_{x} =int limits _{6}^{15}left(3cdot x-14cdot sin left(0,31cdot x-1,57right)-4right)cdot dx =]
[=int limits _{6}^{15}3cdot xcdot dx +int limits _{6}^{15}left(-14cdot sin left(0,31cdot x-1,57right)right)cdot dx +int limits _{6}^{15}left(-4right)cdot dx =]
[=3cdot int limits _{6}^{15}xcdot dx -14cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dx -4cdot int limits _{6}^{15}dx =]
[=3cdot left[frac{x^{2} }{2} right]_{6}^{15} -14cdot left[-frac{1}{0,31} cdot cos left(0,31cdot x-1,57right)right]_{6}^{15} -4cdot left[xright]_{6}^{15} =]
[=1,5cdot left(15^{2} -6^{2} right)+frac{14}{0,31} cdot left(cos left(0,31cdot 15-1,57right)-cos left(0,31cdot 6-1,57right)right)-]
[-4cdot left(15-6right)=135,15.]
Находим работу силы вдоль оси $Oy$: $A_{y} =int limits _{6}^{15}Qleft(x,yleft(xright)right)cdot y’cdot dx $.
Согласно условию задачи имеем:
[Qleft(x,yright)=4cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2. ]
Поэтому:
[Qleft(x,yleft(xright)right)=4cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=28cdot sin left(0,31cdot x-1,57right)+8;]
[y’=7cdot 0,31cdot cos left(0,31cdot x-1,57right)=2,17cdot cos left(0,31cdot x-1,57right).]
Далее получаем:
[A_{y} =int limits _{6}^{15}left(28cdot sin left(0,31cdot x-1,57right)+8right)cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}28cdot 2,17cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}8cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}60,76cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}17,36cdot cos left(0,31cdot x-1,57right)cdot dx .]
Вычисляем первый интеграл $I_{1} $:
[I_{1} =60,76cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=60,76cdot frac{1}{0,31} cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dleft(sin left(0,31cdot x-1,57right)right) =]
[=196cdot left[frac{sin ^{2} left(0,31cdot x-1,57right)}{2} right]_{6}^{15} =]
[=98cdot left(sin ^{2} left(0,31cdot 15-1,57right)-sin ^{2} left(0,31cdot 6-1,57right)right)approx -7,64.]
Вычисляем второй интеграл $I_{2} $:
[I_{2} =17,36cdot int limits _{6}^{15}cos left(0,31cdot x-1,57right)cdot dx =]
[=17,36cdot frac{1}{0,31} cdot left[sin left(0,31cdot x-1,57right)right]_{6}^{15} =]
[=56cdot left(sin left(0,31cdot 15-1,57right)-sin left(0,31cdot 6-1,57right)right)approx -12,57.]
Работа силы вдоль оси $Oy$:
[A_{y} =I_{1} +I_{2} =-7,64-12,57=-20,21.]
Общая работа силы при перемещении вдоль кривой:
[A=A_{x} +A_{y} =135,15-20,21=114,94.]
Работой силы FF, действующей на материальную точку, называют физическую величину, равную скалярному произведению вектора действующей силы на вектор перемещения точки drdr:
dA=(F⃗dr⃗)=Fdrcos(F⃗,dr⃗^)dA=(vec{F}dvec{r})=Fdrcos(widehat{vec{F},dvec{r}})
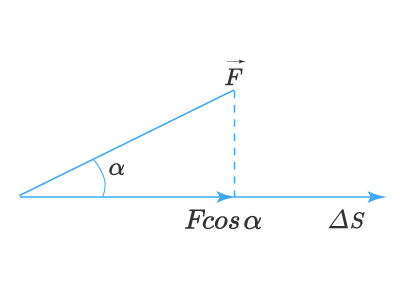
Иначе записывают dA=FcosαdsdA=Fcosalpha ds:
Выражают работу в СИ в джоулях. Джоуль – это работа силы в 1 Н на пути в 1 м условии, что направление действия силы и направление перемещения совпадают. В аналитическом виде
1 Дж = 1Н · 1м= 1 (кг·м2)/с2
Нулевая работа
Работа – скалярная величина. В зависимости от угла между направлениями действующей силы и перемещения она может быть положительной, отрицательной и равна нулю. Нулевой будет работа силы, которая перпендикулярна к направлению перемещения, в частности нулевой является работа центростремительных сил, работа силы тяжести во время движения тела в горизонтальной плоскости и др.
В основном, например, во время равномерного подъема тела, работа действующей силы сводится к преодолению силы тяжести. В случае равномерного движения тела на горизонтальной поверхности – к преодолению силы трения, в производственной сфере – к преодолению сопротивления почвы, сопротивления различных материалов при обработке и тому подобное. Поэтому под работой на практике понимают процесс преодоления сопротивления при перемещениях тел.
Работа переменной силы
Выше мы рассмотрели способ вычисления работы постоянной силы при прямолинейном перемещении тела. Работу переменной силы или произведение переменной проекции силы на направление перемещения, также определяют по формуле:
dA=(F⃗dr⃗)=Fdrcos(F⃗,dr⃗^)dA=(vec{F}dvec{r})=Fdrcos(widehat{vec{F},dvec{r}}),
которую можно применить только для бесконечно малого перемещения drdr.
Работу на всем пути найдем как сумму работ на всех элементарных перемещениях, на которые разделены путь. Эта операция сводится к вычислению интеграла:
A=∫SFcosαdsA=intlimits_{S}{Fcosalpha ds}
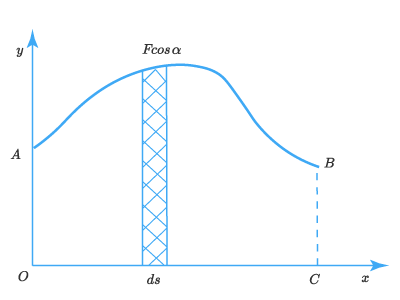
Наряду с аналитическим широко используют графический способ определения работы. Отложив по оси ОуОу проекцию действующей силы FcosаF cos а, а по оси ОхОх – пройденный телом путь ss, получим графическую зависимость между ними в виде кривой АВАВ:
Отсюда следует, что работа при элементарном перемещении
dA=FcosαdsdA=Fcos alpha ds:
равна площади заштрихованной полоски, а работа на всем пути – площади фигуры ОАВС. Например, если вычислить площадь фигуры с помощью индикатора.
Прибор, фиксирующий изменения любого параметра или объекта в форме, удобной для непосредственного восприятия человеком, то можно определить работу газа в цилиндре тепловой машины.
Работа силы тяжести
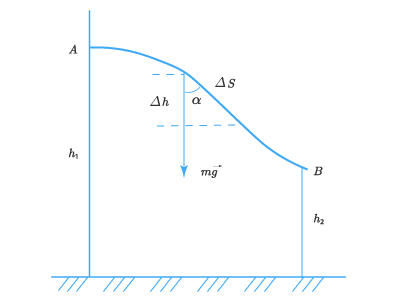
Рассмотрим важный пример работы силы тяжести при движении тела по некоторой кривой АВ:
Поделим весь путь на такие малые части, чтобы их можно было считать прямолинейными. Работа на одной из них:
ΔA=FΔscosα=mgΔscosα=mgΔhDelta A=FDelta scos alpha =mgDelta scos alpha =mgDelta h
Работу на всем пути найдем как сумму работ на отдельных его частях:
A=∑mgΔh=mg∑Δh=mg∑(h1−h2)A=sum{mgDelta h}=mgsum{Delta h}=mgsum{({{h}_{1}}-{{h}_{2}}})
Как видим, работа силы тяжести (или работа против силы тяжести) для тела, которое перемещается в поле тяготения, не зависит от формы траектории, а зависит только от разности высот его начальной и конечной точек приложения.
Если бы тело в поле притяжения описывало замкнутую траекторию, то суммарная работа силы тяжести равнялась бы нулю: положительная работа тела, возникающая в случае, когда оно опускается, компенсируется отрицательной работой тела, когда оно поднимается.
Силы, работа которых не зависит от траектории движения тела, а зависит только от начального и конечного его положений, называются потенциальными.
Таковы, например, силы всемирного тяготения, силы упругости, электростатические силы. Поля, в которых проявляется действие таких сил, называются потенциальными.
Система тел называется консервативной, если в ней внутренние силы взаимодействия потенциальные, а внешние силы, действующие на эти тела, –стационарные и потенциальные.


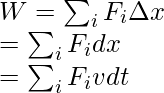
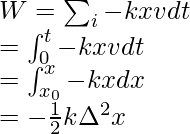

![Rendered by QuickLaTeX.com int^{x}_{0}Fdx \ = int^{x}_{0}xdx \ = [frac{x^2}{2}]^{x}_{0} \ = frac{x^2}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-65c5f8e518dfcc356aad74d2e4673f1a_l3.png)
![Rendered by QuickLaTeX.com int^{x}_{0}Fdx \ = int^{x}_{0}x^2dx \ = [frac{x^3}{3}]^{x}_{0} \ = frac{x^3}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-65cb36228b7aef5e7e5f12a7cb7b741d_l3.png)
![Rendered by QuickLaTeX.com int^{x}_{0}Fdx \ = int^{x}_{0}(x + 4)dx \ = [frac{x^2}{2} + 4x]^{x}_{0} \ = frac{x^2}{2} + 4x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54540c8109188a35b5be07b5a95c71ec_l3.png)
![Rendered by QuickLaTeX.com int^{1}_{-1}Fdx \ = int^{1}_{-1}sin(x)dx \ = [-cos(x)]^{1}_{-1} \ = cos(-1) - cos(1) \ = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1057a8e06af8309fce2bd667940245fa_l3.png)