Как и любая другая сила, сила Ампера имеет возможность совершить работу. По определению механической работы:
(1)

Рис. 1. Работа силы Ампера
Пусть в нашей системе проводник длиной , находящийся в однородном магнитном поле индукции
, по которому течёт ток
, движется под действием силы Ампера и перемещается на расстояние
(рис. 1). Тогда, при условии, что сила Ампера равна
, получим:
(2)
Пометим — площадь, «заметаемая» при движении проводника. Т.е. площадь, которую «прошёл» проводник во время движения. Тогда, в общем случае:
(3)
Соотношение (3) указывает на работу сил Ампера. Однако, если использовать определение изменения потока магнитного поля:
Ф
(4)
получим:
Ф (5)
- где
Сила Ампера — сила, которая действует на проводник с током, помещенный в магнитное поле.
Модуль силы Ампера обозначается как FA. Единица измерения — Ньютон (Н).
Математически модуль силы Ампера определяется как произведение модуля вектора магнитной индукции B, силы тока I, длины проводника l и синуса угла α между условным направлением тока и вектором магнитной индукции:
FA=BIlsinα
Максимальное значение сила Ампера принимает, когда ток в проводнике направлен перпендикулярно вектору магнитной индукции, так как sin90°=1. И сила Ампера отсутствует совсем, если ток в проводнике направлен относительно вектора магнитной индукции вдоль одной линии. В этом случае угол между ними равен 0, а sin0°=1.
Пример №1. Максимальная сила, действующая в однородном магнитном поле на проводник с током длиной 10 см, равна 0,02 Н. Сила тока в проводнике равна 8 А. Найдите модуль вектора магнитной индукции этого поля.
10 см = 0,1 м
Так как речь идет о максимальной силе, действующей на проводник с током, тоsinα при этом равен 1 (проводник с током расположен перпендикулярно вектору магнитной индукции).
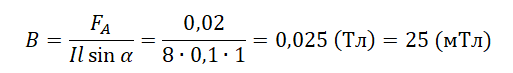
Определение направления силы Ампера
Направление вектора силы Ампера определяется правилом левой руки.
Правило левой руки
Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции →B входила в ладонь, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на отрезок проводника (направление силы Ампера).
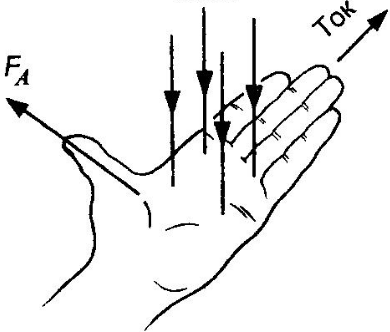
Пример №2. В однородном магнитном поле находится рамка, по которой начинает течь ток (см. рисунок). Какое направление (вверх, вниз, влево, вправо, от наблюдателя, наблюдателю) имеет сила, действующая на нижнюю сторону рамки?
Так как в нижней стороне рамки ток направлен вправо, то четыре пальца левой руки нужно направить вправо. Саму левую руку при этом нужно расположить перпендикулярно плоскости рисунка ладонью вверх, чтобы в нее входили линии вектора магнитной индукции. Если отогнуть большой палец на прямой угол, то он покажет направление силы Ампера, действующей на нижнюю часть рамки. В данном случае она направлена в сторону от наблюдателя.
Работа силы Ампера
Проводники, на которые действует сила Ампера, могут перемещаться под действием этой силы. В этом случае говорят, что сила Ампера совершает работу. Из курса механики вспомним, что работа равна:
A=Fscosα
F — сила, совершающая работу, s — перемещение, совершенное телом под действием этой силы, α — угол между вектором силы и вектором перемещения.
Отсюда работа, совершаемая силой Ампера, равна:
A=FAscosα=BIlsinβscosα
α — угол между вектором силы и вектором перемещения, β — угол между условным направлением тока и вектором магнитной индукции.
Пример №3. Проводник длиной l = 0,15 м перпендикулярен вектору магнитной индукции однородного магнитного поля, модуль которого B = 0,4 Тл. Сила тока в проводнике I = 8 А. Найдите работу, которая была совершена при перемещении проводника на 0,025 м по направлению действия силы Ампера.
Так как проводник расположен перпендикулярно вектору магнитной индукции, и поле однородно, то синус угла между ними равен «1». Так как направление перемещение проводника совпадает с направлением действия силы Ампера, то косинус угла между ними тоже равен «1». Поэтому формула для вычисления работы силы Ампера принимает вид:
A=BIls
Подставим известные данные:
A=0,4·8·0,15·0,025=0,012 (Дж)=12 (мДж)
Задание EF17704
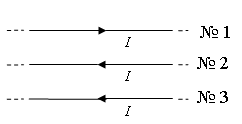 Как направлена сила Ампера, действующая на проводник № 3 со стороны двух других (см. рисунок), если все проводники тонкие, лежат в одной плоскости и параллельны друг другу? По проводникам идёт одинаковый ток силой I.
Как направлена сила Ампера, действующая на проводник № 3 со стороны двух других (см. рисунок), если все проводники тонкие, лежат в одной плоскости и параллельны друг другу? По проводникам идёт одинаковый ток силой I.
а) вверх
б) вниз
в) к нам
г) от нас
Алгоритм решения
1.Определить направление вектора результирующей магнитной индукции первого и второго проводников в любой точке третьего проводника.
2.Используя правило левой руки, определить направление силы Ампера, действующей на третий проводник со стороны первых двух проводников.
Решение
На третьем проводнике выберем произвольную точку и определим, в какую сторону в ней направлен результирующий вектор →B, равный геометрической сумме векторов магнитной индукции первого и второго проводников (→B1и →B2). Применим правило буравчика. Мысленно сопоставим острие буравчика с направлением тока в первом проводнике. Тогда направление вращения его ручки покажем, что силовые линии вокруг проводника 1 направляются относительно плоскости рисунка против хода часовой стрелки. Ток во втором проводнике направлен противоположно току в первом. Следовательно, его силовые линии направлены относительно плоскости рисунка по часовой стрелке.
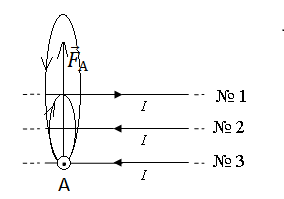
В точке А вектор →B1 направлен в сторону от наблюдателя, а вектор →B2— к наблюдателю. Так как второй проводник расположен ближе к третьему, создаваемое им магнитное поле в точке А более сильное (силы тока во всех проводниках равны по условию задачи). Следовательно, результирующий вектор →B направлен к наблюдателю.
Теперь применим правило левой руки. Расположим ее так, чтобы четыре пальца были направлены в сторону течения тока в третьем проводнике. Ладонь расположим так, чтобы результирующий вектор →B входил в ладонь. Теперь отставим большой палец на 90 градусов. Относительно рисунка он покажет «вверх». Следовательно, сила Ампера →FА, действующая на третий проводник, направлена вверх.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18417
Чему равна сила Ампера, действующая на стальной прямой проводник с током длиной 10 см и площадью поперечного сечения 2⋅10–2 мм2 , если напряжение на нём 2,4 В, а модуль вектора магнитной индукции 1 Тл? Вектор магнитной индукции перпендикулярен проводнику. Удельное сопротивление стали 0,12 Ом⋅мм2/м.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Ампера.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Длина проводника: l = 10 см.
• Площадь поперечного сечения проводника: S = 2⋅10–2 мм2.
• Напряжение в проводнике: U = 2,4 В.
• Модуль вектора магнитной индукции: B = 1 Тл.
• Удельное сопротивление стали: r = 0,12 Ом⋅мм2/м.
• Угол между проводником с током и вектором магнитной индукции: α = 90о.
10 см = 0,1 м
Сила Ампера определяется формулой:
FA=BIlsinα
Так как α = 90о, синус равен 1. Тогда сила Ампера равна:
FA=BIl
Силу тока можно выразить из закона Ома:
I=UR
Сопротивление проводника вычисляется по формуле:
R=rlS
Тогда сила тока равна:
I=USrl
Конечная формула для силы Ампера принимает вид:
FA=BlUSrl=BUSr=1·2,4·2·10−20,12=0,4 (Н)
Ответ: 0,4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17725
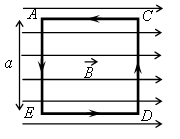 На непроводящей горизонтальной поверхности стола лежит жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата AСDЕ со стороной a(см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции B которого перпендикулярен сторонам AE и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
На непроводящей горизонтальной поверхности стола лежит жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата AСDЕ со стороной a(см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции B которого перпендикулярен сторонам AE и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
Алгоритм решения
1.Сделать список известных данных.
2.Определить, при каком условии рамка с током будет вращаться вокруг стороны CD.
3.Выполнить решение в общем виде.
Решение
По условию задачи известными данными являются:
• Сторона квадратной рамки с током: a.
• Вектор магнитной индукции однородного горизонтального магнитного поля, в котором лежит рамка: B.
Пусть по рамке течёт ток I. На стороны АЕ и CD будут действовать силы Ампера:
FA1=FA2=IaB
Для того чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз. Момент силы Ампера относительно оси, проходящей через сторону CD:
MA=Ia2B
Момент силы тяжести относительно оси CD:
Mmg=−12mga
Чтобы рамка с током оторвалась от горизонтальной поверхности, нужно чтобы суммарный момент сил был больше нуля:
MA+Mmg>0
Так как момент силы тяжести относительно оси CD отрицательный, это неравенство можно записать в виде:
Ia2B>12mga
Отсюда выразим силу тока:
I>mga2a2B
I>mg2aB
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10.7k
Работ сил Ампера A = IΔΦ. Здесь ΔΦ имеет смысл модуля магнитного потока сквозь поверхность, заметённую проводником с постоянным током I при его перемещении: ΔΦ = |Φзам|. Знак работы определяется по направлению движения проводника (см. пример 8.1). ΔΦ имеет также смысл изменения магнитного потока Φ сквозь поверхность, натянутую на контур с постоянным током, при его перемещении: ΔΦ = Φкон – Φнач.
Примеры решения задач
Пример8.1
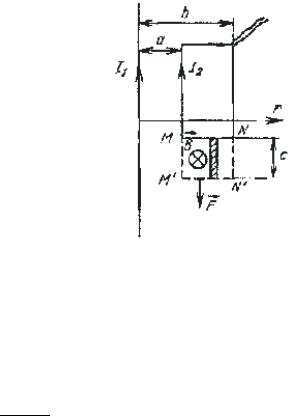
В одной плоскости с длинным* прямым проводником, по которому идёт ток I1 = 10 А, находится плоская прямоугольная рамка. Длинные стороны рамки
|
параллельны проводу, расстояния от них до провода |
a = 5 см, |
||
|
b = 10 см. По рамке протекает ток I1 = 2 А, его направление |
в |
||
|
ближайшей длинной стороне совпадает с направлением |
тока в |
||
|
проводе. Рамка может растягиваться за счёт перемещения |
её короткой |
||
|
стороны MN параллельно самой себе. Найти работу сил |
Ампера при |
||
|
удлинении рамки на c = 2,0 см. |
|||
|
При перемещении стороны рамки MN она заметает |
площадь S в |
||
|
виде прямоугольника MNM’N’ (рис. 8.1). Работа сил Ампера |
равна |
||
|
A = I2|Φзам|, где Φзам – магнитный поток через площадь S |
|||
|
зам = ∫S BdS . |
|||
|
по |
|||
|
Направление B – магнитной индукции, созданной |
проводом с |
||
|
током – от нас в пределах площади S, B = μ0I/(2πr), где r – |
Рис. 8.1 |
расстояние |
|
|
от прямого провода (см. пример 6.2). |
Вектор dS параллелен B , а так как нас интересует |Φзам|, направим его коллинеарно B . Тогда
BdS = BdS . Модуль dS – это площадь бесконечно малого участка площади S прямоугольника, в пределах которого магнитную индукцию B можно считать постоянной. Эти участки представляют собой прямоугольники бесконечно малой ширины dr и высоты c и показаны на рис. 8.1, dS = cdr. Тогда
|
Φзам |
a |
2 |
2 |
ln |
||
|
b |
μ I cdr |
μ I c |
b |
|||
|
= ∫ |
0 πr1 |
= 0πr1 |
a |
, |
||
где пределы интегрирования соответствуют положению на оси r длинный сторон прямоугольника. Работа
|
A= 2πr0 |
I1I2cln a =2,8 10−6 |
Дж. |
|
|
μ |
b |
Сила Ампера F , действующая на рассматриваемую сторону, направлена в сторону перемещения рамки (рис. 8.1), следовательно, её работа положительна.
Задачи
8.1.Квадратная рамка со стороной a = 20 см помещена в однородное магнитное поле с магнитной индукцией B = 0,040 Тл. Нормаль к плоскости рамки составляет угол α = 60° с направлением вектора магнитной индукции. Найти магнитный поток, пронизывающий рамку.
8.2.Обмотка соленоида длиной l = 1,0 м и радиусом r = 25 мм содержит n = 11 витков/см, обтекаемых током I = 2,0 А. Считая, что витки плотно прилегают друг к другу, найти потокосцепление соленоида.
8.3. Обмотка тора (кольцевого соленоида) квадратного сечения со стороной a = 4 см состоит из N = 1000 витков, по которым идет ток I = 2,0 А. Внутренний радиус тора r1 = 8 см. Найти магнитный поток внутри тора.
65
8.4.По длинному* медному проводу кругового сечения идет ток I = 10 А. Плотность тока постоянна, относительная магнитная проницаемость меди μ = 1. Найти магнитный поток, приходящийся на единицу длины, в пределах самого провода.
8.5.Ток I = 5 А течёт по внутреннему медному проводу длинного* коаксиального кабеля и
возвращается по его внешней металлической оболочке. Диаметр внутреннего провода d1 = 2 мм, внешней оболочки – d2 = 10 мм. Найти магнитный поток, приходящийся на единицу длины кабеля. Плотность тока во внутреннем проводе постоянна по сечению.
8.6.Прямоугольная рамка со сторонами a = 10 см и b = 5 см лежит в одной плоскости с длинным* прямым проводом, по которому идет ток I = 10 А. Длинные стороны рамки параллельны проводу,
ближайшая сторона находится на расстоянии x1 = 5 см от прямого проводника. Рамка, оставаясь в той же плоскости, перемещается параллельно самой себе, удаляясь от прямого провода так, что
кратчайшее расстояние между ними возрастает до x2 = 10 см. Найти изменение магнитного потока, пронизывающего рамку, если ток, обтекающий рамку, по стороне, ближайшей к проводу, направлен: а) так же, как ток I; б) противоположно току I.
8.7.В однородном магнитном поле с индукцией B = 2,0·10–5 Тл в плоскости, перпендикулярной линиям индукции, проложены длинные* параллельные шины. Шины соединены подвижным проводником, длина которого l = 0,5 м равна расстоянию между ними. При токе I = 5 А проводник под действием силы Ампера перемещается на расстояние x = 4,0 см. Найти работу силы Ампера при этом перемещении. Ток в цепи считать постоянным.
8.8.Два параллельных достаточно длинных* провода находятся на расстоянии h1 = 2 см друг от друга. По проводам идут токи I1 = I2 = 2,0 А взаимно противоположного направления. Какую работу на единицу длины проводов совершают силы Ампера при медленном удалении проводов друг от друга до расстояния h2 = 8 см?
8.9.В плоскости, перпендикулярной линиям индукции однородного магнитного поля с индукцией B = 3,0·10–5 Тл лежит тонкое* кольцо, радиус которого r = 5 см. По кольцу идёт ток I = 1,5 А.
1. Каково должно быть направление тока в кольце, чтобы работа внешних сил при повороте кольца вокруг его диаметра на 180° была положительной?
2. Какую работу совершат внешние силы при этом повороте?
8.10.В однородном магнитном поле с индукцией B = 2,0·10–5 Тл помещена квадратная рамка со
стороной a = 10 см, обтекаемая током I = 1,0 А. Магнитный момент рамки параллелен B . Какую работу совершают силы Ампера при медленном повороте рамки вокруг одной из её сторон на угол
α = 90°; 180°; 360°?
8.11. В одной плоскости с длинным* прямым проводом, по которому идёт ток I1 = 10 А, находится плоская прямоугольная рамка со сторонами a = 10 см, b = 7,5 см. Длинные стороны рамки параллельны прямому проводу, расстояние от него до ближайшей длинной стороны рамки x0 = 2,5 см. По рамке идет ток I2 = 1,0 А. В стороне, ближайшей к прямому проводу, ток I2 направлен противоположно току I1. Рассчитать, какую работу совершат силы Ампера при медленном повороте рамки на угол α = 180°: а) вокруг оси, параллельной прямому проводу и проходящей через середину рамки; б) вокруг оси, совпадающей с длинной стороной, ближайшей к прямому проводу.
8.12. В одной плоскости с длинным* прямым проводом, по которому идёт ток I1 = 10 А, находится прямоугольная рамка со сторонами a = 5 см, b = 10 см. Длинные стороны рамки параллельны прямому проводу и ближайшая отстоит от него на расстояние x1 = 5 см. Рамка обтекается током I2 = 3 А, в прямом проводнике и ближайшей к нему стороне рамки токи направлены одинаково. Какую работу совершают внешние силы при поступательном прямолинейном перемещении рамки в её плоскости в направлении нормали к проводу? Конечное расстояние от прямого провода до ближайшей к нему длинной стороны рамки x2 = 10 см.
8.13. В длинный* соленоид вдоль его оси медленно втягивается маленькая* плоская рамка. Обмотка рамки состоит из N = 10 витков площадью S = 2,0 см2 каждый. Ток в обмотке рамки I1 = 1,0 А. Обмотка
66
соленоида содержит n = 100 витков/см, по которым идёт ток I2 = 5 А. Какую работу совершают силы Ампера при перемещении рамки из середины основания соленоида в середину его оси? Плоскость рамки нормальна к оси соленоида, токи I1 и I2 направлены одинаково.
8.14.Маленькая* квадратная рамка из мягкой проволоки со стороной a = 3,0 см, обтекаемая током
I1 = 0,10 А, медленно втягивается в середину длинного* соленоида. Обмотка соленоида состоит из n = 10 витков/см, ток в соленоиде I = 1,0 А. Перемещение рамки происходит вдоль оси соленоида, её плоскость всё время перпендикулярна оси соленоида. Токи в соленоиде и в рамке направлены одинаково. Найти суммарную работу, совершенную силами Ампера при перемещении рамки из середины основания до середины оси и при деформации рамки, если диаметр соленоида D >> a.
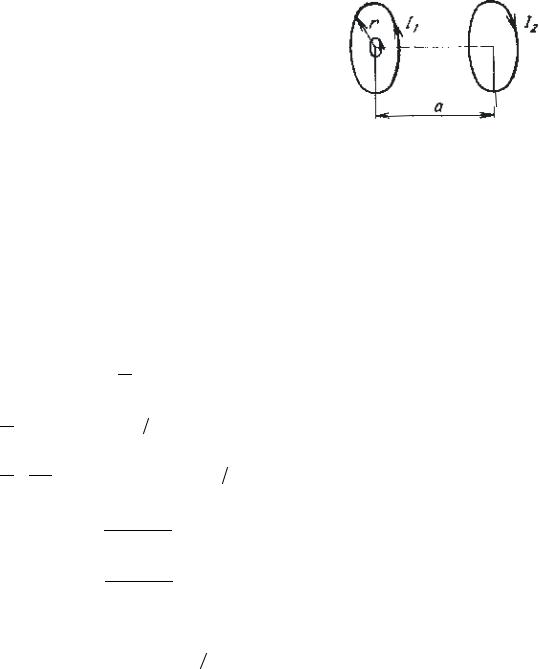
8.15.Два плоских круглых витка радиуса r = 10 см каждый расположены параллельно друг другу на расстоянии a = 10 см, причём прямая, соединяющая центры витков, перпендикулярна плоскостям обоих витков. По виткам протекают токи
|
взаимопротивоположных направлений, но одинаковые |
по величине |
||
|
I1 = I2 = 2,0 А. Концентрично первому витку расположен |
маленький |
||
|
виток площадью S = 0,20 см2. По витку течёт ток I = 0,10 А, |
|||
|
направленный так же, как ток I1 (рис. 8.2). Какую работу |
должны |
||
|
совершить внешние силы, чтобы переместить маленький |
виток |
||
|
(параллельно самомусебе) в середину второго витка? |
|||
|
8.16. Две тонкие катушки с током, векторы магнитных |
Рис. 8.2 |
моментов |
|
которых коллинеарны и по модулю равны соответственно pm1 = 8·10–2 А·м2 и pm2 = 0,12 А·м2, удалены друг от друга на расстояние x1 = 1,0 м. Расстояние между центрами катушек x1 >> l, где l – длина каждой катушки. Найти: а) работу, которую совершат внешние силы, чтобы увеличить расстояние
|
между |
центрами |
катушек |
до |
x2 = 1,1 м; |
|
б) силу взаимодействия катушек на расстоянии x1. |
Ответы
|
8.1. |
= Ba |
α = |
|
|
8.2. |
= μ0πn r lI = |
8.3.Φ= 2μ0 NIaln 1+ a =6,5 10−6 Вб.
πr1
8.4.= μ40I =1,0 10−6 Вб м. l π
8.5.= μ40I 1 +2ln d2 =2,1 10−6 Вб м. l π d1
8.6.а) ΔΦ= 2μ0 Ialn x1 (x2 +b)= −5,8 10−8 Вб;
πx2 (x1 +b)
|
ΔΦ |
μ |
ln |
−1 |
( |
2 |
+b |
) |
5,8 10 Вб |
|||||||||
|
( |
) |
||||||||||||||||
|
x |
x |
||||||||||||||||
|
б) |
= π0 Ia |
x2 |
x1 |
+b |
= |
−8 . |
|||||||||||
|
8.7. |
A |
= IBlx |
= |
. |
|||||||||||||
|
8.8. |
l |
= |
π0 |
I1I2 ln h12 |
=1,1 10−6 Дж м. |
||||||||||||
|
A |
μ |
h |
|||||||||||||||
|
n0 |
2 |
− |
|||||||||||||||
|
8.9. 1. |
↑↑B . |
||||||||||||||||
|
2. |
A′= |
πBIr |
= |
. |
A2 = − BIa = − − |
||||||||||||
|
8.10. |
A1 = −BIa |
= − |
− |
; |
; A3 = 0. |
67

8.11.а) A = μ0 I1I2aln 1 + b0 =5,5 10−7 Дж;
πx
|
б) A = |
π0 |
I1I2aln b− x0 |
=1,4 10−7 Дж. |
|||||||||||||||||
|
μ |
b+ x |
|||||||||||||||||||
|
μ |
2 |
2 |
ln |
(x |
( |
+a)0 x |
1,7 |
10 |
− |
Дж |
||||||||||
|
8.12. |
A′= |
μ2 |
1 |
b |
x |
1 |
2 |
− |
) |
7 |
. |
|||||||||
|
π0 |
I I |
1 x |
+a2 = |
|||||||||||||||||
|
8.13. |
A = |
0 I1I2NnS =6 10 5 Дж. |
8 |
Дж |
||||||||||||||||
|
0 1 |
2 |
2 |
π |
2 |
8,7 |
10 |
||||||||||||||
|
8.14. |
A = |
μ2I I na |
− |
= |
− |
. |
||||||||||||||
|
8.15. |
A = μ I I |
S |
− |
1 |
+ a2 |
− |
|||||
|
0 1 |
r |
1 |
1 |
r2 |
2 |
||||||
|
2 |
|||||||||||
|
μ |
1 |
pm |
2 |
3 |
− x |
3 |
|||||
|
8.16. |
а) A = π0 pm |
x |
 =3,2 10−11 Дж.
=3,2 10−11 Дж.
=4,8 10−10 Дж.
|
б) F = π0 |
mx14 m2 |
=5,8 10−9 Н. |
|
2 |
1 |
|
|
μ |
p p |
68
Соседние файлы в папке 3 – практ_зан
- #
- #
Общее представление об электромагнитном поле
Длительное время представления об электрическом и магнитном поле не связывались между собой. Практические эксперименты подтверждали, что каждое из них имеет свои особенные свойства. Исследования Фарадея и Максвелла показали, что существует электромагнитное поле, которое может проявлять себя как электрическое или магнитное. Его можно описать с мощью вектора напряжённости. Если знать величину и направление данного вектора, то можно рассчитать силу воздействия.
Первым из учёных, кто обратил внимание на взаимное влияние магнитного поля и тока был известный учёный Х. К. Эрстед. Он исследовал влияние проводника с текущим по нему током на положение стрелки компаса. После этого учёные стали систематически изучать различные варианты взаимодействия.
Ампер появился на свет в 1775 году в Лионе. С детства он проявлял страсть к математике. Будучи подростком, изучал труды Эйлера и Лагранжа. Профессором математики Ампер стал в 1809 году, а в 1814 году был избран в академию наук. Хотя он преимущественно занимался математикой, его интересовала физика и некоторые другие науки.
Ампер был не первым человеком, который проявил интерес к связи магнитных и электрических полей, однако он впервые постарался найти точное математическое описание происходящих процессов. Им был не только установлен факт взаимодействия между электрическими токами, но и сформулирован закон данного явления.
Ампер доказал, что проводники начинают взаимодействовать, если по каждому из них протекает ток. В этом случае между ними возникают силы отталкивания или притягивания. В 1826 году Ампер впервые опубликовал результаты своего исследования, с помощью которого он изучал взаимодействие параллельных токов.
На рисунке ниже представлена схема одного из экспериментов Ампера, с помощью которого измеряется сила, действующая на проводник с током в магнитном поле. Стрелка красного цвета на рисунке показывает направление тока.
Основываясь на экспериментах, учёный сделал предположение, которое впоследствии получило название «гипотеза Ампера». Понимая, как влияет ток на магнитное поле, он сумел доказать, что вещество состоит из совокупности чрезвычайно маленьких круговых токов. Каждый из них порождает очень слабое магнитное поле. Поскольку все эти токи ориентированы хаотично, то внешне магнитное поле практически не проявляется. Однако в магнитах все круговые токи одинаково направлены и их воздействие складывается. Этим объясняются их особые свойства и практическое использование.
Ампер, используя свой закон, также объяснил эффект намагничивания. Согласно ему, у некоторых веществ под воздействием магнитного поля происходит упорядочивание круговых токов, и они постепенно ориентируются в одну сторону.
Эта гипотеза стала одним из источников теории магнетизма. Она смогла объяснить явление только частично, так как не дала ответа на вопрос о том, почему некоторые вещества подвергаются воздействию внешнего магнитного поля незначительно. Также остался необъяснённым вопрос, почему при намагничивании одни вещества создают магнитный поток сонаправленный внешнему полю (парамагнетики), а другие — противоположно направленный (диамагнетики).
Что такое сила Ампера
Собственно сила ампера и является той силой действия магнитного поля на проводник, по которому идет ток. Сила Ампера вычисляется по формуле как результат умножения плотности тока, идущего по проводнику на индукцию магнитного поля, в котором находится проводник. Как результат формула силы Ампера будет выглядеть так
са=ст*дчп*ми
Где, са – сила Ампера, ст – сила тока, дчп – длина части проводника, ми – магнитная индукция.
Значение закона Ампера
Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.
Для прямолинейного проводника сила Ампера имеет вид:
где: — сила тока, которая течет в проводнике, — вектор индукции магнитного поля, в которое проводник помещен, — длина проводника в поле, направление задано направлением тока, — угол между векторами .
Этой формулой можно пользоваться:
- если длина проводника такая, что индукция во всех точках проводника может считаться одинаковой;
- если магнитное поле однородное (тогда длина проводника может быть любой, но при этом проводник целиком должен находиться в поле).
Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:
На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную на каждый метр длины.
Ток в один ампер – это такой ток, при котором два однородных параллельных проводника, расположенные в вакууме на расстоянии один метр друг от друга взаимодействуют с силой Ньютона.
Закон взаимодействия токов – два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.
Формула силы Ампера
С учетом всего перечисленного можно получить формулу силы Ампера, которую еще называют законом Ампера:
Модуль силы Ампера равен произведению силы тока в проводнике, вектора магнитной индукции, длины проводника и синуса угла между направлениями векторов магнитной индукции и тока.

Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Связь с другими единицами СИ
Если сила тока в проводнике равна 1 амперу, то за одну секунду через поперечное сечение проходит заряд, равный 1 кулону.
Разность потенциалов в 1 вольт на концах проводника с электрическим сопротивлением 1 ом создаёт в нём ток 1 ампер.
Если конденсатор ёмкостью в 1 фарад заряжать током 1 ампер, то напряжение на обкладках будет возрастать на 1 вольт каждую секунду.
Если изменять ток со скоростью 1 ампер в секунду в проводнике, имеющем индуктивность 1 генри, в нём создаётся ЭДС индукции, равная одному вольту.
Направление силы Ампера
Принимая к сведению то, что сила – векторная величина, определим её направление. Рассмотрим случай, когда проводник с током расположен между двумя полюсами магнитов под прямым углом к линиям магнитной индукции.
Выше мы установили, что согласно закону Ампера, действующая на данный проводник сила, равна: F = B*L*I. Направление вектора рассматриваемой силы определяется по результатам векторного произведения:
![]()
Если полюса магнита статичны (неподвижны), то векторное произведение будет зависеть только от параметров электричества, в частности, от того, в какую сторону оно течёт.
Направление силы Ампера определяют по известному правилу левой руки: ладонь располагают навстречу магнитным линиям, а пальцы размещают вдоль проводника, в сторону устремления тока. На ориентацию силы Ампера указывает большой палец, образующий прямой угол с ладонью (см. рис. 4).
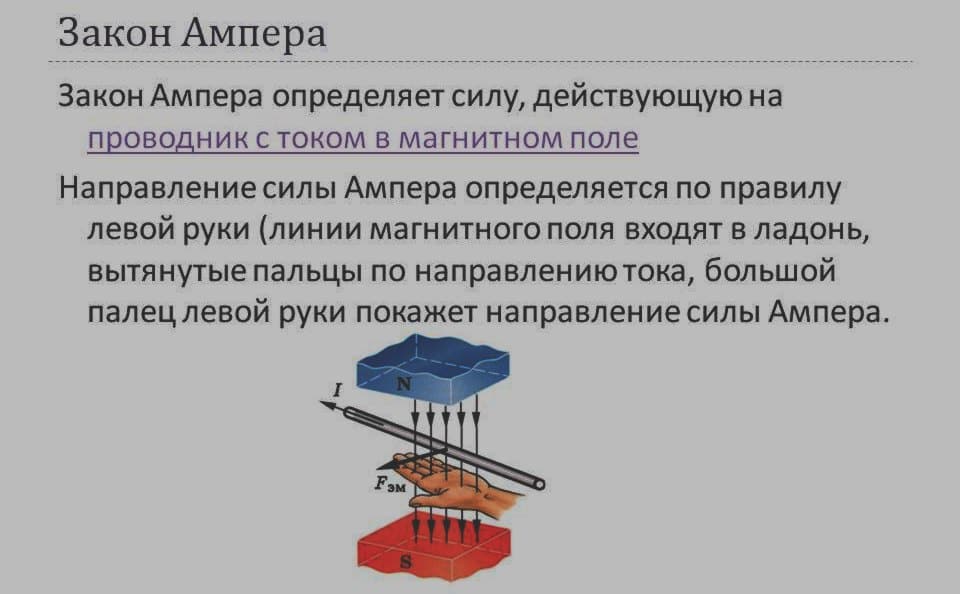
Рис. 4. Интерпретация правила
Измените мысленно направление электрического тока, и вы увидите, что направление вектора Амперовой силы изменится на противоположное. Модуль вектора имеет прямо пропорциональную зависимость от всех сомножителей, но на практике эту величину удобно регулировать путём изменения параметров в электрической цепи (например, для регулировки мощности электродвигателя).
Правило левой руки
Формулировка правила левой руки для силы ампера звучит так:
Если расположить левую руку так, чтобы четыре пальца были направлены по направлению движения тока в проводнике, а перпендикулярная составляющая индукции $B_{perp}$ входила в ладонь, то отставленный большой палец покажет направление силы Ампера.
Как пользоваться этим правилом? Разберем примеры.
- Допустим, проводник расположен горизонтально, и ток по нему идет вперед. Следовательно, четыре пальца левой руки надо вытянуть вперед по этому направлению.
- Теперь допустим, что линии магнитного поля направлены сверху вниз (сверху «север» подковообразного магнита, снизу — «юг»). Следовательно, левую руку надо повернуть ладонью вверх, чтобы линии магнитного поля входили в ладонь и «прокалывали» ее (четыре пальца по-прежнему должны быть вытянуты вперед).
- Отставленный большой палец левой руки будет направлен влево. Это и есть направление силы Ампера для данной ситуации.
Другой пример.
- Пусть проводник расположен вертикально. А магнитное поле направлено справа налево (справа «север» магнита, слева — «юг»).
- Располагаем левую руку четырьмя пальцами вверх. Ладонь открытой стороной должна «смотреть вправо», чтобы магнитные линии входили и «прокалывали» ее.
- Отставленный большой палец покажет назад. Именно так и будет направлена сила Ампера в данном случае.
Обратите внимание, что силу Ампера порождает только перпендикулярная составляющая магнитного поля. А значит, руку надо располагать так, чтобы линии магнитного поля всегда входили в нее под углом, максимально близким к прямому.
Особым случаем является ситуация, когда направление тока и магнитной индукции совпадает. В этом случае руку невозможно расположить так, чтобы линии магнитной индукции входили в нее. Следовательно, силы Ампера здесь не возникнет. В самом деле, если линии магнитной индукции параллельны направлению тока, то перпендикулярная составляющая этих линий равна нулю, и значение силы Ампера в вышеприведенной формуле также равно нулю.
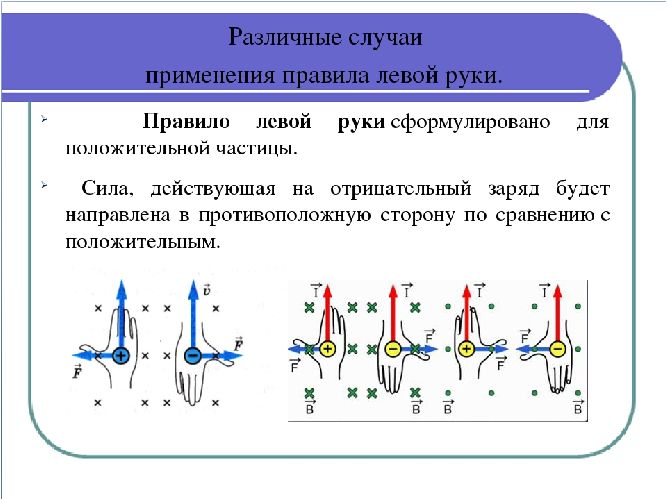
Рис. 3. Различные случаи применения правила левой руки.
Работа силы Ампера
Проводники, на которые действует сила Ампера, могут перемещаться под действием этой силы. В этом случае говорят, что сила Ампера совершает работу. Из курса механики вспомним, что работа равна:
A=Fscos.α
F — сила, совершающая работу, s — перемещение, совершенное телом под действием этой силы, α — угол между вектором силы и вектором перемещения.
Отсюда работа, совершаемая силой Ампера, равна:
A=FAscos.α=BIlsin.βscos.α
α — угол между вектором силы и вектором перемещения, β — угол между условным направлением тока и вектором магнитной индукции.
Пример №3. Проводник длиной l = 0,15 м перпендикулярен вектору магнитной индукции однородного магнитного поля, модуль которого B = 0,4 Тл. Сила тока в проводнике I = 8 А. Найдите работу, которая была совершена при перемещении проводника на 0,025 м по направлению действия силы Ампера.
Так как проводник расположен перпендикулярно вектору магнитной индукции, и поле однородно, то синус угла между ними равен «1». Так как направление перемещение проводника совпадает с направлением действия силы Ампера, то косинус угла между ними тоже равен «1». Поэтому формула для вычисления работы силы Ампера принимает вид:
A=BIls
Подставим известные данные:
A=0,4·8·0,15·0,025=0,012 (Дж)=12 (мДж)
Задание EF17704
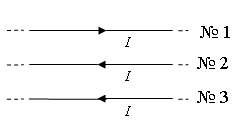
Как направлена сила Ампера, действующая на проводник № 3 со стороны двух других (см. рисунок), если все проводники тонкие, лежат в одной плоскости и параллельны друг другу? По проводникам идёт одинаковый ток силой I.
а) вверх
б) вниз
в) к нам
г) от нас
Алгоритм решения
1.Определить направление вектора результирующей магнитной индукции первого и второго проводников в любой точке третьего проводника.2.Используя правило левой руки, определить направление силы Ампера, действующей на третий проводник со стороны первых двух проводников.
Решение
На третьем проводнике выберем произвольную точку и определим, в какую сторону в ней направлен результирующий вектор →B, равный геометрической сумме векторов магнитной индукции первого и второго проводников (→B1и →B2). Применим правило буравчика. Мысленно сопоставим острие буравчика с направлением тока в первом проводнике. Тогда направление вращения его ручки покажем, что силовые линии вокруг проводника 1 направляются относительно плоскости рисунка против хода часовой стрелки. Ток во втором проводнике направлен противоположно току в первом. Следовательно, его силовые линии направлены относительно плоскости рисунка по часовой стрелке.
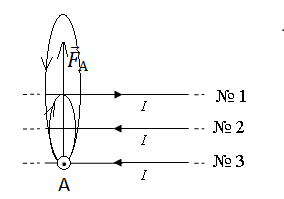
В точке А вектор →B1 направлен в сторону от наблюдателя, а вектор →B2— к наблюдателю. Так как второй проводник расположен ближе к третьему, создаваемое им магнитное поле в точке А более сильное (силы тока во всех проводниках равны по условию задачи). Следовательно, результирующий вектор →B направлен к наблюдателю.
Теперь применим правило левой руки. Расположим ее так, чтобы четыре пальца были направлены в сторону течения тока в третьем проводнике. Ладонь расположим так, чтобы результирующий вектор →B входил в ладонь. Теперь отставим большой палец на 90 градусов. Относительно рисунка он покажет «вверх». Следовательно, сила Ампера →FА, действующая на третий проводник, направлена вверх.
Ответ: а
Задание EF18417
Чему равна сила Ампера, действующая на стальной прямой проводник с током длиной 10 см и площадью поперечного сечения 2⋅10–2 мм2 , если напряжение на нём 2,4 В, а модуль вектора магнитной индукции 1 Тл? Вектор магнитной индукции перпендикулярен проводнику. Удельное сопротивление стали 0,12 Ом⋅мм2/м.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.2.Записать формулу для определения силы Ампера.3.Выполнить решение в общем виде.4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Длина проводника: l = 10 см.• Площадь поперечного сечения проводника: S = 2⋅10–2 мм2.• Напряжение в проводнике: U = 2,4 В.• Модуль вектора магнитной индукции: B = 1 Тл.• Удельное сопротивление стали: r = 0,12 Ом⋅мм2/м.• Угол между проводником с током и вектором магнитной индукции: α = 90о.
10 см = 0,1 м
Сила Ампера определяется формулой:
FA=BIlsin.α
Так как α = 90о, синус равен 1. Тогда сила Ампера равна:
FA=BIl
Силу тока можно выразить из закона Ома:
I=UR..
Сопротивление проводника вычисляется по формуле:
R=rlS..
Тогда сила тока равна:
I=USrl..
Конечная формула для силы Ампера принимает вид:
FA=BlUSrl..=BUSr..=1·2,4·2·10−20,12..=0,4 (Н)
.
.
Ответ: 0,4
Задание EF17725
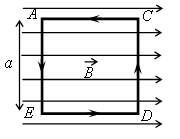
На непроводящей горизонтальной поверхности стола лежит жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата AСDЕ со стороной a(см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции B которого перпендикулярен сторонам AE и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
Алгоритм решения
1.Сделать список известных данных.2.Определить, при каком условии рамка с током будет вращаться вокруг стороны CD.3.Выполнить решение в общем виде.
Решение
По условию задачи известными данными являются:
• Сторона квадратной рамки с током: a.• Вектор магнитной индукции однородного горизонтального магнитного поля, в котором лежит рамка: B.• Масса рамки: m.
Пусть по рамке течёт ток I. На стороны АЕ и CD будут действовать силы Ампера:
FA1=FA2=IaB
Для того чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз. Момент силы Ампера относительно оси, проходящей через сторону CD:
MA=Ia2B
Момент силы тяжести относительно оси CD:
Mmg=−12..mga
Чтобы рамка с током оторвалась от горизонтальной поверхности, нужно чтобы суммарный момент сил был больше нуля:
MA+Mmg>0
Так как момент силы тяжести относительно оси CD отрицательный, это неравенство можно записать в виде:
Ia2B>12..mga
Отсюда выразим силу тока:
I>mga2a2B..
I>mg2aB..
Практическое применение
Сила Ампера используется практически во всех электромеханических устройствах, где необходимо с помощью электрических процессов вызвать движение реальных объектов. Одним из примеров применения являются измерительные приборы.
При пропускании тока через проводник появляется магнитное взаимодействие, и рамка начинает вращаться. При этом смещается стрелка указателя до тех пор, пока сила Ампера не уравновесит силу упругости обеих пружин. Полученный показатель будет характеризовать ток, протекающий через проводник. Чем больше сила тока, тем сильнее отклонится стрелка.
На законе Ампера основывается и такая отрасль, как электротехника. Например, электромагнитная индукция применяется в электродвигателях.
Двигатель обеспечивает преобразование электроэнергии во вращение вала. Ток на рамку поступает через скользящие щётки. Она взаимодействует с постоянным магнитом, что приводит к её повороту под действием силы Ампера. В современных двигателях может использоваться одновременно несколько рамок. Это позволяет увеличить мощность мотора и сделать вращение оси более плавным.
Двигатели, работающие на основе рассматриваемого эффекта, активно используются в различных видах электротранспорта — трамваях, троллейбусах, электропоездах.
Еще одно применение закона Ампера — это громкоговорители. Внутри них находится постоянный магнит. Изменение силы тока вызывает изменение силы воздействия магнитного поля, что приводит к вибрации мембраны, производящей звук нужной частоты.
Притяжение между проводниками с током легло в основу точного определения единицы измерения 1 Ампер. При этом рассматривалась абстрактная ситуация, предполагающая наличие двух параллельно расположенных проводников с бесконечной длиной. Считалось, что каждый из них имеет бесконечно малое сечение, размерами которого можно пренебречь.
Принято, что на всём протяжении они находятся точно на расстоянии один метр и в вакууме. При прохождении тока величиной 1 Ампер сила, действующая на каждый метр проводников, должна составлять 0.0000002 Ньютона. Это определение вступило в силу в 1948 году.
Эксперимент
Для того чтобы иметь возможность своими глазами увидеть действие силы Ампера, можно провести дома небольшой эксперимент. Для начала необходимо взять магнит-подкову, в котором между полюсами поместить проводник. Всё желательно воспроизвести так, как на картинке.
Если замкнуть ключ, то можно увидеть, что проводник начнёт двигаться, смещаясь от начальной точки равновесия. Можно поэкспериментировать с направлениями пропускания тока и увидеть, что зависимо от направления движения меняется направление отклонения проводника. Из самого эксперимента можно вынести несколько наблюдений, которые подтверждают вышесказанное:
- Магнитное поле действует исключительно на проводник с током.
- На проводник с током в магнитном поле действует сила, которая является следствием их взаимодействия. Именно под воздействием этой силы проводник движется в пространстве в границах магнитного поля.
- Характер взаимодействия прямо зависит от напряжения электрического тока и силовых линий магнитного поля.
- Поле не действует на проводник с током, если ток в проводнике течёт параллельно направлению линий поля.
Предыдущая
ТеорияЗакон сохранения электрического заряда
Следующая
ТеорияПочему в странах разные розетки?
Формула силы Ампера в физике
Содержание:
- Определение и формула силы Ампера
- Закон Ампера
- Силы, действующие на проводники с током в магнитном поле
- Единицы измерения силы Ампера
- Примеры решения задач
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$bar{F}, bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
большой палец укажет направление силы Ампера (рис.1).
Закон Ампера
Элементарная сила Ампера
($dbar{F}_A$) определена законом (или формулой) Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(1)$$
где I – сила тока,
$d bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d bar{F}_{A}=bar{j} times bar{B} d V(2)$$
где $bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I cdot B cdot d l cdot sin alpha(3)$$
где $alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$bar{F}_{A}=I int_{l} d bar{l} times bar{B}(4)$$
где $bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl.
Интегрирование в формуле (4) проводят по всей длине проводника (l). {7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$frac{F}{l}=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B operatorname{lsin} alpha$$
где $alpha$ – искомый угол.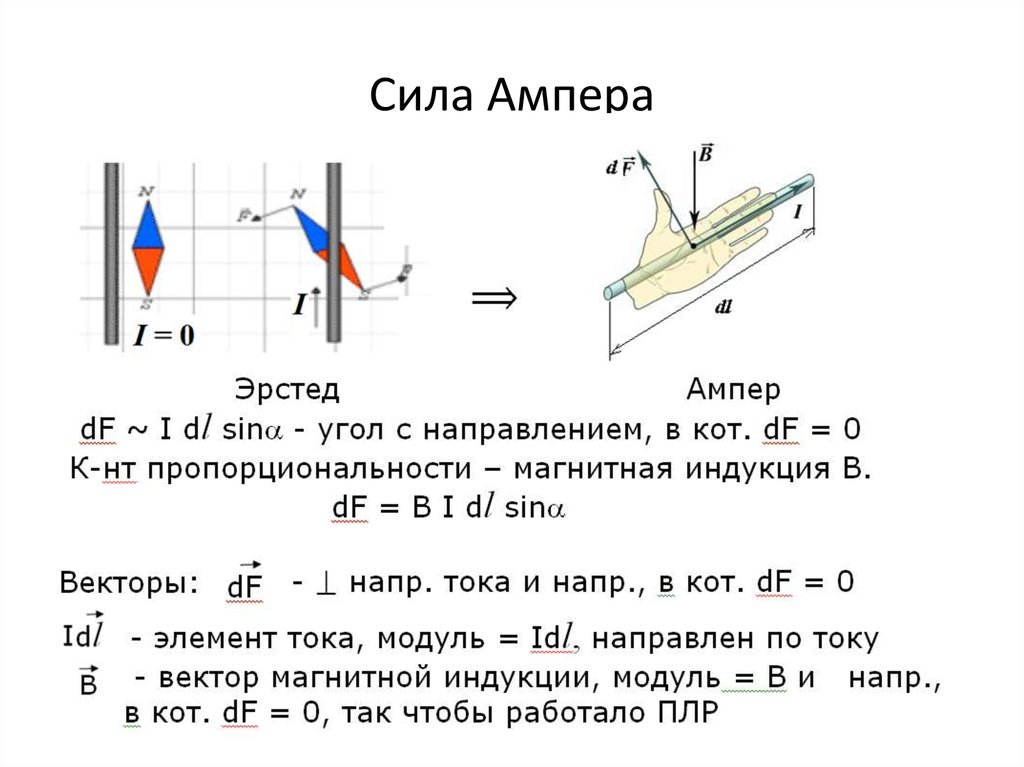 Следовательно:
Следовательно:
$$alpha=arcsin left(frac{F}{I B l}right)$$
Ответ. $alpha=arcsin left(frac{F}{I B l}right)$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
Ширина правого проводника равна a. По проводникам текут токи I
1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится. Станем искать силу
Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Тогда выражение для dFA, учитывая (2. {a+b} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$$
{a+b} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$
Читать дальше: Формула силы выталкивания.
Сила Ампера | СПАДИЛО
Определение
Сила Ампера — сила, которая действует на проводник с током, помещенный в магнитное поле.
Модуль силы Ампера обозначается как FA. Единица измерения — Ньютон (Н).
Математически модуль силы Ампера определяется как произведение модуля вектора магнитной индукции B, силы тока I, длины проводника l и синуса угла α между условным направлением тока и вектором магнитной индукции:
FA=BIlsin.α
Максимальное значение сила Ампера принимает, когда ток в проводнике направлен перпендикулярно вектору магнитной индукции, так как sin.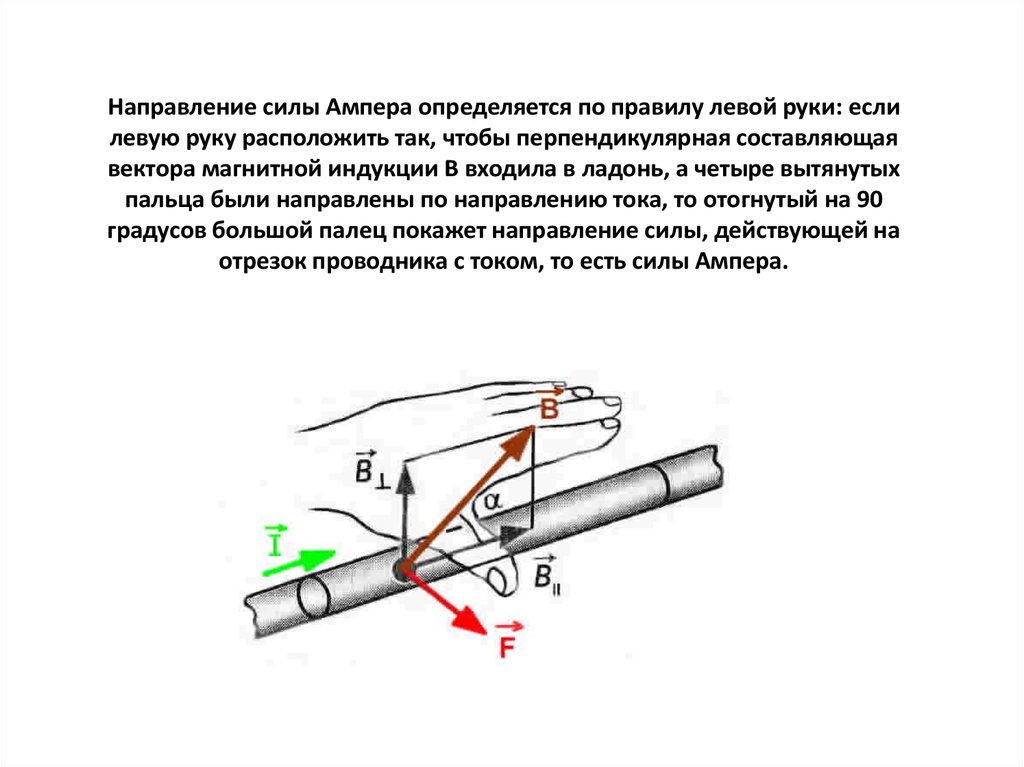
90°=1. И сила Ампера отсутствует совсем, если ток в проводнике направлен относительно вектора магнитной индукции вдоль одной линии. В этом случае угол между ними равен 0, а sin.0°=1.
Пример №1. Максимальная сила, действующая в однородном магнитном поле на проводник с током длиной 10 см, равна 0,02 Н. Сила тока в проводнике равна 8 А. Найдите модуль вектора магнитной индукции этого поля.
10 см = 0,1 м
Так как речь идет о максимальной силе, действующей на проводник с током, тоsin.α при этом равен 1 (проводник с током расположен перпендикулярно вектору магнитной индукции).
Определение направления силы Ампера
Направление вектора силы Ампера определяется правилом левой руки.
Правило левой руки
Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции →B входила в ладонь, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на отрезок проводника (направление силы Ампера).
Пример №2. В однородном магнитном поле находится рамка, по которой начинает течь ток (см. рисунок). Какое направление (вверх, вниз, влево, вправо, от наблюдателя, наблюдателю) имеет сила, действующая на нижнюю сторону рамки?
Так как в нижней стороне рамки ток направлен вправо, то четыре пальца левой руки нужно направить вправо. Саму левую руку при этом нужно расположить перпендикулярно плоскости рисунка ладонью вверх, чтобы в нее входили линии вектора магнитной индукции. Если отогнуть большой палец на прямой угол, то он покажет направление силы Ампера, действующей на нижнюю часть рамки. В данном случае она направлена в сторону от наблюдателя.
Проводники, на которые действует сила Ампера, могут перемещаться под действием этой силы. В этом случае говорят, что сила Ампера совершает работу. Из курса механики вспомним, что работа равна:
A=Fscos.α
F — сила, совершающая работу, s — перемещение, совершенное телом под действием этой силы, α — угол между вектором силы и вектором перемещения.
Отсюда работа, совершаемая силой Ампера, равна:
A=FAscos.α=BIlsin.βscos.α
α — угол между вектором силы и вектором перемещения, β — угол между условным направлением тока и вектором магнитной индукции.
Пример №3. Проводник длиной l = 0,15 м перпендикулярен вектору магнитной индукции однородного магнитного поля, модуль которого B = 0,4 Тл. Сила тока в проводнике I = 8 А. Найдите работу, которая была совершена при перемещении проводника на 0,025 м по направлению действия силы Ампера.
Так как проводник расположен перпендикулярно вектору магнитной индукции, и поле однородно, то синус угла между ними равен «1». Так как направление перемещение проводника совпадает с направлением действия силы Ампера, то косинус угла между ними тоже равен «1». Поэтому формула для вычисления работы силы Ампера принимает вид:
A=BIls
Подставим известные данные:
A=0,4·8·0,15·0,025=0,012 (Дж)=12 (мДж)
Задание EF17704
Как направлена сила Ампера, действующая на проводник № 3 со стороны двух других (см. рисунок), если все проводники тонкие, лежат в одной плоскости и параллельны друг другу? По проводникам идёт одинаковый ток силой I.
рисунок), если все проводники тонкие, лежат в одной плоскости и параллельны друг другу? По проводникам идёт одинаковый ток силой I.
а) вверх
б) вниз
в) к нам
г) от нас
Алгоритм решения
1.Определить направление вектора результирующей магнитной индукции первого и второго проводников в любой точке третьего проводника.
2.Используя правило левой руки, определить направление силы Ампера, действующей на третий проводник со стороны первых двух проводников.
Решение
На третьем проводнике выберем произвольную точку и определим, в какую сторону в ней направлен результирующий вектор →B, равный геометрической сумме векторов магнитной индукции первого и второго проводников (→B1и →B2). Применим правило буравчика. Мысленно сопоставим острие буравчика с направлением тока в первом проводнике. Тогда направление вращения его ручки покажем, что силовые линии вокруг проводника 1 направляются относительно плоскости рисунка против хода часовой стрелки. Ток во втором проводнике направлен противоположно току в первом. Следовательно, его силовые линии направлены относительно плоскости рисунка по часовой стрелке.
Ток во втором проводнике направлен противоположно току в первом. Следовательно, его силовые линии направлены относительно плоскости рисунка по часовой стрелке.
В точке А вектор →B1 направлен в сторону от наблюдателя, а вектор →B2— к наблюдателю. Так как второй проводник расположен ближе к третьему, создаваемое им магнитное поле в точке А более сильное (силы тока во всех проводниках равны по условию задачи). Следовательно, результирующий вектор →B направлен к наблюдателю.
Теперь применим правило левой руки. Расположим ее так, чтобы четыре пальца были направлены в сторону течения тока в третьем проводнике. Ладонь расположим так, чтобы результирующий вектор →B входил в ладонь. Теперь отставим большой палец на 90 градусов. Относительно рисунка он покажет «вверх». Следовательно, сила Ампера →FА, действующая на третий проводник, направлена вверх.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18417
Чему равна сила Ампера, действующая на стальной прямой проводник с током длиной 10 см и площадью поперечного сечения 2⋅10–2 мм2 , если напряжение на нём 2,4 В, а модуль вектора магнитной индукции 1 Тл? Вектор магнитной индукции перпендикулярен проводнику. Удельное сопротивление стали 0,12 Ом⋅мм2/м.
Удельное сопротивление стали 0,12 Ом⋅мм2/м.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Ампера.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Длина проводника: l = 10 см.
• Площадь поперечного сечения проводника: S = 2⋅10–2 мм2.
• Напряжение в проводнике: U = 2,4 В.
• Модуль вектора магнитной индукции: B = 1 Тл.
• Удельное сопротивление стали: r = 0,12 Ом⋅мм2/м.
• Угол между проводником с током и вектором магнитной индукции: α = 90о.
10 см = 0,1 м
Сила Ампера определяется формулой:
FA=BIlsin.α
Так как α = 90о, синус равен 1. Тогда сила Ампера равна:
FA=BIl
Силу тока можно выразить из закона Ома:
I=UR.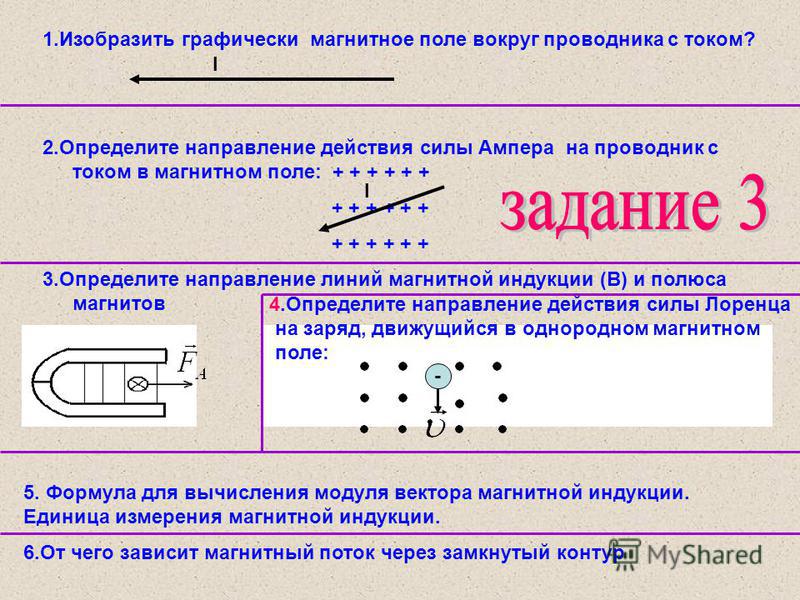 .
.
Сопротивление проводника вычисляется по формуле:
R=rlS..
Тогда сила тока равна:
I=USrl..
Конечная формула для силы Ампера принимает вид:
FA=BlUSrl..=BUSr..=1·2,4·2·10−20,12..=0,4 (Н)
.
.
Ответ: 0,4
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17725
На непроводящей горизонтальной поверхности стола лежит жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата AСDЕ со стороной a(см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции B которого перпендикулярен сторонам AE и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
Алгоритм решения
1.Сделать список известных данных.
2.Определить, при каком условии рамка с током будет вращаться вокруг стороны CD.
3.Выполнить решение в общем виде.
Решение
По условию задачи известными данными являются:
• Сторона квадратной рамки с током: a.
• Вектор магнитной индукции однородного горизонтального магнитного поля, в котором лежит рамка: B.
• Масса рамки: m.
Пусть по рамке течёт ток I. На стороны АЕ и CD будут действовать силы Ампера:
FA1=FA2=IaB
Для того чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз. Момент силы Ампера относительно оси, проходящей через сторону CD:
MA=Ia2B
Момент силы тяжести относительно оси CD:
Mmg=−12..mga
Чтобы рамка с током оторвалась от горизонтальной поверхности, нужно чтобы суммарный момент сил был больше нуля:
MA+Mmg>0
Так как момент силы тяжести относительно оси CD отрицательный, это неравенство можно записать в виде:
Ia2B>12. .mga
.mga
Отсюда выразим силу тока:
I>mga2a2B..
I>mg2aB..
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 9.3k
Формула закона Ампера — GeeksforGeeks
Согласно закону Ампера, магнитное поле, образованное электрическим током, пропорционально его величине. В этом случае константа пропорциональности равна проницаемости пустого пространства. Это также говорит о том, что магнитное поле связано с определенным током или наоборот, пока электрическое поле остается постоянным. Он используется для определения магнитной индукции, возникающей при использовании длинного провода с током. Он также используется для расчета магнитного поля, создаваемого длинным проводящим цилиндром с током.
Формула закона Ампера
Формула закона Ампера равна линейному интегралу магнитного поля вокруг замкнутого контура, равному количеству раз, которое алгебраическая сумма токов проходит через контур.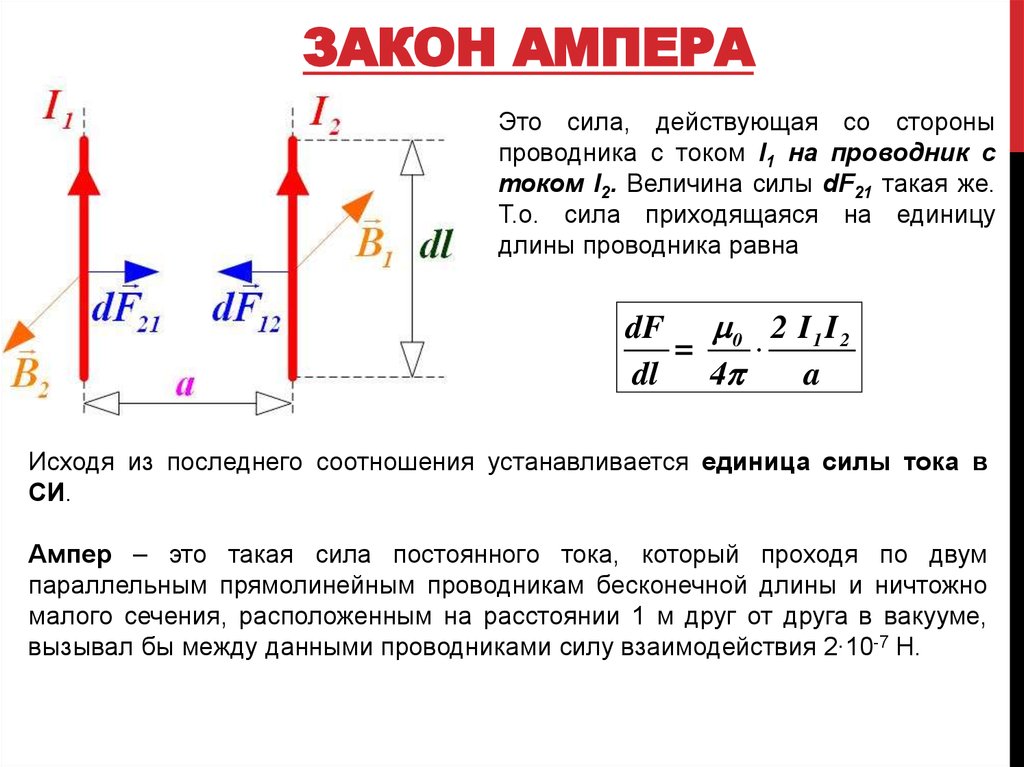 Для проводника с током I, в котором поток тока создает магнитное поле вокруг провода, эту формулу можно использовать для расчета поля.
Для проводника с током I, в котором поток тока создает магнитное поле вокруг провода, эту формулу можно использовать для расчета поля.
где,
μ или – постоянная магнитной проницаемости со значением 4π × 10 -7 N/A 2 ,
B – магнитное поле,
I – поток тока, проходящий через замкнутый контур,
L – длина петли.
Для замкнутого провода значение равно 2πr. Итак, величина магнитного поля в этом случае равна
B = μ o I/2πr
0,2 м, если через него протекает ток силой 2 А.
Решение:
.
= 2πr
= 2 (22/7) (0,2)
= 1,25 м
Используя формулу, которую мы имеем, ) (2)/(1.25)
= 2,011 × 10 -6 T
Задача 2. Найти магнитное поле замкнутого провода радиусом 0,5 м, если по нему течет ток силой 3 А .
Решение:
.
= 2πr
= 2 (22/7) (0,5)
= 6,28 м
Используя формулу, которую мы имеем, ) (3)/(6.28)
= 6 × 10 -7 T
Задача 3. Найти магнитное поле замкнутого провода радиусом 0,8 м, если по нему течет ток силой 5 А .
Решение:
.
= 2πr
= 2 (22/7) (0,8)
= 5,02 м
Используя формулу, которую мы имеем, ) (5)/(5.02)
= 1,25 × 10 -6 T
Задача 4. Найти магнитное поле замкнутого провода радиусом 0,4 м, если по нему течет ток силой 10 А .
Решение:
.
= 2πr
= 2 (22/7) (0,4)
= 2,51 м
Используя формулу, которую мы имеем, ) (10)/(2.51)
= 5 × 10 -6 T
Задача 5. Найти ток, протекающий по замкнутому проводу радиусом 0,7 м, если его поле равно 3,4 × 10 -6 T.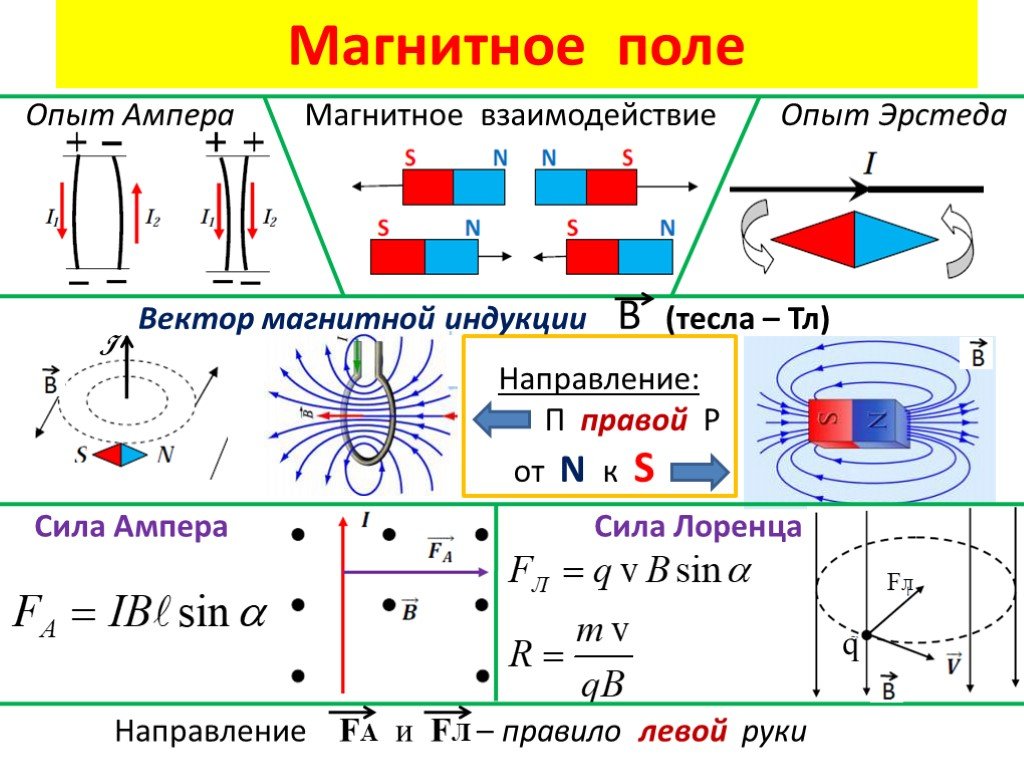
Решение:
Мы имеем,
R = 0,7
B = 3,4 × 10 -6
μ O = 4π × 10002029
μ o = 4π × 100020 -7 9 9 μ o = 4π -7 9 o = 4π × 100020 -7 9 o = 4.
В нашем случае длина петли равна
= 2πr
= 2 (22/7) (0,7)
= 4,4 м
Используя формулу, которую мы имеем, 2πr
3,4 × 10 -6 = (4π × 10 -7 ) (I)/(2,51)
I = 85,3/12,57
I = 6,78 А
Задача 6. Найти силу тока, протекающего по замкнутому проводу радиусом 0,32 м, если его поле равно 2,76 × 10 -7 Тл.
7 2 Решение:
8 Мы имеем,
R = 0,32
B = 2,76 × 10 -7
μo = 4π × 10 -7
В нашем случае длина петли равен,
= 2πr
= 2.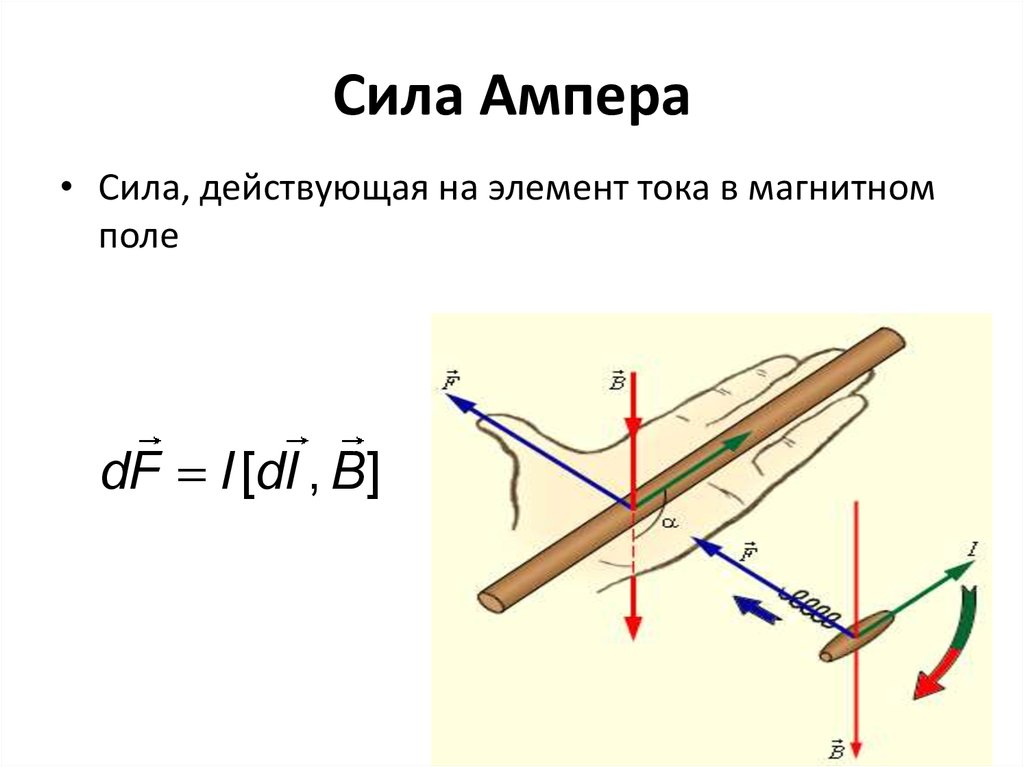 (22/7) (0,32)
(22/7) (0,32)
= 2,011 м
Используя формулу, которую мы имеем,
B = μ O I/2πr
2,76 × 10 -7 = (4π × 10 -7 ) (I)/(2,011)
I = 5,55/12,57
I = 0,44 A
Задача 7. Найти радиус замкнутого провода, если его поле 8,21 × 10 -5 Тл и сила тока 7 А.
Решение:
3 = 8,21 × 10
-5
μ о = 4π × 10 -7
I = 7
Используя формулу, которую мы имеем,
B = μ о I/2πr
8,21 × 10 -5 = (4π × 10 -7 ) (7)/r 9 ×
10 -2 )/8.21
r = 0,017 м
12.6: Закон Ампера — Physics LibreTexts
-
- Последнее обновление
-
-
Сохранить как PDF
-
- Идентификатор страницы
- 4425
-
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Объяснять, как закон Ампера связывает магнитное поле, создаваемое током, со значением тока
- Рассчитайте магнитное поле длинного прямого провода, тонкого или толстого, по закону Ампера
Фундаментальное свойство статического магнитного поля заключается в том, что, в отличие от электростатического поля, оно не является консервативным.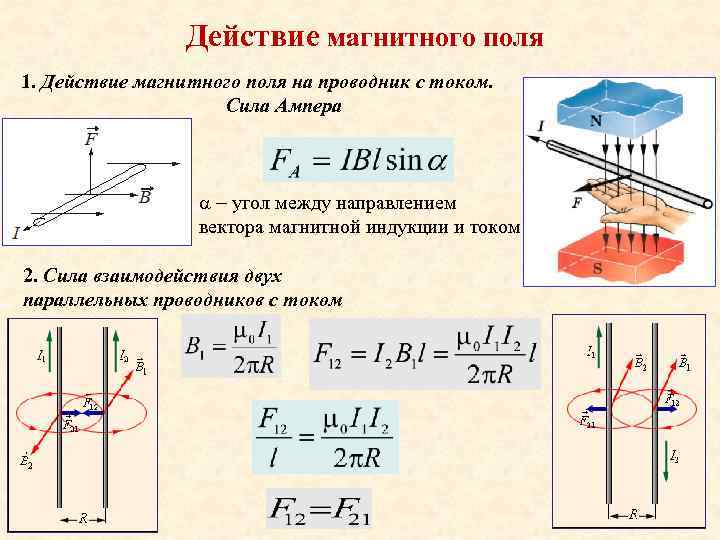 Консервативное поле — это такое поле, которое совершает одинаковую работу над частицей, перемещающейся между двумя разными точками, независимо от выбранного пути. Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от (vec{B}) и известен как закон Ампера . Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.
Консервативное поле — это такое поле, которое совершает одинаковую работу над частицей, перемещающейся между двумя разными точками, независимо от выбранного пути. Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от (vec{B}) и известен как закон Ампера . Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.
На рисунке (PageIndex{1}) показана произвольная плоскость, перпендикулярная бесконечному прямому проводу, ток которого I направлен за пределы страницы. Линии магнитного поля представляют собой окружности, направленные против часовой стрелки и центрированные на проводе. Для начала рассмотрим (oint vec{B} cdot dvec{l}) по замкнутым путям M и N . Обратите внимание, что один путь ( M ) охватывает провод, а другой ( N ) нет. Поскольку силовые линии круглые, (vec{B} cdot dvec{l}) является произведением B и проекции dl на окружность, проходящую через (dvec{l }). Если радиус этого конкретного круга равен r , проекция равна (rdtheta) и
Поскольку силовые линии круглые, (vec{B} cdot dvec{l}) является произведением B и проекции dl на окружность, проходящую через (dvec{l }). Если радиус этого конкретного круга равен r , проекция равна (rdtheta) и
[vec{B} cdot dvec{l} = Br , dtheta.]
Рисунок (PageIndex{1}): Ток I длинного прямого провода направлен за пределы страницы. Интеграл (oint dtheta) равен (2pi) и 0 соответственно для путей M и N.
С (vec{B}), заданным уравнением 12.4.1,
[oint vec{B} cdot dvec{l} = oint left(frac{mu_0 I}{2pi r}right) , r , dtheta = frac{mu_0 I}{2pi} oint dtheta.]
Для пути M , который циркулирует по проводу, (oint_M dtheta = 2pi) и
[oint_M vec{B} cdot dvec{l} = mu_0 I.]
Путь N , с другой стороны, циркулирует как через положительный (против часовой стрелки), так и через отрицательный (по часовой стрелке) (dtheta) (см. рисунок (PageIndex{1})), и поскольку он замкнут, (oint_N dтета = 0). Таким образом, для пути Н ,
рисунок (PageIndex{1})), и поскольку он замкнут, (oint_N dтета = 0). Таким образом, для пути Н ,
[oint_N vec{B} cdot dvec{l} = 0.]
Распространение этого результата на общий случай есть закон Ампера.
Закон Ампера
По произвольному замкнутому пути,
[oint vec{B} cdot dvec{l} = mu_0 I]
где I — полный ток, проходящий через любой открытый поверхность S , периметр которой является путем интегрирования. Необходимо учитывать только токи внутри пути интегрирования.
Чтобы определить, является ли конкретный ток I положительный или отрицательный, согните пальцы правой руки в направлении пути интегрирования, как показано на рисунке (PageIndex{1}). Если I проходит через S в том же направлении, что и ваш вытянутый большой палец, I положителен; если I проходит через S в направлении, противоположном вашему вытянутому большому пальцу, это отрицательно.
Стратегия решения задач: закон Ампера
Чтобы рассчитать магнитное поле, создаваемое током в проводах, выполните следующие действия:
- Определите симметрию тока в проводах. Если симметрии нет, используйте закон Био-Савара для определения магнитного поля.
- Определите направление магнитного поля, создаваемого проводом(ами), по правилу правой руки 2.
- Выберите петлю пути, в которой магнитное поле либо постоянно, либо равно нулю.
- Рассчитать ток внутри контура.
- Вычислите линейный интеграл (oint vec{B} cdot dvec{l}) вокруг замкнутого контура.
- Приравнять (oint vec{B} cdot dvec{l}) к (mu_0 I_{enc}) к (mu_0 I_{enc}) и найти (vec {В}).
Использование закона Ампера для расчета магнитного поля, создаваемого проводом
Использование закона Ампера для расчета магнитного поля, создаваемого постоянным током I в бесконечно длинном тонком прямом проводе, как показано на рисунке (PageIndex{ 2}).
Рисунок (PageIndex{2}): Возможные компоненты магнитного поля B из-за текущего I , который направлен за пределы страницы. Радиальная составляющая равна нулю, потому что угол между магнитным полем и траекторией прямой.
Стратегия
Рассмотрим произвольную плоскость, перпендикулярную проводу, с током, направленным за пределы страницы. Возможные компоненты магнитного поля в этой плоскости (B_r) и (B_{theta}) показаны в произвольных точках на окружности радиусом r с центром на проводе. Поскольку поле цилиндрически симметрично, ни (B_r), ни (B_{theta}) не меняются в зависимости от положения на этой окружности. Также из симметрии радиальные линии, если они есть, должны быть направлены либо все внутрь, либо все наружу от провода. Это означает, однако, что должен существовать чистый магнитный поток через произвольный цилиндр, концентричный проводнику. Радиальная составляющая магнитного поля должна быть равна нулю, поскольку (vec{B}_r cdot dvec{l} = 0). Следовательно, мы можем применить закон Ампера к круговому пути, как показано на рисунке.
Следовательно, мы можем применить закон Ампера к круговому пути, как показано на рисунке.
Решение
По этому пути (vec{B}) постоянна и параллельна (dvec{l}), поэтому
[oint vec{B} cdot d vec{l} = B_{theta} oint dl = B_{theta}(2pi r).]
Таким образом, закон Ампера сводится к
[B_{theta}(2pi r ) = mu_0 I.]
Наконец, поскольку (B_{theta}) является единственным компонентом (vec{B}), мы можем опустить индекс и написать
[B = frac{mu_0 I}{2pi r}.]
Это согласуется с приведенным выше расчетом Био-Савара.
Значимость
Закон Ампера хорошо работает, если у вас есть путь интегрирования, по которому (vec{B} cdot dvec{l}) дает результаты, которые легко упростить. Для бесконечного провода это легко работает с круговым путем вокруг провода, так что магнитное поле не учитывается при интегрировании. Если зависимость от пути кажется сложной, вы всегда можете вернуться к закону Био-Савара и использовать его для нахождения магнитного поля.
Пример (PageIndex{2}): Расчет магнитного поля толстой проволоки по закону Ампера
Радиус длинного прямого провода на рисунке (PageIndex{3}) равен a , и по проводу течет ток (I_0), равномерно распределенный по его поперечному сечению. Найдите магнитное поле как внутри, так и снаружи провода.
Рисунок (PageIndex{3}): (a) Модель провода с током радиусом a и током (I_0). (b) Поперечное сечение того же провода с радиусом х и петлей Ампера радиусом х .
Стратегия
Эта задача имеет ту же геометрию, что и пример (PageIndex{1}), но замкнутый ток изменяется по мере того, как мы перемещаем путь интегрирования снаружи провода внутрь провода, где он не захватывает весь ток прилагается (см. рисунок (PageIndex{3})).
Решение
Для любого кругового пути радиусом r с центром на проводе
[oint vec{B} cdot dvec{l} = oint Bdl = Boint dl = B(2pi r). ]
]
Согласно закону Ампера это равно полному току, проходящему через любую поверхность, ограниченную путем интегрирования. 92} (r leq a).]
Вне провода ситуация идентична ситуации бесконечного тонкого провода из предыдущего примера; то есть
[B = frac{mu_0 I_0}{2pi r} (r geq a).]
Вариант B с r показан на рисунке ( Индекс страницы{4}).
Рисунок (PageIndex{4}): Изменение магнитного поля, создаваемого током (I_0) в длинном прямом проводе радиусом a .
Значение
Результаты показывают, что по мере увеличения радиального расстояния внутри толстой проволоки магнитное поле увеличивается от нуля до известного значения магнитного поля тонкой проволоки. Вне провода поле падает независимо от того, толстый провод или тонкий.
Этот результат аналогичен тому, как закон Гаусса для электрических зарядов ведет себя внутри равномерного распределения зарядов, за исключением того, что закон Гаусса для электрических зарядов имеет равномерное объемное распределение заряда, тогда как закон Ампера здесь имеет однородную область распределения тока.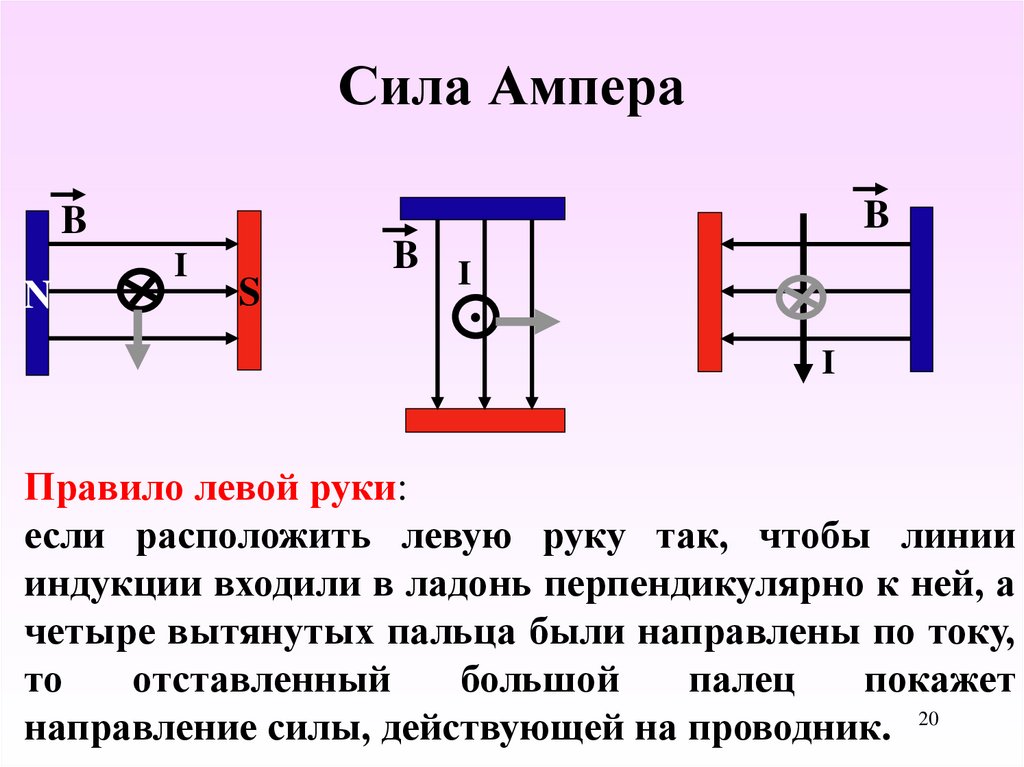 Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.
Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.
Использование закона Ампера с произвольными путями
Используйте закон Ампера для оценки (oint vec{B} cdot dvec{l}) для текущих конфигураций и путей на рисунке (PageIndex{5} ).
Рисунок (PageIndex{5}): Текущие конфигурации и пути для примера (PageIndex{3}).
Стратегия
Закон Ампера гласит, что (oint vec{B} cdot dvec{l} = mu_0 I), где I — это полный ток, проходящий через замкнутый контур. Самый быстрый способ вычислить интеграл — вычислить (mu_0 I), найдя чистый ток через контур. Положительные токи текут по большому пальцу правой руки, если ваши пальцы скручиваются в направлении петли. Это подскажет нам знак ответа.
Решение
(a) Ток, протекающий вниз по контуру, равен току, выходящему из контура, поэтому чистый ток равен нулю. {-6} T cdot m.) 9{-6} T cdot m).
{-6} T cdot m.) 9{-6} T cdot m).
Значение
Если бы все токи закручивались таким образом, что один и тот же ток входил бы в петлю и из петли, чистый ток был бы равен нулю и магнитное поле не присутствовало бы. Вот почему провода в электрическом шнуре расположены очень близко друг к другу. Токи, протекающие к устройству и от устройства по проводу, равны нулевому общему току, протекающему через петлю Ампера вокруг этих проводов. Следовательно, никакие блуждающие магнитные поля не могут присутствовать в проводах с током.
Упражнение (PageIndex{1})
Попробуйте использовать закон Ампера для расчета магнитных полей конечного прямого провода и круглой проволочной петли. Почему это не полезно для этих расчетов?
- Ответить
-
В этих случаях интегралы вокруг петли Ампера очень сложны из-за отсутствия симметрии, поэтому этот метод бесполезен.
Сэмюэля Дж. Линга (Государственный университет Трумэна), Джеффа Санни (Университет Лойолы Мэримаунт) и Билла Мёбса с многими соавторами.
 (22/7) (0,32)
(22/7) (0,32) 3 = 8,21 × 10
-5
μ о = 4π × 10 -7
I = 7
Используя формулу, которую мы имеем,
B = μ о I/2πr
8,21 × 10 -5 = (4π × 10 -7 ) (7)/r 9 ×
10 -2 )/8.21
r = 0,017 м
- Последнее обновление
- Идентификатор страницы
- 4425
 Консервативное поле — это такое поле, которое совершает одинаковую работу над частицей, перемещающейся между двумя разными точками, независимо от выбранного пути. Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от (vec{B}) и известен как закон Ампера . Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.
Консервативное поле — это такое поле, которое совершает одинаковую работу над частицей, перемещающейся между двумя разными точками, независимо от выбранного пути. Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от (vec{B}) и известен как закон Ампера . Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.  Поскольку силовые линии круглые, (vec{B} cdot dvec{l}) является произведением B и проекции dl на окружность, проходящую через (dvec{l }). Если радиус этого конкретного круга равен r , проекция равна (rdtheta) и
Поскольку силовые линии круглые, (vec{B} cdot dvec{l}) является произведением B и проекции dl на окружность, проходящую через (dvec{l }). Если радиус этого конкретного круга равен r , проекция равна (rdtheta) и  рисунок (PageIndex{1})), и поскольку он замкнут, (oint_N dтета = 0). Таким образом, для пути Н ,
рисунок (PageIndex{1})), и поскольку он замкнут, (oint_N dтета = 0). Таким образом, для пути Н , 

 Следовательно, мы можем применить закон Ампера к круговому пути, как показано на рисунке.
Следовательно, мы можем применить закон Ампера к круговому пути, как показано на рисунке. 
 ]
]  Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.
Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.  {-6} T cdot m.) 9{-6} T cdot m).
{-6} T cdot m.) 9{-6} T cdot m). В этих случаях интегралы вокруг петли Ампера очень сложны из-за отсутствия симметрии, поэтому этот метод бесполезен.

