Как найти работу сторонних сил формула - Сайт, где вы сможете решить свои вопросы

Содержание:

Определение и формула ЭДС
Закон Ома для произвольного участка цепи
Единицы измерения
Примеры решения задач

Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал
(учтем, что носители тока предполагаются положительными зарядами) постоянно убирались доставляемые током заряды, при этом к концу с
большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны
перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения.
Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи
или на отдельных участках цепи.

Определение и формула ЭДС

Определение

Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется
электродвижущей силой (ЭДС), действующей в цепи или на участке цепи. ЭДС обозначается
$varepsilon$ . Математически определение ЭДС запишем как:

$$varepsilon=frac{A}{q}(1)$$

где A – работа сторонних сил, q – заряд, над которым производится работа.

Электродвижущая сила источника численно равна разности потенциалов на концах элемента, если он разомкнут, что дает возможность измерить ЭДС по напряжению.

ЭДС, которая действует в замкнутой цепи, может бытьопределена как циркуляция вектора напряжённости сторонних сил:

$$varepsilon=oint_{L} bar{E}^{*} d bar{l}(2)$$

где $bar{E}^{*}$ – напряженность поля сторонних сил. Если напряженность поля сторонних
сил не равна нулю только в части цепи, например, на отрезке 1-2, тогда интегрирование в выражении (2) можно вести только по
данному участку. Соответственно, ЭДС, действующая на участке цепи 1-2 определяется как:

$$varepsilon=int_{1}^{2} bar{E}^{*} d bar{l}(3)$$

Формула (2) дает самое общее определение ЭДС, которое можно использовать для любых случаев.

Закон Ома для произвольного участка цепи

Участок цепи, на котором действуют сторонние силы, называют неоднородным. Для него выполняется равенство:

$$U_{12}=varphi_{1}-varphi_{2}+varepsilon_{12}(4)$$

где U₁₂=IR₂₁ – падение напряжения (или напряжение) на участке цепи 1-2 (I-сила тока);
$varphi_{1}-varphi_{2}$ – разность потенциалов концов участка;
$varepsilon_12$ – электродвижущая сила, которую содержит участок цепи.
$varepsilon_12$ равна алгебраической сумме ЭДС всех источников, которые находятся на данном участке.

Следует учитывать, что ЭДС может быть положительной и отрицательной. ЭДС называют положительной, если она увеличивает потенциал в
направлении тока (ток течет от минуса к плюсу источника).

Единицы измерения

Размерность ЭДС совпадает с размерностью потенциала. Основной единицей измерения ЭДС в системе СИ является: [$varepsilon$]=В

1В=1Дж/1Кл

Примеры решения задач

Пример

Задание. Электродвижущая сила элемента равна 10 В. Он создает в цепи силу тока равную 0,4 А.
Какова работа, которую совершают сторонние силы за 1 мин?

Решение. В качество основы для решения задачи используем формулу для вычисления ЭДС:

$$varepsilon=frac{A}{q}(1.1)$$

Заряд, который проходит в рассматриваемой цепи за 1 мин. можно найти как:

$$q=I Delta t(1.2)$$

Выразим из (1.1) работу, используем (1.2) для вычисления заряда, получим:

$$A=varepsilon I Delta t$$

Переведем время, данной в условиях задачи в секунды ($Delta t$ мин=60 с), проведем вычисления:

$A=10 cdot 0,4 cdot 60=240$ (Дж)

Ответ. A=240 Дж

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

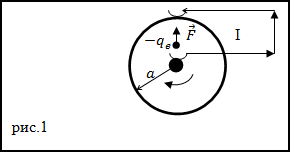
Задание. Металлический диск, имеющий радиус a, вращается с угловой скоростью
$omega$, включен в электрическую цепь при
помощи скользящих контактов, которые касаются оси диска и его окружности (рис.1). Какой будет ЭДС, которая появится между осью
диска и его наружным краем?

Решение. В условиях, которые описаны в задаче, на каждый электрон проводника действует центробежная сила (F)
которая является сторонней. Вследствие ее действия, в диске возникает ЭДС и между осью диска и его наружным краем появляется напряжение.
Формулу для вычисления центробежной силы запишем как:

$$F=m r omega^{2}(2.1)$$

где m – масса электрона, r – расстояние от оси диска.Fдействует на заряженную частицу (электрон), следовательноучитывая (2.1), имеем:

$$E^{*}=frac{F}{q}=frac{m r omega^{2}}{q}$$

где q – заряд электрона.

В соответствии с формулой, определяющей ЭДС участка цепи, получаем:

$$varepsilon=int_{1}^{2} bar{E} d bar{l}=int_{0}^{a} E^{*} d r=int_{0}^{a} frac{m r omega^{2}}{q} d r=frac{m r omega^{2} a^{2}}{2 q}$$

Ответ. $varepsilon=frac{m r omega^{2} a^{2}}{2 q}$

Читать дальше: Формулы по физике.

Источник

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

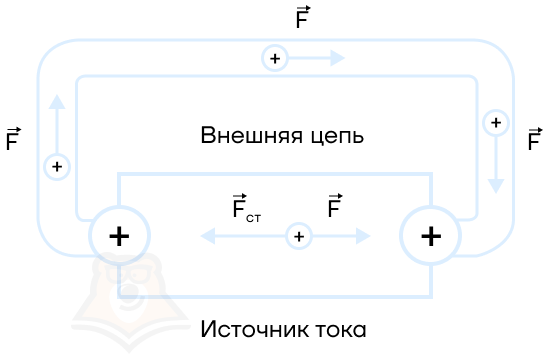
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд q = It . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0) , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При r = 0 формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина R + r неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный (r = 0) .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома U = IR справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор R + r ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд q = It , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем U = IR — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на R + r :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда Кл.

Ответ: 1500.

Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

На этой странице вы узнаете

Где самое большое сопротивление в теле человека?
Какой ученый променял бильярд на физику?
К чему может привести авария среди электронов?

Весь современный мир держится на электричестве. Наряду с глобальной интернет-сетью, наш мир «опутан» сетью электрических проводов. Что такого происходит в этих тоненьких проводах, что от них зависит жизнь целого города? Давайте поближе познакомимся с электрическим током и узнаем, откуда он появляется.

Мы с вами уже познакомились с электрическими схемами в теме «Законы постоянного тока», где выяснили, какие приборы существуют и как используются в схемах. В этой статье мы поговорим о том, как в элементарных электрических цепях появляется ток. Начало положено, сопротивление бесполезно.

Источник тока

Как мы уже выяснили, электрические схемы не могут работать просто так. Представим, что вы хотите поехать на машине, в которой нет бензина. Конечно, машина не заведется, так как ее нужно заправить. Электрические схемы работают по такому же принципу. Если их не подпитывать током, то они не будут работать.

Электрический ток — это направленное, упорядоченное движение электрических зарядов. Поэтому, чтобы поддерживать в цепи ток длительное время, в нем должен быть участок, на котором будет происходить перенос зарядов против сил электростатического поля (поля, создаваемого неподвижными зарядами). То есть, то место, где электроны будут принудительно приходить в движение.

Источник тока — элемент электрической цепи, в котором на заряды действует сторонняя сила, задающая направление движения зарядов (тока).

Перемещение зарядов на этом участке возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Эти силы приводят заряды в движение. Благодаря этому поддерживается ток в цепи. Действие сторонних сил характеризуется величиной, называемой электродвижущей силой источника тока (ЭДС), о которой поговорим чуть позднее.

Примером источника тока может служить обычная батарейка. Вы наверняка замечали, что на пальчиковых батарейках с одной стороны пишется «плюс», а с другой — «минус». Это означает, что электрический ток пойдет от положительной части батарейки к отрицательной. А почему ток выходит из одной части, но заходит в другую?

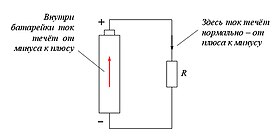
Для объяснения этого явления рассмотрим картинку ниже. Главным критерием рабочей электрической цепи является ее замкнутость, то есть вся цепь неразрывно связана. Подключим нашу батарейку (источник тока) к электрической цепи, которую также называют внешней электрической цепью.

Как мы видим на этом рисунке, на заряды внутри источника тока действует сторонняя сила ((F_{ст})), от плюса к плюсу) и сила электростатического поля ((F)), которая направлена от плюса к минусу. Без действия сторонних сил внутри источника положительный заряд будет двигаться от «+» к «-» (по направлению силы (F)).

Мы действуем сторонними силами так, чтобы он стал двигаться к «+» (по направлению (F_{ст})), то есть против сил электростатического поля. Тогда заряды вылетают из источника тока и далее по внешней цепи, уже под действием обычного электростатического поля, движутся по стандартным законам от «+» к «-». Это и есть наш долгожданный электрический ток – движущиеся заряды. Если бы мы не действовали сторонними силами, все заряды бы просто сидели на месте («+» окружили бы «-», и наоборот). То есть, сама сторонняя сила задает направление движения заряда.

После того как заряд выходит из источника тока, на него действует только одна сила F. Поэтому он обходит всю цепь и возвращается в этот же источник тока. Там на него вновь действует сторонняя сила, ну а дальше вы уже знаете.

Если бы в источнике тока не было сторонних сил, то все положительные заряды застряли бы у минуса.

Основные параметры источника тока

Как и любой другой элемент электрической цепи, источник тока обладает своими характеристиками, которые могут меняться в зависимости от условий использования. Главными характеристиками являются ЭДС источника тока (электродвижущая сила) и его внутреннее сопротивление.

ЭДС источника тока (ε) — это физический параметр, который характеризует работу сторонних сил ((А_{ст})), затраченную на перемещение зарядов (q) внутри источника.

(ε =frac{А_{ст}}{q}), где

(ε) – ЭДС источника тока (В);
(А_{ст})– работа сторонних сил (Дж);
(q) – заряд, помещенный внутри источника (Кл).

Внутреннее сопротивление определяет количество потерь энергии при прохождении тока через источник тока.

Стоит понимать, что внутреннее сопротивление появляется из-за неидеальности реальных предметов. Только у идеальных источников тока отсутствует внутреннее сопротивление.

Однако при расчете характеристик электрических схем никакой сложности не возникает, так как мы просто представляем, что в цепи появляется дополнительный резистор (на схемах обозначается прямоугольником и буквой R), сопротивление которого будет равняться внутреннему сопротивлению источника тока.

Раз уж мы затронули расчеты электрических схем, то пора вплотную к ним приблизиться.

Закон Ома для участка цепи

Какой ученый променял бильярд на физику?

Георг Ом рос в небогатой семье. Также он был довольно азартным человеком, любил играть в бильярд в компании друзей. В университетские годы Ом был лучшим игроком в бильярд среди студенческой молодежи, показывал прекрасные результаты в конькобежном спорте.

Но его очень манили точные науки: физика и математика. Однажды он смог собрать всю свою волю «в кулак» и начать проводить опыты в лаборатории обычной школы, где работал учителем. И так он окончательно вжился в статус ученого-физика. После этого он играл в бильярд только для получения удовольствия, а не использовал его как способ заработка.

Дальше мы с вами поговорим о напряжении на элементах электрической цепи, и, в частности, на источнике тока. Поэтому вспомним, что такое напряжение из темы «Законы постоянного тока». Напряжение – физическая величина, которая показывает, какую работу сторонние силы должны приложить, чтобы перенести заряд от одной точки до другой.

Так как у источника тока имеется внутреннее сопротивление, значит, внутри него также будет и напряжение. Чтобы найти его, воспользуемся законом Ома — умножим внутреннее сопротивление источника тока r на сам ток I и получим:

U_r = Ir.

Также мы можем найти напряжение, которое будет выделяться на внешней цепи. Для этого снова умножим ток I на общее сопротивление цепи R:

U_R = IR.

Оказывается, что не вся энергия источника тока уходит в цепь. Как раз таки та часть энергии, которая уходит на преодоление внутреннего сопротивления, и будет характеризовать потери. Тогда мы можем записать еще одну формулу для нахождения ЭДС источника тока:

ε = U_R+ U_r , где

ε – ЭДС источника тока (В);
U_R – напряжение на самой электрической цепи (В);
U_r – напряжение внутри источника тока (В).

Теперь давайте подставим вместо напряжений полученные формулы через токи и сопротивления и выразим силу тока. Так мы получим закон Ома для полной цепи:

(I=frac{ε}{R + r}) , где

I – ток в цепи (А);
ε – ЭДС источника тока (В);
R – сопротивление в цепи (Ом);
r – внутреннее сопротивление источника (Ом).

Сила тока в цепи с заданным источником тока (при неизменной ЭДС и с постоянным внутренним сопротивлением) зависит только от сопротивления внешней цепи R.

Где самое большое сопротивление в теле человека?

Самое большое электрическое сопротивление на теле человека — поверхность верхнего рогового слоя кожи человека. Оно может достигать 40000–100000 Ом. Но это не значит, что можно хвататься за оголенные провода голыми руками! Этого сопротивления далеко не достаточно, чтобы защитить человека от опасного электрического тока.

Резко уменьшают сопротивление человека потливость кожного покрова, переутомление, нервное возбуждение. Значение снижается до 800–1000 Ом. Поэтому даже самое небольшое напряжение может вызвать ожог кожи.

Задачи на данную тему встречаются в №12 ЕГЭ. Давайте рассмотрим один пример.

Задача. Найдите внутреннее сопротивление источника ЭДС, если сопротивление в цепи R = 4 Ом, а ЭДС ε=10 В. Сила тока в цепи 2 А.

Решение.Воспользуемся законом Ома для полной цепи и выразим из него внутреннее сопротивление источника ЭДС:

(I=frac{ε}{R + r}),
(r=frac{ε}{I}-R=frac{10}{2}-4=1) (Ом).

Ответ: 1 Ом

Короткозамкнутая цепь

Рассмотрим частный случай электрической цепи, в котором источник тока будет подключен сам на себя. Иначе говоря, он будет короткозамкнутым.

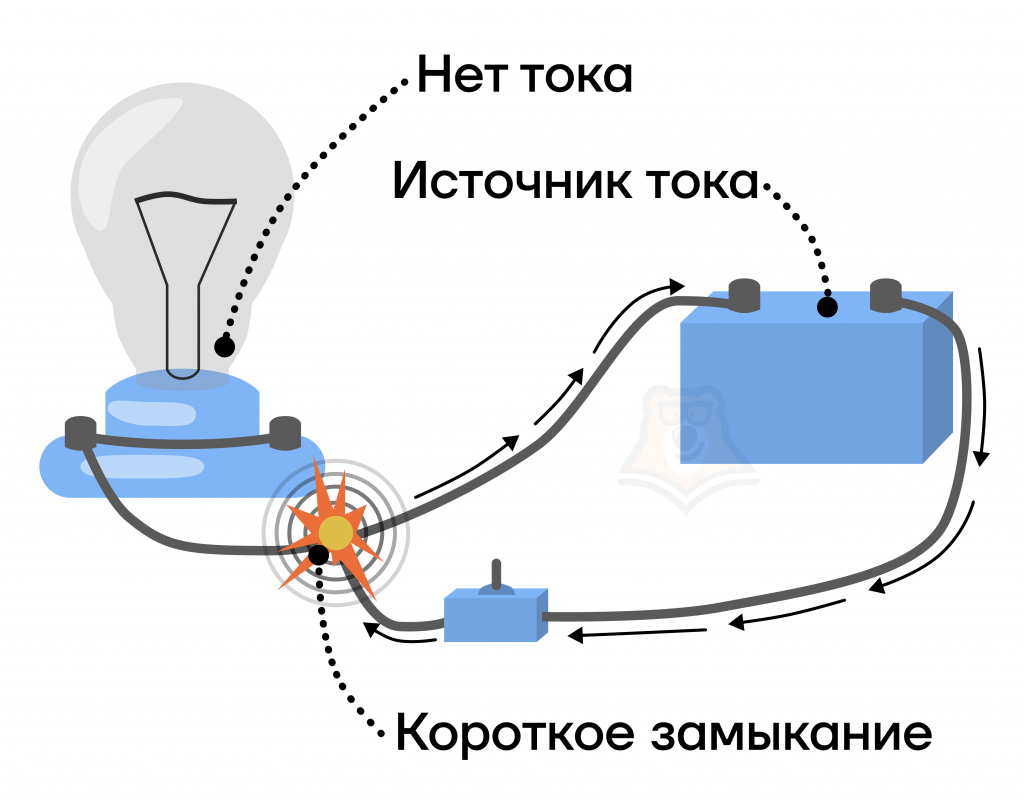
В этом случае отсутствует сопротивление внешней цепи и закон Ома для цепи будет выглядеть так:

(I_{кз}=frac{ε}{r}) , где

(I_{кз}) – ток короткого замыкания (А);
(ε) – ЭДС источника тока (В);
(r) – сопротивление источника ЭДС (Ом).

Короткое замыкание — это такой случай соединения проводов, при котором практически весь ток проходит по пустому проводу и возвращается в источник тока.

Короткое замыкание приводит к сильному нагреву, расплавлению металлов, а иногда и к пожарам.

К чему может привести авария среди электронов?

Если сравнить поток электронов с потоком машин, то ток короткого замыкания – это авария на автодороге. Один поток машин решил влезть в другой. В результате на дороге образовалась авария. Но машины продолжают налетать одна на другую (как в метель в Норильске).

При коротком замыкании сила тока будет увеличиваться до тех пор, пока отключающие механизмы не прекратят поступление силы тока.

Теперь, когда мы уже рассмотрели основные характеристики источника тока, можем перейти к мощности и КПД источника тока.

Мощность и КПД источника тока

Мы уже не раз говорили о том, что при протекании тока выделяется энергия. Источники тока не исключение. При подключении их к цепи на них выделяется энергия. При этом энергия выделяется и в самой цепи.

Чтобы найти мощность передачи энергии (P), выделяемой источником тока, необходимо умножить силу тока на ЭДС этого источника тока. Тогда получим:

(P_{ист}=εI), где

(P_{ист}) – мощность источника тока (Вт);
(ε) – ЭДС источника тока (В);
(I) – сила тока (А).

При этом часть этой мощности уходит на элементы внешней цепи, а другая часть – на преодоление внутреннего сопротивления источника тока:

(εI = I^2R + I^2r).

Тогда мощность, выделяемая на внешней цепи:

(P_R=I^2R).

А мощность, которая теряется на внутреннее сопротивление источника тока:

(P_r=I^2r).

Теперь давайте рассмотрим коэффициент полезного действия (КПД, ) источника тока. Как мы уже говорили ранее, часть ЭДС источника тока уходит на внутреннее сопротивление, а часть – на внешнюю цепь. При этом вспомним, что КПД – это отношение полезной мощности к затраченной.

Запишем формулы для мощности:

(P_{ист}=εI=I^2(R+r)),
(P_R=IU =I^2R).

Тогда КПД:

(eta=frac{IU}{εI}*100%=frac{U}{ε}*100%=frac{R}{R+r}*100%), где

(eta) – КПД источника тока;
(ε) – ЭДС источника тока (В);
(U) – напряжение на внешней цепи (В);
(I) – сила тока (А):
(R) – сопротивление на внешней цепи (Ом);
(r) – сопротивление источника тока (Ом).

Также задачи на тему ЭДС встречаются и в №16 ЕГЭ. Сложность данных задач заключается в установлении правильной зависимости величин друг от друга.

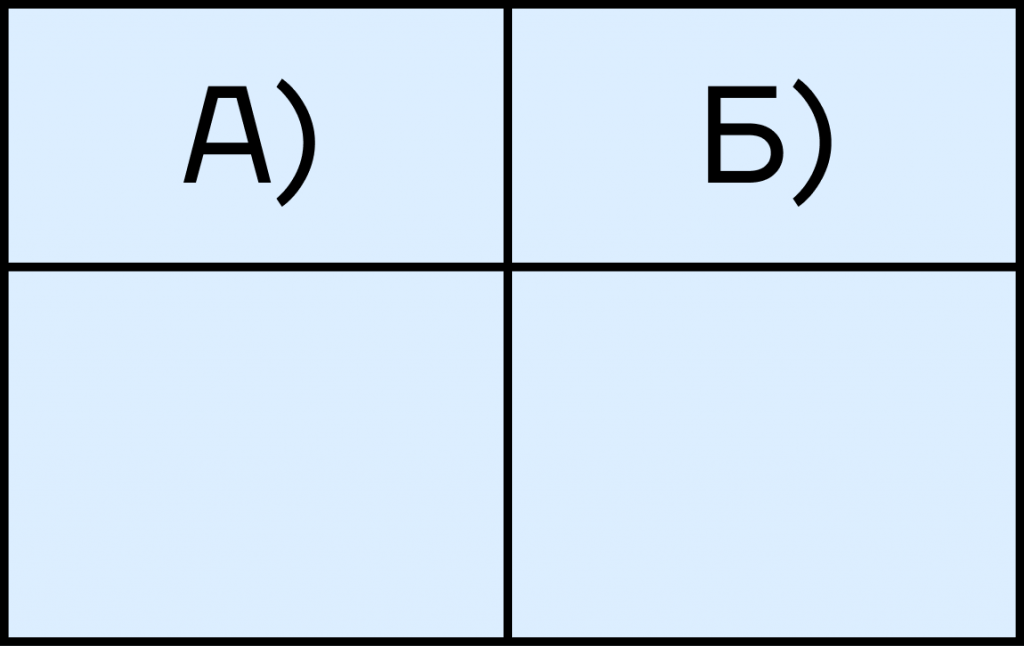
Задача.Определите, как изменятся сила тока (А) в цепи и сопротивление резистора (Б), если ЭДС источника тока заменить на такую же ЭДС, но с большим внутренним сопротивлением.
1) увеличится
2) уменьшится
3) не изменится

Решение.
Б) Внешнее сопротивление никак не зависит от источника тока. Поэтому оно не изменится — выбираем ответ 3.

А) Запишем закон Ома для полной цепи:
(I=frac{ε}{R + r})
При увеличении внутреннего сопротивления знаменатель увеличится. Следовательно, сила тока уменьшится, так что вариант 2 тоже нам подходит.

Ответ: 23

Мы с вами выяснили, что источники тока – элементы электрической цепи, без которых самой цепи не существовало бы. Хотя, конечно, она бы существовала, но была бы бесполезной. Однако и они «не без греха», так как существует опасное внутреннее сопротивление, которое является головной болью для многих инженеров. А все потому, что оно снижает КПД источников тока. Дальше вы можете ознакомиться с полноценными электрическими схемами и посмотреть, как ток ведет себя за пределами источника тока.

Термины

Напряжение – произведение сопротивления элемента и протекающего через него тока.

Резистор (или резистивный элемент) – элемент электрической цепи, который может только потреблять энергию и не может ее создавать.

Сторонние силы — это все внешние силы, воздействующие на заряд.

Электростатическое поле — невидимое поле, создаваемое постоянными электрическими зарядами.

Фактчек

ЭДС источника тока (ε) — это физический параметр, который характеризует работу, затраченную на перемещение зарядов внутри источника сторонними силами: (ε =frac{А_{cт}}{q}).
Внутреннее сопротивление (r) — определяет количество потерь энергии при прохождении тока через источник тока.
Закон Ома для полной цепи: Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее полному сопротивлению: (I =frac{ε}{R + r}).
Предельное значение силы тока для данного источника тока называется током короткого замыкания: (I_{кз} =frac{ε}{r}).
Полная мощность цепи — это есть мощность источника тока: (P_ист=εI).

Проверь себя

Задание 1.
Как рассчитывается ЭДС источника тока?

(ε =frac{А_{ст}}{q})
(ε =frac{U}{q})
(ε =frac{А_{ст}}{I})
(ε =frac{А_{ст}}{qt})

Задание 2.
Короткое замыкание — это:

Соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи.
Соединение концов участка цепи проводником, сопротивление которого очень велико по сравнению с сопротивлением участка цепи.
Соединение концов участка цепи проводником, сопротивление которого не зависит от сопротивления участка цепи.
Отсутствие электрического тока в цепи.

Задание 3.
Чему равно ЭДС источника тока?

(ε = U_R- U_r)
(ε = U_R+ U_r)
(ε = U_R U_r)
(ε = U_R)

Задание 4.
От чего зависит сила тока в цепи с заданным источником тока?

от внутреннего сопротивления цепи
от внутреннего сопротивления источника тока
от внешнего сопротивления цепи
не зависит ни от каких величин

Задание 5.
Где самое большое сопротивление в человеке?

в сердце
в пищеварительной системе
на коже
в голове

Ответы: 1. — 1; 2. — 1; 3. — 2; 4. — 3; 5. — 3.

Источник

Если в проводнике
создать электрическое поле и не принять
мер для его поддержания, то, как было
уже установлено, перемещение носителей
заряда приведет очень быстро к тому,
что поле внутри проводника исчезнет и,
следовательно, ток прекратиться. Для
того чтобы поддерживать ток достаточно
долго, нужно от конца проводника с
меньшим потенциалом (носители тока
предполагаются положительными) непрерывно
отводить приносимые сюда заряды, а к
концу с большим потенциалом непрерывно
их подводить. Т.е. необходимо осуществить
круговорот зарядов, при котором они
двигались бы по замкнутому пути (13.2).
Циркуляция вектора напряженности
электростатического поля, как известно
равна нулю. Поэтому в замкнутой цепи
наряду с участками, на которых положительные
заряды движутся в сторону убывания
потенциала, должны иметься участки, на
которых перенос положительных зарядов
происходит в направлении возрастания
потенциала, т.е. против сил электростатического
поля. Перемещение, зарядов на этих
участках возможно лишь с помощью сил
не электростатического происхождения,
называемых сторонними
силами.

Таким образом, для
поддержания тока необходимы сторонние
силы, действующие либо на всем протяжении
цепи, либо на отдельных ее участках.
Они могут быть обусловлены химическими
процессами, диффузией носителей заряда
в неоднородной среде или через границу
двух разнородных, веществ, электрическими
(но не электростатическими) полями,
порожденными меняющимися во времени
магнитными полями и т.д.

Например, в
гальванических элементах и аккумуляторах
происхождение сторонних сил – химическое.
В генераторах электрического тока
сторонние силы – это силы Лоренца,
действующие со стороны магнитного поля.

Устройства,
обеспечивающие возникновение и действие
сторонних сил, называют источниками
тока. В
этих устройствах происходит разделение
разноимённых зарядов. Под действием
сторонних сил электрические заряды
внутри источника тока движутся в
направлении, противоположном действию
сил электрического поля. В результате
этого на полюсах источника тока
поддерживается постоянная разность
потенциалов.

Подобно тому,
как насос сообщает энергию воде, поднимая
её вверх, источник тока сообщает энергию
заряженным частицам. Как для работы
насоса, поднимающего воду, так и для
работы источника тока необходима
энергия. В зависимости от типа источника
тока, в нём происходит преобразование
механической, внутренней или ещё
какой-либо энергии в электрическую. В
зависимости от вида энергии, которая
внутри источника тока преобразуется в
электрическую энергию, различают
механические, химические, тепловые
источники тока.

Сторонние силы
совершают работу по перемещению
электрических зарядов.

Физическая
величина, определяемая работой,
совершаемой сторонними силами при
перемещении единичного положительного
заряда, называется
электродвижущей силой (э.д.с.) ε, действующей
в цепи.

Сторонняя сила
F_ст,
действующая на заряд q₀,
может быть выражена как

F_ст
= E_ст
q₀,

где E_ст
– напряжённость поля сторонних сил.
Работа же сторонних сил по перемещению
заряда q₀
на замкнутом участке цепи равна

(13.6)

Разделив на q₀,
получим выражение для э.д.с., действующей
в цепи:

(13.7)

т.е. эдс, действующая
в замкнутой цепи, может быть определена
как циркуляция вектора напряжённости
поля сторонних сил. ЭДС, действующая на
участке 1-2, равна

На
заряд q₀помимо
сторонних сил действует также силы
электростатического поля F_э
= E
q₀.
Таким образом, результирующая сила,
действующая в цепи на заряд q₀,
равна

F
=F_ст
+ F_э
= q₀(Е_ст
+ E_э)
(13.8)

Рисунок – 13.3

Работа, совершаемая
результирующей силой над зарядом q₀на участке 1-2, равна

(13.9)

Используя выражения

и ,
можем записать

А₁₂
= q₀ε₁₂
+ q₀
(φ₁-φ₂)
(13.10)

Для замкнутой цепи
работа электростатических сил равна
нулю, поэтому в данном случае
А₁₂
= q₀ε₁₂

Напряжением
U
на участке 1-2 называется физическая
величина, определяемая работой,
совершаемой суммарным полем кулоновских
и сторонних сил при перемещении
положительного единичного заряда на
данном участке цепи.

U₁₂
= ε₁₂
+ (φ₁-φ₂)
(13.11)

Соседние файлы в папке Физика

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 декабря 2022 года; проверки требуют 7 правок.

У этого термина существуют и другие значения, см. Сила (значения).

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил (то есть любых сил, кроме электростатических и диссипативных), действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура^[1]^[2].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил ${vec E}_{{ex}}$ , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре ЭДС будет равна:

${displaystyle {mathcal {E}}=oint limits _{L}{vec {E}}_{ex}cdot d{vec {l}}}$

где — элемент контура.

Несмотря на наличие слова «сила» в наименовании понятия, электродвижущая сила не является одной из сил в физике и не имеет размерности силы.

ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах.
Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.

ЭДС и закон Ома[править | править код]

Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи имеет вид^[1]

${displaystyle varphi _{1}-varphi _{2}+{mathcal {E}}=IR,}$

где ${displaystyle varphi _{1}-varphi _{2}}$ — разность между значениями потенциала в начале и в конце участка цепи, — сила тока, текущего по участку, а — сопротивление участка.

Если точки 1 и 2 совпадают (цепь замкнута), то ${displaystyle varphi _{1}-varphi _{2}=0}$ и предыдущая формула переходит в формулу закона Ома для замкнутой цепи^[1]:

где теперь — полное сопротивление всей цепи.

В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи ( $R_{e}$ ) и внутреннего сопротивления самого́ источника тока (). С учётом этого следует:

${displaystyle {mathcal {E}}=IR_{e}+Ir.}$

ЭДС источника тока[править | править код]

Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:

${displaystyle varphi _{1}-varphi _{2}=IR.}$

Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода ${displaystyle varphi _{a}}$ и катода можно записать:

${displaystyle varphi _{a}-varphi _{k}=IR_{e},}$

где как и ранее $R_{e}$ — сопротивление внешнего участка цепи.

Поделив данное соотношение на закон Ома для замкнутой цепи, записанный в виде ${displaystyle {mathcal {E}}=I(R_{e}+r)}$ , мы получим:

${displaystyle {frac {varphi _{a}-varphi _{k}}{mathcal {E}}}={frac {R_{e}}{R_{e}+r}}}$

и затем ${displaystyle varphi _{a}-varphi _{k}={frac {R_{e}}{R_{e}+r}}{mathcal {E}}.}$

Из последнего соотношения следуют два вывода:

Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока ${displaystyle varphi _{a}-varphi _{k}}$ меньше, чем ЭДС источника.
В предельном случае, когда $R_{e}$ бесконечно (цепь разорвана), выполняется ${displaystyle {mathcal {E}}=varphi _{a}-varphi _{k}.}$

Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи^[1].

ЭДС индукции[править | править код]

Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

${displaystyle {mathcal {E}}=-{frac {dPhi }{dt}},}$

где Phi — поток магнитного поля через указанную поверхность. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.

Неэлектростатический характер ЭДС[править | править код]

Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектростатической природы, преодолевающей силу электрического отталкивания

Как показано на рисунке, электрический ток, нормальное направление которого — от «плюса» к «минусу», внутри источника ЭДС (например, внутри гальванического элемента) течёт в противоположном направлении. Направление от «плюса» к «минусу» совпадает с направлением электростатической силы, действующей на положительные заряды. Поэтому для того, чтобы заставить ток течь в противоположном направлении, необходима дополнительная сила неэлектростатической природы (центробежная сила, сила Лоренца, силы химической природы, сила со стороны вихревого электрического поля) которая бы преодолевала силу со стороны электростатического поля. Диссипативные силы, хотя и противодействуют электростатическому полю, не могут заставить ток течь в противоположном направлении, поэтому они не входят в состав сторонних сил, работа которых используется в определении ЭДС.

Сторонние силы[править | править код]

Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца^[3].

См. также[править | править код]

Правила Кирхгофа

Примечания[править | править код]

↑ ¹ ² ³ ⁴ Сивухин Д. В. Общий курс физики. — М.: Физматлит, МФТИ, 2004. — Т. III. Электричество. — С. 193—194. — 656 с. — ISBN 5-9221-0227-3.
↑ Калашников С. Г. Общий курс физики. — М.: Гостехтеориздат, 1956. — Т. II. Электричество. — С. 146, 153. — 664 с.
↑ Кабардин О. Ф. Физика. – М., Просвещение, 1985. – Тираж 754 000 экз. – с. 131

Источник

Определение и формула ЭДС

Закон Ома для произвольного участка цепи

Единицы измерения

Примеры решения задач

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

Сторонняя сила

Закон Ома для полной цепи

КПД электрической цепи

Закон Ома для неоднородного участка

На этой странице вы узнаете

Источник тока

Основные параметры источника тока

Закон Ома для участка цепи

Короткозамкнутая цепь

Мощность и КПД источника тока

Термины

Фактчек

Проверь себя

ЭДС и закон Ома[править | править код]

ЭДС источника тока[править | править код]

ЭДС индукции[править | править код]

Неэлектростатический характер ЭДС[править | править код]

Сторонние силы[править | править код]

См. также[править | править код]

Примечания[править | править код]

Вам также может понравиться

Как составить композиционный план произведения

Файлы облако мэйл как найти

Найти как нарисовать виноград

Добавить комментарий Отменить ответ