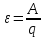Как найти работу сторонних сил в цепи - Сайт, где вы сможете решить свои вопросы

Определение 1

Во время протекания тока по однородному участку цепи электрическое поле совершает работу. За пройденное время Δt по цепи имеется заряд Δq=IΔt.

Электрическое поле выделенного участка выполняет работу, формулу которой мы запишем так: ΔA=(φ1–φ2) Δq=Δφ12IΔt=UIΔt, где U=Δφ12 – напряжение. Такая величина называется работой электрического тока.

Обе части формулы RI=U выражают закон Ома для однородного участка цепи с сопротивлением R, умноженным на IΔt. В итоге получим соотношение RI2Δt=UIΔt=ΔA, выражающее закон сохранения энергии для однородного участка цепи. Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике. ΔQ=ΔA=RI2Δt.

Закон Джоуля-Ленца

Дж. Джоуль и Э. Ленц установили закон преобразования работы тока в тепло.

Определение 2

Формула мощности электрического тока (измеряется в амперах) записывается в виде отношения изменения работы тока ΔA за определенный промежуток времени Δt:

P=∆A∆t=UI=I2R=U2R.

Работа и мощность электрического тока обратно пропорциональны.

По таблице СИ понятно, в чем измеряется мощность: в ваттах (ВТ), а работа в Джоулях (Дж).

Перейдем к рассмотрению полной цепи постоянного тока, которая состоит из источника с электродвижущей силой ε и внутренним сопротивлением r на участке R. Запись основного закона Ома для полной цепи имеет вид (R + r)I=ε. При умножении обеих частей на Δq=IΔt получаем, что соотношение для выражения сохранения энергии полной цепи постоянного тока запишется: R I2Δt+r I2Δt=ε IΔt=ΔAст. Из левой части видно, что ΔQ=R I2Δt обозначает выделяющееся тепло на внешнем участке за промежуток времени Δt, а ΔQист=rI2Δt – внутри источника за тот же время.

εIΔt – это обозначение работы сторонних сил ΔAст,действующих внутри. Если имеется замкнутая цепь, тогда ΔAстпереходит в тепло, которое выделяется во внешней цепи (ΔQ) и внутри источника (ΔQист).

ΔQ+ΔQист=ΔAст=εIΔt.

Работа сторонних сил

Работа электрического поля не входит в данное соотношение, так как в замкнутой цепи работа не совершается, следовательно, тепло идет только от внутренних сторонних сил. В данном случае электрическое поле перераспределяет тепло по всем участкам цепи.

Внешняя цепь может иметь не только проводник с R сопротивлением, но и механизм, потребляющий мощность. Такой случай говорит о том, что R эквивалентно сопротивлению нагрузки. Энергия, которая выделяется по внешней цепи, преобразуется в тепло и другие виды энергии.

Определение 3

Работа, совершаемая сторонними силами за единицу времени, равняется Pист=εI=ε2R+r. Внешняя цепь характеризуется мощностью P=RI2=εI-rI2=ε2R(R+r)2.

Коэффициентом полезного источника называют отношение η=PPист, записываемое как η=PPист=1-rεI=RR+r.

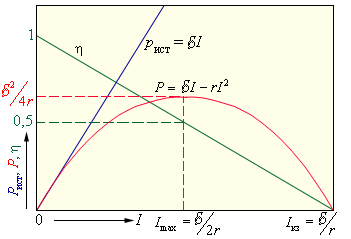
Рисунок 1.11.1 показывает зависимость Pист, полезной Р, выделяемой во внешней цепи, кпд η от тока I для источника с ЭДС, равной ε, и внутренним сопротивлением r. Изменение тока в цепи происходит в пределах от I=0( при R=∞) до I=Iкз=εr( при R=0).

Рисунок 1.11.1. Зависимость мощности источника Pист, мощности во внешней цепи Р и КПД источника η от силы тока.

Приведенные графики показывают, что максимальная мощность во внешней цепи может быть достигнута при R=r и запишется Pmax=ε24r. Формула тока в цепи будет иметь вид Imax=12Iкз=ε2r, где КПД источника не превышает 50%. При I→0 может достигаться максимальное значение КПД, тогда сопротивление R→∞. При коротком замыкании значение мощности Р=0. Тогда она только выделяется внутри источника, что грозит перегревом, причем КПД обращается в ноль.

Источник

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд q = It . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0) , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При r = 0 формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина R + r неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный (r = 0) .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома U = IR справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор R + r ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд q = It , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем U = IR — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на R + r :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда Кл.

Ответ: 1500.

Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Содержание:

Определение и формула ЭДС
Закон Ома для произвольного участка цепи
Единицы измерения
Примеры решения задач

Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал
(учтем, что носители тока предполагаются положительными зарядами) постоянно убирались доставляемые током заряды, при этом к концу с
большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны
перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения.
Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи
или на отдельных участках цепи.

Определение и формула ЭДС

Определение

Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется
электродвижущей силой (ЭДС), действующей в цепи или на участке цепи. ЭДС обозначается
$varepsilon$ . Математически определение ЭДС запишем как:

$$varepsilon=frac{A}{q}(1)$$

где A – работа сторонних сил, q – заряд, над которым производится работа.

Электродвижущая сила источника численно равна разности потенциалов на концах элемента, если он разомкнут, что дает возможность измерить ЭДС по напряжению.

ЭДС, которая действует в замкнутой цепи, может бытьопределена как циркуляция вектора напряжённости сторонних сил:

$$varepsilon=oint_{L} bar{E}^{*} d bar{l}(2)$$

где $bar{E}^{*}$ – напряженность поля сторонних сил. Если напряженность поля сторонних
сил не равна нулю только в части цепи, например, на отрезке 1-2, тогда интегрирование в выражении (2) можно вести только по
данному участку. Соответственно, ЭДС, действующая на участке цепи 1-2 определяется как:

$$varepsilon=int_{1}^{2} bar{E}^{*} d bar{l}(3)$$

Формула (2) дает самое общее определение ЭДС, которое можно использовать для любых случаев.

Закон Ома для произвольного участка цепи

Участок цепи, на котором действуют сторонние силы, называют неоднородным. Для него выполняется равенство:

$$U_{12}=varphi_{1}-varphi_{2}+varepsilon_{12}(4)$$

где U₁₂=IR₂₁ – падение напряжения (или напряжение) на участке цепи 1-2 (I-сила тока);
$varphi_{1}-varphi_{2}$ – разность потенциалов концов участка;
$varepsilon_12$ – электродвижущая сила, которую содержит участок цепи.
$varepsilon_12$ равна алгебраической сумме ЭДС всех источников, которые находятся на данном участке.

Следует учитывать, что ЭДС может быть положительной и отрицательной. ЭДС называют положительной, если она увеличивает потенциал в
направлении тока (ток течет от минуса к плюсу источника).

Единицы измерения

Размерность ЭДС совпадает с размерностью потенциала. Основной единицей измерения ЭДС в системе СИ является: [$varepsilon$]=В

1В=1Дж/1Кл

Примеры решения задач

Пример

Задание. Электродвижущая сила элемента равна 10 В. Он создает в цепи силу тока равную 0,4 А.
Какова работа, которую совершают сторонние силы за 1 мин?

Решение. В качество основы для решения задачи используем формулу для вычисления ЭДС:

$$varepsilon=frac{A}{q}(1.1)$$

Заряд, который проходит в рассматриваемой цепи за 1 мин. можно найти как:

$$q=I Delta t(1.2)$$

Выразим из (1.1) работу, используем (1.2) для вычисления заряда, получим:

$$A=varepsilon I Delta t$$

Переведем время, данной в условиях задачи в секунды ($Delta t$ мин=60 с), проведем вычисления:

$A=10 cdot 0,4 cdot 60=240$ (Дж)

Ответ. A=240 Дж

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

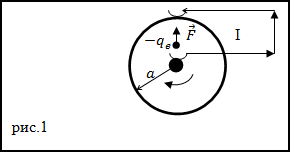
Задание. Металлический диск, имеющий радиус a, вращается с угловой скоростью
$omega$, включен в электрическую цепь при
помощи скользящих контактов, которые касаются оси диска и его окружности (рис.1). Какой будет ЭДС, которая появится между осью
диска и его наружным краем?

Решение. В условиях, которые описаны в задаче, на каждый электрон проводника действует центробежная сила (F)
которая является сторонней. Вследствие ее действия, в диске возникает ЭДС и между осью диска и его наружным краем появляется напряжение.
Формулу для вычисления центробежной силы запишем как:

$$F=m r omega^{2}(2.1)$$

где m – масса электрона, r – расстояние от оси диска.Fдействует на заряженную частицу (электрон), следовательноучитывая (2.1), имеем:

$$E^{*}=frac{F}{q}=frac{m r omega^{2}}{q}$$

где q – заряд электрона.

В соответствии с формулой, определяющей ЭДС участка цепи, получаем:

$$varepsilon=int_{1}^{2} bar{E} d bar{l}=int_{0}^{a} E^{*} d r=int_{0}^{a} frac{m r omega^{2}}{q} d r=frac{m r omega^{2} a^{2}}{2 q}$$

Ответ. $varepsilon=frac{m r omega^{2} a^{2}}{2 q}$

Читать дальше: Формулы по физике.

Источник

❶❼ Электродвижущая сила. Работа сторонних сил

Электродвижущая
сила (ЭДС)
— физическая величина, характеризующая
работу сторонних (непотенциальных) сил
в источниках постоянного или переменного
тока. В замкнутом проводящем контуре
ЭДС равна работе этих сил по перемещению
единичного положительного заряда вдоль
контура.

ЭДС
можно выразить через напряжённость
электрического поля сторонних сил
(Eex). В замкнутом контуре (L) тогда ЭДС
будет равна:

где dl — элемент
длины контура.

ЭДС
так же, как и напряжение, измеряется в
вольтах. Можно говорить об электродвижущей
силе на любом участке цепи. Это удельная
работа сторонних сил не во всем контуре,
а только на данном участке. ЭДС
гальванического элемента есть работа
сторонних сил при перемещении единичного
положительного заряда внутри элемента
от одного полюса к другому. Работа
сторонних сил не может быть выражена
через разность потенциалов, так как
сторонние силы непотенциальны и их
работа зависит от формы траектории.
Так, например, работа сторонних сил при
перемещении заряда между клеммами тока
вне самого источника равна нулю.

Величина,
равная работе сторонних сил по перемещению
единичного положительного заряда в
цепи, называется электродвижущей силой
(ЭДС), действующей в цепи:

Стороннюю
силу, действующую на заряд, можно
представить в виде:

– напряженность
поля сторонних сил.

Работа
сторонних сил на участке 1 – 2:

Тогда

Для
замкнутой цепи:

❶❽ Законы Ома
для участка цепи, неоднородного участка
цепи, замкнутой системы.

Цепь
постоянного тока можно разбить на
отдельные участки. Те участки, на которых
не действуют сторонние силы (т. е. участки,
не содержащие источников тока), называются
однородными.
Участки, включающие источники тока,
называются неоднородными.

При
перемещении единичного положительного
заряда по некоторому участку цепи работу
совершают как электростатические
(кулоновские), так и сторонние силы.
Работа электростатических сил равна
разности потенциалов Δφ12 = φ1 – φ2 между
начальной (1) и конечной (2) точками
неоднородного участка. Работа сторонних
сил равна по определению электродвижущей
силе 12, действующей на данном участке.
Поэтому полная работа равна

U₁₂
= φ₁
– φ₂
+
₁₂.

Величину
U12 принято называть напряжением на
участке цепи 1–2. В случае однородного
участка напряжение равно разности
потенциалов:

U12
= φ1 – φ2.

Немецкий
физик Г. Ом в 1826 году экспериментально
установил, что сила тока I, текущего по
однородному металлическому проводнику
(т. е. проводнику, в котором не действуют
сторонние силы), пропорциональна
напряжению U на концах проводника:

где
R = const.

Величину
R принято называть электрическим
сопротивлением. Проводник, обладающий
электрическим сопротивлением, называется
резистором. Данное соотношение выражает
закон
Ома для однородного участка цепи:
сила тока в проводнике прямо пропорциональна
приложенному напряжению и обратно
пропорциональна сопротивлению проводника.

В
СИ единицей электрического сопротивления
проводников служит ом (Ом). Сопротивлением
в 1 Ом обладает такой участок цепи, в
котором при напряжении 1 В возникает
ток силой 1 А.

Для
участка цепи, содержащего ЭДС, закон
Ома записывается в следующей форме:

IR
= U12 = φ1 – φ2 +

= Δφ12 +

.

Это
соотношение принято называть обобщенным
законом Ома или законом
Ома для неоднородного участка цепи.

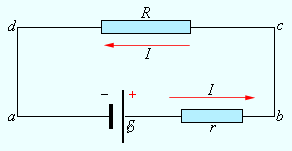
На
рисунке изображена замкнутая цепь
постоянного тока. Участок цепи (cd)
является однородным.

По
закону Ома: IR = Δφcd.

Участок
(ab) содержит источник тока с ЭДС, равной
.

По
закону Ома для неоднородного участка,
Ir
= Δφab +.

Сложив
оба равенства, получим:

I
(R
+ r)
= Δφcd
+ Δφab
+.

Но
Δφcd = Δφba = – Δφab. Поэтому

Эта
формула выражет закон Ома
для полной цепи:
сила тока в полной цепи равна электродвижущей
силе источника, деленной на сумму
сопротивлений однородного и неоднородного
участков цепи.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
11.04.2015501.76 Кб37kr.doc
#
#

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 декабря 2022 года; проверки требуют 7 правок.

У этого термина существуют и другие значения, см. Сила (значения).

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил (то есть любых сил, кроме электростатических и диссипативных), действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура^[1]^[2].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил ${vec E}_{{ex}}$ , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре ЭДС будет равна:

${displaystyle {mathcal {E}}=oint limits _{L}{vec {E}}_{ex}cdot d{vec {l}}}$

где — элемент контура.

Несмотря на наличие слова «сила» в наименовании понятия, электродвижущая сила не является одной из сил в физике и не имеет размерности силы.

ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах.
Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.

ЭДС и закон Ома[править | править код]

Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи имеет вид^[1]

${displaystyle varphi _{1}-varphi _{2}+{mathcal {E}}=IR,}$

где ${displaystyle varphi _{1}-varphi _{2}}$ — разность между значениями потенциала в начале и в конце участка цепи, — сила тока, текущего по участку, а — сопротивление участка.

Если точки 1 и 2 совпадают (цепь замкнута), то ${displaystyle varphi _{1}-varphi _{2}=0}$ и предыдущая формула переходит в формулу закона Ома для замкнутой цепи^[1]:

где теперь — полное сопротивление всей цепи.

В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи ( $R_{e}$ ) и внутреннего сопротивления самого́ источника тока (). С учётом этого следует:

${displaystyle {mathcal {E}}=IR_{e}+Ir.}$

ЭДС источника тока[править | править код]

Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:

${displaystyle varphi _{1}-varphi _{2}=IR.}$

Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода ${displaystyle varphi _{a}}$ и катода можно записать:

${displaystyle varphi _{a}-varphi _{k}=IR_{e},}$

где как и ранее $R_{e}$ — сопротивление внешнего участка цепи.

Поделив данное соотношение на закон Ома для замкнутой цепи, записанный в виде ${displaystyle {mathcal {E}}=I(R_{e}+r)}$ , мы получим:

${displaystyle {frac {varphi _{a}-varphi _{k}}{mathcal {E}}}={frac {R_{e}}{R_{e}+r}}}$

и затем ${displaystyle varphi _{a}-varphi _{k}={frac {R_{e}}{R_{e}+r}}{mathcal {E}}.}$

Из последнего соотношения следуют два вывода:

Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока ${displaystyle varphi _{a}-varphi _{k}}$ меньше, чем ЭДС источника.
В предельном случае, когда $R_{e}$ бесконечно (цепь разорвана), выполняется ${displaystyle {mathcal {E}}=varphi _{a}-varphi _{k}.}$

Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи^[1].

ЭДС индукции[править | править код]

Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

${displaystyle {mathcal {E}}=-{frac {dPhi }{dt}},}$

где Phi — поток магнитного поля через указанную поверхность. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.

Неэлектростатический характер ЭДС[править | править код]

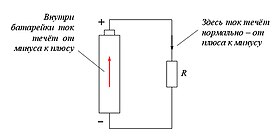
Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектростатической природы, преодолевающей силу электрического отталкивания

Как показано на рисунке, электрический ток, нормальное направление которого — от «плюса» к «минусу», внутри источника ЭДС (например, внутри гальванического элемента) течёт в противоположном направлении. Направление от «плюса» к «минусу» совпадает с направлением электростатической силы, действующей на положительные заряды. Поэтому для того, чтобы заставить ток течь в противоположном направлении, необходима дополнительная сила неэлектростатической природы (центробежная сила, сила Лоренца, силы химической природы, сила со стороны вихревого электрического поля) которая бы преодолевала силу со стороны электростатического поля. Диссипативные силы, хотя и противодействуют электростатическому полю, не могут заставить ток течь в противоположном направлении, поэтому они не входят в состав сторонних сил, работа которых используется в определении ЭДС.

Сторонние силы[править | править код]

Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца^[3].

См. также[править | править код]

Правила Кирхгофа

Примечания[править | править код]

↑ ¹ ² ³ ⁴ Сивухин Д. В. Общий курс физики. — М.: Физматлит, МФТИ, 2004. — Т. III. Электричество. — С. 193—194. — 656 с. — ISBN 5-9221-0227-3.
↑ Калашников С. Г. Общий курс физики. — М.: Гостехтеориздат, 1956. — Т. II. Электричество. — С. 146, 153. — 664 с.
↑ Кабардин О. Ф. Физика. – М., Просвещение, 1985. – Тираж 754 000 экз. – с. 131

Источник

Закон Джоуля-Ленца

Работа сторонних сил

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

Сторонняя сила

Закон Ома для полной цепи

КПД электрической цепи

Закон Ома для неоднородного участка

Определение и формула ЭДС

Закон Ома для произвольного участка цепи

Единицы измерения

Примеры решения задач

❶❼ Электродвижущая сила. Работа сторонних сил

ЭДС и закон Ома[править | править код]

ЭДС источника тока[править | править код]

ЭДС индукции[править | править код]

Неэлектростатический характер ЭДС[править | править код]

Сторонние силы[править | править код]

См. также[править | править код]

Примечания[править | править код]

Вам также может понравиться

Как исправить ошибку в бухгалтерском учете прошлого периода

Как найти координаты третьего вектора

Садится аккумулятор в машине как найти утечку

Добавить комментарий Отменить ответ