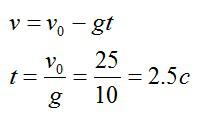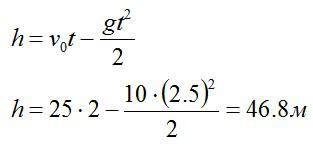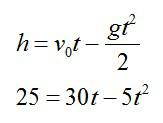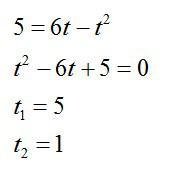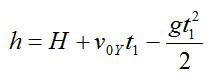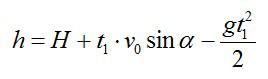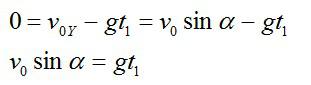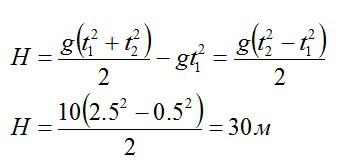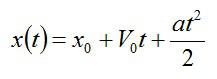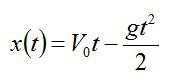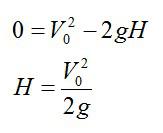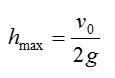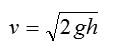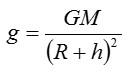- Авторы
- Резюме
- Файлы
Иванов Е.М.
Показано, что работа подъема тела в однородном поле тяжести всегда больше величины потенциальной энергии mgh. Величина работы имеет минимум, величина которого зависит от способа подъема тела.
В школьных [1] и вузовских [2-4] курсах физики утверждается, что если тело массы m равномерно поднимать вверх на высоту h с помощью силы F=mg, то сила совершает положительную работу AF=mgh, равную потенциальной энергии П=mgh, а сила тяжести отрицательную работуAP=-mgh [1]. Рассматривается также случай бросания тела вертикально вверх с начальной скоростью V0, обеспечивающей подъем тела на высоту h на основании закона сохранения и превращения энергии: K=П или . Работу бросания считают равной
. В этих безобидных, на первый взгляд, утверждениях, содержится нечто, противоречащее одному из положений физики. В физике используется понятие КОЭФФИЦИЕНТА ПОЛЕЗНОГО ДЕЙСТВИЯ (η ) – КПД. КПД не может быть больше единицы. КПД всегда меньше единицы, поскольку часть энергии превращается тоже в энергию, но не в ту, что нужна, и поэтому теряется для полезного использования. КПД всегда меньше единицы вследствие самой физической природы вещей и явлений. Если же записать КПД для выше приведенных случаев подъема тела на высоту h, то получим:
. Рассмотрим более подробно ряд случаев подъема тела на высоту h.
§ 1. Рассмотрим движение тела, брошенного вертикально вверх с начальной скоростью V0, за счет действия мгновенной силы в виде 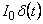
– δ- функция Дирака [7, 8]. Величину I0 будем называть единичным импульсом силы, численно равным количеству движения (импульсу), полученным телом I0=mV0. Дифференциальное уравнение движения (II закон Ньютона) имеет вид:
(1)
при нулевых начальных условиях:
;
(2)
Где x– вертикальная координата, отсчитываемая от поверхности Земли. Для решения задачи воспользуемся двусторонним преобразованием Лапласа [9]
(3)
Для решения этой задачи используется дифференциальное уравнение для односторонней функции где H(t) – единичная (ступенчатая) функция Хевисайда [8, 9]. Тогда производные функции x*(t) имеют вид [9]
;
После соответствующих преобразований, решение получается в следующем виде
(4)
Вычислим работу, совершаемую силами
(5)
Вычисляя интегралы, получим [9]
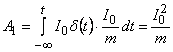
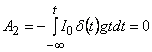
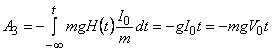
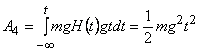
Работа, совершаемая силами, запишется в виде:
(6)
Работа, совершенная единичным импульсом силы I0=mV0 (или начальная энергия, полученная телом) будет равна
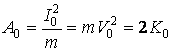
где – начальная кинетическая энергия тела. Время подъема до максимальной высоты
, а максимальная высота подъема
. Подставляя в выражение (6) значение t0, получим конечное значение совершенной работы:
(8)
Поскольку начальная энергия полученная телом A0=2K0, то КПД процесса бросания тела вертикально вверх будет равен
То, что начальная энергия тела A0=2K0 можно объяснить эффектом удвоения массы (силы тяжести) в случае внезапно приложенной нагрузки при бросании [5, 10].
§ 2. Рассмотрим случай движения тела вертикально вверх под действием постоянной вертикальной силы тяги FT. Уравнение движения (II закон Ньютона) запишется в следующем виде
(9)
Если FT=mg, то правая часть тождественно равна нулю, и движения тела вверх не происходит, но в этом случае сила давления тела на опору (например, на поверхность Земли) равна нулю, поскольку сила тяги нейтрализует «тяжелую» массу, и тело находится в квазиневесомом состоянии (состояние левитации). Обозначим силу тяги, равную mg, значком “Л”: FЛ=mg. Если сила тяги больше mg на величину ΔF, то уравнение (9) можно переписать в виде
или
(10)
Таким образом, часть силы тяги FЛ =mg не будет принимать непосредственного участия в работе по подъему тела вверх. Тело будет подниматься вверх только благодаря действию силы ΔF с ускорением . За время t высота подъема будет равна
(11)
Работа подъема составит величину, равную
(12)
Поскольку есть импульс силы, численно равный импульсу (количеству движения), полученному телом
, где V1 – скорость тела в момент времени t, то можно записать
.
Однако чтобы остановить тело на данной высоте h, необходимо еще совершить работу торможения, численно равную кинетической энергии, приобретенной телом ;
(13)
Отдельного разговора заслуживает вопрос о том, что же делает другая часть силы тяги FЛ=mg? Ведь она не принимает участия в подъеме тела на высоту h, она лишь нейтрализует силу тяжести, обеспечивая условия левитации. Можно записать баланс импульсов сил в виде:
(14)
Возведя обе части равенства в квадрат и разделив на 2m, получим баланс энергий (работ):
(15)
Работу, совершаемую силой FT, можно переписать в следующем виде:
(16)
Или, с учетом выражений (11) и (12):
(17)
Первый член в правых частях выражений (15)-(17) представляет собой работу силы левитации в стационарном (неподвижном) состоянии
(18)
Второй член выражает работу, связанную с ускоренным перемещением силы левитации
(19)
Третий член – это обычная работа силы ΔF, обеспечивающей ускоренное движение тела в соответствии со II законом Ньютона:
(20)
Произведение работ . На рис. 1 показана зависимость величины работы левитации AЛ от величины работы AΔ, выраженных в долях потенциальной энергии mgh.
Выражение (17) имеет минимум, равный при
. На графике (рис. 2) показана зависимость работы
, совершаемой силой тяги FT, выраженной в долях потенциальной энергии П=mgh, от величины соотношения ΔF / mg. Если использовать обычную формулу определения работы подъема тела на высоту h с некоторым ускорением a, то будем иметь A=m(g+a)h = (FЛ + ΔF)h . Ее зависимость от величины соотношения ΔF / mg показана на графике (рис. 3). Самое нелепое на этом графике то, что при ΔF=0 совершается работа подъема, равная mgh, хотя, согласно условиям статики, тело должно оставаться неподвижным.
Отрицательная работа, совершаемая силой тяжести при подъеме тела вверх вовсе не равна mgh. Она равна
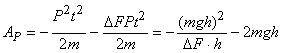
Сумма работ (17) и (21) дает величину , т.е. величину кинетической энергии, приобретенной телом на высоте h.
КПД подъема при без учета работы торможения составляет
.
§3. Тело находится в состоянии левитации (приложена сила тяги ). Для того, чтобы тело двигалось вверх, в начальный момент времени на тело действует направленный вверх единичный импульс силы
. В этом случае дифференциальное уравнение движения запишется в виде
(22)
при нулевых начальных условиях. Решая уравнение с помощью преобразования Лапласа, получим
(23)
Вычисляем работу, совершаемую всеми силами

где , а t1 – время движения до высоты
. Вычисляя интегралы, выделим положительную и отрицательную работы
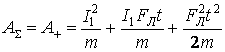
(26)
Преобразуем выражения, входящие в (25)
, где
Тогда суммарную положительную работу (работу подъема) можно записать в виде
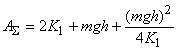
Эта работа имеет минимум, равный при величине
. График зависимости суммарной работы подъема AΣ в зависимости от величины 2K1, выраженных в долях потенциальной энергии П=mgh, показана на графике (рис. 4). Отрицательная работа, совершаемая силой тяжести (27), может быть представлена в виде:
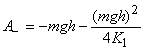
При больших значениях начального импульса ( ) она асимптотически стремится к своему обычному значению
.
Величина энергии, приобретенной в результате ударного нагружения мгновенным импульсом силы I1=mV1, равна . Двойная энергия является результатом удвоения массы при внезапно приложенной нагрузке (в рамках модели материальной точки). В рамках реального упругого тела половина энергии идет на возбуждение упругих колебаний, которые вследствие дисперсии и внутреннего трения с течением времени затухают, переходя во внутреннюю энергию (тело нагревается).
СПИСОК ЛИТЕРАТУР
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. средн. шк. – М.: Просвещение, 1990.
- Сивухин Д.В. Общий курс физики. Том I. Механика. – М.: Наука, 1989.
- Детлаф А.А., Яворский Б.М. Курс физики. Учебн. пособие для вузов. – М.: Высш. шк., 1989.
- Матвеев А.Н. Механика и теория относительности: Учебн. пособие для физ. спец. вузов. – М.: Высш. шк., 1986.
- Иванов Е.М. Дополнительные главы классической механики: – Димитровград: ДИТУД УлГТУ, 2004.
- Иванов Е.М. Работа центростремительных и гироскопических //Успехи современного естествознания, № 9, 2004.
- Арсенин В.Я. Математическая физика. – М.: Наука, 1966.
- Арфкен Г. Математические методы в физике. М.: Атомиздат, 1970.
- Б. Ван Дер Поль, Х. Бреммер. Операционное исчисление на основе двустороннего преобразования Лапласа. – М.: Изд. Иностр.Лит. 1952.
- Иванов Е.М. Закон инерции Галилея (I закон Ньютона) //Вестник ДИТУД, № 1, 2003.
Библиографическая ссылка
Иванов Е.М. РАБОТА ПОДЪЕМА ТЕЛА В ОДНОРОДНОМ ПОЛЕ ТЯЖЕСТИ // Современные наукоемкие технологии. – 2005. – № 3.
– С. 9-12;
URL: https://top-technologies.ru/ru/article/view?id=22372 (дата обращения: 19.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Вторник, а это значит, что сегодня мы снова решаем задачи. На это раз, на тему «свободное падение тел».
Присоединяйтесь к нам в телеграм и получайте актуальную рассылку каждый день!
Задачи на свободное падение тел с решением
Задача №1. Нахождение скорости при свободном падении
Условие
Тело падает с высоты 20 метров. Какую скорость оно разовьет перед столкновением с Землей?
Решение
Высота нам известна по условию. Для решения применим формулу для скорости тела в момент падения и вычислим:
Ответ: примерно 20 метров в секунду.
Задача №2. Нахождение высоты и времени движения тела, брошенного вертикально.
Условие
Индеец выпускает стрелу из лука вертикально вверх с начальной скоростью 25 метров в секунду. За какое время стрела окажется в наивысшей точке и какой максимальной высоты она достигнет стрела?
Решение
Сначала запишем формулу из кинематики для скорости. Как известно, в наивысшей точке траектории скорость стрелы равна нулю:
Теперь запишем закон движения для вертикальной оси, направленной вертикально вверх.
Ответ: 2,5 секунды, 46 метров.
Задача №3. Нахождение времени движения тела, брошенного вертикально вверх
Условие
Мячик бросили вертикально вверх с начальной скоростью 30 метров в секунду. Через какое время мяч окажется на высоте 25 метров?
Решение
Запишем уравнение для движения мячика:
Мы получили квадратное уравнение. Упростим его и найдем корни:
Как видим, уравнение имеет два решения. Первый раз мячик побывал на высоте через 1 секунду (когда поднимался), а второй раз через 5 секунд (когда падал обратно).
Ответ: 1с, 5с.
Задача №4. Нахождение высоты при движении тела под углом к горизонту
Условие
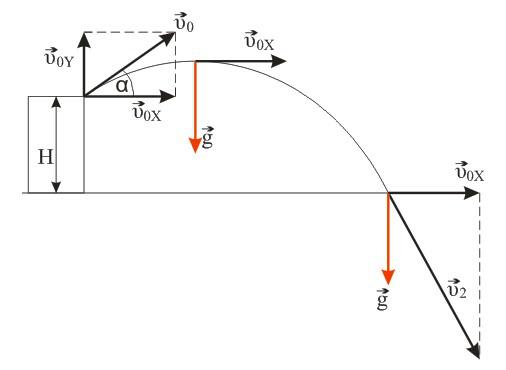
Камень, брошенный с крыши дома под углом альфа к горизонту, через время t1=0,5c достиг максимальной высоты, а еще через время t2=2,5c упал на землю. Определите высоту Н дома. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.
Решение
Камень брошен со скоростью v0 под углом α к горизонту с дома высотой Н. Эту скорость можно разложить на две составляющие: v0X (горизонтальная) и v0Y (вертикальная). В горизонтальном направлении на камень не действует никаких сил (сопротивлением воздуха пренебрегаем), поэтому горизонтальная составляющая скорости неизменна на протяжении всего времени полета камня (равномерное движение). Максимальная точка траектории камня над уровнем земли (исходя из кинематических соотношений):
Здесь t1 – время подъема камня с высоты Н на высоту h; g – ускорение свободного падения.
Вертикальную составляющую скорости можно вычислить исходя из геометрических соображений:
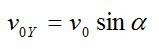
Подставив выражение для скорости в первое уравнение, получим:
Также высоту h можно выразить через время t2 падения камня с высоты h на землю (исходя из кинематических соотношений и учитывая, что с вертикальная составляющая скорости в наивысшей точке равна нулю):
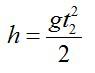
Для высоты дома можно записать:
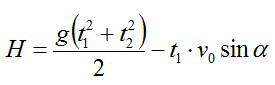
Так как вертикальная составляющая скорости камня в максимальной точке траектории равна нулю:
Подставляем в формулу для высоты H и вычисляем:
Ответ: H = 30 м.
Задача №5. Нахождение закона движения тела
Условие
Найти закон движения тела против силы тяжести, при начальной скорости V0. И на какую максимальную высоту поднимется тело? Тело бросили под углом 90 градусов.
Решение
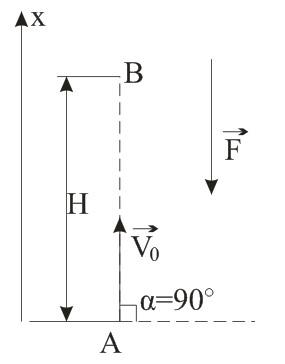
Тело брошено под углом α=90° к горизонту. Другими словами, тело брошено вертикально вверх с начальной скоростью V0. Направим координатную ось х вертикально вверх, так ее направление совпадает с вектором начальной скорости. F – сила тяжести, направленная вниз. В начальный момент тело находится в точке А.
В задаче нужно найти закон движения тела, то есть зависимость координаты тела от времени. В общем случае этот закон задается кинематическим соотношением:
где х0 – начальная координата тела; a – ускорение.
Так как мы поместили начало координат в точку А, х0=0. Тело движется с ускорением свободного падения g, при этом сила тяжести направлена против начальной скорости, поэтому в проекции на вертикальную ось a=-g. Таким образом, искомый закон движения перепишется в виде:
Далее будем использовать еще одно общее кинематическое соотношение:
где V – конечная скорость.
Максимальная высота подъема тела указана на рисунке точной B, в этот момент конечная скорость V равна нулю, а координата х равна максимальной высоте Н подъема тела. Отсюда можно найти выражение для этой величины:
Полезные формулы для решения задач на свободное падение
Свободное падение описывается формулами кинематики. Мы не будем приводить их вывод, но запишем самые полезные.
Формула для максимальной высоты подъема тела, брошенного вертикально вверх c некоторой начальной скоростью:
Кстати, как выводится именно эта формула можно посмотреть в последней задаче.
Формула для времени подъема и падения тела, брошенного вертикально вверх:
Скорость тела в момент падения с высоты h:
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Вопросы с ответами на свободное падение тел
Вопрос 1. Как направлен вектор ускорения свободного падения?
Ответ: можно просто сказать, что ускорение g направлено вниз. На самом деле, если говорить точнее, ускорение свободного падения направлено к центру Земли.
Вопрос 2. От чего зависит ускорение свободного падения?
Ответ: на Земле ускорение свободного падения зависит от географической широты, а также от высоты h подъема тела над поверхностью. На других планетах эта величина зависит от массы M и радиус R небесного тела. Общая формула для ускорения свободного падения:
Вопрос 3. Тело бросают вертикально вверх. Как можно охарактеризовать это движение?
Ответ: В этом случае тело движется равноускоренно. Причем время подъема и время падения тела с максимальной высоты равны.
Вопрос 4. А если тело бросают не вверх, а горизонтально или под углом к горизонту. Какое это движение?
Ответ: можно сказать, что это тоже свободное падение. В данном случае движение нужно рассматривать относительно двух осей: вертикальной и горизонтальной. Относительно горизонтальной оси тело движется равномерно, а относительно вертикальной – равноускоренно с ускорением g.
Баллистика – наука, изучающая особенности и законы движения тел, брошенных под углом к горизонту.
Вопрос 5. Что значит «свободное» падение.
Ответ: в данном контексте понимается, что тело при падении свободно от сопротивления воздуха.
Свободное падение тел: определения, примеры
Свободное падение – равноускоренное движение, происходящее под действием силы тяжести.
Первые попытки систематизированно и количественно описать свободное падение тел относятся к средневековью. Правда, тогда было широко распространено заблуждение, что тела разной массы падают с разной скоростью. На самом деле, в этом есть доля правды, ведь в реальном мире на скорость падения сильно влияет сопротивление воздуха.
Однако, если им можно пренебречь, то скорость падающих тел разной массы будет одинакова. Кстати, скорость при свободном падении возрастает пропорционально времени падения.
Ускорение свободно падающих тел не зависит от их массы.
Рекорд свободного падения для человека на данный момент принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который в 2012 году прыгнул с высоты 39 километров и находился в свободном падении 36 402,6 метра.
Примеры свободного падения тел:
- яблоко летит на голову Ньютона;
- парашютист выпрыгивает из самолета;
- перышко падает в герметичной трубке, из которой откачан воздух.
При свободном падении тела возникает состояние невесомости. Например, в таком же состоянии находятся предметы на космической станции, движущейся по орбите вокруг Земли. Можно сказать, что станция медленно, очень медленно падает на планету.
Конечно, свободное падение возможно не только не Земле, но и вблизи любого тела, обладающего достаточной массой. На других комических телах падения также будет равноускоренным, но величина ускорения свободного падения будет отличаться от земной. Кстати, раньше у нас уже выходил материал про гравитацию.
При решении задач ускорение g принято считать равным 9,81 м/с^2. В реальности его величина варьируется от 9,832 (на полюсах) до 9,78 (на экваторе). Такая разница обусловлена вращением Земли вокруг своей оси.
Нужна помощь в решении задач по физике? Обращайтесь в профессиональный студенческий сервис в любое время.
Рассмотрим несколько примеров решения задач на вычисление работы сил.
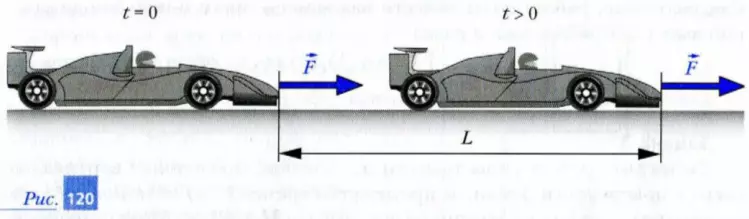
Задача 1. Гоночный автомобиль разгоняется на прямолинейной дороге под действием постоянной силы тяги, значение которой F = 5 кН (рис. 120). Определите работу этой силы при перемещении автомобиля на расстояние L =100 м.
Решение. Поскольку направление силы тяги и направление движения автомобиля совпадают, то
A = F · L = 5000 Н · 100 м = 500000 Дж = 500 кДж = 0,5 МДж.
Ответ: работа силы тяги равна 0,5 МДж.
Отметим, что сила тяги, действующая на автомобиль, создается в результате действия сил трения со стороны дороги на ведущие колеса в направлении движения автомобиля. У гоночных автомобилей с реактивным двигателем она создается непосредственно этим двигателем.
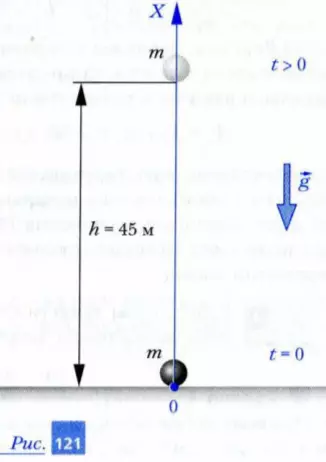
Задача 2. С поверхности Земли вертикально вверх брошен камень, как показано на рис. 121. Какую работу совершит сила тяжести к тому моменту, когда камень поднимется на высоту h = 45 м? Масса камня равна m = 1 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с2.
Решение. Поскольку сила тяжести и перемещение камня во время подъема направлены в противоположные стороны, работа силы тяжести будет величиной отрицательной. Как вы помните, модуль силы тяжести равен m · g. Следовательно, работа силы тяжести над камнем при его подъеме до заданной высоты отрицательна и равна
A = -(m · g) · h = -(1 кг · 10 м/с2) · 45 м = -10 Н · 45 м= -450Дж.
Ответ: работа силы тяжести равна -450 Дж.
Задача 3. Вычислите работу силы тяжести над камнем, брошенным вертикально вверх с поверхности Земли, за промежутки времени: а) от момента броска до момента подъема на максимальную высоту H = 60 м; б) от момента достижения максимальной высоты до момента, когда камень окажется на высоте h = 45 м; *в) от момента начала движения с поверхности Земли до момента, когда, опускаясь, камень второй раз за время полета окажется на высоте h = 45 м. Масса камня равна M = 1 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с2.
Решение.
а) Повторяя решение предыдущей задачи, получаем:
Aa = -(M · g) · H = -(1 кг · 10 м/с2) · 60 м = -10 Н · 60 м = -600 Дж.
б) При падении камня из верхней точки направления силы тяжести и движения камня совпадают. Поэтому на этом участке свободного падения работа силы тяжести положительна и равна
Aб = M · g · (H – h) = 10 Н · 15 м = 150 Дж.
*в) Работа силы тяжести в этом случае может быть определена как сумма работ силы тяжести при подъеме камня до верхней точки и при движении камня вниз из верхней точки до высоты h, т. е.
Aв = Aа + Aб = -(M · g) · H + M · g (H – h) = -M · g · h = -450 Дж.
Сопоставим этот результат с результатом из задачи 2. Можно заметить, что в обоих случаях начальные положения камня (поверхность Земли) и его конечные положения (45 м от поверхности Земли) совпадают. При этом сила тяжести совершает одну и ту же работу. Можно сделать следующий вывод.
Работа силы тяжести определяется разностью высот, на которых находилось тело в начальный и конечный моменты времени.
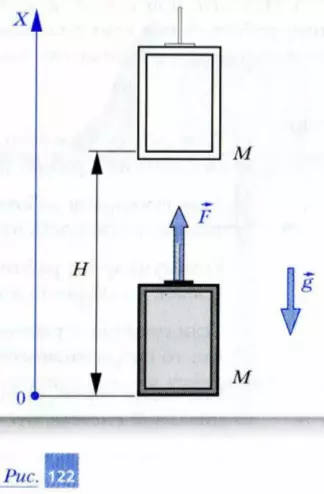
Задача 4. На движущуюся кабину лифта массой M в течение некоторого промежутка времени трос действовал с постоянной силой F. Найдите работу: а) силы F; б) силы тяжести; в) суммы этих сил над кабиной лифта, если за указанный промежуток времени она поднялась вертикально вверх на высоту H.
Решение. Пусть ось Х системы отсчета, связанной с Землей, направлена вертикально вверх, как показано на рис. 122. Тогда значение силы тяжести будет отрицательным, а значение силы F и изменение координаты кабины лифта — положительными.
Поэтому работа силы F положительна и равна
Aа = F · H,
а работа силы тяжести — отрицательна и равна
Aб = -M · g · H.
При рассмотрении законов динамики неоднократно подчеркивалось, что при одновременном действии на точечное тело нескольких сил его ускорение будет таким же, как и при действии на это тело одной силы, равной сумме всех действующих на него сил. Заменим действующие на кабину лифта силы одной суммарной. Значение этой силы равно сумме значений силы тяжести и силы F со стороны троса: Fс = F – M · g. Поэтому работа суммарной силы над кабиной при ее перемещении на высоту H равна
Aв = Fс · H = (F – M · g) · H = F · H – M · g · H = Aа + Aб.
При одновременном действии на тело нескольких сил их суммарная работа равна сумме работ этих сил.
Таким образом, для рассмотренного случая можно сделать следующие выводы.
1. При F > M · g суммарная работа этих сил положительна. Поэтому, если на кабину не действуют другие силы, она должна разгоняться, т. е. ее ускорение должно быть положительным. Это же заключение легко сделать и непосредственно из второго закона Ньютона.
2. При F = M · g суммарная сила равна нулю. Поэтому и суммарная работа этих сил равна нулю. Кабина будет двигаться без ускорения, т. е. ее скорость не будет изменяться.
3. Наконец, при F
Итоги
Если на точечное тело одновременно действуют несколько сил, их суммарная работа равна сумме работ этих сил.
Если суммарная работа всех действующих на тело сил положительна, то скорость этого тела увеличивается.
Если суммарная работа всех действующих на тело сил отрицательна, то скорость этого тела уменьшается.
Если суммарная работа всех действующих на тело сил равна нулю, то скорость этого тела остается неизменной.
Сказанное верно, если движение тела рассматривается в инерциальной системе отсчета.
Упражнения
1. Найдите работу силы трения, тормозящей грузовой автомобиль на отрезке пути L = 40 м, если модуль силы равен 25 кН.
2. Определите работу силы тяжести над камнем массой m = 5 кг при его падении с высоты h = 80 м на Землю.
3. Найдите работу пороховых газов над пулей к моменту ее вылета из ствола снайперской винтовки длиной L = 1 м. Считайте, что сила действия газов постоянна и ее модуль равен 5 кН. Винтовку во время выстрела удерживает неподвижной стоящий на Земле человек.
4. Определите работу силы тяжести над свободно падающим камнем массой m = 1 кг за промежуток времени, в течение которого скорость камня изменяется от v0 = 0 до vк = 30 м/с.
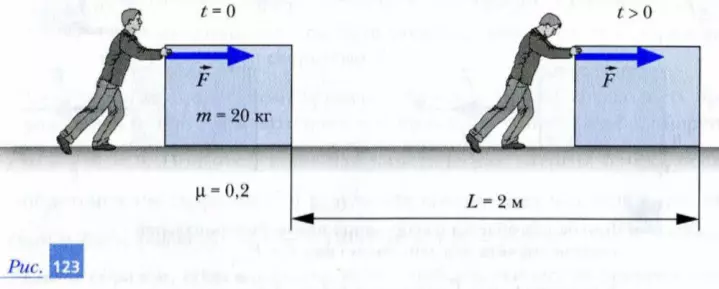
5. Мальчик действует на движущийся по горизонтальному полу ящик массой m = 20 кг силой, направленной в сторону движения ящика (рис. 123) и равной по модулю 50 Н. Коэффициент трения ящика о пол μ = 0,2. При этом за некоторое время ящик передвинулся на расстояние L = 2 м. Какую работу за это время совершат: а) мальчик; б) сила тяжести; в) сила трения; г) сумма всех сил, действующих на ящик? Увеличится или уменьшится скорость ящика за это время?
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,939 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Задачи на Свободное падение с решениями
Формулы, используемые в 9 классе на уроках
«Задачи на Свободное падение тел».
| Название величины | Обозначение | Единица измерения | Формула |
| Время |
t |
с | 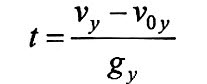 |
| Проекция начальной скорости |
v0y |
м/с |  |
| Проекция мгновенной скорости |
vy |
м/с |  |
| Проекция ускорения |
gy |
м/с2 |  |
| Проекция перемещения |
Sy |
м | 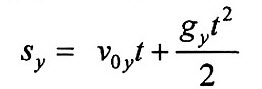 |
| Координата |
y |
м | 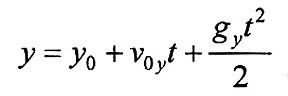 |
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Задача № 1.
С балкона 8-го этажа здания вертикально вниз бросили тело, которое упало на землю через 2 с и при падении имело скорость 25 м/с. Какова была начальная скорость тела?
Задача № 2.
Какой высоты достигнет мяч, брошенный вертикально вверх со скоростью 20 м/с? Сколько времени для этого ему понадобится?
Задача № 3.
Мяч бросили вертикально вверх со скоростью 15 м/с. Через какое время он будет находиться на высоте 10 м?
Задача № 4.
Через сколько секунд мяч будет на высоте 25 м, если его бросить вертикально вверх с начальной скоростью 30 м/с?

Задача № 5.
Лифт начинает подниматься с ускорением а = 2,2 м/с2. Когда его скорость достигла v = 2,4 м/с, с потолка кабины лифта оторвался болт. Чему равны время t падения болта и перемещение болта относительно Земли за это время? Высота кабины лифта Н = 2,5 м.
Ответ: 0,645 с; болт перемещается относительно Земли на 0,49 м вниз.
Задача № 6. (повышенной сложности)
Одно тело свободно падает с высоты h1; одновременно с ним другое тело начинает движение с большей высоты h2. Какой должна быть начальная скорость v0 второго тела, чтобы оба тела упали одновременно?
Задача № 7. (олимпиадного уровня)
Из окна, расположенного на высоте 30 м, начинает падать без начальной скорости тяжелый цветочный горшок. В этот момент точно под окном проезжает велосипедист. При какой скорости движения велосипедиста расстояние между ним и горшком будет все время увеличиваться?
Ответ: v > 17 м/с.
Задача № 8.
ЕГЭ
С воздушного шара, поднимающегося со скоростью v0 = 1 м/с, падает камень и достигает земли спустя t = 16 с. На какой высоте h находился шар в момент сбрасывания камня? С какой скоростью v камень упал на землю?
Задача № 9.
На какой высоте скорость тела, брошенного вертикально вверх с начальной скоростью v0, уменьшится в 4 раза?
Дано: Vo, V = Vo/4.
Найти: h — ?
Решение:
Если принять, что g ≈ 10 м/с2 , то h = 15 • Vo^2 / 320 ≈ 0,047 • Vo^2.
Ответ: h = (15 • Vo^2) / (32 • g) ≈ 0,047 • Vo^2.
Краткое пояснение для решения ЗАДАЧИ на Свободное падение тел.
Свободное падение — это движение тела под действием силы тяжести (другие силы — сила сопротивления, выталкивающая сила — отсутствуют либо ими пренебрегают).
Так как сила тяжести направлена вниз, то ускорение, которое она сообщает телу, тоже направлено вниз. Свободное падение — это равноускоренное движение. Ускорение, сообщаемое телу силой тяжести, называют ускорением свободного падения. Оно одинаково для всех тел вблизи поверхности Земли и имеет значение 9,8 м/с2. При решении задач в большинстве случаев это число округляется до 10 м/с2.
При решении задач применяются формулы равноускоренного движения. Для нахождения проекций векторов координатную ось обычно обозначают буквой у, так как движение происходит по вертикали. Направляют ее вверх или вниз — как удобней при решении конкретной задачи. Скорость свободно падающего тела возрастает.
Движение тела, брошенного вертикально вверх — частный случай свободного падения. Только скорость тела уменьшается, так как оно движется против силы тяжести, и вектор начальной скорости и вектор ускорения противоположно направлены. Достигая некоторой точки (наивысшей точки подъема), тело на мгновение останавливается (в это время его скорость равна нулю), а затем начинает падать. Так как движение вверх и вниз происходит с одинаковым ускорением, то время подъема и время падения тела равны.
Если координатную ось направить вверх, то проекция ускорения будет отрицательна, если вниз — положительна. Но при любом направлении оси для падающего тела векторы ускорения и скорости сонаправлены, а для тела, брошенного вверх — противоположно направлены.
Это конспект по теме «ЗАДАЧИ на Свободное падение тел с решениями». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на применение Законов Ньютона
- Посмотреть конспект по теме КИНЕМАТИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.