Как найти работу тела в тепловом двигателе

В этой главе…

• Достигаем теплового равновесия
• Сохраняем тепловую энергию при различных условиях
• Повышаем эффективность тепловых двигателей
• Падаем почти до абсолютного нуля

Каждому, кому когда-либо приходилось работать летом на открытом воздухе, хорошо известны понятия “тепло” и “работа”, связь между которыми изучает термодинамика. В данной главе, наконец-то, встречаются эти два незабвенных понятия, о которых подробно рассказывается в главе 8 (о работе) и в главе 13 (о тепле, теплоте и тепловой энергии). В термодинамике имеется три закона, а точнее начала, которые также важны для термодинамики, как и законы Ньютона для механики. Кроме того, уж в одном отношении они даже превосходят законы Ньютона, а именно в том, что в термодинамике имеется еще и нулевой закон, который чаще называют нулевым началом термодинамики. В этой главе рассказывается о термодинамическом равновесии (нулевое начало), сохранении энергии (первое начало), о тепловых потоках (второе начало) и недостижимости абсолютного нуля (третье начало). Итак, самое время обратиться к термодинамике.

Стремимся к тепловому равновесию: нулевое начало термодинамики

Основные законы термодинамики начинаются с нулевого начала. Возможно, эта нумерация покажется странной, ведь мало какой набор вещей из повседневной жизни начинается подобным образом (“Будь осторожен на нулевой ступеньке…”), но, знаете ли, физикам нравятся их традиции. Так вот, нулевое начало термодинамики гласит, что два тела находятся в тепловом равновесии, если они могут передавать друг другу теплоту, но не делают этого. (В русскоязычной научной литературе нулевое начало термодинамики называют также общим началом термодинамики. — Примеч. ред.)

Например, если у вас и у воды в плавательном бассейне, в котором вы находитесь, одна и та же температура, то никакое тепло от вас к воде или от воды к вам не передается (хотя такая передача возможна). Ваше тело и бассейн находятся в тепловом равновесии. Однако, если вы прыгнете в бассейн зимой, проломив при этом его ледяную корку, то первое время вряд ли будете в тепловом равновесии с его водой. Впрочем, вы и не захотите этого. (Не пытайтесь проделать этот физический опыт дома!)

Чтобы обнаружить тепловое равновесие (особенно в замерзших бассейнах, куда вы собираетесь прыгнуть), надо использовать термометр. Измерьте с его помощью температуру воды в бассейне, а затем — свою температуру. Если обе температуры совпадают (другими словами, наблюдается тепловое равновесие: ваше — с термометром, а термометра — с водой в бассейне), то в таком случае вы находитесь в тепловом равновесии с водой бассейна.

Использование термометра показывает: два тела, находящиеся в тепловом равновесии с третьим, также находятся в тепловом равновесии друг с другом; вот вам еще одна формулировка нулевого начала.

Кроме всего прочего, нулевое начало содержит идею, что температура — это индикатор теплового равновесия. То, что два тела, упомянутые в нулевом законе, находятся в тепловом равновесии с третьим, дает все нужное дая задания температурной шкалы, например шкалы Кельвина. Ну а с физической точки зрения нулевой закон устанавливает точку отсчета, утверждая, что между двумя телами, имеющими одинаковую температуру, тепловой поток в целом отсутствует.

Сохраняем энергию: первое начало термодинамики

Первое начало термодинамики — это, попросту говоря, закон сохранения энергии. Он утверждает, что энергия никуда не исчезает. Когда системой поглощается или высвобождается тепловая энергия ​( Q )​, а сама система выполняет над окружающими телами работу ​( W )​ (или, наоборот, окружающие тела выполняют работу над ней), то внутренняя энергия системы, имевшая начальное значение ​( U_н )​, становится равной ( U_к ) следующим образом:

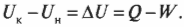
В главе 8 немало говорится о сохранении механической энергии. Там показано, что общая механическая энергия (сумма потенциальной и кинетической энергии) сохраняется. Чтобы утверждать такое, надо было работать с системами, где энергия не тратится на нагревание, — например, когда отсутствует трение. Теперь все изменилось. Тепловая энергия, наконец-то, учитывается нами (как вы, вероятно, поняли из рассуждений), и теперь общую энергию системы можно рассматривать с учетом передачи тепловой энергии, проделанной работы и внутренней энергии системы.

На основании комбинации этих трех величин (тепловой энергии, работы и внутренней энергии) определяется общая энергия системы, которая в целом сохраняется. Если передать системе количество тепловой энергии, равное ( Q ), то при отсутствии работы ее количество внутренней энергии, обозначаемое как ( U ), изменится на ( Q ). Система может терять энергию, выполняя работу над окружающими телами, например, когда машина поднимает груз, висящий на конце каната. Так вот, когда система выполняет работу над окружающими телами и никакой тепловой энергии не тратит, ее внутренняя энергия ( U ) изменится на ( W ). Иначе говоря, если учитывать тепловую энергию, то с учетом всех этих трех величин (тепловой энергии, работы и внутренней энергии) общая энергия системы сохраняется.

Польза первого начала термодинамики состоит в том, что оно связывает все три основные величины: тепловую энергию, работу и внутреннюю энергию. Зная две из них, всегда можно определить третью.

Применяем закон сохранения энергии

Величина передаваемой тепловой энергии ( Q ) является положительной или отрицательной, когда система, соответственно, поглощает или высвобождает тепловую энергию. Величина работы ( W ) является положительной или отрицательной, когда работа, соответственно, выполняется системой над окружающими телами или окружающими телами над системой.

Новички часто путаются, пытаясь определить, являются ли значения каждой из величин положительными или отрицательными. Чтобы не запутаться, при работе с первым началом термодинамики рекомендуется исходить из общей идеи сохранения энергии. Допустим, что мотор выполняет над окружающими телами работу в 2000 Дж, высвобождая при этом 3000 Дж тепловой энергии. Насколько меняется его внутренняя энергия? В данном случае известно, что мотор выполняет над окружающими телами работу в 2000 Дж, поэтому ясно, что его внутренняя энергия уменьшается на 2000 Дж. Кроме того, выполняя работу, он еще высвобождает 3000 Дж тепловой энергии, так что внутренняя энергия мотора уменьшается еще на 3000 Дж.

Значения работы и передаваемой тепловой энергии следует считать отрицательными. Тогда в предыдущем примере получим такое изменение внутренней энергии:

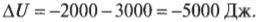
Внутренняя энергия системы уменьшается на 5000 Дж, что определенно имеет смысл, ведь система выполняет над окружающими телами работу в 2000 Дж и высвобождает 3000 Дж тепловой энергии. С другой стороны, а что если система, выполняя над окружающими телами работу в 2000 Дж, поглощает 3000 Дж их тепловой энергии? В таком случае получилось бы 2000 Дж входящей и 3000 Дж исходящей энергии. Теперь понятно, какими должны быть знаки:

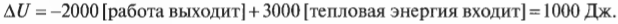
В данном случае общее изменение внутренней энергии системы равно +1000 Дж. Отрицательное значение работа принимает, когда она выполняется над системой окружающими телами. Например, система поглощает 3000 Дж, в то время как окружающие тела выполняют над ней работу в 4000 Дж. Это значит, что внутренняя энергия системы увеличивается на 3000 Дж + 4000 Дж = 7000 Дж. А если нужно все просчитать, то воспользуйтесь следующей формулой:

а затем обратите внимание, что поскольку окружающие тела выполняют работу над системой, значение ​( W )​ считается отрицательным. Таким образом, получаем:

Изучаем изобарические, изохорические, изотермические и адиабатические процессы

В этой главе рассматриваются процессы, при анализе которых приходится работать с такими параметрами, как объем, давление, температура и энергия. Причем полученные результаты очень сильно зависят от того, как эти величины меняются. Например, если газ выполняет работу, сохраняя свой объем постоянным, то этот процесс будет отличаться от того, при котором остается постоянным не объем, а давление газа.

В термодинамике обычно рассматривают четыре стандартных режима, которые отличаются постоянством одного из вышеперечисленных параметров (давление, объем, температура и энергия).

Обратите внимание, что изменения в процессах, описанных в последующих разделах, называются квазистатическими, т.е. эти изменения проходят достаточно медленно, позволяя давлению и температуре оставаться одинаковыми в любом месте системы.

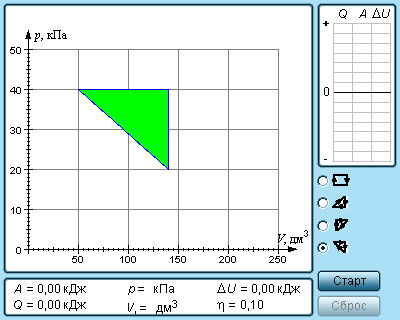
Постоянное давление: изобарический процесс

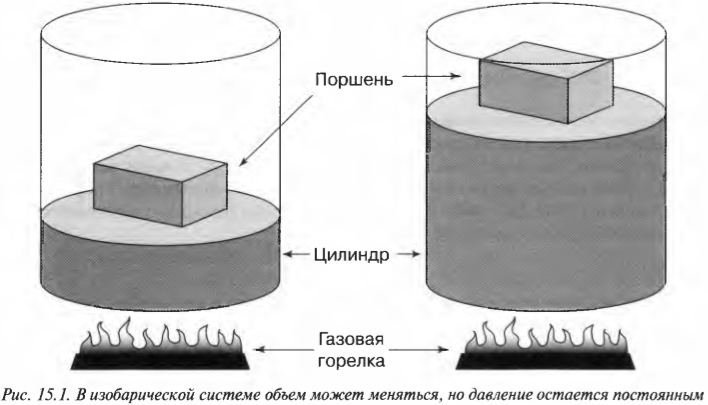
Процесс, в котором давление остается постоянным, называется изобарическим (“барический” означает “относящийся к давлению”). На рис. 15.1 показан цилиндр с поршнем, поднимаемым некоторым количеством газа, когда этот газ нагревается. Объем газа меняется, но утяжеленный поршень сохраняет давление постоянным.

Какую работу выполняет система при расширении газа? Работа равна произведению ​( F )​ на ​( s )​, означающих, соответственно, силу и перемещение. Кроме того, сила равна произведению ​( P )​ на ​( A )​, означающих, соответственно, давление и площадь. Это значит, что:

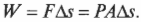
Но произведение площади ( A ) и перемещения ( s ) равно изменению объема ​( Delta!V )​. Таким образом:

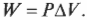
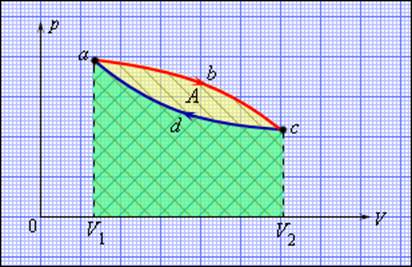
Изобарический процесс можно показать в виде графика (как на рис. 15.2), на котором видно, что объем меняется, в то время как давление остается постоянным. Так как ​( W=PDelta!V )​, то работа — это площадь, ограниченная графиком.

Допустим, имеется 60 м³ идеального газа под давлением в 200 Па (см. главу 2), который нагревается до тех пор, пока он не расширится до объема в 120 м³ (​( PV= nRT )​, где ​( n )​, ​( R )​ и ​( Т )​ означают, соответственно, количество молей, универсальную газовую постоянную (8,31) и температуру; см. главу 14). Какую работу выполняет газ? Все, что вам нужно, — это подставить в формулу численные значения:

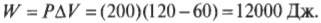
Расширяясь при постоянном давлении, газ выполняет работу в 12000 Дж.

Постоянный объем: изохорический процесс

А что если давление в системе не постоянно? В конце концов, не так уж и часто попадаются устройства с утяжеленным поршнем, как на рис. 15.1. Чаще всего приходится иметь дело с простым замкнутым сосудом, как на рис. 15.3, где показан баллончик с дезодорантом, кем-то неосторожно брошенный в огонь. В этом случае объем остается постоянным, а такой процесс называется изохорическим. По мере того как газ внутри баллончика нагревается, его давление возрастает, но объем остается постоянным (если, конечно, баллончик не взорвется).

Какая работа выполняется с баллончиком распылителя? Посмотрите на график (рис. 15.4). В данном случае объем постоянный, поэтому ​( Fs )​ (произведение силы и перемещения) равно нулю. Никакая работа не выполняется — площадь под графиком равна нулю.

Постоянная температура: изотермический процесс

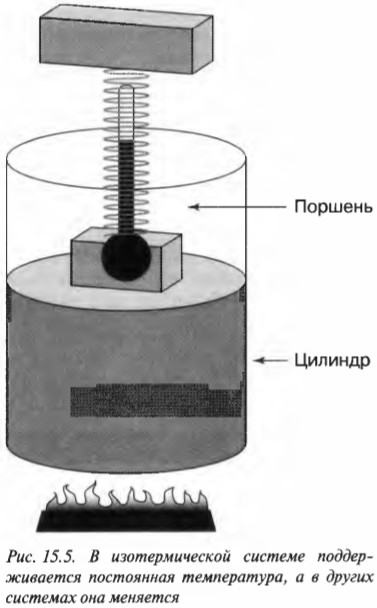
В изотермическом процессе температура остается постоянной, в то время как другие величины меняются. Посмотрите, какой замечательный аппарат показан на рис. 15.5. Этот аппарат специально предназначен для того, чтобы сохранять температуру газа постоянной, причем даже при подъеме поршня. При добавлении к системе (или отводе от системы) тепловой энергии поршень медленно поднимается (или медленно опускается) таким образом, чтобы произведение давления и объема сохранялось постоянным. Так как ( PV= nRT ) (см. главу 14), то температура также остается постоянной.

Какая работа выполняется при изменении объема? Поскольку ( PV= nRT ), то получается такое отношение между ​( P )​ и ​( V )​:

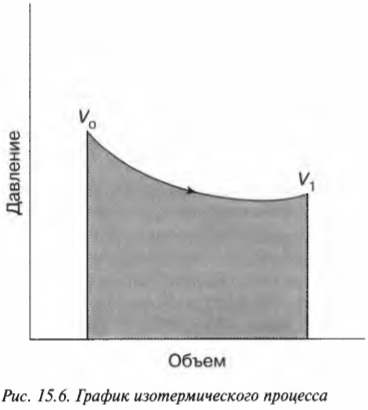
Эту формулу иллюстрирует график, показанный на рис. 15.6.

Выполненную работу “показывает” область, лежащая под графиком. Но какова же площадь этой области? Выполненная работа определяется следующей формулой, где ​( ln )​ — натуральный логарифм, ​( R )​ — газовая постоянная (8,31), ​( V_1 )​ и ​( V_0 )​ означают, соответственно, конечный и начальный объем:

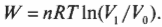
Так как при изотермическом процессе температура остается постоянной, а внутренняя энергия идеального газа равна ​( (3/2)nRT )​ (см. главу 14), то эта энергия не меняется. Таким образом:

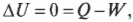
другими словами:

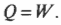
Итак, что произойдет, если цилиндр, показанный на рис. 15.5, погрузить в горячую ванну? В аппарат должна перейти тепловая энергия ​( Q )​, а поскольку температура газа остается постоянной, вся эта тепловая энергия должна превратиться в работу, выполненную системой. Скажем, к примеру, у вас имеется моль гелия при температуре 20°С, и, забавы ради, вы решили увеличить его объем с ​( V_0 )​ = 0,010 м³ до ( V_1 )​ = 0,020 м³. Какую работу выполнит газ при расширении? Все, что вам нужно, — это подставить в формулу численные значения:

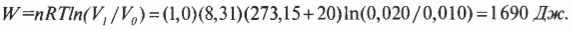
Работа, выполняемая газом, равна 1690 Дж. Изменение его внутренней энергии равно 0 Дж, как всегда при изотермическом процессе. А так как ​( Q=W )​, то добавляемая к газу тепловая энергия также равна 1690 Дж.

Постоянная энергия: адиабатический процесс

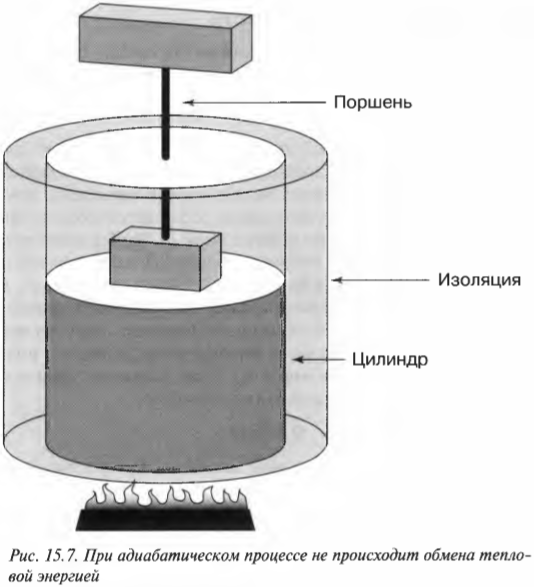
При адиабатическом процессе общая тепловая энергия системы остается постоянной. Посмотрите на рис. 15.7, где показан цилиндр, окруженный изоляционным материалом. Тепловая энергия из системы никуда не уходит, поэтому если происходит изменение, то оно является адиабатическим.

Вычисляя работу, выполняемую при адиабатическом процессе, вы можете сказать, что ​( Q )​ = 0, таким образом:

Так как внутренняя энергия ​( U )​ идеального газа равна ​( (3/2)nRT )​ (см. главу 14), то выполняется работа:

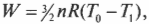
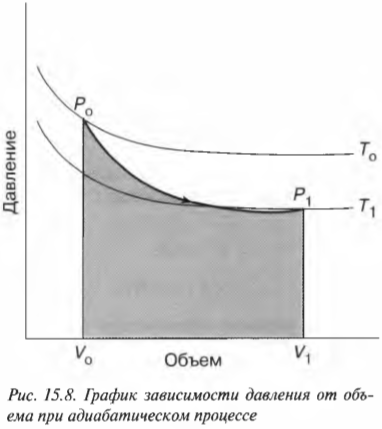
где ​( T_0 )​ и ( T_1 ) означают, соответственно, начальную и конечную температуру. Таким образом, если газ выполняет работу, то это происходит благодаря изменению температуры — при падении температуры газ выполняет работу над окружающими телами. На рис. 15.8 показан график зависимости давления от объема при адиабатическом процессе. Адиабатическая кривая, показанная на этом рисунке, так называемая адиабата, отличается от изотермических кривых, так называемых изотерм. Работа, выполненная, когда общая тепловая энергия системы постоянна, — это область под адиабатой (см. рис. 15.8).

Вычисляем удельную теплоемкость

Начальные значения давления и объема можно так связать с их конечными значениями по следующей формуле:

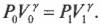
Что такое ​( gamma )​? Это отношение ​( C_p/C_v )​ двух удельных теплоемкостей идеального газа: в числителе — теплоемкость при постоянном давлении ​( C_p )​, а в знаменателе — теплоемкость при постоянном объеме ( C_v ). Удельной теплоемкостью называется отношение тепловой энергии, полученной телом единичной массы, к соответствующему приращению его температуры; подробнее об этом можно узнать в главе 13. Чтобы вычислить удельную теплоемкость, надо найти количество тепловой энергии ​( Q )​, необходимой для изменения температуры тела единичной массы на величину ​( Delta T )​, т.е. ​( c=Q/mDelta T )​, где ​( c )​, ​( m )​ и ( Delta T ) означают, соответственно, удельную теплоемкость, массу и изменение температуры. Впрочем, сейчас удобнее использовать молярную удельную теплоемкость, которая определяется как и удельная, но только рассчитывается не на единицу массу, а на один моль. Она обозначается символом ​( C )​ и измеряется в Дж/(моль·К). Итак, молярная удельная теплоемкость используется вместе с количеством молей ​( n )​, а не массой ​( m )​:

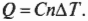
Как найти ​( C )​? Надо вычислить две разные величины: ​( C_mathrm{p} )​ (при постоянном давлении) и ( C_mathrm{v} ) (при постоянном объеме). Согласно первому началу термодинамики (см. предыдущий раздел этой главы), ​( Q=Delta U+W )​. Поэтому достаточно только выразить ​( Delta U )​ через ​( T )​. Выполняемая работа ​( W )​ равна ​( PDelta!V )​, тогда при постоянном объеме ​( W )​ = 0. А изменение внутренней энергии идеального газа равно ​( (3/2)nRDelta T )​ (см. главу 14), поэтому ​( Q )​ при постоянном объеме выражается следующей формулой:

При постоянном давлении работа ​( W )​ равна ( PDelta!V ). А поскольку ​( PV= nRT )​, то ​( W=P(V_1-V_0)=nR(T_1-T_0) )​. Поэтому ​( Q )​ при постоянном давлении выражается следующей формулой:

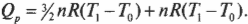
Каким образом можно получить из всего этого значения молярных удельных теплоемкостей? Как уже нам известно, ​( Q=CnDelta T )​, поэтому ( C=Q/nDelta T ). Деля предыдущие две формулы на ( nDelta T ), получаем:

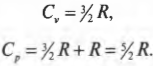
Теперь вы имеете молярные удельные теплоемкости идеального газа. Нужное вам отношение ​( gamma )​ равно отношению этих двух формул:

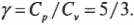
Связать давление и объем в любых двух точках адиабаты (см. предыдущий раздел об адиабатическом процессе) можно таким образом:

Например, если сначала 1 л газа находился под давлением 1 атм, а после адиабатического изменения (когда обмена тепловой энергией нет), объем газа стал 2 л, то каким должно быть новое давление ​( P_1 )​? Путем простой алгебраической операции деления на ​( V_1^{5/3} )​ оставляем в левой части равенства только ( P_1 )​ и получаем:

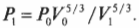
Подставив в эту формулу численные значения, получим:

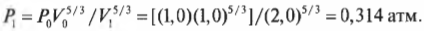
Итак, новое давление должно быть равно 0,314 атмосферы.

Передаем тепловую энергию: второе начало термодинамики

Формально говоря, второе начало термодинамики гласит, что тепловая энергия естественно переходит из тела с более высокой температурой в тело с более низкой температурой, но не в обратном направлении.

Это начало, конечно же, появилось в результате простых наблюдений: приходилось ли вам когда-либо видеть, чтобы тело само становилось холоднее окружающих его тел, если только другое тело не проделало над ним определенной работы? Путем определенной работы можно заставить теплоту переходить из тела, когда естественно ожидать перехода тепловой энергии в тело (вспомните холодильники или кондиционеры), но такое явление само по себе не происходит.

Заставим тепловую энергию работать: тепловые двигатели

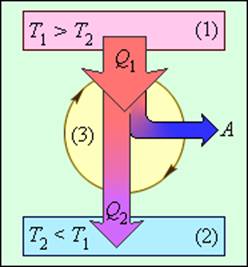
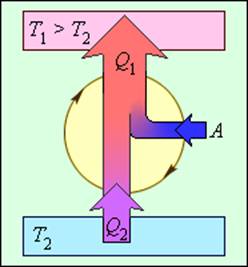
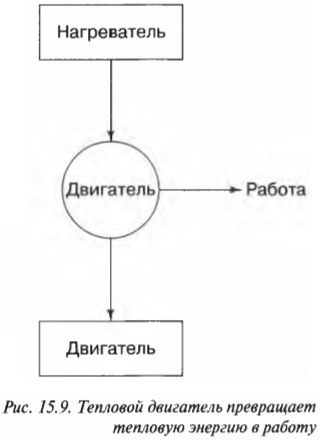
Имеется много способов заставить тепловую энергию работать. Возможно, у вас имеется, например, паровая машина с котлом и поршнями или атомный реактор, производящий перегретый пар, который может вращать турбину. Двигатели, выполняющие работу благодаря источнику тепловой энергии, называются тепловыми. Как они это делают, можно увидеть на рис. 15.9. Тепловая энергия идет от нагревателя к двигателю, который выполняет работу, а неизрасходованная тепловая энергия отправляется в холодильник. Им может быть, например, окружающий воздух или наполненный водой радиатор. Если температура холодильника меньше температуры нагревателя, то тепловой двигатель может работать — хотя бы теоретически.

Оцениваем эффективность работы: КПД теплового двигателя

Тепловая энергия, подаваемая нагревателем, обозначается как ​( Q_{нг} )​, а отправляемая в холодильник (см. предыдущий раздел) — как ​( Q_{mathrm{x}} )​. Путем некоторых вычислений можно найти коэффициент полезного действия (КПД) теплового двигателя. Он равен отношению работы ​( W )​, выполняемой двигателем, к входящей тепловой энергии — иными словами, это та доля входящей тепловой энергии, которую двигатель превращает в работу:

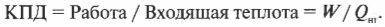
Когда вся входящая тепловая энергия превращается в работу, КПД равен 1. Если никакая входящая тепловая энергия не превращается в работу, КПД равен 0. Часто КПД выражается в виде процентов, поэтому только что названные значения можно представить как 100% и 0%. Поскольку общая энергия сохраняется, то тепловая энергия, входящая в двигатель, должна быть равна сумме выполняемой работы и тепловой энергии, отправляемой в холодильник, то есть:

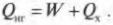
Это значит, что для записи КПД достаточно использовать ( Q_{нг} ) и ( Q_{mathrm{x}} ):

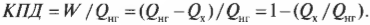
Допустим, что имеется тепловой двигатель с КПД, равным 78%. Этот двигатель производит работу величиной 2,55·10⁷ Дж. Сколько тепловой энергии он использует, а сколько выбрасывает? Известно, что ​( W )​ = 2,55·10⁷ Дж и

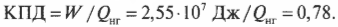
Это значит, что:

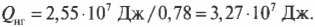
Количество входящей тепловой энергии равно 3,27·10⁷ Дж. А сколько тепловой энергии ( Q_{mathrm{x}} ) остается неизрасходованной и отправляется в холодильник? Как известно:

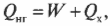
поэтому:

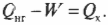
Подставив в эту формулу численные значения, получим:

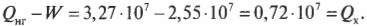
Количество тепловой энергии, отправляемое в холодильник, равно 0,72·10⁷ Дж.

Как сказал Карно: нельзя все тепло превратить в работу

Зная работу и КПД теплового двигателя, можно вычислить количество входящей и исходящей тепловой энергии (тут нам, конечно, поможет закон сохранения энергии, связывающий друг с другом работу, входящую и исходящую тепловую энергию; см. главу 8). А как насчет создания тепловых двигателей со 100%-ным КПД? С точки зрения производительности было бы прекрасно превращать в работу всю тепловую энергию, какая поступает в тепловой двигатель, но это невозможно. Кроме того, в реально работающих тепловых двигателях неизбежны определенные потери, например, из-за трения поршней в паровом двигателе. В XIX веке эту проблему изучал один инженер, которого звали Сади Карно, и он пришел к выводу: в сущности, лучшее, что можно сделать, — это попытаться изобрести двигатель, не имеющий таких потерь.

А если в двигателе нет потерь, то система будет возвращаться в то же состояние, что и перед началом процесса. Такой процесс называется обратимым. Например, если тепловой двигатель тратит энергию на преодоление трения, то обратимым процесс назвать нельзя, так как он не заканчивается в том же состоянии, в каком был сначала. При каких условиях работы тепловой двигатель будет иметь самый высокий КПД? Когда работа двигателя обратима (т.е. в системе нет потерь). Сегодня физики называют это принципом Карно. Итак, принцип Карно гласит, что ни у одного необратимого двигателя не будет такого же высокого КПД, как у обратимого, а все обратимые двигатели, работающие в промежутке между одинаковыми максимальными и одинаковыми минимальными температурами, имеют один и тот же КПД.

Построение двигателя Карно

Карно предложил свою идею двигателя — двигателя Карно. Этот двигатель должен работать обратимо, что не может быть ни в одном реально работающем двигателе, поэтому он представляет собой нечто идеальное. В двигателе Карно тепловая энергия идет от нагревателя, имеющего постоянную температуру ​( T_{нг} )​. А отработанная тепловая энергия уходит в холодильник, имеющий постоянную температуру ( T_{х} ). Поскольку температуры нагревателя и холодильника никогда не меняются, то можно сказать, что отношение подаваемой и отводимой тепловой энергии равно отношению их температур (в кельвинах):

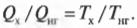
А так как КПД теплового двигателя вычисляется по следующей формуле:

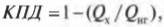
то получается такая формула для вычисления КПД двигателя Карно:

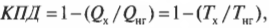
где температура выражается в кельвинах.

В этой формуле показан максимально возможный КПД теплового двигателя. И лучшего результата достичь нельзя. А как гласит третье начало термодинамики (в последнем разделе этой главы), абсолютного нуля достичь нельзя, т.е. ( T_{х} ) никогда не будет равна нулю, следовательно, невозможно получить тепловой двигатель со 100%-ным КПД.

Используем формулу Карно

Формулу максимально возможного КПД (см. предыдущий раздел) использовать довольно легко. Предположим, сделано потрясающее новое изобретение: машина Карно, в которой самолет совершает работу, причем земная поверхность играет роль нагревателя (с температурой примерно 27°С), а воздух на высоте 10000 м — роль холодильника (с температурой примерно -27°С). Какой максимальный КПД такой машины? Преобразуем значения температуры в кельвины и подставив их в формулу машины Карно:

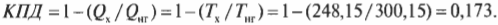
Итак, КПД такой машины Карно равен всего 17,3%. Результат, скажем, не очень. А теперь представим, что в качестве нагревателя используется поверхность Солнца (примерно 5800 К), а в качестве холодильника — межзвездное пространство (примерно 3,4 К), совсем как в научно-фантастических рассказах. Тогда совсем другое дело:

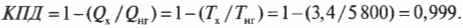
Итак, в таких научно-фантастических условиях для машины Карно можно получить КПД, равный 99,9% и близкий к теоретически максимальному значению.

Охлаждаемся: третье (и абсолютно последнее) начало термодинамики

Третье начало термодинамики достаточно просто формулируется: нельзя достичь абсолютного нуля с помощью любого процесса, состоящего из конечного числа этапов, к нему можно лишь бесконечно приближаться. Иначе говоря, никогда нельзя достичь абсолютного нуля. Каждое действие по понижению температуры физического тела до абсолютного нуля может немного приблизить к цели, но достигнуть ее нельзя, если не выполнить бесконечного числа действий, что невозможно.

Странные явления вблизи абсолютного нуля

Хотя до абсолютного нуля нельзя добраться с помощью какого-либо известного конечного процесса, но к нему можно приблизиться. Причем, имея очень дорогое оборудование, вблизи абсолютного нуля можно столкнуться с множеством странных физических явлений и фактов. Один мой приятель изучает поведение жидкого гелия при очень низких температурах. Например, гелий становится таким эксцентричным, что может самостоятельно выбраться из любого сосуда, в котором он находится. За открытие и исследования этого явления сверхтекучести гелия и некоторые другие наблюдения кое-кто получил Нобелевскую премию. Везет же людям!

(Сверхтекучесть жидкого гелия-4 была открыта в 1938 году П. Л. Капицей, за что он был удостоен Нобелевской премии по физике за 1978 год. Теория сверхтекучего гелия-Н была разработана Л. Д. Ландау, за что он был удостоен Нобелевской премии по физике за 1962 год. — Примеч. ред.)

Физика, 10 класс

Урок 25. Тепловые двигатели. КПД тепловых двигателей

Перечень вопросов, рассматриваемых на уроке:

1) Понятие теплового двигателя;

2)Устройство и принцип действия теплового двигателя;

3)КПД теплового двигателя;

4) Цикл Карно.

Глоссарий по теме

Тепловой двигатель – устройство, в котором внутренняя энергия топлива превращается в механическую.

КПД (коэффициент полезного действия) – это отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.

Двигатель внутреннего сгорания – двигатель, в котором топливо сгорает непосредственно в рабочей камере (внутри) двигателя.

Реактивный двигатель – двигатель, создающий необходимую для движения силу тяги посредством преобразования внутренней энергии топлива в кинетическую энергию реактивной струи рабочего тела.

Цикл Карно – это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов.

Нагреватель – устройство, от которого рабочее тело получает энергию, часть которой идет на совершение работы.

Холодильник – тело, поглощающее часть энергии рабочего тела (окружающая среда или специальные устройства для охлаждения и конденсации отработанного пара, т.е. конденсаторы).

Рабочее тело – тело, которое расширяясь, совершает работу (им является газ или пар)

Основная и дополнительная литература по теме урока:

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 269 – 273.

2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа,2014. – С. 87 – 88.

Открытые электронные ресурсы по теме урока

http://kvant.mccme.ru/1973/12/teplovye_mashiny.htm

Теоретический материал для самостоятельного изучения

Сказки и мифы разных народов свидетельствуют о том, что люди всегда мечтали быстро перемещаться из одного места в другое или быстро совершать ту или иную работу. Для достижения этой цели нужны были устройства, которые могли бы совершать работу или перемещаться в пространстве. Наблюдая за окружающим миром, изобретатели пришли к выводу, что для облегчения труда и быстрого передвижения нужно использовать энергию других тел, к примеру, воды, ветра и т.д. Можно ли использовать внутреннюю энергию пороха или другого вида топлива для своих целей? Если мы возьмём пробирку, нальём туда воду, закроем её пробкой и будем нагревать. При нагревании вода закипит, и образовавшие пары воды вытолкнут пробку. Пар расширяясь совершает работу. На этом примере мы видим, что внутренняя энергия топлива превратилась в механическую энергию движущейся пробки. При замене пробки поршнем способным перемещаться внутри трубки, а саму трубку цилиндром, то мы получим простейший тепловой двигатель.

Тепловой двигатель – тепловым двигателем называется устройство, в котором внутренняя энергия топлива превращается в механическую.

Вспомним строение простейшего двигателя внутреннего сгорания. Двигатель внутреннего сгорания состоит из цилиндра, внутри которого перемещается поршень. Поршень с помощью шатуна соединяется с коленчатым валом. В верхней части каждого цилиндра имеются два клапана. Один из клапанов называют впускным, а другой – выпускным. Для обеспечения плавности хода поршня на коленчатом вале укреплен тяжелый маховик.

Рабочий цикл ДВС состоит из четырех тактов: впуск, сжатие, рабочий ход, выпуск.

Во время первого такта открывается впускной клапан, а выпускной клапан остается закрытым. Движущийся вниз поршень засасывает в цилиндр горючую смесь.

Во втором такте оба клапана закрыты. Движущийся вверх поршень сжимает горючую смесь, которая при сжатии нагревается.

В третьем такте, когда поршень оказывается в верхнем положении, смесь поджигается электрической искрой свечи. Воспламенившаяся смесь образует раскаленные газы, давление которых составляет 3 -6 МПа, а температура достигает 1600 -2200 градусов. Сила давления толкает поршень вниз, движение которого передается коленчатому валу с маховиком. Получив сильный толчок маховик будет дальше вращаться по инерции, обеспечивая движение поршня и при последующих тактах. Во время этого такта оба клапана остаются закрытыми.

В четвертом такте открывается выпускной клапан и отработанные газы движущимся поршнем выталкиваются через глушитель (на рисунке не показан) в атмосферу.

Любой тепловой двигатель включает в себя три основных элемента: нагреватель, рабочее тело, холодильник.

Для определения эффективности работы теплового двигателя вводят понятие КПД.

Коэффициентом полезного действия называют отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.

Q₁ – количество теплоты полученное от нагревания

Q₂ – количество теплоты, отданное холодильнику

– работа, совершаемая двигателем за цикл.

Этот КПД является реальным, т.е. как раз эту формулу и используют для характеристики реальных тепловых двигателей.

Зная мощность N и время работы t двигателя работу, совершаемую за цикл можно найти по формуле

Передача неиспользуемой части энергии холодильнику.

В XIX веке в результате работ по теплотехнике французский инженер Сади Карно предложил другой способ определения КПД (через термодинамическую температуру).

Главное значение этой формулы состоит в том, что любая реальная тепловая машина, работающая с нагревателем, имеющим температуру Т₁, и холодильником с температурой Т₂, не может иметь КПД, превышающий КПД идеальной тепловой машины. Сади Карно, выясняя при каком замкнутом процессе тепловой двигатель будет иметь максимальный КПД, предложил использовать цикл, состоящий из 2 адиабатных и двух изотермических процессов

Цикл Карно – самый эффективный цикл, имеющий максимальный КПД.

Не существует теплового двигателя, у которого КПД = 100% или 1.

Формула дает теоретический предел для максимального значения КПД тепловых двигателей. Она показывает, что тепловой двигатель тем эффективнее, чем выше температура нагревателя и ниже температура холодильника. Лишь при температуре холодильника, равной абсолютному нулю, η = 1.

Но температура холодильника практически не может быть ниже температуры окружающего воздуха. Повышать температуру нагревателя можно. Однако любой материал (твердое тело) обладает ограниченной теплостойкостью, или жаропрочностью. При нагревании он постепенно утрачивает свои упругие свойства, а при достаточно высокой температуре плавится.

Сейчас основные усилия инженеров направлены на повышение КПД двигателей за счет уменьшения трения их частей, потерь топлива вследствие его неполного сгорания и т. д. Реальные возможности для повышения КПД здесь все еще остаются большими.

Повышение КПД тепловых двигателей и приближение его к максимально возможному — важнейшая техническая задача.

Тепловые двигатели – паровые турбины, устанавливают также на всех АЭС для получения пара высокой температуры. На всех основных видах современного транспорта преимущественно используются тепловые двигатели: на автомобильном – поршневые двигатели внутреннего сгорания; на водном – двигатели внутреннего сгорания и паровые турбины; на железнодорожном – тепловозы с дизельными установками; в авиационном – поршневые, турбореактивные и реактивные двигатели.

Сравним эксплуатационные характеристики тепловых двигателей.

КПД:

Паровой двигатель – 8%.

Паровая турбина – 40%.

Газовая турбина – 25-30%.

Двигатель внутреннего сгорания – 18-24%.

Дизельный двигатель – 40– 44%.

Реактивный двигатель – 25%.

Широкое использование тепловых двигателей не проходит бесследно для окружающей среды: постепенно уменьшается количество кислорода и увеличивается количество углекислого газа в атмосфере, воздух загрязняется вредными для здоровья человека химическими соединениями. Возникает угроза изменения климата. Поэтому нахождение путей уменьшения загрязнения окружающей среды является сегодня одной из наиболее актуальных научно-технических проблем.

Примеры и разбор решения заданий

1. Какую среднюю мощность развивает двигатель автомобиля, если при скорости 180 км/ч расход бензина составляет 15 л на 100 км пути, а КПД двигателя 25%?

Дано: v=180км/ч = 50 м/с, V = 15 л = 0,015 м³, s = 100 км = 10⁵ м, ɳ = 25% = 0,25, ρ = 700 кг/м³, q = 46 × 10⁶ Дж/кг.

Найти: N.

Решение:

Запишем формулу для расчёта КПД теплового двигателя:

Работу двигателя, можно найти, зная время работы и среднюю мощность двигателя:

Количество теплоты, выделяющееся при сгорании бензина, находим по формуле:

Учитывая всё это, мы можем записать:

Время работы двигателя можно найти по формуле:

Из формулы КПД выразим среднюю мощность:

.

Подставим числовые значения величин:

После вычислений получаем, что N=60375 Вт.

Ответ: N=60375 Вт.

2. Тепловая машина имеет КПД 25 %. Средняя мощность передачи теплоты холодильнику составляет 4 кВт. Какое количество теплоты рабочее тело получает от нагревателя за 20 с?

Дано: ɳ = 25%, N = 4000 Вт, t = 20 с.

Найти: Q₁.

Решение

  =

– это количество теплоты, отданное холодильнику

Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.

Как следует из первого закона термодинамики, полученное газом количество теплоты Q полностью превращается в работу A при изотермическом процессе, при котором внутренняя энергия остается неизменной (ΔU = 0):

Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме (p, V) газообразного рабочего тела с помощью замкнутых кривых (рис. 3.11.1). При расширении газ совершает положительную работу A₁, равную площади под кривой abc, при сжатии газ совершает отрицательную работу A₂, равную по модулю площади под кривой cda. Полная работа за цикл A = A₁ + A₂ на диаграмме (p, V) равна площади цикла. Работа A положительна, если цикл обходится по часовой стрелке, и A отрицательна, если цикл обходится в противоположном направлении.

Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd

Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q₁ > 0 и отдает холодильнику количество теплоты Q₂ < 0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно

При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (ΔU = 0). Согласно первому закону термодинамики,

Отсюда следует:

Работа A, совершаемая рабочим телом за цикл, равна полученному за цикл количеству теплоты Q. Отношение работы A к количеству теплоты Q₁, полученному рабочим телом за цикл от нагревателя, называется коэффициентом полезного действия η тепловой машины:

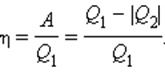
Модель. Термодинамические циклы.

Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1). Энергетическая схема тепловой машины изображена на рис. 3.11.2.

Рисунок 3.11.2. Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1 > 0, A > 0, Q2 < 0; T1 > T2

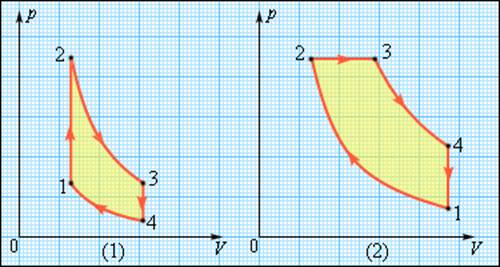
В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.

Рисунок 3.11.3. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2)

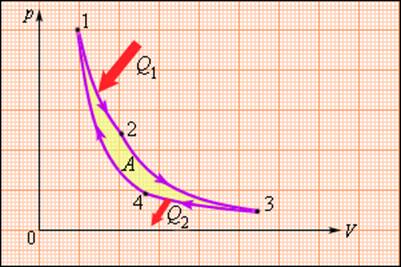
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).

Рисунок 3.11.4. Цикл Карно

Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T₁. Газ изотермически расширяется, совершая работу A₁₂, при этом к газу подводится некоторое количество теплоты Q₁ = A₁₂. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A₂₃ > 0. Температура газа при адиабатическом расширении падает до значения T₂. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T₂ < T₁. Происходит процесс изотермического сжатия. Газ совершает работу A₃₄ < 0 и отдает тепло Q₂ < 0, равное произведенной работе A₃₄. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T₁, газ совершает работу A₄₁ < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:

На диаграмме (p, V) эта работа равна площади цикла.

Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1–2 и 3–4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником).

Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для 1 моля газа

где T₁ и T₂ – начальная и конечная температуры газа.

Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам

По определению, коэффициент полезного действия η цикла Карно есть

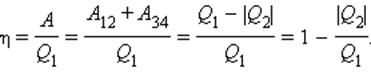
С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T₁ и холодильника T₂:

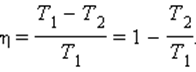
Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, т. е. бесконечно близким к состоянию теплового равновесия с окружающими телами (тепловыми резервуарами или термостатами). Цикл Карно исключает теплообмен при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника:

Модель. Цикл Карно.

Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях. Обход цикла по часовой стрелке соответствует тепловому двигателю, когда полученное рабочим телом тепло частично превращается в полезную работу. Обход против часовой стрелки соответствует холодильной машине, когда некоторое количество теплоты отбирается от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Поэтому идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной.

В реальных холодильных машинах используются различные циклические процессы. Все холодильные циклы на диаграмме (p, V) обходятся против часовой стрелки. Энергетическая схема холодильной машины представлена на рис. 3.11.5.

Рисунок 3.11.5. Энергетическая схема холодильной машины. Q1 < 0, A < 0, Q2 > 0, T1 > T2

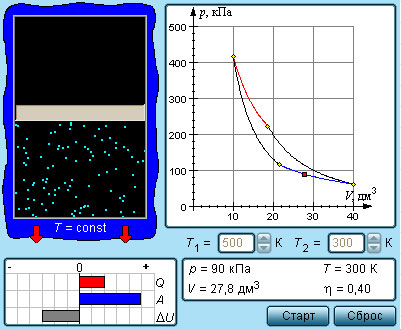
Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q₂| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением

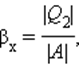
т. е. эффективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении β_х может быть и больше, и меньше единицы. Для обращенного цикла Карно

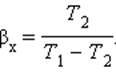
Если полезным эффектом является передача некоторого количества тепла |Q₁| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность β_Т теплового насоса может быть определена как отношение

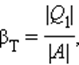
т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:

следовательно, β_Т всегда больше единицы. Для обращенного цикла Карно

Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.

Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.

Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений (ΔU=0): 

A=Q

Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3.11.1 в виде диаграммы (p, V) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A1, эквивалентную площади под кривой abc. При сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A=A1+A2 на диаграмме (p, V) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.

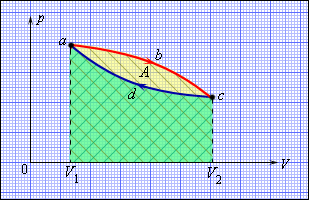
Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd.

Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.

Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.

Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q1>0 и теряет, отдавая холодильнику, количество теплоты Q2<0. Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:

Q=Q1+Q2=Q1-Q2.

Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется ΔU=0. Основываясь на первом законе термодинамики, запишем: 

∆U=Q-A=0.

Из этого следует: 

A=Q=Q1-Q2.

Работа A, которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q.

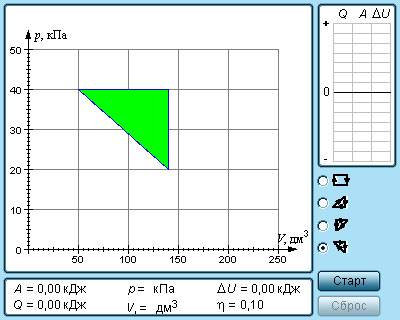
Рисунок 3.11.2. Модель термодинамических циклов.

Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть (1–η) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η<1. На рисунке 3.11.3 проиллюстрирована энергетическая схема тепловой машины.

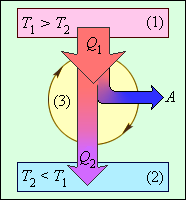
Рисунок 3.11.3. Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1>0, A>0, Q2<0; T1>T2.

Виды тепловых двигателей

В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3.11.3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры (1–2, 3–4) и две адиабаты (2–3, 4–1), дизельного двигателя -две адиабаты (1–2, 3–4), одну изобару (2–3) и одну изохору (4–1). Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 %, у дизельного двигателя – приблизительно 40 %.

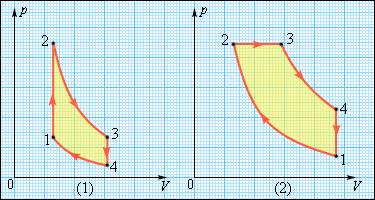
Рисунок 3.11.4. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2).

Цикл Карно

Круговой процесс, изображенный на рисунке 3.11.5, состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.

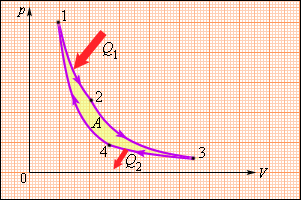
Рисунок 3.11.5. Цикл Карно.

Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы (1–2) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T1. Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A12 количество теплоты Q1=A12. После этого на участке адиабаты (2–3) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A23>0. Его температура при адиабатическом расширении снижается до величины T2. На идущем следующим участке изотермы (3–4) газ приводится в тепловой контакт с холодильником в условиях температуры T2<T1. Производится процесс изотермического сжатия. Газом совершается некоторая работа A34<0 и отдается тепло Q2<0, эквивалентное произведенной им работе A34. Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T1, также совершается работа A41<0. совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках: 

A=A12+A23+A34+A41.

На диаграмме (p, V) данная работа равняется площади цикла.

Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1–2 и 3–4, относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.

Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения ΔU его внутренней энергии. Для 1 моля газа верно следующее выражение:

A=-∆U=-CV(T2-T1),

в котором T1 и T2 представляют собой начальную и конечную температуры рабочего тела.

Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:

A23=-A41.

Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений: 

η=AQ1=A12+A34Q12=Q1-Q2Q1=1-Q2Q1.

С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T2 и нагревателя T1: 

η=T1-T2T1=1-T2T1.

Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника: 

ηКарно=ηmax

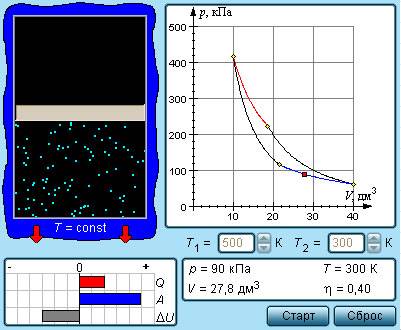
Рисунок 3.11.6. Модель цикла Карно.

Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.

Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.

В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме (p, V) обходятся против часовой стрелки. На рисунке 3.11.7 проиллюстрирована энергетическая схема холодильной машины.

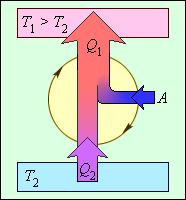
Рисунок 3.11.7. Энергетическая схема холодильной машины. Q1<0, A>0, Q2 > 0, T1>T2.

Работающее по холодильному циклу устройство может обладать двояким предназначением.

Если полезным эффектом является отбор некоторого количества тепла Q2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.

Эффективность работы холодильника может быть охарактеризована следующим отношением: 

βx=Q2A.

Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. В условиях подобного определения βх может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:

βx=T2T1-T2.

В случае, когда полезным эффектом является передача некоего количества тепла
|Q1| нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.

Эффективность βТ теплового насоса может быть определена с помощью отношения: 

βт=Q1A.

То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует: 

Q1>A.

Следовательно, βТ всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:

βт=1η=T1T1-T2.

В данном разделе вы уже познакомились с устройством и принципом работы двух видов теплового двигателя: двигателя внутреннего сгорания и паровой турбины. Используя эти механизмы, мы совершаем какую-то работу. Очевидно, что работа будет совершаться за счет энергии, которая выделяется при сгорании топлива. Но большая часть этой энергии теряется в окружающей среде. То есть эта часть энергии не используется полезно.

Следовательно, и работу таких механизмов тогда нужно рассчитывать специальным образом. Для этого в физике разделяют работу на полную и полезную, вводят понятие коэффициента полезного действия (КПД) механизма. На данном уроке мы познакомимся с этими величинами и рассмотрим решение задач с использованием КПД.

Полезная работа теплового двигателя

Для того чтобы судить о полезной работе теплового двигателя, обратимся еще раз к его устройству. Если рассматривать его принцип работы, то устройство любого теплового двигателя можно представить в виде простой схемы (рисунок 1).

Тепловой двигатель состоит из нагревателя, рабочего тела и холодильника.

Рабочим телом является газ или пар. Например, в паровой турбине — это пар, в газовой — газ, в двигателе внутреннего сгорания — смесь паров бензина и воздуха.

Этот газ получает некоторое количество теплоты $Q_1$ от нагревателя. Под нагревателем подразумевается не какое-то специальное механическое устройство, как можно подумать. Нагреватель в схеме теплового двигателя — это горящее топливо.

Газ нагревается и расширяется. Так он совершает работу $A_п$, используя свою внутреннюю энергию.

Но важно понимать, что часть этой внутренней энергии $Q_2$ не совершает какую-то полезную для нас работу. Она передается вместе с отработанным паром или выхлопными газами атмосфере — холодильнику. 

В качестве холодильника может использоваться резервуар с водой. Отработавший пар будет в таком случае приносить дополнительную пользу — нагревать воду для ее дальнейшего использования. Но этот процесс уже требует отдельного рассмотрения. 

Итак, нас интересует именно та часть энергии топлива, выделяемая при его сгорании, которая превращается в полезную работу. От величины этой части энергии зависит экономичность двигателя.

Для этой характеристики мы вводим новое понятие — коэффициент полезного действия (КПД) теплового двигателя.

КПД теплового двигателя

Коэффициент полезного действия (КПД) теплового двигателя — это отношение совершенной полезной работы двигателя к энергии, полученной от нагревателя.

КПД теплового двигателя также как и КПД простейших механизмов, изученных вами в прошлом курсе, обозначается греческой буквой “эта” — $eta$ и выражается в процентах.

Формула для расчета КПД теплового двигателя имеет следующий вид:

$eta = frac{A_п}{Q_1}$,

или

$eta = frac{Q_1 — Q_2}{Q_1} cdot 100 %$,

где $A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику,
$Q_1 — Q_2 = A_п$ — количество теплоты, которое пошло на совершение работы.

Например, при сгорании топлива выделяется определенное количество энергии. Одна пятая этой энергии пошла на совершение полезной работы. Это означает, что КПД двигателя равен $frac{1}{5}$ или $20 %$.

Средние значения КПД различных тепловых двигателей

В таблице 1 представлены средние значения КПД некоторых двигателей.

Двигатель	КПД, %
Паровой двигатель	8
Двигатель внутреннего сгорания	18 — 40
Газовая турбина	25 — 30
Паровая турбина	40
Дизельный двигатель	40 — 44
Реактивный двигатель на жидком топливе	47

Обратите внимание, что КПД всегда меньше единицы — меньше $100 %$. Это означает, что холодильник всегда получает некоторое количество теплоты от нагревателя.

Одной из важнейших технических задач при проектировании двигателей является повышение значения КПД.

Упражнения

$A_п — ?$

Посмотреть решение и ответ

Скрыть

Дано:
$Q_1 = 155 space Дж$
$Q_2 = 85 space Дж$ 

$eta — ?$

Посмотреть решение и ответ

Скрыть

$eta -?$

Посмотреть решение и ответ

Скрыть