Как найти работу тока за час

Как найти работу если известно напряжение и сила тока?

Чтобы подсчитать работу электрического тока, вспомним определение понятия напряжения: U=А/q

Следовательно, работа электрического тока равна:

Электрический заряд можно выразить через силу тока и его время протекания q=It:

Итак, работа электрического тока равна произведению силы тока на напряжение и на время протекания тока по цепи.

Работа электрического тока выражается в джоулях (Дж) . В качестве внесистемной единицы принята работа тока силой 1 А в течение 1 ч на участке цепи с напряжением 1 В. Эту единицу работы назвали ватт-час (1 Вт-ч) : 1 Вт-ч = 3600 Дж = 3,6 кДж. На практике используют более крупные, кратные ей единицы:

1 гВт-ч= 102 Вт-ч = 3,6·105Дж,
1 кВт-ч= 103 Вт-ч = 3,6·106Дж,
1 МВт-ч = 106 Вт-ч = 3,6·109Дж.

Из курса физики VII класса вы знаете, что мощность равна отношению совершенной работы ко времени, в течение которого эта работа была совершена. Мощность в механике принято обозначать буквой N, в электротехнике — буквой Р. Следовательно, мощность равна:

Пользуясь этой формулой, найдем мощность электрического тока. Так как работа тока определяется формулой А = IUt, то мощность электрического тока равна:

За единицу мощности ватт (Вт) принята мощность тока силой 1 А на участке с напряжением 1 В. Следовательно, 1 Вт = 1 А·1 В.

Ватт сравнительно небольшая мощность, на практике используют более крупные единицы, кратные ватту: 1 гВт (гектоватт) = 102 Вт, 1 кВт (киловатт) = 103 Вт, 1 МВт (мегаватт) = 106 Вт, 1 ГВт (гигаватт) = 109 Вт.

Источник

Работа электрического тока. Закон Джоуля-Ленца.

Для определения работы, которая совершается током, проходящим по некоторому участку цепи, нужно воспользоваться определением напряжения: . Значит,

где А — работа тока; q — электрический заряд, который прошел за определенное время через исследуемый участок цепи. Подставив в последнее равенство формулу q = It, имеем:

Работа электрического тока на участке цепи является произведением напряжения на концах это­го участка на силу тока и на время, на протяжении которого совершалась работа.

Закон Джоуля-Ленца .

Закон Джоуля — Ленца гласит: количество теплоты, которое выделяется в проводнике на участке электрической цепи с сопротивлением R при протекании по нему постоянного тока I в течение времени t равно произведению квадрата тока на сопротивление и время:

Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтверж­ден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которо­му удалось раскалить железную спираль, пропустив через нее электрический ток.

Из закона Джоуля — Ленца видно, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на про­воднике с наибольшим сопротивлением. Это применяется в технике, например, для распыления металлов.

При параллельном соединении каждый проводник находятся под одинаковым напряжением, но токи в них разные. Из формулы (Q = I 2 Rt) видно, что, так как, согласно закону Ома , то

Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.

Если в формуле (А = IUt) выразить U через IR, воспользовавшись законом Ома, получим Закон Джоуля — Ленца. Это лишний раз подтверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.

Источник

Как узнать, сколько киловатт-часов потребляет прибор, исходя из его заявленной мощности?

Прочитав данный пост, вы можете узнать, сколько энергии (Вт/ч, кВт/ч) потребляет прибор, исходя из его заявленной мощности (Вт, кВт), а также — сколько нужно платить за энергию, используя этот прибор.

Пример 1: Предположим, у вас есть чайник, мощностью 2100 Вт. И вам нужно узнать, сколько платить за энергию, используя чайник. 2100 Вт он потребляет в час. То есть, 2,1 кВт — это тоже самое, что 2,1 кВт/ч. На кипячение, как известно — тратится 5 минут. Поэтому 2100 Вт поделим на 60, чтобы узнать сколько тратится ватт в минуту.

2100 / 60 = 35 ватт в минуту.

Чтобы узнать, сколько тратится энергии за 5 минут, мы 35 должны умножить на 5.

35 * 5 = 175 ватт за 5 минут.

Кипятить мы будем по 5 раз в день, поэтому умножим еще на 5.

175 * 5 = 875 ватт за 5 кипячений.

Как известно, платить нужно 1 раз в месяц. Поэтому 875 ватт мы умножим на 30 дней.

875 * 30 = 26250 ватт = 26,25 киловатт в месяц.

Округлим 27 киловатт в месяц.

Итак, цена за 1 киловатт — 4 рубля 68 копеек. Поэтому, 27 умножим на 5. Всякие копейки в расчет не берем.

27 * 5 = 135 рублей.

Итог: плата за электроэнергию составит 135 рублей.

Еще один пример: энергосберегающая светодиодная лампа на 7 Вт. Эти 7 Вт она потребляет в час. Гореть она будет по 5 часов в день.

7 * 5 = 35 Вт за 5 часов горения

Далее, 35 умножим на 30 дней.

35 * 5 = 1050 Вт в месяц = 1,05 кВт в месяц

1,05 умножим на 5.

1,05 * 5 = 5 рублей.

Итог: плата — 5 рублей.

И последний пример: электроплита на 7 кВт. Эти 7 кВт она потребляет в час.

Готовить на ней мы будем по 3 часа в день.

7000 Вт * 3 = 21000 Вт = 21 кВт за 3 часа готовки

21000 Вт умножим на 30 дней.

21000 * 30 = 630000 Вт = 630 кВт в месяц.

И 630 умножим на 5 рублей

630 * 5 = 3150 руб.

Плата за энергию составит 3150 руб.

Поэтому, у кого дома электроплита — у того тариф на электроэнергию, где 1 кВт стоит дешевле. То есть — не 5 а 3 рубля.

630 * 3 = 1890 руб плата с тарифом для электроплит.

Дубликаты не найдены

более того придётся ещё и выключить регуляторы

чтобы комфорки и духовка не выключались при наборе температуры

таже фигня и с чайником. по факту он 1.8 а не 2.2

Мда. Аффтор пишет бред. Ну а про 7 кВт в течении 5 часов. У авффтора в квартире ресторан, что у него плита пашет во все 4 конфорки непрерывно?

Это какой класс школьной программы?

Школота, мать её.

Думал, осенью их хоть поменьше будет — хрен там.

кстати твой ПК консоль во время игры кушают от розетки от 300-500вт в час

зарядка от телефона от 8-15вт в час

А ватт-часов в час, или просто ватт.

Ватт-час — это количество энергии.

А Ватт — моментальная мощность, со временем она не меняется.

О чём я и говорил.

Кстати о единице скорости строительства я тока счас узнал))

Да это прикол такой)

Технически всё верно, но никто в своём уме не будет это использовать в работе)

Слышал раньше, но подобной картинки не встречал.

А что это за единица такая — кВт/ч?

Правильно Вт×ч, а не делить

Справочник сначала открывай, а потом статьи пиши.

правильно кВт*ч) приставка кило- с маленькой буквы пишется)

Внесистемная единица количества используемой энергии. Используется в расчётах за потреблённое электричество.

Серьезно? Киловатт делить на час?

Написание через дробь неправильно с точки зрения физики, но используется в половине случаев. Так что привыкайте, с этим уже ничего не поделать.

Сколько потребляет стиралка за месяц

Да, я знаю, что после поста про кипячение чая в микроволновке все ждут сравнения чайника с электроплитой, но для этого ваттметр не годится, т.к. у плиты другая розетка, и для измерений придется использовать электросчетчик, отключив все остальные потребители в квартире, а до этого никак не доходят руки. Я обязательно это сделаю в скором времени.

А пока я постараюсь ответить на вопрос, действительно ли стоит заморачиваться с тем, чтобы ставить стиралку на ночь, чтобы сэкономить на ночном тарифе на электроэнергию, и вообще, много ли она потребляет. Неожиданно? Сам в шоке, но меня давно интересовал этот вопрос.

Стиралка у меня Electrolux EWS 10410W, вот такая:

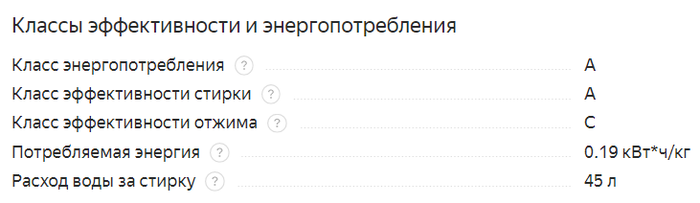
Она имеет следующие параметры эффективности:

Тут, кстати, указано расчетное потребление энергии, в конце попробуем прикинуть расчеты с ним.

Так как классах энергоэффективности я не шарю, нарыл шпаргалку:

Добавлю, что современные стиралки имеют класс «А» с кучей плюсов, то есть моя стиралка считается еще середнячком.

Я взял ваттметр и засунул его куда-то под кухонный гарнитур в зад стиралки, оставив в таком виде на месяц. Через месяц доставать его было лень (туда очень трудно подлезть), поэтому показания я снял на 37-й день измерений. Вот что я там увидел:

За 37 дней стиралка потребила 10.67 кВт*ч, что соответствует 8.8 кВт*ч/месяц.

Теперь о количестве стирок. За это время было сделано 10 стирок. Чаще всего стирка ставилась на 2 часа при 60 градусах, отжим 1000 об/мин, но пару раз было час-полтора, 40 градусов и 900 об/мин.

Перейдем к подсчетам.

У нас в Санкт-Петербурге дневной тариф 4.06 руб/кВт*ч, ночной — 2.34 руб/кВт*ч.
Таким образом, при дневном тарифе стиралка намотает за месяц 35.72 руб, при ночном — 20.59 руб. Разница составляет 15.13 руб в месяц. Это даже меньше, чем экономия за счет отказа от электрочайника! При этом цена одной стирки получилась 4.3/2.5 руб за день и ночь соответственно (не считая 3 руб за воду).

А теперь сравним наши замеры с расчетами исходя из паспорта стиралки. Для этого возьмем:

суммарное время стирок — 18.5 ч, средняя загрузка стиралки — 3 кг (прикинул исходя из 4.5 кг максимальных по паспорту), расход по паспорту 0.19 кВт*ч/кг, все перемножаем, получаем расчетное потребление за 37 дней — 10.55 кВт*ч, за месяц — 8.7 кВт*ч. Божечки, сошлось!

Вывод: утверждение о возможности сэкономить на ночных стирках немного преувеличено, проще не париться и запускать стиралку когда удобно. Но если 15 руб в месяц не лишние, то лучше ставить на ночь.

Источник

Работа и мощность тока

Какую работу совершает электрический ток, проходя по тому или иному участку цепи? Чтобы определить это, вспомним, что такое напряжение. Согласно формуле (11.1) U = A/q. Отсюда следует, что

где A — работа тока; q — электрический заряд, прошедший за данное время через рассматриваемый участок цепи. Подставляя в последнее равенство выражение q = It, получаем

Итак, чтобы найти работу тока на участке цепи, надо напряжение на концах этого участка U умножить на силу тока I и на время t, в течение которого совершалась работа.

Действие тока характеризуют не только работой A, но и мощностью P. Мощность тока показывает, какую работу совершает ток за единицу времени. Если за время t была совершена работа A, то мощность тока P = A/t. Подставляя в это равенство выражение (18.2), получаем

Итак, чтобы найти мощность электрического тока P, надо силу тока I умножить на напряжение U.

В Международной системе единиц (СИ) работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время — в секундах (с). При этом

1 Вт = 1 Дж/с, 1 Дж = 1 Вт · с.

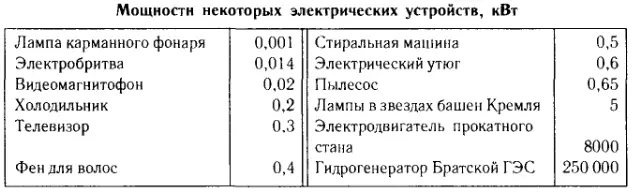
Мощности некоторых электроустройств, выраженные в киловаттах (1 кВт = 1000 Вт), приведены в таблице 5.

Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать I = 10 А, то при напряжении U = 220 В соответствующая электрическая мощность оказывается равной:

P = 10 A · 220 В = 2200 Вт = 2,2 кВт.

Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока и потому недопустимо.

В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком (счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения оказывается пропорциональной силе тока и напряжению. Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в киловатт-часах (кВт·ч).

1 кВт·ч — это работа, совершаемая электрическим током мощностью 1 кВт в течение 1 ч. Так как 1 кВт = 1000 Вт, а 1 ч = 3600 с, то

1 кВт·ч = 1000 Вт · 3600 с = 3 600 000 Дж.

. 1. Как находится работа электрического тока? 2. По какой формуле находится мощность тока? 3. С помощью какого прибора измеряют работу тока? Какая единица работы при этом используется? 4. Сложите мощности всех имеющихся у вас дома электрических устройств. Допустимо ли их одновременное включение в сеть? Почему?

Экспериментальное задание. Рассмотрите у себя дома счетчик электроэнергии. Выясните, как снимаются с него показания. Измерьте с его помощью электроэнергию, израсходованную задень. В течение следующего дня старайтесь экономить энергию — не оставляйте включенным свет, если это не нужно; выключайте электроприборы, которыми в данный момент не пользуетесь; не смотрите все подряд по телевизору. После этого определите с помощью счетчика, сколько электроэнергии вам удалось сэкономить. Вычислите стоимость этой энергии. Сколько денег вам удастся сберечь при подобной экономии энергии за месяц?

Источник

Какую работу совершает электрический ток, проходя по тому или иному участку цепи? Чтобы определить это, вспомним, что такое напряжение. Согласно формуле (11.1) U = A/q. Отсюда следует, что

A = qU,     (18.1)

где A — работа тока; q — электрический заряд, прошедший за данное время через рассматриваемый участок цепи. Подставляя в последнее равенство выражение q = It, получаем

A = IUt.     (18.2)

Итак, чтобы найти работу тока на участке цепи, надо напряжение на концах этого участка U умножить на силу тока I и на время t, в течение которого совершалась работа.

Действие тока характеризуют не только работой A, но и мощностью P. Мощность тока показывает, какую работу совершает ток за единицу времени. Если за время t была совершена работа A, то мощность тока P = A/t. Подставляя в это равенство выражение (18.2), получаем

P = IU.      (18.3)

Итак, чтобы найти мощность электрического тока P, надо силу тока I умножить на напряжение U.

В Международной системе единиц (СИ) работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время — в секундах (с). При этом

1 Вт = 1 Дж/с, 1 Дж = 1 Вт · с.

Мощности некоторых электроустройств, выраженные в киловаттах (1 кВт = 1000 Вт), приведены в таблице 5.

Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать I = 10 А, то при напряжении U = 220 В соответствующая электрическая мощность оказывается равной:

P = 10 A · 220 В = 2200 Вт = 2,2 кВт.

Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока и потому недопустимо.

В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком (счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения оказывается пропорциональной силе тока и напряжению. Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в киловатт-часах (кВт·ч).

1 кВт·ч — это работа, совершаемая электрическим током мощностью 1 кВт в течение 1 ч. Так как 1 кВт = 1000 Вт, а 1 ч = 3600 с, то

1 кВт·ч = 1000 Вт · 3600 с = 3 600 000 Дж.

??? 1. Как находится работа электрического тока? 2. По какой формуле находится мощность тока? 3. С помощью какого прибора измеряют работу тока? Какая единица работы при этом используется? 4. Сложите мощности всех имеющихся у вас дома электрических устройств. Допустимо ли их одновременное включение в сеть? Почему?

Экспериментальное задание. Рассмотрите у себя дома счетчик электроэнергии. Выясните, как снимаются с него показания. Измерьте с его помощью электроэнергию, израсходованную задень. В течение следующего дня старайтесь экономить энергию — не оставляйте включенным свет, если это не нужно; выключайте электроприборы, которыми в данный момент не пользуетесь; не смотрите все подряд по телевизору. После этого определите с помощью счетчика, сколько электроэнергии вам удалось сэкономить. Вычислите стоимость этой энергии. Сколько денег вам удастся сберечь при подобной экономии энергии за месяц?

Чтобы подсчитать работу электрического тока, вспомним определение понятия напряжения: U=А/q

Следовательно, работа электрического тока равна:

A=qU

Электрический заряд можно выразить через силу тока и его время протекания q=It:

А = IUt

Итак, работа электрического тока равна произведению силы тока на напряжение и на время протекания тока по цепи.

Работа электрического тока выражается в джоулях (Дж) . В качестве внесистемной единицы принята работа тока силой 1 А в течение 1 ч на участке цепи с напряжением 1 В. Эту единицу работы назвали ватт-час (1 Вт-ч) : 1 Вт-ч = 3600 Дж = 3,6 кДж. На практике используют более крупные, кратные ей единицы:

1 гВт-ч= 102 Вт-ч = 3,6·105Дж,
1 кВт-ч= 103 Вт-ч = 3,6·106Дж,
1 МВт-ч = 106 Вт-ч = 3,6·109Дж.

Из курса физики VII класса вы знаете, что мощность равна отношению совершенной работы ко времени, в течение которого эта работа была совершена. Мощность в механике принято обозначать буквой N, в электротехнике — буквой Р. Следовательно, мощность равна:

Р = А/t.

Пользуясь этой формулой, найдем мощность электрического тока. Так как работа тока определяется формулой А = IUt, то мощность электрического тока равна:

Р = IU.

За единицу мощности ватт (Вт) принята мощность тока силой 1 А на участке с напряжением 1 В. Следовательно, 1 Вт = 1 А·1 В.

Ватт сравнительно небольшая мощность, на практике используют более крупные единицы, кратные ватту: 1 гВт (гектоватт) = 102 Вт, 1 кВт (киловатт) = 103 Вт, 1 МВт (мегаватт) = 106 Вт, 1 ГВт (гигаватт) = 109 Вт.

Вы уже знаете, что работа электрического тока измеряется в джоулях. Но на практике часто используются другие величины, о которых вы и узнаете на данном уроке.

Почему неудобно выражать работу тока в джоулях на практике?

Начнем с того, что в паспортах электроприборов обычно указывают мощность тока в них. Как можно выразить работу тока через мощность и время?

Зная мощность потребителя электроэнергии, можно рассчитать и работу тока, совершенную за определенное время: $A = Pt$.

Рассмотрим единицы измерения величин в этой формуле. Мощность у нас измеряется в ваттах, время — в секундах, а работа — в джоулях.

$1 space Вт = 1 frac{Дж}{с}$,
$1 space Дж = 1 space Вт cdot с$.

Обратите внимание на то, что время выражается в секундах. Но обычно в потребителе электроэнергии ток совершает работу более продолжительное время.

Некоторые приборы мы используем часами, а некоторые — круглосуточно. Например, тот же холодильник. Расчет же электроэнергии по счетчику производится раз в месяц.

Логично, что очень неудобно переводить такие большие промежутки времени в секунды каждый раз при расчете работы электрического тока. Поэтому и используются другие единицы измерения.

Внесистемные единицы измерения работы электрического тока

По вышеуказанным причинам при расчете работы электрического тока время намного удобнее выражать в часах. Сама же работа часто выражается в следующих единицах: $ватт cdot час$ ($Вт cdot ч$), $гектоватт cdot час$ ($гВт cdot ч$), $киловатт cdot час$ ($кВт cdot ч$).

$1 space Вт cdot ч = 3600 space Дж$,
$1 space гВт cdot ч = 100 space Вт cdot ч = 360 space 000 space Дж$,
$1 space кВт cdot ч = 1000 space Вт cdot ч = 3 space 600 space 000 space Дж$.

Снятие показаний счетчика и расчет потребляемой энергии

Каждый месяц люди платят за «электричество». То есть за использованную электроэнергию в течение месяца, которая определяется совершенной работой электрического тока.

Сумма платежа рассчитывается исходя из показаний счетчика и действующего тарифа на электроэнергию.

В начале нового месяца фиксируются показания счетчика (рисунок 1, а). В конце месяца эти показания фиксируются еще раз (рисунок 1, б). Обратите внимание, что обычно последнее число, показанное на счетчике, — это десятые доли $кВт cdot ч$. Эта последняя цифра может быть выделена цветной рамкой, или перед ней будет стоять точка.

Разница между этими показаниями — это и есть израсходованная за месяц электроэнергия. Она же эквивалентна работе электрического тока, совершенной во всех электроприборах за месяц. Рассчитаем ее:
$A = 11706.6 space кВт cdot ч space — space 10982.6 space кВт cdot ч = 724 space кВт cdot ч$.

Действующий тариф (стоимость $1 space кВт cdot ч$) указывается в квитанциях на оплату. Он может различаться в зависимости от страны или ее региона.

Возьмем тариф, равный $3 frac{р.}{кВт cdot ч}$ (3 рубля за $1 space кВт cdot ч$).

Чтобы рассчитать стоимость потребленной энергии, нужно тариф умножить на количество (численное значение) этой энергии:
$Стоимость = Тариф cdot A$.

В нашем случае получается:
$Стоимость = 3 frac{р.}{кВт cdot ч} cdot 724 space кВт cdot ч = 2172 space р.$

Пример задачи

Электрическая лампа рассчитана на ток мощностью $100 space Вт$. Ежедневно лампа горит в течение $6 space ч$. Найдите работу тока за один месяц (30 дней) и стоимость израсходованной энергии, считая, что тариф составляет 300 копеек за $1 space кВт cdot ч$.

Дано:
$P = 100 space Вт$
$t = 6 space ч cdot 30 = 180 space ч$
$Тариф = 300 frac{к.}{кВт cdot ч}$

$A — ?$
$Стоимость — ?$

Решение:

Работу электрического тока рассчитаем по формуле: $A = Pt$.
$A = 100 space Вт cdot 180 space ч = 18 space 000 Вт cdot ч = 18 space кВт cdot ч$.

Рассчитаем стоимость. Для этого умножим тариф на работу, совершаемую электрическим током:
$Стоимость = 300 frac{к.}{кВт cdot ч} cdot 18 space кВт cdot ч = 540 space к. = 54 space р.$

Ответ: $A = 18 space кВт cdot ч$, $стоимость = 54 space рубля$.

Упражнения

Дано:
$P = 0.6 space кВт$
$t = 1.5 space ч$

$A — ?$

Показать решение и ответ

Скрыть

Дано:
$P_1 = P_2 = 60 space Вт$
$P_3 = P_4 = 40 space Вт$
$t = 3 space ч cdot 30 = 90 space ч$
$Тариф = 3.3 frac{р.}{кВт cdot ч}$

$Стоимость — ?$

Показать решение и ответ

Скрыть

Дано:
$U = 220 space В$
$P_1 = P_2 = P_3 = 40 space Вт$
$t_1 = t_2 = t_3 = 4 space ч cdot 30 = 120 space ч$
$P_4 = 800 space Вт$
$t_4 = 1 space ч cdot 30 = 30 space ч$
$P_5 = 1000 space Вт$
$t_5 = 0.5 space ч cdot 30 = 15 space ч$
$P_6 = 600 space Вт$
$t_6 = 0.5 space ч cdot 4 = 2 space ч$
$Тариф = 3.3 frac{р.}{кВт cdot ч}$

$Стоимость — ?$

Показать решение и ответ

Скрыть