Как найти работу тормозящей силы

Как найти работу тормозящей силы

Известно, что грузовой автомобиль массой пять тысяч килограмм движется по горизонтальному пути со скоростью семьдесят два километра в час (20 метров в секунду).
Необходимо: определить силу и время торможения автомобиля, если тормозной путь составил пять метров.

Дано: m=5000 кг; v=20 м/сек; s=5 м
Найти: F-?; t-?

Решение

Исходя из того, что работа силы торможения численно равна изменению кинетической энергии движущегося автомобиля F*s={m*v^2}/2, получаем формулу для определения силы торможения

F={m*v^2}/{2*s}

Подставив в формулу численные значения, рассчитаем силу торможения грузового автомобиля

F={5000*20^2}/{2*5}=200000н

Из формулы v_t=v+at, при условии, что vt=0: t=-{v/a}, где a=-{v^2/{2*s}}, получаем формулу времени торможения

t={2*s}/v

Время торможения автомобиля

t={2*5}/20=0,5сек

Ответ: сила торможения автомобиля составила двести тысяч ньютон, время торможения равно половине секунды.

Источник

Лабораторная работа № 4

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА

Цели работы

1.Оценить момент тормозящей силы, действующий на тело в процессе вращения.

2.Определить момент инерции тела с учетом момента тормозящей силы.

3.Произвести расчет моментов, пользуясь энергетическими соотношениями.

Описание установки

Установка представляет собой тело со шкивом, которое вращается в шарикоподшипниках. На шкив намотана нить, один конец которой прикреплен к шкиву, а другой – к подставке массой mпод . На подставку могут помещаться

подгрузки массой mп . Груз под действием силы тяжести может опускаться,

приводя во вращение тело. После того, как груз от отметки h0 опустится на полную длину нити до отметки h1 (см. рис. 4.1), тело, вращаясь по инерции, поднимет груз снова на некоторую высоту до отметки h2.

В процессе движения часть механической энергии системы тело-груз расходуется на работу против тормозящей силы и, следовательно, превращается во внутреннюю энергию системы и окружающего воздуха, которые нагреваются. Из этого следует, что тело поднимет груз на высоту меньшую начальной, то есть отметка h2 всегда будет расположена ниже отметки h0. Тормозящая сила складывается из силы трения в подшипниках и из силы трения о воздух при движении тела и груза.

Рис. 4.1

ВЫВОД РАБОЧИХ ФОРМУЛ

Вывод формулы для косвенных измерений момента тормозящей силы

Для оценки момента тормозящей силы воспользуемся энергетическими соотношениями. Поскольку силы трения являются диссипативными, то работа тормозящей силы АТ при переходе системы тело-груз из начального состояния в конечное равна

где Eнач – механическая энергия системы тело-груз в начальном состоянии; Eкон – механическая энергия системы тело-груз в конечном состоянии.

Механическая энергия системы складывается из кинетической и потенциальной энергий. В те моменты времени, когда система покоится, кинетическая энергия равна нулю и, следовательно, механическая энергия становится равной только потенциальной энергии системы. Такие состояния системы возникают в начальный момент времени, когда груз находится на отметке h0 , и в тот момент, когда, спустившись вниз, груз за счет вращения

тела поднимается до отметки h2 (рис. 4.1). Если принять, что на высоте h1

потенциальная энергия груза равна нулю, то приращение механической энергии для выбранных начального и конечного состояний системы равно

E2 E0 mg

h2 h1

mg

h0 h1

mg(h21 h01 ) ,

(4.2)

где h01

– расстояние между отметками h0

и h1;

h21

– расстояние между отметками h2

и h1.

Будем считать, что момент тормозящей силы в основном

связан с

вращательным движением тела, т. е. тормозящей силой, действующей на груз, пренебрежем. Тогда элементарная работа момента тормозящей силы равна скалярному произведению

AT M T d ,

где M T – вектор момента тормозящей силы;

d – вектор бесконечно малого углового перемещения тела.

Оба вектора M T и d направлены вдоль оси вращения, но в противоположные стороны. Следовательно,

A

M

T

d

cos180

M

T

d

M

T

d .

T

Полная работа момента тормозящей силы, если предположить, что он постоянен, тогда равна

2

AT MT d MT 02 ,

(4.3)

0

где 02 – угол поворота тела вокруг оси при переходе системы из начального состояния в конечное (груз при этом перемещается от отметки h0 до отметки

h2 ).

При движении груза вниз от отметки h0 до отметки h1 со шкива

сматывается нить длиной

h0 h1

.

Учитывая,

что длина окружности шкива

равна 2 r и каждый оборот шкива соответствует углу 2 радиан, найдем угол

поворота шкива при движении груза вниз:

01

h1

2

h0

h1

радиан.

(4.4)

h0

2 r

r

Очевидно, что при дальнейшем вращении тела до момента, когда груз

остановится на отметке h2 , оно повернется на угол

h2 h1

радиан.

12

r

Тогда общий угол поворота тела, соответствующий переходу груза от

отметки h0 до отметки h2 , равен

02

01

h0 h1

h2 h1

радиан.

(4.5)

12

r

Подставляя (4.2) и (4.3) в (4.1) найдем

MT 02 mg

h2 h1

mg

h0 h1

mg(h21 h01 ) .

Отсюда, используя (4.5), получаем формулу для оценки модуля вектора

момента тормозящей силы

M

T

mgr

h1

h2

h1

mgr

h01 h21

.

(4.6)

h0

h0

h1

h2

h1

h01 h21

Вывод формулы для косвенных измерений момента инерции тела с учетом момента тормозящей силы

Рассмотрим систему тело-груз в начальный момент времени, когда груз находится на отметке h0 , а в качестве конечного выберем тот момент времени, когда груз опустился до нижней отметки h1, соответствующей полной длине

нити. Опять будем исходить из энергетического соотношения (4.1). Для выбранных начального и конечного состояний получим

где MT – момент тормозящей силы (4.6);

01 – угол поворота тела, соответствующий перемещению груза от

отметки h0 до h1 (4.4).

Начальная механическая энергия системы тело-груз равна

E0 mg h0

h1

mgh01.

(4.8)

Конечная механическая энергия системы складывается из кинетической энергии вращательного движения тела и кинетической энергии поступательного движения груза в момент прохождения им отметки h1:

I 2

mv 2

E E

E

1

1

,

вращ

пост

1

2

2

где I – момент инерции тела;

1 – угловая скорость вращения тела в момент t1 (см. рис. 4.1); v1 – скорость поступательного движения груза в момент t1 .

Строго говоря, в процессе движения груз за счет упругого растяжения

нити опускается чуть ниже отметки h1,

тормозится нитью, а затем за счет

упругого сжатия нити возвращается на эту отметку.

Предполагая, что движение системы является равноускоренным, для

скорости груза на отметке h1 получаем

v

2

h0 h1

2h01

,

(4.10)

1

t1

t1

где t1 – время, за которое груз опустится от отметки h0

до h1.

Угловая скорость вращения тела в тот же момент времени равна

v1

,

(4.11)

1

r

где r – радиус шкива, на который намотана нить.

Подставляя (4.7), (4.8), (4.9) в (4.1), получим

I2

mv 2

M

1

1

mg

h h

.

T

01

2

2

0

1

Из этой формулы, учитывая (4.4), (4.10) и (4.11), выражаем момент

инерции I :

(mgr M

T

)rt 2

(mgr M

T

)rt 2

I

1

mr 2

1

mr 2 ,

(4.12)

2

h0 h1

2h01

где MT – момент тормозящей силы, который вычисляется по формуле (4.6).

Получение формул для определения погрешностей косвенных измерений момента тормозящей силы и момента инерции тела

Методика получения оценок истинных значений величин и погрешностей при прямых и косвенных измерениях описана в [1]. При выполнении данной

h21 и

лабораторной работы прямыми будут являться измерения длины

h2 h1

времени t1 . Остальные величины, входящие в рабочие формулы (4.6) и (4.12),

измеряются заранее и их истинные значения с указанием погрешностей приведены в таблице исходных данных, помещенной около экспериментальной установки.

Выполнив прямые многократные измерения величин h21 и t1 (см. задание к работе) и проведя их статистическую обработку по методике, описанной в [1],

21 h21 и

найдите

h

t1 t1 для выбранного значения доверительной

вероятности. Эти величины будут в дальнейшем использованы для оценки истинного значения и погрешности при косвенных измерениях.

Подставляя в рабочую формулу (4.6) истинные значения всех аргументов, получим оценку истинного значения момента тормозящей силы:

21

,

mg

h01

h

M

(4.13)

T

r

h01

h21

где черта над величиной означает «оценка истинного значения».

h h

01 21 r h h

01 21

h h 2 01 21 m h h

01 21

Абсолютная погрешность косвенных измерений величины MT определяется формулой, приведенной в [1]

M

T

2

M

T

2

M

T

2

m

g

r

m

g

r

M

T

M

2

M

2

T

T

h

h

h

h

01

21

01

21

12

С помощью этой формулы, взяв частные производные по всем аргументам, получаем

2

12

h

h

01

21

mr

g

h

h

21

01

2

(4.14)

(h01

h21)

1

mgr

h01

)2

h01 h21

(h h

21

01

2

(h01

h21)

1

mgr

h21

h

(h h )2

h

21

01

21

01

Вформулу (4.14) входят пять квадратичных членов, вклад каждого из них

впогрешность величины MT не одинаков. Поэтому, чтобы упростить

вычисления, прежде чем применять эту формулу, необходимо оценить вклад каждого квадратичного слагаемого и оставить в формуле только наибольшие. Эта оценка, кроме того, позволит выявить те величины, точность измерения которых определяет точность получаемого результата.

Оценку истинного значения величины момента инерции тела, определяемого в опытах с помощью формулы (4.12), получим, подставив в нее истинные значения входящих аргументов:

I (mgr M T )rt12 mr 2 .

2h01

Абсолютная погрешность косвенных измерений величины I формулой, приведенной в [1].

I

2

I

2

I

2

I

2

m

g

r

h

m

g

r

h

01

01

I

2

2

I

I

M

t

M

T

T

t

1

1

С помощью этой формулы, взяв частные производные по всем аргументам, получаем

2

2

2

2

2

12

t

t

gr

mr

1

2

1

2

r

m

g

2h

2h

01

01

2

2

2

M

t

mgrt

1

T 1

2mr r

h

2h

01

01

2

2

2

2

mgr

t

M

rt

T

I

1

1

h

(4.16)

2

2

01

2h

2h

01

01

2

2

rt

1

M

T

2h01

2

2

mgr

t

M

rt

1

T

1

t

1

h

h

01

01

В формулу (4.16) входит шесть квадратичных членов. Один из них (пятый) связан с погрешностью величины MT , которая определяется формулой (4.14).

Как было сказано выше, прежде чем применять формулу (4.16) необходимо оценить вклад каждого квадратичного слагаемого, сохранив только наибольшие.

Задание к работе

1.

Заготовьте таблицу

для

прямых пятикратных измерений длины

h2 h1

h21 и времени t1

с

последующей статистической обработкой

полученных результатов.

2.Заранее выберите отметку h0 (от 30 до 50 см), от которой начнется

движение груза m .

3. Вращая тело рукой, размотайте нить на полную длину и заранее определите численное значение отметки h1. Обычно можно считать h1 0.

Внесите длину h0 h1 h01 в таблицу. Оцените погрешность измерения этой длины как систематическую погрешность измерительной линейки.

4.Включите электронный секундомер.

5.Вращая тело рукой, намотайте нить на шкив так, чтобы груз занял

положение соответствующее выбранной Вами начальной отметке h0 .

6. Проведите первый опыт, используя в качестве груза, тянущего нить, только одну подставку массой mпод без подгрузков. Предварительно нажатием

кнопки «Режим» установите режим №2 (светится индикатор «Реж.2»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее тело, и одновременно включится секундомер. При включенном режиме №2 секундомер в момент прохождения грузом отметки h1 автоматически остановится, но тормозная система при этом не остановит движение, позволив грузу подняться до отметки h2 . Дождитесь момента, когда

груз поднимется до

отметки

h2 , и зафиксируйте ее численное значение.

Внесите результаты

первого

опыта в таблицу измерений (ими будут

h2 h1

h21 и t1 ).

7.Пятикратно повторите этот опыт, не меняя массу груза, что необходимо для определения случайной погрешности прямых измерений.

8.Проведите по одному опыту, поместив на подставку сначала один, а затем сразу два подгрузка. Результаты внесите в таблицу измерений.

9.Проведите статистическую обработку пятикратно проведенных

прямых измерений величин

h2 h1

h21 и t1 (п. 6,7), пользуясь методикой,

изложенной в [1]. Получите оценку истинных значений и доверительных погрешностей для этих величин. Результаты вычислений внесите в таблицу.

10. Проведите оценку истинного значения момента тормозящей силы MT , пользуясь формулой (4.13).

11. Проведите численную оценку квадратичных членов формулы (4.14) и, отбросив малые, оцените погрешность косвенных измерений момента тормозящей силы MT .

12.Проведите оценку истинного значения момента инерции тела I , пользуясь формулой (4.15).

13.Проведите численную оценку квадратичных членов формулы (4.16) и,

отбросив малые, оцените погрешность косвенных измерений момента инерции тела I .

14.С помощью формулы (4.6) или (4.13) проведите расчет моментов тормозящей силы для однократных опытов с другими грузами (см. п.8). Погрешности измерений для этих опытов вычислять не надо. Обратите внимание на закономерное изменение момента тормозящей силы с ростом массы груза.

15.С помощью формулы (4.12) или (4.15) проведите расчет момента инерции тела для однократных опытов с другими грузами (см. п.8). Погрешности измерений для этих опытов вычислять не надо. Наблюдается ли закономерное изменение момента инерции с ростом массы груза?

Контрольные вопросы

1.Какая часть системы совершает в процессе опыта поступательное, а какая – вращательное движение?

2.Почему для описания вращательного движения удобней пользоваться угловыми кинематическими характеристиками, а для поступательного – линейными?

3.Что такое момент силы? Какие силы и моменты сил действуют на тело во время его движения?

4.Какие силы создают момент тормозящей силы? Можно ли указать точку приложения этих сил?

5.Как определить работу момента силы?

6.Сохраняется ли механическая энергия системы тело-груз в процессе опыта?

7.Как можно оценить момент тормозящей силы, пользуясь энергетическими соотношениями? Какие упрощающие предположения при этом делаются?

8.Изменяется ли момент тормозящей силы при увеличении массы груза, как и почему?

9.Что такое момент инерции тела, какое свойство тела он характеризует?

10.Как найти кинетическую энергию при поступательном и при вращательном движении?

11.Как можно определить момент инерции тела, пользуясь энергетическими соотношениями.

12.Зависит ли момент инерции тела от массы груза, закрепленного на конце нити?

13.Выведите формулу кинетической энергии тела, совершающего вращательное движение вокруг неподвижной оси.

14.Выведите рабочую формулу для оценки момента тормозящей силы. 15.Выведите рабочую формулу для момента инерции тела с учетом и без учета

момента тормозящей силы. Примените эти формулы, чтобы ответить на вопрос, имеет ли смысл учет момента тормозящей силы в проделанных опытах.

Индивидуальные задания для членов бригады, выполняющих лабораторную работу на одной установке

Номер

Индивидуальное задание

члена

бригады

1

Постройте, пользуясь формулой (6), график зависимости момента

тормозящей силы MT от величины h2 . При расчете считайте

величины h0 и h1, входящие в формулу, равными h0 50см ,

h1 0см . Численные значения радиуса шкива возьмите в таблице

исходных данных, помещенной в Приложении или около

лабораторной установки, на которой Вам предстоит выполнять

опыты. Массу m считайте равной массе подставки mпод (без

подгрузков).

2

Выполните задание аналогичное заданию для первого номера, но

для массы m равной сумме масс подставки и одного подгрузка:

m mпод mп .

3

Выполните задание аналогичное заданию для первого номера, но

для массы m равной сумме масс подставки и двух подгрузков:

m mпод 2mп .

Литература

1.Введение (эти методические указания).

2.Савельев И.В. Курс общей физики. – М, Наука, 1982 г. Т.1. и последующие издания.

Источник

88 / 0 / 1

Регистрация: 19.09.2013

Сообщений: 10

1

Определение работы силы торможения

17.10.2013, 20:18. Показов 6849. Ответов 6

Студворк — интернет-сервис помощи студентам

Маховик в виде сплошного диска, момент инерции которого I, вращаясь про торможении равнозамедленно, за время t уменьшил частоту с ω1 до ω2. Определите работу силы торможения.

Помогите разобраться что к чему, а то голова уже кругом..



0

Programming

Эксперт

94731 / 64177 / 26122

Регистрация: 12.04.2006

Сообщений: 116,782

 17.10.2013, 20:18

6

Хочу в Исландию

1041 / 840 / 119

Регистрация: 10.11.2010

Сообщений: 1,630

17.10.2013, 21:00

2

Чему равна кинетическая энергия вращающегося диска?



1

88 / 0 / 1

Регистрация: 19.09.2013

Сообщений: 10

17.10.2013, 21:41

 [ТС]

3

кинетическая энергия равна W= (Iω^2)2, насколько я понимаю.

Добавлено через 7 минут
ой, то есть W= (Iω^2)/2 забыл знак дроби
но мне все еще не понятно как от этого оттолкнуться



0

Хочу в Исландию

1041 / 840 / 119

Регистрация: 10.11.2010

Сообщений: 1,630

17.10.2013, 22:38

4

Правильно! А работа равна разности энергий:
https://www.cyberforum.ru/cgi-bin/latex.cgi?A=frac{Iomega _1^2}{2}-frac{Iomega _2^2}{2}.



1

88 / 0 / 1

Регистрация: 19.09.2013

Сообщений: 10

17.10.2013, 23:06

 [ТС]

5

То есть это и будет ответ на поставленный вопрос? Просто в условии фигурирует еще и время, вот я и думал, как же время присунуть сюда



0

Хочу в Исландию

1041 / 840 / 119

Регистрация: 10.11.2010

Сообщений: 1,630

17.10.2013, 23:25

6

Да, время кажется здесь лишнее… Например если мы передвигаем ящик против сил трения , то работа будет та же если мы его будем двигать пять минут или три часа, так ведь? То же самое с махрвиком, который надо остановить.



1

88 / 0 / 1

Регистрация: 19.09.2013

Сообщений: 10

17.10.2013, 23:38

 [ТС]

7

Хорошо, спасибо больше за разъяснение



0
Источник

Рассмотрим несколько примеров решения задач на вычисление работы сил.

Задача 1. Гоночный автомобиль разгоняется на прямолинейной дороге под действием постоянной силы тяги, значение которой F = 5 кН (рис. 120). Определите работу этой силы при перемещении автомобиля на расстояние L =100 м.

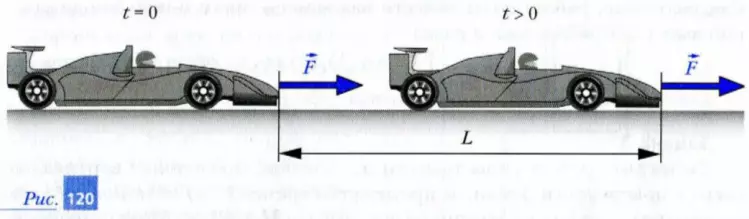
Работа силы тяги

Решение. Поскольку направление силы тяги и направление движения автомобиля совпадают, то

A = F · L = 5000 Н · 100 м = 500000 Дж = 500 кДж = 0,5 МДж.

Ответ: работа силы тяги равна 0,5 МДж.

Отметим, что сила тяги, действующая на автомобиль, создается в результате действия сил трения со стороны дороги на ведущие колеса в направлении движения автомобиля. У гоночных автомобилей с реактивным двигателем она создается непосредственно этим двигателем.

Задача 2. С поверхности Земли вертикально вверх брошен камень, как показано на рис. 121. Какую работу совершит сила тяжести к тому моменту, когда камень поднимется на высоту h = 45 м? Масса камня равна m = 1 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с2.

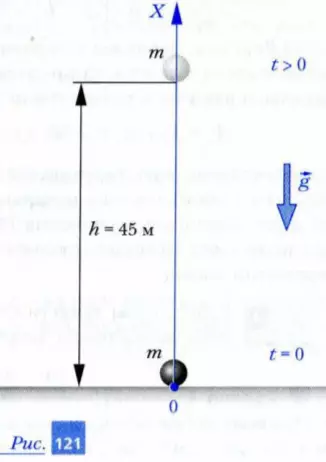
Работа силы тяжести над брошенным вверх камнем

Решение. Поскольку сила тяжести и перемещение камня во время подъема направлены в противоположные стороны, работа силы тяжести будет величиной отрицательной. Как вы помните, модуль силы тяжести равен m · g. Следовательно, работа силы тяжести над камнем при его подъеме до заданной высоты отрицательна и равна

A = -(m · g) · h = -(1 кг · 10 м/с2) · 45 м = -10 Н · 45 м= -450Дж.

Ответ: работа силы тяжести равна -450 Дж.

Задача 3. Вычислите работу силы тяжести над камнем, брошенным вертикально вверх с поверхности Земли, за промежутки времени: а) от момента броска до момента подъема на максимальную высоту H = 60 м; б) от момента достижения максимальной высоты до момента, когда камень окажется на высоте h = 45 м; *в) от момента начала движения с поверхности Земли до момента, когда, опускаясь, камень второй раз за время полета окажется на высоте h = 45 м. Масса камня равна M = 1 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с2.

Решение.

а) Повторяя решение предыдущей задачи, получаем:

Aa = -(M · g) · H = -(1 кг · 10 м/с2) · 60 м = -10 Н · 60 м = -600 Дж.

б) При падении камня из верхней точки направления силы тяжести и движения камня совпадают. Поэтому на этом участке свободного падения работа силы тяжести положительна и равна

Aб = M · g · (H – h) = 10 Н · 15 м = 150 Дж.

*в) Работа силы тяжести в этом случае может быть определена как сумма работ силы тяжести при подъеме камня до верхней точки и при движении камня вниз из верхней точки до высоты h, т. е.

Aв = Aа + Aб = -(M · g) · H + M · g (H – h) = -M · g · h = -450 Дж.

Сопоставим этот результат с результатом из задачи 2. Можно заметить, что в обоих случаях начальные положения камня (поверхность Земли) и его конечные положения (45 м от поверхности Земли) совпадают. При этом сила тяжести совершает одну и ту же работу. Можно сделать следующий вывод.

Работа силы тяжести определяется разностью высот, на которых находилось тело в начальный и конечный моменты времени.

Задача 4. На движущуюся кабину лифта массой M в течение некоторого промежутка времени трос действовал с постоянной силой F. Найдите работу: а) силы F; б) силы тяжести; в) суммы этих сил над кабиной лифта, если за указанный промежуток времени она поднялась вертикально вверх на высоту H.

Решение. Пусть ось Х системы отсчета, связанной с Землей, направлена вертикально вверх, как показано на рис. 122. Тогда значение силы тяжести будет отрицательным, а значение силы F и изменение координаты кабины лифта — положительными.

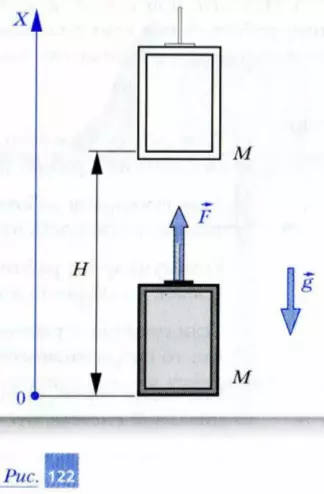
Суммарная работа сил

Поэтому работа силы F положительна и равна

Aа = F · H,

а работа силы тяжести — отрицательна и равна

Aб = -M · g · H.

При рассмотрении законов динамики неоднократно подчеркивалось, что при одновременном действии на точечное тело нескольких сил его ускорение будет таким же, как и при действии на это тело одной силы, равной сумме всех действующих на него сил. Заменим действующие на кабину лифта силы одной суммарной. Значение этой силы равно сумме значений силы тяжести и силы F со стороны троса: Fс = F – M · g. Поэтому работа суммарной силы над кабиной при ее перемещении на высоту H равна

Aв = Fс · H = (F – M · g) · H = F · H – M · g · H = Aа + Aб.

При одновременном действии на тело нескольких сил их суммарная работа равна сумме работ этих сил.

Таким образом, для рассмотренного случая можно сделать следующие выводы.

1. При F > M · g суммарная работа этих сил положительна. Поэтому, если на кабину не действуют другие силы, она должна разгоняться, т. е. ее ускорение должно быть положительным. Это же заключение легко сделать и непосредственно из второго закона Ньютона.

2. При F = M · g суммарная сила равна нулю. Поэтому и суммарная работа этих сил равна нулю. Кабина будет двигаться без ускорения, т. е. ее скорость не будет изменяться.

3. Наконец, при F

Итоги

Если на точечное тело одновременно действуют несколько сил, их суммарная работа равна сумме работ этих сил.

Если суммарная работа всех действующих на тело сил положительна, то скорость этого тела увеличивается.

Если суммарная работа всех действующих на тело сил отрицательна, то скорость этого тела уменьшается.

Если суммарная работа всех действующих на тело сил равна нулю, то скорость этого тела остается неизменной.

Сказанное верно, если движение тела рассматривается в инерциальной системе отсчета.

Упражнения

1. Найдите работу силы трения, тормозящей грузовой автомобиль на отрезке пути L = 40 м, если модуль силы равен 25 кН.

2. Определите работу силы тяжести над камнем массой m = 5 кг при его падении с высоты h = 80 м на Землю.

3. Найдите работу пороховых газов над пулей к моменту ее вылета из ствола снайперской винтовки длиной L = 1 м. Считайте, что сила действия газов постоянна и ее модуль равен 5 кН. Винтовку во время выстрела удерживает неподвижной стоящий на Земле человек.

4. Определите работу силы тяжести над свободно падающим камнем массой m = 1 кг за промежуток времени, в течение которого скорость камня изменяется от v0 = 0 до vк = 30 м/с.

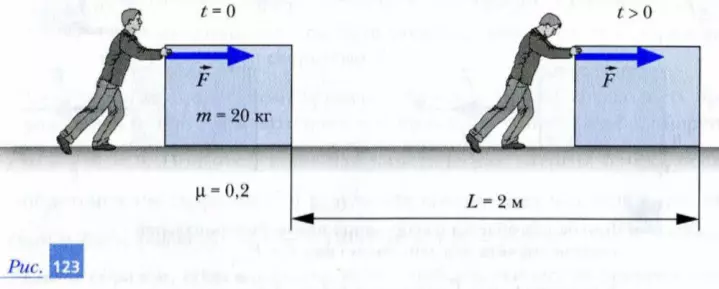
5. Мальчик действует на движущийся по горизонтальному полу ящик массой m = 20 кг силой, направленной в сторону движения ящика (рис. 123) и равной по модулю 50 Н. Коэффициент трения ящика о пол μ = 0,2. При этом за некоторое время ящик передвинулся на расстояние L = 2 м. Какую работу за это время совершат: а) мальчик; б) сила тяжести; в) сила трения; г) сумма всех сил, действующих на ящик? Увеличится или уменьшится скорость ящика за это время?

Работы разных сил при перемещении ящика

Источник

Инфоурок

›

Физика

›Другие методич. материалы›ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ НА СИЛУ ТОРМОЖЕНИЯ

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ НА СИЛУ ТОРМОЖЕНИЯ

  • Настоящий материал опубликован пользователем Кенжаев Зафар Муродуллаевич. Инфоурок является
    информационным посредником и предоставляет пользователям возможность размещать на сайте
    методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
    сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

    Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
    сайта, Вы можете оставить жалобу на материал.

    Удалить материал

  • Кенжаев Зафар Муродуллаевич

    • На сайте: 7 лет и 4 месяца
    • Подписчики: 2
    • Всего просмотров: 26996
    • Всего материалов:

      36

Источник

Добавить комментарий