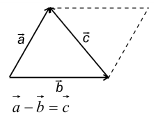
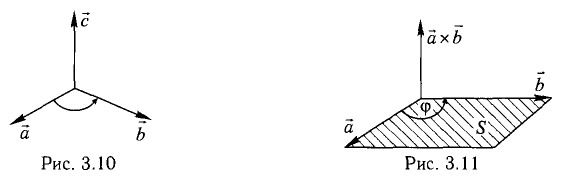
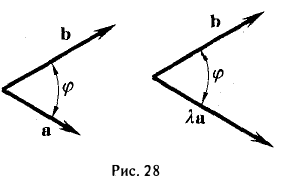
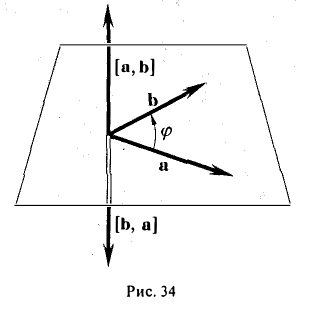
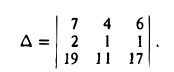
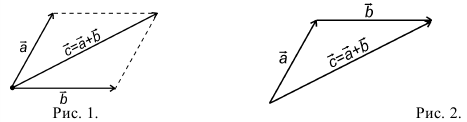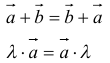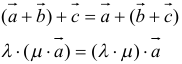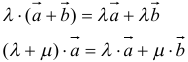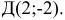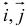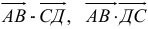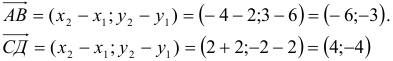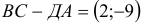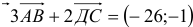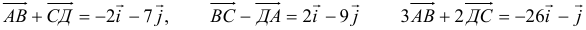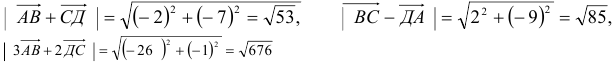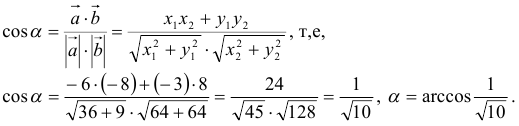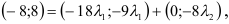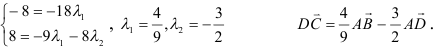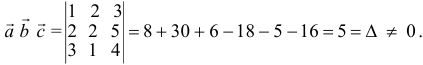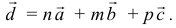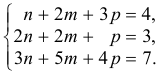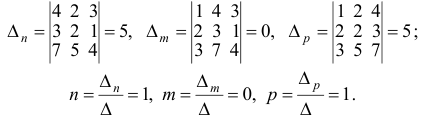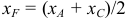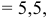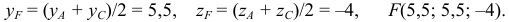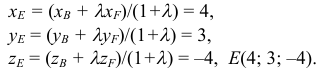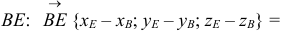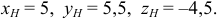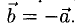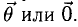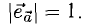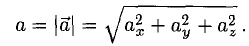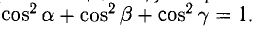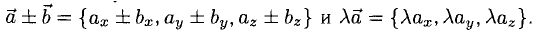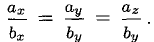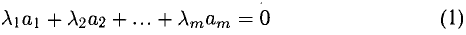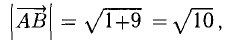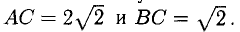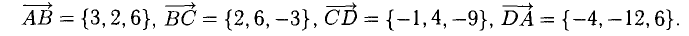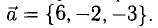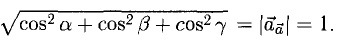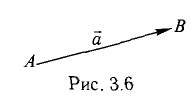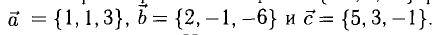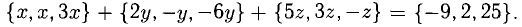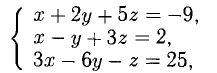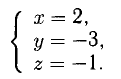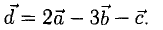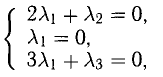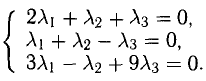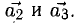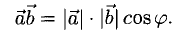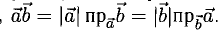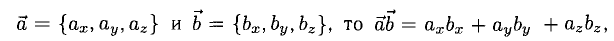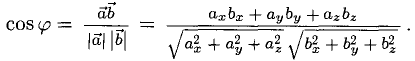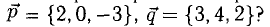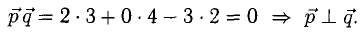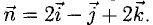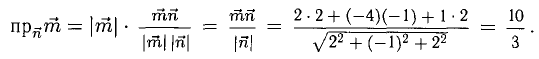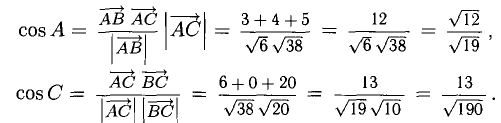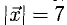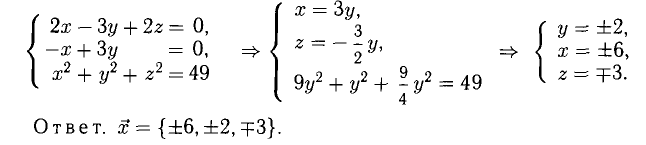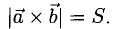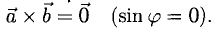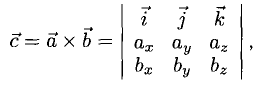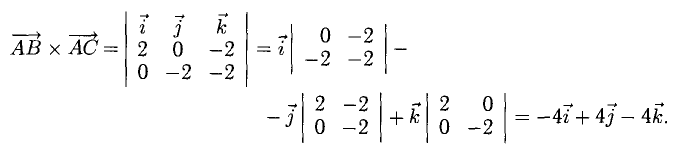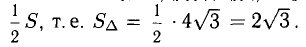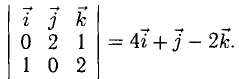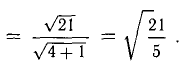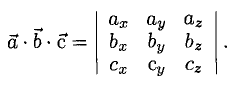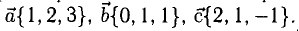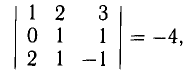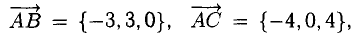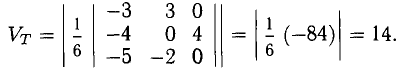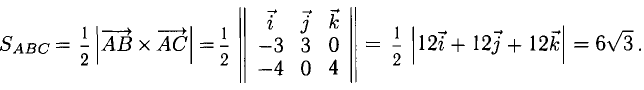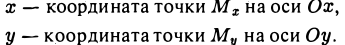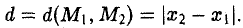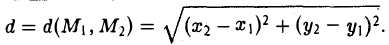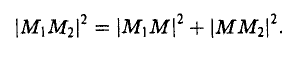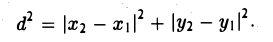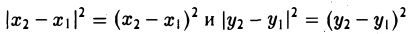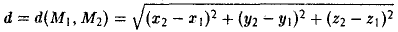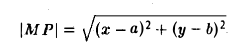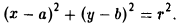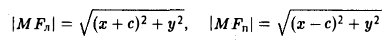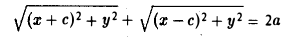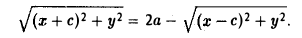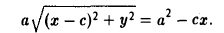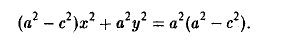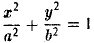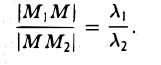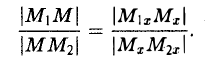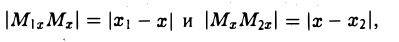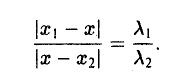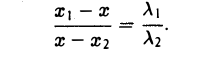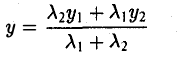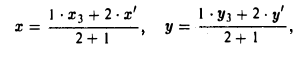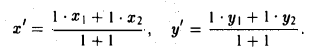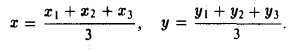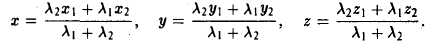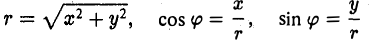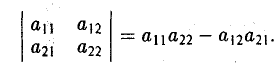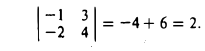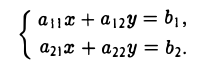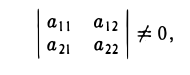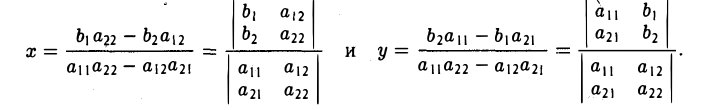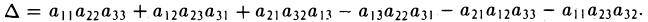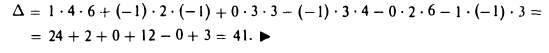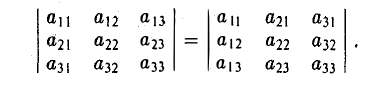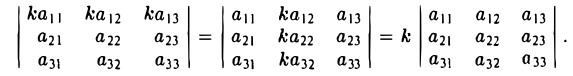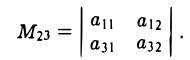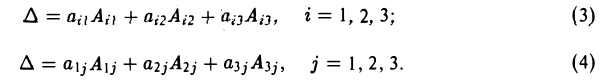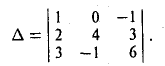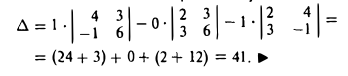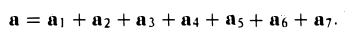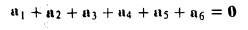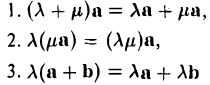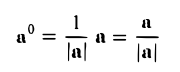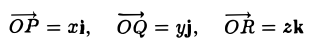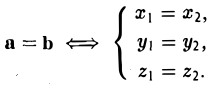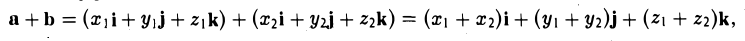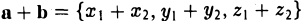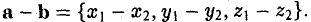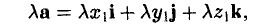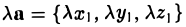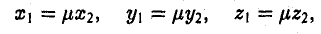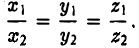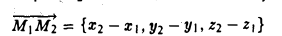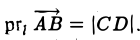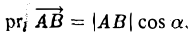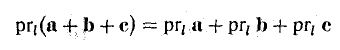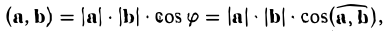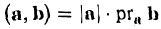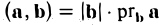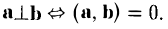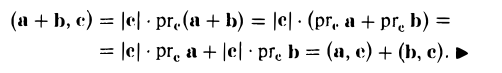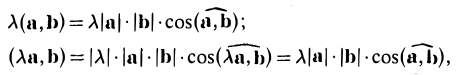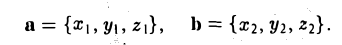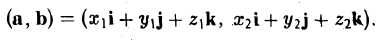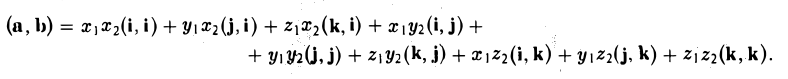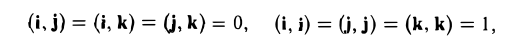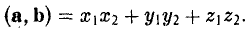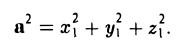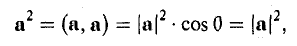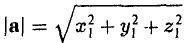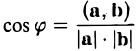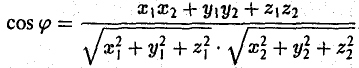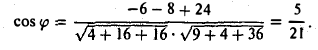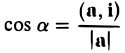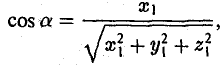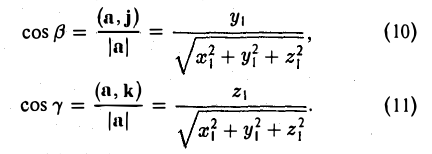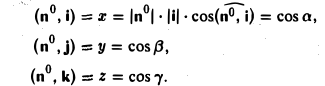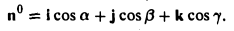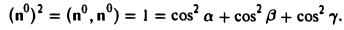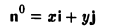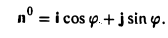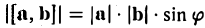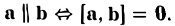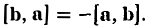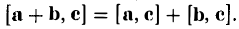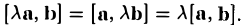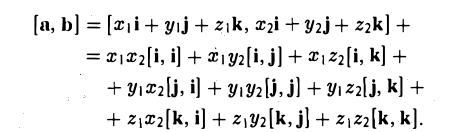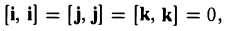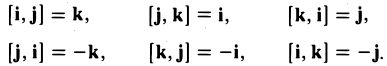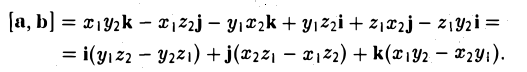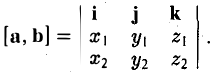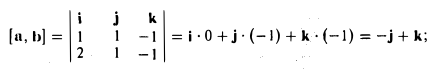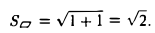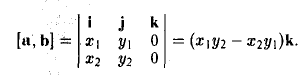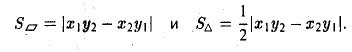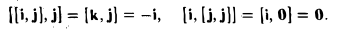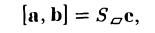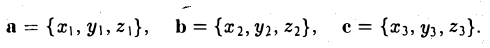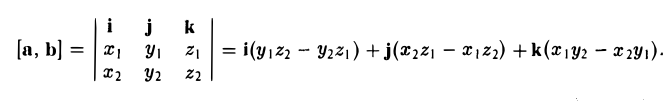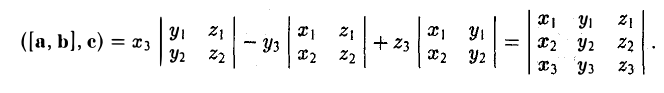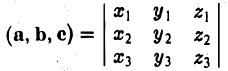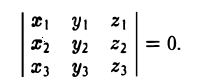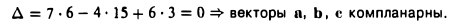Примеры решений по векторной алгебре
Векторная алгебра для чайников
В этом разделе вы найдете бесплатные решения задач по векторной алгебре: вектора, углы, взаимное расположение на плоскости и пространстве, базис из векторов, действия с векторами и т.п.
Решения задач с векторами
Задача 1. На оси $Ох$ найти точку, равноудаленную от точек $А(2;-4;5)$ и $В(-3;2;7)$.
Задача 2. Написать разложение вектора $X$ по векторам $(a, b, c)$.
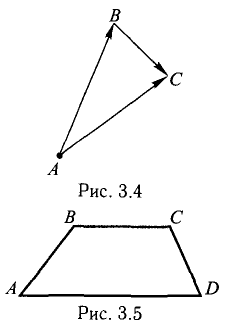
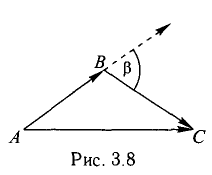
Задача 3. Найти косинус угла между векторами $AB$ и $AC$.
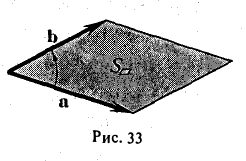
Задача 4. Вычислить площадь треугольника с вершинами $$A=(-4;4;4), B=(3;1;0), C=(-1;0;6).$$
Задача 5. Компланарны ли вектора $a, b, c$? $$a=(-3;2;1), b=(3;1;2), c=(3;-1;4)$$
Задача 6. Заданы два вектора в пространстве. Найти:
а) их сумму;
б) их разность; косинус угла между ними;
в) их векторное произведение.
$a=(0;1;1), b=(-2;0;1).$
Задача 7. Сила $F$ приложена к точке $А$. Вычислить:
а) работу силы $F$ в случае, когда точка её приложения, двигаясь прямолинейно, перемещается в точку $В$;
b) модуль момента силы $F$ относительно точки $В$.
Задача 8. Найти ранг и базис системы векторов, перейти к новому базису. Записать разложения векторов по найденным базисам.
Задача 11. Написать разложение вектора $bar$ по векторам $bar, bar, bar$.
Задача 13. Вычислить площадь параллелограмма, построенного на векторах $bar
$, $bar$.
Найти работу через вектора
Механическая работа
О чем эта статья:
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа
А = FScosα
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
α — угол между векторами силы и перемещения []
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия
Еп = mgh
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
h — высота [м]
На планете Земля g ≈ 9,8 м/с 2
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
- За счет чего происходит процесс?
- Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность
N = A/t
N — мощность [Вт]
A — механическая работа [Дж]
t — время [с]
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
Мощность
N = Fv
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность
N = Fvcosα
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
α — угол между векторами силы и скорости []
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
- Выталкивающая сила.
- Сила вязкого трения.
- Сила тяжести.
- Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Линейная алгебра для разработчиков игр
Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.
Зачем нам линейная алгебра?
Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.
Что такое вектор?
В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора:
Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.
Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.
Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.
Сложение векторов
Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:
(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)
Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.
Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.
Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.
Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).
Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).
Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.
Вычитание векторов
Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:
(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).
Умножение вектора на скаляр
Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:
0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).
Длина вектора
Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.
Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x 2 + y 2 = h 2
В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x 2 + y 2 ).
Итак, скорость нашего корабля равна:
|V| = sqrt(4 2 + 3 2 ) = sqrt(25) = 5
Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x 2 + y 2 + z 2 )
Расстояние
Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.
Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2 2 +1 2 ) = sqrt(5) = 2.23
Нормализация
Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?
Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.
Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:
(3/5) 2 + (4/5) 2 = 9/25 + 16/25 = 25/25 = 1
Скалярное произведение векторов
Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе
(a1, a2) • (b1, b2) = a1b1 + a2b2
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:
Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:
V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1
Так как единица больше нуля, то главный герой находится в поле зрения стражника.
Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:
Где Θ (произносится как «theta») — угол между векторами A и B.
Это позволяет нам найти Θ (угол) с помощью выражения:
Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.
D’ = D / |D| = (1, 1) / sqrt(1 2 + 1 2 ) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(2 2 + (-1) 2 ) = (2,-1) / sqrt(5) = (0.89, -0.45)
Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72
Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.
Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:
Векторное произведение
Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?
Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).
А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».
Для решения этой задачи мы используем векторное произведение: S = M x W.
Подставим теперь нужные нам значения:
S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)
Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.
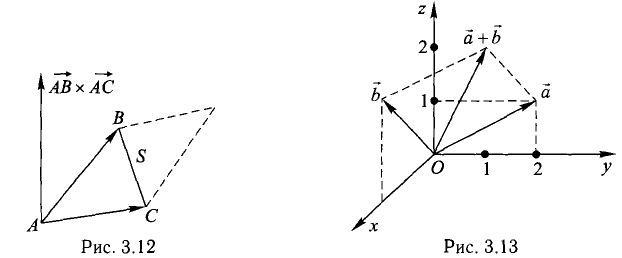
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.
Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».
Вот так это выглядит в коде:
В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.
Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).
Для начала изучим «строительные блоки» матрицы преобразований.
Базисный вектор
Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:
Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:
Применяя эту функцию ко всем трём точкам, мы получим следующую картину:
Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).
Пусть теперь наш корабль выглядит вот так:
Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»
Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.
По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:
Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:
0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)
Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:
-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)
Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y
1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)
Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.
Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:
Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.
Матрицы
Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:
Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:
Будучи записанным по-другому, это выражение выглядит так:
Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:
Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:
Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:
Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.
К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:
И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:
Теперь, когда мы перемножаем их, мы получаем:
(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)
Что, в свою очередь, может быть записано как:
x(a, b) + y(c, d) + (e, f)
Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.
Трехмерные матрицы
Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:
Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:
И добавляем единицу [1] в вектор, как здесь:
Вращение в двухмерном пространстве
Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:
Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:
(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))
Затем, мы включаем координатную ось Y (0, 1). Получим:
(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))
Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.
Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:
Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T -1 . Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:
Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.
Теперь рассмотрим трёхмерное вращение.
Трёхмерное вращение
Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:
Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.
То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?
Вращение, определяемое осью и углом (Axis-angle rotation)
Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.
Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?
Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:
Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.
Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.
У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.
Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.
На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:
Тут показана иллюстрация для каждого шага:
Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.
Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.
Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M -1 RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.
Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.
Эйлеровские углы
Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.
Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).
Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.
Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.
Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.
Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?
Вращение с помощью матриц
Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:
Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.
Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).
Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.
Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.
Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.
Кватернионы
Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.
Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.
Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.
Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.
Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.
«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.
Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.
Векторы на ЕГЭ по математике. Действия над векторами
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения 
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Вот другой пример.
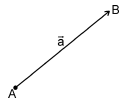
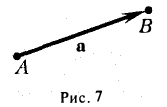
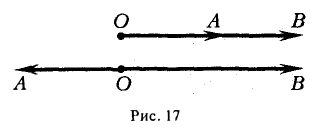
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор 
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:
Здесь в скобках записаны координаты вектора 
Находятся они просто: координата конца вектора минус координата его начала.
Если координаты вектора заданы, его длина находится по формуле
Сложение векторов
Для сложения векторов есть два способа.
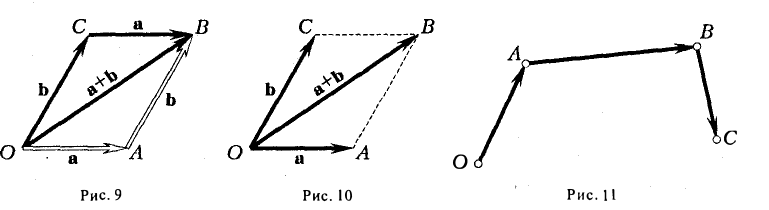
1 . Правило параллелограмма. Чтобы сложить векторы 



Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
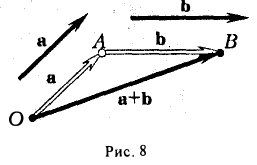
2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы 



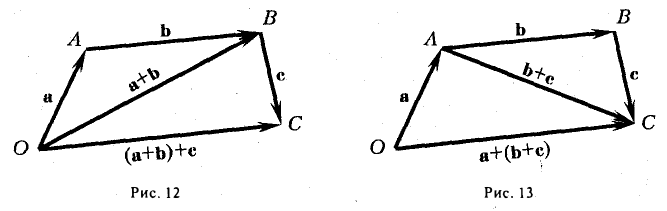
По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .
При сложении векторов 

Вычитание векторов
Вектор 



Теперь понятно, что такое вычитание векторов. Разность векторов 



Умножение вектора на число
При умножении вектора 



Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов 

Из формулы для скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
Векторная алгебра — основные понятия с примерами решения и образцами выполнения
Вектором называется направленный отрезок. Вектор обозначается либо символом 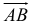
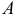
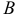

2. Длиной (модулем) вектора 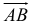
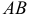
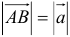
3.Вектор называется единичным, если его длина равна «1»; единичный вектор 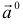


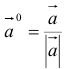
4. Вектор называется нулевым, если его начало и конец совпадают 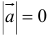
5. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарность векторов обозначается: 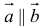

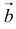
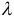
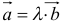
6. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.
7. Вектор 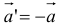

8. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
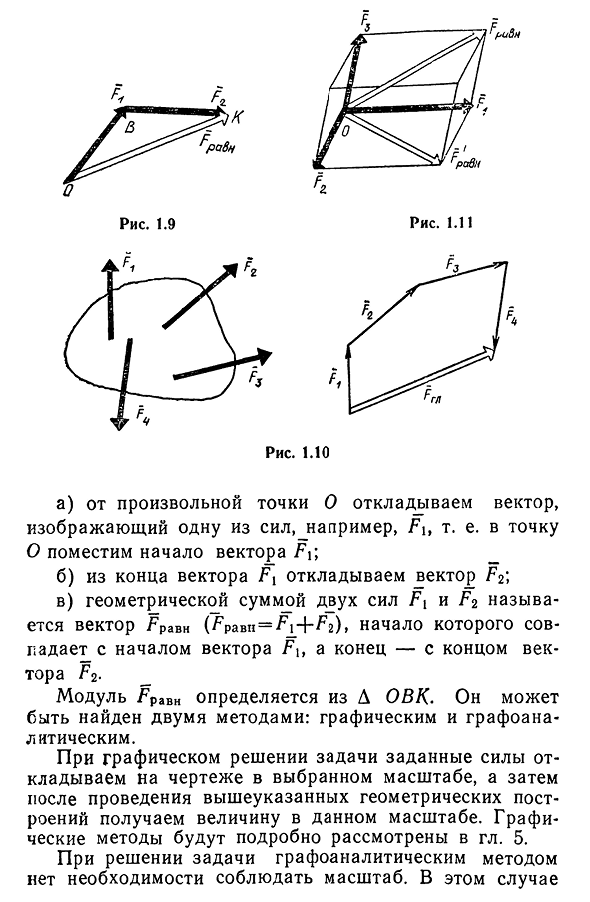
Для решения задач необходимо уметь выполнять линейные операции над вектором в геометрической форме, то есть над вектором, как над
направленным отрезком: сложение, вычитание векторов и умножение вектора на число.
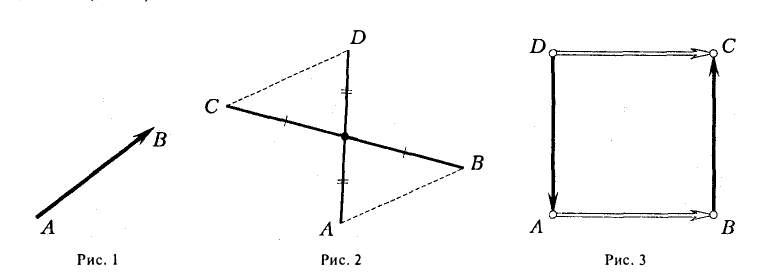
9. Сложение двух векторов можно выполнить по правилу параллелограмма (рис. 1) или по правилу треугольника (рис. 2).
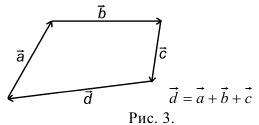
При сложении более двух векторов, лежащих в одной плоскости, используется правило «замыкающей линии многоугольника» (рис. 3).
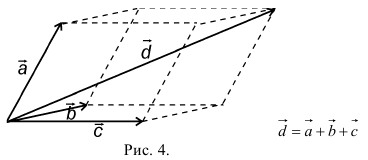
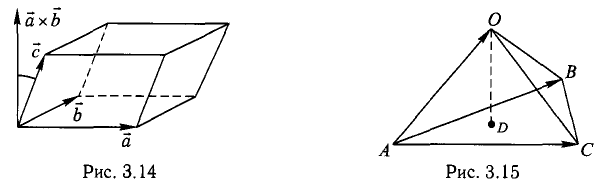
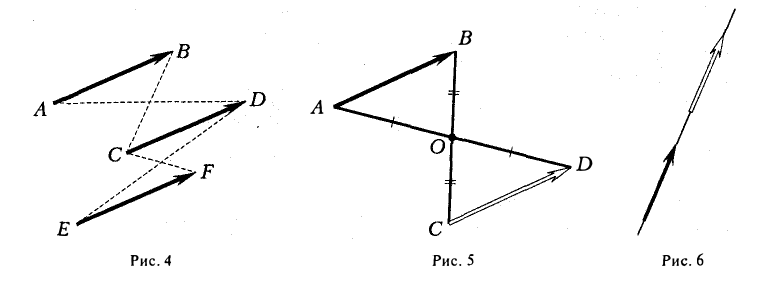
При сложении трех некомпланарных векторов удобно пользоваться правилом «параллелепипеда» (рис. 4).
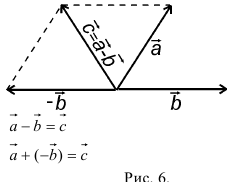
10. Действие вычитания двух векторов связано с действием сложения (рис.5).
Разностью двух векторов называется вектор, проведенный из конца вычитаемого в конец уменьшаемого. Заметим, что разностью является вектор, служащий второй диагональю параллелограмма.
Разность можно также представить в виде сложения с противоположным вектором (рис. 6).
11. Произведением вектора 
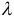
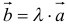
12. Для решения задач полезно знать также следующие законы и свойства:
- переместительный:
- сочетательный:
- распределительный:
Примеры задач решаемых с применением векторной алгебры
Задача:
Пусть даны точки
1) Найти координаты векторов
2) Написать разложение этих векторов по базису
3) Найти длины этих векторов
4) Найти скалярное произведение
5) Найти угол между векторами 

6) Найти разложение вектора 

Решение:
1) Вычислим координаты векторов 
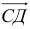
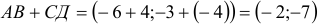
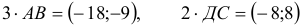
2)
4) Для вычисления угла между векторами воспользуемся формулой:
5) Разложить вектор 

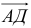


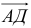
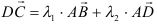
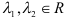
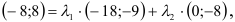
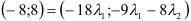
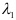
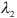
Задача:
а). Даны векторы 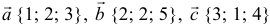
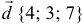
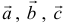
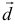
Решение:
Три вектора образуют базис, если 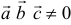
Найдем координаты вектора 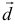
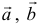
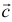
Два вектора равны, если их соответствующие координаты равны.
Решим систему методом Крамера:
Ответ: 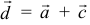
Задача:
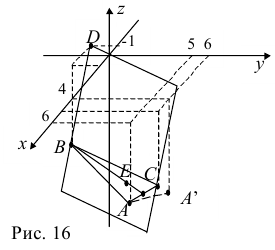
Даны координаты вершин тетраэдра 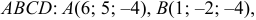
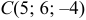
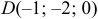
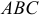

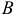
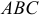


Решение:
1) Найдем координаты т. 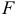
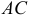
Точка 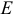
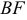
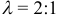
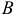
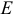
2) Найдем направляющий вектор прямой 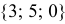

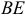
3) Найдем уравнение плоскости 
Найдем каноническое уравнение прямой, перпендикулярной плоскости 

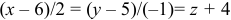
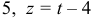
Найдем координаты точки 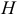

Координаты точки 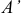


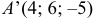
Ответ: 1) координаты точки пересечения медиан 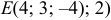
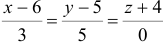
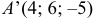
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Векторная алгебра — решение заданий и задач по всем темам с вычислением
Понятие вектора. Линейные операции над векторами
1°. Любые две точки 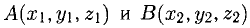
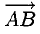
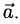
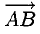
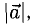
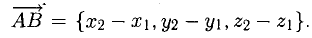
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора 
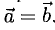
Векторы 
Вектор называется нулевым, если его модуль равен нулю, и обозначается
2°. Линейными называются действия сложения, вычитания векторов и умножения вектора на число.
1.Если начало 

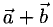


2.Если начала векторов 




3.При умножении вектора 
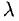
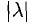
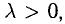
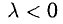
Вектор 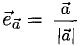

3°. Запись ci — 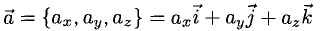

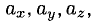

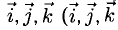
4°. Числа 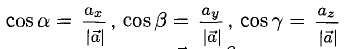
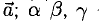

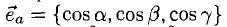

5°. Линейные операции над векторами, которые заданы своими координатами, определяются так: пусть 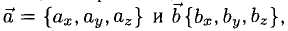
Следовательно, при сложении векторов складываются их соответствующие координаты, а при умножении вектора на число умножаются на число все координаты вектора.
6°. Необходимое и достаточное условие коллинеарности векторов 
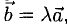
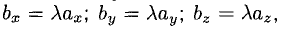
Если один из членов какого-нибудь из этих отношений равен нулю, то и второй член того же отношения должен быть нулем. Геометрически это значит, что в этом случае оба вектора перпендикулярны соответствующей координатной оси (например, если 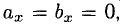
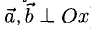
7°. Система векторов 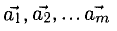
( 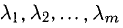

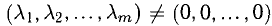
Примеры с решениями
Пример:
Доказать, что треугольник с вершинами в точках A(1,2), B(2,5), С(3,4) прямоугольный.
Решение:
Построим векторы, совпадающие со сторонами треугольника (см. п. 1°): 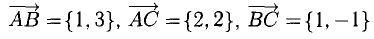
Найдем длины сторон: 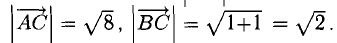
Нетрудно видеть, что 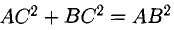
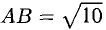
Пример:
Проверить, что точки А( 2,-4,3), В(5, —2,9), С( 7,4,6) и D(6,8, -3) являются вершинами трапеции.
Решение:
Составим векторы-стороны с целью обнаружения коллинеарности векторов (в трапеции ВС || AD) (рис. 3.5):
Имеем 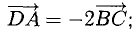
Пример:
Найти орт и направляющие косинусы вектора
Решение:
Имеем 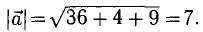
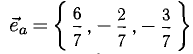
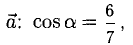
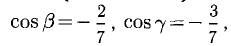
Пример:
Определить точку В, которая является концом вектора 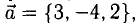
Решение:
Пусть точка В имеет координаты B(x,y,z) (рис. 3.6). Тогда координа- ^ ты вектора (п. 1°)
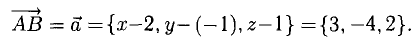
Следовательно, 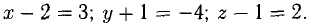
Пример:
Вектор 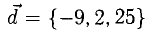
Решение:
Необходимо найти такие числа х, у, z, что 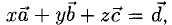
Имея в виду, что при сложении векторов складываются их координаты и равные векторы имеют равные координаты, приходим к системе уравнений
Ответ.
Пример:
Показать, что система векторов 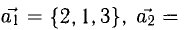
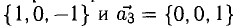
Решение:
В данном случае равенство (1) имеет вид 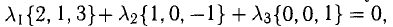
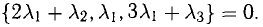
из которой следует, что 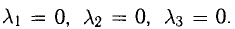
Пример:
Показать, что система векторов 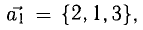
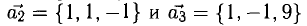
Решение:
Равенство (1) равносильно системе уравнений
Она имеет ненулевое решение, например, 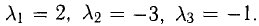
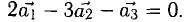
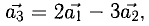
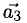
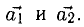
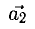
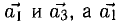
Скалярное произведение векторов
1°. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению их длин на косинус угла 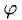
Из 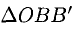
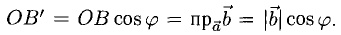
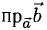


Итак,
т.е. скалярное произведение векторов равно сумме произведений одноименных координат этих векторов.
При этом 
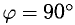
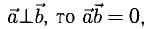
3°. Из определения скалярного произведения следует формула для вычисления угла между двумя векторами:
Примеры с решениями
Пример:
Перпендикулярны ли векторы 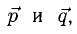
Решение:
Условие перпендикулярности векторов (п. 2°) 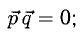
Пример:
Найти проекцию вектора 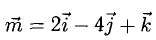
Решение:
Имеем 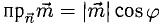
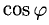
Ответ
Пример:
Зная векторы, совпадающие с двумя сторонами: 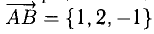
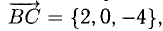
Решение:
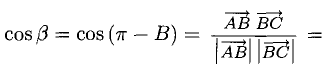
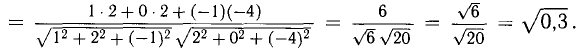
При помощи таблиц находим 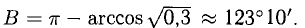
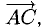
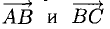
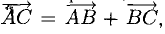
Ответ. 123° 10′, 19°29′, 37°21′.
Пример:
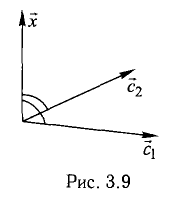
Найти координаты вектора 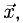
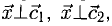
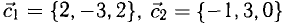
Решение:
На рис. 3.9 имеем 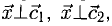
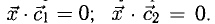
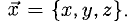
Векторное произведение векторов
1°. Векторы 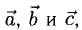

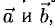
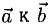
2°. Векторным произведением ненулевых векторов 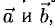

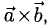
1) 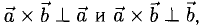
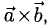
2) Вектор 
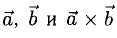
3) 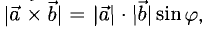
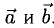
Если векторы 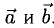

3°. Если известны координаты векторов-сомножителей 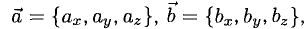
в которой определитель следует разложить по элементам первой строки.
Примеры с решениями
Пример:
Найти площадь треугольника, вершины которого находятся в точках А(1,2,3), В<3,2,1), С(1,0,1).
Решение:
Найдем координаты векторов 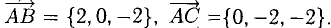
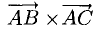
Найдем длину этого вектора, которая равна численно площади параллелограмма S (п. 2°): 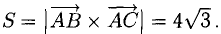
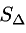
Пример:
Построить параллелограмм на векторах 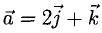
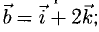

Сделаем чертеж (рис. 3.13). Имеем 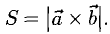
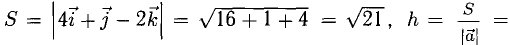
Смешанное произведение векторов
1°. Смешанным произведением трех ненулевых векторов 


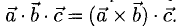

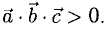

Модуль смешанного произведения векторов 
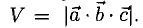
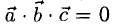

Объем тетраэдра с вершинами в точках 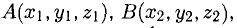
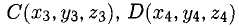
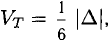
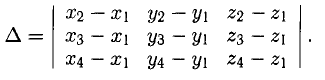
2°. Условие 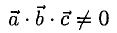

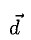
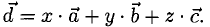
Примеры с решениями
Пример:
Найти объем параллелепипеда, построенного на векторах
Решение:
Искомый объем 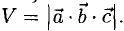
Пример:
В точках 0(0,0,0), А(5,2,0), В(2,5,0) и С(1,2,4) находятся вершины пирамиды. Вычислить ее объем, площадь грани ABC и высоту пирамиды, опущенную на эту грань.
Решение:
1) Сделаем схематический чертеж (рис. 3.15).
2) Введем векторы 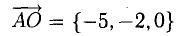
3) Площадь грани ABC
4) Объем пирамиды 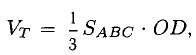
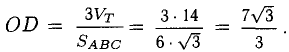
Ответ.
Основные понятия векторной алгебры




Прямоугольные декартовы координаты
Координатная ось
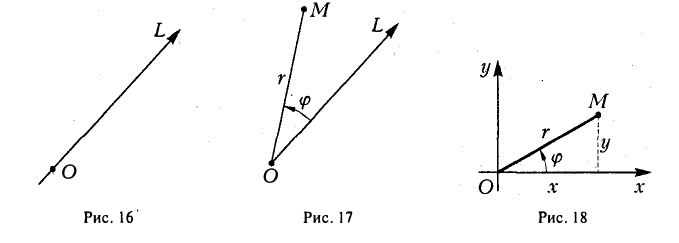
Пусть на плоскости или в пространстве задана произвольная прямая L: Ясно, что по этой прямой L сы можем перемещаться в oднoм из двух противоположных направлений. Выбор любого (одного) из этих направлений будем называть ориентацией прямой L.
Оnределение:
Прямая с заданной на ней ориентацией называется осью. На чертеже ориентация оси указывается стрелкой (рис. 1 ) . Фиксируем на оси 
Пусть М — произвольная точка оси 
Оnределение:
Ось 
Прямоугольные декартовы координаты на плоскости
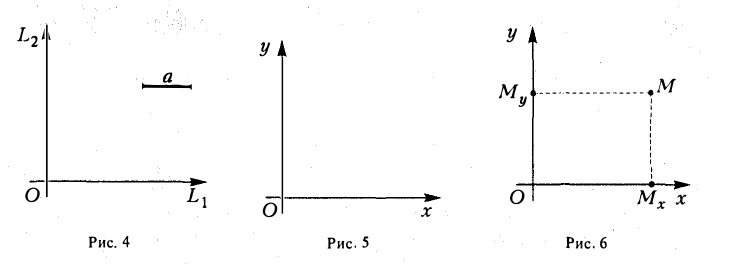
Пусть П — произвольная плоскость. Возьмем на ней некоторую точку О и проведем через эту точку взаимно перпендикулярные прямые L 1 и L 2. Зададим на каждой из nрямых L 1 и L 2 ориентацию и выберем единый масштабный отрезок а. Тогда эти прямые nревратятся в координатные оси с общей точкой отсчета О (рис. 4).
Назовем одну из координатных осей осью абсцисс (осью Ох), друrую —осью ординат (осью Оу) (рис. 5). Точка О называется началом координат. Пусть М — произвольная точка плоскости П (рис. 6). Проведем через точку М прямые, перпендикулярные координатным осям, и поставим ей в соответствие упорядоченную пару чисел (х, у) по следующему nравилу:
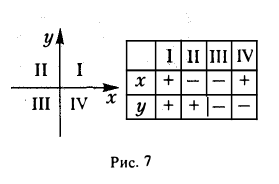
Числа х и у называются прямоугольными декартовыми при этом х называется ее абсциссой, а у — ординатой. координатами точки М; Обозначение: М(х, у). Чтобы кратко охарактеризовать описанную конструкцию, говорят, что на плоскости П задана прямоугольная декартова система координат Ох у. Координатные оси разбивают плоскость на четыре части, называемые четвертями или квадрантами. На рисунке и в таблице показано, как эти квадранты нумеруются (рис. 7).
Замечание:
Масштабные от резки на координатных осях могут быть и разной длины. В этом случае координатная система называется просто прямоугольной.
Прямоугольные декартовы координаты в пространстве
Возьмем в пространстве некоторую точку О и проведем через нее три взаимно перпендикулярные прямые L 1 , L 2 и L 3 . Выберем на каждой из nрямых ориентацию и единый масштаб. Прямые L 1 , L 2 и L 3 превратятся в координатные оси с общей точкой отсчета О (рис. 8).
Назовем одну из этих осей осью абсцисс (осью Ох), вторую — осью ординат (осью Оу) и третью — осью аппликат (осью Oz) (рис. 9). Точка О называется началом координат. Пусть М — nроизвольная точка (рис. 10). Проведем через точку М nлоскости, перпендикулярные координатным осям, и поставим ей в соответстnие упорядоченную тройку чисел (х, у, z) по следующему правилу:
Числа х, у и z называются прямоугольными декартовыми координатами точки М; при этом х называется абсциссой точки М, у — ее ординатой, а z —аппликатой. Обозначение: М(х, у, z). Таким образом, в пространстве введена прямоугольная декартова система координат.
Оnределение:
Плоскость, проходящая через любую пару координатных осей, называется координатной плоскостью.
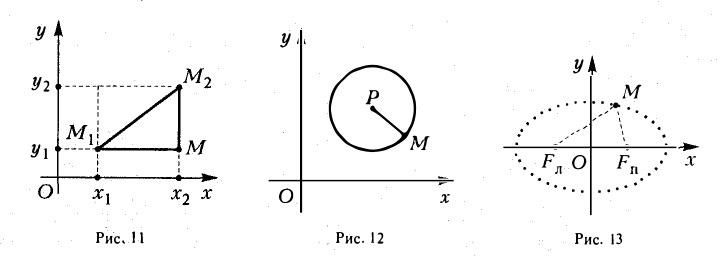
Координатных плоскостей три: Оху, Oyz и Oxz. Эти плоскости разбивают пространство на восемь частей — октантов. 1 .4. Простейшие задачи аналитической геометрии А. Расстояние между точками Пусть М 1 (х 1 ) и М 2 (х 2 )- две точки на координатной оси. Тогда расстояние d между ними вычисляется по формуле
Если на плоскости задана прямоугольная декартова система координат Оху, то расстояние d между любыми двумя точками М 1 (х 1 , у1 и М2 (х2 , y2) вычисляется по следующей формуле
Рассмотрим прямоугольный треугольник ∆MM1M2 (pиc. l l). По теореме Пифагора
,и извлекая из обеих частей равенства квадратный корень, приходим к требуемой формуле .
Замечание:
Расстояние между точками 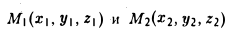
Задача:
Написать уравнение окружности радиуса т с центром в точке Р(а, b).
Пусть М(х, у) — точка окружности (рис. 12). Это означает, что |M P| = r. Заменим |M P|его выражением
и возведем обе части полученного равенства в квадрат:
Это есть каноническое уравнение окружности радиуса r с центром в точке Р(а, b) .
Задача:
Пусть F л (-с, 0) и F n (c, 0) -фиксированные точки плоскости, а -заданное число (а > с ≥ 0). Найти условие, которому удовлетворяют координаты х и у точки М, обладающей следующим свойством: сумма расстояний от точки М до Fл и до F n равна 2а.
Вычислим расстояния между точками М и F л и между точками М и F n . Имеем
Перенесем второй корень в правую часть
Возводя обе части в квадрат, после простых преобразований получим
С целью дальнейших упрощений вновь возводим обе части в квадрат. В результате nриходим к равенству
Полагая b 2 = а 2 — с 2 и деля обе части nоследнего соотноwения на а 2 b 2 , nолучаем уравнение эллипса
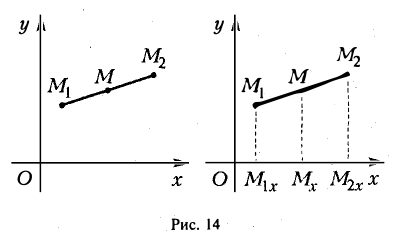
Деление отрезка в данном отношении:
Требуется выразить координаты х и у этой точки через координаты концов отрезка М1М2 и числа λ 1 и λ 2 . Предположим сначала, что отрезок М1М2 не параллелен оси ординат Оу (рис. 14). Тогда
то из последних двух соотношений получаем, что
Точка М лежит между точками М1 и М2 , поэтому либо х 1 х > х 2 . В любом из этих случаев разности х1 — х и х — х 2 имеют одинаковые знаки. Это позволяет переписать последнее равенство в следующей форме
В случае, когда отрезок М1М2 параллелен оси Оу, х 1 = х 2 = х. Заметим, что тот же результат дает формула (*), если nоложить в ней х 1 = х 2 . Справедливость формулы
доказывается аналогичным рассуждением .
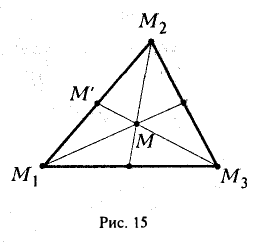
Задача:
Найти координаты центра тяжести М треугольника с вершинами в точках . М1 ( х 1 , у 1 ), М2 ( х 2 , у 2 ) и М3 ( х 3 , у 3 ). Восnользуемся тем, что центр тяжести треугольника совпадает с точкой пересечения его медиан. Точка М делит каждую медиану в отношении 2 : 1, считая от вершины (рис. 15). Тем самым, ее координаты х и у можно найти по формулам
где х’ и у’ — координаты второго конца М’ медианы М3 М’. Так как М’ — середина отрезка М1М2, то
Полученные соотношения позволяют выразить координаты z и у центра тяжести М треугольника ∆М1М2М3 через координаты его вершин:
Замечание:
Полярные координаты
Предположим, что задана точка О, ось 
Пусть М — произвольная точка плоскости, отличная от точки О (рис.17). Ее положение на плоскости однозначно определяется двумя числами: расстоянием г между точками О и М и отсчитываемым против часовой стрелки углом φ между положительным лучом оси 
Точка О называется полюсом, 
Ясно, что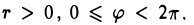
Таким образом, на плоскости можно задать еще одну координатную систему — полярную.
Прямоугольную декартову систему координат Оху будем называть согласованной с заданной полярной, если начало координат 0(0, 0) — полюс, ось Ох — полярная ось, а ось Оу составляете осью Ох угол, равный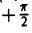
(рис.18). В свою очередь
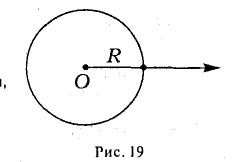
Пример:
Пусть R > О — заданное число. Множество точек плоскости, полярные координаты (г,
Определители 2-го и 3-го порядков
Определителем второго порядка называется число
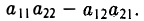
Обозначение:
Тем самым, для вычисления определителя второго порядка нужно из произведения а11, а22 элементов главной диагонали вычесть произведение а12, а21 элементов его побочной диагонали (рис. 20).
Пример:
По правилу (1) имеем
С определителями второго порядка мы встречаемся уже при отыскании решения системы двух линейных алгебраических уравнений с двумя неизвестными
Решая эту систему методом исключения неизвестных при условии, что
Пусгь теперь даны девять чисел aij (i = I, 2, 3; j = I, 2, 3).
Определителем третьего порядка называется число, обозначаемое символом
и вычисляемое по следующему правилу:
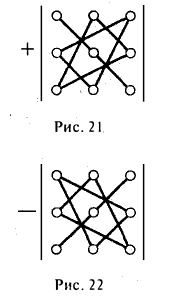
Первый индекс i элемента aij указывает номер строки, в которой он расположен, а второй индекс j — номер столбца.
Чтобы разобраться с распределением знаков в правой части формулы (2), обратим внимание на следующее: произведение элементов а11, а22, а33 главной диагонали входит в формулу со своим знаком, также как и произведение а11, а22, а33 и а11, а22, а33 элементов, расположенных в вершинах треугольников, основания которых параллельны главной диагонали (рис. 21); с другой стороны, произведение а13, а22, а31 элементов побочной диагонали, а также произведения а12, а21, а33 и а11, а23, а32 — с противоположным знаком (рис.22). Такой подход к вычислению определителя третьего порядка называется правилом треугольника.
Пример:
Применяя правило треугольника, находим
Установим некоторые свойства определителей 3-го порядка, легко проверяемые при помощи разложений (1) и (2).
Свойство:
Величина определителя не изменится, если все его строки заменить его столбцами с теми же номерами
Свойство:
При перестановке любых двух строк (или любых двух столбцов) определителя он изменяет свой знак на противоположный.
Свойство:
Общий множитель всех элементов одной строки (или одного столбца) определителя можно вынести за знак определителя
Следующие три свойства определителя вытекают из свойств 1-3. Впрочем, в их справедливости можно убедиться и непосредственно, пользуясь формулами (1) и (2).
Свойство:
Если определитель имеет две равные строки (или дна равных столбца), то он равен нулю.
Свойство:
Если все элементы некоторой строки (или некоторого столбца) равны нулю, то и сам определитель равен нулю.
Свойство:
Если соответствующие элементы двух строк (или двух столбцов) пропорциональны, то определитель равен нулю.
Укажем еще один способ вычисления определителя 3-го порядка
Минором Mij элемента aij определителя ∆ называется определитель, получаемый изданного путем вычеркивания элементов i-й строки и j-ro столбца, на пересечении которых находится этот элемент. Например, минором элемента a23 будет определитель
Алгебраическим дополнением элемента Aij называется минор Mij — этого элемента, взятый со своим знаком, если сумма i + j номеров строки и столбца, на пересечении которых расположен элемент aij, есть число четное, и с противоположным знаком, если это число нечетное:
Теорема:
Определитель равен сумме произведений элементов любой его строки (любого его столбца) на их алгебраические дополнения, так что имеют место следующие равенства
Покажем, например, что
Пользуясь формулой (2), получаем, что
Правило (3) называется разложением определителя по элементам i-й строки, а правило (4) — разложением определителя по элементам j -го столбца.
Пример:
Раскладывая определитель по элементам 1-ой строки, получим
Понятия связанного и свободного векторов
Рассмотрим две точки А и В. По соединяющему их отрезку можно перемещаться в любом из двух противоположных направлений. Если считать, например, точку А начальной, а точку В конечной, то тогда получаем направленный отрезок АВ, в другом случае — направленный отрезок В А. Направленные отрезки часто называют связанными или закрепленными векторами. На чертеже заданное направление указывается стрелкой (рис. 1).
В случае, когда начальная и конечная точки совпадают, А = В, связанный вектор называется нулевым.
Определение:
Будем говорить, что связанные векторы АВ и CD равны, если середины отрезков AD и ВС совпадают (рис. 2).
Обозначение:
Заметим, что в случае, когда точки А, В, С и D не лежат на одной прямой, это равносильно тому, что четырехугольник ABCD — параллелограмм. Ясно, что равные связанные векторы имеют равные длины.
Пример:
Рассмотрим квадрат и выберем векторы, как указано на рис.3. Векторы АВ и DC равны, а векторы ВС и DA не равны.
Укажем некоторые свойства равных связанных векторов:
- Каждый связанный вектор равен самому себе: АВ = АВ.
- Если АВ = CD, той CD = АВ.
- Если АВ = CD и CD = EF,то АВ = EF (рис.4).
Пусть АВ — заданный связанный вектор и С — произвольная точка. Ясно, что, опираясь на определение, всегда можно построить точку D так, чтобы
CD = АВ.
Тем самым, от каждой точки можно отложить связанный вектор, равный исходному (рис. 5).
Мы будем рассматривать свободные векторы, т. е. такие векторы, начальную точку которых можно выбирать произвольно, или, что то же самое, которые можно произвольно переносить параллельно самим себе. Ясно, что свободный вектор 
Если в качестве начальных выбирать лишь те точки, которые лежат на прямой, определяемой заданным (ненулевым) связанным вектором, то мы приходим к понятию скользящего вектора (рис. 6).
Связанные и скользящие векторы широко используются в теоретической механике.
Для обозначен ия свободных векторов будем пользоваться полужирными строчными латинскими буквами — а, b, с,… ; нулевой вектор обозначается через 0.
Пусть заданы вектор а и точка А. Существует ровно одна точка В, для которой

(рис.7). Операция построения связанного вектора АВ, для которого выполняется это равенство, называется откладыванием свободного вектора а от точки А.
Заметим, что связанные векторы, получаемые в результате описанной операции откладывания, равны между собой и, значит, имеют одинаковую дли ну. Это позволяет ввести длину свободного вектора а, которую мы будем обозначать символом |а. Длина нулевого вектора равна нулю. Если а = b, то |а| = |b; обратное неверно.
Линейные операции над векторами
Сложение векторов
Пусть заданы два вектора а и b. Возьмем какую-нибудь точку О и отложим от нее вектор a: 


Нетрудно заметить, что сложение векторов коммутативно, т. е. для любых векторов а и b справедливо равенство
а + b = b + а
Если отложить векторы а и 1» от обшей точки О и построить на них как на сторонах параллелограмм, то вектор 
Пусть заданы три вектора, например, a, b и с. Отложим от произвольной точки О вектор a: 

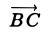

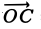
(а +b) + с = а + (b + с),
т. е. сложение векторов ассоциативно. Опуская скобки, можно говорить о сумме трех векторов и записывать ее так:
а + b + с.
Аналогично определяется сумма любого числа векторов: это есть вектор, который замыкает ломаную, построенную из заданных векторов. На рис. 14 показан», как построить сумму семи векторов:
Приведенный способ сложения произвольного числа векторов называется правилом замыкающего ломаную.
Пример:
Найти сумму векторов, идущих из центра правильного шестиугольника в его вершины.
По правилу замыкающего ломаную получаем
Умножение вектора на число
Определение:
Свободные векторы а и b называются коллинеарными, если определяющие их связанные векторы лежат на параллельных или на совпадающих прямых (рис. 16).
Обозначение: а||b.
Замечание:
Из определения следует, что если хотя бы один из векторов a и b нулевой, то они коллинеарны.
Если отложить коллинеарные векторы а и b от обшей точки О, 

Если векторы имеют равные длины и одинаково направлены, то они равны. Пусть а — вектор, λ — вещественное число.
Определение:
Произведением вектора а на число λ называется вектор b такой, что
2) векторы а и b одинаково (соответственно, противоположно) направлены, если λ > 0 (соответственно, λ
(здесь λ и μ — любые действительные числа, а и Ь — произвольные векторы).
Определение:
Вектор, длина которого равна единице, называется единичным вектором, или ортом, и обозначается а° (читается: а с нуликом), |а°| = 1.
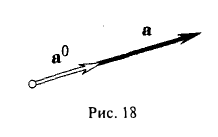
Если а ≠ 0, то вектор
есть единичный вектор (орт) направления вектора а (рис. 18).
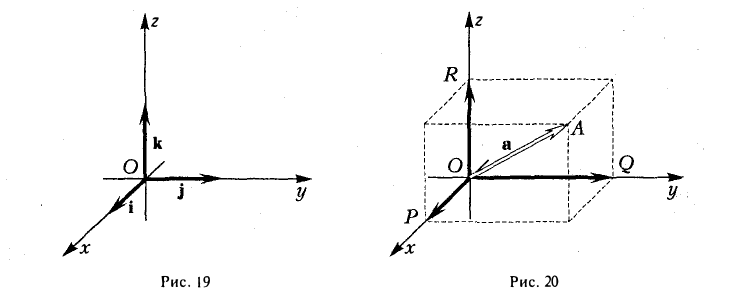
Координаты и компоненты вектора
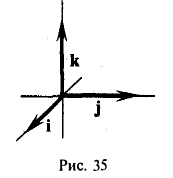
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ox, Оу, Oz (рис. 19). Рассмотрим произвольный вектор п, начало которого лежит в начале координат О, а конец — в точке А. Проведем через точку А плоскости, перпендикулярные осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Р, Q и R соответственно. Из рис. 20 видно, что
Векторы 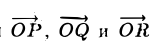
поэтому найдутся числа х, у, z такие, что
а = xi + yj + zk. (2)
Формула (2) называется разложением вектора а по векторам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k.
Векторы i, j, к попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. е. коэффициенты х, у, z в разложении вектора а по векторам i, j, к определены однозначно. Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки А — конца вектора а. Мы пишем в этом случае
а = <х, y,z>.
Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы xi, yj, zk, сумма которых равна вектору а, называются компонентами вектора а.
Из вышеизложенного следует, что два вектора а = < х1, у1, z1 > и b = <х2, у2, z2> равны тогда и только тогда, когда соответственно равны их координаты, т. е.
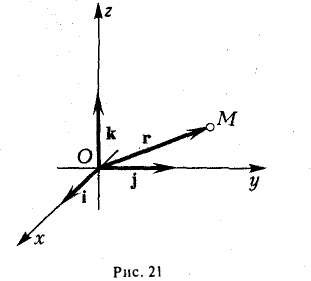
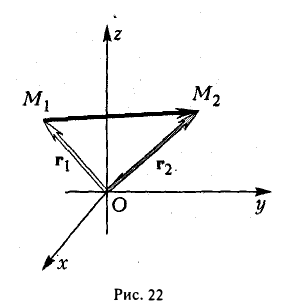
Радиус-вектором точки М(х,у, z) называется вектор г = xi + yj + zk, идущий из начала координат О в точку М (рис. 21).
Линейные операции над векторами в координатах
— при сложении векторов их координаты попарно складываются. Аналогично получаем
— при умножении вектора на число все его координаты умножаются на это число.
Пусть а = < х1, у1, z1>, b = < х2, у2, z2 > — коллинеарные векторы, причем b ≠ 0. Тогда а = μb, т.е.
Обратно, если выполняются соотношения (3), то а = μb, т. е. векторы a и b коллинеарны.
Таким образом, векторы а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Пример:
Найти координаты вектора 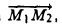
Из рис. 22 видно, что 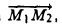
— координаты вектора ММг равны разностям одноименных координат конечной М2 и начальной М точек этого вектора.
Проекция вектора на ось
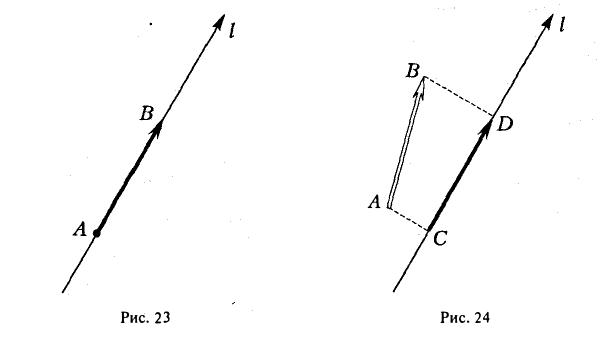
Рассмотрим на оси l ненулевой направленный отрезок АВ (рис.23). Величиной направленного отрезка АВ на оси l называется число, равное длине отрезка АВ, взятой со знаком «+», если направление отрезка АВ совпадаете направлением оси l, и со знаком «-», если эти направления противоположны.
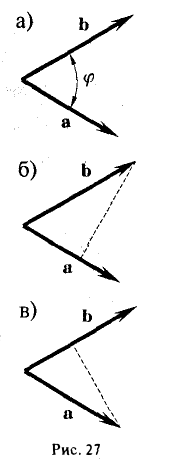
Рассмотрим теперь произвольный вектор 
Определение:
Проекцией вектора 
Обозначение:
Основные свойства проекций
- Проекция вектора АВ на какую-либо ось l равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25)
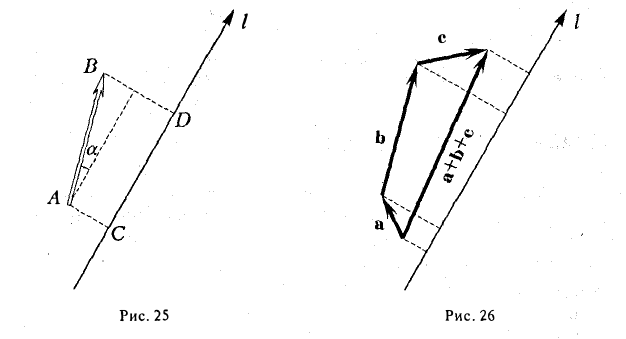
- Проекция суммы векторов на какую-либо ось l равна сумме проекций векторов на ту же ось.
Скалярное произведение векторов
Пусть имеем два вектора a и b.
Определение:
Скалярным произведением вектора а на вектор b называется число, обозначаемое символом (а, b) и определяемое равенством
(1)
где φ, или в иной записи (
Заметив, что |b| cos φ есть проекция вектора b на направление вектора а, можем написать
(рис. 27 б) и, аналогично,’ (2)
(рис. 27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или b — нулевой, будем считать, что
(a, b) = 0.
Свойства скалярного произведения
- Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и b ортогональны, a ⊥ b.
Это следует из формулы (1), определяющей скалярное произведение.
Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так:
2. Скалярное произведение коммутативно:
(а, b) = (b, а).
Справедливость утверждения вытекает из формулы (I), если учесть четность функции cos φ: cos(- φ) = cos φ.
3. Скалярное произведение обладает распределительным свойством относительно сложения:
(а + b, с) = (а, с) + (b, c).
4. Числовой множитель А можно выносить за знак скалярного произведения
(λа, b) = (а, λb) = λ (а, b).
- Действительно, пусть λ > 0. Тогда
поскольку при λ > 0 углы (

Аналогично рассматривается случай λ
Замечание:
В общeм случае (а, b)c ≠ a(b, c).
Скалярное произведение векторов, заданных координатами
Пусть векторы а и b заданы своими координатами в ортонормированном базисе i, j, k:
Рассмотрим скалярное произведение векторов а и b:
Пользуясь распределительным свойством скалярного произведения, находим
То есть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат.
Пример:
Найти скалярное произведение векторов n = 4i — 2j + k и b = 6i + 3j + 2k.
(a, b) = 4 • 6 + (-2) • 3 + 1 • 2 = 20.
Скалярное произведение вектора на себя называется скалярным квадратом:
(а, а) = а 2 .
Применяя формулу (4) при b = а, найдем (5)
С другой стороны,
так что из (5) следует, что (6)
— в ортонормированном базисе длина вектора равна квадратному корню из суммы квадратов его координат.
Косинус угла между векторами. Направляющие косинусы
Согласно определению
(а, b) = |а| • |b| • cos φ,
где φ — у гол между векторами а и b. Из этой формулы получаем
(7)
(предполагается, что векторы а и b — ненулевые).
Пример:
Найти угол между векторами a = <2, -4,4,>и d = <-3,2,6>. Пользуясь формулой (8), находим
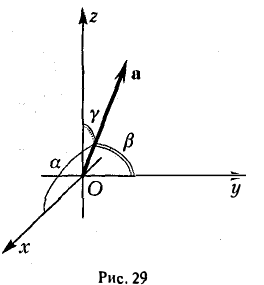
или, в координатной записи, (9)
где а есть угол, образованный вектором я с осью Ох. Аналогично получаем формулы
Формулы (9)-(11) определяют направляющие косинусы вектора а, т. е. косинусы углов, образуемых вектором n с осями координат (рис. 29).
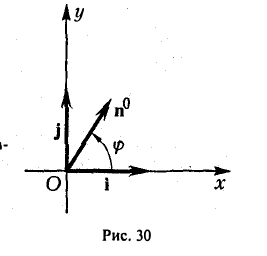
Пример:
Найти координаты единичного вектора n°. По условию | n°| = 1. Пусть n° = zi+ yj+ zk. Тогда
Таким образом, координатами единичного вектора являются косинусы углов, образованных этим вектором с осями координат:
Пример:
Пусть единичный вектор n° ортогонален оси z:
(рис. 30). Тогда его координаты г и у соответственно равны
x=cos φ, y = sin φ.
Векторное произведение векторов
Определение:
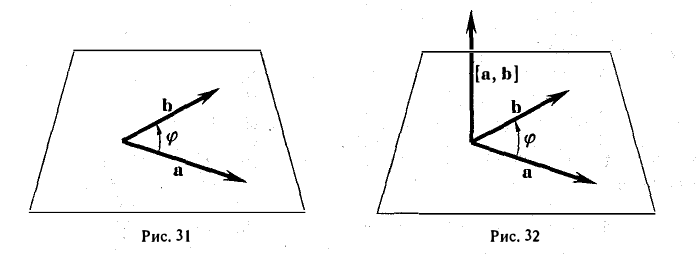
Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [a, b] (или a х b), такой, что
1) длина вектора [а, b] равна |а| • |Ь| • sin φ, где φ — угол между векторами а и b (рис.31);
2) вектор [а, b] перпендикулярен векторам а и b, т.е. перпендикулярен плоскости этих векторов;
3) вектор [а, Ь] направлен так, что из конца этого вектора кратчайший поворот от л к Ь виден происходящим против часовой стрелки (рис. 32).
Иными словами, векторы я, b и [a, b] образуют правую тройку векторов, т.е. расположены так, как большой, указательный и средний пальцы правой руки. В случае, если векторы a и b коллинеарны, будем считать, что [a, b] = 0.
По определению длина векторного произведения (1)
численно равна площади 
|[a, b]| = 
Свойства векторного произведения
- Векторное произведение равно нулевому вектору тогда и только тогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы я и b коллинеарны, то угол между ними равен либо 0, либо тг).
Это легко получить из того, что |[a, b]| = |a| • |b| • sin φ.
Если считать нулевой вектор коллинеарным любому вектору, то условие коллинеарности векторов a и b можно выразить так
2. Векторное произведение антикоммутативно, т. е. всегда (2)
В самом деле, векторы [а, b] и [b, а] имеют одинаковую длину и коллинеарны. Направления же этих векторов противоположны, так как из конца вектора [a, b] кратчайший поворот от a к b будет виден происходящим против часовой стрелки, а из конца вектора [b, a] — почасовой стрелке (рис. 34).
3. Векторное произведение обладает распределительным свойством по отношению к сложению
4. Числовой множитель λ можно выносить за знак векторного произведения
Векторное произведение векторов, заданных координатами
Пусть векторы a и b заданы своими координатами в базисе i,j, k: а = < х1, у1, z1>, b = < х2, у2, z2 >. Пользуясь распределительным свойством векторного произведения, находим (3)
Выпишем векторные произведения координатных ортов (рис. 35):
Поэтому для векторного произведения векторов a и b получаем из формулы (3) следующее выражение (4)
Формулу (4) можно записать в символической, легко запоминающейся форме, если воспользоваться определителем 3-го порядка: (5)
Разлагая этот определитель по элементам 1-й строки, получим (4). Примеры:
- Найти площадь параллелограмма, построенного на векторах а = i + j- k, b = 2i + j- k.
Искомая площадь 
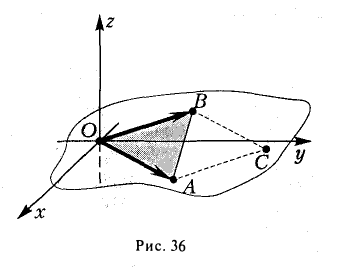
2. Найти площадь треугольника ОАВ (рис.36).
Ясно, что площадь S∆ треугольника ОАВ равна половине площади S параллелограмма О АС В. Вычисляя векторное произведение [a, b] векторов a= 

Замечание:
Векторное произведение не ассоциативно, т.е. равенство [[а, b], с] = [а, b,с]] в общем случае неверно. Например, при а = i, b = j. c= j имеем
Смешанное произведение векторов
Пусть имеем три вектора а, b и с. Перемножим векторы а и b векторно. В результате получим вектор [а, b). Умножим его скалярно на вектор с:
([a, b], с).
Число ([а, b], с) называется смешанным произведением векторов а, b, с и обозначается символом (а, b, с).
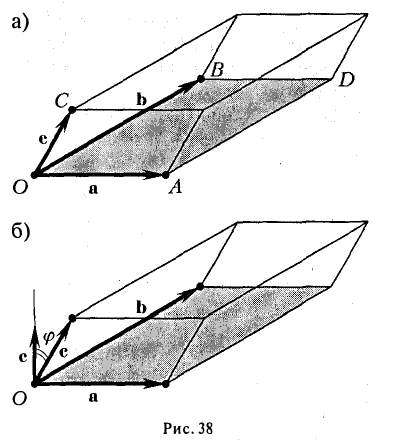
Геометрический смысл смешанного произведения
Отложим векторы а, b и с от общей точки О (рис. 37). Если все четыре точки О, А, В, С лежат в одной плоскости (векторы a, b и с называются в этом случае компланарными), то смешанное произведение ([а, b], с) = 0. Это следует из того, что вектор [а, b] перпендикулярен плоскости, в которой лежат векторы а и b, а значит, и вектору с.
Если же точки О, А, В, С не лежат в одной плоскости (векторы a, b и с некомпланарны), построим на ребрах OA, OB и ОС параллелепипед (рис. 38 а). По определению векторного произведения имеем
где 
Умножая обе части последнего равенства справа скалярно на вектор с, получаем, что
Число ргe с равно высоте h построенного параллелепипеда, взятого со знаком « + », если угол ip между векторами с и с острый (тройка а, b, с — правая), и со знаком «-», если угол — тупой (тройка а, b, с — левая), так что
Тем самым, смешанное произведение векторов a, b и с равно объему V параллелепипеда, построенного на этих векторах как на ребрах, если тройка а, b, с — правая, и -V, если тройка а, b, с — левая.
Исходя из геометрического смысла смешанного произведения, можно заключить, что, перемножая те же векторы a, b и с в любом другом порядке, мы всегда будем О получать либо +V, либо -V. Знак произведения будет зависеть лишь от того, какую тройку образуют перемножаемые векторы — правую или левую. Если векторы а, b, с образуют правую тройку, то правыми будут также тройки b, с, а и с, а, b. В то же время все три тройки b, а, с; а, с, b и с, b, а — левые. Тем самым,
(а, b, с) = (b, с, а) = (с, a,b) = -(b, а, с) = -(а, с, b) = -(с, b, а).
Еще раз подчеркнем, что смешанное произведение векторов равно нулю тогда и только тогда, когда перемножаемые векторы а, b, с компланарны:
Смешанное произведение в координатах
Пусть векторы а, b, с заданы своими координатами в базисе i, j, k:
Найдем выражение для их смешанного произведения (а, b, с). Имеем
— смешанное произведение векторов, заданных своими координатами в базисе i, j, k, равно определителю третьего порядка, строки которого составлены соответственно из координат первого, второго и третьего из перемножаемых векторов.
Пример:
Проверить, компланарны ли векторы
Рассматриваемые векторы будут компланарны или некомпланарны в зависимости от того, будет равен нулю или нет определитель
Разлагая его по элементам первой строки, получим
Двойное векторное произведение
Двойное векторное произведение [а, [b, с]] представляет собой вектор, перпендикулярный к векторам а и [b, с]. Поэтому он лежит в плоскости векторов b и с и может быть разложен по этим векторам. Можно показать, что справедлива формула
[а, [b, с]] = b(а, с) — с(а, b).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/nayti-rabotu-cherez-vektora
http://lfirmal.com/vektornaya-algebra-osnovnyie-ponyatiya-i-opredeleniya/
[/spoiler]
Примеры решений по векторной алгебре
Векторная алгебра для чайников
В этом разделе вы найдете бесплатные решения задач по векторной алгебре: вектора, углы, взаимное расположение на плоскости и пространстве, базис из векторов, действия с векторами и т.п.
Лучшее спасибо – порекомендовать эту страницу
Решения задач с векторами
Задача 1. На оси $Ох$ найти точку, равноудаленную от точек $А(2;-4;5)$ и $В(-3;2;7)$.
Задача 2. Написать разложение вектора $X$ по векторам $(a, b, c)$.
$$X=(-4;4;4), a=(3;1;0), b=(-1;0;6), c=(-1;2;0).$$
Задача 3. Найти косинус угла между векторами $AB$ и $AC$.
$$A=(-4;4;4), B=(3;1;0), C=(-1;0;6).$$
Задача 4. Вычислить площадь треугольника с вершинами $$A=(-4;4;4), B=(3;1;0), C=(-1;0;6).$$
Задача 5. Компланарны ли вектора $a, b, c$? $$a=(-3;2;1), b=(3;1;2), c=(3;-1;4)$$
Задача 6. Заданы два вектора в пространстве. Найти:
а) их сумму;
б) их разность; косинус угла между ними;
в) их векторное произведение.
$a=(0;1;1), b=(-2;0;1).$
Задача 7. Сила $F$ приложена к точке $А$. Вычислить:
а) работу силы $F$ в случае, когда точка её приложения, двигаясь прямолинейно, перемещается в точку $В$;
b) модуль момента силы $F$ относительно точки $В$.
$$F=(5;-3;9), A(3;4;-6), B(2;6;5).$$
Задача 8. Найти ранг и базис системы векторов, перейти к новому базису. Записать разложения векторов по найденным базисам.
Задача 9. Дано $|bar{a}|=4, |bar{b}|=6$, $angle phi=pi/6$. Найти:
А) косинус угла между векторами $bar{a}-2bar{b}$ и $2bar{a}-bar{b}$.
Б) площадь параллелограмма, построенного на векторах $2bar{a}+bar{b}$ и $2bar{a}-bar{b}$.
Задача 10. Найти вектор $bar{a}$, если он перпендикулярен векторам $bar{b}=(1;4;2)$, $bar{c}=bar{i}-bar{j}-bar{k}$, и удовлетворяет условию $(bar{a},bar{d})=5$, где $bar{d}=(2;1;3)$.
Задача 11. Написать разложение вектора $bar{x}$ по векторам $bar{a}, bar{b}, bar{c}$.
$$
bar{x}=(-4;4;4), bar{a}=(3;1;0), bar{b}=(-1;0;6), bar{c}=(-1;2;0).
$$
Задача 12. Даны векторы $bar{a}$ и $bar{b}$. При каких значениях $m$ эти векторы перпендикулярны?
$$ bar{a} = 2bar{i}-3bar{j}+mbar{k}, bar{b}=4bar{i}+7bar{j}-6bar{k}. $$
Задача 13. Вычислить площадь параллелограмма, построенного на векторах $bar{p}$, $bar{q}$.
$$ bar{p}=2bar{a}+3bar{b}, bar{q}=3bar{a}-bar{b}, |bar{a}|=1, |bar{b}|=3, (bar{a},bar{b})=pi/6.
$$
Задача 14. Компланарны ли вектора?
$$ bar{a}=(-3;2;1), bar{b}=(3;1;2), bar{c}=(3;-1;4). $$
Задача 15. Найти:
1) Проекцию $text{пр}_b overline{AB}$;
2) Площадь треугольника со сторонами, совпадающими с векторами $bar{a}$ и $bar{b}$;
3) Смешанное произведение $(bar{b} cdot bar{a} cdot overline{AB})$;
4) При каком $lambda$ векторы $overline{AB}$ и $bar{a}+lambda bar{b}$ ортогональны?
$$ bar{a} = 3bar{i}-bar{j}+2bar{k}, bar{b} = (-1;2;1), A=(0,-2,1), B=(-1,1,3). $$
Задача 16. Найти координаты вектора $bar{x}$, если известно, что он перпендикулярен векторам $bar{a}_1=(4,-2,-3)$ и $bar{a}_2=(0,1,3)$, образует с ортом $bar{j}$ острый угол и $|bar{x}|=26$.
Задача 17. Даны векторы $bar{a}$, $bar{b}$ и $bar{c}$. Необходимо:
а) вычислить смешанное произведение трех векторов;
b) найти модуль векторного произведения;
с) проверить, будут ли коллинеарны или ортогональны два вектора;
d) проверить, будут ли компланарны три вектора.
$$ bar{a} = 2bar{i}-3bar{j}+bar{k}, bar{b} = bar{j}+4bar{k}, bar{c} = 5bar{i}+2bar{j}-3bar{k}.$$
$$ a. bar{a} cdot 3bar{b} cdot bar{c};\
b. |3 bar{a} times 2 bar{c}|;\
c. bar{a} text{ и } bar{c};\
d. bar{a}, 2bar{b} text{ и } 3bar{c}.
$$
Не получаются задачи? Решим быстро и недорого!
Ученик
(197),
закрыт
9 лет назад
Александр Титов
Гений
(50749)
10 лет назад
Работа силы по перемещению на пути из точки А в точку B определяется как скалярное произведение вектора силы на вектор перемещения. Вектор перемещения равен АВ = (-1-0; -1-0 -1-1) = (-1; -1: -2). Скалярное произведение векторов, заданных своими координатами (x1, y1, z1) и (x2, y2, z2), вычисляется по формуле (x1x2 + y1y2 + z1z2). Подставляя сюда координаты векторов силы и перемещеня, получаем ответ A = -5. Обратите внимание на знак минус перед числом.
artem92 писал(а):
Позарез надо решение
2. Вычислить поток векторного поля [math]vec{a}=x^2,vec{i}+y^2,vec{j}+z^2,vec{k}[/math] через часть поверхности [math]1-z=x^2+y^2[/math], лежащую в первом октанте.
Заранее огромное спасибо.
Я так понимаю – в задаче подразумевается, что нормаль внешняя.
[math]begin{aligned}z &=1-x^2-y^2\z’_x&=-2x\z’_y &=-2y\[5pt] vec{n}&=-z’_x,vec{i}-z’_y,vec{j}+vec{k}=2x,vec{i}+2y,vec{j}+vec{k}\[5pt] langlevec{a}&,vec{n}rangle= a_x(-z’_x)+a_y(-z’_y)+a_z= 2x^3+2y^3+(1-x^2-y^2)^2\[9pt] Pi&=iintlimits_{D_{xy}}langle{vec{a},vec{n}}rangle,dxdy= iintlimits_{x^2+y^2leqslant1}Bigl[2x^3+2y^3+(1-x^2-y^2)^2Bigr],dxdy=\ &= left{begin{gathered}x=rsinvarphi,hfill\y=rcosvarphihfillend{gathered}right}= intlimits_0^{2pi}dvarphi intlimits_0^1Bigl[2r^3sin^3varphi+2r^3cos^3varphi+(1-r^2)^2Bigr]r,dr=\ &=intlimits_0^{2pi}dvarphi intlimits_0^1Bigl[2(sin^3varphi+cos^3varphi)r^4+r-2r^3+r^5Bigr]dr=\ &=intlimits_0^{2pi}!{left.{left(frac{2}{5}(sin^3varphi+cos^3varphi)r^5+frac{1}{2}r^2-frac{1}{2}r^4+frac{1}{6}r^6right)}!right|_{r=0}^{r=1}dvarphi=\ &=intlimits_0^{2pi}!left(frac{2}{5}(sin^3varphi+cos^3varphi)+frac{1}{6}right)!dvarphi= frac{2}{5}cdot0+frac{pi}{3}= frac{pi}{3}end{aligned}[/math]
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
33
Добавлен:
13.05.2015
Размер:
829.55 Кб
Скачать
|
Федеральное агентство по образованию РФ |
||
|
ГОУВПО «Удмуртский государственный университет» |
УДК |
514.12 |
|
Факультет информационных технологий |
ББК |
22.151 |
|
и вычислительной техники |
Г 60 |
|
|
Рецензенты: к.ф.-м.н. М.А. Воронецкая |
||
|
к.ф.-м.н. В.И. Родионов |
||
|
В.В. Головизин |
Головизин В.В. |
|
|
Г60 |
Основные задачи курса «Алгебра и геометрия». |
|
|
Часть I: Основные задачи векторной алгебры: учеб.- |
||
|
метод. пособие. Ижевск, 2009. 156 с. |
||
|
Основные задачи курса «Алгебра и геометрия». |
Первая часть учебно-методического пособия предна- |
|
|
Часть I. Основные задачи векторной алгебры |
значена для студентов, изучающих векторную алгебру в |
|
|
рамках любого курса высшей математики. Пособие может |
||
|
быть полезно преподавателям при проведении практиче- |
||
|
ских занятий и при подготовке индивидуальных заданий |
||
|
Учебно-методическое пособие |
студентам. |
|
|
Пособие содержит решения задач, которые тематически |
разбиты на главы, и имеют сквозную нумерацию. Номера упражнений, помещенных в конце пособия, совпадают номерами соответствующих задач.
УДК 514.12 ББК 22.151
|
Ижевск 2009 |
© Головизин В.В., 2009 |
2
Предисловие
Для любого вузовского преподавателя математики не является секретом то обстоятельство, что в последние годы в университет приходят студенты с весьма разным уровнем математической подготовки. Автор данного пособия преследовал цель помочь нашим студентам первого курса обучения (в первую очередь, студентам, имеющим невысокий уровень) в освоении одного из самых основных, фундаментальных курсов учебной программы – курса алгебры и геометрии, и очень надеется, что эта помощь не будет отвергнута или проигнорирована.
Наибольшую трудность у студентов вызывает решение задач, даже стандартных. Практические занятия, на которых студентов обучают решению задач, имеют жесткие временные рамки. В соответствии со стандартами образовательных программ часть обучения каждый студент обязан проводить самостоятельно, и на это в учебных планах отводится немало часов. Представляемое Вашему вниманию, уважаемый читатель, пособие предназначено помочь Вам в Вашей самостоятельной работе.
Автор стремился донести до читателя идеи решения, дать образцы логического мышления, научить применять полученный теоретический материал в конкретных задачах, помогая тем самым читателю пробрести необходимые практические навыки, умение думать и размышлять над задачей.
Все основные задачи курса тематически разбиты на главы, но основной методической единицей пособия является задача. При этом соблюдается единый принцип подачи учебного материала. После формулировки каждой задачи приводятся необходимые теоретические сведения, затем следует подробное решение задачи в общем виде, которое иллюстрируются конкретными числовыми примерами.
Ориентироваться в пособии довольно легко. С помощью оглавления читатель находит интересующую его тему
– главу. В начале пособия приводится полный список задач, имеющих сквозную нумерацию. Упражнения, приведенные в конце пособия, для удобства читателя имеют номера, совпадающие с номерами задач.
Читатель может по своему желанию проработать отдельную главу, решая все задачи главы последовательно, или же ознакомиться с решением отдельной задачи. Можно сразу же проверить понимание материала, решив соответствующее упражнение. Впрочем, вдумчивый читатель может не торопиться с чтением предложенного решения и попытаться справиться с задачей самостоятельно.
В заключение отметим, что пособие может быть полезно преподавателям при проведении практических занятий, коллоквиумов и, особенно, для подготовки индивидуальных заданий студентам.
|
СПИСОК ЗАДАЧ |
15. |
Построить точку с заданными полярными координата- |
||
|
Глава 1. Метод координат |
ми в полярной системе координат. |
|||
|
16. |
Найти расстояние между двумя точками в полярной |
|||
|
1. |
Найти расстояние между двумя точками. |
системе координат. |
||
|
17. |
Найти площадь треугольника с известными вершинами |
|||
|
2. |
На координатной прямой найти точки, удаленные от |
в полярной системе координат. |
||
|
данной точки на заданное расстояние. |
18. |
Найти внутренний угол треугольника с известными |
||
|
3. |
Найти отношение, в котором данная точка делит дан- |
вершинами в полярной системе координат. |
||
|
ный отрезок. |
Глава 4. Полярная система координат и ПДСК |
|||
|
4. |
Найти координаты точки, которая делит данный отре- |
|||
|
зок в данном отношении. |
||||
|
5. |
Найтицентртяжестисистемыиздвухматериальныхточек. |
19. |
Найти декартовые координаты точки по ее полярным |
|
|
6. |
Найтицентртяжестисистемыизтрехматериальныхточек. |
координатам. |
||
|
7. |
Найти центр тяжести однородного треугольника. |
20. |
Найти полярные координаты точки по ее декартовым |
|
|
8. |
Найти центр тяжести трапеции. |
координатам. |
||
|
9. |
Найти центр тяжести однородного многоугольника. |
Глава 5. Действия с векторами |
||
|
Глава 2. Косоугольная система координат |
||||
|
21. |
Построить вектор, равный сумме двух данных векторов |
|||
|
10. |
Построить точку с заданными координатами в косо- |
по правилу параллелограмма. |
||
|
угольной системе координат и найти расстояние до нее |
22. |
Построить вектор, равный сумме двух или более дан- |
||
|
от начала координат. |
ных векторов по правилу треугольника. |
|||
|
11. |
Найти координаты заданной точки в косоугольной сис- |
23. Построитьвектор, равныйпроизведениювектораначисло. |
||
|
теме координат. |
24. |
Построить вектор, противоположный данному. |
||
|
12. |
Найти расстояние от точки с заданными координатами |
25. |
Построить разность векторов. |
|
|
в косоугольной системе координат до осей координат. |
26. |
Построить и вычислить проекцию вектора на ось. |
||
|
13. |
Найти координаты точки в косоугольной системе коорди- |
27. |
Построить и вычислить проекцию вектора на вектор. |
|
|
нат, если известны расстояния от нее до осей координат. |
28. |
Вычислить скалярное произведение векторов, исполь- |
||
|
Глава 3. Полярная система координат |
зуя его определение и простейшие свойства. |
|||
|
29. |
Найти угол между векторами, если известно их скаляр- |
|||
|
ное произведение и их модули. |
||||
|
14. |
Найти полярные координаты заданной точки в поляр- |
30. |
Вычислить скалярное произведение векторов, исполь- |
|
|
ной системе координат. |
зуя его определение и свойство линейности. |
|
31. |
Определить ориентацию данной тройки векторов. |
44. |
Найти декартовые координаты вектора координатного |
|
32. |
Построить векторное произведение двух векторов. |
пространства, его модуль, орт и направляющие косину- |
|
|
33. |
Вычисление модуля векторного произведения векторов |
сы по известным координатам его начала и конца. |
|
|
с использованием его определения и свойств. |
45. |
Найти декартовые координаты суммы векторов и про- |
|
|
34. |
Вычисление смешанного произведения векторов с ис- |
изведения вектора на число для векторов координатно- |
|
|
пользованием его определения и свойств. |
го пространства. |
||
|
35. |
Определить ориентацию данной тройки векторов, ис- |
46. |
Найти декартовые координаты радиус-вектора точки с |
|
пользуя свойства смешанного произведения. |
известными координатами и координаты точки, если |
||
|
Глава 6. Линейные операции с векторами |
известны декартовые координаты ее радиус-вектора. |
||
|
47. |
Определить, коллинеарные ли векторы, заданные в ко- |
||
|
в координатной форме |
ординатной форме. |
||
|
36. |
Найти декартовую координату вектора числовой оси, |
Глава 7. Разложение вектора по произвольному базису |
|
|
записать его в координатной форме, найти его модуль, |
геометрическим способом |
||
|
орт и направляющий косинус, определить его ориента- |
|||
|
цию на координатной оси. |
48. |
Построить разложение вектора по произвольному бази- |
|
|
37. |
Найти декартовую координату вектора координатной |
су на прямой и вычислить его координату. |
|
|
оси по известным координатам его начала и конца и за- |
49. |
Построить разложение вектора по произвольному бази- |
|
|
писать его в координатной форме. Найти его модуль, |
су на плоскости и вычислить его координаты. |
||
|
орт и направляющий косинус. Определить его ориента- |
50. |
Построить разложение вектора по произвольному бази- |
|
|
цию на координатной оси. |
су пространства и вычислить его координаты. |
||
|
38. |
Найти координаты суммы векторов и произведения |
Глава 8. Линейные операции с векторами |
|
|
вектора на число для векторов координатной оси. |
|||
|
39. |
Найти декартовые координаты вектора координатной |
в произвольном базисе |
|
|
плоскости, его модуль, орт и направляющие косинусы. |
|||
|
40. |
Найти декартовые координаты вектора координатной |
51. |
Линейные операции с векторами в координатной форме |
|
плоскости, его модуль, орт и направляющие косинусы |
относительно произвольного базиса на прямой. |
||
|
по известным координатам его начала и конца. |
52. |
Линейные операции с векторами в координатной форме |
|
|
41. |
Найти координаты суммы векторов и произведения век- |
относительно произвольного базиса на плоскости. |
|
|
тора на число для векторов координатной плоскости. |
53. |
Линейные операции с векторами в координатной форме |
|
|
42. Найтиполярныйуголвекторанакоординатнойплоскости. |
относительно произвольного базиса пространства. |
43.Найти декартовые координаты вектора координатного пространства, егомодуль, ортинаправляющие косинусы.
|
Глава 9. Координатывекторавортонормированномбазисе |
63. |
Найти проекцию вектора на вектор, если оба вектора |
||
|
54. |
Построить нормированный базис на прямой и найти |
заданы в координатной форме относительно ортонор- |
||
|
мированного базиса, и найти, в частности, проекции |
||||
|
координату вектора данной прямой относительно по- |
вектора на координатные оси. |
|||
|
строенного базиса. |
64. |
Найти работу, производимую вектором силы вдоль век- |
||
|
55. |
Построить ортонормированный базис плоскости и най- |
тора перемещения материальной точки, если оба векто- |
||
|
ти координаты вектора плоскости относительно по- |
ра заданы в координатной форме относительно орто- |
|||
|
строенного базиса. |
нормированного базиса. |
|||
|
56. |
Построить ортонормированный базис пространства и |
Глава 12. Применениевекторногопроизведениявекторов |
||
|
найти координаты произвольного вектора относительно |
||||
|
построенного базиса. |
65. |
Найти синус угла между двумя векторами, заданными в |
||
|
Глава 10. Произведения векторов в координатной форме |
||||
|
координатной форме. |
||||
|
66. |
Определить, являются ли два вектора, заданные в коор- |
|||
|
57. |
Найти скалярное произведение векторов, заданных в коор- |
динатной форме, коллинеарными. |
||
|
динатнойформеотносительноортонормированногобазиса. |
67. Найти координаты вектора, перпендикулярного двум не- |
|||
|
58. |
Найти векторное произведение векторов, заданных в коор- |
коллинеарнымвекторам, заданнымвкоординатнойформе. |
||
|
динатнойформеотносительноортонормированногобазиса. |
68. |
Найти двугранный угол между гранями треугольной |
||
|
59. |
Найти смешанное произведение векторов, заданных в коор- |
пирамиды, если известны координаты ее вершин. |
||
|
динатнойформеотносительноортонормированногобазиса. |
69. |
Найти площадь треугольника, если известны координа- |
||
|
Глава 11. Применениескалярного произведениявекторов |
ты его вершин. |
|||
|
70. |
Определить момент силы относительно данной точки. |
|||
|
71. |
Найти линейную скорость точки тела, вращающегося |
|||
|
60. |
Найти модуль, орт и направляющие косинусы вектора, |
вокруг оси с заданной угловой скоростью. |
||
|
заданного в координатной форме относительно орто- |
Глава 13. Применениесмешанногопроизведениявекторов |
|||
|
нормированного базиса. |
||||
|
61. |
Найти угол между векторами, заданными в координат- |
|||
|
ной форме относительно ортонормированного базиса. |
72. |
Определить, компланарны ли три вектора, заданные в |
||
|
62. |
Определить, являются ли два вектора, заданные в коор- |
координатной форме. |
||
|
динатной форме относительно ортонормированного ба- |
73. |
Определить ориентацию трех некомпланарных векто- |
||
|
зиса, ортогональными. |
ров, заданных в координатной форме. |
|||
|
74. |
Вычислить объем треугольной пирамиды, если извест- |
|||
|
ны координаты ее вершин. |

75.Вычислить высоту треугольной пирамиды, если известны координаты ее вершин.
Глава 14. Разложение вектора по произвольному базису алгебраическим способом
76.Найти координаты вектора относительно данного базиса на прямой, если вектор и базис даны в координатной форме.
77.На плоскости найти координаты вектора относительно данного базиса, если вектор и базис даны в координатной форме.
78.В пространстве найти координаты вектора относительно данного базиса, если вектор и базис даны в координатной форме.
Глава 15. Вычисление модуля и направляющих косинусов вектора в произвольном базисе
79.Найти модуль и направляющий косинус вектора, заданного в координатной форме относительно произвольного базиса на прямой.
80.Найти модуль и направляющие косинусы вектора, заданного в координатной форме относительно произвольного базиса на плоскости.
81.Найти модуль и направляющие косинусы вектора, заданного в координатной форме относительно произвольного базиса в пространстве.
Глава 1. Метод координат
Задача 1. Найти расстояние между двумя точками.
Решение. Мы полагаем, что в пространстве введена прямоугольная декартовая система координат (в дальнейшем сокращенно ПДСК) Oxyz. Пусть A(xA , yA , zA ) и
B(xB , yB , zB ) – две произвольные точки пространства. Тогда расстояние между ними можно найти по формуле:
AB = (xB −xA )2 +(yB − yA )2 +(zB −zA )2 .
Если точки А и В даны на координатной плоскости Оху, то
A(xA , yA ) , B(xB , yB ) и AB = (xB −xA )2 +(yB − yA )2 .
Если точки даны на координатной оси Ох, то A(xA ) , B(xB ) и AB = (xB −xA )2 =| xB −xA | .
Замечание. Расстояние между точками А и В можно нахо-
дить и как модуль вектора AB . Для этого находим декар-
товые координаты вектора AB и используем формулу вычисления его модуля. Понятно, что при этом получаются те же самые формулы.
Пример. Найти длины сторон треугольника АВС, если даны координаты его вершин:
А(1; –1; 0), В(0; 1; 0), С(3; 1; 1).
Решение. Очевидно,
|
AB = (0 −1)2 +(1+1)2 = |
5 , |
||
|
AC = |
(3 −1)2 +(1+1)2 +(1−0)2 |
= 3 , |
|
|
BC = |
(3 −0)2 +(1−1)2 +(1−0)2 |
= |
10 . |
Ответ: 10, 3, 5 .

Задача 2. На координатной прямой найти точки, удаленные от данной точки на заданное расстояние.
Решение. Пусть на координатной оси Ох дана точка A(xA ) и положительное число а. Нужно найти координаты
точек М(х), таких, что AM = a . Так как AM =| x −xA | , то,
по сути, нужно решить уравнение
| x − xA | = a .
Нет никакой необходимости решать это уравнение алгебраическими методами, т.к. с геометрической точки зрения ответ очевиден.
|
M1 |
A |
M2 х |
|
• |
• |
• |
|
xA −a |
xA |
xA + a |
|
Рис. 1. |
Здесь AM1 = AM2 = a , поэтому координата точки M1 на
величину а меньше координаты точки А, а координата точки M2 на величину а больше координаты точки А.
Ответ: M1 (xA −a) , M2 (xA + a) .
Пример. На оси Ох найти точки, удаленные от точки А(–7) на расстояние, равное 11.
Ответ: M1 (−18) , M2 (4) .
Замечание. Аналогично решаются неравенства
| x −xA | < a , | x −xA | ≤ a , | x −xA | > a , | x −xA | ≥ a .
Решим, например, неравенство | x −xA | < a . С геометриче-
ской точки зрения решить данное неравенство означает найти координаты всех точек М(х) на оси Ох, которые уда-
лены от точки А на расстояние меньшее чем а, то есть для которых AM < a .
Из рисунка 1 мы видим, что все точки, удаленные от точки А на расстояние меньшее чем а, находятся на интервале (M1 , M2 ) , т.е. решением данного неравенства являет-
ся интервал x (M1 , M2 ) . Аналогично решаются и другие, указанные выше, неравенства.
Задача 3. Найти отношение, в котором данная точка делит данный отрезок.
Определение. Говорят, что точка С делит отрезок прямой АВ, считая от точки А, в отношении λ, если AC = λ CB .
Обозначение. Отношение, в котором точка С делит отрезок АВ, считая от точки А, обозначаем λCAB .
Решение. Рассмотрим различные случаи этой задачи.
1)Известно, что точка С находится на отрезке АВ и известны расстояния АС и ВС. Тогда точка С делит отрезок АВ внутренним образом и
λCAB = АСВС .
2)Известно, что точка С находится вне отрезка АВ и известны расстояния АС и ВС. Тогда точка С делит отрезок АВ внешним образом и
λCAB = − АСВС .
3)Известны координаты всех трех точек:
A(xA , yA , zA ) , B(xB , yB , zB ) и C(xC , yC , zC ) .
Тогда

|
λCAB = |
xC − xA |
= |
yC − yA |
= |
zC − zA |
. |
(1) |
|
xB − xC |
yB − yC |
||||||
|
zB − zC |
Пример. Известно, что точки А(0; –3; z), В(2; –2; 1) и С(4; у; –2) находятся на одной прямой. Найти отношение, в котором точка С делит отрезок АВ, ординату точки С и аппликату точки А.
Решение. С помощью формулы (1) находим искомое отношение:
|
λCAB |
= |
xC − xA |
= |
4 −0 |
= −2 . |
|
|
xB − xC |
2 − 4 |
|||||
Используя формулу (1) и найденное отношение, находим:
|
λCAB = |
yC − yA |
, −2 = |
y +3 |
, |
4 + 2y = y +3 , y = −1. |
|||||
|
−2 − y |
||||||||||
|
yB − yC |
||||||||||
|
Аналогично, λCAB = |
zC − zA |
, |
−2 |
= |
−2 − z |
, z = 4 . |
||||
|
1+ 2 |
||||||||||
|
zB − zC |
||||||||||
|
Ответ: λCAB = −2 , |
yC = −2 , zA = 4 . |
Задача 4. Найти координаты точки, которая делит данный отрезок в данном отношении.
Решение. Пусть известны координаты концов отрезка АВ и λCAB . Тогда координаты точки С легко находятся из равенств (1):
|
xC = |
xA + λ xB |
, |
yC |
= |
yA + λ yB |
, zC = |
zA +λ zB |
. |
(2) |
||
|
1 + λ |
1 + λ |
||||||||||
|
1+λ |
|||||||||||
|
В частности, если точка С – это середина отрезка АВ, то |
|||||||||||
|
xC = |
xA + xB |
, |
yC |
= |
yA + yB |
, |
zC = |
zA + zB |
. |
(3) |
|
|
2 |
2 |
2 |
Пример 1. Пусть А(–2; –7), В(13; 4), λCAB = 34 . Найти ко-
|
ординаты точки С. |
|||||||||||||||||||||||
|
Решение. По формулам (3) находим: |
|||||||||||||||||||||||
|
xA + λxB |
−2 + |
3 |
13 |
31 |
|||||||||||||||||||
|
4 |
|||||||||||||||||||||||
|
xC |
= |
= |
= |
, |
|||||||||||||||||||
|
1+ λ |
3 |
7 |
|||||||||||||||||||||
|
1+ |
|||||||||||||||||||||||
|
4 |
|||||||||||||||||||||||
|
yA + λyB |
−7 + |
3 |
4 |
16 |
|||||||||||||||||||
|
yC |
= |
= |
4 |
= − |
. |
||||||||||||||||||
|
1+ λ |
3 |
7 |
|||||||||||||||||||||
|
1+ |
|||||||||||||||||||||||
|
31 |
16 |
4 |
|||||||||||||||||||||
|
; − |
|||||||||||||||||||||||
|
Ответ: С |
. |
||||||||||||||||||||||
|
7 |
|||||||||||||||||||||||
|
7 |
Пример 2. Пусть А(–1; –7; 4), В(13; 5; –6). Найти коорди-
наты середины отрезка АВ. Решение.
|
xC |
= |
xA + xB |
= |
−1+13 |
= 6 , |
yC |
= |
yA + yB |
= |
−7 +5 |
= −1, |
|||
|
2 |
2 |
|||||||||||||
|
2 |
zA + zB |
4 −6 |
2 |
|||||||||||
|
zC |
= |
= |
= −1. |
|||||||||||
|
2 |
||||||||||||||
|
2 |
Ответ: С(6; –1; –1).
Задача 5. Найти центр тяжести системы из двух материальных точек.
Определение. Пусть имеется отрезок АВ, концы которого являются материальными точками с массами mA и mB со-
ответственно. Точка С отрезка АВ, для которой выполняется равенство

mA AC = mB BC ,
где АС и ВС – длины соответствующих отрезков, называется геометрическим центром тяжести (в дальнейшем просто ГЦТ) системы из двух материальных точек.
Из определения следует, что ГЦТ системы из двух материальных точек А и В является точка С, которая делит отрезок АВ внутренним образом в отношении
λC = AC = mB . AB CB mA
Справедлива следующая теорема.
Теорема. (О координатах ГЦТ системы двух материальных точек.) Пусть A(xA , yA , zA ) , B(xB , yB , zB ) – две произ-
вольные материальные точки с массами mA и mB соответственно. Пусть точка C(xC , yC , zC ) является их ГЦТ. Тогда
|
xC |
= |
xA mA + xB mB |
, |
yC = |
yA mA + yB mB |
, |
|
|
mA + mB |
mA + mB |
||||||
|
zC = |
zA mA + zB mB |
. |
(4) |
||||
|
mA + mB |
Пример. Пусть А(–1; –7; 4), В(13; 5; –6) – две материаль-
ные точки, причем масса точки А в три раза меньше массы точки В. Найти координаты их ГЦТ.
Решение. По условию, mB = 3mA . Подставляя данные задачи в формулы (4), находим:
|
xC = |
xA mA + xB mB |
= |
mA (xA +3xB ) |
= |
−1+39 |
= |
19 |
, |
|
mA + mB |
4 |
2 |
||||||
|
4mA |
|
yC |
= |
yA mA + yB mB |
= |
mA (yA +3yB ) |
= |
−7 +15 = 2 , |
||||||||||
|
mA + mB |
4mA |
4 |
||||||||||||||
|
zC |
= |
zA mA + zB mB |
= |
mA (zA +3zB ) |
= |
4 −18 |
= − |
7 . |
||||||||
|
4 |
||||||||||||||||
|
mA + mB |
4mA |
2 |
||||||||||||||
|
19 |
; 2; − |
7 |
||||||||||||||
|
Ответ: |
. |
|||||||||||||||
|
2 |
||||||||||||||||
|
2 |
Задача 6. Найти центр тяжести системы из трех материальных точек.
Определение. ГЦТ системы из n ( n ≥ 3 ) материальных точек A1 , A2 , …, An с массами m1 , m2 , …, mn называется ГЦТ
системы из двух материальных точек: С и An с массами mC = m1 + m2 + … + mn−1 и mn соответственно, где С – это ГЦТ системы из (n−1) -й материальных точек
A1 , A2 , …, An−1 .
Справедлива следующая теорема.
Теорема. (О ГЦТ системы из n материальных точек.)
Пусть A1 (x1 , y1 , z1 ), …, An (xn , yn , zn ) – система из n ( n ≥ 2 ) материальных точек с массами m1 , …, mn соответ-
ственно, и точка С является их ГЦТ. Тогда
|
xC |
= |
x1 |
m1 + x2 m2 +… + xn mn |
, |
||||
|
m1 + m2 +… + mn |
||||||||
|
yC |
= |
y1 |
m1 + y2 m2 +… + yn mn |
, |
||||
|
m1 + m2 +… + mn |
||||||||
|
zC |
= |
z1 m1 + z2 m2 +… + zn mn |
. |
(5) |
||||
|
m1 + m2 +… + mn |

В частности, при n = 3, получаем:
|
xC |
= |
x1 m1 + x2 m2 + x3 m3 |
, |
||
|
m1 + m2 + m3 |
|||||
|
yC |
= |
y1 m1 + y2 m2 + y3 m3 |
, |
||
|
m1 + m2 + m3 |
|||||
|
zC |
= |
z1 m1 + z2 m2 + z3 m3 |
. |
(6) |
|
|
m1 + m2 + m3 |
Пример. Пусть на оси Ох даны три материальные точки:
А(–17), mA = 3 , В(9), mB =1, С(30), mC = 2 . Найти их
ГЦТ.
Решение. Используем первую из формул (6):
|
x = |
x1 m1 + x2 m2 + x3 m3 |
= |
−17 3 +9 1+30 2 |
= |
15 = 5 . |
|
|
m + m |
+ m |
3 +1+ 2 |
||||
|
2 |
3 |
6 2 |
||||
|
1 |
Ответ: 2,5.
Задача7. Найтицентртяжестиоднородноготреугольника.
Решение. Если известны координаты вершин треугольника (вырезанного из однородного материала), то его ГЦТ можно найти по формулам:
|
x = |
xA + xB + xC |
, |
y = |
yA + yB + yC |
, z = |
zA + zB + zC |
. (7) |
|
3 |
3 |
3 |
Пример. Найти ГЦТ треугольника с вершинами А(0; 3; 9),
В(–2; –3; 17), С(11; –12; 10).
Решение. Вычисляем по формулам (7):
|
x = |
xA + xB + xC |
= 0 − 2 +11 |
= 3, |
||||||
|
yA + yB + yC |
3 |
3 |
zA + zB + zC |
||||||
|
y = |
= |
3 −3 −12 |
= −4 , |
z = |
=12 . |
||||
|
3 |
|||||||||
|
3 |
3 |
Ответ: (3; –4; 12).
Задача 8. Найти центр тяжести трапеции.
Решение. Разобьем трапецию ABCD на два треугольника АВС и ACD. Найдем центры тяжести обоих треугольников. Пусть Е – центр тяжести треугольника АВС, F – центр тяжести треугольника ACD. Поместим в точку Е массу, численно равную площади треугольника АВС:
mE = 12 BC h , где h – высота трапеции. В точку F помеща-
ем массу, численно равную площади треугольника ACD: mF = 12 AD h . Обозначим a = AD длину нижнего основа-
ния, b = BC длину верхнего основания. Тогда mE = bh2 ,
mF = ah2 . Теперь ГЦТ трапеции совпадает с ГЦТ системы из двух материальных точек Е и F.
|
b |
С |
|||||||||||||||||
|
В • E |
||||||||||||||||||
|
h |
• F |
|||||||||||||||||
|
А |
D |
|||||||||||||||||
|
а |
||||||||||||||||||
|
Рис. 2. |
||||||||||||||||||
|
xE mE + xF mF |
xE |
bh |
+ xF |
ah |
bxE |
+ axF |
||||||||||||
|
x = |
= |
2 |
2 |
= |
. |
|||||||||||||
|
mE + mF |
bh |
+ |
ah |
a + b |
||||||||||||||
|
2 |
2 |
По аналогичным формулам находятся остальные координаты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
17.03.2016187.73 Кб15Часть 1.docx
- #
- #
- #
- #

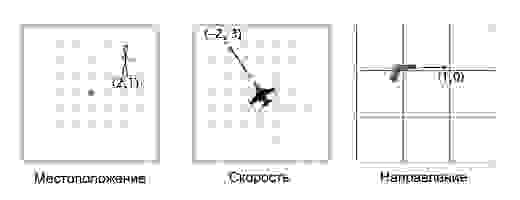
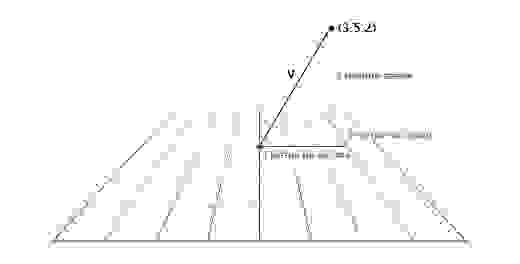
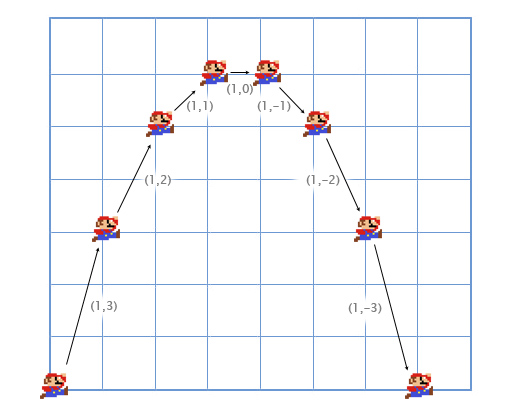
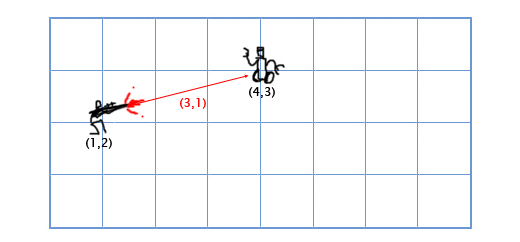
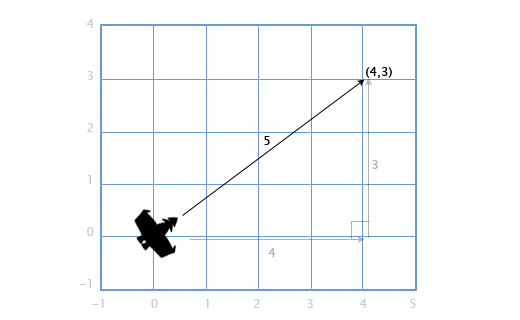
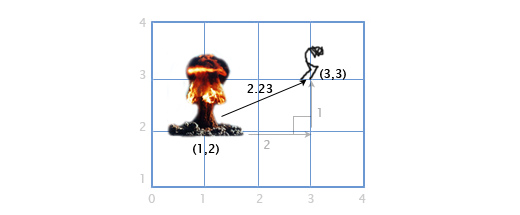
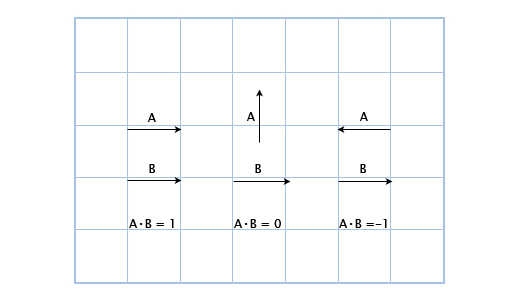
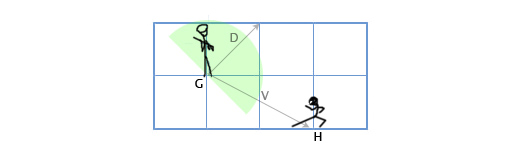
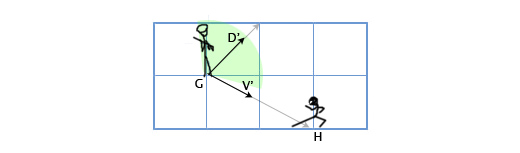
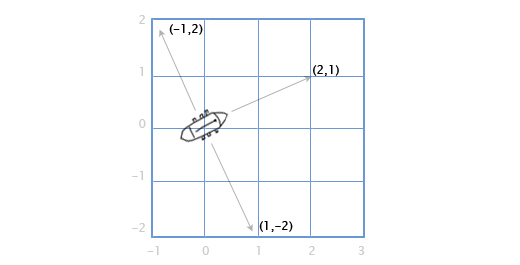
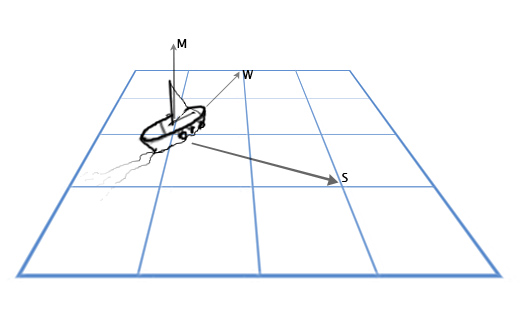
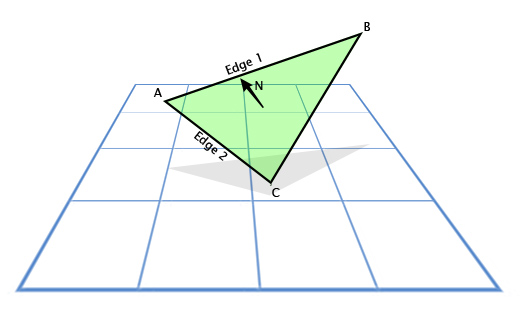
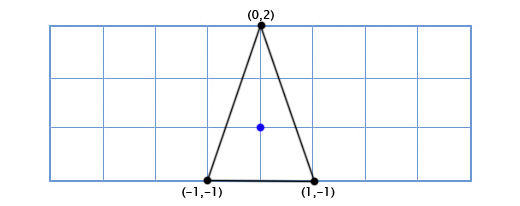
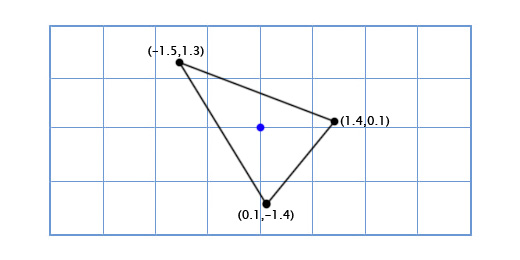
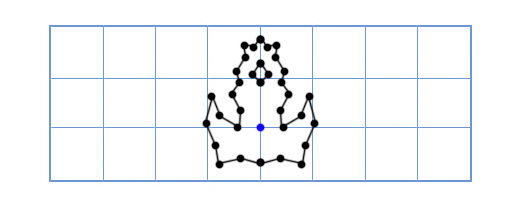
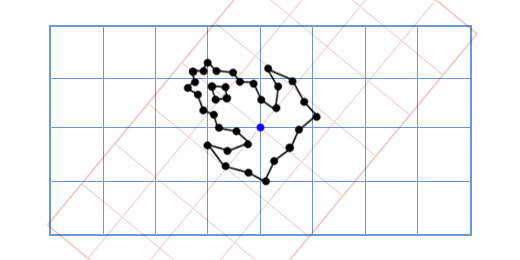
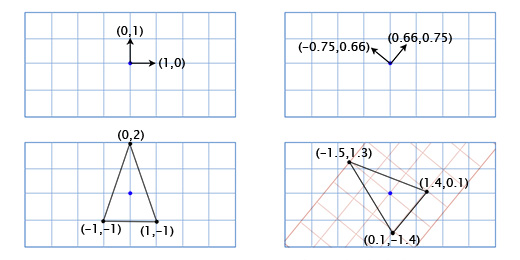
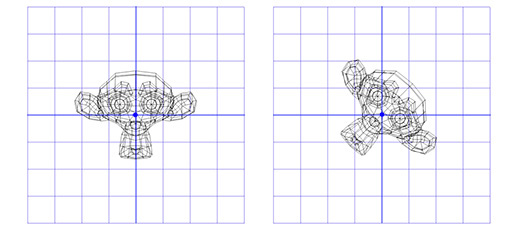
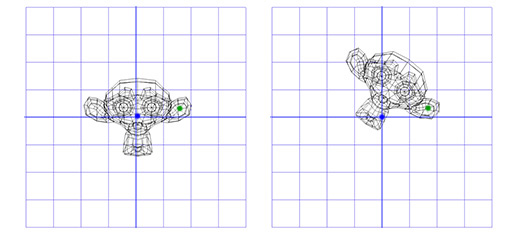
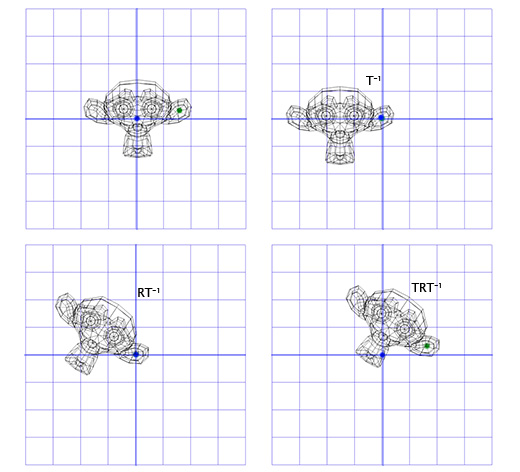
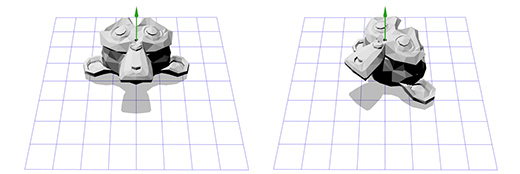
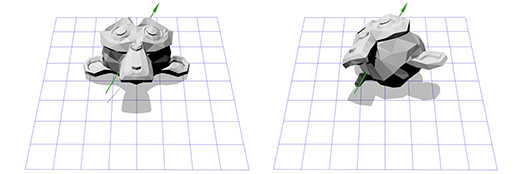
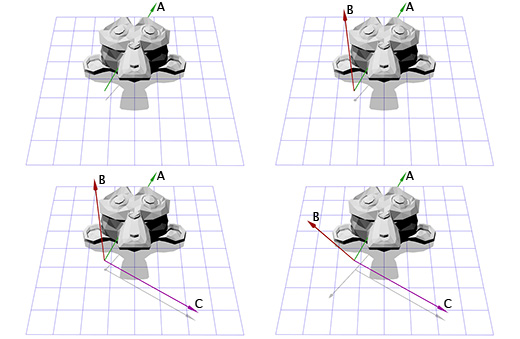
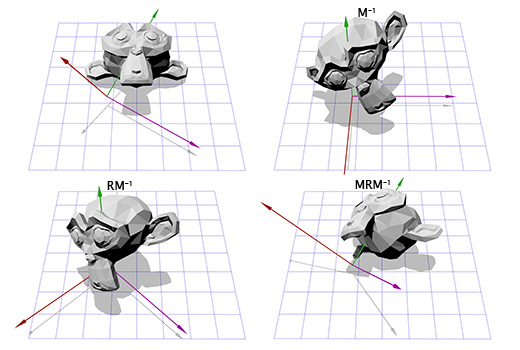
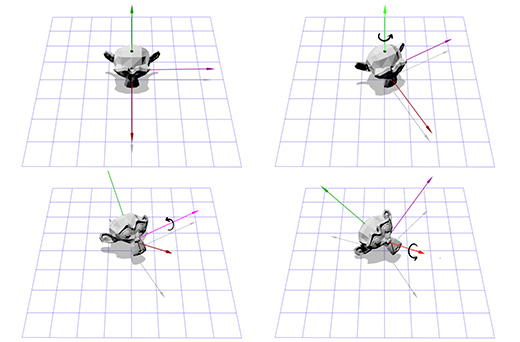

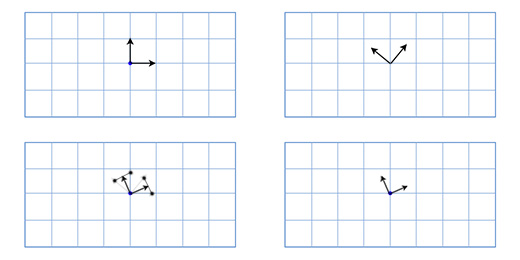


















 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»