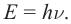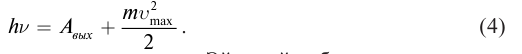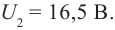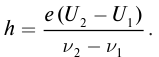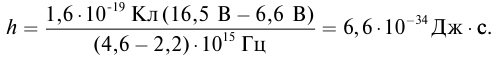Физика, 11 класс
Урок 22. Фотоэффект
Перечень вопросов, рассматриваемых на уроке:
- предмет и задачи квантовой физики;
- гипотеза М. Планка о квантах;
- опыты А.Г. Столетова;
- определение фотоэффекта, кванта, тока насыщения, задерживающего напряжения, работы выхода, красной границы фотоэффекта;
- уравнение Эйнштейна для фотоэффекта;
- законы фотоэффекта.
Глоссарий по теме:
Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
Фотоэффект – это вырывание электронов из вещества под действием света.
Квант – (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике.
Ток насыщения – некоторое предельное значение силы фототока.
Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.
Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.
Основная и дополнительная литература по теме урока:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.
3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г. С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.
4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.
Теоретический материал для самостоятельного изучения
В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.
Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.
Коэффициент пропорциональности получил название постоянной Планка, и она равна:
h = 6,63 ∙ 10-34 Дж∙с.
После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.
Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.
В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.
Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.
Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.
Схема установки для изучения законов фотоэффекта
Первый закон фотоэффекта: фототок насыщения – максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, – прямо пропорционален интенсивности падающего излучения.
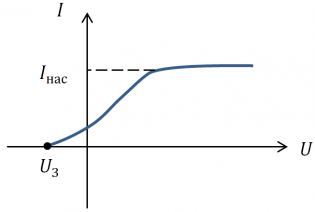
Зависимость силы тока от приложенного напряжения
Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.
Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.
hνmin = Aв
где Ав – работа выхода электронов;
h – постоянная Планка;
νmin – частота излучения, соответствующая красной границе фотоэффекта;
с – скорость света;
λкр – длина волны, соответствующая красной границе.
Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, “затрудняющее” вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.
Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.
Задерживающее напряжение
Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:
где 
Е – заряд электрона;

Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:
В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».
Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны – фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.
Примеры и разбор решения заданий
1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Работа выхода |
Запирающее напряжение |
Решение:
Работа выхода – это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.
Запирающее напряжение – это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:
Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.
Ответ:
|
Работа выхода |
Запирающее напряжение |
|
не изменится |
увеличится |
2. Красная граница фотоэффекта для вещества фотокатода λ0 = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.
Решение.
Запишем уравнение для фотоэффекта через длину волны:
Условие связи красной границы фотоэффекта и работы выхода:
Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:
Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:
Подставляя численные значения, получаем: λ ≈ 215 нм.
Ответ: λ ≈ 215 нм.
Начало теории электромагнитной природы света заложил Максвелл, который заметил сходство в скоростях распространения электромагнитных и световых волн. Но согласно электродинамической теории Максвелла любое тело, излучающее электромагнитные волны, должно в итоге остынуть до абсолютного нуля. В действительности этого не происходит. Противоречия между теорией и опытными наблюдениями были разрешены в начале XX века, вскоре после того, как был открыт фотоэффект.
Что такое фотоэффект
Фотоэффект — испускание электронов из вещества под действием падающего на него света.
Александр Столетов
Явление фотоэффекта было открыто в 1887 году Генрихом Герцем. Фотоэффект также был подробно изучен русским физиком Александром Столетовым в период с 1888 до 1890 годы. Этому явлению он посвятил 6 научных работ.
Для наблюдения фотоэффекта нужно провести опыт. Для этого понадобится электрометр и подсоединенная к нему пластинка из цинка (см. рисунок ниже). Если дать пластинке положительный заряд, то при ее освещении электрической дугой скорость разрядки электрометра не изменится. Но если цинковую пластинку зарядить отрицательно, то свет от дуги заставить электрометр разрядиться очень быстро.
Наблюдаемое во время этого эксперимента явление имеет простое объяснение. Свет вырывает электроны с поверхности цинковой пластинки. Если она имеет отрицательный заряд, электроны отталкиваются от нее, что приводит к полному разряжению электрометра. Причем при повышении интенсивности освещения скорость разрядки увеличивается, ровно, как и наоборот: при уменьшении интенсивности освещения электрометр разряжается медленно. Если же зарядить пластинку положительно, то электроны, которые вырываются светом, притягиваются к ней. Поэтому они оседают на ней, не изменяя заряд электрометра.
Если между световым пучком и отрицательно заряженной пластиной поставить лист стекла, пластинка перестанет терять электроны независимо от интенсивности излучения. Это связано с тем, что стекло задерживает ультрафиолетовое излучение. Отсюда можно сделать следующий вывод:
Явление фотоэффекта может вызвать только ультрафиолетовый участок спектра.
Волновая теория света не может объяснить, почему электроны могут вырываться только под действием ультрафиолета. Ведь даже при большой амплитуде и силе волн электроны остаются на месте, когда, казалось бы, они должны непременно быть вырванными.
Законы фотоэффекта
Чтобы получить более полное представление о фотоэффекте, выясним, от чего зависит количество электронов, вырванных светом с поверхности вещества, а также, от чего зависит их скорость, или кинетическая энергия. Выяснить все это нам помогут эксперименты.
Первый закон фотоэффекта
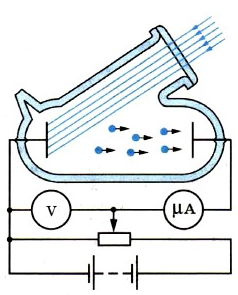
Возьмем стеклянный баллон и выкачаем из него воздух (смотрите рисунок выше). Затем поместим в него два электрода. На электроды подадим напряжение и будем регулировать его с помощью потенциометра и измерять при помощи вольтметра.
В верхней части нашего баллона есть небольшое кварцевое окошко, которое пропускает весь свет, в том числе ультрафиолетовый. Через него падает свет на один из электродов (в нашем случае на левый электрод, к которому присоединен отрицательный полюс батареи). Мы увидим, что под действием света этот электрод начнет испускать электроны, которые при движении в электрическом поле будут создавать электрический ток. Вырванные электроны будут направляться ко второму электроду. Но если напряжение небольшое, второго электрода достигнут не все электроны. Если интенсивность излучения сохранить, но увеличить между электродами разность потенциалов, то сила тока будет увеличиваться. Но как только она достигнет некоторого максимального значения, рост силы тока при дальнейшем увеличении напряжения прекратится. Максимальное значение силы тока будем называть током насыщения.
Ток насыщения — максимальное значение силы тока, также называемое предельным значением силы фототока.
Ток насыщения обозначается как Iн. Единица измерения — А (Кл/с). Численно величина равна отношению суммарному заряду вырванных электронов в единицу времени:
Iн=qt
Если же мы начнем изменять интенсивность излучения, то сможем заметить, что фототок насыщения также начинается меняться. Если интенсивность излучения ослабить, максимальное значение силы тока уменьшится. Если интенсивность светового потока увеличить, ток насыщения примет большее значение. Отсюда можно сделать вывод, который называют первым законом фотоэффекта.
Первый закон фотоэффекта:
Число электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны. Иными словами, фототок насыщения прямо пропорционален падающему световому потоку Ф.
Второй закон фотоэффекта
Теперь произведем измерения кинетической энергии, то есть, скорости вырывания электронов. Взгляните на график, представленный ниже. Видно, что сила фототока выше нуля даже при нулевом напряжении. Это говорит о том, что даже при нулевой разности потенциалов часть электронов достигает второго электрода.
Если мы поменяем полярность батареи, то будем наблюдать уменьшение силы тока. Если подать на электроды некоторое значение напряжения, равное Uз, сила тока станет равно нулю. Это значит, что электрическое поле тормозит вырванные электроны, останавливает их, а затем возвращает на тот же электрод.
Напряжение, равное Uз, называют задерживающим напряжением. Оно зависит зависит от максимальной кинетической энергии электронов, которые вырываются под действием света. Измеряя задерживающее напряжение и применяя теорему о кинетической, можно найти максимальное значение кинетической энергии электронов. Оно будет равно:
mv22=eUз
Опыт показывает, что при изменении интенсивности света (плотности потока излучения) задерживающее напряжение не меняется. Значит, не меняется кинетическая энергия электронов. С точки зрения волновой теории света этот факт непонятен. Ведь чем больше интенсивность света, тем большие силы действуют на электроны со стороны электромагнитного поля световой волны и тем большая энергия, казалось бы, должна передаваться электронам. Но экспериментальным путем мы обнаруживаем, что кинетическая энергия вырываемых светом электронов зависит только от частоты света. Отсюда мы можем сделать вывод, являющийся вторым законом фотоэффекта.
Второй закон фотоэффекта:
Максимальная кинетическая энергия фотоэлектронов линейно растет с частотой света и не зависит от его интенсивности.
Причем, если частота света меньше определенной для данного вещества минимальной частоты νmin, фотоэффект наблюдаться не будет.
Теория фотоэффекта
Все попытки объяснить явление фотоэффекта электродинамической теорией Максвелла, согласно которой свет — это электромагнитная волна, непрерывно распределенная в пространстве, оказались тщетными. Нельзя было понять, почему энергия фотоэлектронов определяется только частотой света и почему свет способен вырывать электроны лишь при достаточно малой длине волны.
В попытках объяснить это явление физик Макс Планк предложил, что атомы испускают электромагнитную энергию отдельными порциями — квантами, или фотонами. И энергия каждой порции прямо пропорциональна частоте излучения:
E=hν
h — коэффициент пропорциональности, который получил название постоянной Планка. Она равна 6,63∙10–34 Дж∙с.
Пример №1. Определите энергию фотона, соответствующую длине волны λ = 5∙10–7 м.
Энергия фотона равна:
E=hν
Выразим частоту фотона через скорость света:
ν=cλ
Следовательно:
Идею Планка продолжил развивать Эйнштейн, которому удалось дать объяснение фотоэффекту в 1905 году. В экспериментальных законах фотоэффекта Эйнштейн увидел убедительное доказательство того, что свет имеет прерывистую структуру и поглощается отдельными порциями. Причем энергия Е каждой порции излучения, по его расчетам, полностью соответствовала гипотезе Планка.
Из того, что свет излучается порциями, еще не вытекает вывода о прерывистости структуры самого света. Ведь и воду продают в бутылках, но отсюда не следует, что вода состоит из неделимых частиц. Лишь фотоэффект позволил доказать прерывистую структуру света: излученная порция световой энергии Е = hν сохраняет свою индивидуальность и в дальнейшем. Поглотиться может только вся порция целиком.
Кинетическую энергию фотоэлектрона можно найти, используя закон сохранения энергии. Энергия порции света hν идет на совершение работы выхода А и на сообщение электрону кинетической энергии. Отсюда:
hν=A+mv22
Работа выхода — минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Полученное выражение объясняет основные факты, касающиеся фотоэффекта. Интенсивность света, по Эйнштейну, пропорциональна числу квантов (порций) энергии hν в пучке света и поэтому определяет количество вырванных электронов. Скорость же электронов согласно зависит только от частоты света и работы выхода, которая определяется типом металла и состоянием его поверхности. От интенсивности освещения кинетическая энергия фотоэлектронов не зависит.
Для каждого вещества фотоэффект наблюдается лишь при освещении его светом с минимальной частотой волны νmin. Это объясняется тем, что для вырывания электрона без сообщения ему скорости нужно выполнять как минимум работу выхода. Поэтому энергия кванта должна быть больше этой работы:
hν>A
Предельную частоту νmin называют красной границей фотоэффекта. При этой частоте фотоэффект уже наблюдается.
Красная граница фотоэффекта равна:
νmin=Ah
Минимальной частоте, при которой возможен фотоэффект для данного вещества, соответствует максимальная длина волны, которая также носит название красной границы фотоэффекта. Это такая длина волны, при которой фотоэффект еще наблюдается. Обозначается она как λmах или λкр.
Максимальная длина волны, при которой еще наблюдается фотоэффект, равна:
λmax=hcA
Работа выхода А определяется родом вещества. Поэтому и предельная частота vmin фотоэффекта (красная граница) для разных веществ различна. Отсюда вытекает еще один закон фотоэффекта.
Третий закон фотоэффекта:
Для каждого вещества существует максимальная длина волны, при которой фотоэффект еще наблюдается. При больших длинах волн фотоэффекта нет.
Вспомните опыт, который мы описали в самом начале. Когда между цинковой пластинкой и световым пучком мы поставили зеркало, фотоэффект был прекращен. Это связано с тем, что красная граница для цинка определяется величиной λmах = 3,7 ∙ 10-7 м. Эта длина волны соответствует ультрафиолетовому излучению, которое не пропускало стекло.
Пример №2. Чему равна красная граница фотоэффекта νmin, если работа выхода электрона из металла равна A = 3,3∙10–19 Дж?
Применим формулу для вычисления красной границы фотоэффекта:
Задание EF15717
При увеличении в 2 раза частоты света, падающего на поверхность металла, задерживающее напряжение для фотоэлектронов увеличилось в 3 раза. Первоначальная частота падающего света была равна 0,75 ⋅1015 Гц. Какова длина волны, соответствующая «красной границе» фотоэффекта для этого металла? Ответ записать в нм.
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Переписать формулу закона сохранения энергии применительно к опытам 1 и 2.
4.Используя формула, связывающую задерживающее напряжение и кинетическую энергию фотона, определить работу выхода.
5.Записать формулу для красной границы фотоэффекта.
6.Выполнить решение в общем виде.
7.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Частота света в опыте 1: ν1 = ν = 0,75∙1015 Гц.
• Частота света в опыте 2: ν2 = 2ν1 = 2ν Гц.
• Задерживающее напряжение в опыте 1: U1 = U В.
• Задерживающее напряжение в опыте 2: U2 = 3U1 = 3U В.
Запишем формулу закона сохранения энергии:
hν=A+mv22
Применим ее к 1 и 2 опыту, составив систему из двух уравнений:
⎧⎪⎨⎪⎩hν1=A+mv212hν2=A+mv222
Преобразуем:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+mv222
Формула, связывающая задерживающее напряжение и кинетическую энергию фотона:
mv22=eUз
Известно, что при увеличении частоты в 2 раза задерживающее напряжение увеличилось в 3 раза. Так как задерживающее напряжение прямо пропорционально кинетической энергии фотона, то она (кинетическая энергия), также увеличивается в 3 раза. Следовательно:
mv222=3mv212
Тогда:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+3mv212
Умножим первое уравнение системы на «–3» и сложим оба уравнения:
⎧⎪⎨⎪⎩−3hν=−3A−3mv2122hν=A+3mv212
−hν=−2A
Отсюда работа выхода равна:
A=hν2
Формула для нахождения красной границы фотоэффекта:
νmin=Ah
Формула длины волны:
λ=cν
Следовательно, длина волны для красной границы фотоэффекта:
λmin=cνmin=chA=2chhν=2cν
Ответ: 800
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17645
При исследовании зависимости кинетической энергии фотоэлектронов от частоты падающего света фотоэлемент освещался через светофильтры. В первой серии опытов использовался красный светофильтр, а во второй – жёлтый. В каждом опыте измеряли напряжение запирания.
Как изменяются длина световой волны, напряжение запирания и кинетическая энергия фотоэлектронов? Для каждой величины определите соответствующий характер её изменения:
| 1) | увеличится |
| 2) | уменьшится |
| 3) | не изменится |
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
Алгоритм решения
1.Определить, от чего зависит и как меняется длина световой волны.
2.Записать закон сохранения энергии, формулу зависимости кинетической энергии от напряжения запирания.
3.Используя формулы, становить, как меняется напряжение запирания и кинетическая энергия.
Решение
Длина световой волны определяется ее цветом. Красный свет имеет большую длину волны. Следовательно, во втором опыте длина световой волны уменьшится.
Закон сохранения энергии для фотоэффекта:
hν=A+mv22
Формула зависимости кинетической энергии от напряжения запирания:
mv22=eUз
Следовательно:
hν=A+eUз
Работы выхода — величина постоянная для данного вещества. Следовательно, напряжение запирания зависит только от частоты световой волны. Частота — величина обратная длине волны. Так как длина волны уменьшилась, частота увеличилась. Следовательно, увеличилось и напряжение запирания.
Поскольку напряжение запирания прямо пропорционально кинетической энергии фотонов, то эта энергия также увеличивается.
Ответ: 211
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17973
На металлическую пластинку падает монохроматическая электромагнитная волна, выбивающая электроны из пластинки. Максимальная кинетическая энергия фотоэлектронов, вылетевших из пластинки в результате фотоэффекта, составляет 3 эВ, а работа выхода из металла в 2 раза больше этой энергии. Чему равна энергия фотонов в падающей волне?
Ответ:
а) 9 эВ
б) 2 эВ
в) 3 эВ
г) 6 эВ
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Выполнить решение в общем виде.
4.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Максимальная кинетическая энергия выбитых электронов: Emax = 3 эВ.
• Работа выхода из металла: A = 2 Emax.
Закона сохранения энергии для фотоэффекта:
hν=A+mv22
Или:
E=A+Emax=2Emax+Emax=3Emax=3·3=9 (эВ)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.3k
88
Цель
работы:
изучение явления внешнего фотоэффекта,
нахождение его красной границы и работы
выхода электрона из металла.
1. Введение
Внешним
фотоэффектом
называется испускание электронов
веществом под действием света.
Энергетический баланс при фотоэффекте
выражается уравнением Эйнштейна
, (1)
где
hν
– энергия светового кванта, переданная
электрону; A
–
работа выхода электрона за пределы
вещества;
– максимальная кинетическая энергия
освободившегося электрона. Уравнение
(1) получено в предположении, что
электромагнитное излучение представляет
собой поток частиц, называемых фотонами.
Фотон несет энергию,
при этом он неделим и при взаимодействии
отдает свою энергию полностью. Фотон
обладает также импульсом.
Фотоэффект можно рассматривать как
процесс соударения фотона с электроном.
Уравнение
(1) дает теоретическое обоснование
законов фотоэффекта, экспериментально
установленных Столетовым:
1)
фототок насыщения пропорционален
световому потоку;
2)
максимальная скорость фотоэлектронов
определяется частотой света
и не зависит от его интенсивности;
3)
для каждой поверхности существует
минимальная частота ν0
(красная граница фотоэффекта), ниже
которой фотоэффект не возможен:
. (2)
Определив
ν0
экспериментально,
из формулы (2) можно найти работу выхода
электронов A
для данного вещества.
Простейшим
прибором для наблюдения фотоэффекта
является вакуумный фотоэлемент (рис.1).
Это откачанный стеклянный баллон, одна
половина которого покрыта изнутри
металлом, играющим роль фотокатода К.
Анод А
обычно выполняется в форме кольца или
шарика. Между катодом и анодом с помощью
батареи Б
создается ускоряющая разность потенциалов.
При освещении катода он испускает
электроны, которые подхватываются полем
и попадают на анод. Цепь замыкается, и
в ней течет ток. В данной установке
использован фотоэлемент с катодом,
красная граница которого лежит в видимой
области спектра. Это позволяет использовать
в качестве источника света лампу
накаливания.
|
Один |
Рис. |
разности
потенциалов Uзадер.
ни одному из электронов, даже обладающему
при вылете из катода К
наибольшим значением скорости
,
не удастся достигнуть анодаА.
Фототок прекращается. Это условие можно
записать:
, (3)
Измерив
задерживающее напряжение Uзадер
и, зная частоту излучения ,
из формулы (1) можно найти работу выхода
А,
затем по формуле (2) определить красную
границу фотоэффекта 0.
В
данной работе для определения красной
границы при неизменной ускоряющей
разности потенциалов будем изменять
частоту падающего излучения .
При некоторой частоте 0
фототок должен прекратится. Однако этот
метод требует более тщательного, хотя
бы качественного анализа причин,
определяющих величину фототока. Очевидно,
что фототок при данной частоте излучения
определяется числом фотонов Nфот(),
падающих на фотокатод в единицу времени,
и вероятностью взаимодействия фотона
с электроном P(),
приводящего к выходу электрона из
вещества:
. (4)
Число
фотонов в световом потоке Nфот()
определяется излучательной способностью
источника света R,T.
Если предположить, что лампа накаливания
излучает как чёрное тело (см. введение
к работе 14), то её излучательная способность
может быть представлена графиком,
приведенным на рис. 2.
|
Рис. |
Рис. |
Количество
энергии, излучаемой лампой в области
частот от
до +,
определяется площадью, заштрихованной
на графике рис. 2: W=
R,T·.
Тогда число фотонов, излучаемых в
интервале частот
будет равно:
.
В
области низких частот справедлив закон
Релея-Джинса, согласно которому R,T
~ 2.
Следовательно, в этой области отношение
,
равное,
будет пропорционально
(рис. 3). В области ожидаемого значения
красной границы, R,T
растет линейно (в районе точки перегиба
R,T
~ )
и, следовательно, отношение
остается величиной постоянной для
разных частот. При больших частотах (
> экстр)
излучательная способность тела
уменьшается и одновременно растет
“удельный вес” фотонов h.
В результате отношение
резко падает. Следовательно, в области
значения частоты0,
число фотонов, испускаемых лампой
накаливания на разных частотах, остается
величиной постоянной.
Величина
второго сомножителя
в формуле (4) определяется многими
причинами. Одним из решающих факторов
является число электронов, взаимодействие
с которыми может привести к появлению
фототока. Электроны проводимости в
металле не могут самопроизвольно
покинуть вещество, так как металл
представляет для них потенциальную
яму. При температуреT
= 0 К все нижние энергетические уровни
ямы заняты электронами. Последний
занятый уровень носит название уровня
Ферми. Разность между глубиной
потенциальной ямы Ep0
и энергией Ферми EF
определяет работу выхода электрона из
металла:
(рис. 4). Если энергия фотона
,
то такой фотон не может “вытащить”
электрон из потенциальной ямы. При
взаимодействии с фо-
|
тоном, |
Рис. |
ности
,
которая равна.
Следовательно, вероятность выбивания
электрона из металла.
В
итоге, в формуле (4) число фотонов,
испускаемых лампой накаливания в единицу
времени в области частот, лежащих вблизи
красной границы, остается величиной
постоянной на разных частотах, а
вероятность взаимодействия фотона с
электроном пропорциональна разности
частот
.
Следовательно, в области красной границы
фототок пропорционален разности.
При больших частотах фототок должен
уменьшаться с ростом
за счет
уменьшения числа фотонов, излучаемых
источником света в этой спек
тральной области. Таким образом,
ожидаемая зависимость фототока от
частоты должна
|
иметь |
Рис. |
Итак,
для экспериментального определения
красной границы фотоэффекта и работы
выхода необходимо снять зависимость
фототока от частоты излучения и,
аппроксимируя линейный участок графика
в области низких частот до пересечения
с осью частот, определить 0.
По формуле (2) можно определить работу
выхода электронов из металла.
| Квантовая механика |
|---|
|
|
Основа
|
|
Фундаментальные понятия
|
|
Эксперименты
|
|
Формулировки
|
|
Уравнения
|
|
Интерпретации
|
|
Развитие теории
|
|
Сложные темы
|
|
Известные учёные
|
|
См. также
|
| См. также: Портал:Физика |
Фотоэффе́кт, или фотоэлектри́ческий эффе́кт, — явление взаимодействия света или любого другого электромагнитного излучения с веществом, при котором энергия фотонов передаётся электронам вещества. В конденсированных (твёрдых и жидких) веществах выделяют внешний (поглощение фотонов сопровождается вылетом электронов за пределы вещества) и внутренний (электроны, оставаясь в веществе, изменяют в нём своё энергетическое состояние) фотоэффект. Фотоэффект в газах состоит в ионизации атомов или молекул под действием излучения[1].
Внешний фотоэффект[править | править код]
Внешним фотоэффектом (фотоэлектронной эмиссией) называется испускание электронов веществом под действием электромагнитных излучений. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.
Фотокатод — электрод вакуумного электронного прибора, непосредственно подвергающийся воздействию электромагнитных излучений и эмитирующий электроны под действием этого излучения.
Фототок насыщения — максимальный ток выбитых электронов, ток между фотокатодом и анодом, при котором все выбитые электроны собираются на аноде.
Спектральная характеристика фотокатода — зависимость спектральной чувствительности от частоты или длины волны электромагнитного излучения.
История открытия[править | править код]
Внешний фотоэффект был открыт в 1887 году Генрихом Герцем[2][3][4]. При работе с открытым резонатором он заметил, что если посветить ультрафиолетом на цинковые разрядники, то прохождение искры заметно облегчается.
В 1888—1890 годах фотоэффект систематически изучал русский физик Александр Столетов[5], опубликовавший 6 работ[6][7][8][9][10][11]. Им были сделаны несколько важных открытий в этой области, в том числе выведен первый закон внешнего фотоэффекта[12].
Ещё Столетов пришёл к выводу, что «Разряжающим действием обладают, если не исключительно, то с громадным превосходством перед прочими лучами, лучи самой высокой преломляемости, недостающие в солнечном спектре», то есть вплотную подошёл к выводу о существовании красной границы фотоэффекта. В 1891 г. Эльстер и Гейтель при изучении щелочных металлов пришли к выводу, что, чем выше электроположительность металла, тем ниже граничная частота, при которой он становится фоточувствительным[13].
Томсон в 1898 году экспериментально установил, что поток электрического заряда, выходящий из металла при внешнем фотоэффекте, представляет собой поток открытых им ранее частиц (позже названных электронами). Поэтому увеличение фототока с ростом освещённости следует понимать как увеличение числа выбитых электронов с ростом освещённости.
Исследования фотоэффекта Филиппом Ленардом в 1900—1902 годах показали, что, вопреки классической электродинамике, энергия вылетающего электрона всегда строго связана с частотой падающего излучения и практически не зависит от интенсивности облучения.
Схема учебного эксперимента по исследованию фотоэффекта. Из света берётся узкий диапазон частот и направляется на катод внутри вакуумного прибора. Напряжением между катодом и анодом устанавливается энергетический порог между ними. По току судят о достижении электронами анода.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Карла Вильгельма Озеена, получил Нобелевскую премию) на основе гипотезы Макса Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк в 1900 году предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций (фотонов) с энергией hν каждый, где h — постоянная Планка.
В 1906—1915 годах фотоэффект обрабатывал Роберт Милликен. Он смог установить точную зависимость запирающего напряжения от частоты (действительно оказавшуюся линейной) и на его основании смог вычислить постоянную Планка. «Я потратил десять лет моей жизни на проверку этого эйнштейновского уравнения 1905 г., — писал Милликен, — и вопреки всем моим ожиданиям я вынужден был в 1915 г. безоговорочно признать, что оно экспериментально подтверждено, несмотря на его несуразность, так как казалось, что оно противоречит всему, что мы знаем об интерференции света». В 1923 году Милликен был удостоен Нобелевской премии в области физики «за работы по определению элементарного электрического заряда и фотоэлектрического эффекта».
Исследования фотоэффекта были одними из самых первых квантовомеханических исследований.
Законы внешнего фотоэффекта[править | править код]
Законы внешнего фотоэффекта:
1-й закон фотоэффекта (закон Столетова): Сила фототока насыщения прямо пропорциональна интенсивности светового излучения[14]. При неизменном спектральном составе электромагнитного излучения, падающего на фотокатод, фототок насыщения пропорционален энергетической освещённости катода (иными словами, число фотоэлектронов, выбиваемых из катода в единицу времени прямо пропорционально интенсивности излучения).
2-й закон фотоэффекта: Максимальная кинетическая энергия выбиваемых светом электронов возрастает с частотой света и не зависит от его интенсивности[14].
3-й закон фотоэффекта: Для каждого вещества при определённом состоянии его поверхности существует граничная частота света, ниже которой фотоэффект не наблюдается. Эта частота и соответствующая ей длина волны называется красной границей фотоэффекта[14].
Внешний фотоэффект практически безынерционен. Фототок немедленно возникает при освещении поверхности тела, при условии что фотоэффект может существовать[14].
При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла, полупроводника или диэлектрика и там поглощается. Поглотив фотон, электрон получает от него энергию.
Согласно теории 1905 года, из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
- где
— т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества). Для обозначения работы выхода в современной научной литературе буква A не используется;
— максимальная кинетическая энергия вылетающего электрона;
— частота падающего фотона с энергией
;
- h — постоянная Планка .
Из этой формулы следует существование красной границы фотоэффекта при T = 0 K, то есть существование наименьшей частоты (
Напряжение обратной полярности, подаваемое на электроды, уменьшает ток фотоэффекта, поскольку электронам приходится совершать дополнительную работу по преодолению электростатических сил. Минимальное напряжение, полностью прекращающее фототок, называется задерживающим или запирающим напряжением. Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:
Фотоэффект разделяют на поверхностный, когда фотоэлектрон вылетает из поверхностного слоя атомов, и объёмный, когда фотоэлектрон вылетает из объёма твердого тела. Объёмный фотоэффект рассматривается трёхстадийный:
на первой стадии происходит возбуждение электрона атома в возбуждённое состояние, на второй стадии под действием тянущего электрического поля электрон достигает поверхности, на третьей стадии если энергия электрона достаточна для преодоления потенциального барьера на поверхности, тогда он вылетает из твердого тела. В общем виде можно записать:

где 


Теория Фаулера[править | править код]
Основные закономерности внешнего фотоэффекта для металлов хорошо описываются теорией Фаулера[15][16]. Согласно ей после поглощения в металле фотона его энергия переходит электронам проводимости, в результате чего электронный газ в металле оказывается состоящим из смеси газов с обычным распределением распределением Ферми — Дирака и возбуждённым (сдвинутым на 
Плотность фототока определяется формулой Фаулера:
где 


- Замечание. Термин “с нормальным распределением распределением Ферми — Дирака” заменен на “с обычным распределением распределением Ферми — Дирака”, поскольку есть математический термин нормальное распределение, который здесь может ошибочно иметься в виду.
Квантовый выход[править | править код]
Важной количественной характеристикой фотоэффекта является квантовый выход Y — число эмитированных электронов в расчёте на один фотон, падающий на поверхность тела. Величина Y определяется свойствами вещества, состоянием его поверхности и энергией фотонов.
Квантовый выход фотоэффекта из металлов в видимой и ближней УФ-областях Y < 0,001 электрон/фотон. Это связано, прежде всего, с малой глубиной выхода фотоэлектронов, которая значительно меньше глубины поглощения света в металле. Большинство фотоэлектронов рассеивает свою энергию до подхода к поверхности и теряет возможность выйти в вакуум. При энергии фотонов вблизи порога фотоэффекта большинство фотоэлектронов возбуждается ниже уровня вакуума и не даёт вклада в фотоэмиссионный ток. Кроме того, коэффициент отражения в видимой и ближней УФ-областях велик и лишь малая часть излучения поглощается в металле. Эти ограничения частично снимаются в дальней УФ-области спектра, где Y достигает величины 0,01 электрон/фотон при энергии фотонов E > 10 эВ.
Векториальный фотоэффект[править | править код]
Векториальным фотоэффектом называется зависимость фототока от направления поляризации падающего света, являющаяся следствием проявления волновых свойств света. Особенно сильно фототок увеличивается, когда вектор напряженности электрического поля лежит в плоскости падения (чувствительность значительно больше по величине и спектральная характеристика имеет избирательный максимум) по сравнению с тем, когда он перпендикулярен плоскости падения (фототок монотонно возрастает с увеличением частоты). Векториальный фотоэффект объясняется фототоком электронов, находящихся в поверхностном слое металла, где действует электрическое поле двойного слоя, создающее потенциальный барьер[17][18][19].
Замечание[править | править код]
- Вероятно, используемый здесь термин векториальный фотоэффект есть не что иное, как используемый в других изданиях аналогичный термин селективный или избирательный фотоэффект [20].
Внутренний фотоэффект[править | править код]
Внутренним фотоэффектом называется явление возрастания электропроводности и уменьшения сопротивления, вызванное облучением[21]. Он объясняется перераспределением электронов по энергетическим состояниям в твёрдых и жидких полупроводниках и диэлектриках, происходящее под действием излучений, проявляется в изменении концентрации носителей зарядов в среде и приводит к возникновению фотопроводимости или вентильного фотоэффекта[22].
Фотопроводимостью называется увеличение электрической проводимости вещества под действием излучения.
История открытия[править | править код]
В 1839 году Александр Беккерель наблюдал[23] фотовольтаический эффект в электролите.
В 1873 году Уиллоуби Смит обнаружил, что селен является фотопроводящим[24][25].
Виды[править | править код]
Вентильный фотоэффект[править | править код]
Вентильный фотоэффект или фотоэффект в запирающем слое — явление, при котором фотоэлектроны покидают пределы тела, переходя через поверхность раздела в другое твёрдое тело (полупроводник) или жидкость (электролит).
Фотовольтаический эффект[править | править код]
Фотовольтаический эффект — возникновение электродвижущей силы под действием электромагнитного излучения[26]. Применяется для измерения интенсивности падающего света (например в фотодиодах) или для получения электричества в солнечных батареях.
Сенсибилизированный фотоэффект[править | править код]
Сенсибилизированным фотоэффектом называется фотоэффект, сопровождающийся явлением сенсибилизации, то есть изменением величины и спектра фоточувствительности в широкозонных фотопроводниках органической и неорганической природы в зависимости от структуры молекулярных соединений[27].
Фотопьезоэлектрический эффект[править | править код]
Фотопьезоэлектрическим эффектом называется явление появления в полупроводнике фото электродвижущей силы в условиях внешнего неравномерного сжатия полупроводника[28].
Фотомагнитный эффект[править | править код]
Фотомагнитным эффектом называется возникновение электродвижущей силы в освещенном однородном полупроводнике в магнитном поле[28].
Ядерный фотоэффект[править | править код]
При поглощении гамма-кванта ядро получает избыток энергии без изменения своего нуклонного состава, а ядро с избытком энергии является составным ядром. Как и другие ядерные реакции, поглощение ядром гамма-кванта возможно только при выполнении необходимых энергетических и спиновых соотношений. Если переданная ядру энергия превосходит энергию связи нуклона в ядре, то распад образовавшегося составного ядра происходит чаще всего с испусканием нуклонов, в основном нейтронов. Такой распад ведёт к ядерным реакциям 

Многофотонный фотоэффект[править | править код]
В сильном электромагнитном поле с электронной оболочкой атома в элементарном акте фотоэффекта могут взаимодействовать несколько фотонов. В этом случае ионизация атома возможна с помощью излучения с энергией квантов 
Современные исследования[править | править код]
Как показали эксперименты в национальном метрологическом институте Германии Physikalisch-Technische Bundesanstalt, результаты которых опубликованы 24 апреля 2009 года в Physical Review Letters[31], в мягком рентгеновском диапазоне длин волн при плотности мощности на уровне нескольких петаватт (1015 Вт) на квадратный сантиметр общепринятая теоретическая модель фотоэффекта может оказаться неверной.
Сравнительные количественные исследования различных материалов показали, что глубина взаимодействия между излучением и веществом существенно зависит от структуры атомов этого вещества и корреляции между внутренними электронными оболочками. В случае c ксеноном, который использовался в экспериментах, воздействие пакета фотонов в коротком импульсе приводит, по всей видимости, к одновременной эмиссии множества электронов с внутренних оболочек[32].
См. также[править | править код]
- Фотоэлектронная спектроскопия
- Солнечная генерация
- Эффект Комптона
Примечания[править | править код]
- ↑ Яворский Б. М., Детлаф А. А., Лебедев А. К. Справочник по физике для инженеров и студентов вузов. — М., Оникс, 2007. — Тираж 5100 экз. — ISBN 978-5-488-01248-6. — с. 725
- ↑ http://www.britannica.com/science/photoelectric-effect Архивная копия от 10 января 2016 на Wayback Machine «The photoelectric effect was discovered in 1887 by the German physicist Heinrich Rudolf Hertz.»
- ↑ H. Hertz (1887), Ueber einen Einfluss des ultravioletten Lichtes auf die electrische Entladung Архивная копия от 24 января 2016 на Wayback Machine (An effect of ultraviolet light on electrical discharge) / Ann. Phys., 267: 983—1000. doi: 10.1002/andp.18872670827 (нем.)
- ↑ Stig Lundqvist, Physics, 1901—1921 Архивная копия от 4 февраля 2016 на Wayback Machine // World Scientific, 1998, ISBN 9789810234010, p.121 (англ.)
- ↑ БСЭ, ФОТОЭФФЕКТ
- ↑ Stoletow, A. Sur une sorte de courants electriques provoques par les rayons ultraviolets (фр.) // Comptes Rendus (англ.) (рус. : magazine. — 1888. — Vol. CVI. — P. 1149. (Reprinted in Stoletow, M.A. On a kind of electric current produced by ultra-violet rays (англ.) // Philosophical Magazine Series 5 : journal. — 1888. — Vol. 26, no. 160. — P. 317. — doi:10.1080/14786448808628270.; abstract in Beibl. Ann. d. Phys. 12, 605, 1888).
- ↑ Stoletow, A. Sur les courants actino-electriques au travers deTair (фр.) // Comptes Rendus (англ.) (рус. : magazine. — 1888. — Vol. CVI. — P. 1593. (Abstract in Beibl. Ann. d. Phys. 12, 723, 1888).
- ↑ Stoletow, A. Suite des recherches actino-électriques (фр.) // Comptes Rendus (англ.) (рус.. — 1888. — Vol. CVII. — P. 91. (Abstract in Beibl. Ann. d. Phys. 12, 723, 1888).
- ↑ Stoletow, A. Sur les phénomènes actino-électriques (фр.) // Comptes Rendus (англ.) (рус.. — 1889. — Vol. CVIII. — P. 1241.
- ↑ Столетов, А. Актино-электрические исследовaния (рус.) // Журнал Русского физико-химического общества. — 1889. — Т. 21. — С. 159.
- ↑ Stoletow, A. Sur les courants actino-électriques dans l’air raréfié (фр.) // Journal de Physique : magazine. — 1890. — Vol. 9. — P. 468. — doi:10.1051/jphystap:018900090046800.
- ↑ БСЭ, СТОЛЕТОВ АЛЕКСАНДР ГРИГОРЬЕВИЧ
- ↑ Дуков В. М. Исторические обзоры в курсе физики средней школы. — М.: Просвещение, 1983. — 160 с.
- ↑ 1 2 3 4 Яворский Б. М., Пинский А. А. Основы физики. Том 2. — М., Наука, 1974. — Тираж 169 000 экз. — с. 197
- ↑ Добрецов Л. Н., Гомоюнова М. В. Эмиссионная электроника. — М.: Наука, 1966. — С. 564. (недоступная ссылка)
- ↑ Fowler, 1931, pp. 45—56.
- ↑ Ворончев Т. А., Соболев В. Д. Физические основы электровакуумной техники. — М.: Высшая школа, 1967. — с. 217—220
- ↑ Лукирский, 1933.
- ↑ Лукьянов, 1948.
- ↑ Ландсберг Г. С. Оптика. Учебное пособие. 6-е изд., стереотип. М.: Физматлит, 2003. Глава XXXII. § 179. Зависимость силы фототока от длины световой волны. С.586-589. Рис.32.8, 32.9, 32.10, 32.11
- ↑ Яворский Б. М., Пинский А. А. Основы физики. Том 2. — М.: Наука, 1974. — Тираж 169 000 экз. — с. 336
- ↑ Киреев П. С. Физика полупроводников. — М.: Высшая школа, 1975. — Тираж 30000 экз. — с. 537—546
- ↑ A. E. Becquerel (1839). «Mémoire sur les effets électriques produits sous l’influence des rayons solaires». Comptes Rendus 9: 561—567
- ↑ Smith, W. (1873). «Effect of Light on Selenium during the passage of an Electric Current». Nature 7 (173): 303. Bibcode:1873Natur…7R.303.. doi:10.1038/007303e0
- ↑ БСЭ, ФОТОПРОВОДИМОСТЬ
- ↑ Фотовольтаический эффект — статья из Большой советской энциклопедии.
- ↑ Акимов И. А., Черкасов Ю. А., Черкашин М. И. Сенсибилизированный фотоэффект. — М.: Наука, 1980. — С. 384.
- ↑ 1 2 Тауц Я. Фото- и термоэлектрические явления в полупроводниках. — М.: ИЛ, 1962. — С. 141.
- ↑ Климов А. Н. Ядерная физика и ядерные реакторы. — М.: Энергоатомиздат, 1985. — С. 352.
- ↑ Квантовая электроника. Маленькая энциклопедия. — М.: Советская энциклопедия, 1969. — С. 431.
- ↑ Extreme Ultraviolet Laser Excites Atomic Giant Resonance // Phys. Rev. Lett. — 2009. — Vol. 102. — P. 163002.
- ↑ Обнаружены ограничения классического фотоэффекта для рентгеновского излучения. Nanonewsnet.ru. Архивировано 28 апреля 2009 года.
Ссылки[править | править код]
- Фотоэффект // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Фотоэффект — статья из Физической энциклопедии
Литература[править | править код]
- Ландсберг Г. С. Оптика. — М.: Физматлит, 2003. — 848 с.
- Лукирский П. И. О фотоэффекте. — Л.; М.: Гос. техн.-теорет. изд-во, 1933. — 94 с.
- Лукьянов С. Ю. Фотоэлементы. — Москва ; Ленинград :: Изд-во и 2-я тип. Изд-ва Акад. наук СССР, 1948. — 372 с.
- Рывкин С. М. Фотоэлектрические явления в полупроводниках. — М.: Физматлит, 1963. — 494 с.
- Fowler R. H. The Analysis of Photoelectric Sensitivity Curves for Clean Metals at Various Temperatures // Phys. Rev. — 1931. — Vol. 38.
Содержание:
Фотоэффект:
Рассмотрим фотоэффект с точки зрения классической электродинамики.
На основе волновой теории света можно предположить, что:
- – свет любой длины волны должен вырывать электроны из металла;
- – на вырывание электрона из металла требуется определенное время;
- – число вырванных электронов и их энергия должны быть пропорциональны интенсивности света.
Александр Григорьевич Столетов (1839–1896) – русский физик. Исследовал внешний фотоэффект, открыл первый закон фотоэффекта. Исследовал газовый разряд, критическое состояние, получил кривую намагничивания железа.
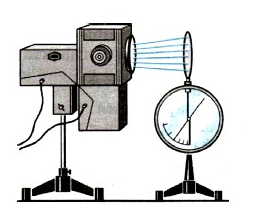
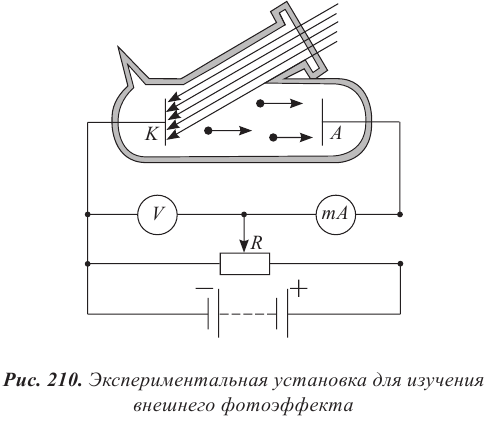
Современная установка для исследования фотоэффекта
Современная установка для изучения фотоэффекта представляет собой два электрода, помещенных в стеклянный баллон, из которого выкачан воздух (рис. 210). На один из электродов через кварцевое «окошко» падает свет. В отличие от обычного стекла кварц пропускает ультрафиолетовое излучение. На электроды подается напряжение, которое можно менять с помощью потенциометра R и измерять вольтметром V. К освещаемому электроду К − катоду подсоединяют отрицательный полюс батареи. Под действием света катод испускает электроны, которые направляются электрическим полем к аноду, создается электрический ток. Значение силы тока фиксируется миллиамперметром.
Законы фотоэффекта Столетова
Исследования, проведенные русским ученым А.Г. Столетовым и немецким ученым Ф. Ленардом, показали, что законы фотоэффекта не соответствуют классическим представлениям.
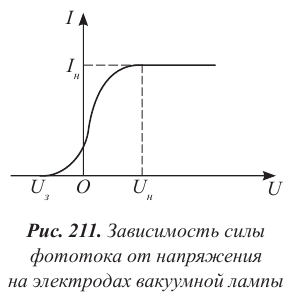
На рисунке 211 представлена вольтамперная характеристика, полученная в результате измерений при различных значениях напряжения между электродами.
Из графика следует, что:
1. Сила фототока не зависит от напряжения, если оно достигает некоторого значения
Максимальное значение силы тока 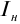
Сила тока насыщения − это максимальный заряд, переносимый фотоэлектронами за единицу времени:
где n − число фотоэлектронов, вылетающих с поверхности освещаемого металла за 1 с, е − заряд электрона.
2. Сила фототока отлична от нуля при нулевом значении напряжения.
3. Если изменить направление электрического поля, соединив катод с положительным полюсом источника тока, а анод − с отрицательным, то скорость фотоэлектронов уменьшится, об этом можно судить по показаниям миллиамперметра: сила тока уменьшается при увеличении отрицательного значения напряжения. При некотором значении напряжения 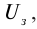
При известном значении 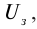
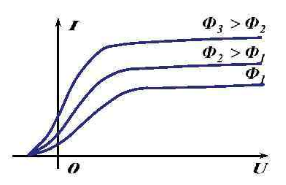
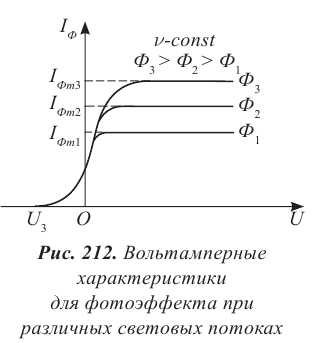
Исследование фотоэффекта при освещении катода световыми потоками равной частоты, но различной интенсивности дал результат, представленный вольтамперными характеристиками, изображенными на рисунке 212.
Сила фототока насыщения увеличивается с увеличением интенсивности падающего света.
Вспомните! Фотоэффект – это испускание электронов веществом под действием света или любого другого электромагнитного излучения.
Величина запирающего напряжения от интенсивности света не зависит, для всех потоков она имеет одно и то же значение.
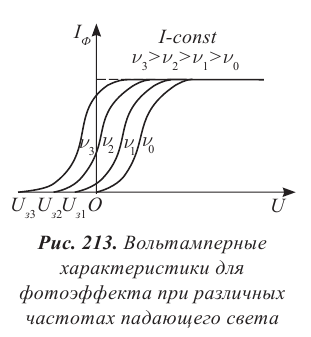
Освещение катода светом одной и той же интенсивности, но разной частоты дало серию вольтамперных характеристик, представленных на рисунке 213. Как следует из графиков, величина задерживающего напряжения 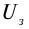
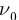
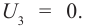
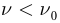
Минимальную частоту падающего света 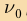
На основании экспериментальных данных Столетовым были сформулированы законы фотоэффекта:
- Сила фототока прямо пропорциональна интенсивности светового потока.
- Максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от интенсивности.
- Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света
(максимальная длина
), при которой возможен фотоэффект, если
то фотоэффект не происходит.
- Заказать решение задач по физике
Квантовая теория фотоэффекта
Теоретическое обоснование фотоэффекта было дано в 1905 г. А. Эйнштейном. Он предположил, что свет не только излучается квантами, как утверждал М. Планк, но и распространяется и поглощается порциями, представляет собой поток частиц − фотонов, энергия которых равна
Сам фотоэффект состоит в том, что световые частицы, сталкиваясь с электронами металла, передают им свою энергию и импульс и сами при этом исчезают. Если энергия квантов падающего света больше той работы, которую электрон должен совершить против сил притяжения к положительно заряженным частицам вещества, то электрон вылетает из металла. Становится понятным смысл красной границы фотоэффекта: для вырывания электрона из металла энергия квантов должна быть не меньше, чем 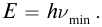
Это и есть формула Эйнштейна для фотоэффекта. Обычно ее пишут в виде:
Зависимость силы фототока от интенсивности света Эйнштейн объяснил следующим образом: число вылетающих в единицу времени электронов пропорционально интенсивности света, поскольку интенсивность определяется числом квантов, испускаемых источником в единицу времени. Мощная лампа испускает больше квантов, следовательно, число вырванных электронов светом такой лампы будет больше, чем светом менее мощной лампы.
Энергия вылетающих электронов зависит не от силы света лампы, а от того, какой частоты свет она испускает, от этого зависит энергия фотона и кинетическая энергия фотоэлектрона.
Фотоны, энергия, масса и импульс фотона
Фотон – это частица света. Он не делится на части: испускается, отражается, преломляется и поглощается целым квантом. У него нет массы покоя, неподвижных фотонов не существует.
Энергия фотона
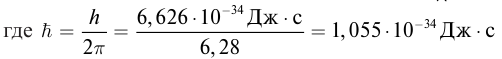
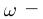
Масса фотона
Массу фотона определяют, исходя из закона о взаимосвязи массы и энергии:
Измерить массу фотона невозможно, ее следует рассматривать как полевую массу, обусловленную тем, что электромагнитное поле обладает энергией.
Импульс фотона
Фотон – частица света, следовательно, ее импульс равен:
Применение фотоэффекта в технике
Фотоэлементы:
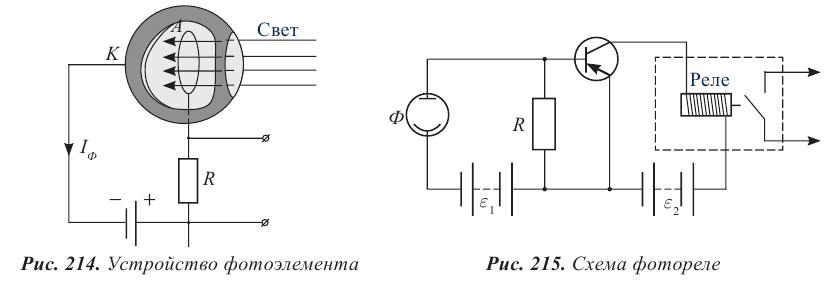
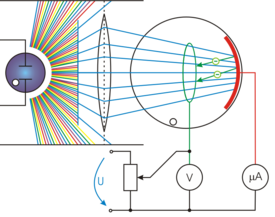
Приборы, принцип действия которых основан на явлении фотоэффекта, называют фотоэлементами. Устройство фотоэлемента изображено на рисунке 214. Внутренняя поверхность К (катод) стеклянного баллона, из которого выкачан воздух, покрыта светочувствительным слоем с небольшим прозрачным для света участком для доступа света внутрь баллона. В центре баллона находится металлическое кольцо А (анод). От электродов сделаны выводы для подключения фотоэлемента к электрической цепи. В качестве светочувствительного слоя обычно используют напыленные покрытия из щелочных металлов, имеющих малую работу выхода, т.е. чувствительных к видимому свету.
Фотоэлементы используют для автоматического управления электрическими цепями с помощью световых пучков.
Фотореле:
Фотоэлектрическое реле срабатывает при прерывании светового потока, падающего на фотоэлемент (рис. 215). Фотореле состоит из фотоэлемента Ф, усилителя фототока, в качестве которого используют полупроводниковый триод, и электромагнитного реле, включенного в цепь коллектора транзистора. Напряжение на фотоэлемент подают от источника тока 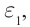
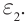
Когда фотоэлемент освещен, в его цепи, содержащей резистор R, идет слабый ток, потенциал базы транзистора выше потенциала эмиттера, и ток в коллекторной цепи транзистора отсутствует.
Если же поток света, падающий на фотоэлемент, прерывается, ток в его цепи сразу прекращается, переход эмиттер – база открывается для основных носителей, и через обмотку реле, включенного в цепь коллектора, пойдет ток. Реле срабатывает, и его контакты замыкают исполнительную цепь. Ее функциями могут быть остановка пресса, в зону действия которого попала рука человека, выдвигание преграды в турникете метро, автоматическое включение освещения на улицах.
Пример решения задачи
Определите постоянную Планка h, если известно, что электроны, вырываемые из металла светом с частотой 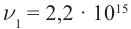
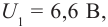
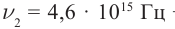
Дано:
U1 = 6,6 B
U2 = 16,5 B
h – ?
Решение: Запишем уравнение Эйнштейна для электрона, вырванного из металла светом с частотами 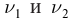
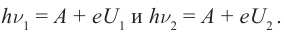
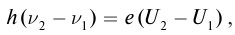
Выполним расчеты:
Ответ: h = 6,6 · 10–34 Дж · с.
- Оптические явления в природе по физике
- Оптические приборы в физике
- Оптика в физике
- Волновая оптика в физике
- Разложение белого света на цвета и образование цветов
- Давление света в физике
- Химическое действие света
- Корпускулярно-волновая природа света














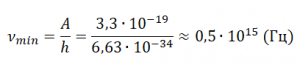
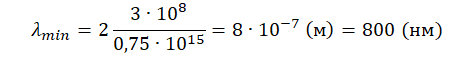














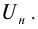
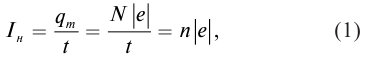
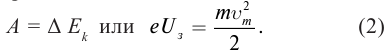
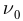 (максимальная длина
(максимальная длина 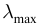 ), при которой возможен фотоэффект, если
), при которой возможен фотоэффект, если 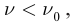 то фотоэффект не происходит.
то фотоэффект не происходит.