Как найти работу выхода с поверхности металла

Формула работа выхода электронов

В металлах имеются электроны проводимости, образующие электронный газ и участвующие в тепловом движении. Так как электроны проводимости удерживаются внутри металла, то, следовательно, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. Эта работа, естественно, различна для разных металлов.

Потенциальная энергия электрона внутри металла постоянна и равна:

W_p = -eφ , где j – потенциал электрического поля внутри металла.

При переходе электрона через поверхностный электронный слой потенциальная энергия быстро уменьшается на величину работы выхода и становится вне металла равной нулю. Распределение энергии электрона внутри металла можно представить в виде потенциальной ямы.

В рассмотренной выше трактовке работа выхода электрона равна глубине потенциальной ямы, т.е.

Этот результат соответствует классической электронной теории металлов, в которой предполагается, что скорость электронов в металле подчиняется закону распределения Максвелла и при температуре абсолютного нуля равна нулю. Однако в действительности электроны проводимости подчиняются квантовой статистике Ферми-Дирака, согласно которой при абсолютном нуле скорость электронов и соответственно их энергия отлична от нуля.

Максимальное значение энергии, которой обладают электроны при абсолютном нуле, называется энергией Ферми E_F . Квантовая теория проводимости металлов, основанная на этой статистике, дает иную трактовку работы выхода. Работа выхода электрона из металла равна разности высоты потенциального барьера eφ и энергии Ферми.

где φ’ – среднее значение потенциала электрического поля внутри металла.

Таблица работа выхода электронов из простых веществ

В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.

Источник

Как найти работу выхода электрона с поверхности некоторого металла

КВАНТОВАЯ ОПТИКА И ЯДЕРНАЯ ФИЗИКА

Красная граница фотоэффекту для некоторого металла равняется 275 нм. Найти:

а) работу выхода электрона из металла;

б) максимальную скорость электронов, которые вырываются из металла
светом с длиной волны 180 нм ;

в) максимальную кинетическую энергию электронов.

Дано:

λ_кр = 275 нм =275·10 -9 м

λ_кр = 180 нм =180 · 10 -9 м

Решение:

Зная красную границу фотоэффекта, найдем работу выхода

Уравнение Эйнштейна для внешнего фотоэффекта

Откуда максимальная кинетическая энергия

Максимальная скорость фотоэлектронов

Ответ: ; ; .

Источник

Примеры решенных задач по физике на тему «Фотоэффект»

Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.

Явление фотоэффекта заключается в испускании веществом электронов под действием падающего света. Теория фотоэффекта разработана Эйнштейном и заключается в том, что поток света представляет собой поток отдельных квантов(фотонов) с энергией каждого фотона h n . При попадании фотонов на поверхность вещества часть из них передает свою энергию электронов. Если этой энергия больше работы выхода из вещества, электрон покидает металл. Уравнение эйнштейна для фотоэффекта: где — максимальная кинетическая энергия фотоэлектрона.

Длина волны красной границы фотоэффекта для некоторого металла составляет 307 нм. Максимальная кинетическая энергия фотоэлектронов – 1 эВ. Найти отношение работы выхода электрона к энергии падающего фотона.

Частота света красной границы фотоэффекта для некоторого металла составляет 6*10 14 Гц, задерживающая разность потенциалов для фотоэлектронов – 2В. Определить частоту падающего света и работу выхода электронов.

Работа выхода электрона из металла составляет 4,28эВ. Найти граничную длину волны фотоэффекта.

На медный шарик радает монохроматический свет с длиной волны 0,165 мкм. До какого потенциала зарядится шарик, если работа выхода электрона для меди 4,5 эВ?

Работа выхода электрона из калия составляет 2,2эВ, для серебра 4,7эВ. Найти граничные длину волны фотоэффекта.

Длина волны радающего света 0,165 мкм, задерживающая разность потенциалов для фотоэлектронов 3В. Какова работа выхода электронов?

Красная граница фотоэффекта для цинка 310 нм. Определить максимальную кинетическую энергию фотоэлектронов, если на цинк падает свет с длиной волны 200нм.

На металл с работой выхода 2,4эВ падает свет с длиной волны 200нм. Определить задерживающую разность потенциалов.

На металл падает свет с длиной волны 0,25 мкм, задерживающая разность потенциалов при этом 0,96В. Определить работу выхода электронов из металла.

При изменении длины волны падающего света максимальные скорости фотоэлектронов изменились в 3/4 раза. Первоначальная длина волны 600нм, красная граница фотоэффекта 700нм. Определить длину волны после изменения.

Работы выхода электронов для двух металлов отличаются в 2 раза, задерживающие разности потенциалов — на 3В. Определить работы выхода.

Максимальная скорость фотоэлектронов равно 2,8*10 8 м/с. Определить энергию фотона.

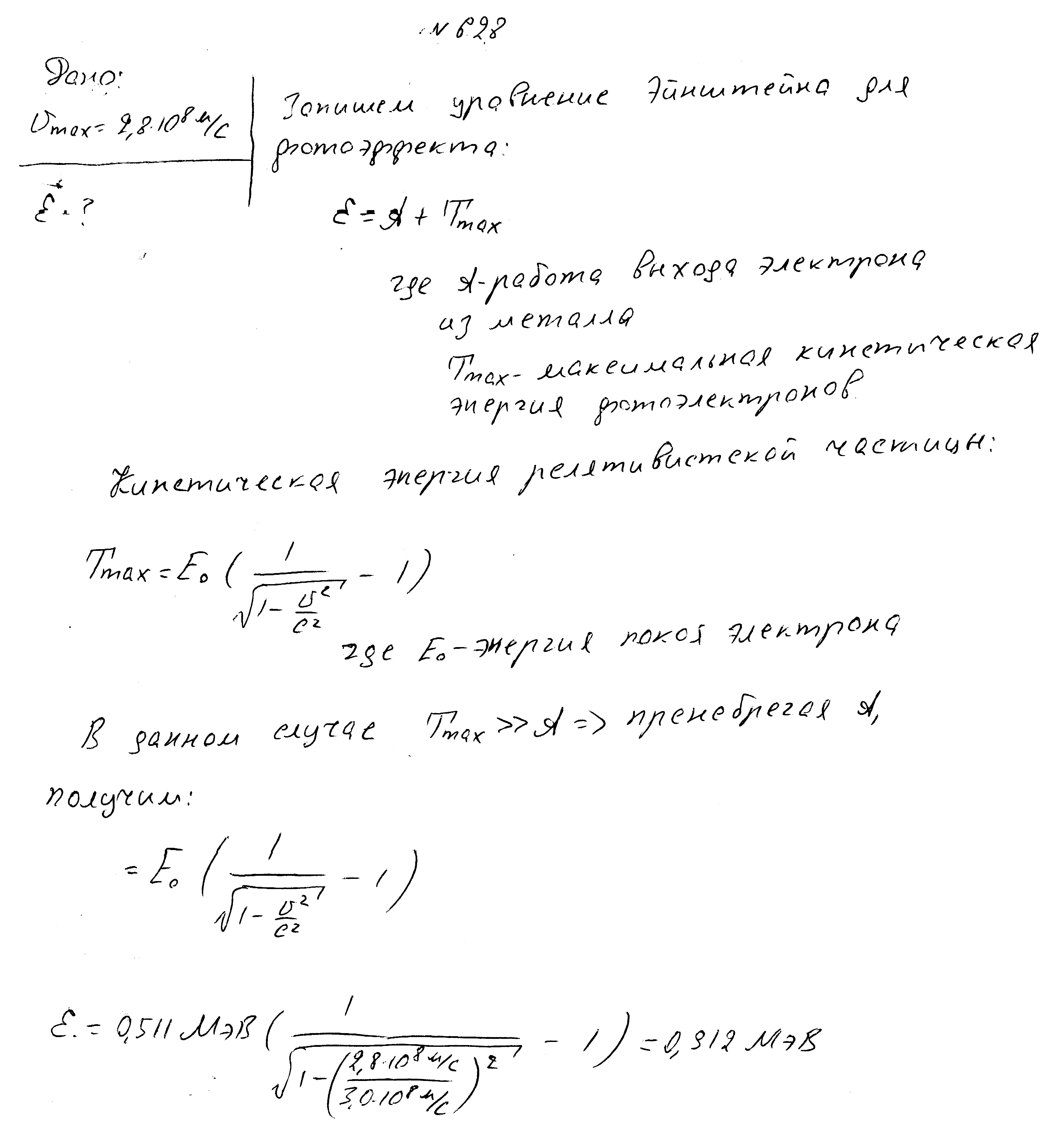
Энергии падающих на металл фотонов равны 1,27 МэВ. Найти максимальную скорость фотоэлектронов.

Максимальная скорость фотоэлектронов равно 0,98с, где с — скорость света в вакууме. Найти длину волны падающего света.

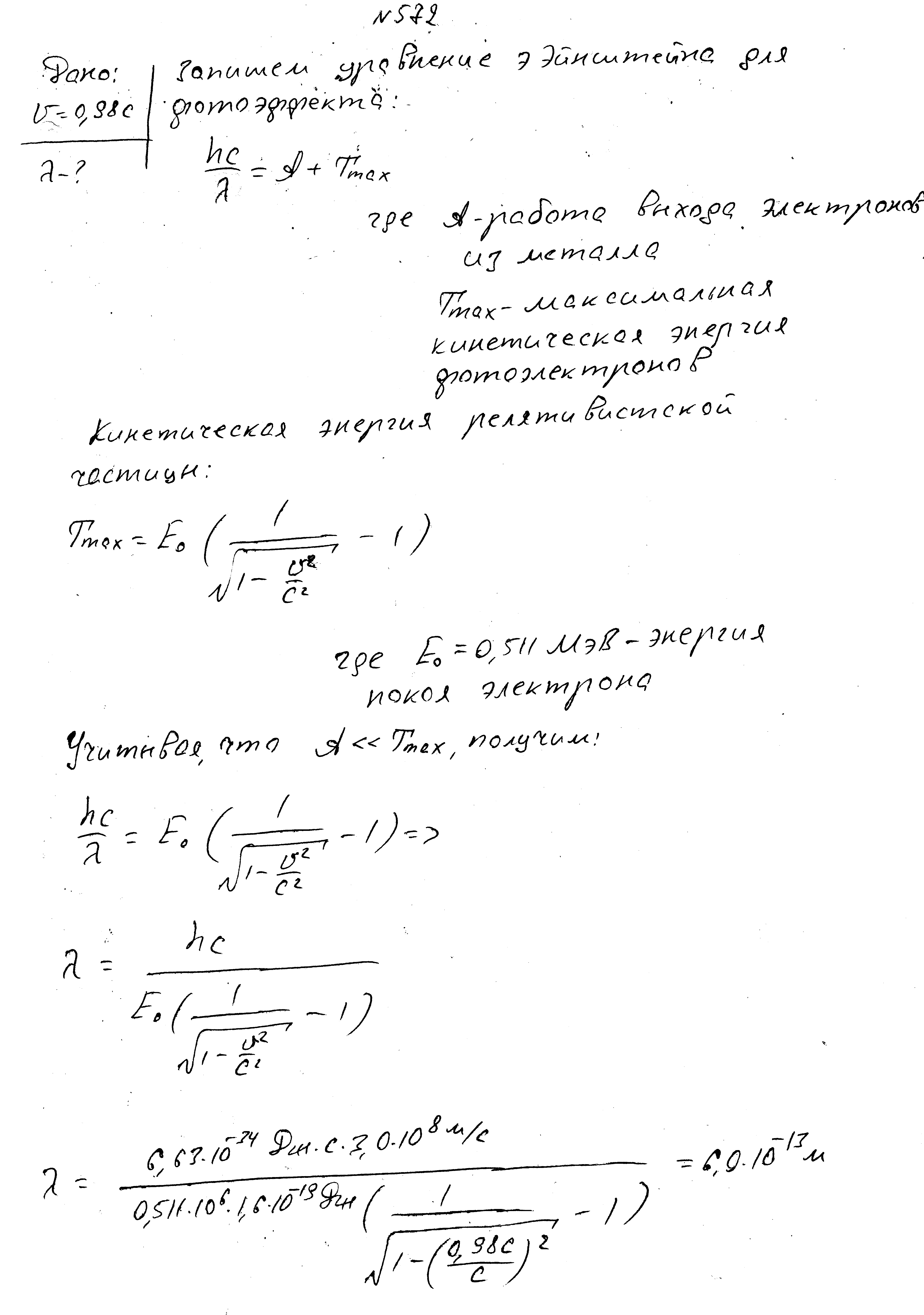
Энергия фотона в пучке света, падающего на поверхность металла, равно 1,53 МэВ. Определить максимальную скорость фотоэлектронов.

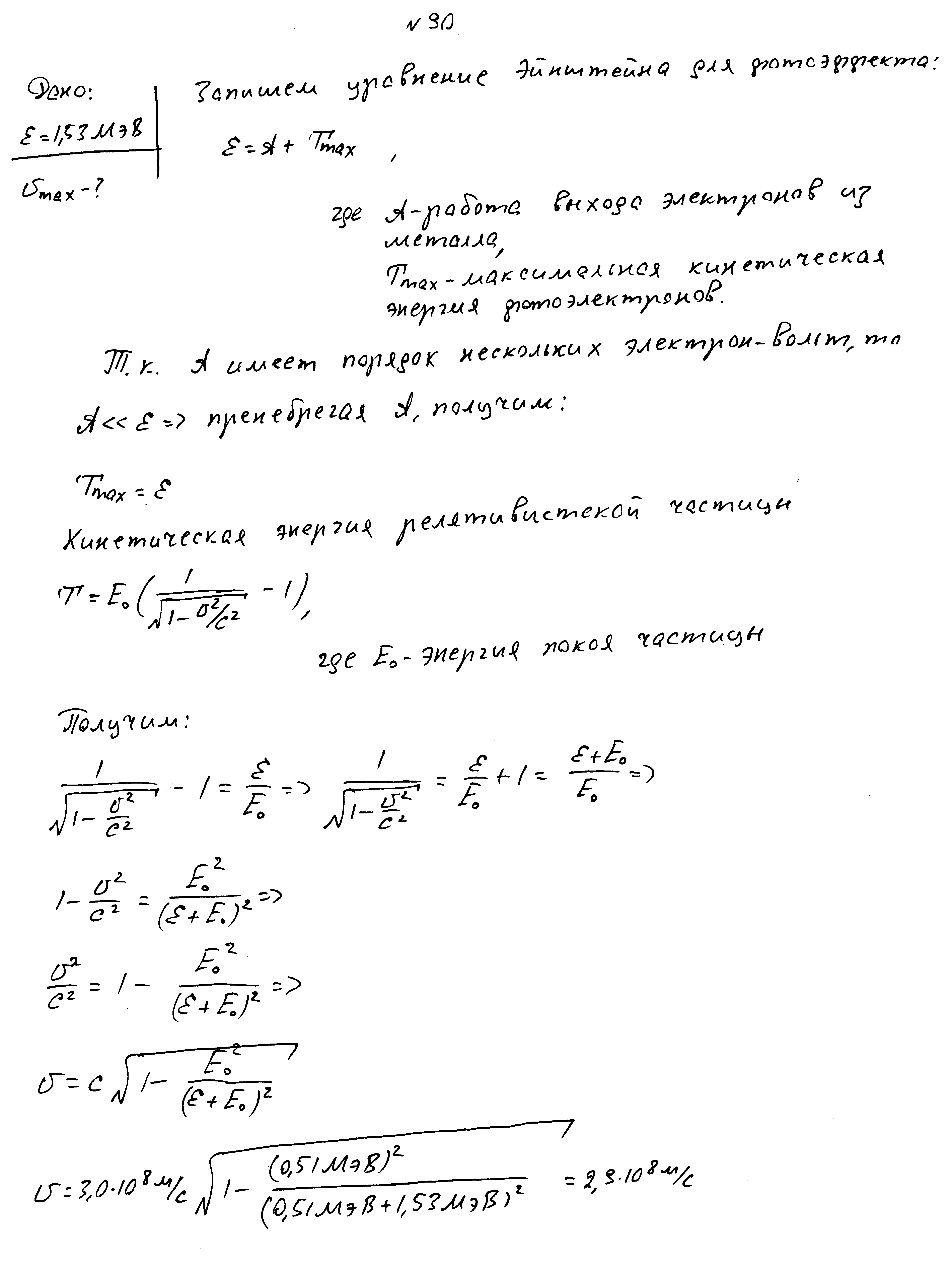
На шарик из металла падает свет с длиной волны 0,4 мкм, при этом шапик заряжается до потенциала 2В. До какого потенциала зарядится шарик, если длина волны станет равной 0,3 мкм?

После изменения длины волны падающего света в 1,5 раза задерживающая разность потенциалов изменилась с 1,6В до 3В. Какова работа выхода?

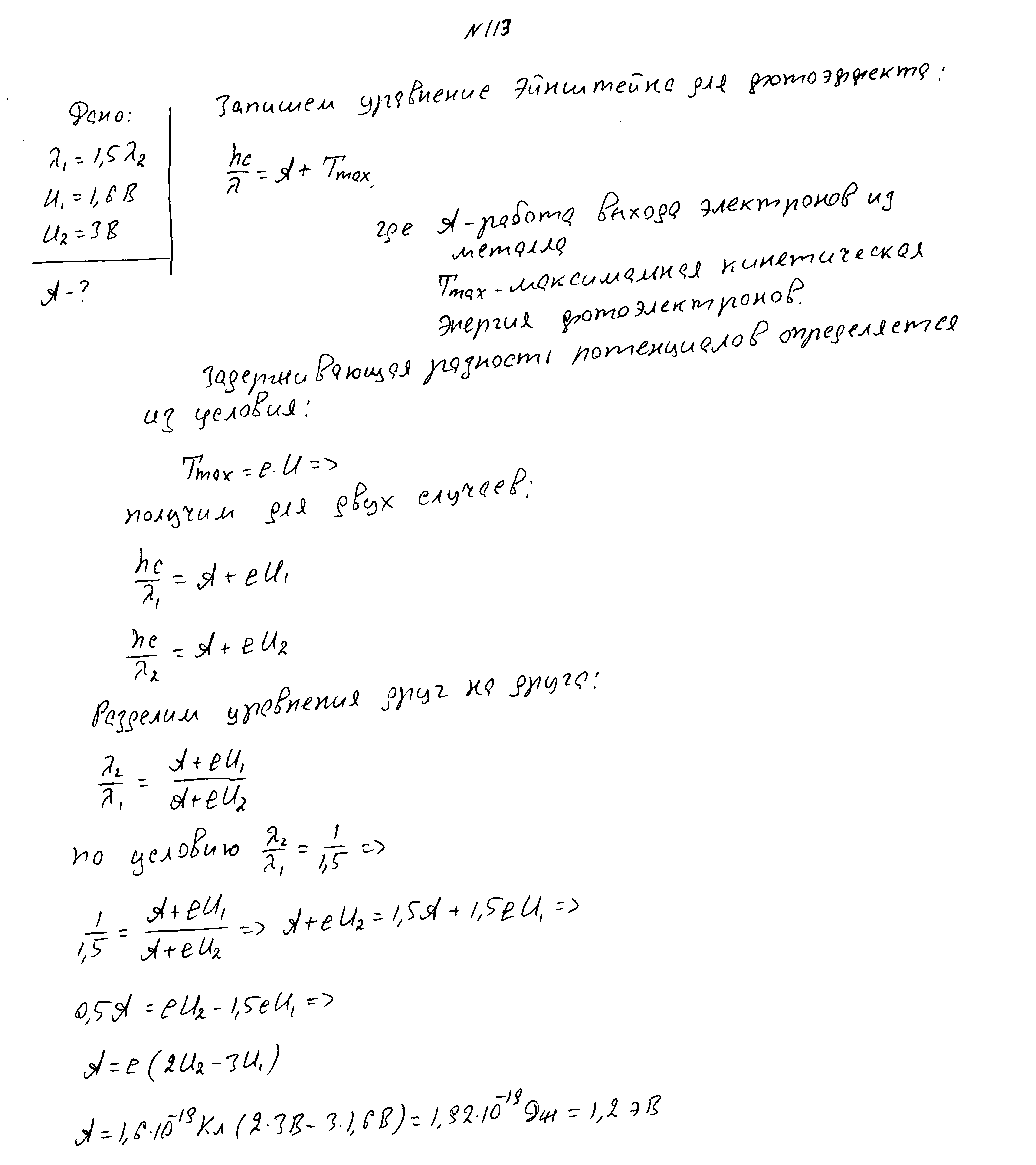
Красная граница фотоэффекта 560нм, частота падающего света 7,3*10 14 Гц. Найти максимальную скорость фотоэлектронов.

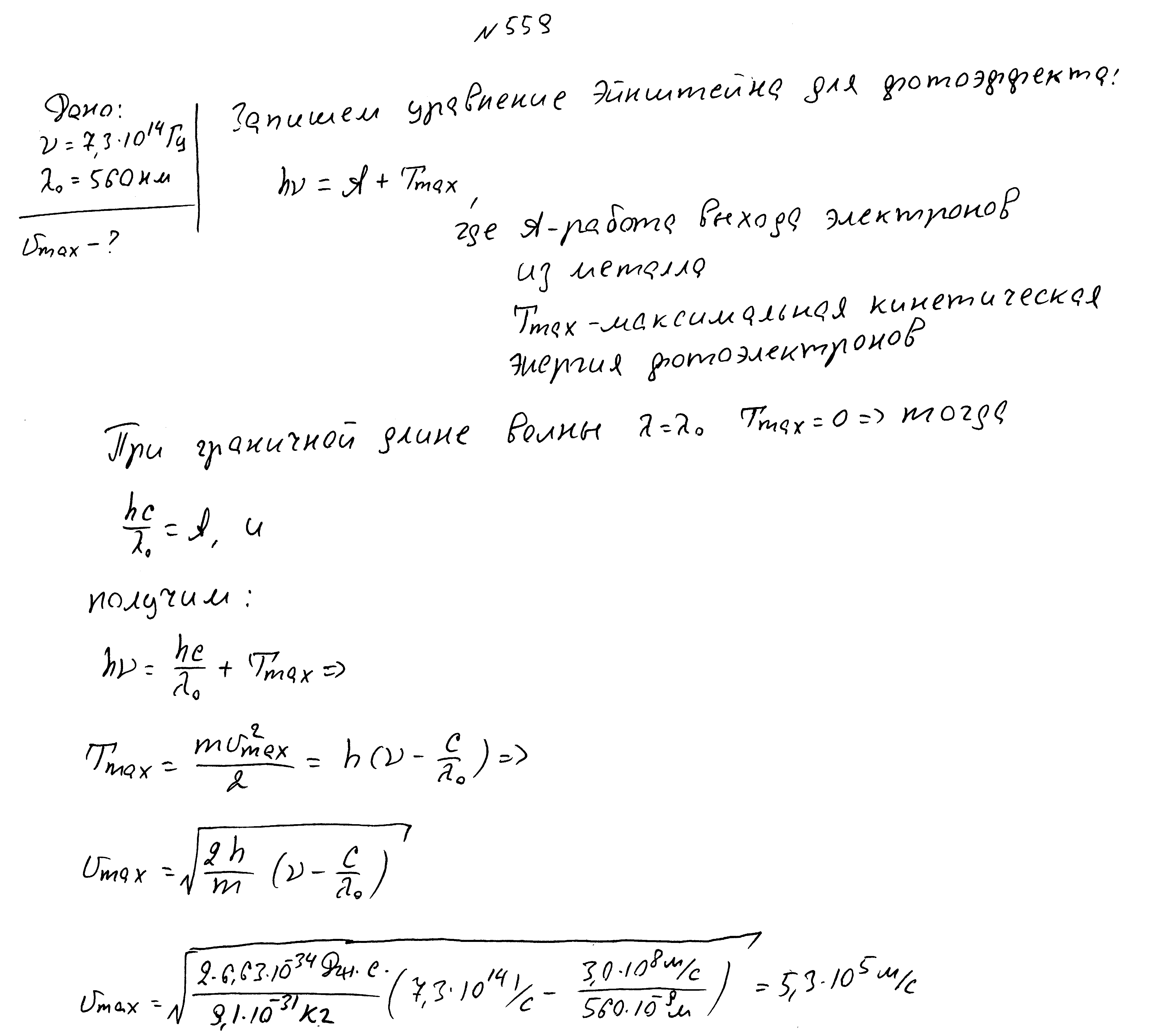
Красная граница фотоэффекта 2800 ангстрем, длина волны падающего света 1600 ангстрем. Найти работу выхода и максимальную кинетическую энергию фотоэлектрона.

Задерживащая разность потенциалов 1,5В, работа выхода электронов 6,4*10 -19 Дж. Найти длину волны падающего света и красную границу фотоэффекта.

Работа выхода электронов из металла равна 3,3 эВ. Во сколько раз изменилась кинетическая энергия фотоэлектронов. если длина волны падающего света изменилась с 2,5*10 -7 м до 1,25*10 -7 м?

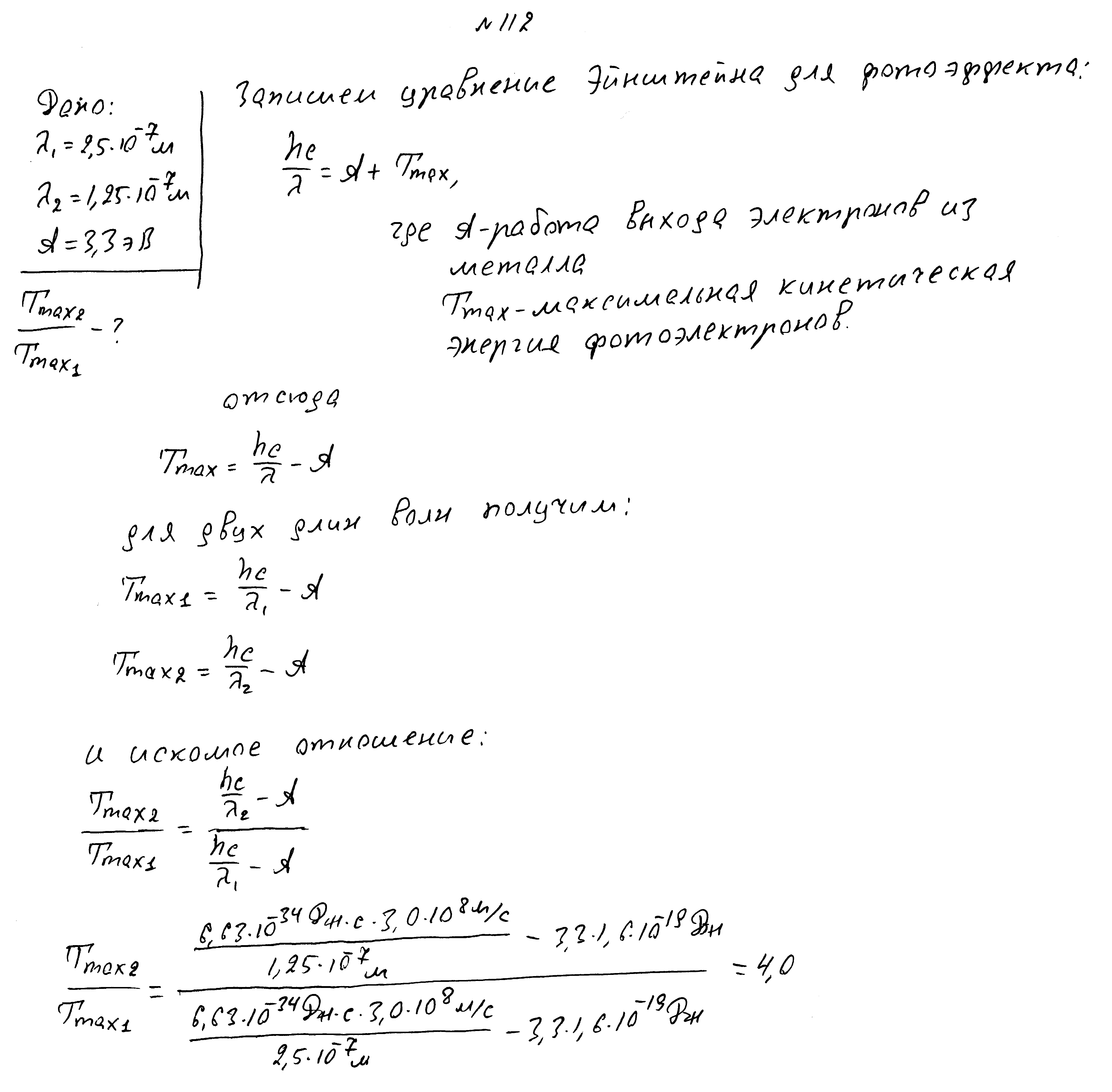
Найти максимальную скорость фотоэлектронов для видимого света с энергией фотона 8 эВ и гамма излучения с энергией 0,51 МэВ. Работа выхода электронов из металла 4,7 эВ.

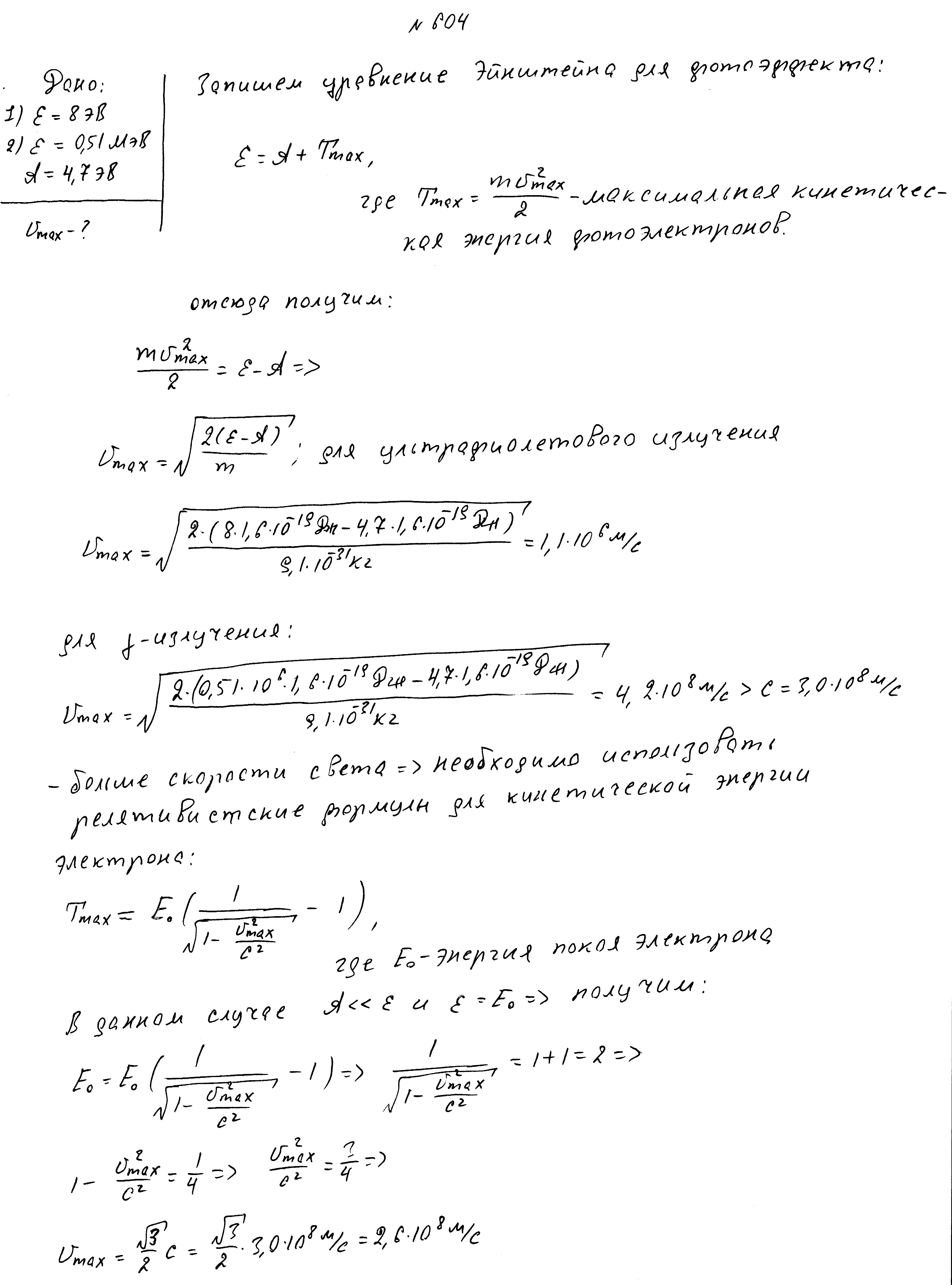
Фототок прекращается при задерживающей разности потенциалов 3,7 В. Работа выхода электронов равна 6,3 эВ. Какая работа выхода электронов у другого металла, если там фототок прекращается при разности потенциалов, большей на 2,3В.

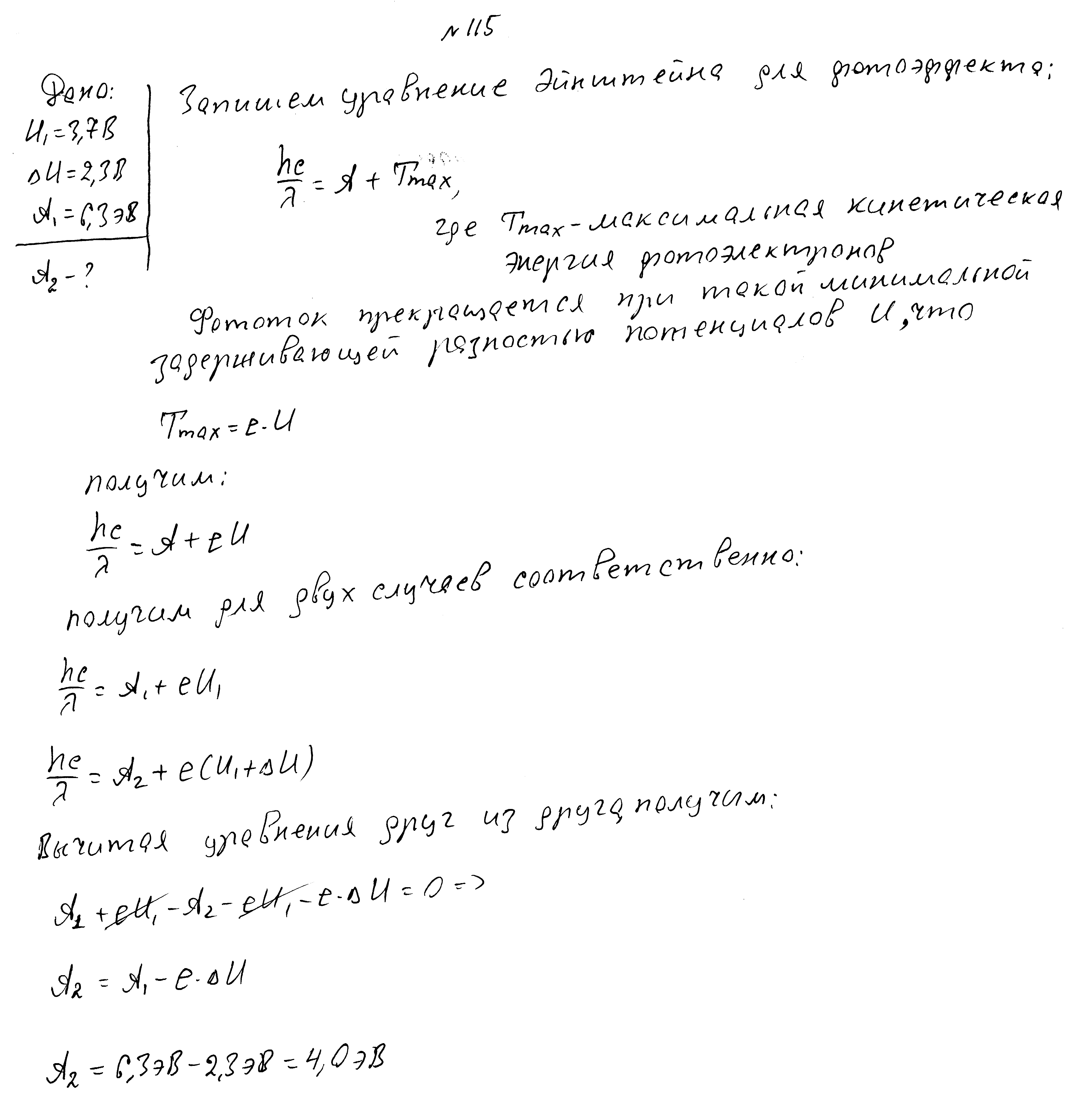
Работа выхода электронов из металла 4,5 эВ, энергия падающих фотонов 4,9 эВ. Чему равен максимальный импульс фотоэлектронов?

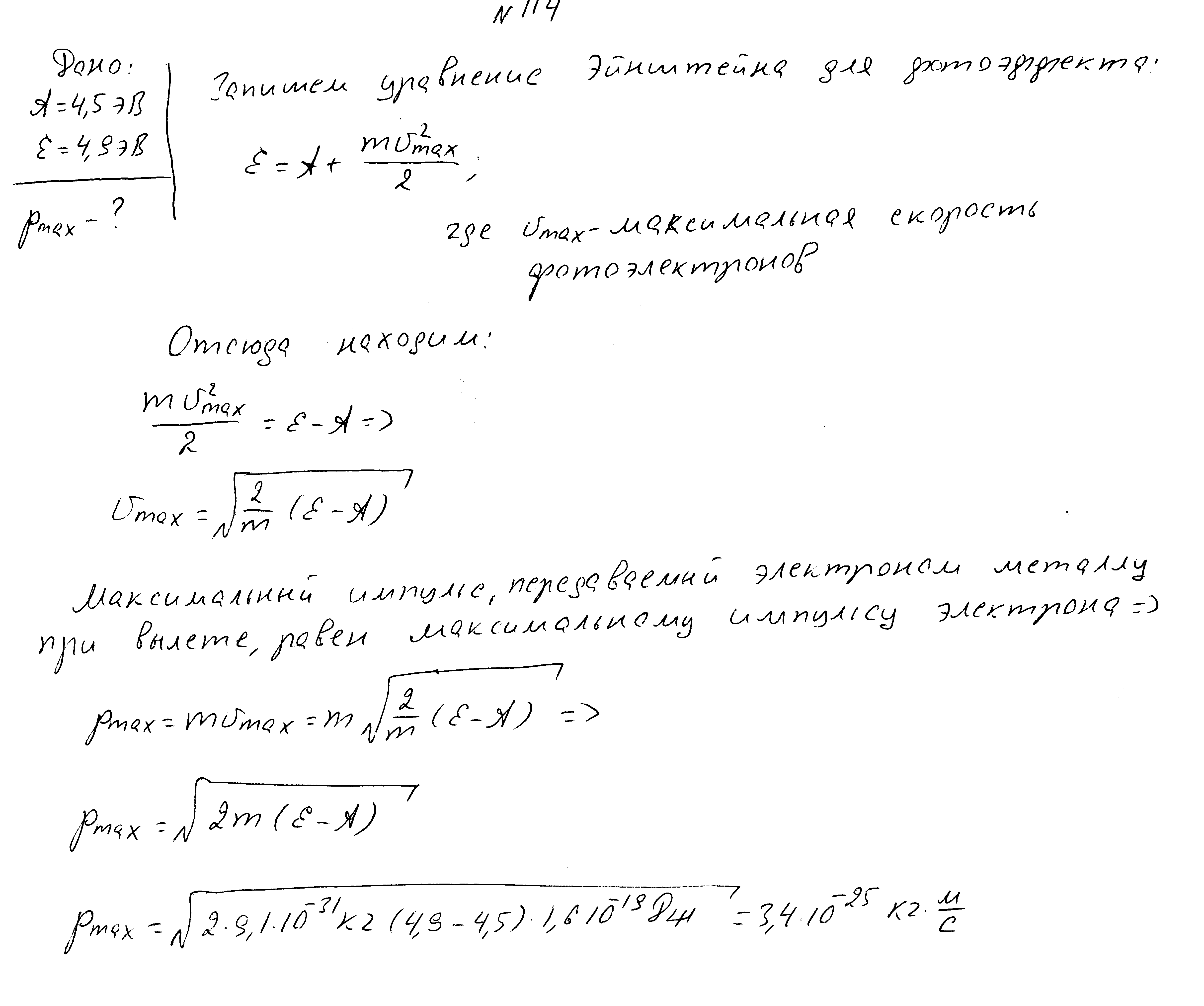
Красная граница фотоэффекта 2900 ангстрем, максимальная скорость фотоэлектронов 10 8 м/с. Найти отношение работы выхода электронов к энергии палающих фотонов.

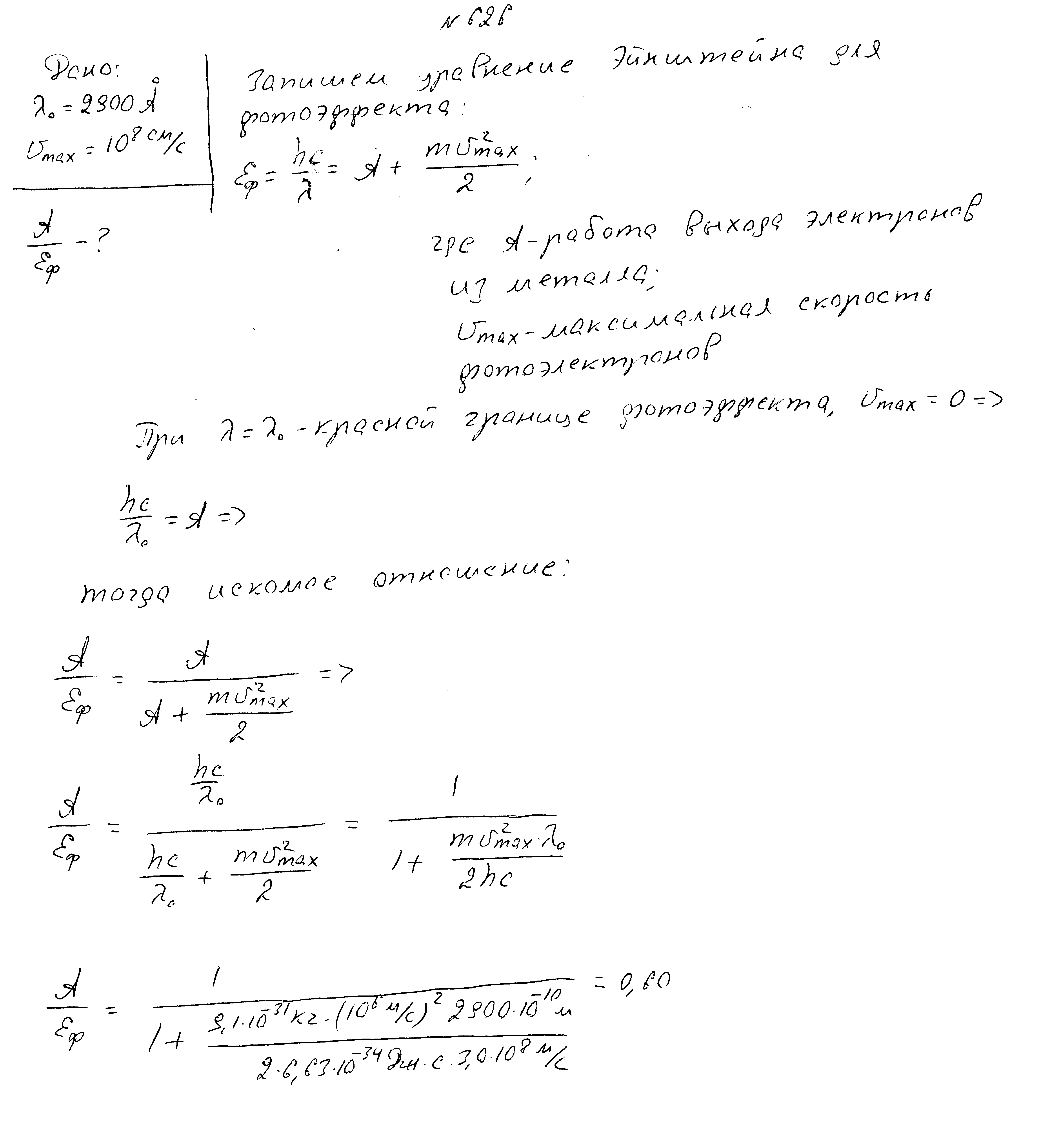
Длина волны падающего света 400нм, красная граница фотоэффекта равна 400нм. Чему равна максимальная скорость фотоэлектронов?

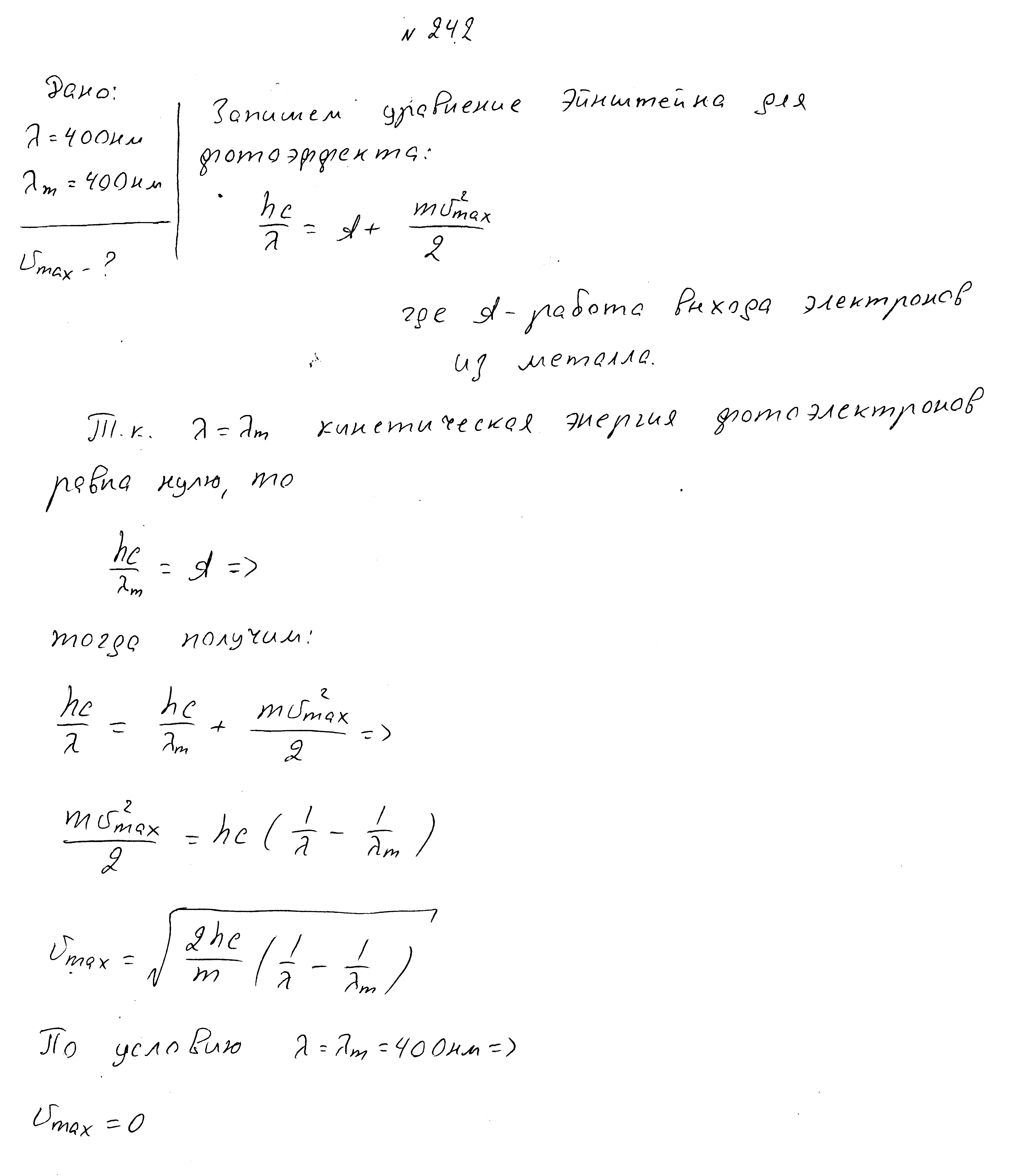
Длина волны падающего света 300нм, работа выхода электронов 3,74 эВ. Напряженность задерживающего электростатического поля 10 В/см.Какой максимальный путь фотоэлектронов при движении в направлении задерживающего поля?

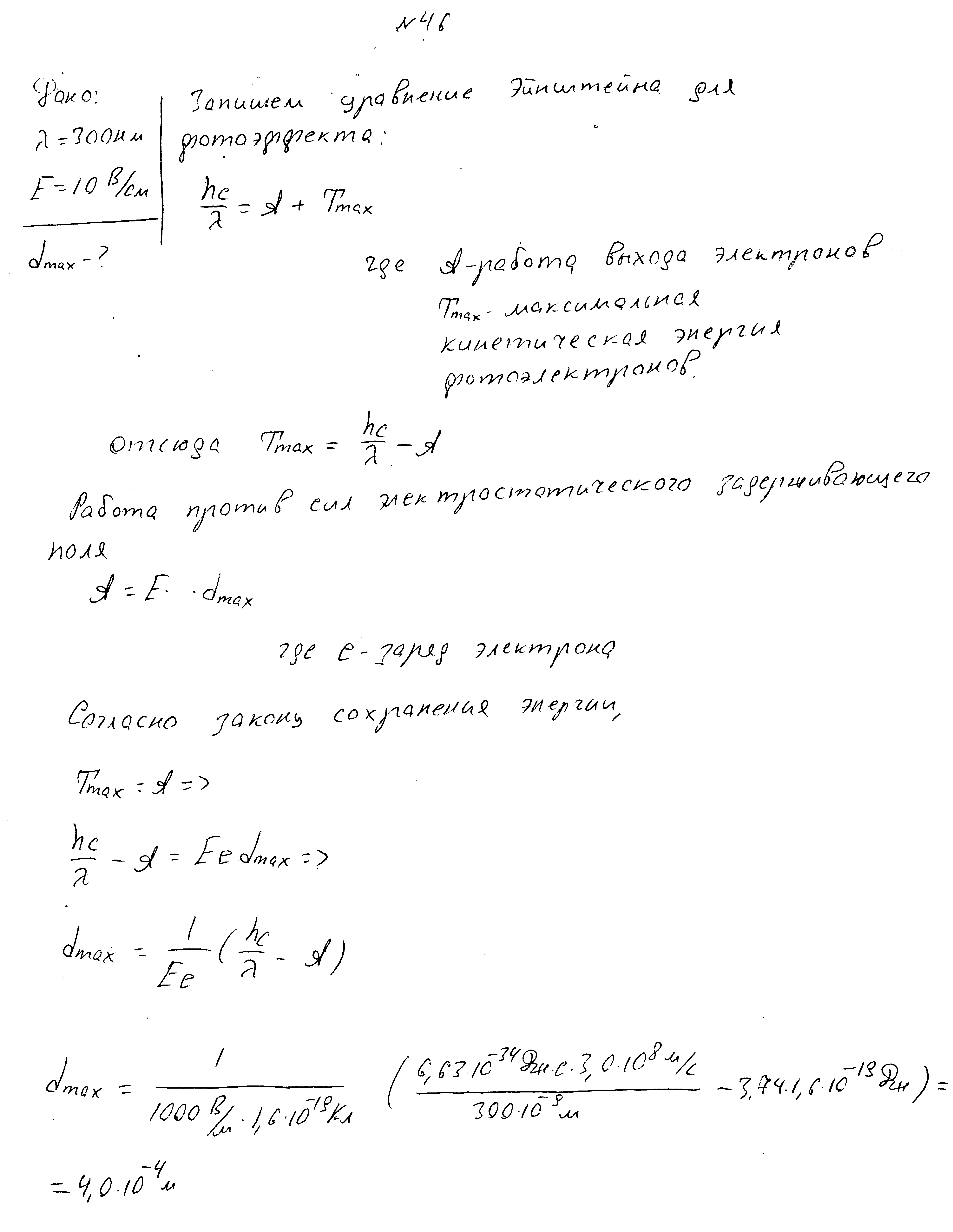
Длина волны падающего света 100 нм, работа выхода электронов 5,30эВ. Найти максимальную скорость фотоэлектронов.

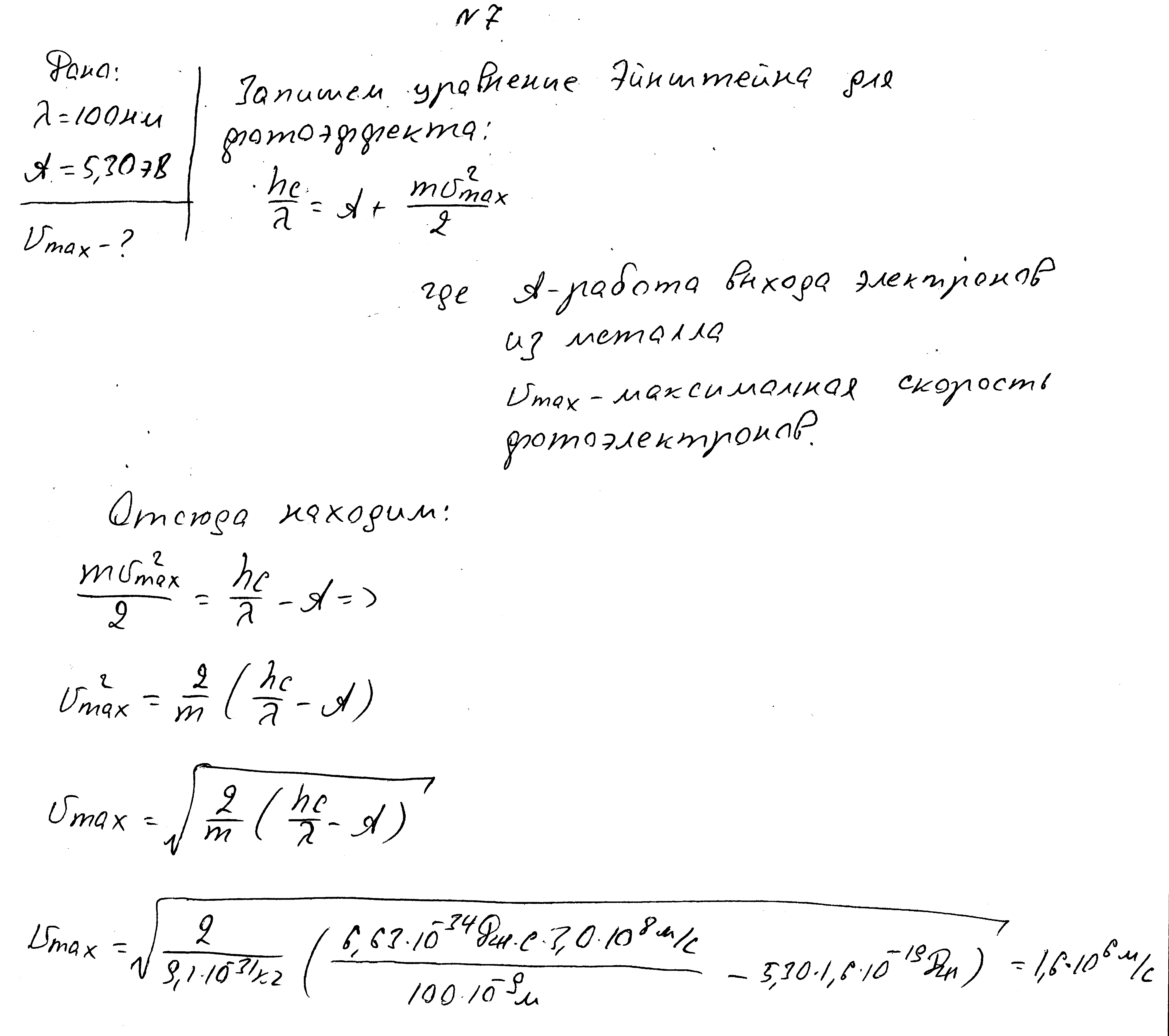
При длине волны радающего света 491нм задерживающая разность потенциалов 0,71В. Какова работа выхода электронов? Какой стала длина волны света, если задерживающая разность потенциалов стала равной 1,43В?

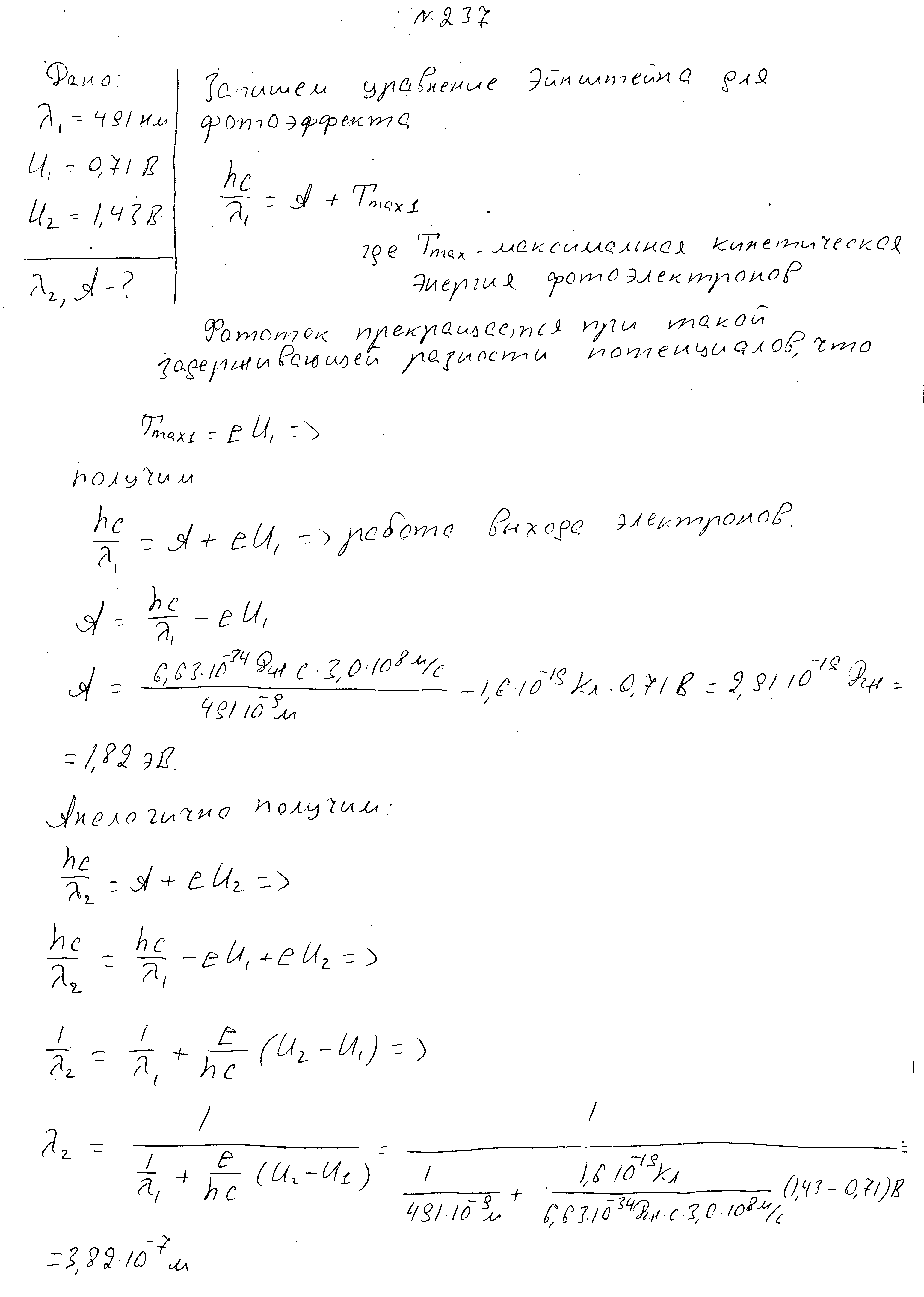
Кинетическая энергия фотоэлектронов 2,0 эВ, красная граница фотоэффекта 3,0*10 14 Гц. Определить энергию фотонов.

Красная граница фотоэффекта 0,257 мкм, задерживающая разность потенциалов 1,5В. Найти длину волны падающего света.

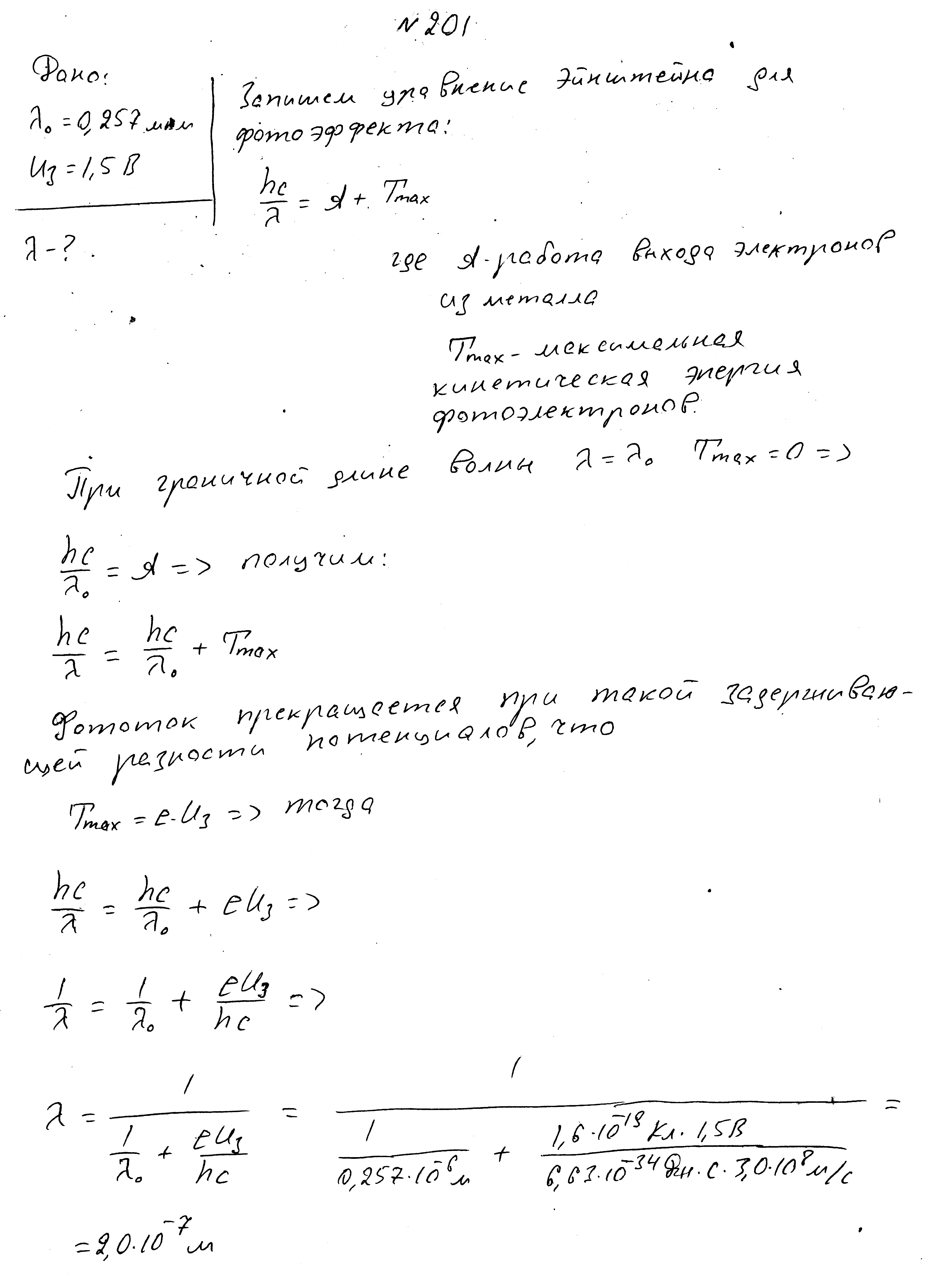
Красная граница фотоэффекта 2850 ангстрем. Минимальное значение энергии фотона, при котором возможен фотоэффект?

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 декабря 2021 года; проверки требуют 15 правок.

Рабо́та вы́хода — разность значений энергий уровня вакуума и уровня Ферми , то есть минимальная энергия, которую необходимо сообщить электрону для его «непосредственного» удаления из объёма твёрдого тела, обычно металла или полупроводника:

Работа выхода обычно указывается в электрон-вольтах, типичные величины лежат в диапазоне 3—5 эВ.

Возможные обозначения: и другие.

Здесь «непосредственность» означает то, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности по атомным масштабам, достаточным чтобы электрон прошёл весь двойной слой, но достаточно близко по сравнению с размерами макроскопических граней кристалла.

Определение и комментарий[править | править код]

Работа выхода находится как где энергия уровня вакуума берётся на небольшом расстоянии от места выхода электрона из образца, хотя и значительно большем, чем постоянная кристаллической решётки.

При удалении электрона от поверхности его взаимодействие с зарядами, остающимися внутри твёрдого тела, приводит к индуцированию поверхностных зарядов (в электростатике для расчёта взаимодействия применяется «метод изображения заряда»). Удаление электрона на бесконечность происходит в поле индуцированного поверхностного заряда на что требуется дополнительная работа, зависящая от диэлектрической проницаемости вещества, геометрии образца и свойств всех его поверхностей.

При нахождении величины удаление от конкретной грани полагается небольшим, и эта дополнительная работа не учитывается. оказывается разной для различных кристаллографических плоскостей поверхности вещества. В отличие от работа по перемещению электрона далее в бесконечность не зависит от того, через какую плоскость был удален электрон, ввиду потенциальности электростатического поля.

Работа выхода в фотоэффекте[править | править код]

Работа выхода во внешнем фотоэффекте — минимальная энергия фотонов, необходимая для удаления электрона из вещества под действием света при

Работа выхода из различных металлов[править | править код]

Единицей измерения работы в СИ являются джоуль (Дж), но в физике твердого тела принято использовать электронвольт (эВ)^[1].
Диапазоны изменения работы выхода для типичных кристаллографических плоскостей указаны в таблице^[2]:

Элемент	эВ	Элемент	эВ	Элемент	эВ	Элемент	эВ	Элемент	эВ
Ag:	4,52 — 4,74	Al:	4,06 — 4,26	As:	3,75	Au:	5,1 — 5,47	B:	~4,45
Ba:	2,52 — 2,7	Be:	4,98	Bi:	4,31	C:	~5	Ca:	2,87
Cd:	4,08	Ce:	2,9	Co:	5	Cr:	4,5	Cs:	2,14
Cu:	4,53 — 5,10	Eu:	2,5	Fe:	4,67 — 4,81	Ga:	4,32	Gd:	2,90
Hf:	3,9	Hg:	4,475	In:	4,09	Ir:	5,00 — 5,67	K:	2,29
La:	3,5	Li:	2,93	Lu:	~3,3	Mg:	3,66	Mn:	4,1
Mo:	4,36 — 4,95	Na:	2,36	Nb:	3,95 — 4,87	Nd:	3,2	Ni:	5,04 — 5,35
Os:	5,93	Pb:	4,25	Pd:	5,22 — 5,6	Pt:	5,12 — 5,93	Rb:	2,261
Re:	4,72	Rh:	4,98	Ru:	4,71	Sb:	4,55 — 4,7	Sc:	3,5
Se:	5,9	Si:	4,60 — 4,85	Sm:	2,7	Sn:	4,42	Sr:	~2,59
Ta:	4,00 — 4,80	Tb:	3,00	Te:	4,95	Th:	3,4	Ti:	4,33
Tl:	~3,84	U:	3,63 — 3,90	V:	4,3	W:	4,32 — 5,22	Y:	3,1
Yb:	2,60[3]	Zn:	3,63 — 4,9	Zr:	4,05

Работу выхода можно определить методом контактной разности потенциалов, основанном на сравнении работ выхода из металлов – эталонного и контролируемого^[4].

Работа выхода для полупроводника[править | править код]

Для полупроводников работа выхода определяется точно так же, как и для металлов (и данные для некоторых собственных полупроводников включены в таблицу).

На практике полупроводник обычно легирован и величина зависит от типа и концентрации легирующих примесей. Уровень при сильном легировании донорами находится у края зоны проводимости , а при сильном легировании акцепторами — близко к краю валентной зоны (соответственно, вариации составляют около ширины запрещённой зоны

Более универсальной величиной, вместо для полупроводников является энергия сродства к электрону, равная Например, для кремния сродство составляет 4,05 эВ, а работа выхода примерно от 4,0 до 5,2 эВ (для собственного материала около 4,6 эВ).

Примечания[править | править код]

Литература[править | править код]

• Solid State Physics, by Ashcroft and Mermin. Thomson Learning, Inc, 1976
• Гончаренко В.И., Олешко В.С. Метод контактной разности потенциалов в оценке энергетического состояния поверхности металлических деталей авиационной техники: монография. – М.: Изд-во МАИ, 2019. – 160 с. – ISBN 978-5-4316-0631-1 http://elibrary.mai.ru/MegaPro/UserEntry?Action=Link_FindDoc&id=68387&idb=0

Как
показывает опыт, свободные электро­ны
при обычных температурах практиче­ски
не, покидают металл. Следовательно, в
поверхностном слое металла должно быть
задерживающее электрическое поле,
препятствующее выходу электронов из
ме­талла в окружающий вакуум. Работа,
ко­торую нужно затратить для удаления
электрона из металла в вакуум, называет­ся
работой
выхода. Укажем
две вероятные причины появления работы
выхода:

1. Если электрон
по какой-то причине удаляется из металла,
то в том месте, которое электрон покинул,
возникает из­быточный положительный
заряд и элект­рон притягивается к
индуцированному им самим положительному
заряду.

2.
Отдельные электроны, покидая ме­талл,
удаляются от него на расстояния порядка
атомных и создают тем самым над
поверхностью металла «электронное
облако», плотность которого быстро
убы­вает с расстоянием. Это облако
вместе с наружным слоем положительных
ионов решетки образует двойной
электрический слой, поле
которого подобно полю плоско­го
конденсатора. Толщина этого слоя рав­на
нескольким межатомным расстояниям
(10^-10
— 10^-9
м). Он не создает элек­трического поля
во внешнем пространстве, но препятствует
выходу свободных элек­тронов из
металла.

Таким
образом, электрон при вылете из металла
должен преодолеть задержи­вающее его
электрическое поле двойного слоя.
Разность потенциалов 
в этом слое, называемая поверхностным
скачком потенциала, определяется
работой выхода (А)
электрона
из металла:

=A/e,

где е
—
заряд электрона. Так как вне двойного
слоя электрическое поле отсут­ствует,
то потенциал среды равен нулю, а внутри
металла потенциал положителен и равен
.
Потенциальная энергия сво­бодного
электрона внутри металла равна — е
и является относительно вакуума
отрицательной. Исходи из этого можно

167

считать,
что весь объем металла для элек­тронов
проводимости представляет потен­циальную
яму с плоским дном, глубина которой
равна работе выхода А.

Работа
выхода выражается в элект­рон-вольтах
(эВ):
1 эВ равен работе, со­вершаемой силами
поля при перемещении элементарного
электрического заряда (за­ряда, равного
заряду электрона) при про­хождении
им разности потенциалов в 1 В. Так как
заряд электрона равен 1,6•l0^-19
Кл,
то 1 эВ = 1,6•10^-19
Дж.

Работа
выхода зависит от химической природы
металлов и от чистоты их по­верхности
и колеблется в пределах не­скольких
электрон-вольт (например, у ка­лия
Л=2,2 эВ, у платины A
= б,3 эВ). Подобрав определенным образом
покры­тие поверхности, можно значительно
уменьшить paботу
выхода. Например, если нанести на
поверхность вольфрама (А
=4,5
эВ) слой оксида щелочно-земельного
металла (Са, Sr,
Ba), то
работа выхода снижается до 2 эВ.

§ 105. Эмиссионные явления и их применение

Если
сообщить электронам в металлах энергию,
необходимую для преодоления работы
выхода, то часть электронов может
покинуть металл, в результате чего
на­блюдается явление испускания
электро­нов, или электронной
эмиссии. В
зависи­мости от способа сообщения
электронам энергии различают
термоэлектронную, фо­тоэлектронную,
вторичную электронную и автоэлектронную
эмиссии.

1.
Термоэлектронная эмиссия — это
испускание электронов нагретыми
метал­лами. Концентрация свободных
электро­нов в металлах достаточно
высока, поэто­му даже при средних
температурах вслед­ствие распределения
электронов по скоро­стям (по энергии)
некоторые электроны обладают энергией,
достаточной для прео­доления
потенциального барьера на гра­нице
металла. С повышением температуры число
электронов, кинетическая энергия
теплового движения которых больше
ра­боты выхода, растет и явление
термоэлек­тронной эмиссии становится
заметным.

Исследование
закономерностей термо­электронной
эмиссии можно провести с по­мощью
простейшей двухэлектродной лам­пы —
вакуумного
диода, представляюще­го
собой откачанный баллон, содержащий
два электрода: катод К
и
анод А.
В
про­стейшем случае катодом служит
нить из тугоплавкого металла (например,
воль­фрама), накаливаемая электрическим
то­ком. Анод чаще всего имеет форму
ме­таллического цилиндра, окружающего
ка­тод. Если диод включить в цепь, как
это показано на рис. 152, то при накаливании
катода и подаче на анод положительного
напряжения (относительно катода) в
анодной цепи диода возникает ток. Если
поменять полярность батареи Б_а,
то ток прекращается, как бы сильно катод
ни накаливали. Следовательно, катод
ис­пускает отрицательные частицы —
элек­троны.

Если
поддерживать температуру на­каленного
катода постоянной и снять за­висимость
анодного тока I_а
от анодного напряжения U_a
—
вольт-амперную
харак­теристику (рис.
153), то оказывается, что она не является
линейной, т. е. для ваку­умного диода
закон Ома не выполняется. Зависимость
термоэлектронного тока I
от
анодного напряжения в области малых

168

положительных
значений U
описывается
законом
трех вторых (установлен
русским физиком С. А. Богуславским (1883—
1923) и американским физиком И. Ленгмюром
(1881 — 1957)):

I=BU^3/2,

где В
— коэффициент,
зависящий от фор­мы и размеров
электродов, а также их взаимного
расположения.

При
увеличении анодного напряжения ток
возрастает до некоторого максималь­ного
значения I_нас,
называемого током
на­сыщения. Это
означает, что почти все электроны,
покидающие катод, достигают анода,
поэтому дальнейшее увеличение
на­пряженности поля не может привести
к увеличению термоэлектронного тока.
Следовательно, плотность тока насыщения
характеризует эмиссионную способность
материала катода.

Плотность
тока насыщения определя­ется формулой
Ричардсона — Дешмана, выведенной
теоретически на основе кван­товой
статистики:

j_нас=CT²e^-A/(kT).

где А
— работа
выхода электронов из ка­тода, Т
— термодинамическая
температу­ра, С
—
постоянная, теоретически одина­ковая
для всех металлов (это не подтвер­ждается
экспериментом, что, по-видимому,
объясняется поверхностными эффектами).
Уменьшение работы выхода приводит к
резкому увеличению плотности тока
на­сыщения. Поэтому применяются
оксидные катоды (например, никель,
покрытый ок­сидом щелочно-земельного
металла), ра­бота выхода которых равна
1 —1,5 эВ.

На
рис. 153 представлены вольт-ам­перные
характеристики для двух темпера­тур
катода: T₁
и
Т₂,
причем
T₂>T₁.
С
по­вышением температуры катода
испуска­ние электронов с катода
интенсивнее, при этом увеличивается и
ток насыщения. При U_a=0
наблюдается
анодный ток, т. е. некоторые электроны,
эмиттируемые катодом, обладают энергией,
достаточной для преодоления работы
выхода и дости­жения анода без
приложения электриче­ского поля.

Явление
термоэлектронной эмиссии ис­пользуется
в приборах, в которых необхо­димо
получить поток электронов в вакуу­ме,
например в электронных лампах,
рен­тгеновских трубках, электронных
микро­скопах и т. д. Электронные лампы
широко применяются в электро- и
радиотехнике, автоматике и телемеханике
для выпрямле­ния переменных токов,
усиления электри­ческих сигналов и
переменных токов, гене­рирования
электромагнитных колебаний и т. д. В
зависимости от назначения в лампах
используются дополнительные управляющие
электроды.

2.
Фотоэлектронная эмиссия — это
эмиссия электронов из металла под
действием света, а также коротковол­нового
электромагнитного излучения (например,
рентгеновского). Основные закономерности
этого явления будут разобраны при
рассмотрении фотоэлек­трического
эффекта.

3.
Вторичная электронная эмиссия — это
испускание электронов поверхностью
металлов, полупроводников или диэлек­триков
при бомбардировке их пучком электронов.
Вторичный электронный поток состоит
из электронов, отраженных повер­хностью
(упруго и неупруго отраженные электроны),
и «истинно» вторичных элек­тронов —
электронов, выбитых из металла,
полупроводника или диэлектрика
первич­ными электронами.

Отношение
числа вторичных электро­нов n₂
к числу первичных п₁,
вызвавших
эмиссию, называется коэффициентом
вто­ричной электронной эмиссии:

=n₂/n₁.

Коэффициент б
зависит от природы мате­риала
поверхности, энергии бомбардиру­ющих
частиц и их угла падения на поверх­ность.
У полупроводников и диэлектриков б
больше, чем у металлов. Это объясняется
тем, что в металлах, где концентрация
электронов проводимости велика,
вторич­ные электроны, часто сталкиваясь
с ними, теряют свою энергию и не могут
выйти из металла. В полупроводниках и
диэлектри­ках же из-за малой концентрации
элек­тронов проводимости столкновения
вто­ричных электронов с ними происходят
гораздо реже и вероятность выхода
вторич­ных электронов из эмиттера
возрастает в несколько раз.

169

Для
примера на рис. 154 приведена качественная
зависимость коэффициента вторичной
электронной эмиссии б от энер­гии Е
падающих
электронов для KCl.
С увеличением энергии электронов б
воз­растает, так как первичные электроны
все глубже проникают в кристаллическую
ре­шетку и, следовательно, выбивают
больше вторичных электронов. Однако
при некото­рой энергии первичных
электронов 6 на­чинает уменьшаться.
Это связано с тем, что с увеличением
глубины проникновения первичных
электронов вторичным все труднее
вырваться на поверхность. Значе­ние
_max
для KCl
достигает 12
(для чистых металлов оно не превышает
2).

Явление
вторичной электронной эмис­сии
используется в фотоэлектронных
ум­ножителях (ФЭУ),
применяемых для уси­ления слабых
электрических токов. ФЭУ представляет
собой вакуумную трубку с фотокатодом
К и анодом А, между кото­рыми расположено
несколько электро­дов— эмиттеров
(рис.155).
Электроны, вырванные с фотокатода под
действием света, попадают на эмиттер
Э₁,
пройдя
ускоряющую разность потенциалов между
К и Э₁.
Из
эмиттера Э₁
выбивается 
электронов.
Усиленный таким образом

электронный
поток направляется на эмит­тер Э2, и
процесс умножения повторяется на всех
последующих эмиттерах. Если ФЭУ содержит
n
эмиттеров,
то на аноде А, называемом коллектором,
получается
уси­ленный в б” раз фотоэлектронный
ток.

4.
Автоэлектронная эмиссия — это
эмиссия электронов с поверхности
метал­лов под действием сильного
внешнего электрического поля. Эти
явления можно наблюдать в откачанной
трубке, конфигу­рация электродов
которой (катод — острие, анод — внутренняя
поверхность трубки) позволяет при
напряжениях при­мерно 10³
В получать электрические поля
напряженностью примерно 10⁷
В/м. При постепенном повышении напряжения
уже при напряженности поля у поверхности
катода примерно 10⁵—10⁶
В/м возникает слабый ток, обусловленный
электронами, испускаемыми катодом. Сила
этого тока увеличивается с повышением
напряжения на трубке. Токи возникают
при холодном катоде, поэтому описанное
явление назы­вается также холодной
эмиссией. Объяс­нение
механизма этого явления возможно лишь
на основе квантовой теории.

Соседние файлы в папке Трофимова Курс физики

• #

  16.03.2016155.65 Кб1141.doc

• #

  16.03.2016662.53 Кб21010.doc

• #

  16.03.2016592.38 Кб25011.doc

• #
• #

  16.03.2016181.76 Кб16713.doc

• #

  16.03.2016336.38 Кб13614.doc

• #

  16.03.2016206.34 Кб14115.doc

• #

  16.03.2016169.98 Кб9616.doc
• #

  16.03.2016123.39 Кб9417.doc

• #

  16.03.2016629.25 Кб22318.doc

Работа выхода в металлах

В металлах, согласно электронной теории проводимости, свободные электроны находятся в состоянии постоянного хаотичного теплового движения. Однако при нормальных температурах они не покидают металл. У поверхности металла существует задерживающее электрическое поле. Чтобы вылететь из металла электрон должен совершить работу по преодолению задерживающих сил. Эта работа называется работой выхода.

Как у поверхности металла образуется задерживающее поле?

1. Вследствие теплового движения электроны с поверхности металла могут отрываться и образуют над поверхностью электронное облако.
2. На местах покинувших металл электронов образуются положительные ионы. По закону Кулона, они стремяться вернуть покинувшие металл электроны обратно.

В результате у поверхности металла образуется двойной электрический слой.

В вакууме за пределами задерживающего слоя поле отсутствует, поэтому формула для работы выхода запишется в виде:

A=eφ,

где φ – потенциал выхода, равный потенциалу поля внутри металла.

Контактная разность потенциалов

Явление контактной разности потенциалов в 1797 году открыл Алессандро Вольта (1745 -1827).

Причины возникновения контактной разности потенциалов:

1. Разная работа выхода для разных металлов.
2. Разная концентрация свободных электронов в разных металлах.

Схематически рассмотрим контакт двух металлов. Пусть у металла 1 работа выхода больше, чем у металла 2, и в металле 1 концентрация свободных электронов больше.

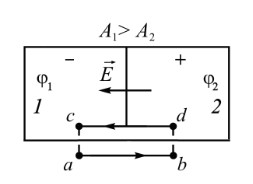
Между точками a и b, лежащими рядом с поверхностью, но не принадлежащими проводнику, возникает внешняя контактная разность потенциалов. 

Электроны диффундируют из одного металла в другой, при этом из металла 1 в металл 2 уходит больше электронов, так как n1>n2. В результате металл 1 приобретает положительный, а металл 2 – отрицательный заряд. Возникшая разность потенциалов называется внутренней контактной разностью потенциалов.

Решение: воспользуемся уравнением Эйнштейна для фотоэффекта:
[ frac{hcdot c}{lambda } =A+frac{mcdot upsilon ^{2}}{2}, ]
здесь h = 6,63 ∙ 10^-34 Дж∙с – постоянная Планка, с = 3 ∙ 10⁸ – скорость света, A – искомая работа выхода электронов из металла, m = 9,1 ∙ 10^-31 кг – масса электрона, υ – максимальная скорость фотоэлектронов. По условию задачи, скорость в первом случае в n раз больше, чем во втором (в первом случае длина волны падающего излучения меньше, следовательно, энергия падающих фотонов больше, что приводит к более высокой скорости выбиваемых электронов) Запишем уравнение для двух случаев:
[ begin{array}{l} {frac{hcdot c}{lambda _{1}} =A+frac{mcdot left(ncdot upsilon right)^{2} }{2} =A+n^{2} cdot frac{mcdot upsilon ^{2}}{2},} \ {frac{hcdot c}{lambda _{2} } =A+frac{mcdot upsilon ^{2}}{2},{rm ; ; ; ; ; }frac{mcdot upsilon ^{2}}{2} =frac{hcdot c}{lambda _{2}} -A,} \ {frac{hcdot c}{lambda _{1}} =A+n^{2} cdot left(frac{hcdot c}{lambda _{2}} -Aright)=A+n^{2} cdot frac{hcdot c}{lambda _{2}} -n^{2} cdot A,} \ {Acdot left(n^{2} -1right)=n^{2} cdot frac{hcdot c}{lambda _{2}} -frac{hcdot c}{lambda _{1}},} \ {A=frac{hcdot c}{n^{2} -1} cdot left(frac{n^{2}}{lambda _{2}} -frac{1}{lambda _{1}} right).} end{array} ]
Ответ: 3,4 ∙ 10^-19 Дж = 2,13 эВ.