Как найти работу за сутки физика

Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.

Работы силы, формула

Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Работа силы — это скалярное произведение вектора силы на вектор перемещения.

Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:

Векторный вид записи

[ large boxed{ A = left( vec{F} , vec{S} right) }]

Для решения задач правую часть этой формулы удобно записывать в скалярном виде:

[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]

( F left( H right) ) – сила, перемещающая тело;

( S left( text{м} right) ) – перемещение тела под действием силы;

( alpha ) – угол между вектором силы и вектором перемещения тела;

Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.

В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.

Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.

Рассмотрим несколько случаев, следующих из формулы:

1. Когда угол между силой и перемещением острый, работа силы положительная;
2. А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
3. Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!

Работа — разность кинетической энергии

Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.

( E_{k1} left(text{Дж} right) )  – начальная кинетическая энергия машины;

( E_{k2} left(text{Дж} right) )  – конечная кинетическая энергия машины;

( m left( text{кг}right) ) – масса автомобиля;

( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.

Кинетическую энергию будем вычислять, используя формулу:

[ large E_{k} = m cdot frac{v^{2}}{2} ]

[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]

[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]

Теперь найдем разницу кинетической энергии в конце и вначале разгона.

[ large boxed{ A = Delta E_{k} }]

[ large Delta E_{k} = E_{k2} — E_{k1} ]

[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]

Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.

Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.

[ large boxed{ A = Delta E }]

Работа силы тяжести — разность потенциальной энергии

Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.

( E_{p1} left(text{Дж} right) )  – начальная потенциальная энергия яблока;

( E_{p2} left(text{Дж} right) )  – конечная потенциальная энергия яблока;

Примечание: Работу можно рассчитать через разность потенциальной энергии тела.

Потенциальную энергию будем вычислять, используя формулу:

[ large E_{p} = m cdot g cdot  h]

( m left( text{кг}right) ) – масса яблока;

Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.

( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.

Начальная высота яблока над поверхностью земли равна 3 метрам

[ large E_{p2} = 0,2 cdot 10 cdot  3 = 6 left(text{Дж} right) ]

Потенциальная энергия яблока на столе

[ large E_{p1} = 0,2 cdot 10 cdot  1 = 2 left(text{Дж} right) ]

Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.

[ large Delta E_{p} = E_{p2} — E_{p1} ]

[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]

Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!

Чтобы работа получилась положительной, в правой части формулы перед ( Delta  E_{p}) дополнительно допишем знак «минус».

[ large boxed{ A = — Delta E_{p} }]

Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.

Примечания:

1. Если тело падает на землю, работа силы тяжести положительна;
2. Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
3. Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
4. Работа силы тяжести не зависит от траектории, по которой двигалось тело;
5. Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.

Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Мощность

В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.

Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.

Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).

Расчет работы осуществляем, используя любую из формул:

[ large A = Delta E_{k} ]

[ large A = Delta E_{p} ]

[ large A = F cdot S cdot cos(alpha) ]

Разделив эту работу на время, в течение которого она совершалась, получим мощность.

[ large boxed{ P = frac{A}{Delta t} }]

Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.

Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.

Еще одна формула для расчета мощности

Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:

[ large P = left( vec{F} , vec{v} right) ]

Формулу можно записать в скалярном виде:

[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]

( F left( H right) ) – сила, перемещающая тело;

( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;

( alpha ) – угол между вектором силы и вектором скорости тела;

Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:

[ large boxed{ P = F cdot v }]

Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).

КПД

КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.

Примечания:

1. Процент – это дробь, у которой в знаменателе число 100.
2. КПД — это либо правильная дробь, или дробь, равная единице.

Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.

[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]

(eta) – КПД;

( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;

(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;

Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.

[ large boxed{ eta leq 1 }]

Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:

[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]

Выводы

1. Сила, приложенная к телу и перемещающая его, совершает работу;
2. Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
3. Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
4. Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
5. Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
6. Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
7. Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
8. Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
9. Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
10. КПД — это либо правильная дробь, или дробь, равная единице.
11. Можно вычислять КПД, подставляя в формулу работу, или мощности

В сегодняшней статье кратко расскажем про работу и мощность в механике, а также приведем примеры задач для тех, кто учится их решать.

Больше полезной информации для студентов всех специальностей — на нашем телеграм-канале. Подписывайтесь!

Задачи на механическую работу и мощность с решениями

Задача №1. Нахождение механической работы

Условие

Грузчик равномерно толкает ящик с осциллографами по горизонтальному полу. Сила трения равна 450 Н. Найдите работу, совершенную грузчиком, если ящик передвинули на 20 метров.

Решение

Так как ящик двигался равномерно, то сила тяги грузчика равна силе трения.

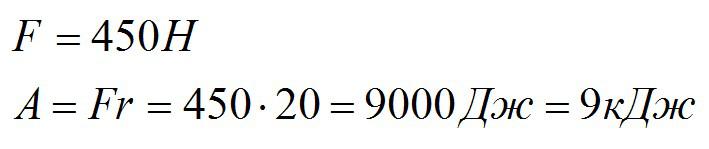
Ответ: 9кДж

Задача №2. Расчет работы силы тяжести

Условие

Гантель массой 1 кг падает с высоты 10 метров. Какую работу совершает сила тяжести?

Решение

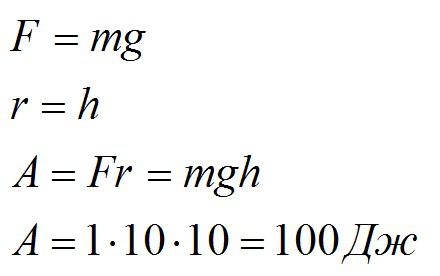
Ответ: 100 Дж.

mgh – выражение для потенциальной энергии камня в наивысшей точке.

Задача №3. Расчет механической мощности и работы

Условие

Деревенский житель поднимает ведро из колодца за 20 секунд, действуя с постоянной силой 80 Н. Глубина колодца равна h=10 м. Какую мощность развивает человек?

Решение

Сначала найдем работу, совершаемую при подъеме ведра, а затем вычислим мощность:

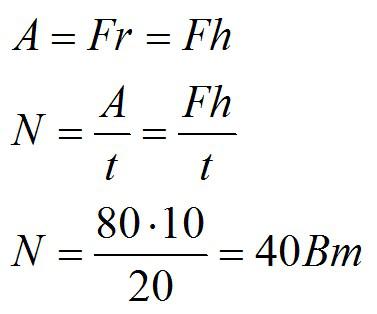
Ответ: 40 Вт.

Задача №4. Нахождение мощности. Связь мощности, силы и скорости

Условие

Мотороллер движется со скоростью 60 км/ч. Сила тяги двигателя равна 245 Н. Какую мощность развивает двигатель?

Решение

Переведем значение скорости в систему СИ и применим формулу, связывающую мощность, силу и скорость: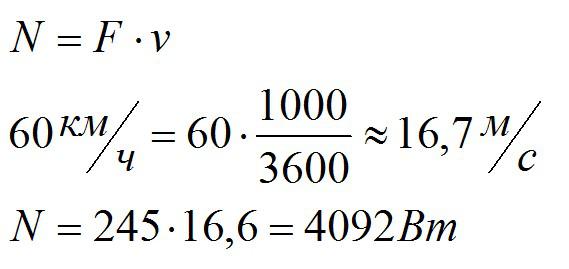

Ответ: 4092 Вт.

Задача №5. Нахождение механической работы.

Условие

Мощность двигателя трамвая равна 86 кВт. Какую работу может совершить трамвай за 2 часа непрерывной езды?

Решение

Работу можно вычислить из определения мощности:

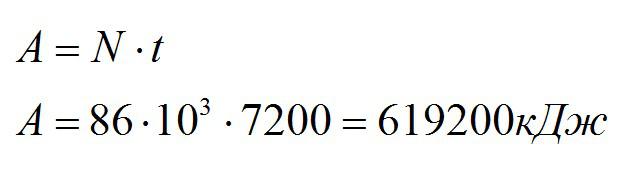
Ответ: 619200 кДж

Вопросы на механическую мощность и работу

Вопрос 1. Сила тяжести действует на автомобиль, едущий по прямой и горизонтальной дороге. Совершает ли эта сила работу?

Ответ. Не совершает. Работу в данном случае совершает сила тяги двигателя автомобиля.

Вопрос 2. Приведите примеры механической работы.

Ответ. Примеры в которых совершается механическая работа:

• лошадь тянет телегу (работу совершает сила тяги лошади);
• бурлаки на Волге тянут баржу (работу совершает мускульная сила рук бурлаков);
• спортсмен поднимает штангу (работу совершает мускульная сила рук спортсмена).

Вопрос 3. Камень падает с неба. Совершает ли сила тяжести работу?

Ответ. Да, совершает. Это работа так называемых потенциальных, или диссипативных, сил.

Вопрос 4. Какие есть внесистемные единицы измерения мощности?

Ответ. Самая распространенная внесистемная единица измерения мощности – лошадиная сила.

1 лошадиная сила равна примерно 745 Ваттам.

Вопрос 5. Какая еще величина выражается в Джоулях?

Ответ. Джоуль — единица измерения не только работы, но и энергии.

Работа и мощность в механике

Работа в механике

Для работы существует множество определений. Нас в данном случае интересует лишь одно:

Механическая работа – скалярная физическая величина, равная произведению силы, действующей на тело, на модуль перемещения, которое совершает тело под действием этой силы.

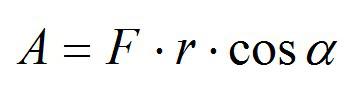
Если направления векторов силы и перемещения не совпадают, в определение добавляется третий множитель: косинус угла альфа между векторами.

Единица измерения работы: Джоуль

Мощность в механике

Мощность показывает, какая работа совершается за единицу времени.

Механическая мощность – скалярная физическая величина, равная отношению работы ко времени, за которое она совершалась.

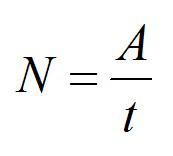
Мощность измеряется в Ваттах.

Нужна помощь в решении задач и других заданий? Обращайтесь в профессиональный студенческий сервис.

Рассмотрим несколько примеров решения задач на вычисление работы сил.

Задача 1. Гоночный автомобиль разгоняется на прямолинейной дороге под действием постоянной силы тяги, значение которой F = 5 кН (рис. 120). Определите работу этой силы при перемещении автомобиля на расстояние L =100 м.

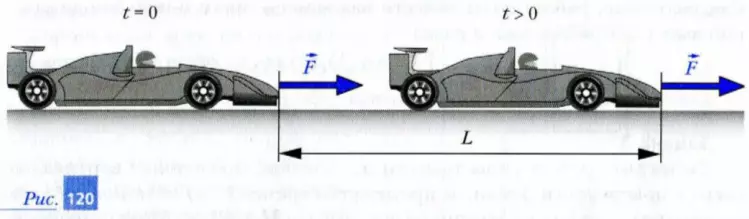
Решение. Поскольку направление силы тяги и направление движения автомобиля совпадают, то

A = F · L = 5000 Н · 100 м = 500000 Дж = 500 кДж = 0,5 МДж.

Ответ: работа силы тяги равна 0,5 МДж.

Отметим, что сила тяги, действующая на автомобиль, создается в результате действия сил трения со стороны дороги на ведущие колеса в направлении движения автомобиля. У гоночных автомобилей с реактивным двигателем она создается непосредственно этим двигателем.

Задача 2. С поверхности Земли вертикально вверх брошен камень, как показано на рис. 121. Какую работу совершит сила тяжести к тому моменту, когда камень поднимется на высоту h = 45 м? Масса камня равна m = 1 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с².

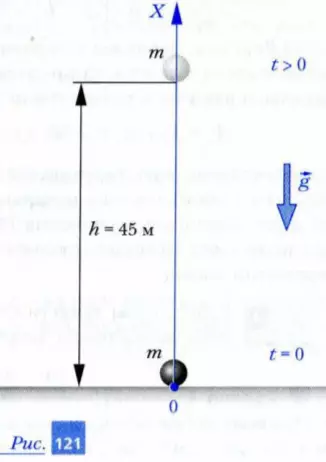
Решение. Поскольку сила тяжести и перемещение камня во время подъема направлены в противоположные стороны, работа силы тяжести будет величиной отрицательной. Как вы помните, модуль силы тяжести равен m · g. Следовательно, работа силы тяжести над камнем при его подъеме до заданной высоты отрицательна и равна

A = -(m · g) · h = -(1 кг · 10 м/с²) · 45 м = -10 Н · 45 м= -450Дж.

Ответ: работа силы тяжести равна -450 Дж.

Задача 3. Вычислите работу силы тяжести над камнем, брошенным вертикально вверх с поверхности Земли, за промежутки времени: а) от момента броска до момента подъема на максимальную высоту H = 60 м; б) от момента достижения максимальной высоты до момента, когда камень окажется на высоте h = 45 м; *в) от момента начала движения с поверхности Земли до момента, когда, опускаясь, камень второй раз за время полета окажется на высоте h = 45 м. Масса камня равна M = 1 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с².

Решение.

а) Повторяя решение предыдущей задачи, получаем:

A_a = -(M · g) · H = -(1 кг · 10 м/с²) · 60 м = -10 Н · 60 м = -600 Дж.

б) При падении камня из верхней точки направления силы тяжести и движения камня совпадают. Поэтому на этом участке свободного падения работа силы тяжести положительна и равна

A_б = M · g · (H – h) = 10 Н · 15 м = 150 Дж.

*в) Работа силы тяжести в этом случае может быть определена как сумма работ силы тяжести при подъеме камня до верхней точки и при движении камня вниз из верхней точки до высоты h, т. е.

A_в = A_а + A_б = -(M · g) · H + M · g (H – h) = -M · g · h = -450 Дж.

Сопоставим этот результат с результатом из задачи 2. Можно заметить, что в обоих случаях начальные положения камня (поверхность Земли) и его конечные положения (45 м от поверхности Земли) совпадают. При этом сила тяжести совершает одну и ту же работу. Можно сделать следующий вывод.

Работа силы тяжести определяется разностью высот, на которых находилось тело в начальный и конечный моменты времени.

Задача 4. На движущуюся кабину лифта массой M в течение некоторого промежутка времени трос действовал с постоянной силой F. Найдите работу: а) силы F; б) силы тяжести; в) суммы этих сил над кабиной лифта, если за указанный промежуток времени она поднялась вертикально вверх на высоту H.

Решение. Пусть ось Х системы отсчета, связанной с Землей, направлена вертикально вверх, как показано на рис. 122. Тогда значение силы тяжести будет отрицательным, а значение силы F и изменение координаты кабины лифта — положительными.

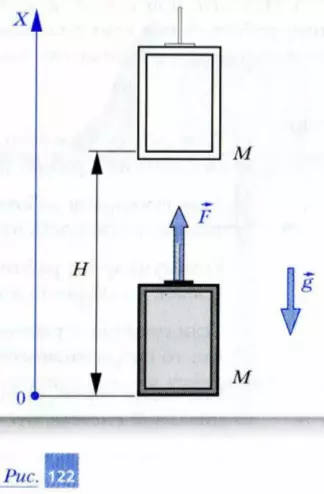
Поэтому работа силы F положительна и равна

A_а = F · H,

а работа силы тяжести — отрицательна и равна

A_б = -M · g · H.

При рассмотрении законов динамики неоднократно подчеркивалось, что при одновременном действии на точечное тело нескольких сил его ускорение будет таким же, как и при действии на это тело одной силы, равной сумме всех действующих на него сил. Заменим действующие на кабину лифта силы одной суммарной. Значение этой силы равно сумме значений силы тяжести и силы F со стороны троса: F_с = F – M · g. Поэтому работа суммарной силы над кабиной при ее перемещении на высоту H равна

A_в = F_с · H = (F – M · g) · H = F · H – M · g · H = A_а + A_б.

При одновременном действии на тело нескольких сил их суммарная работа равна сумме работ этих сил.

Таким образом, для рассмотренного случая можно сделать следующие выводы.

1. При F > M · g суммарная работа этих сил положительна. Поэтому, если на кабину не действуют другие силы, она должна разгоняться, т. е. ее ускорение должно быть положительным. Это же заключение легко сделать и непосредственно из второго закона Ньютона.

2. При F = M · g суммарная сила равна нулю. Поэтому и суммарная работа этих сил равна нулю. Кабина будет двигаться без ускорения, т. е. ее скорость не будет изменяться.

3. Наконец, при F

Итоги

Если на точечное тело одновременно действуют несколько сил, их суммарная работа равна сумме работ этих сил.

Если суммарная работа всех действующих на тело сил положительна, то скорость этого тела увеличивается.

Если суммарная работа всех действующих на тело сил отрицательна, то скорость этого тела уменьшается.

Если суммарная работа всех действующих на тело сил равна нулю, то скорость этого тела остается неизменной.

Сказанное верно, если движение тела рассматривается в инерциальной системе отсчета.

Упражнения

1. Найдите работу силы трения, тормозящей грузовой автомобиль на отрезке пути L = 40 м, если модуль силы равен 25 кН.

2. Определите работу силы тяжести над камнем массой m = 5 кг при его падении с высоты h = 80 м на Землю.

3. Найдите работу пороховых газов над пулей к моменту ее вылета из ствола снайперской винтовки длиной L = 1 м. Считайте, что сила действия газов постоянна и ее модуль равен 5 кН. Винтовку во время выстрела удерживает неподвижной стоящий на Земле человек.

4. Определите работу силы тяжести над свободно падающим камнем массой m = 1 кг за промежуток времени, в течение которого скорость камня изменяется от v₀ = 0 до v_к = 30 м/с.

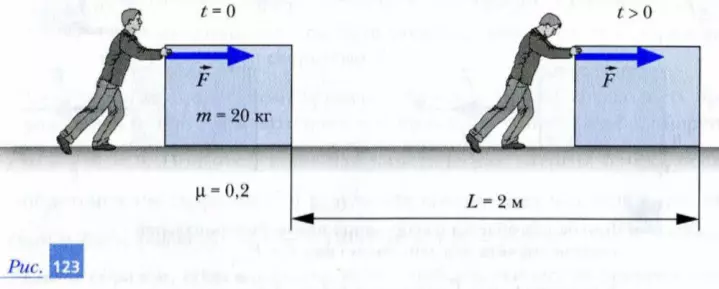
5. Мальчик действует на движущийся по горизонтальному полу ящик массой m = 20 кг силой, направленной в сторону движения ящика (рис. 123) и равной по модулю 50 Н. Коэффициент трения ящика о пол μ = 0,2. При этом за некоторое время ящик передвинулся на расстояние L = 2 м. Какую работу за это время совершат: а) мальчик; б) сила тяжести; в) сила трения; г) сумма всех сил, действующих на ящик? Увеличится или уменьшится скорость ящика за это время?

Вы уже знаете, что работа электрического тока измеряется в джоулях. Но на практике часто используются другие величины, о которых вы и узнаете на данном уроке.

Почему неудобно выражать работу тока в джоулях на практике?

Начнем с того, что в паспортах электроприборов обычно указывают мощность тока в них. Как можно выразить работу тока через мощность и время?

Зная мощность потребителя электроэнергии, можно рассчитать и работу тока, совершенную за определенное время: $A = Pt$.

Рассмотрим единицы измерения величин в этой формуле. Мощность у нас измеряется в ваттах, время — в секундах, а работа — в джоулях.

$1 space Вт = 1 frac{Дж}{с}$,
$1 space Дж = 1 space Вт cdot с$.

Обратите внимание на то, что время выражается в секундах. Но обычно в потребителе электроэнергии ток совершает работу более продолжительное время.

Некоторые приборы мы используем часами, а некоторые — круглосуточно. Например, тот же холодильник. Расчет же электроэнергии по счетчику производится раз в месяц.

Логично, что очень неудобно переводить такие большие промежутки времени в секунды каждый раз при расчете работы электрического тока. Поэтому и используются другие единицы измерения.

Внесистемные единицы измерения работы электрического тока

По вышеуказанным причинам при расчете работы электрического тока время намного удобнее выражать в часах. Сама же работа часто выражается в следующих единицах: $ватт cdot час$ ($Вт cdot ч$), $гектоватт cdot час$ ($гВт cdot ч$), $киловатт cdot час$ ($кВт cdot ч$).

$1 space Вт cdot ч = 3600 space Дж$,
$1 space гВт cdot ч = 100 space Вт cdot ч = 360 space 000 space Дж$,
$1 space кВт cdot ч = 1000 space Вт cdot ч = 3 space 600 space 000 space Дж$.

Снятие показаний счетчика и расчет потребляемой энергии

Каждый месяц люди платят за «электричество». То есть за использованную электроэнергию в течение месяца, которая определяется совершенной работой электрического тока.

Сумма платежа рассчитывается исходя из показаний счетчика и действующего тарифа на электроэнергию.

В начале нового месяца фиксируются показания счетчика (рисунок 1, а). В конце месяца эти показания фиксируются еще раз (рисунок 1, б). Обратите внимание, что обычно последнее число, показанное на счетчике, — это десятые доли $кВт cdot ч$. Эта последняя цифра может быть выделена цветной рамкой, или перед ней будет стоять точка.

Разница между этими показаниями — это и есть израсходованная за месяц электроэнергия. Она же эквивалентна работе электрического тока, совершенной во всех электроприборах за месяц. Рассчитаем ее:
$A = 11706.6 space кВт cdot ч space — space 10982.6 space кВт cdot ч = 724 space кВт cdot ч$.

Действующий тариф (стоимость $1 space кВт cdot ч$) указывается в квитанциях на оплату. Он может различаться в зависимости от страны или ее региона.

Возьмем тариф, равный $3 frac{р.}{кВт cdot ч}$ (3 рубля за $1 space кВт cdot ч$).

Чтобы рассчитать стоимость потребленной энергии, нужно тариф умножить на количество (численное значение) этой энергии:
$Стоимость = Тариф cdot A$.

В нашем случае получается:
$Стоимость = 3 frac{р.}{кВт cdot ч} cdot 724 space кВт cdot ч = 2172 space р.$

Пример задачи

Электрическая лампа рассчитана на ток мощностью $100 space Вт$. Ежедневно лампа горит в течение $6 space ч$. Найдите работу тока за один месяц (30 дней) и стоимость израсходованной энергии, считая, что тариф составляет 300 копеек за $1 space кВт cdot ч$.

Дано:
$P = 100 space Вт$
$t = 6 space ч cdot 30 = 180 space ч$
$Тариф = 300 frac{к.}{кВт cdot ч}$

$A — ?$
$Стоимость — ?$

Решение:

Работу электрического тока рассчитаем по формуле: $A = Pt$.
$A = 100 space Вт cdot 180 space ч = 18 space 000 Вт cdot ч = 18 space кВт cdot ч$.

Рассчитаем стоимость. Для этого умножим тариф на работу, совершаемую электрическим током:
$Стоимость = 300 frac{к.}{кВт cdot ч} cdot 18 space кВт cdot ч = 540 space к. = 54 space р.$

Ответ: $A = 18 space кВт cdot ч$, $стоимость = 54 space рубля$.

Упражнения

Дано:
$P = 0.6 space кВт$
$t = 1.5 space ч$

$A — ?$

Показать решение и ответ

Скрыть

Дано:
$P_1 = P_2 = 60 space Вт$
$P_3 = P_4 = 40 space Вт$
$t = 3 space ч cdot 30 = 90 space ч$
$Тариф = 3.3 frac{р.}{кВт cdot ч}$

$Стоимость — ?$

Показать решение и ответ

Скрыть

Дано:
$U = 220 space В$
$P_1 = P_2 = P_3 = 40 space Вт$
$t_1 = t_2 = t_3 = 4 space ч cdot 30 = 120 space ч$
$P_4 = 800 space Вт$
$t_4 = 1 space ч cdot 30 = 30 space ч$
$P_5 = 1000 space Вт$
$t_5 = 0.5 space ч cdot 30 = 15 space ч$
$P_6 = 600 space Вт$
$t_6 = 0.5 space ч cdot 4 = 2 space ч$
$Тариф = 3.3 frac{р.}{кВт cdot ч}$

$Стоимость — ?$

Показать решение и ответ

Скрыть