При прохождении тока в цепи электрическое поле совершает работу по перемещению заряда. В этом случае работу электрического поля называют работой электрического тока.
При прохождении заряда (q) по участку цепи электрическое поле будет совершать работу: (A=qcdot U), где (U) — напряжение электрического поля, (A) — работа, совершаемая силами электрического поля по перемещению заряда (q) из одной точки в другую.
Для выражения любой из этих величин можно использовать приведённый ниже рисунок.
Рис. (1). Зависимость между работой, напряжением и зарядом
Количество заряда, прошедшее по участку цепи, пропорционально силе тока и времени прохождения заряда:
q=I⋅t
.
Работа электрического тока на участке цепи пропорциональна напряжению на её концах и количеству заряда, проходящего по этому участку:
A=U⋅q
.
Работа электрического тока на участке цепи пропорциональна силе тока, времени прохождения заряда и напряжению на концах участка цепи:
A=U⋅I⋅t
.
Чтобы выразить любую из величин из данной формулы, можно воспользоваться рисунком.
Рис. (2). Зависимость между работой, силой тока и временем прохождения заряда
Единицы измерения величин:
работа электрического тока ([A]=1) Дж;
напряжение на участке цепи ([U]=1) В;
сила тока, проходящего по участку ([I]=1) А;
время прохождения заряда (тока) ([t]=1) с.
Для измерения работы электрического тока нужны вольтметр, амперметр и часы. Например, для определения работы, которую совершает электрический ток, проходя по спирали лампы накаливания, необходимо собрать цепь, изображённую на рисунке. Вольтметром измеряется напряжение на лампе, амперметром — сила тока в ней. А при помощи часов (секундомера) засекается время горения лампы.
Рис. (3). Схема и часы для измерения
Например:
I = 1,2 АU = 5 Вt = 1,5 мин = 90 сА = U⋅I⋅t = 5⋅1,2⋅90 = 540 Дж
Обрати внимание!
Работа чаще всего выражается в килоджоулях или мегаджоулях.
(1) кДж = 1000 Дж или (1) Дж = (0,001) кДж;
(1) МДж = 1000000 Дж или (1) Дж = (0,000001) МДж.
Для потребителей электрической энергии существуют приборы, позволяющие в пределах ошибки измерения получать числовые данные о ее расходе в единицу времени.
Рис. (4). Электросчетчик
Механическая мощность численно равна работе, совершённой телом в единицу времени:
N = Аt
. Чтобы найти мощность электрического тока, надо поступить точно также, т.е. работу тока,
A=U⋅I⋅t
, разделить на время.
Мощность электрического тока обозначают буквой (Р):
. Таким образом:
Мощность электрического тока равна произведению напряжения на силу тока:
P=U⋅I
.
Из этой формулы можно определить и другие физические величины.
Для удобства можно использовать приведённый ниже рисунок.
Рис. (5). Зависимость между мощностью, напряжением и силой тока
За единицу мощности принят ватт: (1) Вт = (1) Дж/с.
Из формулы
P=U⋅I
следует, что
(1) ватт = (1) вольт ∙ (1) ампер, или (1) Вт = (1) В ∙ А.
Обрати внимание!
Используют также единицы мощности, кратные ватту: гектоватт (гВт), киловатт (кВт), мегаватт (МВт).
(1) гВт = (100) Вт или (1) Вт = (0,01) гВт;
(1) кВт = (1000) Вт или (1) Вт = (0,001) кВт;
(1) МВт = (1 000 000) Вт или (1) Вт = (0,000001) МВт.
Пример:
Измерим силу тока в цепи с помощью амперметра, а напряжение на участке — с помощью вольтметра.
Рис. (6). Схема
Так как мощность тока прямо пропорциональна напряжению и силе тока, протекающего через лампочку, то перемножим их значения:
.
Ваттметры измеряют мощность электрического тока, протекающего через прибор. По своему назначению и техническим характеристикам ваттметры разнообразны.
В зависимости от сферы применения у них различаются пределы измерения.
|
Аналоговый ваттметр |
Аналоговый ваттметр |
Аналоговый ваттметр |
Цифровой ваттметр |
|
|
|
|
|
Рис. (7). Приборы для измерения
Подключим к цепи по очереди две лампочки накаливания, сначала одну, затем другую и измерим силу тока в каждой из них. Она будет разной.
Рис. (8). Лампы различной мощности в цепи
Сила тока в лампочке мощностью (25) ватт будет составлять (0,1) А. Лампочка мощностью (100) ватт потребляет ток в четыре раза больше — (0,4) А. Напряжение в этом эксперименте неизменно и равно (220) В. Легко можно заметить, что лампочка в (100) ватт светится гораздо ярче, чем (25)-ваттовая лампочка. Это происходит оттого, что её мощность больше. Лампочка, мощность которой в (4) раза больше, потребляет в (4) раза больше тока. Значит:
Обрати внимание!
Мощность прямо пропорциональна силе тока.
Что произойдёт, если одну и ту же лампочку подсоединить к источникам различного напряжения? В данном случае используется напряжение (110) В и (220) В.
Рис. (8). Лампа, подключенная к источнику тока с различным напряжением
Можно заметить, что при большем напряжении лампочка светится ярче, значит, в этом случае её мощность будет больше. Следовательно:
Обрати внимание!
Мощность зависит от напряжения.
Рассчитаем мощность лампочки в каждом случае:
| I=0,2АU=110ВP=U⋅I=110⋅0,2=22Вт | I=0,4АU=220ВP=U⋅I=220⋅0,4=88Вт. |
Можно сделать вывод о том, что при увеличении напряжения в (2) раза мощность увеличивается в (4) раза.
Не следует путать эту мощность с номинальной мощностью лампы (мощность, на которую рассчитана лампа). Номинальная мощность лампы (а соответственно, ток через нить накала и её расчётное сопротивление) указывается только для номинального напряжения лампы (указано на баллоне, цоколе или упаковке).
Рис. (9). Маркировка
В таблице дана мощность, потребляемая различными приборами и устройствами:
Таблица (1). Мощность различных приборов
|
Название |
Рисунок |
Мощность |
| Калькулятор |
|
(0,001) Вт |
| Лампы дневного света |
|
(15 — 80) Вт |
| Лампы накаливания |
|
(25 — 5000) Вт |
| Компьютер |
|
(200 — 450) Вт |
| Электрический чайник |
|
(650 — 3100) Вт |
| Пылесос |
|
(1500 — 3000) Вт |
| Стиральная машина |
|
(2000 — 4000) Вт |
| Трамвай |
|
(150 000 — 240000) Вт |
Источники:
Рис. 1. Зависимость между работой, напряжением и зарядом. © ЯКласс.
Рис. 3. Схема и часы для измерения. © ЯКласс.
Рис. 5. Зависимость между мощностью, напряжением и силой тока. © ЯКласс.
Рис. 6. Схема. © ЯКласс.
Таблица 1. Мощность различных приборов. Компьютер. Указание авторства не требуется, 2021-08-14, Pixabay License, https://pixabay.com/ru/photos/яблоко-стул-компьютер-1834328/.
Роман LT*****
Ученик
(170),
на голосовании
10 лет назад
Голосование за лучший ответ
Scarabey
Искусственный Интеллект
(110810)
10 лет назад
работа (или энергия) равна мощность умножить на время. согласно системе единиц си Вт*ч
Иван Дулин
Профи
(727)
10 лет назад
Сначала надо время перевести в секунды: t=10х60=600 секунд
A=Pt=700Втх600сек=420 000 Дж=420 КДж
Ответ: 420 килоджоулей
Похожие вопросы
В этой статье я объясню, что такое работа электрического тока, какие единицы измерения для нее используются и какие важные формулы необходимо знать.
Что такое работа электрического тока?
Давайте рассмотрим обычную батарейку. По сути, батарейка преобразует химическую энергию в электрическую энергию электронов. Если теперь подключить её в электрическую цепь, то электроны могут совершать работу, используя свою электрическую энергию, например, зажигать лампочку.
Если вы хотите узнать, сколько электрической энергии было преобразовано в другой вид энергии, то вам нужно рассчитать работу электрического тока.
Определение понятия «электрическая работа» и её единицы измерения.
Работа электрического тока [A] позволяет определить, сколько электрической энергии было или может быть преобразовано в другие виды энергии.
Когда вы рассчитываете работу электрического тока, вы знаете, сколько электрической энергии было преобразовано в другие формы энергии. А уже какие другие формы энергии могут быть — это зависит от ситуации (несколько примеров в списке ниже):
- Ваш тостер преобразует электрическую энергию в тепловую;
- Когда вы включаете лампочку, электрическая энергия преобразуется в световую;
- Электродвигатель преобразует электрическую энергию в механическую.
Единицей измерения работы электрического тока в СИ является Джоуль [Дж], также часто используется в качестве единицы измерения Ватт-секунда [Вт·с]. Один джоуль всегда соответствует одной ватт-секунде. То есть 1 Дж = 1 Вт·с .
Другой важной единицей измерения является киловатт-час [кВт·ч]. Один киловатт-час равен 3 600 000 ватт-секунд или джоулей.
1 кВт·ч = 1 * 103 Вт·ч = 1 * 103 * 3600 Вт·с = 3,6 * 106 Вт·с = 3,6 * 106 Дж.
Полезный факт: а вы знали, что именно электрическую работу измеряют электросчётчики установленные в наших домах и квартирах! Электросчётчики измеряют работу электрического тока в кВт·ч.
По какой формуле вычисляется работа электрического тока?
Если вы на каком-либо участке электрической цепи под действием электрического напряжения U привели в движение заряд q, то вы можете рассчитать электрическую работу A как напряжение U, приложенное на концах этого участка цепи, умноженное на электрический заряд q, который прошёл по нему, то есть: A = U * q .
Зная, что электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения: q = I * t. Тогда электрическую работу A [Дж] можно определить как напряжение U [В], умноженное на силу тока I [А] и умноженное на время t [с], то есть: A = U * I * q .
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Чуть ниже в статье мы разберем два практических примера, которые покажут применение данных формул. Однако перед этим мы кратко рассмотрим еще несколько важных формул.
Примечание: Вы обязательно должны запомнить первые две формулы. Следующие ниже формулы менее важны, но могут быть полезны для вас при решении тех или иных задач.
Другие формулы для определения работы электрического тока.
Закон Ома для участка цепи связывает напряжение U и ток I. Это позволяет нам рассчитать электрическую работу A другим способом.
Итак, согласно закона Ома, U = I * R или I = U / R , где R — это электрическое сопротивление.
Тогда вы можете подставить эти формулы в A = U * I * t. В итоге получатся другие формулы для нахождения работы электрического тока:
- A = I2 * R * t ;
- A = (U2 * t ) / R .
Примеры задач
Пример 1.
У вас есть батарея, подающая постоянное напряжение 12 В и ток 2,3 А. Вы используете эту батарею для освещения лампочки в течение 1 часа. Теперь вы хотите знать, какая работа электрического тока была произведена.
Мы знаем формулу для определения работы электрического тока: A = U * I * q, тогда получаем:
A = 12 В * 2,3 А * 1 ч = 27,6 Вт·ч .
Чтобы дать вам представление о единицах измерения, давайте переведем результат в ватт-секунды и джоули
27,6 Вт·ч = 27,6 * 3600 Вт·с = 99360 Вт·с = 99360 Дж.
Пример 2.
У вас есть батарейка с напряжением 5 В. Эта батарейка совершает электрическую работу в 10*10-2 Вт·с. Нам нужно рассчитать рассчитать количество электрического заряда q, перемещенного между полюсами батареи.
Мы знаем формулу для определения работы электрического тока: A = U * q, тогда q = A / U. Подставляя значения в формулу получаем:
q = 10*10-2 Вт·с / 5 В = 0,02 Кл.
Чтобы подсчитать работу электрического тока, вспомним определение понятия напряжения: U=А/q
Следовательно, работа электрического тока равна:
A=qU
Электрический заряд можно выразить через силу тока и его время протекания q=It:
А = IUt
Итак, работа электрического тока равна произведению силы тока на напряжение и на время протекания тока по цепи.
Работа электрического тока выражается в джоулях (Дж). В качестве внесистемной единицы принята работа тока силой 1 А в течение 1 ч на участке цепи с напряжением 1 В. Эту единицу работы назвали ватт-час (1 Вт-ч): 1 Вт-ч = 3600 Дж = 3,6 кДж. На практике используют более крупные, кратные ей единицы:
1 гВт-ч= 102 Вт-ч = 3,6·105Дж,
1 кВт-ч= 103 Вт-ч = 3,6·106Дж,
1 МВт-ч = 106 Вт-ч = 3,6·109Дж.
Из курса физики VII класса вы знаете, что мощность равна отношению совершенной работы ко времени, в течение которого эта работа была совершена. Мощность в механике принято обозначать буквой N, в электротехнике — буквой Р. Следовательно, мощность равна:
Р = А/t.
Пользуясь этой формулой, найдем мощность электрического тока. Так как работа тока определяется формулой А = IUt, то мощность электрического тока равна:
Р = IU.
За единицу мощности ватт (Вт) принята мощность тока силой 1 А на участке с напряжением 1 В. Следовательно, 1 Вт = 1 А·1 В.
Ватт сравнительно небольшая мощность, на практике используют более крупные единицы, кратные ватту: 1 гВт (гектоватт) = 102 Вт, 1 кВт (киловатт) = 103 Вт, 1 МВт (мегаватт) = 106 Вт, 1 ГВт (гигаватт) = 109 Вт.
Господа, так уж сложилось на этом свете, такова эгоистичная человеческая натура, что если кто-то или что-то не может сделать для тебя какую-то полезность, как-то поработать, оказать какую-то услугу, чем-то помочь, то обычно это кто-то или что-то являются нафиг никому не нужными. Это грустно, наверное, должно быть не совсем так, но опыт указывает именно на такое положение дел…
Что же касается электрического тока – то с ним все отлично. Он с удовольствием рад поработать и вообще всячески готов помогать людям, поэтому он никогда не сталкивается с тем, что он кому-то не нужен. Вы встречали людей, которые бы говорили, что им не нужно электричество? Лично я нет.
Это все замечательно, но мы здесь собрались отнюдь не для праздных философских бесед. Наша задача выяснить, чем именно ток может быть полезен и как количественно оценить его пользу. Давайте вспомним статью про напряжение. Что мы там говорили? Кажется, то, что напряжение по сути своей это отношение работы, которую надо совершить по переносу заряда с одной клеммы на другую к этому самому заряду. А давайте-ка выразим работу! Что в итоге получится?
То есть, если у нас на концах проводника напряжение U и через проводник протек заряд Δq, то, очевидно, поле совершило работу А, равную произведению этого заряда на напряжение. Обращаю внимание, господа, мы пока что ничего не выводили! Это все исключительно из определения напряжения. При создании напряжения надо поработать и запасти энергию, зато потом она может высвободиться и поработать уже сама.
Отлично, скажет читатель! Опять мне предлагают считать какой-то В статье про силу тока предлагали, теперь здесь! И как я его посчитаю?! Залезу что ли в проводник и ручками переберу заряды?!
Господа, спокойно! Не зря вспомнилась статья про силу тока. Чему, кстати, она равна? Как вы, надеюсь, еще не забыли, она равна
А раз пошло такое дело, давайте выразим отсюда Δq и подставим это в выражении для работы. Что получим?
Видите, как все отлично вышло! Заряды ушли и мы можем легко посчитать работу тока: мы же помним, что для Δt есть секундомер в нашем айфоне!
То есть что у нас получается? Мы совершенно спокойно можем взять вольтметр, амперметр и айфон с секундомером. Далее, включить это все (кроме айфона, конечно 
) в цепь с нагрузкой. Померить напряжение, ток и засечь время. И мы сможем точно узнать, какую ток совершил работу.
Допустим, мы намерили, что в цепи протекает ток I=2 А при напряжении на нагрузке U=12 В. Как найти работу тока в течении 1 минуты? Считаем
Но на этом преобразования не закончены. Я надеюсь, вы не забыли закон Ома? Так вот, нам никто не мешает выразить из него напряжение через ток и сопротивление:
Теперь подставляем это в формулку для работы. Получаем
Таким образом у нас появилась еще одна формула, с помощью которой можно высчитать работу, совершаемую током. То есть, оказывается, достаточно замерить в цепи ток и, если мы знаем сопротивление, то мы найдем и работу тока. В принципе, это логично. Ведь ток, напряжение и сопротивление как раз-таки сязаны между собой через уже известный вам закон Ома. Поэтому абсолютно аналогично можно выразить из закона Ома силу тока и вставить и подставить ее в выражение для работы. Получим
То есть, зная напряжение источника и сопротивление нагрузк, можно высчитать работу тока. Замечу, что все эти соотношения получились всего-навсего из определений что такое ток, что такое напряжение и из закона Ома.
Господа, еще с курса механики вам было известно, что часто интерес представляет даже не работа, а мощность – количество работы в единицу времени. Ну, то есть что бы найти мощность, надо работу разделить на время. Получаем в итоге
Господа, обратите свое пристальное внимание на эти формулки и запомните их очень хорошо. Они правда очень нужны и используются весьма часто, так же, как и закон Ома. Мощность вещь нужная. И ее не так сложно измерить. Например это можно сделать, воспользовавшись схемой, изображенной на рисунке 1.
Рисунок 1 – Измерение мощности
Теперь коснемся чуть подробнее вопросов размерности. В чем там мощность в механике измерялась? Кажется, в ваттах? Так и тут. Размерности сохранились. Мощность электрического тока измеряется все в тех же ваттах. Один ватт здесь – это когда сила тока равна 1 амперу при напряжении 1 вольт.
Еще кроме ватта есть такая интересная величина, как лошадиная сила. На первый взгляд может показаться странным, что это величина мощности, а не… хотя бы уж силы. Я тоже в детстве недоумевал, что это такое и при чем тут лошади? Оказалось, они были непосредственно в этом замешаны. Как гласит легенда, Джеймс Уатт, который является изобретателем паровой машины, хотел наглядно показать, насколько его машины круты. Понятное дело, что если бы он просто написал там что-то про килоуатты киловатты его никто бы в то время не понял. Нужен был наглядный пример, доступный для понимания людям без высшего образования. И вот, если его паровая машина могла совершать ту же самую работу за то же самое время, что и лошадь, то, выходит, что она развивала мощность в одну лошадиную силу. Это было всем более-менее наглядно понятно. Конечно, способ очень неточный. Конечно, один молодой жеребец разовьет гораздо большую мощность, чем старая кобыла. Но термин устоялся и даже численно связан с ваттами:
В наше время этот термин, как ни странно, все также используется в автомобильной индустрии для показания мощности двигателя. Если вы кому-то скажете, что ваш двигатель имеет мощность в 72 кВт вас вряд ли поймут, зато если скажете, что он в 98 л.с., всем все сразу станет ясно. Вот такие вот отпечатки накладывает история.
А как с энергией или работой? Помнится, они в джоулях в механике измерялась? Здесь все чуть по-другому. Нет-нет, джоули все так же имеют право на жизнь. Просто исторически сложилось (по крайней мере на практике), что работу электричества измеряют в кВт⋅ч. Именно эти цифры вы можете видеть на своем электрическом счетчике в квартире. Именно за них вы платите деньги каждый месяц. Заметьте, господа, именно кВт умножить на час. Накаких кВт/ч. Киловатты на часы мы не делим, ни в коем случае! Как же связаны между собой и джоуль? Это легко вывести:
Как видим, одному киловатту соответствует весьма не мало джоулей!
Теперь давайте рассмотрим, а как мы можем использовать эту энергию электричества? Самыми разными способами! Она может вращать двигатели. Она может трансформироваться в свет. Она может способствовать протеканию химических реакций. Способов куча! Но пока что мы рассмотрим один из них – нагрев, то есть трансформация электрической энергии в тепловую.
Если у нас в цепи с постоянным током нет моторчиков, нет светодиодов и лампочек, нет ванночек с химическими реактивами, а есть только обычный резистор (проводник с некоторым сопротивлением) – ток будет просто нагревать его. Полагаю, понимание физики процесса нагрева проводника не должно вызвать вопросов. Тут все просто. Под действием электрического поля электроны в проводнике ускоряются. Они начинают чаще и сильнее соударяться с узлами кристаллической решетки проводника и вообще с неоднородностями внутри него. При ударах они будут отдавать часть своей энергии узлам решетки, из-за чего те начнут колебаться чуточку быстрее. А как мы все знаем – чем быстрее колеблются элементы структуры вещества, тем больше его температура. То есть происходит нагрев проводника. Вы спросите – а как посчитать это количество теплоты? Как ни странно, формулу мы уже писали сегодня:
Почему это так должно быть очевидно. Если работа тока расходуется только на нагрев проводника, то вся эта энергия и пойдет в тепло по закону сохранения энергии. Но есть один тонкий момент, связанный с терминологией. Если вы запишите это выражение вот так
то это будет называться законом Джоуля-Ленца в честь двух весьма уважаемых господ.
Да, другие формулы ничуть от этой не отличаются и по ним все так же можно считать количество теплоты, но именно вот эта формула получила такое название.
А теперь, господа, для закрепления пройденного материала, я бы хотел рассмотреть одну задачку, которая может реально иметь место в жизни. Звучит она так.
Определите, на сколько градусов перегреется проволока из нихрома, имеющая площадь поперечного сечения 1 квадратный миллиметр и длиной в 30 метров, при протекании через нее кратковременного тока силой в 50 А и длительностью 1 секунда.
Такая задача вполне может иметь место на практике. Байку про то, как мне пришлось решать нечто подобное для мегамощной установки я рассказывал в статье про сопротивление. Кто не читал, можете ознакомиться.
Давайте порассуждаем, как нам решать эту задачу. У нас есть все габариты нашей проволоки и мы знаем материал. Значит, мы можем найти ее сопротивление.
Далее, мы знаем сопротивление, силу тока и время – по закону Джоуля-Ленца мы легко считаем энергию.
Теперь остается вспомнить формулу, которая была в каком-то там курсе, связанном с тепловыми процессами. Ну, она связывала между собой энергию, теплоемкость, массу и перегрев. Помните?
Теплоемкость нихрома нагуглим. Массу можно найти, зная плотность нихрома и объем проволоки. И остается одна величина – перегрев ΔT. Его и высчитываем. План ясен – теперь вперед, погнали считать!
По формуле из статьи про сопротивление находим сопротивление нихромовой проволоки:
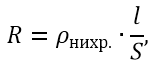
где l – длина проволоки, ро – плотность нихрома, S – площадь поперечного сечения проволоки.
Теперь воспользуемся нашим законом Джоуля-Ленца. Получаем, что на нашей бедной нихромовой проволоке рассеется вот столько энергии:
где I – заданный в задаче ток, R – посчитанное в предыдущем пункте сопротивление, дельта t – заданное в задаче время протекания тока.
Идем дальше, найдем объем проволоки. Проволока имеет форму цилиндра. Как известно из геометрии, для нахождения объема цилиндра надо умножить площадь его основания на высоту. Имеем
Ну и теперь, зная объем проволоки и ее плотность, которую мы легко нагуглим, мы находим массу нашей нихромовой проволоки
Теперь осталось только выразить из формулы, написанной в начале задачи перегрев и собрать все величины воедино. Получаем
Такой общий вид формулы для расчета перегрева проволоки, если нам известен ее материал, площадь сечения, сила тока и длительность его протекания. Обратите внимание, господа, что у нас сократилась длина проволоки. Получается, перегрев от нее не зависит.
Проанализируем эту формулу чуть глубже. Мы видим, что перегрев прямо пропорционален времени протекания тока. То есть, если подходить формально, получается, что даже при самых маленьких токах при очень большом времени протекания будет бесконечно большой перегрев. Разумеется, мы знаем из практики, что это не так. Проволока будет отдавать тепло в окружающее пространство и охлаждаться таким образом. Будут идти два процесса: первый подводит к проволоке энергию (протекающий ток) и второй отводит ее от проволоки (теплообмен с окружающей средой). В итоге наступит некоторое термодинамическое равновесие и проволока приобретет некоторую постоянную температуру. Какую именно – это весьма сложный вопрос и так просто на него не ответить, потому что это зависит от множества факторов. Когда же верна наша формула? И можно ли ей вообще пользоваться? Пользоваться можно, но осторожно 
. Следует понимать, что этот перегрев считался без обмена температурой с окружающей средой. То есть по этой формуле можно считать для случая весьма коротких импульсов тока для весьма грубой оценки пикового перегрева материала, когда процесс термодинамического равновесия не успевает наступить. Тем не менее с импользованием этой формулы можно давать оценку, выживет ли наш материал при таких коротких импульсах тока или лучше взять что-то понадежнее. Ну и в заключение, имея в виду все вышенаписанное, подставим конкретные цифры и посчитаем перегрев. Само собой, подставлять все будем в кошерной системе СИ. Вообще рекомендую всегда все расчеты вести только в ней, путаницы будет в разы меньше. Получим:
Таким образом, наша проволока перегреется на 803 градуса. Температура плавления нихрома составляет порядка 1300 градусов, то есть наша проволока выдержит. На деле температура будет скорее всего гораздо меньше из-за неизбежного процесса теплообмена с окружающей средой. То есть данную проволоку можно смело использовать для такой нагрузки.
Итак, господа, статья получилась не маленькая и включала в себя довольно много изученного ранее материала. Математики тут тоже получилось порядком. Надеюсь, кому-то эти сведения будут полезными . За сим прощаюсь, всем удачи и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
