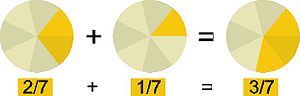
Данная статья посвящена изучению темы “Рациональные числа”. Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет.
Рациональные числа. Определения
Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой.
Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.
Рациональные числа – числа, которые можно представить в виде положительной обыкновенной дроби ab, отрицательной обыкновенной дроби -ab или числа ноль.
Таким образом, можно оставить ряд свойств рациональных чисел:
- Любое натуральное число является рациональным числом. Очевидно, каждое натуральное число n можно представить в виде дроби 1n.
- Любое целое число, включая число 0, является рациональным числом. Действительно, любое целое положительное и целое отрицательное число легко представляется в виде соответственно положительной или отрицательной обыкновенной дроби. Например, 15=151, -352=-3521.
- Любая положительная или отрицательная обыкновенная дробь ab является рациональным числом. Это следует напрямую из данного выше определения.
- Любое смешанное число является рациональным. Действительно, ведь смешанное число можно представить в виде обыкновенной неправильной дроби.
- Любую конечную или периодическую десятичную дробь можно представить в виде обыкновенной дроби. Поэтому, каждая периодическая или конечная десятичная дробь является рациональным числом.
- Бесконечные и непериодическое десятичные дроби не являются рациональными числами. Их невозможно представить в форме обыкновенных дробей.
Приведем примеры рациональных чисел. Числа 5, 105, 358, 1100055 являются натуральными, положительными и целыми. Сдедовательно, это рациональные числа. Числа -2, -358, -936 представляют собой целые отрицательные числа, и они также рациональны в соответствии с определением. Обыкновенные дроби 35, 87, -358 также являются примерами рациональных чисел.
Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.
Рациональные числа – это такие числа, которые можно представить в виде дроби ±zn, где z – целое число, n – натуральное число.
Можно показать, что данное определение равносильно предыдущему определению рациональных чисел. Чтобы сделать это, вспомним, что черта дроби равносильна знаку деления. С учетом правил и свойств деления целых чисел, можно записать следующие справедливые неравенства:
0n=0÷n=0; -mn=(-m)÷n=-mn.
Таким образом, можно записать:
zn=zn, при z>00, при z=0-zn, при z<0
Собственно, данная запись и является доказательством. Приведем примеры рациональных чисел, основываясь на втором определении. Рассмотрим числа -3, 0, 5, -755, 0,0125 и -135. Все эти числа являются рациональными, так как их можно записать в виде дроби с целым числителем и натуральным знаменателем: -31, 01,-755, 12510000, 85.
Приведем еще одну эквивалентную форму определения рациональных чисел.
Рациональное число – это такое число, которое можно записать в виде конечной или бесконечной периодической десятичной дроби.
Данное определение напрямую следует из самого первого определения этого пункта.
Подведем итог и сформулируем резюме по данному пункту:
- Положительные и отрицательные дробные и целые числа составляют множество рациональных чисел.
- Каждое рациональное число можно представить в виде обыкновенной дроби, числитель которой является целым числом, а знаменатель – натуральным числом.
- Каждое рациональное число можно также представить в виде десятичной дроби: конечной или бесконечной периодической.
Какое из чисел является рациональным?
Как мы уже выяснили, любое натуральное число, целое число, правильная и неправильная обыкновенная дробь, периодическая и конечная десятичная дробь являются рациональными числами. Вооружившись этими знаниями можно без труда определить, является ли какое-то число рациональным.
Однако на практике часто приходится иметь дело не с числами, а с числовыми выражениями, которые содержат корни, степени и логарифмы. В некоторых случаях ответ на вопрос “рационально ли число?” является далеко не очевидным. Рассмотрим методы ответа на этот вопрос.
Если число задано в виде выражения, содержащего только рациональные числа и арифметические действия между ними, то результат выражения – рациональное число.
Например, значение выражения 2·318-0,250,(3) является рациональным числом и равно 18.
Таким образом, упрощение сложного числового выражения позволяет определить, рационально ли заданное им число.
Теперь разберемся со знаком корня.
Оказывается, что число mn, заданное в видя корня степени n от числа m рационально лишь тогда, когда m является n-ой степенью какого-то натурального числа.
Обратимся к примеру. Число 2 не является рациональным. Тогда как 9, 81 – рациональные числа. 9 и 81 – полные квадраты чисел 3 и 9 соответственно. Числа 199, 28, 151 не являются рациональными числами, так как числа под знаком корня не являются полными квадратами каких-либо натуральных чисел.
Теперь возьмем более сложный случай. Является ли рациональным число 2435? Если возвести 3 в пятую степень, получается 243, поэтому исходное выражение можно переписать так: 2435=355=3. Следовательно, данное число рационально. Теперь возьмем число 1215. Это число нерационально, так как не существует натурального числа, возведение которого в пятую степень даст 121.
Для того, чтобы узнать, является ли логарифм какого-то числа a по основанию b рациональным числом необходимо применить метод от противного. К примеру, узнаем, рационально ли число log25. Предположим, что данное число рационально. Если это так, то его можно записать в виде обыкновенной дроби log25=mn.По свойствам логарифма и свойствам степени справедливы следующие равенства:
5=2log25=2mn5n=2m
Очевидно, последнее равенство невозможно так как в левой и правой частях находятся соответственно нечетное и четное числа. Следовательно, сделанное предположение неверно, и число log25 не является рациональным числом.
Стоит отметить, что при определении рациональности и иррациональности чисел не стоит принимать скоропостижных решений. Например, результат произведения иррациональных чисел не всегда является иррациональным числом. Наглядный пример: 2·2=2.
Также существуют иррациональные числа, возведение которых в иррациональную степень дает рациональное число. В степени вида 2log23 основание и показатель степени являются иррациональными числами. Однако само число является рациональным: 2log23=3.
Рационáльное числó (от лат. ratio «отношение, деление, дробь») — число, которое можно представить в виде обыкновенной дроби 
, где 
— целое число, а 
— натуральное[1]. Пример: 
, где 
, а 
.
Целые числа также могут быть записаны в виде дроби, например:
Поэтому целые числа также являются рациональными. Таким образом, множество рациональных чисел представляет собой расширение множества целых чисел путём добавления к ним дробей.
Понятие дроби возникло несколько тысяч лет назад, когда, сталкиваясь с необходимостью измерять некоторые величины (длину, вес, площадь и т. п.), люди поняли, что целых чисел недостаточно и необходимо ввести понятие доли: половины, трети, четверти и т. п. Дробями и операциями над ними пользовались, например, шумеры, древние египтяне и греки.
Множество рациональных чисел[править | править код]
Множество рациональных чисел обозначается 
(от лат. quotient, «частное») и может быть записано в таком виде:
При этом оказывается, что разные записи могут представлять одну и ту же дробь, например, 
и 
, (все дроби, которые можно получить друг из друга умножением или делением числителя и знаменателя на одно и то же натуральное число, представляют одно и то же рациональное число). Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:
Здесь 
— наибольший общий делитель чисел и .
Множество рациональных чисел является естественным обобщением множества целых чисел. Легко видеть, что если у рационального числа 
знаменатель 
, то 
является целым числом.
Множество рациональных чисел располагается всюду плотно на числовой оси: между любыми двумя различными рациональными числами расположено хотя бы одно рациональное число (а значит, и бесконечное множество рациональных чисел). Тем не менее, оказывается, что множество рациональных чисел имеет счётную мощность (то есть все его элементы можно перенумеровать). Со времён древних греков известно о существовании чисел, не представимых в виде дроби: они доказали в частности, что 
не рациональное число. Недостаточность рациональных чисел для выражения всех величин привела в дальнейшем к понятию вещественного числа. В отличие от множества вещественных чисел (которое соответствует одномерному пространству), множество рациональных чисел имеет меру нуль.
Терминология[править | править код]
Формальное определение[править | править код]
Формально рациональные числа определяются как множество классов эквивалентности пар 
по отношению эквивалентности 
, если 
. При этом операции сложения и умножения определяются следующим образом:
Из определения видно, что никакие операции сложения или умножения не приводят к появлению пары вида 
Связанные определения[править | править код]
Правильные, неправильные и смешанные дроби[править | править код]
Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Правильные дроби представляют рациональные числа, по модулю меньшие единицы. Дробь, не являющаяся правильной, называется неправильной и представляет рациональное число, большее или равное единице по модулю.
Неправильную дробь можно представить в виде суммы целого числа и правильной дроби, называемой смешанным числом. Например, 
. Подобная запись (с пропущенным знаком сложения), хотя и употребляется в элементарной арифметике, избегается в строгой математической литературе из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь.
Высота дроби[править | править код]
Высота обыкновенной дроби — это сумма модуля числителя и знаменателя этой дроби.
Высота рационального числа — это сумма модуля числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу[2].
Например, чтобы узнать высоту дроби 
, нужно сначала из неё получить несократимую дробь. Несократимая дробь будет выглядеть так: 
. Потом нужно сложить модуль числителя и знаменатель: 
. Значит высота дроби равна 
.
Комментарий[править | править код]
Термин дробное число (дробь) иногда[уточнить] используется как синоним к термину рациональное число, а иногда синоним любого нецелого числа. В последнем случае дробные и рациональные числа являются разными вещами, так как тогда нецелые рациональные числа — всего лишь частный случай дробных.
Свойства[править | править код]
Основные свойства[править | править код]
Множество рациональных чисел удовлетворяют шестнадцати основным свойствам, которые легко могут быть получены из свойств целых чисел.[3]
- Упорядоченность. Для любых рациональных чисел
и () существует правило, позволяющее однозначно идентифицировать между ними одно и только одно из трёх отношений: «», «» или «». Это правило называется правилом упорядочения и формулируется следующим образом:
-
- Операция сложения. Для любых рациональных чисел и () существует бинарная операция сложения, которая ставит им в соответствие некоторое рациональное число . При этом само число называется суммой чисел и и обозначается , а процесс отыскания такого числа называется сложением. Правило сложения имеет следующий вид:
- Операция умножения. Для любых рациональных чисел и () существует бинарная операция умножения, которая ставит им в соответствие некоторое рациональное число . При этом само число называется произведением чисел и и обозначается , а процесс отыскания такого числа также называется умножением. Правило умножения имеет следующий вид:
- Транзитивность отношения порядка. Для любой тройки рациональных чисел , и ) если меньше и меньше , то меньше , а если равно и равно , то равно .
- Коммутативность сложения. От перемены мест рациональных слагаемых сумма не меняется.
- Ассоциативность сложения. Порядок сложения трёх рациональных чисел не влияет на результат.
- Наличие нуля. Существует рациональное число 0, которое сохраняет любое другое рациональное число при суммировании.
- Наличие противоположных чисел. Любое рациональное число имеет противоположное рациональное число, при суммировании с которым даёт 0.
- Коммутативность умножения. От перемены мест рациональных множителей произведение не меняется.
- Ассоциативность умножения. Порядок перемножения трёх рациональных чисел не влияет на результат.
- Наличие единицы. Существует рациональное число 1, которое сохраняет любое другое рациональное число при умножении.
- Наличие обратных чисел. Любое ненулевое рациональное число имеет обратное рациональное число, умножение на которое даёт 1.
- Дистрибутивность умножения относительно сложения. Операция умножения согласована с операцией сложения посредством распределительного закона:
- Связь отношения порядка с операцией сложения. К левой и правой частям рационального неравенства можно прибавлять одно и то же рациональное число.
- Связь отношения порядка с операцией умножения. Левую и правую части рационального неравенства можно умножать на одно и то же положительное рациональное число.
- Аксиома Архимеда. Каково бы ни было рациональное число , можно взять столько единиц, что их сумма превзойдёт .
Дополнительные свойства[править | править код]
Все остальные свойства, присущие рациональным числам, не выделяют в основные, потому что они, вообще говоря, уже не опираются непосредственно на свойства целых чисел, а могут быть доказаны исходя из приведённых основных свойств или непосредственно по определению некоторого математического объекта. Таких дополнительных свойств очень много. Здесь имеет смысл привести лишь некоторые из них.
- Отношение порядка «>» (с противоположным порядком аргументов) также транзитивно.
- Произведение любого рационального числа на ноль равно нулю.
- Рациональные неравенства одного знака можно почленно складывать.
- Множество рациональных чисел является полем (а именно, полем частных кольца целых чисел ) относительно операций сложения и умножения дробей.
- — поле
- В позиционной системе счисления рациональное число представляется периодической дробью. Более того, наличие представления в виде периодической дроби является критерием рациональности вещественного числа.
- Каждое рациональное число является алгебраическим.
- Между любыми двумя различными рациональными числами и существует хотя бы одно рациональное число , такое, что и . (В качестве примера такого числа можно взять .) Ясно, что между и , а также между и тоже существует хотя бы по одному рациональному числу. Отсюда следует, что между любыми двумя различными рациональными числами и существует бесконечно много рациональных чисел. Иначе говоря, не существует двух соседних рациональных чисел. В частности, не существует наименьшего положительного рационального числа.
- Не существует наибольшего и наименьшего рационального числа. Для любого рационального числа найдутся рациональные (и даже целые) числа и такие, что и .
Счётность множества рациональных чисел[править | править код]
Нумерация положительных рациональных чисел
Чтобы оценить количество рациональных чисел, нужно найти мощность их множества. Легко доказать, что множество рациональных чисел счётно. Для этого достаточно привести алгоритм, который нумерует рациональные числа, то есть устанавливает биекцию между множествами рациональных и натуральных чисел.
Примером такого построения может служить следующий простой алгоритм. Составляется бесконечная таблица обыкновенных дробей, на каждой 
-ой строке в каждом 
-ом столбце которой располагается дробь 
. Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются 
, где — номер строки таблицы, в которой располагается ячейка, а — номер столбца.
Полученная таблица обходится «змейкой» по следующему формальному алгоритму.
Эти правила просматриваются сверху вниз и следующее положение выбирается по первому совпадению.
В процессе такого обхода каждому новому рациональному числу ставится в соответствие очередное натуральное число. То есть дроби 
ставится в соответствие число 1, дроби 
— число 2, и т. д. Нумеруются только несократимые дроби. Формальным признаком несократимости является равенство единице наибольшего общего делителя числителя и знаменателя дроби.
Следуя этому алгоритму, можно занумеровать все положительные рациональные числа. Это значит, что множество положительных рациональных чисел 
счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, поставив в соответствие каждому рациональному числу противоположное ему. Таким образом множество отрицательных рациональных чисел 
тоже счётно. Их объединение 
также счётно по свойству счётных множеств. Множество же рациональных чисел 
тоже счётно как объединение счётного множества с конечным.
Существуют и другие способы занумеровать рациональные числа. Например, воспользовавшись такими структурами как дерево Калкина — Уилфа, дерево Штерна — Броко или ряд Фарея.
Утверждение о счётности множества рациональных чисел может вызывать некоторое недоумение, так как на первый взгляд складывается впечатление, что оно гораздо обширнее множества натуральных чисел (ведь между любыми двумя натуральными числами находится бесконечное множество рациональных). На самом деле это не так, и натуральных чисел хватает, чтобы занумеровать все рациональные.
Недостаточность рациональных чисел[править | править код]
Гипотенуза такого треугольника не выражается никаким рациональным числом
В геометрии следствием так называемой аксиомы Архимеда (в более общем понимании, чем упомянуто выше) является возможность построения сколь угодно малых (то есть, коротких) величин, выражаемых рациональными числами вида 
. Этот факт создаёт обманчивое впечатление, что рациональными числами можно измерить вообще любые геометрические расстояния. Легко показать, что это не верно.
Из теоремы Пифагора известно, что гипотенуза прямоугольного треугольника выражается как квадратный корень суммы квадратов его катетов. Т. о. длина гипотенузы равнобедренного прямоугольного треугольника с единичным катетом равна , то есть числу, квадрат которого равен 2.
Если допустить, что число представляется некоторым рациональным числом, то найдётся такое целое число и такое натуральное число , что 
, причём дробь несократима, то есть числа и — взаимно простые.
Если , то 
, то есть 
. Следовательно, число 
чётно, но произведение двух нечётных чисел нечётно, что означает, что само число также чётно. А значит найдётся натуральное число 
, такое что число можно представить в виде 
. Квадрат числа в этом смысле 
, но с другой стороны , значит 
, или 
. Как уже показано ранее для числа , это значит, что число — чётно, как и . Но тогда они не являются взаимно простыми, так как оба делятся на 2. Полученное противоречие доказывает, что не есть рациональное число.
Из вышесказанного следует, что существуют отрезки на плоскости, а, значит, и на числовой прямой, которые не могут быть измерены рациональными числами. Это приводит к возможности расширения понятия рациональных чисел до вещественных.
См. также[править | править код]
- Дроби Фарея
- Иррациональные числа
- Непрерывная дробь
Примечания[править | править код]
- ↑ Рациональное число // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Шиханович Ю. А. Введение в современную математику (Начальные понятия). — М.: Наука, 1965. — С. 191. — 376 с.
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 30—31. — 672 с. — ISBN 5-482-00445-7.
Литература[править | править код]
- И.Кушнир. Справочник по математике для школьников. — Киев: АСТАРТА, 1998. — 520 с.
- П. С. Александров. Введение в теорию множеств и общую топологию. — М.: глав. ред. физ.-мат. лит. изд. «Наука», 1977
- И. Л. Хмельницкий. Введение в теорию алгебраических систем
Символы математического языка
Натуральные числа используются при счёте: (1), (2), (3), (4…)
Множество всех натуральных чисел обозначается буквой
ℕ
.
Множество всех целых чисел обозначается буквой
ℤ
. Оно содержит число (0), все натуральные числа: (1), (2), (3), (4…) и все целые отрицательные числа: (-1), (-2), (-3), (-4…).
Множество рациональных чисел обычно обозначается буквой
ℚ
. Оно содержит все целые числа и все обыкновенные дроби:
23;−12;83
и т. д.
Обобщённо говорят, что множество
ℚ
состоит из чисел вида
mn;−mn
, где (m, n) — натуральные числа и число (0) (целое число можно тоже представить в виде
m1
).
Символы
ℕ
,
ℤ
,
ℚ
удобно использовать для указания типа числа.
1. Запись
n∈ℕ
(говорят: «элемент (n) принадлежит множеству
ℕ
») обозначает, что число (n) — натуральное.
2. Запись
m∈ℤ
обозначает, что число (m) — целое.
3. Запись
r∈ℚ
обозначает, что число (r) — рациональное.
4. Записи
ℕ⊂ℤ,ℤ⊂ℚ
обозначают, что
ℕ
— часть множества
ℤ
, а
ℤ
— часть множества
ℚ
.
Обрати внимание!
Символ принадлежности
∈
используется, когда элемент принадлежит множеству.
Символ включения
⊂
используется, когда одно множество содержится в другом.
В математике введены следующие обозначения. Запись
s∈S
обозначает, что (s) — один из элементов множества (S). Запись
A⊂B
обозначает, что множество (A) представляет собой часть множества (B). Говорят: (A) — подмножество множества (B).
Обрати внимание!
Для обозначения множеств в математике используют прописные буквы, а для элементов множеств — строчные буквы.
Для обозначения высказываний «элемент (s) не принадлежит множеству (S)» или «множество (B) не является частью (подмножеством) множества (A)» употребляют такие же символы, но перечёркнутые косой чертой:
s∉S;B⊄A
.
Рациональные числа как бесконечные десятичные периодические дроби
Всякое рациональное число представимо в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби.
Продемонстрируем это на примере: возьмём целое число (4), обыкновенную дробь
711
и десятичную дробь (5,377).
Целое число (4) представимо в виде бесконечной десятичной дроби: (4,0000…) Десятичную дробь (5,377) можно представить в виде бесконечной десятичной дроби: (5,377000…) Обыкновенную дробь
711
преобразуем в десятичную путём «деления уголком»:
766¯11¯0,636363…4033¯7066¯4033¯7066¯4033¯…
Легко заметить, что в дробной части частного появилась одинаковая комбинация цифр: (63), (63), (63…) Дробь
711
(= 0,6363636363…) является бесконечной. Обычно пишут: (0,(63)).
Бесконечная десятичная периодическая дробь — десятичная дробь, у которой после запятой повторяется одна и та же последовательность цифр. Эта последовательность называется периодом.
Целое число можно записать как бесконечную десятичную дробь с периодом (0). Например:
(4 = 4,00000… = 4,(0)).
Обрати внимание!
Вообще, любое рациональное число можно представить бесконечной десятичной периодической дробью.
Практически удобнее пользоваться конечной десятичной дробью (4,377), чем бесконечной дробью в виде (4,377(0)). Но теоретически любую обыкновенную дробь можно записать в виде бесконечной периодической десятичной дроби. И наоборот: любая бесконечная десятичная периодическая дробь представима в виде обыкновенной дроби.
Следовательно, любая бесконечная десятичная периодическая дробь является рациональным числом.
Рациональные и иррациональные числа. Множество действительных чисел
- Понятие рационального числа
- Иррациональные числа
- Алгебраические и трансцендентные числа
- Структура множества действительных чисел
- Примеры
Понятие рационального числа
Рациональное число – это число, представляемое обыкновенной дробью m/n, где числитель m – целое число, а знаменатель n – натуральное число:
$$ q = frac{m}{n}, m in Bbb Z, n in Bbb N iff q in Bbb Q $$
Множество рациональных чисел обозначается $Bbb Q$.
Примеры рациональных чисел:
$$ 1 frac{3}{5}; -7,1; 0; frac{1}{3}; frac{7}{4}; -2 $$
Любое рациональное число представимо в виде конечной или периодической бесконечной десятичной дроби.
Например:
$$ frac{1}{3} = 0,333 … = 0,(3); frac{3}{7} = 0,(428571); frac{3}{8} = 0,125 $$
Несократимая рациональная дробь m/n имеет конечное десятичное представление тогда и только тогда, когда простыми делителями числа n являются только 2 и 5 в различных степенях: $n = 2^a cdot 5^b, a, b ge 0$
Например:
$$ frac{7}{125} = 0,056; frac{11}{20} = 0,55; frac{127}{625} = 0,2032; frac{9}{16} = 0,5625 $$
Алгоритм перевода десятичной периодической дроби в обыкновенную дробь
Шаг 1. Для чистой периодической дроби – в числителе записать период дроби. Для смешанной периодической дроби – в числителе записать всю дробную часть и вычесть из неё число, полученное из цифр до периода.
Шаг 2. Для чистой периодической дроби – в знаменателе записать столько девяток, сколько цифр в периоде.
Для смешанной периодической дроби – в знаменателе записать столько девяток, сколько цифр в периоде и справа дописать столько нулей, сколько цифр в дробной части до периода.
Шаг 3. Если необходимо, сократить полученную дробь
Например:
Чистые периодические дроби:
$$ 0,(3) = frac{3}{9} = frac{1}{3}, 1,(15) = 1 + frac{15}{99} = 1 frac{5}{33} $$
Смешанные периодические дроби:
$$ 2,6(543) = 2+ frac{6543-6}{9990} = 2 + frac{6537}{9990} = 2 frac{2179}{3330} $$
$$ 5,0(13) = 5+ frac{13-0}{990} = 5 frac{13}{990}$$
Множество рациональных чисел счётно, т.е. эквивалентно множеству натуральных чисел: $ Bbb Q sim Bbb N$ (см. §11 данного справочника)
Слева – схема подсчёта всех положительных рациональных чисел (взаимно однозначное соответствие между элементами множеств $ Bbb Q_+ и Bbb N$)
Множество рациональных чисел замкнуто, относительно операций сложения, вычитания, умножения и деления (исключая деление на 0). В алгебре говорят, что рациональные числа образуют поле.
Иррациональные числа
Иррациональное число – это число, которое нельзя представить обыкновенной дробью m/n, где числитель m – целое число, а знаменатель n – натуральное число. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Множество иррациональных чисел обозначается $mathbb I $.
Примеры иррациональных чисел:
$$ sqrt 2; – sqrt[3] 7; π; sin 20^0; e^5; ln7; 0,01001000100001… $$
Множество иррациональных чисел не замкнуто относительно операции сложения.
Например, результатом суммы: $frac{1}{1+sqrt 2} + frac{1}{1-sqrt 2} = frac{1-sqrt 2+1+ sqrt 2}{(1+ sqrt 2)(1- sqrt 2)} = frac{2}{1-2}$ =-2 будет целое число.
Иррациональные числа можно приблизительно записывать десятичными дробями или приближать рациональными дробями. Например, для $ sqrt 2$ можем записать:
$$ 1 lt sqrt 2 lt 2 $$
$$ frac{14}{10} lt sqrt 2 lt frac{15}{10} $$
$$ frac{141}{100} lt sqrt 2 lt frac{142}{100} $$
$$ frac{1414}{1000} lt sqrt 2 lt frac{1415}{1000} и т.д. $$
Число $ π approx 3 $,14 или $π approx frac{22}{7}$ или $π ≈ frac{355}{113}$ – с разной точностью.
Мера иррациональности действительного числа a – действительное число μ, которое показывает, насколько хорошо число a может быть приближено рациональными числами.
$μ(a) = 1 iff a$ – рациональное число
$ μ(a) = 2 Leftarrow a $ – алгебраическое иррациональное число
$ μ(a) ge 2 Leftarrow a $ – трансцендентное число
Для многих трансцендентных чисел мера иррациональности неизвестна, есть только верхняя оценка.
Например:
$$ μ(e) = 2, μ(π) le 7,6063 $$
Алгебраические и трансцендентные числа
Если действительное число является корнем уравнения вида
$$ c_n x^n+c_{n-1} x^{n-1}+⋯+c_1 x+c_0 = 0 $$
с целыми коэффициентами $ c_i in Bbb Z$, такое число называется алгебраическим.
Если действительное число не является корнем никакого такого уравнения с целыми коэффициентами, число называется трансцендентным.
Например:
$$ x^2 = 4 Rightarrow x = pm 2, x^2 = 2 Rightarrow x = pm sqrt 2, x^3 = 2 Rightarrow x = sqrt 2 $$
$$ pm 2, pm √2, sqrt[3] 2 $$ – алгебраические числа. При этом, первая пара является рациональными числами, остальные числа – иррациональные.
Примеры алгебраических чисел: $3,5 frac{1}{5}, sqrt 3, sqrt{5+sqrt 2}, sqrt{1+ sqrt{5- sqrt 2}}, sqrt[5]21$
Алгебраические числа бывают рациональными и иррациональными.
Примеры трансцендентных чисел:$ π,2^{sqrt2}, sin10^0, e^4$
Все трансцендентные числа иррациональны.
Множество алгебраических чисел бесконечно и счётно, т.е. эквивалентно множеству натуральных чисел.
Множество алгебраических чисел замкнуто относительно операций сложения, вычитания, умножения и деления (исключая деление на 0). В алгебре говорят, что алгебраические числа образуют поле.
Множество трансцендентных чисел несчётно.
Т.е., трансцендентных чисел «больше», чем алгебраических. Их слишком много, чтобы можно было представить в виде последовательности.
Структура множества действительных чисел
Из-за несовпадения подмножеств, структуру множества действительных чисел можно представить двумя равносильными схемами:
$$ Bbb R = Bbb Q cup Bbb I = Bbb A cup Bbb T $$
$$ Bbb R = Bbb A cup Bbb T = Bbb Q cup Bbb I $$
Множество действительных чисел несчётно.
Множество действительных чисел замкнуто относительно операций сложения, вычитания, умножения и деления (исключая деление на 0).
Множество действительных чисел упорядочено. Для любых двух действительных чисел a и b можно установить отношение: либо $a lt b$, либо a = b, либо $a gt b$.
В алгебре говорят, что действительные числа образуют непрерывное упорядоченное поле.
Примеры
Пример 1. Найдите рациональные дроби, равные данным бесконечным периодическим десятичным дробям:
а) 0,222…
0,(2) = $frac{2}{9}$
б) 5,18686…
$5,1(86) = 5+ frac{186-1}{990} = 5 frac{185}{990} = 5 frac{37}{198}$
в) 0,35(29)
$0,35(29) = frac{3529-35}{9900} = frac{3494}{9900} = frac{1747}{4950}$
г) 1,9(36)
$1,9(32) = 1+ frac{936-9}{990} = 1 frac{927}{990} = 1frac{103}{110}$
Пример 2*. Докажите, что $ sqrt 2$ не является рациональным числом.
Проведём доказательство от противного.
Допустим, что $ sqrt 2$ – рациональное число. Тогда его можно представить в виде несократимой дроби: $ sqrt 2 = frac{a}{b}$, где числитель и знаменатель – целые числа. Т.к. дробь несократима, одно из чисел – чётное, второе – нечётное.
Возведём обе части уравнения в квадрат:
$$ (sqrt2)^2 = (frac{a}{b})^2 Rightarrow 2 = frac{a^2}{b^2} Rightarrow a^2 = 2b^2 $$
Число $2b^2$ – чётное. Значит, $a^2$ – тоже чётное, и само число a – тоже чётное.
$$ a = 2k Rightarrow a^2 = 4k^2 $$
$$ 4k^2 = 2b^2 Rightarrow 2k^2 = b^2 $$
Число $2k^2$ – чётное. Значит, $b^2$ – тоже чётное, и само число b – тоже чётное.
Мы пришли к противоречию. Ведь для несократимой дроби a и b не могут быть одновременно чётными.
Значит, наше допущение неверно, и $ sqrt 2$ нельзя представить в виде дроби $ frac{a}{b}$.
Что и требовалось доказать.
Пример 3. Изобразите на координатной плоскости отрезки, равные по длине алгебраическим иррациональным числам:
а) a = $ sqrt 2$
По теореме Пифагора:
$$a = sqrt{1^2+1^2} = sqrt 2 $$
б) a = $ sqrt 5$
По теореме Пифагора:
$$a = sqrt{1^2+2^2} = sqrt 5 $$
в) a = $ sqrt 13$
По теореме Пифагора:
$$a = sqrt{2^2+3^2} = sqrt 13 $$
г*) a = $ sqrt 3$
По теореме Пифагора:
$$b = sqrt{1^2+1^2} = sqrt 2 $$
$$b = sqrt{(sqrt{2})^2+1^2} = sqrt 3 $$
Содержание:
- Определение рационального числа
- Операции над рациональными числами
Рациональные числа появились как форма записи чисел, более “мелких”, нежели
натуральных.
Определение рационального числа
Определение
Рациональное число (лат. ratio – отношение, деление, дробь) –
это число которое может быть представлено в виде дроби $frac{m}{n}$ , где
числитель$m$ – целое число, а
знаменатель
$n$ – натуральное. Множество рациональных чисел $Q$ обозначается (от англ. quotient “частное”) и
может быть записано в виде: $Q=left{frac{m}{n} : m in Z, n in Nright}$ . Числа вида
$frac{m}{n}$ – называют еще
обыкновенными дробями. Если
$m lt n$, то дробь $frac{m}{n}$ называется правильной, если $m geq n$, то – неправильной.
Пример
Задание. Указать какие из записанных чисел являются рациональными:
$$-49 ; 17 ; frac{14}{3} ; frac{3}{4} ; 3,2 ; sqrt[3]{11} ; sqrt{7}$$
Решение. Рациональными будут числа:
$frac{14}{3} ; frac{3}{4}$ а так же
$-49 ; 17 ; 3,2$ так как их можно представить в виде рациональных дробей –
$frac{-49}{1} ; frac{17}{1} ; frac{32}{10}$ соответственно.
Ответ. $-49 ; 17 ; frac{14}{3} ; frac{3}{4} ; 3,2$
Если $m$ – нацело делится на $n$ или $n=1$, то рациональное число $frac{m}{n}$ также будет
целым числом; если при этом
$m$ будет натуральным, то в таком случае дробь $frac{m}{n}$ будет еще и натуральным числом. Поэтому для этих чисел имеет место такая цепочка вложений:
$N subset Z subset Q$ .
Операции над рациональными числами
На множестве рациональных можно ввести четыре арифметические операции:
сложение,
вычитание,
умножение и
деление; которые вычисляются по следующим правилам.
Правило вычисления суммы двух рациональных чисел:
$$frac{m}{n}+frac{p}{q}=frac{m cdot q+n cdot p}{n cdot q}$$
Правило вычисления разности двух рациональных чисел:
$$frac{m}{n}-frac{p}{q}=frac{m cdot q-n cdot p}{n cdot q}$$
Правило вычисления произведения двух рациональных чисел:
$$frac{m}{n} cdot frac{p}{q}=frac{m cdot p}{n cdot q}$$
Правило вычисления частного двух рациональных чисел:
$$frac{m}{n} : frac{p}{q}=frac{m cdot q}{n cdot p}$$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму, разность, произведение и частное чисел
$frac{5}{7}$ и $frac{2}{3}$
Решение. По правилу вычисления суммы двух рациональных чисел:
$$frac{5}{7}+frac{2}{3}=frac{5 cdot 3+7 cdot 2}{7 cdot 3}=frac{15+14}{21}=frac{29}{21}$$
По правилу вычисления разности двух рациональных чисел:
$$frac{5}{7}-frac{2}{3}=frac{5 cdot 3-7 cdot 2}{7 cdot 3}=frac{15-14}{21}=frac{1}{21}$$
По правилу вычисления произведения двух рациональных чисел:
$$frac{5}{7} cdot frac{2}{3}=frac{5 cdot 2}{7 cdot 3}=frac{10}{21}$$
По правилу вычисления частного двух рациональных чисел:
$$frac{5}{7} : frac{2}{3}=frac{5 cdot 3}{7 cdot 2}=frac{15}{14}$$
Ответ.
$$frac{5}{7}+frac{2}{3}=frac{29}{21} ; frac{5}{7}-frac{2}{3}=frac{1}{21}$$
$$frac{5}{7} cdot frac{2}{3}=frac{10}{21} ; frac{5}{7} : frac{2}{3}=frac{15}{14}$$
Читать дальше: что такое сумма чисел.
