10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
Теорема 4. Если многочлен с целыми коэффициентами f (x) = anxn + an-1xn-1 + … + a1x+a0 имеет рациональный корень x=p/q (q ≠ 0, дробь p/q несократимая), то р является делителем свободного члена (a0), а q — делителем коэффициента при старшем члене аn.
Если p/q является корнем многочлена f (х), то f(p/q) = 0. Подставляем p/q вместо х в f(x) и из последнего равенства имеем
|
an * pn/qn + an-1 * pn-1/qn-1 + … + a1 * p/q + a0 = 0. |
(1) |
Умножим обе части равенства (1) на (q ≠ 0). Получаем
|
аnрn + an-1pn-1q + … + a1pqn-1 + a0qn = 0. |
(2) |
В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому
a0qn = -(аnрn + an-1pn-1q + … + a1pqn-1) делится на р.
Но когда мы записываем рациональное число в виде p/q, то эта дробь считается несократимой, то есть р и q не имеют общих делителей. Произведение a0qn может делиться на р (если р и q — взаимно простые числа) только тогда, когда a0 делится на р. Таким образом, р — делитель свободного члена a0.
Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда
anpn = -(an-1pn-1q + … + a1pq-1 + a0qn) делится на q. Поскольку р и q — взаимно простые числа, то an делится на q, следовательно, q — делитель коэффициента при старшем члене.
Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a0. Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене f (х) коэффициент аn = 1, то делителями аn могут быть только числа ±1, то есть q =±1, и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Задача 1 Найдите рациональные корни многочлена 2х3 – х2 + 12х – 6.
Пусть несократимая дробь p/q является корнем многочлена. Тогда р необходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.
Таким образом, рациональные корни многочлена необходимо искать среди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.
Кроме того, по схеме Горнера можно записать, что
2х3 – х2 + 12х – 6 = (x – 1/2) (2x2 + 12).
Многочлен 2х2 + 12 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень x =1/2.
Задача 2 Разложите многочлен Р (х) = 2х4 + 3х3 – 2х2 – х – 2 на множители.
Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.
Тогда Р (х) = (х – 1)(2х3 + 5х2 + 3х + 2). Ищем целые корни кубического многочлена 2х3 + 5х2 + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2
Имеем Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Квадратный трехчлен 2х2 + х +1 не имеет действительных корней и на линейные множители не раскладывается.
Ответ: Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х2 + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры доказывается, что многочлен нечетной степени всегда можно разложить на линейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.
Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Задача 3 Разложите на множители многочлен х4 + х3 + 3х2 + х + 6.
Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
|
х4 + х3 + 3х2 + х + 6 = (х2 + ах + b)(х2 + сх + d), |
(3) |
где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
х4 + х3 + 3х2 + х + 6 = x4 + cx3 + dx2 +
+ ax3 + acx2 + adx +
+ bx2 + bcx + bd.
Получаем систему
 |
(4) |
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рассматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.
Для каждой пары значений b и d из третьего равенства системы (4) найдем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.
Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:
Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид
|
x4 + х3 + 3х2 + х + 6 = (х2 – х + 2)(х2 + 2х + 3). |
(5) |
Поскольку квадратные трехчлены х2 – х + 2 и х2 + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
Упражнения
- Найдите целые корни многочлена:
1) х3 – 5х + 4;
2) 2x3 + x2 – 13x + 6;
3) 5х3 + 18х2 – 10х – 8;
4) 4х4 – 11х2 + 9х – 2.
- Найдите рациональные корни уравнения:
1) х3 – 3х2 + 2 = 0;
2) 2х3 – 5х2 – х + 1 = 0;
3) 3х4 + 5х3 – х2 – 5х – 2 = 0;
4) 3х4 – 8х3 – 2х2 + 7х – 2 = 0.
- Разложите многочлен на множители:
1) 2х3 – х2 – 5х – 2;
2) х3 + 9х2 + 23х +15;
3) х4 – 2х3 + 2х – 1;
4) х4 – 2х3 – 24х2 + 50х – 25.
- Найдите действительные корни уравнения:
1) х3 + х2 – 4х + 2 = 0;
2) х3 – 7х – 6 = 0;
3) 2х4 – 5х3 + 5х2 – 2 = 0;
4) 2х3 – 5х2 + 1 = 0.
5*. Разложите многочлен на множители методом неопределенных коэффициентов:
1) х4 + х3 – 5х2 + 13х – 6;
2) х4 – 4х3 – 20х2 + 13х – 2.
6*. Разложите многочлен на множители, заранее записав его с помощью метода неопределенных коэффициентов в виде (х2 + bх + с)2 – (mх + n)2: :
1) х4+ 4х – 1;
2) х4 – 4х3 – 1;
3) х4 + 4а3х – а4.
Содержание:
- Теорема о рациональных корнях
- Задача пример №8
- Задача пример №9
- Задача пример №10
Теорема о рациональных корнях
Если для многочлена 
с целыми коэффициентами существует рациональный корень, то этот корень имеет вид
Доказательство:
Пусть несократимая дробь 
является корнем многочлена 
с целыми коэффициентами:
Умножим обе части равенства на 
:
Так как в последнем равенстве каждый член, кроме члена 
, содержит множитель 
и каждый член, кроме члена 
, содержит множитель 
, то коэффициент 
должен делится на 
, а коэффициент 
должен делится на 
.
Задача пример №8
Найдите рациональные корни многочлена 
.
Решение:
свободный член 6, старший коэффициент 2.
Для 
, 
запишем все возможные числа вида
, т.е. одним из множителей является двучлен 
. Другие множители найдем, используя синтетическое деление:
Так как, 
, получим, что 
являются корнями многочлена.
Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Задача пример №9
Найдите корни многочлена 
.
Решение:
по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 
, то, решив квадратное уравнение 
, получим другие корни: 
. Значит данный многочлен третьей степени имеет три корня: –
.
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 
сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми.
Например, для нахождения корней многочлена 
надо умножить все члены уравнения 
на 12, а затем решить полученное уравнение 
.
Для нахождения рациональных корней выполните следующие действия:
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 
(обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен 
, на который многочлен делится без остатка.
3. Для данного многочлена при помощи синтетического деления на двучлен 
определяется другой множитель.
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 
могут являться числа ±1.
Проверим: 
; 
. Значит, многочленах 
не имеет рациональных корней.
Исследование:
1) Перепишите примеры в тетрадь и проведите обсуждение.
a) Многочлен первой степени 
имеет один корень: 
b) Многочлен второй степени 
имеет два корня: 
, 
; 
c) Многочлен третьей степени 
имеет три корня: 
d) Многочлен четвертой степени 
имеет четыре корня: 
e) Принимая во внимание, что уравнение 
имеет кратные корни, получим 5 корней: 
2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид 
.
3) Равна ли степень произвольного многочлена количеству его корней?
Покажем на примере, что многочлен n-ой степени имеет n корней.
Задача пример №10
Найдите все корни многочлена 
.
Решение:
рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
.
Значит, 
является корнем данного многочлена 
. Другие корни найдем синтетическим делением.
В выражении 
для множителя 
вновь применим теорему о рациональных корнях и синтетическое деление. Тогда 
; 
. Решим уравнение 
; 
; 
(корень кратности 2); 
; 
Корни: 
Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).
Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Свойства прямоугольного треугольника
- Частное решение дифференциального уравнения
- Интегрирование иррациональных функций
- Площадь поверхности. Интеграл по площади поверхности
- Формула Пуассона
- Найти производную функции
- Исследовать функцию на непрерывность: пример решения
- Преобразование графиков функций
- Полный дифференциал функции: пример решения
- Прямые и плоскости в пространстве
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 ноября 2021 года; проверки требуют 7 правок.
В алгебре теоре́ма о рациона́льных корня́х (также тест на рациона́льные ко́рни) определяет рамки для рациональных корней многочлена вида:
с целыми коэффициентами 
и 
.
Теорема утверждает, что каждый рациональный корень 
, где 
и 
— взаимно простые числа, удовлетворяет условию, что
Теорема о рациональных корнях является частным случаем леммы Гаусса.
Применение[править | править код]
Теорема используется для нахождения всех рациональных корней многочлена, если таковые существуют. С её помощью определяется конечное количество возможных решений, подлежащих проверке подстановкой. Если рациональный корень 
найден, исходный многочлен может быть поделён без остатка на 
с получением многочлена меньшей степени, чьи корни также являются корнями исходного многочлена.
Кубическое уравнение[править | править код]
Кубическое уравнение в общем виде:
с целыми коэффициентами имеет три решения в комплексных числах. Если тест на рациональные корни не выявляет таковых, то единственным способом выражения решений является использование кубических корней. Однако в случае выявления хотя бы одного рационального решения r, вынесение (x–r) за скобки приводит к квадратному уравнению, которое возможно решить через дискриминант.
Доказательство[править | править код]
Пусть:
.
Предположим, что 
для некоторых взаимно простых целых и :
.
Умножая обе части уравнения на 
, вынося за скобки и перенося свободный член с противоположным знаком в правую часть уравнения, получаем:
.
Видно, что является делителем 
. Но и — взаимно простые числа, значит, также должно быть делителем 
.
Если, напротив, перенести старший член в правую часть уравнения и вынести за скобки, получим:
.
Сделаем вывод о делимости 
на [1].
Примеры[править | править код]
Пример 1[править | править код]
Каждый рациональный корень многочлена
должен иметь делитель единицы в числителе и делитель двойки в знаменателе. Таким образом, возможными рациональными корнями являются 
и 
. Однако ни один из них не обращает выражение в ноль, следовательно, многочлен рациональных корней не имеет.
Пример 2[править | править код]
Каждый рациональный корень многочлена
должен иметь делитель шестерки в числителе и делитель единицы в знаменателе, откуда возможными корнями являются 
. Из них 
, 
и 
обращают выражение в ноль, являясь, таким образом, корнями многочлена.
Примечания[править | править код]
- ↑ Arnold, Denise. 4 unit mathematics. — Melbourne: Edward Arnold, 1993. — 306 pages с. — ISBN 0340543353, 9780340543351.
Литература[править | править код]
- Miller C. D., Lial M. L., Schneider D. I. Fundamentals of college algebra (англ.). — 3rd edition. — Scott & Foresman/Little & Brown Higher Education, 1990. — P. 216–221. — ISBN 0-673-38638-4.
- Jones P. S., Bedient J. D. The historical roots of elementary mathematics (англ.). — Dover Courier Publications, 1998. — P. 116–117. — ISBN 0-486-25563-8.
- Larson R. Calculus: an applied approach (англ.). — Cengage Learning, 2007. — P. 23–24. — ISBN 978-0-618-95825-2.
Теорема Безу и следствия из неё
19 июля 2022
Теорема Безу позволяет решать уравнения высших степеней, которые на первый взгляд не решаются, и раскладывать на множители многочлены, которые не раскладываются.:)
Формулировка теоремы довольно проста:
Терема Безу. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $x- color{red}{a}$ равен значению этого многочлена в точке $x= color{red}{a}$:
[r=Pleft( color{red}{a} right)]
На практике нас интересует не сама теорема Безу, а некоторые следствия из неё — именно они помогают решать уравнения и раскладывать многочлены на множители. В этом уроке мы рассмотрим все такие следствия и станем настоящими мастерами в работе с многочленами.
Содержание
- Деление с остатком
- Разложение на множители
- Целые корни многочленов
- Рациональные корни многочленов
- Доказательства
В разных учебниках теорему Безу проходят то в 9-м классе, то в 10-м. Этот урок построен так, что вы поймёте его вне зависимости от школы, класса и учебника.
1. Деление с остатком
Итак, есть многочлен $Pleft( x right)$ и двучлен $x- color{red}{a}$. Разделим $Pleft( x right)$ на $x- color{red}{a}$ с остатком:
[Pleft( x right)=Qleft( x right)cdot left( x- color{red}{a} right)+r]
Теперь найдём значение многочлена $Pleft( x right)$ в точке $x= color{red}{a}$:
[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}- color{red}{a} right)+r=r]
Собственно, мы только что доказали теорему Безу. А заодно подготовили основу для первого важного следствия.
Следствие 1. Деление на произвольный двучлен
Теорема Безу прекрасно работает не только для двучлена $x-color{red}{a}$, но и для любого линейного выражения вида $color{blue}{k}x+color{red}{b}$.
Следствие 1. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $color{blue}{k}x+color{red}{b}$ равен значению этого многочлена в точке $x=-color{red}{b}/ color{blue}{k};$:
[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]
На практике для большей надёжности рекомендуется приравнять двучлен $color{blue}{k}x+color{red}{b}$ к нулю:
[begin{align} color{blue}{k}x+color{red}{b} &=0 \ x &=-frac{color{red}{b}}{color{blue}{k}} \ end{align}]
Затем подставить найденное значение $x=-{color{red}{b}}/{color{blue}{k}};$ в многочлен $Pleft( x right)$ и таким образом найти $Pleft( -{color{red}{b}}/{color{blue}{k}}; right)$:
[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]
Пример 1. Стандартный многочлен
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)=4{{x}^{3}}-3{{x}^{2}}+5x-6]
на двучлен $Tleft( x right)=x-2$.
Решение. Это стандартный двучлен вида $x-color{red}{a}$, поэтому решаем по стандартной теореме Безу, согласно которой остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{2}$ равен $Pleft( color{red}{2} right)$:
[begin{align}r &=Pleft( color{red}{2} right)= \ &=4cdot {color{red}{2}^{3}}-3cdot {color{red}{2}^{2}}+5cdotcolor{red}{2}-6 \ &=32-12+10-6=24 end{align}]
Ответ: 24.
Пример 2. Более сложный многочлен
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)={{left( {{x}^{3}}-2{{x}^{2}}+5 right)}^{3}}{{left( 2x+1 right)}^{5}}]
на двучлен $Tleft( x right)=x+1$.
Решение. Многочлен $Pleft( x right)$ представлен в виде произведения двух других многочленов, которые ещё и возведены в степени. Если раскрыть скобки и привести подобные слагаемые, получится обычный многочлен вида
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
По свойствам степеней найдём степень такого многочлена:
[deg Pleft( x right)=3cdot 3+1cdot 5=14]
Раскрывать скобки и приводить подобные в многочлене 14-й степени долго и трудно, а главное — в этом нет никакой необходимости. Ведь по теореме Безу остаток от деления $Pleft( x right)$ на двучлен $x-color{red}{a}$ всегда равен $Pleft( color{red}{a} right)$ — и не важно, как записан исходный многочлен $Pleft( x right)$.
Для надёжности, чтобы найти $color{red}{a}$, приравняем к нулю двучлен $Tleft( x right)=x+1$:
[begin{align}x+1 &=0 \ x &=color{red}{-1} \ end{align}]
Теперь подставим $x=color{red}{-1}$ в многочлен $Pleft( x right)$ и найдём остаток:
[begin{align}r &=Pleft( color{red}{-1} right)= \ &={{left( {{left( color{red}{-1} right)}^{3}}-2cdot {{left( color{red}{-1} right)}^{2}}+5 right)}^{3}}cdot {{left( 2cdot left( color{red}{-1} right)+1 right)}^{5}}= \ &={{left( -1-2+5 right)}^{3}}cdot {{left( -2+1 right)}^{5}}=-8 end{align}]
Ответ: −8.
Пример 3. Рациональные коэффициенты
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)=3{{x}^{20}}+{{x}^{19}}-7x+1]
на двучлен $Tleft( x right)=3x+1$.
Решение. Воспользуемся Следствием 1 из теоремы Безу. Для надёжности приравняем к нулю двучлен $Tleft( x right)$ и найдём $color{red}{a}$:
[begin{align}3x+1 &=0 \ x &=color{red}{-{1}/{3};} end{align}]
Подставим найденное $x=color{red}{-{1}/{3};}$ в многочлен $Pleft( x right)$ и найдём остаток:
[begin{align} Pleft( color{red}{-frac{1}{3}} right) &=3cdot {{left( color{red}{-frac{1}{3}} right)}^{20}}+{{left( color{red}{-frac{1}{3}} right)}^{19}}-7cdot left( color{red}{-frac{1}{3}} right)+1= \ &=frac{1}{{{3}^{19}}}-frac{1}{{{3}^{19}}}+frac{7}{3}+1=frac{10}{3} end{align}]
Ответ: ${10}/{3};$.
Пример 4. Иррациональные коэффициенты
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)={{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}+64]
на двучлен $Tleft( x right)=left( 1-sqrt{3} right)x+2$.
Решение. Вновь воспользуемся Следствием 1 из теоремы Безу. Приравняем двучлен $Tleft( x right)$ к нулю и найдём $color{red}{a}$:
[left( 1-sqrt{3} right)x+2=0]
Это линейное уравнение с иррациональными коэффициентами. Такое уравнение решается стандартно (см. урок «Линейные уравнения»):
[x=-frac{2}{1-sqrt{3}}=frac{2}{sqrt{3}-1}]
Избавимся от иррациональности в знаменателе, домножив числитель и знаменатель на сопряжённое:
[x=frac{2color{blue}{left( sqrt{3}+1 right)}}{left( sqrt{3}-1 right) color{blue}{left( sqrt{3}+1 right)}}=frac{2left( sqrt{3}+1 right)}{2}= color{red}{sqrt{3}+1}]
Степень исходного многочлена: $deg Pleft( x right)=6$. Если подставить в такой многочлен иррациональное число, то это число придётся возводить в шестую степень. Это слишком долго и трудно, поэтому перепишем многочлен $Pleft( x right)$ так:
[begin{align} Pleft( x right) &=left( {{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}-64 right)+128= \ &={{left( {{x}^{2}}-4 right)}^{3}}+128 end{align}]
Мы выделили точный куб разности — классическую формулу сокращённого умножения. Как это работает — см. уроки «Формулы сокращённого умножения» и «Куб суммы и разности».
В такую формулу намного проще подставить $x=color{red}{sqrt{3}+1}$:
[begin{align}Pleft( color{red}{sqrt{3}+1} right) &={{left( {{left( color{red}{sqrt{3}+1} right)}^{2}}-4 right)}^{3}}+128= \ &={{left( {{left( sqrt{3} right)}^{2}}+2sqrt{3}+{{1}^{2}}-4 right)}^{3}}+128= \ &={{left( 2sqrt{3} right)}^{3}}+128= \ &=24sqrt{3}+128 end{align}]
Ответ получился некрасивым, но это и есть искомый остаток от деления.
Ответ: $24sqrt{3}+128$.
2. Разложение на множители
Сейчас будет немного теории, которая может показаться непонятной, но далее на примерах всё встанет на свои места.
Рассмотрим ещё раз деление многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
По теореме Безу мы легко найдём остаток $r=Pleft( color{red}{a} right)$. В частности, при $Pleft( color{red}{a} right)=0$ многочлен примет вид
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
А это значит, что многочлен $Pleft( x right)$ разделился на двучлен $x-color{red}{a}$ без остатка, и мы получили разложение на множители.
Кроме того, равенство $Pleft( color{red}{a} right)=0$ означает, что число $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. И это ещё одно замечательное следствие теоремы Безу.
Следствие 2. Корни многочлена и деление
Следствие 2. Число $x=color{red}{a}$ является корнем многочлена $Pleft( x right)$ тогда и только тогда, когда $Pleft( x right)$ делится без остатка на $left( x-color{red}{a} right)$.
На практике это означает, что для разложения многочлена на множители мы просто перебираем разные числа $x=color{red}{a}$ до тех пор, пока не окажется, что $Pleft( color{red}{a} right)=0$. В этот момент многочлен перепишется в виде
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
Такой перебор особенно эффективен в сочетании со схемой Горнера (см. урок «Схема Горнера»). Потому что параллельно с вычислением $Pleft( color{red}{a} right)$ мы получаем ещё и коэффициенты нового многочлена $Qleft( x right)$.
Пример 10. Обычный многочлен
Разложите на множители многочлен
[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}-11x-6]
Решение. Для наглядности отметим синим цветом коэффициенты многочлена $Pleft( x right)$:
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-11} right)cdot x+left( color{blue}{-6} right)]
Составим из них таблицу для схемы Горнера:
[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline{} & {} & {} & {} & {} & {}\ end{array}]
Все коэффициенты целые, поэтому логично проверять целые $x=color{red}{a}$, начиная с самых простых и маленьких чисел:
[x=pm 1; pm 2; pm 3; ldots ]
Проверим $x=color{red}{1}$ и $x=color{red}{-1}$:
[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline color{red}{1} & 1 & 4 & 1 & -10 & color{red}{-16}\ hline color{red}{-1} & 1 & 2 & -5 & -6 & color{green}{0}\ end{array}]
Проверка числа $x=color{red}{1}$ окончилась неудачей: остаток $r=color{red}{-16}$. Зато проверка $x=color{red}{-1}$ дала остаток $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ является корнем многочлена $Pleft( x right)$, и сам многочлен можно переписать так:
[begin{align}Pleft( x right) &=Qleft( x right)cdot left( x-left( color{red}{-1} right) right) \ &=left( {{x}^{3}}+2{{x}^{2}}-5x-6 right)left( x+1 right) end{align}]
Теперь разложим многочлен $Qleft( x right)$ по схеме Горнера. Проверим ещё раз число $x=color{red}{-1}$:
[begin{array}{r|r|r|r|r|r}{} & 1 & 3 & -3 & -11 & -6\ hline color{red}{-1} & color{blue}{1} & color{blue}{2} & color{blue}{-5} & color{blue}{-6} & color{green}{0}\ hline color{red}{-1} & 1 & 1 & -6 & color{green}{0} & {}\ end{array}]
И вновь получили $r=color{green}{0}$. Исходный многочлен примет вид
[Pleft( x right)=left( {{x}^{2}}+x-6 right){{left( x-1 right)}^{2}}]
В первой скобке стоит квадратный трёхчлен. Разложим его на множители по теореме Виета:
[{{x}^{2}}+x-6=left( x+3 right)left( x-2 right)]
Итого окончательное разложение многочлена $Pleft( x right)$:
[left( x+3 right)left( x-2 right){{left( x-1 right)}^{2}}]
Однако это было довольно простое задание: теорема Безу использовалась лишь в качестве обоснования, почему вместо $Pleft( x right)$ мы пишем $Qleft( x right)left( x-color{red}{a} right)$.
Следующее задание будет намного интереснее.:)
Пример 11. Многочлен с двумя переменными
Разложите на множители многочлен
[Pleft( x,y right)=y{{x}^{2}}+3yx+x-4y-1]
Решение. Это многочлен от двух переменных. Он квадратный относительно переменной $x$ и линейный относительно $y$. Чтобы разложить такой многочлен на множители, сгруппируем его слагаемые относительно переменной $x$:
[Pleft( x,y right)= color{blue}{y}cdot {{x}^{2}}+left( color{blue}{3y+1} right)cdot x+left( color{blue}{-4y-1} right)]
Составляем таблицу:
[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline {} & {} & {} & {}\ end{array}]
Чтобы воспользоваться теоремой Безу, нужно найти такое $x=color{red}{a}$, чтобы $r=Pleft( color{red}{a} right)= color{green}{0}$. Поскольку в роли коэффициентов выступают выражения, содержащие переменную $y$, вновь рассмотрим самые простые варианты, которые приходят в голову:
[x=pm 1; pm y]
Проверим, например, $x=color{red}{1}$:
[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline color{red}{1} & y & 4y+1 & color{green}{0}\ end{array}]
Первая же попытка привела к успеху: $r=color{green}{0}$, поэтому $x=color{red}{1}$ — крень многочлена $Pleft( x,y right)$. Разложим этот многочлен на множители согласно Следствию 2 теоремы Безу:
[Pleft( x,y right)=left( ycdot x+4y+1 right)cdot left( x-color{red}{1} right)]
В первой скобке стоит новый многочлен, линейный по $x$ и по $y$. Его уже нельзя разложить на множители, поэтому ответ окончательный:
[Pleft( x,y right)=left( xy+4y+1 right)left( x-1 right)]
Важное замечание. Строго говоря, линейность многочлена по каждой переменной ещё не означает, что его нельзя разложить на множители. Простой контрпример:
[xy-x+y-1=left( x+1 right)left( y-1 right)]
Однако в нашем случае дальнейшее применение теоремы Безу и проверки по схеме Горнера не даст никаких новых множителей.
3. Целые корни многочленов
До сих пор мы подставляли числа наугад. И если удавалось найти число $x=color{red}{a}$ такое, что $Pleft( color{red}{a} right)=0$, мы объявляли его корнем, а многочлен $Pleft( x right)$ переписывали в виде
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
Однако с помощью теоремы Безу можно значительно ускорить отыскание корней, отбросив заведомо неподходящие варианты. В этом нам поможет следующее утверждение.
Следствие 3. Целочисленные корни
Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:
[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.
Обратите внимание: старший коэффициент при ${{x}^{n}}$ равен единице. Именно поэтому многочлен $Pleft( x right)$ называется приведённым. Кроме того, все коэффициенты ${{a}_{n-1}},ldots ,{{a}_{0}}$ должны быть целыми числами.
И вот тогда целые корни следует искать среди делителей свободного члена ${{a}_{0}}$.
Пример 5. Простое уравнение
Решите уравнение
[{{x}^{3}}-2{{x}^{2}}-x+2=0]
Решение. Это приведённое кубическое уравнение с целыми коэффициентами. Рассмотрим многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-2} right)cdot {{x}^{2}}+left( color{blue}{-1} right)cdot x+color{blue}{2}]
Если у него есть целые корни, то по Следствию 3 теоремы Безу все они находятся среди делителей свободного члена ${{a}_{0}}=2$. Таких делителей всего четыре:
[x=pm 1; pm 2]
Подставим эти числа в схему Горнера:
[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-2} & color{blue}{-1} & color{blue}{2}\ hline color{red}{1} & 1 & -1 & -2 & color{green}{0}\ hline color{red}{-1} & 1 & -2 & color{green}{0} & {}\ end{array}]
Уже на первом шаге мы получили $r=color{green}{0}$. Следовательно, $x=color{red}{1}$ — корень многочлена $Pleft( x right)$, и сам многочлен можно переписать так:
[Pleft( x right)=left( {{x}^{2}}-x-2 right)left( x-color{red}{1} right)]
Впрочем, если учесть третью строку таблицы, то можно вообще записать
[Pleft( x right)=left( x-2 right)left( x-left( color{red}{-1} right) right)left( x-color{red}{1} right)]
В любом случае, корни многочлена, как и корни уравнения — это числа 2, 1 и −1.
Ответ: $x=1$, $x=-1$, $x=2$.
Формула понижения степени
Итак, с помощью теоремы Безу мы можем:
- Найти целый корень многочлена;
- Разложить исходный многочлен на множители;
- Далее искать корни многочлена степени на единицу меньше.
В самом деле, если $Pleft( color{red}{a} right)=0$, тогда по Следствию 2 теоремы Безу мы переписываем многочлен $Pleft( x right)$ в виде
[Pleft( x right)=Qleft( x right)left( x-color{red}{a} right)]
Далее мы ищем корни многочлена $Qleft( x right)$, степень которого на единицу меньше $Pleft( x right)$.
Этот приём называется понижением степени. Он помогает свести исходный многочлен к квадратному, корни которого легко считаются, например, через дискриминант.
Пример 6. Среднее уравнение
Решите уравнение
[{{x}^{3}}-3{{x}^{2}}-4x+12=0]
Решение. Это уравнение третьей степени. Достаточно найти один корень — далее останется решить квадратное уравнение. Заметим, что многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-4} right)cdot x+color{blue}{12}]
является приведённым с целочисленными коэффициентами. По Следствию 3 теоремы Безу все целые корни этого многочлена содержатся среди делителей свободного члена ${{a}_{0}}=12$. Таких делителей довольно много:
[x=pm 1; pm 2; pm 3; pm 4; pm 6; pm 12]
Впрочем, нам достаточно найти всего один корень. Воспользуемся схемой Горнера:
[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-3} & color{blue}{-4} & color{blue}{12}\ hlinecolor{red}{1} & 1 & -2 & -7 & color{red}{5}\ hlinecolor{red}{-1} & 1 & -4 & 0 & color{red}{12}\ hlinecolor{red}{2} & 1 & -1 & -6 & color{green}{0}\ end{array}]
Проверка закончилась неудачей для $x=color{red}{1}$ и $x=color{red}{-1}$. Но для $x=color{red}{2}$ мы нашли то, что искали: остаток $r=color{green}{0}$. Следовательно, $x=color{red}{2}$ — корень многочлена $Pleft( x right)$.
Разложим многочлен на множители согласно теореме Безу:
[Pleft( x right)=left( {{x}^{2}}-x-6 right)left( x-color{red}{2} right)]
В первой скобке стоит квадратный трёхчлен. Его корни легко найти по теореме Виета:
[Pleft( x right)=left( x-3 right)left( x+2 right)left( x-2 right)]
Приравниваем полученное произведение к нулю и решаем уравнение: $x=3$, $x=-2$, $x=2$.
Ответ: $x=2$, $x=-2$, $x=3$.
Пример 7. Сложное уравнение
Решите уравнение
[{{x}^{4}}-{{x}^{3}}-5{{x}^{2}}+3x+2=0]
Решение. Слева приведённый многочлен с целочисленными коэффициентами, поэтому все целые корни находятся среди делителей свободного члена ${{a}_{0}}=2$:
[x=pm 1; pm 2]
Достаточно подобрать два корня — далее уравнение сведётся к квадратному. Воспользуемся схемой Горнера:
[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{-1} & color{blue}{-5} & color{blue}{3} & color{blue}{2}\ hlinecolor{red}{-1} & 1 & -2 & -3 & 6 & color{red}{-4}\ hlinecolor{red}{1} & 1 & 0 & -5 & -2 & color{green}{0}\ hlinecolor{red}{-2} & 1 & -2 & -1 & color{green}{0} & {}\ end{array}]
Получили корни $x=color{red}{1}$ и $x=color{red}{-2}$. Разложим многочлен на множители:
[left( {{x}^{2}}-2x-1 right)left( x-color{red}{1} right)left( x-left( color{red}{-2} right) right)=0]
Решим квадратного уравнение из первой скобки:
[{{x}^{2}}-2x-1=0]
Дискриминант положителен:
[begin{align} D &={{left( -2 right)}^{2}}-4cdot 1cdot left( -1 right)= \ &=4+4=8 end{align}]
Следовательно, уравнение имеет два корня:
[x=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]
Ответ: $x=1$, $x=-2$, $x=1pm sqrt{2}$.
4. Рациональные корни
До сих пор мы работали лишь с приведёнными многочленами, где старший коэффициент равен единице. Однако теорема Безу прекрасно работает и для неприведённых многочленов — при условии что все коэффициенты остаются целыми.
Рассмотрим уравнение
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.
Следствие 4. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.
Это утверждение будет доказано в конце урока. Сейчас важен практический смысл, который состоит в том, что все рациональные корни уравнения
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
имеют вид $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}$ следует искать среди делителей ${{a}_{0}}$, а $color{blue}{q}$ — среди положительных делителей ${{a}_{n}}$.
Пример 8. Простой многочлен
Найдите рациональные корни многочлена
[Pleft( x right)=2{{x}^{5}}-{{x}^{4}}+4x-2]
Решение. Делители свободного члена ${{a}_{0}}=-2$:
[p=pm 1; pm 2]
Положительные делители старшего коэффициента ${{a}_{4}}=2$:
[q=1; 2]
Возможные рациональные корни многочлена $Pleft( x right)$ по Следствию 4 теоремы Безу:
[x=pm 1; pm 2; pm {1}/{2};]
Проверять числа $x=color{red}{pm 1}$ нет смысла, поскольку все коэффициенты многочлена $Pleft( x right)$, за исключением одного, чётные. Следовательно, при подстановке нечётных чисел многочлен принимает нечётные значения, которые точно не равны нулю.
Остальные числа проверим по схеме Горнера:
[begin{array}{r|r|r|r|r|r|r}{} & color{blue}{2} & color{blue}{-1} & color{blue}{0} & color{blue}{0} & color{blue}{4} & color{blue}{-2}\ hlinecolor{red}{2} & 2 & 3 & 6 & 12 & 28 & color{red}{54}\ hlinecolor{red}{-2} & 2 & -5 & 10 & -20 & 44 & color{red}{-90}\ hline color{red}{{1}/{2};} & 2 & 0 & 0 & 0 & 4 & color{green}{0}\ hline color{red}{-{1}/{2};} & 2 & -2 & 1 & -{1}/{2}; & {17}/{4}; & color{red}{-{33}/{8};}\ end{array}]
Подошло лишь одно число: $x=color{red}{{1}/{2};}$. Следовательно, многочлен имеет лишь один рациональный корень.
Ответ: $x={1}/{2};$.
Обратите внимание: проверку дробных чисел можно прекращать, как только в строке таблицы появилась дробь. Потому что дальше это число будет лишь умножаться на новые дроби и складываться с другими целыми числами. При таких обстоятельствах получить $r=color{green}{0}$ уже невозможно.
Пример 9. Сложный многочлен
Найдите рациональные корни многочлена
[Pleft( x right)=3{{x}^{7}}+2{{x}^{6}}-5{{x}^{5}}+3{{x}^{3}}-{{x}^{2}}-7x+5]
Решение. Это многочлен с целыми коэффициентами. Делители свободного члена ${{a}_{0}}=5$:
[p=pm 1; pm 5]
Положительные делители старшего коэффициента ${{a}_{7}}=3$:
[q=1; 3]
Кандидаты в корни согласно Следствию 4 теоремы Безу:
[x=pm 1; pm 5; pm {1}/{3};; pm {1}/{5};]
Всего восемь кандидатов. Проверим их все по схеме Горнера:
[begin{array}{r|r|r|r|r|c|c|c|c}{} & color{blue}{3} & color{blue}{2} & color{blue}{-5} & color{blue}{0} & color{blue}{3} & color{blue}{-1} & color{blue}{-7} & color{blue}{5}\ hlinecolor{red}{1} & 3 & 5 & 0 & 0 & 3 & 2 & -5 & color{green}{0}\ hlinecolor{red}{-1} & 3 & 2 & -2 & 2 & 1 & 1 & color{red}{-6} & {}\ hlinecolor{red}{5} & 3 & 20 & 100 & color{red}{500} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-5} & 3 & -10 & 50 & color{red}{-250} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{1}/{3};} & 3 & 6 & 2 & color{red}{{2}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{1}/{3};} & 3 & 4 & color{red}{-{4}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{5}/{3};} & 3 & 10 & color{red}{{50}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{5}/{3};} & 3 & 0 & 0 & 0 & 3 & -3 & color{green}{0} & {}\ end{array}]
Обратите внимание: для чисел $x=color{red}{5}$ и $x=color{red}{-5}$ мы прекратили вычисления досрочно, поскольку получили явно неадекватные числа, которые дальше будут только расти.
При проверке $x=color{red}{{1}/{3};}$, $x=color{red}{-{1}/{3};}$ и $x=color{red}{{5}/{3};}$ мы в какой-то момент возникли дроби, после чего дальнейшие вычисления теряют смысл.
Итого найдены два рациональных корня: $x=color{red}{1}$ и $x=color{red}{-{5}/{3};}$. Пожалуй, это одно из самых утомительных заданий на применение теоремы Безу, которые я когда-либо решал.:)
5. Доказательства
Рассмотрим доказательства всех ключевых утверждений сегодняшнего урока.
5.1. Теорема Безу
Мы сформулировали эту теорему в самом начале урока:
Терема Безу. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $x-color{red}{a}$ равен значению этого многочлена в точке $x=color{red}{a}$:
[r=Pleft( color{red}{a} right)]
Доказательство. Разделим многочлен $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
Такое представление всегда однозначно (см. урок «Деление многочленов с остатком»). Здесь многочлен $Qleft( x right)$ — неполное частное, $r$ — остаток, причём
[begin{align}deg r lt deg left( x-color{red}{a} right) &=1 \ deg r &=0 \ end{align}]
Другими словами, остаток $r$ — это просто число.
Теперь найдём значение $Pleft( x right)$ в точке $x=color{red}{a}$:
[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}-color{red}{a} right)+r=r]
Теорема Безу доказана. Однако её доказательство опирается на единственность деления с остатком.
5.2. Целочисленные корни
Целочисленные корни приведённого многочлена с целыми коэффициентами следует искать среди делителей свободного члена.
Следствие 3. Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:
[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.
Доказательство. Пусть $color{red}{b}in mathbb{Z}$ — корень многочлена $Pleft( x right)$, т.е. $Pleft( color{red}{b} right)=0$. Подставим число $x=color{red}{b}$ в формулу многочлена и получим уравнение:
[{color{red}{b}^{n}}+{{a}_{n-1}}{color{red}{b}^{n-1}}+ldots +{{a}_{1}}color{red}{b}+{{a}_{0}}=0]
Перенесём последнее слагаемое вправо, а слева из оставшихся слагаемых вынесем множитель $color{red}{b}$ за скобку:
[color{red}{b}cdot left( {color{red}{b}^{n-1}}+{{a}_{n-1}}{color{red}{b}^{n-2}}+ldots +{{a}_{1}} right)=-{{a}_{0}}]
Поскольку $-{{a}_{0}}in mathbb{Z}$, а слева стоят два целочисленных множителя, получаем, что число $-{{a}_{0}}$ делится на $color{red}{b}$. Следовательно, свободный член ${{a}_{0}}$ тоже делится на $color{red}{b}$, что и требовалось доказать.
5.3. Рациональные корни
Рассмотрим уравнение
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.
Утверждение. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения $Pleft( x right)=0$, то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.
Доказательство. Подставим число $x=color{red}{p}/color{blue}{q};$ в исходное уравнение. Поскольку $x=color{red}{p}/color{blue}{q};$ — корень, уравнение обратится в верное числовое равенство:
[{{a}_{n}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n}}+{{a}_{n-1}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n-1}}+ldots +{{a}_{1}}cdot frac{color{red}{p}}{color{blue}{q}}+{{a}_{0}}=0]
Домножим обе части на ${color{blue}{q}^{n}}$. Получим
[{{a}_{n}}{color{red}{p}^{n}}+{{a}_{n-1}}{color{red}{p}^{n-1}}color{blue}{q}+ldots +{{a}_{1}}color{red}{p}{color{blue}{q}^{n-1}}+{{a}_{0}}{color{blue}{q}^{n}}=0]
Перенесём последнее слагаемое ${{a}_{0}}{color{blue}{q}^{n}}$ вправо, а в левой части из оставшихся слагаемых вынесем множитель $color{red}{p}$ за скобку:
[color{red}{p}left( {{a}_{n}}{color{red}{p}^{n-1}}+{{a}_{n-1}}{color{red}{p}^{n-2}}color{blue}{q}+ldots +{{a}_{1}}{color{blue}{q}^{n-1}} right)=-{{a}_{0}}{color{blue}{q}^{n}}]
Слева и справа от знака равенства стоят целые числа, поскольку все слагаемые и множители являются целыми. Мы видим, что левая часть делится на $color{red}{p}$. Следовательно, правая часть тоже делится на $color{red}{p}$:
[-{{a}_{0}}{color{blue}{q}^{n}} vdots color{red}{p}]
По условию теоремы дробь $color{red}{p}/color{blue}{q};$ несократима. Следовательно, числа $color{blue}{q}$ и $color{red}{p}$ не имеют общих делителей, и единственный возможный вариант — это когда ${{a}_{0}}$ делится на $color{red}{p}$.
Аналогично доказывается, что старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$. Теорема доказана.
Вот и всё.:)
Смотрите также:
- Схема Горнера
- Деление многочленов уголком
- Теорема Виета
- Задача B3 — работа с графиками
- Метод коэффициентов, часть 2
- Нестандартная задача B2: студенты, гонорары и налоги
Рациональные корни многочлена с целыми коэффициентами
Вопрос о нахождении
рациональных корней многочлена f(x)
Q[x]
(с рациональными коэффициентами) сводится
к вопросу об отыскании рациональных
корней многочленов k
∙ f(x)
Z[x]
(с целыми коэффициентами). Здесь число
k
является наименьшим общим кратным
знаменателей коэффициентов данного
многочлена.
Необходимые, но
не достаточные условия существования
рациональных корней многочлена с целыми
коэффициентами дает следующая теорема.
Теорема 6.1 (о
рациональных корнях многочлена с целыми
коэффициентами).
Если
–рациональный
корень многочлена f(x)
= an
xn+
+
…+ a1
x
+ a0
с
целыми
коэффициентами,
причем (p,
q)
= 1, то числитель
дроби p
является делителем свободного члена
а0,
а знаменатель q
является делителем старшего коэффициента
а0.
Теорема
6.2. Если
Q
(где
(p,
q)
= 1)
является
рациональным корнем многочлена
f(x)
с целыми
коэффициентами, то
–целые
числа.
Пример. Найти
все рациональные
корни
многочлена
f(x)
= 6
x4
+ x3
+ 2
x2
–
4 х+
1.
1. По теореме 6.1:
если
–рациональный
корень многочлена f(x),
(где
(p,
q)
= 1), то
a0
= 1
p,
an
= 6
q.
Поэтому p
{
1}, q
{1,
2, 3, 6}, значит,
.
2. Известно, что
(следствие 5.3) число а
является корнем многочлена f(x)
тогда и только тогда, когда f(x)
делится на (х
– а).
Следовательно,
для проверки того, являются ли числа 1
и –1 корнями многочлена f(x)
можно воспользоваться схемой Горнера:
|
6 |
1 |
2 |
– 4 |
1 |
|
|
1 |
6 |
7 |
9 |
5 |
6 |
|
– 1 |
6 |
– 5 |
7 |
–11 |
12 |
f(1)
= 6
0,f(–1)
= 12
0,
поэтому 1 и –1 не являются корнями
многочленаf(x).
3. Чтобы отсеять
часть оставшихся чисел
,
воспользуемся теоремой 6.2. Если выражения
или
принимает целые значения для соответствующих
значений числителяp
и знаменателя q,
то в соответствующих клетках таблицы
(см. ниже) будем писать букву “ц”, в
противном случае – “др”.
|
|
|
|
|
|
|
|
|
|
ц |
ц |
ц |
др |
др |
др |
|
|
ц |
ц |
ц |
ц |
др |
др |
=
=
4. С помощью схемы
Горнера проверяем, будут ли оставшиеся
после отсеивания числа
корнямиf(x).
Вначале разделим f(x)
на (х
–
).
|
6 |
1 |
2 |
– 4 |
1 |
|
|
|
6 |
4 |
4 |
–2 |
0 |
В результате
имеем: f(x)
= (х
–
)(6
x3
+ 4
x2
+
4 х
– 2) и
– кореньf(x).
Частное q(x)
= 6 x3
+ 4
x2
+
4 х
– 2 разделим
на (х
+
).
|
6 |
1 |
2 |
– 4 |
1 |
|
|
– |
6 |
–2 |
3 |
–5 |
3 |
Так
как q
(–
)
= 3
0, то (–
) не является корнем многочленаq(x),
а значит и многочлена f(x).
Наконец,
разделим многочлен q(x)
= 6 x3
+ 4
x2
+
+ 4 х
– 2 на (х
–
).
|
6 |
1 |
2 |
– 4 |
1 |
|
|
|
6 |
3 |
3 |
–3 |
0 |
Получили:
q
(
)
= 0, т.е.
– кореньq(x),
а значит,
– кореньf
(x).
Таким образом, многочлен f
(x)
имеет два рациональных корня:
и
.
Освобождение от алгебраической иррациональности в знаменателе дроби
В школьном курсе
при решении некоторых типов задач на
освобождение от иррациональности в
знаменателе дроби достаточно домножить
числитель и знаменатель дроби на число
сопряженное знаменателю.
Примеры. 1.
t
=
.
Здесь в знаменателе
срабатывает формула сокращенного
умножения (разность квадратов), что
позволяет освободиться от иррациональности
в знаменателе.
2. Освободиться от
иррациональности в знаменателе дроби
t
=
. Выражение
– неполный квадрат разности чисела
=
иb
= 1. Воспользовавшись формулой сокращенного
умножения а3
– b3=
(а
+ b)
· (a2
– ab
+ b2),
можно определить множитель m
= (а + b)
=
+ 1, на который следует домножать числитель
и знаменатель дробиt,
чтобы избавиться от иррациональности
в знаменателе дроби t.
Таким образом,
t
=
.
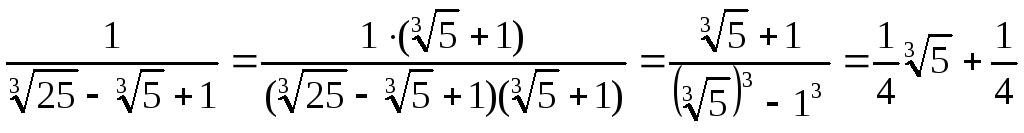В ситуациях, где
формулы сокращенного умножения не
работают, можно использовать другие
приемы. Ниже будет сформулирована
теорема, доказательство которой, в
частности, позволяет найти алгоритм
освобождения от иррациональности в
знаменателе дроби в более сложных
ситуациях.
Определение 6.1.
Число z
называется алгебраическим
над полем
F,
если существует многочлен f(x)
F[x],
корнем которого является z,
в противном случае число z
называется трансцендентным
над полем F.
Определение 6.2.
Степенью
алгебраического над полем
F
числа
z
называется степень неприводимого над
полем F
многочлена p(x)
F[x],
корнем которого является число z.
Пример. Покажем,
что число z
=
является алгебраическим над полемQ
и найдем его
степень.
Найдем неприводимый
над полем Q
многочлен p(х),
корнем которого является x
=
.
Возведем обе части равенстваx
=
в
четвертую степень, получимх4
= 2 или х4
– 2
= 0. Итак, p(х)
= х4
– 2, а степень
числа z
равна deg
p(х)
= 4.
Теорема 6.3
(об освобождении
от алгебраической иррациональности в
знаменателе дроби). Пусть
z
– алгебраическое число над полем F
степени n.
Выражение вида t
=
,где
f(x),
(x)
F[x],
(z)
0
единственным
образом может быть представлено в виде:
t
= сn-1
zn-1
+ cn-2
zn-2
+ … + c1
z
+ c0,
ci
F.
Алгоритм освобождения
от иррациональности в знаменателе дроби
продемонстрируем на конкретном примере.
Пример.
Освободиться от иррациональности в
знаменателе дроби:
t
=
1. Знаменателем
дроби является значение многочлена
(х)
= х2
– х
+1 при х
=
.
В предыдущем примере показано, что
– алгебраическое число над полемQ
степени 4, так как оно является корнем
неприводимого над Q
многочлена p(х)
= х4
– 2.
2. Найдем линейное
разложение НОД (
(х),
p(x))
с помощью алгоритма Евклида.
_
x4
– 2 |
x2
– x
+ 1
x4–
x3+
x2
x2
+ x = q1(x)
_
x3–
x2
–
2
x3–
x2+
x
x2
– x
+ 1 |
– x
–2 = r1
(x)
x2
+ 2x
– x +
3
= q2(x)
_–3x
+
1
–3x
– 6
_
– x
–2 |7
= r2
– x
–2
–
x
–
=q3(x)
0
Итак, НОД (
(х),
p(x))
= r2
=
7. Найдем
его линейное разложение.
Запишем
последовательность Евклида, пользуясь
обозначениями многочленов.
p(x)
=
(x)
· q1(x)
+ r1(x)
r1(x)
=
p(x)
–
(x)
· q1(x)
(x)
= r1(x)
· q2(x)
+ r2(x)
r2(x)
=
(x)
– r1(x)
· q2(x)
r1(x)
= r2(x)
· q2(x).
Подставим в
равенство 7= r2(x)
=
(x)
– r1(x)
· q2(x)
значение остатка r1(x)
= p(x)
–
(x)
· q1(x),
после преобразований получим линейное
разложение НОД(
(х),
p(x)):
7 = p(x)
· (– q2(x))
+
(x)
· [1 + q1(x)
· q2(x)].
Если подставить в последнее равенство
вместо обозначений соответствующие
многочлены и учесть, что p(
)
= 0, то имеем:
(1 –
+
)
· (–
+ 2
+ 3
+ 1)] = 7 (1)
3. Из равенства (1)
следует, что если знаменатель дроби t
умножить на число m
= [1 + (–
+ 2
+ 3
+ 1)], то получим 7. Таким образом,
t
=
=
.
МЕТОДИКА 16.
Тема урока: Стандартный вид многочлена
Класс: 7
Тип урока: урок проверки и контроля
знаний и умений
Цели урока:
– проверить умения приводить многочлен
к стандартному виду
– развивать у учащихся логическое
мышление, внимание
– воспитывать самостоятельность
Структура урока:
-
Организационный момент
-
Инструктаж
-
Самостоятельная работа.
Задания:
1. Дополните предложения:
а) Выражение, содержащее сумму одночленов
называют …(многочленом).
б) Многочлен состоящий из стандартных
одночленов и не содержащий подобных
слагаемых называется … (стандартным
многочленом).
в) Наибольшую из степеней одночленов
входящих в многочлен стандартного вида
называют … (степенью многочлена).
г) Прежде чем определить степень
многочлена, нужно … (привести его к
стандартному виду).
д) Для нахождения значения многочлена
нужно сделать первое…(представить
многочлен в стандартном виде), второе
…(подставить значение переменной в
данное выражение).
2. Найти значение многочлена:
а) 2a4–ab+2b2приa=-1, b=-0,5
б) x2+2xy+y2приx=1,2, y=-1,2
3. Привести многочлен к стандартному
виду:
а) -5ах2
+ 7а2х + 2а2х +
9ах2 – 4ах2 –
8а2х;
б) (5х2
– 7х – 13) – (3х2 – 8х + 17);
в) 2а
– (1,4ав + 2а2 – 1) + (3а + 6,4ав);
г)
(2с2 – 1,6с + 4) – ((10,6с2
+ 4,4с – 0,3) – (3,6с2 – 7с –
0,7));
4.
Привести многочлен к стандартному виду
и выяснить при каких значениях хего значение равно 1:
а)
2x2-3x–x2-5+2x–x2+10;
б)
0,3x3–x2+x–x3+3x2+0,7x3-2x2+0,07
Билет
№ 17.
Делимость
целых чисел
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
