Как найти радианную меру угла выраженного

Углы в математике (а также в тригонометрии и физике) высчитываются и измеряются в градусах или в радианах. Важно понимать и определять связь между этими единицами измерения, и переводить их из одной в другую. Понимание и определение этой связи позволяет оперировать углами и перевести градусы в радианы, а также осуществить перевод из радиан в градусы с помощью специальной тригонометрической формулы – формулы перевода градусов в радианы. В данной статье мы разберемся, зачем все это нужно конвертировать (и что делать с конвертируемым), выведем формулу для перевода градусов в радианы и обратно – из радианов в градусы, а также разберем несколько примеров из практики по конвертации.

Связь между градусами и радианами

Что такое радиан? Радиан вместе с градусом является выражением угловой меры: это величина, которая используется для измерения плоских углов. Поэтому, когда говорят о таблице градусов и радиан, то имеют в виду таблицу, в которой представлены соответствия угловых градусов радианам (что позволяет вам не находить и не считать самостоятельно на калькуляторе, к примеру).

Как перевести радианы в градусы — есть формула? Для нахождения связи между градусами и радианами, необходимо узнать, сколько будет градусная и ридианная (радиальная) мера какого-либо угла (и для этого нам не нужно пользоваться каким-либо переводчиком онлайн). Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла, необходимо рассчитать определенные данные: длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π·r. Разделим длину дуги на радиус и получим радианную меру угла: π·rr=π рад.

Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180°. Следовательно, 180°=π рад. 

Формулы перевода из градусов в радианы и наоборот

Как перевести градусы в радианы не более, чем за минуту? Что делать с координатами в градусах, если нужны в радианах? Из содержания формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и обратно из градусов в радианы (взаимно преобразовывать и пересчитывать).

Как онлайн найти градусную меру угла и сделать пересчет? Выразим 1 радиан в градусах. Для этого разделим левую и правую части радиуса на пи.

1 рад=180π° – град. мера угла в 1 радиан равна 180π.

Также можно выразить один градус в радианах. Чему равен 1 радиан и во что он будет переходить? Вот простой расчет.

1°=π180рад

Можно произвести приблизительные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы. 

1 рад=180π°=1803,1416°=57,2956°

Значит, в одном радиане примерно 57 градусов

1°=π180рад=3,1416180рад=0,0175 рад

Один градус содержит 0,0175 радиана.

По какой формуле перевести радианы в градусы?

Примеры перевода градусов в радианы и радианов в градусы

Рассмотрим пример, как перевести градусы в радианы по формуле.

Конечно, в интернете это все может считаться за секунду, но у самостоятельного подсчета другие преимущества.

Аналогично можно получить формулу перевода в радианы из градусов.

y°=y·π180рад

Угол может измеряться следующими величинами:

1. Градусами (и соответствующими ему величинами: угловыми минутами и секундами);
2. Радианами.

Градусная мера угла

Если взять развернутый угол (это два прямых угла) и поделить его на 180 частей, то одна такая часть будет называться одним градусом. Для того, чтобы измерить градусную меру угла, необходимо посчитать, сколько раз 1 градус входит в данный угол. Полученное число и будет ответом.

Если угол таков, что его нельзя измерить целым числом, либо же он меньше единичного угла, то используют такие меры измерения как угловые минуты и секунды.

Если градус поделить на 60 частей, то одной такой частью будет минута. В свою же очередь, если минуту разделить на те же 60 частей, то полученным числом будет 1 секунда.

Радианная мера угла

Радианом называют угол, образованный дугой окружности длинной равной радиусу этой окружности.

Длина окружности равна:

l=2⋅π⋅rl=2cdotpicdot r,

где rr — радиус этой окружности.

Тогда, разделив на радиус, получаем, что полный угол в радианах равен:

lr=2⋅π⋅rr=2⋅π радианfrac{l}{r}=frac{2cdotpicdot r}{r}=2cdotpitext{ радиан}

В градусах этот же угол равен, как известно, 360∘360^{circ}.

Отсюда находим связь между радианами и градусами:

2⋅π радиан=360∘2cdotpitext{ радиан}=360^{circ}

Это та главная формула, которая нужна, чтобы переводить градусы в радианы и наоборот.

Один радиан равен:

1 радиан=360∘2⋅π≈57.3∘1text{ радиан}=frac{360^{circ}}{2cdotpi}approx57.3^{circ}

Один радиан в минутах:

1 радиан=360∘2⋅π⋅60≈3438′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60approx3438′

Один радиан в секундах:

1 радиан=360∘2⋅π⋅60⋅60≈206280′′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60cdot60approx206280”

Перевод градусов в радианы

Если по условию известна градусная мера угла, то чтобы перевести ее в радианную, нужно сделать следующие действия: умножить ее на πpi и разделить на 180.

Перевод градусов в радианы

y радиан=π180⋅xytext{ радиан}=frac{pi}{180}cdot x

xx — значение угла в градусах;
yy — значение того же угла в радианах.

Пример 1

Переведите 45 градусов в радианную меру измерения. Ответ округлите до десятой доли.

Решение

45∘=π180⋅45 радиан≈0.8 радиан45^{circ}=frac{pi}{180}cdot 45text{ радиан}approx0.8text{ радиан}

Ответ

0.8 радиан0.8text{ радиан}

Задача

Земля совершила треть от половины оборота вокруг Солнца. На какой угол в радианах она повернулась?

Решение

Найдем сначала этот угол в градусах. Полный угол составляет 360∘360^circ. Половина от полного оборота это 180∘180^{circ}. Нам же нужна треть этого угла, то есть:

180∘3=60∘frac{180^circ}{3}=60^circ

Земля отклонилась на угол 60∘60^circ от своего начального положения. Переведем теперь этот угол в радианы:

60∘=π180⋅60 радиан≈1 радиан60^circ=frac{pi}{180}cdot 60text{ радиан}approx1text{ радиан}

Решение

1 радиан1text{ радиан}

Перевод радиан в градусы

Чтобы перевести радианы в градусы, нужно умножить угол в радианах на 180 и разделить на πpi.

Перевод радиан в градусы

y∘=180π⋅xy^{circ}=frac{180}{pi}cdot x

xx — значение угла в радианах;
yy — значение того же угла в градусах.

Пример 2

Переведите 3 радиана в градусную меру угла.

Решение

3 радиана=180π⋅3≈172∘3text{ радиана}=frac{180}{pi}cdot3approx172^circ

Ответ

172∘172^circ

Ищете, где можно заказать задачу по математике недорого? Обратитесь к нашим экспертам в данной области!

Тест по теме «Перевод градусов в радианы и наоборот»

Для того, чтобы дать ответ на поставленный вопрос необходимо выяснить соотношение между градусами и радианами.

Мы чаще сталкивается с тем, что в геометрии углы измеряются градусами. Но есть еще и радианная мера угла.

Чтобы понять, что это такое, возьмем развернутый угол ( 180 градусов ), стороны которого одновременно являются диаметром окружности. Для вычисления радианной меры данного угла нужно длину окружности между сторонами угла разделить на длину радиуса:

(π х r)/r = π ( радиан ), а в градусах этот угол составляет 180.

π радиан = 180 градусов, отсюда 1 градус = π/180 радиан.

Чтобы перевести градусную меру угла в радианную необходимо заданное количество градусов умножить на π и разделить на 180.

Если провести вычисления, то мы узнаем, что 1 градус = 0,0175 радиана. Теперь можно действовать еще проще: заданное количество градусов умножить на 0,0175.

****************­*****************­*****************­******

Рассмотрим пример:

Найдем радианную меру угла 30 градусов.

Для этого 30 х 0,0175 = 0,525 (радиана).

Радианная мера угла 30 градусов составляет 0,525 радиана.

Материалы урока

Прежде, чем приступить к рассмотрению новой темы, давайте вспомним, что градусом называют величину центрального угла, которому соответствует 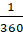 часть окружности. Градусная мера угла – это положительное число, которое показывает, сколько раз градус и его части укладываются в измеряемом угле.

А углы можно измерять только в градусах? Сегодня на уроке мы рассмотрим ещё одну единицу измерения углов.

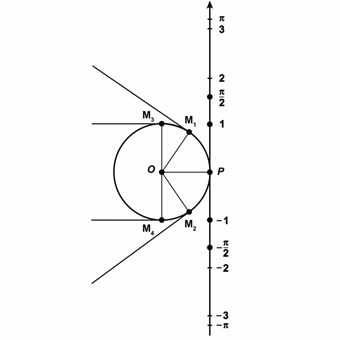
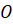
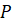
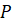
Давайте изобразим окружность с центром в точке  и радиусом . Затем проведём вертикальную прямую, которая касается окружности в точке . Эту прямую мы будем считать числовой осью с началом отсчёта в точке . Положительным направлением на прямой будем считать направление вверх. За единичный отрезок на числовой оси возьмём радиус окружности.

Отметим на прямой несколько точек:  и ,  и ,  и ,  и ,  и .

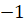
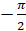
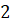
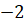
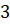
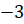
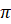
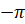
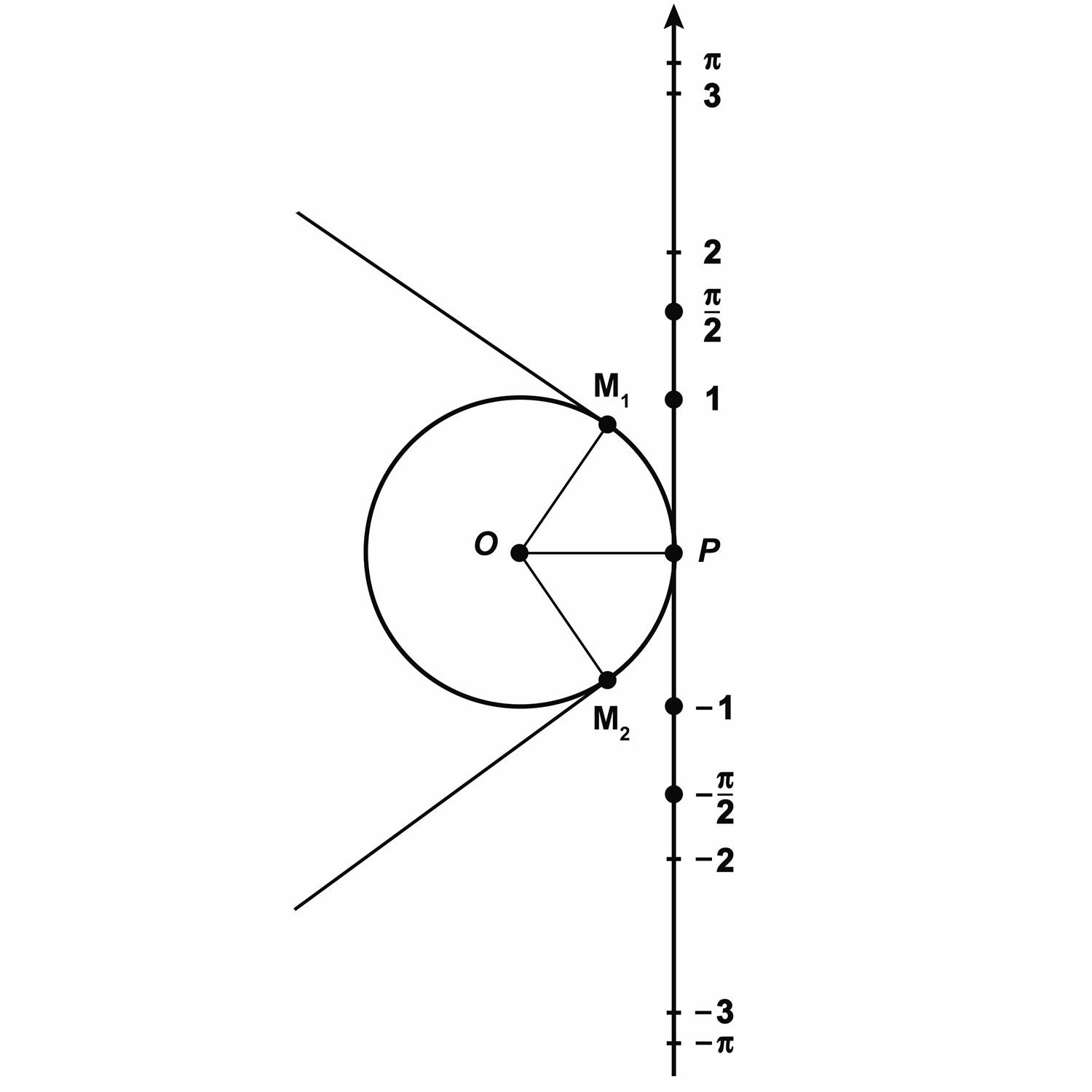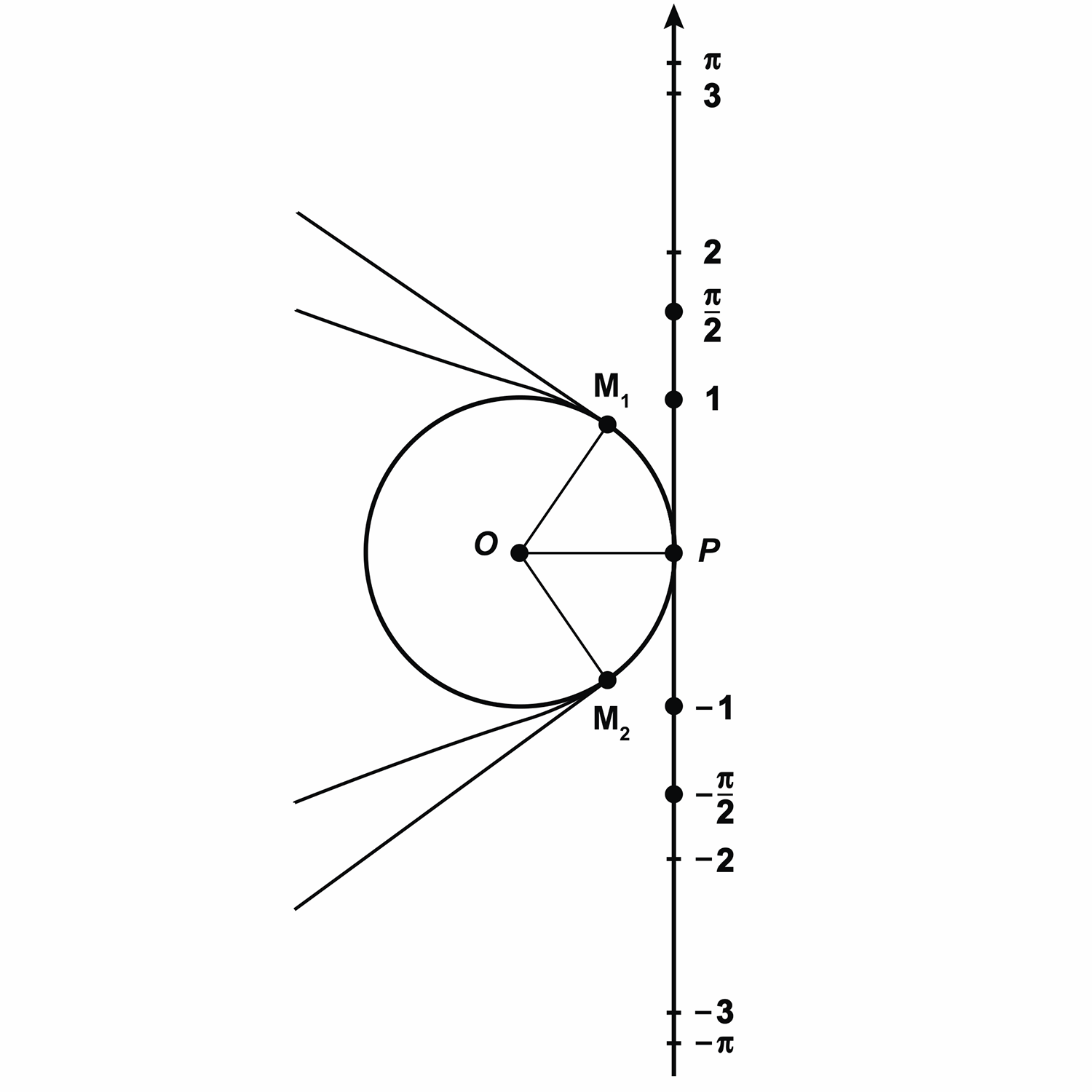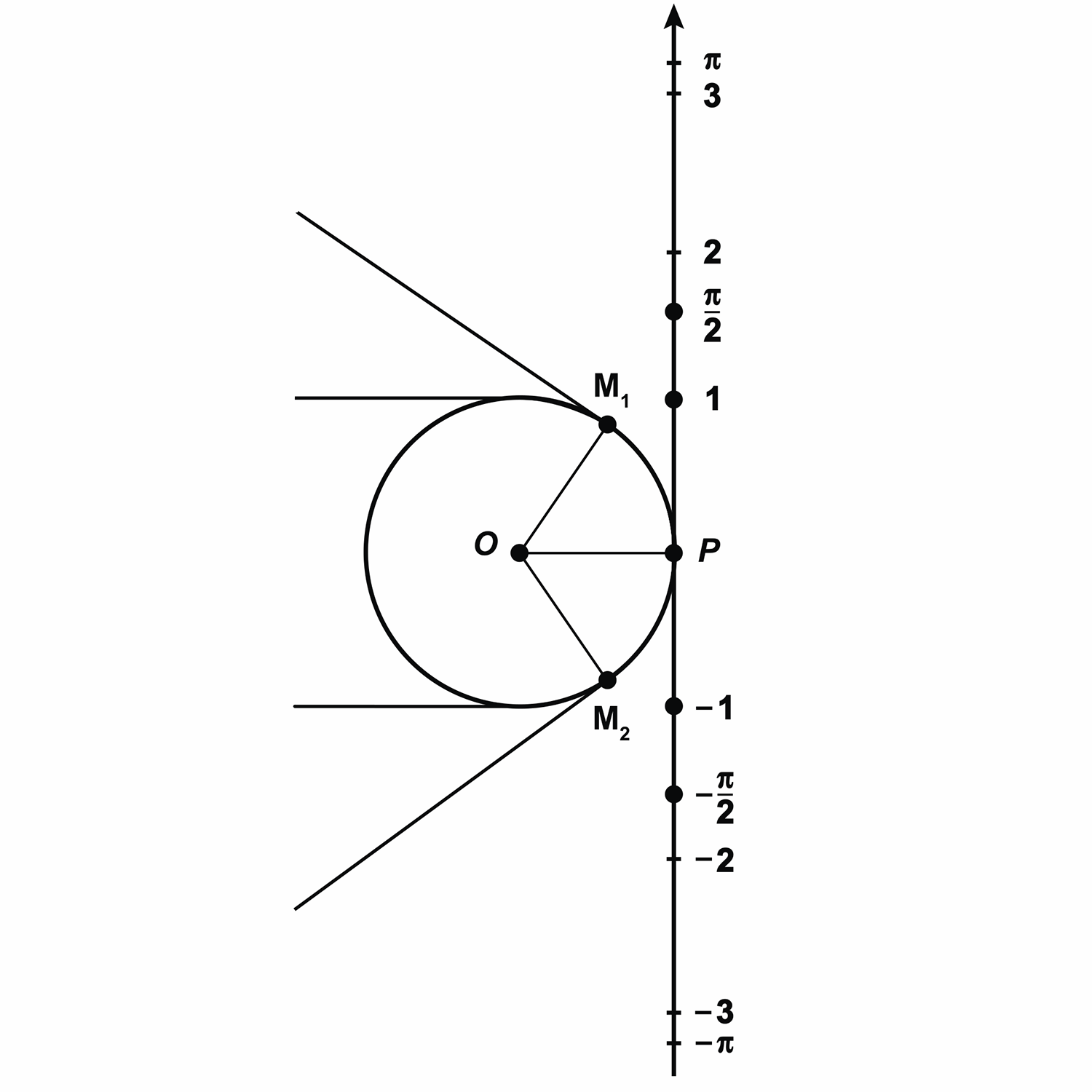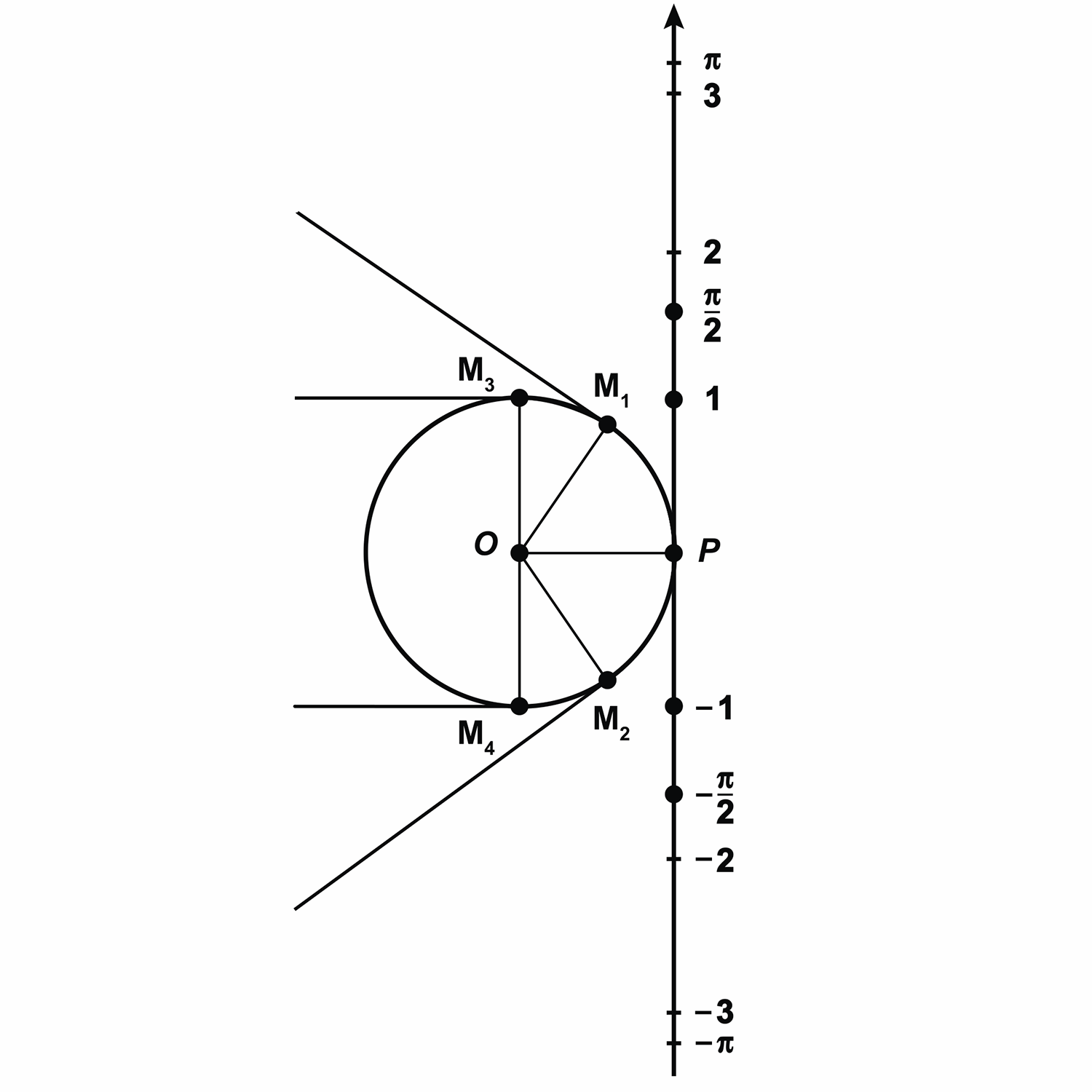
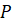
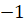
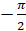
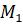
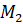
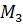
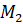
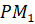
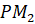
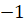
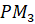
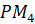
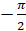
Теперь представим нашу прямую в виде нерастяжимой нити, которая закреплена на окружности в точке . Будем наматывать нить на окружность. При этом точки на числовой прямой с координатами , , ,  перейдут соответственно в точки окружности , , , . При этом длина дуги  равна , длина дуги  равна , длина дуги  равна , длина дуги  равна .

Получается, что каждой точке прямой ставится в соответствие некоторая точка окружности.

Так, точке прямой с координатой  ставится в соответствие точка . А значит, угол  можем считать единичным? Да, и его мерой мы будем измерять другие углы. Например, угол  следует считать равным , а угол  равным .

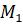
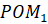
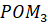
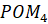
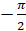
А где используют такой способ измерения углов? Такой способ измерения углов широко используется в математике и физике. Говорят, что углы измеряются в радианной мере.

Единичный угол 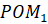 называют углом в один радиан. Записывают так:  рад.

И напомним, что длина дуги 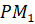 равна радиусу нашей окружности.

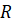
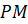
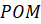
Сейчас давайте рассмотрим окружность радиуса . И отметим на ней дугу , равную длине радиуса окружности, и угол .

И такой угол называется углом в один радиан? Верно.

Запомните! Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.

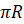
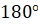
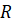
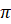
Интересно, а скольким градусам равен угол в один радиан? Давайте найдём градусную меру угла в один радиан. Мы знаем из курса геометрии, что дуге длиной , то есть полуокружности, соответствует центральный угол, равный . Следовательно, дуге окружности длиной  соответствует угол в  раз меньший.

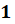
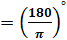
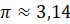
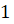
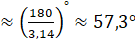
Выше мы назвали такой угол углом в один радиан, а значит, можем записать, что рад . , тогда рад .

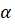
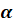
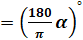
Если угол содержит  рад, то рад . Эту формулу называют формулой перехода от радианной меры к градусной.

Давайте с вами найдём градусную меру угла, равного  рад. Для этого воспользуемся формулой перехода от радианной меры к градусной. Подставим  вместо : . Сократим на  и на . И в результате получим .

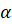
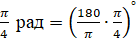
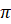
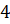
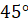
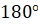
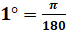
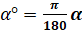
Можно ли, наоборот, перейти от градусной меры к радианной? Конечно, можно, но такой переход будет чуть сложнее. Так как угол в  равен  рад, то  рад. Тогда  рад. Такую формулу называют формулой перехода от градусной меры к радианной.

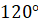
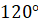
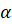
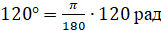
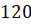
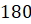
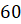
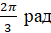
Найдём радианную меру угла, равного . Воспользуемся формулой перехода от градусной меры к радианной. Подставим  вместо : . Сократим  и  на . И в результате получим .

Обратите внимание, что при обозначении меры угла в радианах слово «радиан» обычно не пишут: 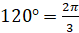. При этом обозначение градуса в записи меры угла пропускать нельзя.

В следующей таблице представлены углы в градусной и радианной мере, с которыми мы будем встречаться чаще всего.

Отметим, что радианная мера углов позволяет значительно упростить многие формулы в математике, физике, механике. В частности, радианная мера угла удобна для вычисления длины дуги окружности. Так, выше мы выяснили, что угол в  рад стягивает дугу, длина которой равна радиусу , а значит, угол в  рад стягивает дугу длиной: . Если , то эта формула принимает совсем простой вид: , то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.

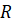
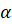
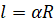
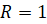
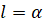
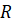
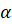
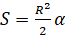
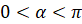
Сейчас, прежде чем приступить к выполнению заданий, мы докажем, что площадь кругового сектора радиуса , образованного углом в  рад, равна , где .

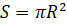
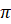
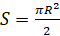
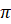
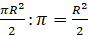
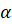
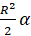
Докажем это. Известно, что площадь круга вычисляется по формуле: . Площадь полукруга, то есть кругового сектора в  рад: . Тогда площадь сектора в  рад в  раз меньше, то есть . Следовательно, площадь сектора в  рад равна .

Ну а сейчас давайте выполним несколько заданий.

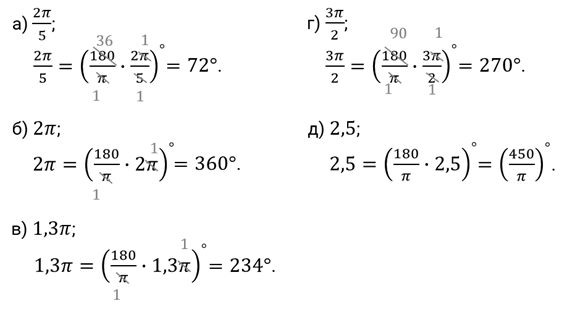
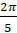
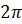
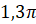
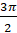
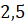
Первое задание. Найдите градусную меру угла, выраженную в радианах: а) ; б) ; в) ; г) ; д) .

Решение.

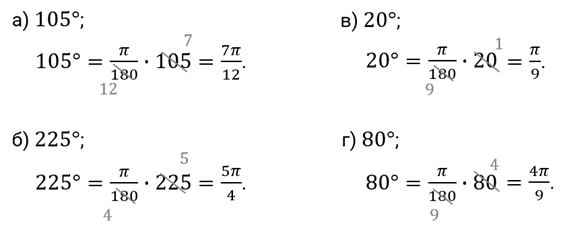
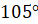
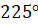
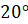
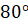
Второе задание. Найдите радианную меру угла, выраженного в градусах: а) ; б) ; в) ; г) .

Решение.

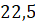
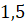
Следующее задание. Чему равен радиус окружности, если дуге длиной  см соответствует центральный угол в  рад?

Решение.

И ещё одно задание. Дуге кругового сектора соответствует угол, равный  рад. Чему равна площадь сектора, если радиус круга равен  см?

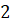
Решение.

Ну а сейчас немного истории.

Впервые радиан как единица измерения был использован английским математиком Роджером Котсом в 1713 году. Он считал, что радиан является наиболее естественной единицей измерения углов. Термин «радиан» впервые появился в печати в 1873 году в экзаменационных билетах Университета Квинса в Белфасте, составленных британским инженером и физиком Джеймсом Томсоном.

В 1960 году XI Генеральной конференцией по мерам и весам радиан был принят в качестве единицы измерения плоских углов в Международной системе единиц (СИ).

Алгебра и начала математического анализа, 10 класс

Урок №29. Радианная мера угла

Перечень вопросов, рассматриваемых в теме:

1) Понятие тригонометрической окружности;

2) Поворот точки вокруг начала координат;

3) Длина дуги окружности и площадь кругового сектора.

Глоссарий по теме

Окружность – это замкнутая линия, все точки которой равноудалены от центра.

Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.

Круг – часть плоскости, ограниченная окружностью.

Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.

Круговой сектор – часть круга, ограниченная двумя радиусами.

Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Теоретический материал для самостоятельного изучения

На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.

Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.

На окружности можно выделить дугу. А если рассмотреть круг – часть плоскости, ограниченной окружностью – то можно выделить круговой сектор.

«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей

Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)

Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии, . А учитывая, что R=1, , осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.

Вычислите длину каждой дуги.

Ответ. длина каждой дуги равна части окружности или

Длина полуокружности равна А так как образовался развернутый угол, то 180.

Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.

рис.3

Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.

Обозначается 1рад.

;

α рад=(180/π α)° (1)

Длину дуги l окружности радиуса R (рис.4)

можно вычислять по формуле(3)

А площадь S кругового сектора радиуса R и дугой рад (рис.5)

находят по формуле: , где (4)

Вернёмся к единичной окружности в координатной плоскости.

Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.

Введём понятие поворота точки. (рис.2)

1. Пусть Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
2. Пусть точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол – α.

При повороте на 0 рад точка остаётся на месте.

Давайте рассмотрим такой пример:

при повороте точки М(1;0) на угол получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на

угол (рис.6)

(рис.6)

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Найти градусную меру угла, равного рад.

Решение: Используя формулу (1),

находим .

Так как , то рад, тогда (2)

Ответ: .

Пример 2. Найти радианную меру угла, равного 60.

Решение:

Вычисляем по формуле (2): рад

рад

При обозначении мер угла, наименование «рад» опускают.

Ответ: рад, рад.

Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера .

Решение: Используя формулу (3),

получим:

Ответ: .

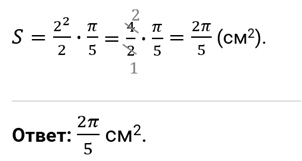
Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла .

Решение:

По формуле (4) вычисляем

Ответ: 45 м²

Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный .

Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как то

прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны Учитывая, что точка М находится в I координатной четверти, её координаты положительны.

На окружности можно найти координаты любой точки.

Ответ: