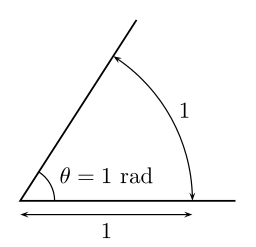Углы в математике (а также в тригонометрии и физике) высчитываются и измеряются в градусах или в радианах. Важно понимать и определять связь между этими единицами измерения, и переводить их из одной в другую. Понимание и определение этой связи позволяет оперировать углами и перевести градусы в радианы, а также осуществить перевод из радиан в градусы с помощью специальной тригонометрической формулы – формулы перевода градусов в радианы. В данной статье мы разберемся, зачем все это нужно конвертировать (и что делать с конвертируемым), выведем формулу для перевода градусов в радианы и обратно – из радианов в градусы, а также разберем несколько примеров из практики по конвертации.
Связь между градусами и радианами
Что такое радиан? Радиан вместе с градусом является выражением угловой меры: это величина, которая используется для измерения плоских углов. Поэтому, когда говорят о таблице градусов и радиан, то имеют в виду таблицу, в которой представлены соответствия угловых градусов радианам (что позволяет вам не находить и не считать самостоятельно на калькуляторе, к примеру).
Как перевести радианы в градусы — есть формула? Для нахождения связи между градусами и радианами, необходимо узнать, сколько будет градусная и ридианная (радиальная) мера какого-либо угла (и для этого нам не нужно пользоваться каким-либо переводчиком онлайн). Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла, необходимо рассчитать определенные данные: длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π·r. Разделим длину дуги на радиус и получим радианную меру угла: π·rr=π рад.
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180°. Следовательно, 180°=π рад.
Связь между радианами и градусами выражается следующей полной формулой
π радиан =180°
Формулы перевода из градусов в радианы и наоборот
Как перевести градусы в радианы не более, чем за минуту? Что делать с координатами в градусах, если нужны в радианах? Из содержания формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и обратно из градусов в радианы (взаимно преобразовывать и пересчитывать).
Как онлайн найти градусную меру угла и сделать пересчет? Выразим 1 радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 рад=180π° – град. мера угла в 1 радиан равна 180π.
Также можно выразить один градус в радианах. Чему равен 1 радиан и во что он будет переходить? Вот простой расчет.
1°=π180рад
Можно произвести приблизительные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 рад=180π°=1803,1416°=57,2956°
Значит, в одном радиане примерно 57 градусов
1°=π180рад=3,1416180рад=0,0175 рад
Один градус содержит 0,0175 радиана.
По какой формуле перевести радианы в градусы?
x рад=х·180π°
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Рассмотрим пример, как перевести градусы в радианы по формуле.
Конечно, в интернете это все может считаться за секунду, но у самостоятельного подсчета другие преимущества.
Пусть α=3,2 рад. Нужно узнать градусную меру этого угла.
Применим формулу перехода от радианов к градусам и получим:
3,2 рад=3,2·180π°≈3,2·1803,14°≈5763,14°≈183,4°
Аналогично можно получить формулу перевода в радианы из градусов.
y°=y·π180рад
Переведем 47 градусов в радианы.
Согласно формуле, умножим 47 на пи и разделим на 180.
47°≈47·3,14180≈0,82 рад
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Угол может измеряться следующими величинами:
- Градусами (и соответствующими ему величинами: угловыми минутами и секундами);
- Радианами.
Градусная мера угла
Если взять развернутый угол (это два прямых угла) и поделить его на 180 частей, то одна такая часть будет называться одним градусом. Для того, чтобы измерить градусную меру угла, необходимо посчитать, сколько раз 1 градус входит в данный угол. Полученное число и будет ответом.
Если угол таков, что его нельзя измерить целым числом, либо же он меньше единичного угла, то используют такие меры измерения как угловые минуты и секунды.
Если градус поделить на 60 частей, то одной такой частью будет минута. В свою же очередь, если минуту разделить на те же 60 частей, то полученным числом будет 1 секунда.
Радианная мера угла
Радианом называют угол, образованный дугой окружности длинной равной радиусу этой окружности.
Длина окружности равна:
l=2⋅π⋅rl=2cdotpicdot r,
где rr — радиус этой окружности.
Тогда, разделив на радиус, получаем, что полный угол в радианах равен:
lr=2⋅π⋅rr=2⋅π радианfrac{l}{r}=frac{2cdotpicdot r}{r}=2cdotpitext{ радиан}
В градусах этот же угол равен, как известно, 360∘360^{circ}.
Отсюда находим связь между радианами и градусами:
2⋅π радиан=360∘2cdotpitext{ радиан}=360^{circ}
Это та главная формула, которая нужна, чтобы переводить градусы в радианы и наоборот.
Один радиан равен:
1 радиан=360∘2⋅π≈57.3∘1text{ радиан}=frac{360^{circ}}{2cdotpi}approx57.3^{circ}
Один радиан в минутах:
1 радиан=360∘2⋅π⋅60≈3438′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60approx3438′
Один радиан в секундах:
1 радиан=360∘2⋅π⋅60⋅60≈206280′′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60cdot60approx206280”
Перевод градусов в радианы
Если по условию известна градусная мера угла, то чтобы перевести ее в радианную, нужно сделать следующие действия: умножить ее на πpi и разделить на 180.
y радиан=π180⋅xytext{ радиан}=frac{pi}{180}cdot x
xx — значение угла в градусах;
yy — значение того же угла в радианах.
Переведите 45 градусов в радианную меру измерения. Ответ округлите до десятой доли.
Решение
45∘=π180⋅45 радиан≈0.8 радиан45^{circ}=frac{pi}{180}cdot 45text{ радиан}approx0.8text{ радиан}
Ответ
0.8 радиан0.8text{ радиан}
Земля совершила треть от половины оборота вокруг Солнца. На какой угол в радианах она повернулась?
Решение
Найдем сначала этот угол в градусах. Полный угол составляет 360∘360^circ. Половина от полного оборота это 180∘180^{circ}. Нам же нужна треть этого угла, то есть:
180∘3=60∘frac{180^circ}{3}=60^circ
Земля отклонилась на угол 60∘60^circ от своего начального положения. Переведем теперь этот угол в радианы:
60∘=π180⋅60 радиан≈1 радиан60^circ=frac{pi}{180}cdot 60text{ радиан}approx1text{ радиан}
Решение
1 радиан1text{ радиан}
Перевод радиан в градусы
Чтобы перевести радианы в градусы, нужно умножить угол в радианах на 180 и разделить на πpi.
y∘=180π⋅xy^{circ}=frac{180}{pi}cdot x
xx — значение угла в радианах;
yy — значение того же угла в градусах.
Переведите 3 радиана в градусную меру угла.
Решение
3 радиана=180π⋅3≈172∘3text{ радиана}=frac{180}{pi}cdot3approx172^circ
Ответ
172∘172^circ
Ищете, где можно заказать задачу по математике недорого? Обратитесь к нашим экспертам в данной области!
Тест по теме «Перевод градусов в радианы и наоборот»
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Что такое радиан
Радиан — это мера угла, альтернативная более привычной градусной.
Определение 1
Один радиан — это угол, который стягивает дуга, длина которой равна радиусу окружности, причём сам угол берёт начало в центре рассматриваемой окружности. Кратко единица измерения «радиан» обозначается сокращением «рад».
Так как радиан является отношением длины к длине, то он является величиной безразмерной. Однако для удобства и избегания путаницы обозначения радианной меры с какой-либо ещё, радианную меру угла принято подписывать «рад».
Формулы и правила
Для того чтобы узнать количество радиан, которые содержит в себе угол, нужно длину дуги разделить на радиус окружности. Размер полного угла из определения радиана равен $2π$ рад.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Через радианную меру можно выразить длину дуги, которая стягивает угол, она будет равна $α cdot R$, где $R$ — радиус окружности, а $α$ – мера угла, выраженная в радианах.
Теперь немного отвлечёмся и узнаем, что такое число $π$.
Определение 2
Число $π$ — это отношение длины окружности к её диаметру. Вне зависимости от диаметра окружности, оно всегда одно и то же и приблизительно равно $3,1415$.
Соответственно определению числа $π$, длина всей окружности равна $2π$, что соответствует величине полного углового оборота, то есть $360º$. Число $π$ используют в радианной мере.
Рисунок 1. Число пи в радианах равно 3,1415. Автор24 — интернет-биржа студенческих работ
«Градусы в радианы: формула» 👇
А сейчас рассмотрим, как осуществить перевод из рад в градусы. Для этого нужно помнить, что число «Пи» равно $180º$ и при необходимости перевода радиан в градусы подставлять вместо $π$ это значение.
Пример 1
Найдите, сколько градусов в 1 радиане.
Решение
В половине окружности, равной 180 градусам, содержится приблизительно 3,1415 радиан, соответственно, для того чтоб найти, сколько градусов в одном радиане, нужно 180 разделить на число «Пи», получим:
$1 рад = frac{180}{ π} ≈ 57,29º$
В случае же если нужно осуществить перевод углов в градусах в радианы, необходимо значение в радианах для одного градуса умножать на градусное значение угла.
Пример 2
Чему равен 1 градус в радианах?
Решение
Число π соответствует $180º$, то есть: $π= 180º$, а один градус в 180 раз меньше, чем 180 градусов. Поэтому необходимо всё выражение разделить на $180$, получаем: $1º= frac{π}{180}left(1right)$. Теперь вы знаете, сколько радиан в 1 градусе.
Для того чтобы перевести любой угол в радианы, достаточно число, полученное для угла в один градус с использованием формулы $(1)$ умножить на значение угла в градусах, например:
$45º=frac{π cdot 45}{180} = frac{ π}{4}$
В общем виде эта формула для перевода угла, заданного в градусах в радианы будет выглядеть так:
$y рад = frac{π cdot x}{180}$, где $x$ — градусная мера угла, а $y$ — мера угла в радианах.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 февраля 2023 года; проверки требует 1 правка.
| Радиан | |
|---|---|
| рад | |
 1 радиан — центральный угол, длина дуги которого равна радиусу окружности |
|
| Величина | величина угла |
| Система | СИ |
| Тип | основная |
 Медиафайлы на Викискладе |
Некоторые важные углы, измеренные в радианах. Все многоугольники, изображённые на диаграммах, — правильные
Радиа́н (русское обозначение: рад, международное: rad; от лат. radius — луч, радиус) — угол, соответствующий дуге, длина которой равна её радиусу[1]. Единица измерения плоских углов в Международной системе единиц (СИ), а также в системах единиц СГС и МКГСС[2].
Радианная мера — угловая мера, в которой за единицу принимается угол в 1 радиан. То есть, радианная мера любого угла — это отношение этого угла к радиану[3]. Из определения следует, что величина полного угла равна 2π радиан (см. рис. справа).
Определить радианную меру можно и так: радианная мера угла — отношение длины дуги окружности, находящейся между сторонами угла, к радиусу этой окружности, когда центр окружности совпадает с вершиной угла. В геометрии для определения радианной меры угла используют единичную окружность с центром в вершине угла; тогда радианная мера угла равна длине дуги единичной окружности между сторонами угла[4][5].
Поскольку длина дуги окружности пропорциональна её угловой мере и радиусу, длина дуги окружности радиуса R и угловой величины α, измеренной в радианах, равна α ∙ R.
Так как величина угла, выраженная в радианах, равна отношению длины дуги окружности (м) к длине её радиуса (м), угол в радианном измерении — величина безразмерная.
Радиан в Международной системе единиц (СИ)[править | править код]
В качестве единицы измерения плоских углов в Международной системе единиц (СИ) радиан был принят XI Генеральной конференцией по мерам и весам в 1960 году одновременно с принятием системы СИ в целом[6]. В настоящее время в системе СИ радиан квалифицируется как когерентная[7] безразмерная производная единица СИ, имеющая специальные наименование и обозначение. Русское обозначение — рад, международное — rad[8].
Безразмерность плоского угла означает, что единицей его измерения является число один. Однако, применительно к плоскому углу единице «один» было присвоено специальное наименование «радиан» для того, чтобы в каждом конкретном случае облегчить понимание того, какая именно величина имеется в виду[9].
Кратные и дольные единицы[править | править код]
Десятичные кратные и дольные единицы радиана образуются с помощью стандартных приставок СИ, однако используются редко. Так, в миллирадианах, микрорадианах и нанорадианах измеряется угловое разрешение в астрономии. В кратных единицах (килорадианах и т. д.) измеряется
набег угловой фазы. Сокращённое обозначение (рад, rad) основной и производных единиц не следует путать с устаревшей единицей измерения поглощённой дозы ионизирующего излучения — рад.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 рад | декарадиан | дарад | darad | 10−1 рад | децирадиан | драд | drad |
| 102 рад | гекторадиан | град | hrad | 10−2 рад | сантирадиан | срад | crad |
| 103 рад | килорадиан | крад | krad | 10−3 рад | миллирадиан | мрад | mrad |
| 106 рад | мегарадиан | Мрад | Mrad | 10−6 рад | микрорадиан | мкрад | µrad |
| 109 рад | гигарадиан | Град | Grad | 10−9 рад | нанорадиан | нрад | nrad |
| 1012 рад | терарадиан | Трад | Trad | 10−12 рад | пикорадиан | прад | prad |
| 1015 рад | петарадиан | Прад | Prad | 10−15 рад | фемторадиан | фрад | frad |
| 1018 рад | эксарадиан | Эрад | Erad | 10−18 рад | атторадиан | арад | arad |
| 1021 рад | зеттарадиан | Зрад | Zrad | 10−21 рад | зепторадиан | зрад | zrad |
| 1024 рад | иоттарадиан | Ирад | Yrad | 10−24 рад | иокторадиан | ирад | yrad |
| 1027 рад | роннарадиан | Ррад | Rrad | 10−27 рад | ронторадиан | ррад | rrad |
| 1030 рад | кветтарадиан | Кврад | Qrad | 10−30 рад | квекторадиан | кврад | qrad |
| рекомендовано к применению применять не рекомендуется не применяются или редко применяются на практике |
Связь радиана с другими единицами[править | править код]
Пропорциональное соотношение радиана с другими единицами измерения углов описывается формулой:
- 1 радиан = 1/(2π) оборотов = 180/π градусов = 200/π градов.
Очевидно, развернутый угол равен 
или 
радианам. Отсюда вытекает тривиальная формула пересчёта из градусов, минут и секунд в радианы и наоборот.
- a[°] = α[рад] × (360° / (2π)) или α[рад] × (180° / π),
- α[рад] = a[°] : (180° / π) = a[°] × (π / 180°),
где α[рад] — угол в радианах, a[°] — угол в градусах.
1 рад (или 
) = 
(мнемоническое правило запоминания в градусах-минутах-секундах: “Число радиана и порядок шутя пишу наизусть”, где число букв в каждом слове равно соответствующей цифре в записи значения радиана, до десятой доли угловой секунды)
(или 1 рад в минутах) = 
(или 1 рад в секундах) = 
В метрической системе угловых мер прямой угол делится на 100 градов и каждый град на 100 сантиградов, который, в свою очередь, делится на сотые доли сантиграда, так что
(или 1 рад в сотых долях «сантиграда») = 
Употреблять его практически не приходится, так как метрическая система угловых мер пока не получила широкого распространения.
Чтобы легче запомнить, как переводят радианы в градусы и обратно, заметим:
Переводя радианы в градусы (или в минуты, или в секунды), мы из отвлеченного числа (
) делаем именованное (
) и поэтому должны множить на 
или 
;
Переводя градусы в радианы, мы, наоборот, уничтожаем наименование: получаем отвлечённое число; значит, здесь надо делить на или 
либо же умножать на перевёрнутую
дробь 
Пример 1. Перевести в радианы 
![{displaystyle {boldsymbol {alpha }}[mathrm {rad} ]eqcirc 5^{circ }={frac {5^{circ }}{displaystyle {rho ^{circ }}}}~mathrm {rad} =0{,}0872_{6}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/199f5d22ca4b2c3e1462f8102b709f2c1a55ebeb)
[10]
[10]
[10]
[10] 
Альтернативный способ предусматривает перевод минут и секунд в десятичные (сотые и десятитысячные) доли градуса,
и однократного деления на 
(как правило, этот способ более точен)
Пример 2. Перевести в градусы 1 радиан.
![a[^{circ }]eqcirc 1cdot {frac {360^{circ }}{2pi }}=1cdot 57{,}29578^{circ }=57{,}{boldsymbol {29578}}^{circ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f43329e10793951c24756957d3c38ae9481215c5)
Итого 
Таблица градусов, радиан и град[править | править код]
| Угол, в долях от полного |
Градусы | Радианы | Грады | Синус | Косинус | Тангенс |
|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не определён |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не определён |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Радианная мера в математическом анализе[править | править код]
При рассмотрении тригонометрических функций в математическом анализе всегда считается, что аргумент выражен в радианах, что упрощает запись; при этом само обозначение рад (rad) часто опускается.
При малых углах синус и тангенс угла, выраженного в радианах, приблизительно равны самому углу (в радианах), что удобно при приближённых вычислениях. При углах менее 
, приближение можно считать верным до третьего знака после запятой. Если угол меньше 
, — то до шестого знака после запятой[12]:
История[править | править код]
Первое использование радиана вместо углового градуса для деления окружности на части с помощью ее собственного радиуса обычно приписывают Роджеру Котсу (XVIII век), который считал эту единицу измерения угла наиболее естественной[13]. Однако идея измерять длину дуги радиусом окружности использовалась и другими математиками. Например, Аль-Каши использовал единицу измерения, названную им «часть диаметра», которая равнялась 1/60 радиана. Также им использовались и более мелкие производные единицы[14].
Термин «радиан» впервые появился в печати 5 июня 1873 года в экзаменационных билетах, составленных Джеймсом Томсоном из Университета Квинса в Белфасте. Томсон использовал термин не позднее 1871 года, в то время как Томас Мьюр из Сент-Эндрюсского университета в 1869 году колебался в выборе между терминами «рад», «радиал» и «радиан». В 1874 году Мьюр, после консультаций с Джеймсом Томсоном, решил использовать термин «радиан»[15][16][17].
См. также[править | править код]
- Град, минута, секунда
- Градус, минута, секунда
- Оборот (единица измерения)
- Парсек
- Стерадиан
- Тысячная (угол)
Примечания[править | править код]
- ↑ Радиан // Математическая энциклопедия (в 5 томах). — М.: Советская энциклопедия, 1984. — Т. 4.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 98. — 240 с. — ISBN 5-7050-0118-5.
- ↑ Выгодский, 1965.
- ↑ Гельфанд, Львовский, Тоом, 2002.
- ↑ David E. Joyce. Measurement of Angles (англ.). Dave’s Short Trig Course. Clark University. Дата обращения: 8 сентября 2015. Архивировано 7 сентября 2015 года.
- ↑ Резолюция 12 XI Генеральной конференции по мерам и весам (1960) (англ.). Международное бюро мер и весов. Дата обращения: 19 декабря 2014. Архивировано 28 июля 2012 года.
- ↑ Производная единица измерения называется когерентной, если она выражается в виде произведения степеней основных единиц измерения с коэффициентом пропорциональности, равным единице.
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин. Дата обращения: 18 сентября 2012. Архивировано из оригинала 10 ноября 2012 года.
- ↑ Units for dimensionless quantities, also called quantities of dimension one (англ.). SI Brochure: The International System of Units (SI). Международное бюро мер и весов (2006). Дата обращения: 19 декабря 2014. Архивировано 7 октября 2014 года.
- ↑ 1 2 3 4 Лишние цифры [после четвёртого знака после запятой] в выражениях минут и секунд зачастую отбрасываются ввиду того, что следующая цифра в выражении градусов неизвестна, и, следовательно, писать цифры дальше четвёртой [обозначены нижним индексом] — напрасный труд.
- ↑ Abramowitz & Stegun, 1972, p. 74, 4.3.46.
- ↑
- (точность нарушается в четвертом знаке после запятой)
- (точность не выдерживается в седьмом знаке после запятой)
Именно поэтому промежутки шкал(ы) на счётной линейке имеют пределы и ; ниже этого значения (до 0) разграфки нет, так как углы (в радианах) совпадают со значениями синусов/тангенсов в пределах точности линейки (Панов Д. Ю. Счётная линейка. — 25-е изд. — М.: изд-во Наука (Гл. ред. физ.-мат. литературы), 1982. — 176 с.)
- ↑ O’Connor, J. J.; Robertson, E. F. Biography of Roger Cotes. The MacTutor History of Mathematics (февраль 2005). Дата обращения: 3 февраля 2014. Архивировано 24 сентября 2012 года.
- ↑ Luckey, Paul. Der Lehrbrief über den kreisumfang von Gamshid b. Mas’ud al-Kasi (нем.) / Siggel, A.. — Berlin: Akademie Verlag, 1953. — S. 40.
- ↑ Florian Cajori. History of Mathematical Notations (неопр.). — 1929. — Т. 2. — С. 147—148. — ISBN 0-486-67766-4.
- ↑ Muir, Thos. The Term “Radian” in Trigonometry (англ.) // Nature. — 1910. — Vol. 83, no. 2110. — P. 156. — doi:10.1038/083156a0. — Bibcode: 1910Natur..83..156M.Thomson, James. The Term “Radian” in Trigonometry (англ.) // Nature. — 1910. — Vol. 83, no. 2112. — P. 217. — doi:10.1038/083217c0. — Bibcode: 1910Natur..83..217T.Muir, Thos. The Term “Radian” in Trigonometry (англ.) // Nature. — 1910. — Vol. 83, no. 2120. — P. 459—460. — doi:10.1038/083459d0. — Bibcode: 1910Natur..83..459M.
- ↑ Miller, Jeff Earliest Known Uses of Some of the Words of Mathematics (23 ноября 2009). Дата обращения: 30 сентября 2011. Архивировано 18 января 2021 года.
Литература[править | править код]
- Выгодский М. Я. Справочник по элементарной математике. — Наука, 1965. — С. 340—343. — 424 с.
- Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия. — М.: МЦНМО, 2002. — С. 7—8. — 199 с. — ISBN 5-94057-050-X.
- Abramowitz, M.; Stegun, I. A. (англ.). — New York: Dover Publications, 1972. — ISBN 0-486-61272-4.
Перевод градусов в радианы и обратно: формулы, примеры
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Связь между градусами и радианами
Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 р а д = 180 π ° – градусная мера угла в 1 радиан равна 180 π .
Также можно выразить один градус в радианах.
1 ° = π 180 р а д
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °
Значит, в одном радиане примерно 57 градусов
1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д
Один градус содержит 0,0175 радиана.
Формула перевода радианов в градусы
x р а д = х · 180 π °
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Пример 1. Перевод из радианов в градусы
Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.
Применим формулу перехода от радианов к градусам и получим:
3 , 2 р а д = 3 , 2 · 180 π ° ≈ 3 , 2 · 180 3 , 14 ° ≈ 576 3 , 14 ° ≈ 183 , 4 °
Аналогично можно получить формулу перевода из градусов в радианы.
Формула перевода из градусов в радианы
y ° = y · π 180 р а д
Переведем 47 градусов в радианы.
Согласно формуле, умножим 47 на пи и разделим на 180.
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
http://skysmart.ru/articles/mathematic/edinichnaya-okruzhnost
[/spoiler]
