Как найти радиус бассейна

Для того что бы вычислить радиус круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить радиус круга.
Радиус круга рассчитывается по следующим формулам:

1. Если нам известна длина:

   Формула для расчета радиуса круга через его длину:
   R=P/(2π)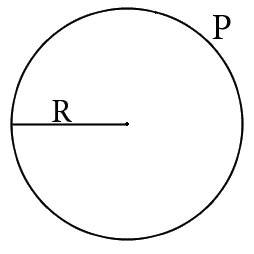

   

2. Если нам известна площадь:

   Формула для расчета радиус круга через площадь:
   R=

   √

   S/π

   

3. Если нам известен диаметр:

   Формула для расчета радиус круга через диаметр:
   R=D/2

   

Где R – радиус круга, S – площадь круга, P – длина круга, D – диаметр, π – число Пи которое всегда примерно равно 3,14.

При строительстве или покупке нового бассейна его полезный объем указывается в технической документации.

Если такая информация утеряна, вычисления можно произвести самостоятельно. Для круглой чаши достаточно минимума данных и пары несложных формул.

Зачем нужно проводить вычисление?

Еще на стадии проектирования необходимо знать количество воды, вмещаемой бассейном. Это поможет окончательно определиться с формой и размерами резервуара, спланировать расходы на установку.

Правильный расчет объема важен для работоспособности всей системы.

От этого параметра зависят:

• требуемая мощность источника, из которого поступает вода для заполнения чаши и последующей замены;
• количество химических средств, дозировка которых на единицу объема указывается производителями в инструкции;
• характеристики фильтров, насосов, шлангов для обеспечения хорошей работы бассейна;
• организация циркуляции воды в больших резервуарах.

Важно! Объем бассейна отражается на затратах по его обслуживанию. Необходимо заранее просчитать финансы, достаточные для выбранного режима эксплуатации.

Какие данные необходимы?

Для расчета вместимости бассейна применяются базовые геометрические правила. Учитывая круглую форму чаши, внутреннее пространство можно представить как идеальный цилиндр.

Для вычислений потребуются 3 величины:

• глубина;
• диаметр или радиус;
• константа π = 3,14.

За глубину принимается не высота бортов, а уровень воды в бассейне. Существуют конструкции, где вода постоянно переливается через край, но в большинстве случаев борта будут выше на 15-20 см.

Предполагается, что глубина бассейна одинакова по всей его площади. Если это не так, для приблизительных подсчетов можно взять среднее значение.

Справка. Если нет возможности узнать диаметр бассейна, можно рулеткой измерить длину его окружности L_окр по внутренней стороне борта. Затем воспользоваться формулой вычисления диаметра: D=L_окр/ 3,14.

Как посчитать: пошаговая инструкция

Чтобы узнать вместимость круглого бассейна, нужно площадь основания S резервуара умножить на его высоту H: V = S x H.

Необходимо внимательно относиться к единицам измерения. Например, все величины могут быть измерены в метрах. Тогда результат будет измеряться в кубометрах. Затем его можно пересчитать в литры, если в этом есть потребность. В зависимости от того, какие параметры бассейна известны, применяются различные алгоритмы расчета.

Если глубина бассейна равномерно изменяется от одного края к другому, для расчетов объема применяется среднее значение: сумму максимальной и минимальной величин нужно поделить на два: H_сред = (H_мин + H _макс)/2.

По диаметру

Площадь основания S вычисляется как произведение 1/4 квадрата диаметра на постоянную π.

Полученное произведение умножают на высоту воды в бассейне: V = π * D²/4 * H.

Поскольку значение π всегда одинаково и равно 3,14, формулу можно упростить: V = D² * H * 0,78.

По радиусу

Радиус составляет ровно половину от диаметра. Для расчета объема можно воспользоваться аналогичной формулой: V = π * R² * H.

Рекомендуется округлять полученное значение в большую сторону, чтобы результат получился с небольшим запасом.

Для овальной чаши

Если бассейн не абсолютно круглой формы, а слегка вытянутый, площадь его поперечного сечения определяют на основании двух измерений: a – половины длины и b – половины ширины резервуара: S = π*a * b.

Тогда: V = 3,14 * a * b * H, где H – высота заливаемой воды.

Примеры расчетов

Чтобы наглядно продемонстрировать применение приведенных выше правил, рассмотрим несколько конкретных примеров.

В кубометрах

Примеры:

1. Бассейн диаметром 3 м планируется наполнить на глубину 1,5 м. Чтобы определить объем, воспользуемся формулой: V = π * D²/4 * H = 3,14 *3² /4 * 1,5 = 10,5975 м³.
2. При величине радиуса круглой чаши 5 м и высоте бортов 2 м в резервуар можно максимально залить: V = π * R² * H = 3,14 * 5² * 2 = 157 м³.
3. Допустим, что минимальная высота наполнения составляет 80 см, а глубина на другой стороне 120 см. При диаметре бассейна 300 см получаем: H_ср = (H₁ + H₂)/2 = (80 + 120)/2 = 100 см, V= 300² * 100 * 0,78 = 7 020 000 (см³) = 7,020 м³.

Справка. В одном кубометре (1 м³) содержится 10⁶ кубических сантиметров воды.

В литрах

Линейные величины традиционно измеряют в метрах и сантиметрах, а жидкости в литрах. Один литр воды теоретически представляет собой кубик со стороной 10 см. В 1 м³ таких кубиков 1000 штук. Таким образом: 1м³ = 1000 литров.

Масса такого объема воды равна 1 тонне.

Примеры:

1. Определим вместимость конструкции диаметром 1 м и глубиной 0,5 м: V = π * D²/4 * H = 3,14 * 1² /4 * 0,5 = 0,3925 м³. Чтобы получить объем в литрах, умножаем на тысячу: V = 392,5 л.
2. Большой резервуар шириной 500 см и глубиной 200 см способен принять: V = D² * H * 0,78 = 500² * 200 * 0,78 = 39 000 000 (см³) = 39 тыс.л.
3. Овальный бассейн с длиной 10 м и шириной 4 м, заполненный на 1,5 м, обсчитывается следующим образом: S =π*ab = 3,14 * (10/2) * (4/2) = 31,4 (м²), V = S * H = 31,4 * 1,5 = 47,1 (м³) = 47 100 л.

Заключение

Определение объема круглого бассейна не требует специальных умений. Провести измерения на местности с помощью рулетки или лазерного дальномера, а потом подставить полученные значения в формулы может любой образованный человек. Если резервуар имеет сложную конфигурацию, лучше обратиться в строительную фирму.

Понимание различных размеров вашего бассейна важно, когда вы покупаете чехлы и другие аксессуары. Вам также необходимо знать объем, чтобы правильно обработать бассейн химикатами. Некоторые общие измерения, которые вы можете знать:

Оценка количества воды в бассейне полезна для добавления химикатов.

• Окружность или периметр бассейна
• Площадь поверхности воды
• Объем воды в бассейне.

Конкретные формулы, используемые для получения этих измерений, будут различаться в зависимости от формы пула, и вычисления могут быть простыми или сложными, в зависимости от этой формы. Например, прямоугольный пул, который является однородным по глубине во всех областях, довольно легко измерить, в то время как неправильная изогнутая форма может быть значительно более сложной.

В некоторых случаях измерения объема воды могут быть точной оценкой, а не точным измерением или расчетом. Но есть ряд основных математических формул, которые дадут вам довольно точные определения важных измерений.

Некоторые измерения требуют только рулетки, в то время как другие – вычисления, основанные на этих измерениях. Лучше всего делать измерения в футах и ​​долях футов. Например, вместо того, чтобы измерять длину бассейна как 30 футов 3 дюйма, измерьте его как 30,25 фута.

Периметр / Окружность

Периметр вашего пула (или окружность, если ваш пул совершенно круглый) – это измерение, которое само по себе не имеет большого количества применений, но может оказаться полезным при выполнении других вычислений. Периметр легко измерить обычной рулеткой.

Прямоугольный или квадратный бассейн

Используя квадратный или прямоугольный пул, вы, конечно, можете измерить каждую из четырех сторон и сложить измерения вместе, чтобы определить полный периметр, хотя на самом деле необходимо измерить только одну сторону квадратного пула, а затем умножить на 4.

С прямоугольным пулом вы можете измерить одну короткую сторону, а затем умножить на 2; затем измерьте длинную сторону и умножьте на 2 – и затем сложите эти измерения вместе, чтобы определить полный периметр.

Например, прямоугольный пул, который имеет 20 футов с одной стороны и 40 футов с другой стороны, может иметь периметр, рассчитанный так: (20 x 2) + (40 x 2) = 120 футов.

Круглый бассейн

Круглый бассейн также можно измерить, уложив рулетку вокруг внешнего края бассейна. Однако, если вы уже знаете диаметр бассейна – таким образом продаются многие надземные бассейны – вы можете определить окружность по формуле: «Окружность = pi x диаметр». Ради этого расчета вы можете использовать 3,14 в качестве значения для пи. Итак, круглый бассейн диаметром 20 футов имеет окружность 3,14 х 20 или 62,8 фута.

Нерегулярный изогнутый бассейн

Здесь также лучший способ (действительно единственный практический метод) состоит в том, чтобы расположить рулетку вдоль края бассейна как можно ближе к воде. Другие способы расчета периметра нерегулярного пула являются сложными.

Площадь поверхности

Площадь поверхности является важным измерением, которое вступает в игру, когда вы хотите рассчитать объем воды или при покупке покрытия для бассейна. Достаточно просто рассчитать площадь поверхности круглого, квадратного или прямоугольного бассейна, но немного сложнее с нерегулярным, изогнутым бассейном.

Прямоугольный или квадратный бассейн

С квадратной или прямоугольной формулой формула для расчета площади просто умножить длину на ширину. Таким образом, бассейн длиной 40 футов и шириной 30 футов будет иметь площадь 1200 квадратных футов (40 х 30).

Круглый бассейн

Формула для площади круга: “pi x r² «где« r »- ​​радиус круга. Поэтому, если у вас есть бассейн диаметром 20 футов, радиус равен 10 футам, и формула будет рассчитана следующим образом: 3,14 x 10² = 314 квадратных футов.

Нерегулярный изогнутый бассейн

кредит: Брайан TrandemSketching неправильной формы на сетке бумаги может помочь вам рассчитать площадь поверхности.

Все становится немного сложнее, когда вы пытаетесь рассчитать площадь поверхности бассейна с почечной или другой неправильной изогнутой формой. Самый простой способ приблизить площадь поверхности – сделать эскиз формы бассейна на миллиметровой бумаге, используя шкалу, в которой квадрат 1/4 дюйма представляет 1 фут. Просто подсчитав количество квадратов, занимаемых формой почки, вы можете точно оценить площадь поверхности вашего бассейна.

Объем воды

Суть расчета объема воды заключается в том, чтобы взять площадь поверхности и умножить ее на глубину бассейна. Этот расчет даст вам объем пула в кубических футах. Но объем пула обычно измеряется в галлонах, поэтому, чтобы преобразовать кубические метры в галлоны, просто умножьте кубические метры на 7,48. (Один кубический фут воды содержит 7,48 галлона.)

Прямоугольный или квадратный бассейн

С абсолютно квадратным или прямоугольным пулом, который имеет постоянную глубину в каждой точке, вычисление может быть сформулировано как «S x D = V», где S представляет площадь поверхности, а D представляет глубину. Таким образом, бассейн, имеющий площадь 1200 квадратных футов и глубину 6 футов, вмещает 7200 кубических футов воды.

Чтобы перевести в галлоны, умножьте это число на 7,48. В этом примере бассейн с 7200 кубическими футами воды вмещает 53 856 галлонов.

Что если у вашего бассейна наклонное дно? Для большинства целей метод, описанный здесь, будет отлично работать, когда вам нужно оценить объем и объем галлона. Если у вас есть пул с глубоким концом или наклонным дном, можно быть более точным, набросав пул и разделив его на разные сегменты, а затем рассчитав объемы по отдельности и сложив их вместе.

кредит: Bryan TrandemA Эскиз вида сбоку может помочь вам рассчитать объем, разделив пул на различные секции.

На прилагаемой диаграмме пул, если смотреть со стороны, в поперечном сечении, показывающий, как вы можете визуализировать пул в виде двух отдельных областей для целей точного расчета объема.

Другой метод состоит в том, чтобы просто измерить бассейн в самой глубокой части и в самой мелкой части, и взять среднее из двух измерений как глубину бассейна. Этот метод может подойти, если вам не нужно быть очень точным в своих расчетах.

Круглый бассейн

Чтобы рассчитать объем круглого пула, снова умножьте площадь поверхности, как описано выше, затем умножьте ее на глубину. Бассейн диаметром 20 футов имел площадь поверхности 314 квадратных футов. Если этот пул имеет глубину 4 фута, объем будет 1256 кубических футов.

Чтобы преобразовать это измерение в галлоны, умножьте на 7,48. Таким образом, пул, содержащий 1256 кубических футов, имеет емкость в 9 394,88 галлона.

Нерегулярный изогнутый бассейн

Для бассейна, имеющего форму почек или другой неправильной формы, метод почти такой же: возьмите оценочную площадь поверхности и умножьте на глубину. Затем возьмите это измерение в кубических метрах и умножьте на 7,48, чтобы получить объем в галлонах вашего бассейна.