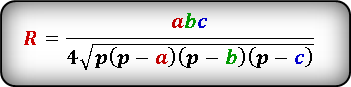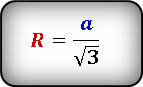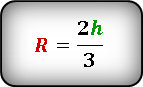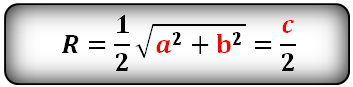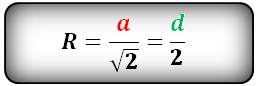Нахождение радиуса вписанной в правильный многоугольник окружности
В публикации представлена формула, с помощью которой можно найти радиус окружности, вписанной в правильный многоугольник, а также приведен пример решения задачи для лучшего понимания представленного материала.
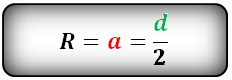
Формула расчета радиуса окружности
На рисунке изображен правильный шестиугольник со вписанной в него окружностью, но формула ниже подходит для любого правильного n-угольника.
где a – длина стороны.
Примечание: зная радиус вписанного круга можно найти сторону равностороннего n-угольника:
Пример задачи
Вычислите радиус вписанной в правильный восьмиугольник окружности, если длина его стороны составляет 12 см.
Решение:
Воспользуемся первой формулой, подставив в нее известное значение.
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6c5e0348da0e3aad • Your IP : 178.45.231.185 • Performance & security by Cloudflare
Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать – как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
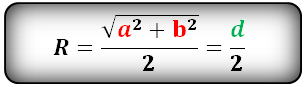
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
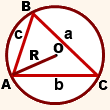
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
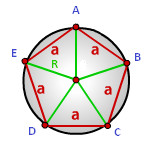
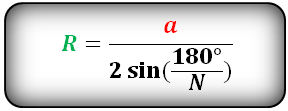
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://mathvox.ru/geometria/mnogougolniki/glava-2-chetirehugolniki-i-ih-svoistva/radius-okrujnosti-opisannoi-okolo-chetirehugolnika/
http://skysmart.ru/articles/mathematic/radius-okruzhnosti
[/spoiler]
Разберем ещё одну очень сложную задачу из открытого банка заданий ФИПИ. Чем она «очень сложная»? Наверное, тем, что в ней для быстрого решения необходимо выполнить дополнительное построение. А это всегда не просто – вариантов всегда очень много, а найти нужно «единственный рабочий».
Задание №25, геометрия, снова окружность. Поехали?
Задача
Рассуждение
- Четырёхугольник вписан. А любой можно вписать?
- Угол между диагоналями известен, возможно площадь через диагонали и угол между ними.
- Может свойство пересекающихся хорд окружности (диагонали).
- Радиус описанной окружности, возможно через теорему синусов.
Решение
Построим вписанный в окружность четырёхугольник, с пересекающимися в точке K диагоналями.
Достроим хорду параллельную любой из диагоналей четырёхугольника.
Четырёхугольник ABDE – трапеция или прямоугольник (квадрат отнесём к прямоугольникам) т.к. противолежащие стороны AE и BD параллельны, а накрестлежащие углы при секущей BD равны, то и дуги (и хорды) равны. Получается, в любом случае AB = DE.
Теперь рассмотрим четырёхугольник ACDE.
Это вписанный в окружность четырёхугольник (все вершины принадлежат окружности).
В отличии от треугольников (можно вписать всегда), четырёхугольник получится вписать в окружность только если выполнено условие: сумма противолежащих углов в сумме равна 180°.
Можно найти угол ∠CDE = 120°.
Рассмотрим ∆CDE.
В этом треугольнике нам известно две стороны (CD и DE) и угол между ними (∠CDE) – теорема косинусов.
По теореме косинусов находим сторону CE (CD = 10; DE = 40; cos∠CDE = -0,5):
CE = 10√21.
И уже по теореме синусов найдём радиус описанной окружности для ∆CDE.
Не забываем, что sin120° = sin60° (формулы приведения).
Ответ: 10√7
Заключение
Что пригодилось:
- Интуиция для удачного построения;
- Свойство углов четырёхугольника вписанного в окружность;
- Теорема косинусов;
- Теорема синусов.
Применение
Подобные задания можно найти на сайте ФИПИ или перейти по этой ссылке. Пробуйте, решайте, рассказывайте о своих способах решения. Удачи!



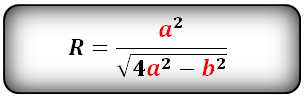
Формула радиуса описанной окружности треугольника ( R ) :



Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
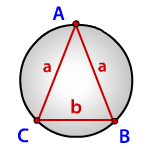
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b – стороны треугольника
Формула радиуса описанной окружности равнобедренного треугольника(R):
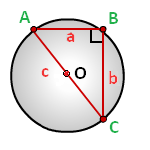
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a, b – катеты прямоугольного треугольника
c – гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
a – боковые стороны трапеции
c – нижнее основание
b – верхнее основание
d – диагональ
p – полупериметр треугольника DBC
p = (a+d+c)/2
Формула радиуса описанной окружности равнобокой трапеции, (R)
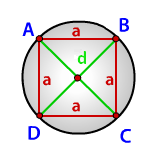
Радиус описанной окружности квадрата равен половине его диагонали
a – сторона квадрата
d – диагональ
Формула радиуса описанной окружности квадрата (R):
Радиус описанной окружности прямоугольника равен половине его диагонали
a, b – стороны прямоугольника
d – диагональ
Формула радиуса описанной окружности прямоугольника (R):
a – сторона многоугольника
N – количество сторон многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
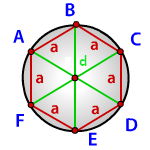
a – сторона шестиугольника
d – диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.
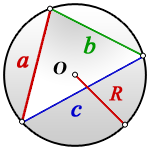
Радиус описанной окружности для произвольного треугольника
Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):
где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.
Центр описанной окружности лежит:
у остроугольного треугольника — внутри треугольника;
у прямоугольного — на середине гипотенузы;
у тупоугольного — вне треугольника, напротив тупого угла.
Радиус описанной окружности для прямоугольного треугольника
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:
Окружность, описанная около многоугольника
Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.
Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.
Радиус окружности, описанной около правильного многоугольника
Формула радиуса описанной окружности для правильного многоугольника
где a — длина стороны многоугольника, n — количество его сторон.
Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.
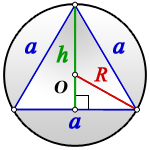
Радиус описанной окружности правильного треугольника

Если без иррациональности в знаменателе —
У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:
Радиус описанной окружности квадрата
Формула радиуса описанной окружности для квадрата
Если без иррациональности в знаменателе —
Радиус описанной окружности правильного шестиугольника
Формула радиуса описанной окружности для правильного шестиугольника
Свойства вписанных и описанных четыехугольников
Содержание:
- Вписанный четырехугольник, особенности, основные свойства фигуры
- Описанный четырехугольник, особенности, основные свойства фигуры
- Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
- Чему равна сумма противоположных углов вписанного в окружность четырехугольника
- Как найти радиус вписанного в окружность четырехугольника, формула
Вписанный четырехугольник, особенности, основные свойства фигуры
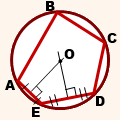
Вписанный в окружность четырехугольник является таким четырехугольником, каждая из вершин которого принадлежит описанной около него окружности.
Вписанный в окружность четырехугольник изображен на рисунке:
Здесь около четырехугольника ABCD описана окружность, а сам этот четырехугольник можно назвать вписанным в данную окружность. Этот вывод можно сделать на основании определения, рассмотренного ранее, так как точки A, B, C, D являются одновременно и вершинами четырехугольника, и принадлежат описанной около него окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Теорема 1
Какой-либо четырехугольник может быть вписан в некую окружность при условии, что его противолежащие углы в сумме дают 180°.
Теорема 2
В том случае, когда противолежащие углы некого четырехугольника в сумме составляют 180°, данный четырехугольник может быть вписан в окружность.
На примере рисунка запишем смысл изложенной теоремы:
(left. begin{array}{l} angle A + angle C = {180^o}\ angle B + angle D = {180^o} end{array} right} Leftrightarrow ABCD) треугольник вписан в окружность.
Следствие 1
Не каждый параллелограмм допустимо вписывать в окружность, лишь прямоугольники — в том числе квадраты.
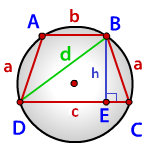
Если какой-то четырехугольник вписан в окружность, то ее центральная точка совпадет с точкой, в которой пересекаются диагонали вписанного четырехугольника. При этом радиус описанной около четырехугольника окружности составит половину от длины его диагонали, то есть:
(R = frac{1}{2}BD)
Радиус, окружности, описанной около некого четырехугольника с прямыми углами, можно вычислить с помощью следующей формулы, содержащей стороны прямоугольника:
(R = frac{1}{2}sqrt {A{B^2} + A{D^2}}.)
Представим, что прямоугольник имеет стороны, которые равны a и b. Тогда справедливо следующее соотношение:
(R = frac{1}{2}sqrt {{a^2} + {b^2}})
Следствие 2
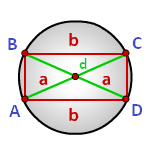
Допустимо вписать в окружность лишь такую трапецию, которая является равнобедренной.
Выведем формулу для вычисления радиуса окружности, которая описана около равнобедренной трапеции. Искомая величина равна радиусу окружности, описанной около одного из треугольников, имеющего те же вершины, что и рассматриваемая трапеция:
ABC, ABD, ACD или BCD.
Описанный четырехугольник, особенности, основные свойства фигуры
Описанным четырехугольником называют такую геометрическую фигуру с четырьмя углами, каждая из сторон которой является касательной к окружности. Данная окружность считается вписанной в рассматриваемый четырехугольник.
Теорема 3
В любой четырехугольник допустимо вписать какую-либо окружность при условии, что его противолежащие стороны в сумме равны.
Заметим, что в данном случае соблюдено условие:
AB+CD=BC+AD
На основе теоремы можно сформулировать обратное утверждение. В том случае, когда противоположные стороны четырехугольника в сумме равны, то есть AB+CD=BC+AD, в такой четырехугольник ABCD допустимо вписать какую-либо окружность.
Теорема 4
Центральная точка окружности, вписанной в четырехугольник, совпадает с точкой, в которой пересекаются биссектрисы данной геометрической фигуры.
Заметим, что на рисунке биссектрисами углов, которые имеет четырехугольник ABCD, являются следующие отрезки:
- AO;
- BO;
- CO;
- DO.
В результате:
(angle BAO = angle DAO)
(angle ABO = angle CBO) и так далее.
Теорема 5
Точки, в которых вписанная окружность касается описанного четырехугольника, расположены на сторонах с началом, совпадающим с одной вершиной, и находятся на одинаковом удалении от данной вершины.
Рассмотрим рисунок. Заметим, что:
BM=BK;
CK=CF;
DF=DN.
Записанные равенства вытекают из того факта, что это отрезки касательных, которые проведены из одной точки.
Запишем следующие соотношения:
(OM bot AB);
(OK bot BC);
(OF bot CD);
(ON bot AD).
Данные соотношения верны, так как включают в себя радиусы, которые проведены в точки касания окружности и описанного четырехугольника.
Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
В том случае, когда в четырехугольник вписана окружность, его площадь определяется по формуле:
(S = p cdot r)
Здесь p обозначает полупериметр четырехугольника.
Вспомним, что противолежащие стороны четырехугольника, в который вписана окружность, в сумме равны. Исходя из данного утверждения, можно сделать вывод: полупериметр такого четырехугольника равен какой-либо из пар сумм противолежащих сторон.
Если рассмотреть некий четырехугольник ABCD, то можно записать формулу для вычисления полупериметра этой геометрической фигуры:
p=AD+BC
p=AB+CD.
Тогда площадь четырехугольника, в который вписана окружность, будет вычислена таким образом:
({S_{ABCD}} = (AD + BC) cdot r;)
({S_{ABCD}} = (AB + CD) cdot r.)
В результате для определения радиуса окружности, которая вписана в некий четырехугольник, можно воспользоваться следующей формулой:
(r = frac{S}{p}.)
В том случае, если рассматривается описанная около четырехугольника ABCD окружность, то формула для вычисления ее радиуса примет вид:
(r = frac{{{S_{ABCD}}}}{{AD + BC}};)
(r = frac{{{S_{ABCD}}}}{{AB + CD}}.)
Чему равна сумма противоположных углов вписанного в окружность четырехугольника
Теорема 6
Если четырехугольник вписан в некую окружность, то его противолежащие углы в сумме дают .
Заметим, что на рисунке изображен четырехугольник ABCD, вписанный в окружность (O; R). Требуется доказать, что:
(angle A+angle C=180^o;)
(angle B+angle D=180^o.)
Представим доказательства. По условию:
(angle A) — угол вписанного четырехугольника, опирается на дугу BCD;
(angle C) — угол, который опирается на дугу DAB.
Зная, что вписанный угол составляет ½ часть дуги, которая является его опорой, запишем:
(angle A = frac{1}{2} cup BCD,)
(angle C = frac{1}{2} cup DAB.)
В результате:
(angle A + angle C = frac{1}{2} cup BCD + frac{1}{2} cup DAB = frac{1}{2}( cup BCD + cup DAB) = frac{1}{2} cdot 360^o = 180^o.)
Аналогичным образом запишем, что:
(angle B + angle D = frac{1}{2}( cup CDA + cup ABC) = frac{1}{2} cdot 360^o = 180^o.)
Теорема доказана.
Теорема 7
Если имеется такой четырехугольник, в котором противолежащие углы в сумме составляют (180^o), то около него можно описать окружность.
Представим, что имеется некий четырехугольник ABCD.
Сумма его противолежащих углов равна: (angle B+angle D=180^o).
Попробуем доказать, что около рассматриваемого четырехугольника можно описать окружность.
В первую очередь построим окружность около треугольника ABC таким образом, чтобы точка D принадлежала данной окружности. Построим доказательства, двигаясь «от обратного».
Допустим, что точка D не принадлежит окружности, которая описана около треугольника ABD. В таком случае точка D должна располагаться во внутренней области, ограниченной данной окружностью, или за пределами окружности.
В том случае, когда точка D расположена во внутреннем пространстве, ограниченном окружностью, какой-то луч AD имеет точку пересечения с окружностью. Обозначим ее, как Е. Заметим, что если вокруг четырехугольника ABCE описана окружность, то его противолежащие углы в сумме составляют (180^o):
(angle B+angle E = 180^o.)
Согласно данным из условия задачи:
(angle B+angle D=180^o.)
Таким образом:
(angle D=angle E.)
С другой стороны, угол D является внешним углом треугольника DCE при его вершине D. Исходя из этого, запишем:
(angle ADC=angle DEC+angle DCE.)
В результате получается, что угол D не равен углу E. Это утверждение противоречиво. Таким образом, точка D не расположена во внутреннем пространстве, ограниченном окружностью, описанной около треугольника ABC.
Луч AD имеет точку пересечения с окружностью, обозначенную буквой Е. В таком случае, ABCE представляет собой вписанный в окружность четырехугольник, а также:
(angle B+angle E=180^o)
Согласно условию задачи:
(angle B+angle D=180^o.)
Тогда:
(angle D=angle E.)
Однако угол Е является внешним углом треугольника ECD и расположен при вершине E.
Таким образом: (angle AEC=angle EDC+angle DCE.)
В результате недопустимо равенство углов D и E. В том случае, когда точка D расположена за пределами окружности, возникает противоречие. Таким образом, остается единственно верный вариант расположения этой точки, согласно которому она принадлежит окружности, описанной около четырехугольника. Теорема доказана.
Согласно свойству и признаку четырехугольника, вписанного в окружность, необходимым и достаточным условием вписанного четырехугольника является следующая теорема.
Теорема 7
Около четырехугольника допустимо описать окружность лишь в том случае, когда его противолежащие углы в сумме составляют 180 градусов.
Как найти радиус вписанного в окружность четырехугольника, формула
Допустим, что имеется некий четырехугольник, стороны которого обозначены, как a, b, c, d, а полупериметр равен p. В таком случае описанная около данного четырехугольника окружность имеет радиус, который можно рассчитать по формуле как отношение:
(R={frac {1}{4}}{sqrt {frac {(ab+cd)(ac+bd)(ad+bc)}{(p-a)(p-b)(p-c)(p-d)}}}.)
Примечание
Формулу радиуса окружности, которая описана около четырехугольника, ввел индийский математик Ватассери Парамешвара в XV веке.
Рассмотрим еще одну закономерность, которую называют формулой Брахмагупты. С ее помощью можно определить площадь S четырехугольника, который вписан в окружность и имеет стороны, равные a, b, c, d:
(S={sqrt {(p-a)(p-b)(p-c)(p-d)}}.)
В данном случае p является полупериметром, то есть в два раза меньше, чем периметр, и определяется как:
(p={tfrac {1}{2}}(a+b+c+d).)
С помощью формулы Брахмагупты представляется возможным изменить форму записи формулы Парамешвары:
(4SR={sqrt {(ab+cd)(ac+bd)(ad+bc)}}.)
Здесь S определяется, как площадь четырехугольника, вписанного в окружность. Диаметр равен двум радиусам и проходит через центр окружности.




2.png)