Как найти радиус через длину нити

Шитье. Как рассчитать радиус и нарисовать окружность без циркуля — 3 способа!

Три способа нарисовать окружность без циркуля.

КАК РАССЧИТАТЬ РАДИУС ОКРУЖНОСТИ.

Для чего он нужен, этот расчет радиуса? Чтобы начертить окружность, нам надо знать радиус этой сомой окружности – то есть расстояние от одной ножки циркуля до другой.

Допустим нам надо нарисовать окружность донышка панамки, и все что мы знаем, это обхват головы ребеночка. Как широко надо раздвинуть ножки циркуля, чтобы в итоге получить окружность, совпадающую с размерами головы ребеночка?

Или нам нужно начертить окружность юбки-солнца, зная только то, что длина окружности должна идеально совпадать с обхватом нашей талии.

Сейчас, чтобы все было предельно ясно и понятно, разберем 2 конкретных случая, которые чаще всего встречаются в работе швей.

Это расчет радиуса донышка панамки. И расчет радиуса на выкройке юбки-солнца.

Ситуация первая – нужно рассчитать радиус и начертить окружность дня панамки для девочки.

Эту история я красиво расписала в картинках прямо с текстом -рассуждением. Чтобы была понятна вся последовательность работы мозга. )))

Значит, чтобы узнать радиус – нам надо наш обхват головы ребеночка поделить на 6,28.

Берем мобильный телефон, находим в нем калькулятор и делим наши 42 см обхвата головы на 6,28 – получаем 6,68 см = то есть 6 см и 6 мм. Это и есть радиус.

Значит, нам надо раздвинуть ножки циркуля на расстояние 6 см 6 мм. И тогда нарисованная нами окружность будет равна 42 см – то есть ляжет ровненько по головке ребенка (только не забудьте ее обвесит отступив на 1 см для припусков на швы).

Ситуация вторая – нужно начертить окружность юбки-солнца. Все что мы знаем это обхват талии и длина юбки которую мы в итоге хотим получить.

В чертеже юбки солнца есть 2 окружности. Маленькая (внутренняя) должна лечь ровненько на нашу талию. То есть длина этой окружности должна совпасть с обхватом талии. Обхват талии 70 см, значит, и длина окружности должна быть 70 см (ну, разве что, там всякие сантиметры туда-сюда в виде припуска на швы, или еще какую дополнительную отделку в виде поясочка или кокеточки)

Значит нам нужно узнать, какого радиуса чертить круг, чтобы окружность в результате получилась длиной в эти нужные нам70 см.

На картинке ниже я все расписала и как рассчитать радиус маленькой окружности и как потом узнать радиус большой окружности.

И когда начерчена маленькая окружность. Все что нам нужно, это к маленькому радиусу прибавить желаемую длину юбки – и мы получаем большой радиус для большой окружности края юбки.

Вот с расчетами мы разобрались. Будем шить юбки и панамки – буду отправлять вас в эту статью.

Теперь давайте разберемся, как нарисовать окружность любого размера без циркуля.

КАК НАРИСОВАТЬ ОКРУЖНОСТЬ БЕЗ ЦИРКУЛЯ.

Вот здесь ниже я проиллюстрировала тремя картинками три способа. Надеюсь что все понятно нарисовано и прописано.

Да это быстрый способ – но надо следить за тем, чтобы карандаши не откланялись в сторону. Угол наклона карандаша изменяем радиус. Или надо чтобы один человек ровно держал один карандаш, а другой ровно перпендикулярно чертил вторым карандашом.

Вообще-то, чем ниже привязана нитка тем точнее будет окружность. Поэтому некоторые пользуются маленькими булавочками. Погрешность при отклонении булавки в сторону небольшая, и при шитье ею можно принебречь.

И все-таки самый вернейший способ начертить точный круг без циркуля, это при помощи обычной линейки и карандаша. Вот как это выглядит:

И далее по кругу, двигаем сантиметр (как часовую стрелку в часах) и отмечаем точки на одном и том же расстоянии – то есть на одной и той же цифре сантиметровой ленты. Вместо ленты можно использовать бечевочку с нанесенной на ней отметкой – главное убедитесь что бечевочка нисколько не тянется.

Ну вот и все – еще один пробел в знаниях устранен – теперь можно и на юбку-солнце замахнуться и на панамку – рассчитывать радиусы мы умеем .

Ольга Клишевская, специально для сайта “Женские разговоры”.

Источник

Как измерить диаметр по нитке?

Математика | 5 — 9 классы

Как измерить диаметр по нитке.

Можно попробовать намотать на карадаш 20 витков, очень близко друг к другу, померять длину всех витков и разделить на их количество.

Пожалуйста помогите решить задачу Начерти окружность радиусом два сантиметра и 1 сантиметра и 3 сантиметра Проведите диаметр каждой окружности на сколько частей диаметр разделил Круг измерить диаметр ?

Пожалуйста помогите решить задачу Начерти окружность радиусом два сантиметра и 1 сантиметра и 3 сантиметра Проведите диаметр каждой окружности на сколько частей диаметр разделил Круг измерить диаметр каждой окружности.

У портнихи 40 катушек с нитками из них 12 катушек с белыми нитками 8 черных остальные с цветными нитками сколько У портнихи катушек с цветными нитками?

У портнихи 40 катушек с нитками из них 12 катушек с белыми нитками 8 черных остальные с цветными нитками сколько У портнихи катушек с цветными нитками.

Начерти окружность 2см ?

Начерти окружность 2см .

Проведи диаметр в каждой окружности.

На скооько частей диаметр разделил круг.

Измерь диамеир каждой окружности.

Начерти окружности радиусом 2см1м3см?

Начерти окружности радиусом 2см1м3см.

Проведи диаметр в каждой окружности.

На сколько частей диаметр разделил круг?

Измерь диаметр каждой окружности.

Нужно начертить 10 кругов, измерить его диаметр и умножить на 3?

Нужно начертить 10 кругов, измерить его диаметр и умножить на 3.

14. И делать так со всеми окружностями.

Начертить окружность произвольного радиуса, измерить ее длину, найти диаметр, вычислить отношение длины окружности с длине диаметра?

Начертить окружность произвольного радиуса, измерить ее длину, найти диаметр, вычислить отношение длины окружности с длине диаметра.

Простой окружности с радиусами 2см и 3см измерь радиусы и диаметры окружностей что ты заметил сделай вывод и нарисуй?

Простой окружности с радиусами 2см и 3см измерь радиусы и диаметры окружностей что ты заметил сделай вывод и нарисуй.

Начерти при помощи циркуля в тетради окружности с радиусами 2 см, 3 см, 1 см?

Начерти при помощи циркуля в тетради окружности с радиусами 2 см, 3 см, 1 см.

Измерь диаметр, каждой окружности .

Вычисли, во сколько раз радиус каждой окружности меньше, чем диаметр.

Какой вывод можно сделать?

Измерить длину окружности ведра и стакана, а также их диаметр?

Измерить длину окружности ведра и стакана, а также их диаметр.

Найти отношение длины окружности к диаметру обоих сосудов.

Ниткой измерить окружность (её длину), измерить её диаметр?

Ниткой измерить окружность (её длину), измерить её диаметр.

На этой странице находится вопрос Как измерить диаметр по нитке?, относящийся к категории Математика. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Математика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Источник

Как при помощи нитки измерить окружность стакана?

Математика | 5 — 9 классы

Как при помощи нитки измерить окружность стакана?

Ставишь стакан, обхватываешь ниткой, после распрямляешь нитку и измеряешь по линейке.

С помощью тонкой нити измерте длину окружности стакана измерте длину диаметра ?

С помощью тонкой нити измерте длину окружности стакана измерте длину диаметра .

Найдите отношение длены окружности к длине диаметра и сравните полученые результаты с чесом П.

Начерти в тетради любую окружность проведи в ней радиус и измерь его?

Начерти в тетради любую окружность проведи в ней радиус и измерь его.

Измерь длину радиуса окружности?

Измерь длину радиуса окружности.

Начерти окружность с тем же центром так, чтобы ее радиус.

Составлял половину радиуса данной окружности.

Лесник измерил длину окружности ствола дерева с помощью верёвки и получили 3?

Лесник измерил длину окружности ствола дерева с помощью верёвки и получили 3.

3 м. найдите диаметр ствола этого дерева?

Как измерить радиус окружности, еслидлину окружности увеличить на 9, 42 см?

Как измерить радиус окружности, еслидлину окружности увеличить на 9, 42 см?

Как нужно измерить радиус чтобы длина окружности увеличилась в 8 раз?

Как нужно измерить радиус чтобы длина окружности увеличилась в 8 раз?

Измерь с помощью полетки площадь данной фигуры?

Измерь с помощью полетки площадь данной фигуры.

Как найти длину окружности с помощью нитки?

Как найти длину окружности с помощью нитки.

Как правильно измерить радиус окружности?

Как правильно измерить радиус окружности?

Длина окружности края стакана равна 18, 85см?

Длина окружности края стакана равна 18, 85см.

Ее диаметр — нам.

Найдите отношение длина края окружности стакана к длине его диаметра.

На этой странице сайта размещен вопрос Как при помощи нитки измерить окружность стакана? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Источник

Изучение способов нахождения длины окружности

Рубрика: Математика: алгебра и начала анализа, геометрия

Дата публикации: 29.12.2019 2019-12-29

Статья просмотрена: 3590 раз

Библиографическое описание:

Бородин, М. В. Изучение способов нахождения длины окружности / М. В. Бородин, О. Б. Никитина. — Текст : непосредственный // Юный ученый. — 2020. — № 1 (31). — С. 37-42. — URL: https://moluch.ru/young/archive/31/1837/ (дата обращения: 28.02.2023).

В своей повседневной жизни мы часто сталкиваемся с задачами, которые связаны с вычислением периметра, то есть суммы длин сторон различных геометрических фигур. В случае, если геометрическая фигура — многоугольник, нахождение его периметра не составляет особого труда: для этого достаточно с помощью линейки измерить длину каждой из сторон и сложить полученные результаты. Что же делать, если необходимо узнать длину окружности? Ответу на этот вопрос посвящена данная статья.

Окружность является самой распространённой кривой практически во всех областях человеческой деятельности. Форму окружности или круга мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны. Многие вещи, окружающие нас, имеют круглую форму, например: обруч, кольцо, мяч, тарелка.

В свободное время я люблю заниматься моделированием из бумаги, пластилина и, особенно, из деталей конструктора Лего. Иногда, для того чтобы подготовить нужную заготовку для модели, необходимо знать длину сторон фигуры, которую хочешь получить. Никогда эта задача не вызывала у меня затруднений, пока я не столкнулся с определением длины окружности.

В учебнике по геометрии 7 класса рассматривается вопрос определения длины окружности. Существует формула, при помощи которой решается эта задача. Мне стало интересно, а как же раньше, в древности, люди находили длину окружности, можно ли ее найти экспериментальным путем без помощи известной формулы, какая существует связь между размером окружности (диаметром) и длиной окружности, и какое практическое применение может иметь решение этой задачи.

Ещё в давние времена люди сталкивались с практическими задачами, для решения которых необходимо было уметь находить длину окружности. Например, для того чтобы изготовить металлический обод для колеса телеги, определить вместительность сосуда, при строительстве зданий, для изготовления ювелирных изделий, при пошиве одежды.

В источниках [1, 4] сказано, что уже 4 тысячи лет назад люди знали, что длина окружности примерно равна трём его диаметрам. В дальнейшем, более 2 тыс. лет назад, большой вклад в развитие геометрии, в том числе в изучение геометрических фигур — окружности и круга — внесли древнегреческий математик Евклид, а позже — Архимед.

Целью исследования является изучение различных способов нахождения длины окружности и получение взаимосвязи между диаметром окружности и её длиной.

Гипотеза исследования: формулу длины окружности можно получить самостоятельно экспериментальным путем.

Основные понятия

Окружность — это замкнутая плоская кривая линия, все точки которой находятся на одинаковом расстоянии от заданной точки О. Эта точка называется центром окружности (рисунок 1,а).

Круг — часть плоскости, ограниченная окружностью (рисунок 1,б).

Можно сказать, что окружность является границей круга.

Основные линии окружности — радиус и диаметр (рисунок 1,а).

Радиус R окружности — это отрезок, соединяющий центр О с любой точкой окружности.

Диаметр D окружности — отрезок, который соединяет две точки окружности и проходит через ее центр.

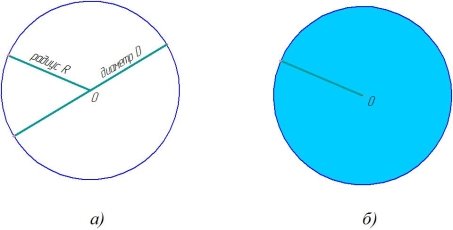
Рис. 1. Окружность и круг

Способы нахождения длины окружности

Рассмотрим некоторые возможные способы нахождения длины окружности.

Нахождение длины окружности с помощью нити

Когда я впервые задумался над решением данной задачи, первое и самое простое, что пришло на ум — это приложить нить к окружности, а затем при помощи линейки измерить ее длину. Подготовиться к эксперименту мне помог папа: он вырезал на станке металлические круги разных диаметров.

Проведем измерение круга диаметром 50 мм. Я обернул круг нитью, шариковой ручкой сделал отметки и при помощи линейки измерил длину нити между отметками (рисунок 2).

Длина нити оказалась равной 158 мм. При измерении я обратил внимание на то, что результат получается приблизительным, так как зависит от силы натяжения нити и ее толщины. И самое главное — не каждую окружность можно измерить таким способом.

То есть данный экспериментальный способ не решает поставленной задачи. Необходимо получить универсальную формулу, при помощи которой можно было бы найти длину окружности любого диаметра.

Рис. 2. Нахождение длины окружности с помощью нити

Нахождение длины окружности с помощью квадратов

Следующий способ, который я решил применить: представить окружность в виде квадрата (рисунок 3).

Продолжаем исследовать окружность диаметром 50 мм (рисунок 3,а).

Построим вокруг окружности квадрат так, чтобы он касался окружности в 4-х точках (рисунок 3,б), то есть сторона квадрата равна диаметру окружности.

Но на рисунке видно, что периметр квадрата явно больше длины вписанной окружности. А что, если внутри окружности построить еще один квадрат? Тогда, возможно, длина окружности будет средней величиной между периметрами двух квадратов.

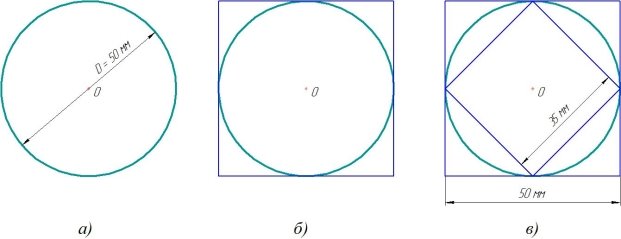
Измерим длины сторон квадратов с помощью линейки (рисунок 3,в). Длина стороны внутреннего квадрата равна 35 мм, наружного — 50 мм.

Найдем периметры квадратов:

Периметр внутреннего квадрата Р _внутр = 35+35+35+35 = 435= 140 (мм);

Периметр внешнего квадрата Р _внешн = 50+50+50+50= 450 = 200 (мм).

Предположим, что длина окружности — это средняя величина двух периметров. Найдём, чему она равна: (140+200):2 = 170 (мм).

Это значение намного отличается от длины окружности, полученной при измерении с помощью нити — 158 мм, что говорит о невысокой точности этого метода.

Нахождение длины окружности с помощью многоугольников

Далее я предположил, что если внутри окружности построить многоугольник с большим количеством сторон, то его периметр будет больше приближен к длине описанной окружности.

Для того чтобы подтвердить своё предположение, я решил исследовать несколько геометрических фигур: шестиугольник, восьмиугольник, двенадцатиугольник. Диаметр окружности — 50 мм (рисунок 4).

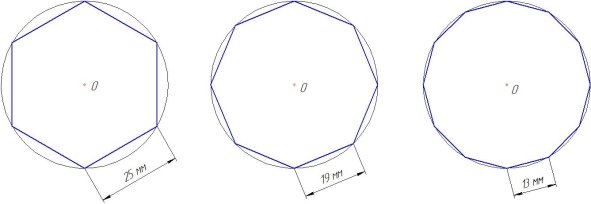
Измерим линейкой длины сторон и с помощью калькулятора найдем периметры построенных фигур.

Периметр шестиугольника (обозначим его Р ₆ ) равен:

Р ₆ = 25+25+25+25+25+25= 625 = 150 (мм).

Найдем периметры восьмиугольника Р ₈ и двенадцатиугольника Р ₁₂ :

Р ₈ = 19+19+19+19+19+19+19+19 = 819 = 152 (мм);

Р ₁₂ = 13+13+13+13+13+13+13+13+13+13+13+13 = 1213 = 156 (мм).

Из полученных результатов можно сделать вывод, что чем больше сторон имеет многоугольник, тем больше его периметр будет приближен к реальной длине окружности, в которую он вписан.

Получение формулы длины окружности экспериментальным методом

От геометрических построений переходим к практическому исследованию и попробуем ответить на вопрос: существует ли связь между диаметром окружности и его длиной.

Экспериментальным способом найдём длины 3-х окружностей диаметром 50, 100 и 200 мм.

Для эксперимента нам понадобятся: 3 металлических круга диаметром 50, 100 и 200 мм, простой карандаш, цветные карандаши, лист ватмана, линейка, рулетка, корпус шариковой ручки, выполняющий роль оси вращения (рисунок 5).

Рис. 5. Подготовка к эксперименту

Для нахождения длины окружности мы будем катить металлический круг, как колесо, по прямой линии, проведенной на листе ватмана. На круге сделана насечка для того, чтобы можно было отметить, когда круг сделает полный оборот. Расстояние, которое пройдет круг за один оборот, и будет являться длиной окружности соответствующего диаметра (рисунок 6).

Рис. 6. Проведение эксперимента

В ходе эксперимента мы получили следующие результаты (рисунок 7).

Длина окружности, диаметр которой D ₁ = 50мм, равна 157мм, то есть L ₁ =157 мм.

Длина окружности диаметром D ₂ =100 мм равна L ₂ =314 мм.

Длина окружности диаметром D ₃ =200 мм равна L ₃ =628 мм.

Рис. 7. Результаты эксперимента

Представим полученные результаты в виде таблицы.

Источник

Взять линейку и померять. От центра до окружности. Или вас интересует аналитический способ? Обычно, окружность задают так: “задана окружность радиусом R”, так вот “R” это и есть радиус. Если вместо “R” говорится “D”, то это диаметр – удвоенный радиус. автор вопроса выбрал этот ответ лучшим Матве­й628 [90.1K] 9 лет назад  Найти радиус окружности обычно требуется тогда, когда известна длина окружности. В этом случае, чтобы найти радиус окружности, нужно просто разделить длину окружности на 6,28. Это и будет радиус. Не так просто найти радиус, когда есть окружность, но нет ничего, кроме линейки. Понятно, что радиус равен половине диаметра, а вот как провести диаметр, если нет центра? Очень просто. Выбираем три точки на окружности, рисуем вписанный треугольник. Далее проводим три перпендикуляра из центров сторон треугольника. Их точка пересечения и будет центром окружности. Далее измеряем расстояние от центра окружности до самой окружности. Это и будет радиус окружности. Ксарф­акс [156K] 6 лет назад  Радиус – отрезок, соединяющий центр окружности и любую точку, которая на ней отмечена. Существует довольно много способов нахождения радиуса окружности. Это зависит от условий задачи, от того, какие исходные данные у вас имеются. Например: 1) R = 0,5D. Здесь D – это диаметр окружности. 2) С помощью линейки можно измерить диаметр, а затем поделить получившееся число на 2. 3) Если известна длина окружности C, то значение R = C/2π. 4) Если известна площадь круга A, то значение R = Корень(Aπ). 5) Если окружность вписана квадрат, то можно найти радиус данной окружности по значению площади квадрата и длине его стороны. Разделите диаметр окружности на 2 Это и будет радиус !!! Maris­ya [10.4K] 10 лет назад  Если известна длина окружности, то радиус окружности можно найти разделив ее длину на два пи. Формула: С = 2*пи*R, откуда R = C/(2*пи). C – длина окружности, R – радиус окружности…………………….. Смотря какие есть исходные данные. Если известен диаметр, то просто разделить на 2, если есть длина окружности, то разделить ее на число Пи умноженное на 2. Если есть площаль окуружности, то следует разделить ее на число Пи и из полученного числа извлечь корень квадратный, это и будет радиус. Ну, или измерьте линейкой, если есть сама окружность. Roxri­te [79.1K] 9 лет назад  Существует несколько способов найти радиус окружности: 1. Если окружность построена на обычном листе, то измерьте её радиус с помощью линейки. 2. Если известен диаметр окружности, то необходимо разделить диаметр пополам. 3. Если известна площадь окружности, то по формуле S=πR², отсюда R=√(S/π). Если это надо сделать экспериментальным путём и без помощи всяческих формул, то легче лёгкого взять линейку и померить всё же диаметр этой окружности, ну а потом, соответственно, разделить его на два, вот и получится радиус. Почему лучше мерить диаметр? Да чтоб центр окружности не искать))) Самый простой способ найти радиус окружности – это диаметр этой окружности, если, конечно, он известен, разделить на 2. Вот формула R = D/2. Если известна длина окружности, то тогда можно использовать следующую формулу: R = L/2П (длина окружности – это L, П – это “пи”, равное 3,14. Nikol­ai Sosiu­ra [152K] 9 лет назад  Радиус окружности найти можно. Если мы знаем диаметр окружность, то можно поделить на два. Получится радиус окружности. Неплохо в этом расчете помогает формула R = L/2π. R – радиус. L – длинна круга (если известна или можно определить). 2π – 2*3,14. CooLW­arK [27.3K] 9 лет назад  Радиус окружности можно найти следующими способами: Если измерить расстояние от центра окружности до одной из её крайних точек. Если известен диаметр окружности, то R = D/2. Если известна длина окружности, то R = C/2*3,14. Алекс Клима­нов [2.9K] 9 лет назад  Это расстояние от центра окружности до одной из её крайних точек. То есть проще всего линейкой. Легче и точнее померить диаметр – делим пополам. Если дана длина окружности С, то r = С/2*П. Знаете ответ?

Для того что бы вычислить радиус круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить радиус круга.
Радиус круга рассчитывается по следующим формулам:

1. Если нам известна длина:

   Формула для расчета радиуса круга через его длину:
   R=P/(2π)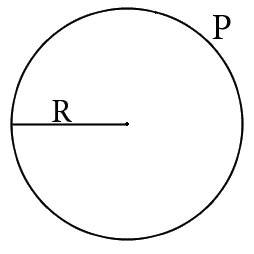

   

2. Если нам известна площадь:

   Формула для расчета радиус круга через площадь:
   R=

   √

   S/π

   

3. Если нам известен диаметр:

   Формула для расчета радиус круга через диаметр:
   R=D/2

   

Где R – радиус круга, S – площадь круга, P – длина круга, D – диаметр, π – число Пи которое всегда примерно равно 3,14.