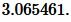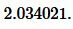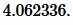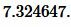Как найти радиус через угол альфа

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

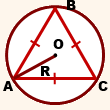
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать – как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

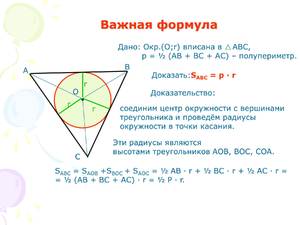
Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Отрезки в окружности

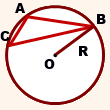
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

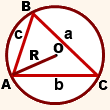
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Нахождение радиуса круга: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:

C = 2 π R

π – число, приближенное значение которого равно 3,14.

2. Через площадь круга

Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:

S = π R 2

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

[spoiler title=”источники:”]

[/spoiler]

Радиус описанной окружности около треугольника онлайн

1. Радиус окружности описанной около треугольника, если известны три стороны треугольника

Пусть известны три стороны a, b, c треугольника. Найдем радиус описанной окружности около треугольника.

Площадь треугольника по трем сторонам a, b, c и радиусу R описанной окружности имеет вид:

откуда

Площадь треугольника по трем сторонам имеет вид:

где

Подставляя (2) в (1), получим формулу радиуса описанной окружности около треугольника:

где p вычисляется из формулы (3).

Пример 1. Известны три стороны треугольника: ( small a=6, b=5, c=4.5 ). Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (4), где ( small р ) вычисляется из формулы (3).

Найдем p из (2):

Подставим значения a, b, c, p в (1):

Ответ:

2. Радиус окружности описанной около треугольника, если известны сторона a и противолежащий угол A

Пусть известны сторона a и противолежащий угол A. Найдем радиус описанной окружности около треугольника. Из расширенной теоремы синусов имеем:

Откуда:

Пример 2. Сторона треугольника равна: 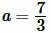а противолежащий угол ( small angle A=35°.) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (5). Подставим значения 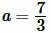и ( small angle A=35° ) в (5):

Ответ:

3. Радиус окружности описанной около треугольника, если известны стороны b и c треугольника и угол между ними A

Пусть известны стороны b и c треугольника и угол между ними A. Найдем радиус описанной окружности около треугольника.

Из теоремы косинусов, имеем:

или

Подставляя (6) в (5), получим требуемую формулу:

Пример 3. Известны две стороны треугольника: и угол между ними: ( small angle A=30°. ) Найти радиус окружности описанной около треугольника.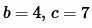

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения 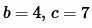и ( small angle A=30° ) в (7):

Ответ:

4. Радиус окружности описанной около треугольника, если известны сторона треугольника a и прилежащие углы B и C

Пусть известны сторона a треугольника и прилежащие к ней углы B и C. Найдем радиус описанной окружности около треугольника. Как известно, сумма углов треугольника равна 180°. Поэтому легко найти треий угол треугольника: ( small angle A=180°- (angle B+ nangle C). ) Тогда для нахождения радиуса описанной около треугольника окружности можно воспользоваться формулой (5):

Получили следующую формулу:

Пример 4. Известны сторона треугольника: и прилежащие к ней углы: ( small angle B=21°, ;angle C=34°. ) Найти радиус окружности описанной около треугольника.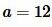

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (8). Подставим значения 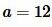и ( small angle B=21°, ;angle C=34° ) в (8):

Ответ:

Смотрите также:

• Радиус описанной окружности около равнобедренного треугольника онлайн
• Радиус описанной окружности около равностороннего треугольника онлайн
• Радиус описанной окружности около прямоугольного треугольника онлайн

Если окружность располагается внутри угла и касается его сторон, её называют вписанной в этот угол. Центр такой вписанной окружности располагается на биссектрисе этого угла.

Если же она лежит внутри выпуклого многоугольника и соприкасается со всеми его сторонами, она называется вписанной в выпуклый многоугольник.

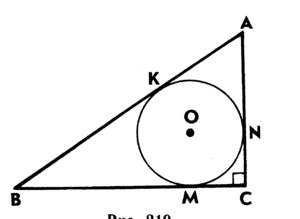
Окружность, вписанная в треугольник

Окружность, вписанная в треугольник, соприкасается с каждой стороной этой фигуры лишь в одной точке. В один треугольник возможно вписать лишь одну окружность.

Радиус такой окружности будет зависеть от следующих параметров треугольника:

1. Длин сторон треугольника.
2. Его площади.
3. Его периметра.
4. Величины углов треугольника.

Для того чтобы вычислить радиус вписанной окружности в треугольник, не всегда обязательно знать все перечисленные выше параметры, поскольку они взаимосвязаны между собой через тригонометрические функции.

Вычисление с помощью полупериметра

Чтобы рассчитать величину радиуса вписанной окружности в треугольник, необходимо учитывать следующие параметры:

1. Если известны длины всех сторон геометрической фигуры (обозначим их буквами a, b и c), то вычислять радиус придётся путём извлечения квадратного корня.
2. Приступая к вычислениям, необходимо добавить к исходным данным ещё одну переменную — полупериметр (р). Его можно рассчитать, сложив все длины и полученную сумму разделив на 2. p = (a+b+c)/2. Таким образом можно существенно упростить формулу нахождения радиуса.
3. В целом формула должна включать в себя знак радикала, под который помещается дробь, знаменателем этой дроби будет величина полупериметра р.
4. Числителем данной дроби будет представлять собой произведение разностей (p-a)*(p-b)*(p-c)
5. Таким образом, полный вид формулы будет представлен следующим образом: r = √(p-a)*(p-b)*(p-c)/p).

Вычисление с учётом площади треугольника

Если нам известна площадь треугольника и длины всех его сторон, это позволит найти радиус интересующей нас окружности, не прибегая к извлечению корней.

1. Для начала нужно удвоить величину площади.
2. Результат делится на сумму длин всех сторон. Тогда формула будет выглядеть следующим образом: r = 2*S/(a+b+c).
3. Если воспользоваться величиной полупериметра, можно получить совсем простую формулу: r = S/p.

Расчёт с помощью тригонометрических функций

Если в условии задачи присутствует длина одной из сторон, величина противоположного угла и периметр, можно воспользоваться тригонометрической функцией — тангенсом. В этом случае формула расчёта будет иметь следующий вид:

r = (P /2- a)* tg (α/2), где r — искомый радиус, Р — периметр, а — значение длины одной из сторон, α — величина противоположного стороне, а угла.

Радиус окружности, которую необходимо будет вписывать в правильный треугольник, можно найти по формуле r = a*√3/6.

Окружность, вписанная в прямоугольный треугольник

В прямоугольный треугольник можно вписать только одну окружность. Центр такой окружности одновременно служит точкой пересечения всех биссектрис. Эта геометрическая фигура имеет некоторые отличительные черты, которые необходимо учесть, вычисляя радиус вписанной окружности.

1. Для начала необходимо выстроить прямоугольный треугольник с заданными параметрами. Построить такую фигуру можно по размеру её одной стороны и величинам двух углов или же по двум сторонам и углу между этими сторонами. Все эти параметры должны быть указаны в условии задачи. Треугольник обозначается как АВС, причём С — это вершина прямого угла. Катеты при этом обозначаются переменными, а и b, а гипотенуза — переменной с.
2. Для построения классической формулы и вычисления радиуса окружности необходимо найти размеры всех сторон описанной в условии задачи фигуры и по ним вычислить полупериметр. Если в условиях даются размеры двух катетов, по ним можно вычислить величину гипотенузы, исходя из теоремы Пифагора.
3. Если в условии дан размер одного катета и одного угла, необходимо понять, прилежащий этот угол или противолежащий. В первом случае гипотенуза находится с помощью теоремы синусов: с=a/sinСАВ, во втором случае применяют теорему косинусов с=a/cosCBA.
4. Когда все расчёты выполнены и величины всех сторон известны, находят полупериметр по формуле, описанной выше.
5. Зная величину полупериметра, можно найти радиус. Формула представляет собой дробь. Её числителем является произведение разностей полупериметра и каждой из сторон, а знаменателем —величина полупериметра.

Следует заметить, что числитель данной формулы является показателем площади. В этом случае формула нахождения радиуса гораздо упрощается — достаточно разделить площадь на полупериметр.

Определить площадь геометрической фигуры можно и в том случае, если известны оба катета. По сумме квадратов этих катетов находится гипотенуза, далее вычисляется полупериметр. Вычислить площадь можно, умножив друг на друга величины катетов и разделив полученное на 2.

Если в условиях даны длины и катетов и гипотенузы, определить радиус можно по очень простой формуле: для этого складываются длины катетов, из полученного числа вычитается длина гипотенузы. Результат необходимо разделить пополам.

Видео

Из этого видео вы узнаете, как находить радиус вписанной в треугольник окружности.

Радиус описанной около треугольника окружности можно найти по одной из двух общих формул.

Кроме того, для правильного и прямоугольного треугольников существуют дополнительные формулы.

Радиус описанной около произвольного треугольника окружности

Формула I (следствие из теоремы синусов)

   

То есть радиус описанной окружности равен отношению длины стороны треугольника к удвоенному синусу противолежащего этой стороне угла.

В общем виде эту формулу записывают так:

   

Формула II.

   

в общем виде —

   

То есть чтобы найти радиус описанной около треугольника окружности, надо произведения длин сторон треугольника разделить на четыре площади треугольника.

Если площадь треугольника находить по формуле Герона

   

где p — полупериметр,

   

то получим формулу радиуса описанной около треугольника окружности через длины сторон:

   

Обе эти формулы можно применить к треугольнику любого вида. Следует только учесть положение центра.

Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника, напротив тупого угла.

Радиус окружности, описанной около прямоугольного треугольника

Формула:

   

То есть в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.

Обычно гипотенузу обозначают через c (AB=c) и формулу записывают так:

   

Радиус окружности, описанной около правильного треугольника

Формула:

   

Если без иррациональности в знаменателе, то

   

В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной окружности:

   

Геометрия круга

Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..

---

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.

• Окружность — линия, ограничивающая круг.
• Дуга — часть окружности.
• Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
• Хорда — отрезок, соединяющий две точки окружности.
• Сегмент — часть круга, ограниченная хордой и дугой.
• Сектор — часть круга, ограниченная двумя радиусами и дугой.

---

Интересующие нас величины и их обозначения:

---

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

• Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
• Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
• Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.

---

1. Даны диаметр D и длина дуги L

;     длина хорды ;
высота сегмента ;    центральный угол .

---

2. Даны диаметр D и длина хорды X

;     длина дуги ;
высота сегмента ;    центральный угол .

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .

---

3. Даны диаметр D и центральный угол φ

;     длина дуги ;
длина хорды ;    высота сегмента .

---

4. Даны диаметр D и высота сегмента H

;     длина дуги ;
длина хорды ;    центральный угол .

---

6. Даны длина дуги L и центральный угол φ

;     диаметр ;
длина хорды ;    высота сегмента .

---

8. Даны длина хорды X и центральный угол φ

;     длина дуги ;
диаметр ;    высота сегмента .

---

9. Даны длина хорды X и высота сегмента H

;     длина дуги ;
диаметр ;    центральный угол .

---

10. Даны центральный угол φ и высота сегмента H

;     диаметр ;
длина дуги ;    длина хорды .

---

Внимательный читатель не мог не заметить, что я пропустил два варианта:

5. Даны длина дуги L и длина хорды X

7. Даны длина дуги L и высота сегмента H

Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?

Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.

---

Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:

длина окружности ;
площадь круга ;
площадь сектора ;
площадь сегмента ;

---

И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.

Программа Segment