Как найти радиус электронной орбиты

Ра́диус а́тома — расстояние между атомным ядром и самой дальней из стабильных орбит электронов в электронной оболочке этого атома. Поскольку, согласно квантовой механике, атомы не имеют четких границ, а вероятность найти электрон, связанный с ядром данного атома, на определённом расстоянии от этого ядра быстро убывает с увеличением расстояния, атому приписывают некоторый определённый радиус, полагая, что в шаре этого радиуса заключена подавляющая часть электронной плотности (порядка 90 процентов). Существуют различные определения радиуса атома^[⇨], три наиболее широко используемых: радиус Ван-дер-Ваальса, ионный радиус и ковалентный радиус.

В зависимости от определения термин «радиус атома» может применяться либо только к изолированным атомам, либо также к атомам в конденсированной среде, ковалентно связанным в молекулах или в ионизированном и возбужденном состояниях; его значение может быть получено путем экспериментальных измерений или вычислено из теоретических моделей. Значение радиуса может зависеть от состояния атома и окружающей среды^[1].

Электроны не имеют четко определённых орбит или границ. Скорее, их положения могут быть описаны как распределения вероятностей, которые постепенно сужаются по мере удаления от ядра без резкого сокращения. Кроме того, в конденсированном веществе и молекулах электронные облака атомов обычно в некоторой степени перекрываются, и некоторые из электронов могут перемещаться в области, охватывающей два или более атомов («принадлежать» нескольким атомам одновременно).

Согласно большинству определений, радиусы изолированных нейтральных атомов колеблются в диапазоне от 30 до 300 пм (или от 0,3 до 3 ангстрем), в то время как радиусы атомных ядер находятся пределах от 0,83 до 10 фм^[2]. Следовательно, радиус типичного атома примерно в 30 тысяч раз больше радиуса его ядра.

Во многих случаях форма атома может быть аппроксимирована сферой. Это лишь грубое приближение, но оно может дать количественные представления и выступить в качестве базовой модели для описания для многих явлений, таких как плотность жидкостей и твердых веществ, диффузия жидкостей через молекулярные сита, расположение атомов и ионов в кристаллах, а также размер и форма молекул.

Радиусы атомов изменяются, подчиняясь определённым закономерностям периодической таблицы химических элементов. Например, радиусы атомов обычно уменьшаются при перемещении слева направо вдоль каждого периода (строки) таблицы, от щелочных металлов до благородных газов, и возрастают по мере продвижения сверху вниз в каждой группе (столбце). Радиусы атомов резко возрастают при переходе между благородным газом в конце каждого периода и щелочным металлом в начале следующего периода. Эти тенденции изменения радиусов атомов (наряду с другими химическими и физическими свойствами элементов) могут быть объяснены с точки зрения теории электронной оболочки атома, а также представляют доказательства подтверждения квантовой теории. Радиусы атомов уменьшаются в периодической таблице, потому что с увеличением атомного номера увеличивается число протонов в атоме, а дополнительные электроны добавляются в одну и ту же квантовую оболочку. Следовательно, эффективный заряд атомного ядра по отношению к внешним электронам увеличивается, притягивая внешние электроны. В результате электронное облако сжимается и атомный радиус уменьшается.

История[править | править код]

В 1920 году, вскоре после того, как стало возможным определять размеры атомов с помощью рентгеноструктурного анализа, было высказано предположение, что все атомы одного и того же элемента имеют одинаковые радиусы^[3]. Однако в 1923 году, когда было получено больше данных о кристаллах, было обнаружено, что аппроксимация атома сферой не всегда корректна при сравнении атомов одного и того же элемента в разных кристаллических структурах^[4].

Определения[править | править код]

Широко используемые определения радиуса атома включают:

• Радиус Ван-дер-Ваальса, Вандерваальсовы радиусы^[5] — эта величина соответствует половине межъядерного расстояния между ближайшими одноимёнными атомами, не связанными между собой химической связью и принадлежащими разным молекулам (например, в молекулярных кристаллах).^[6].
• Ионный радиус: номинальный радиус ионов элемента в определённом состоянии ионизации, выведенный из расстояния между атомными ядрами в кристаллических солях, которые включают эти ионы. В принципе, расстояние между двумя соседними противоположно заряженными ионами (длина ионной связи между ними) должно равняться сумме их ионных радиусов^[6].
• Ковалентный радиус: номинальный радиус атомов элемента, когда они ковалентно связаны с другими атомами, выводится из расстояния между атомными ядрами в молекулах. В принципе, расстояние между двумя атомами, которые связаны друг с другом в молекуле (длина этой ковалентной связи), должно равняться сумме их ковалентных радиусов^[6].
• Металлический радиус: номинальный радиус атомов элемента, когда они соединены с другими атомами металлическими связями.
• Боровский радиус: радиус орбиты электрона с наименьшей энергией, предсказанный Боровской моделью атома (1913)^[7][8]. Он применим только к атомам и ионам с одним электроном, таким как водород, однократно ионизованный гелий и позитроний. Хотя сама модель в настоящее время устарела, радиус Бора для атома водорода считается одной из фундаментальных физических постоянных.

Измерение радиуса атома опытным путём[править | править код]

В таблице приведены измеренные опытным путём ковалентные радиусы для элементов, опубликованные американским химиком Д.Слейтером в 1964 году^[9]. Значения приведены в пикометрах (пм или 1 × 10-12 м) с точностью около 5 пм. Оттенки цвета ячеек варьируются от красного до жёлтого по мере увеличения радиуса; серый цвет — отсутствие данных.

Группы (столбцы)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

Периоды (строки)

1

H 25

He  31

2

Li 145

Be 105

B 85

C 70

N 65

O 60

F 50

Ne  38

3

Na 180

Mg 150

Al 125

Si 110

P 100

S 100

Cl 100

Ar  71

4

K 220

Ca 180

Sc 160

Ti 140

V 135

Cr 140

Mn 140

Fe 140

Co 135

Ni 135

Cu 135

Zn 135

Ga 130

Ge 125

As 115

Se 115

Br 115

Kr

5

Rb 235

Sr 200

Y 180

Zr 155

Nb 145

Mo 145

Tc 135

Ru 130

Rh 135

Pd 140

Ag 160

Cd 155

In 155

Sn 145

Sb 145

Te 140

I 140

Xe

6

Cs 260

Ba 215

*

Hf 155

Ta 145

W 135

Re 135

Os 130

Ir 135

Pt 135

Au 135

Hg 150

Tl 190

Pb 180

Bi 160

Po 190

At

Rn

7

Fr

Ra 215

**

Rf

Db

Sg

Bh

Hs

Mt

Ds

Rg

Cn

Nh

Fl

Mc

Lv

Ts

Og

Лантаноиды

*

La 195

Ce 185

Pr 185

Nd 185

Pm 185

Sm 185

Eu 185

Gd 180

Tb 175

Dy 175

Ho 175

Er 175

Tm 175

Yb 175

Lu 175

Актиноиды

**

Ac 195

Th 180

Pa 180

U 175

Np 175

Pu 175

Am 175

Cm

Bk

Cf

Es

Fm

Md

No

Lr

Объяснение общих тенденций[править | править код]

Изменение радиуса атома с увеличением зарядового числа можно объяснить расположением электронов в оболочках с постоянной ёмкостью. Оболочки обычно заполнены в порядке увеличения радиуса, поскольку отрицательно заряженные электроны притягиваются положительно заряженными протонами атомного ядра. Поскольку зарядовое число увеличивается вдоль каждой строки периодической таблицы, дополнительные электроны входят в ту же самую внешнюю оболочку, а её радиус постепенно сжимается из-за увеличения заряда ядра. В атомах инертных газов внешняя оболочка полностью заполнена; следовательно, дополнительный электрон следующего элемента — щелочного металла — перейдет в следующую внешнюю оболочку, что объясняет внезапное увеличение атомного радиуса.

Увеличивающийся заряд ядра частично уравновешивается ростом числа электронов, это явление известно как экранирование^[en]; он объясняет, почему размер атомов обычно увеличивается в каждом столбце периодической таблицы. Из этой закономерности есть важное исключение, известное как лантаноидное сжатие: меньшие, по сравнению с ожидаемыми, величины ионных радиусов химических элементов, входящих в группу лантаноидов (атомный номер 58—71), которое происходит из-за недостаточного экранирования заряда ядра электронами 4f-орбитали.

По существу, атомный радиус уменьшается на протяжении периодов из-за увеличения количества протонов в ядре. Соответственно, большее количество протонов создает более сильный заряд и сильнее притягивает электроны, уменьшая размер радиуса атома. При движении сверху вниз по столбцам (группам) периодической таблицы атомный радиус увеличивается, поскольку есть больше энергетических уровней и, следовательно, больше расстояние между протонами и электронами. Кроме того, электронное экранирование ослабляет притяжение протонов, поэтому оставшиеся электроны могут удаляться от положительно заряженного ядра. Таким образом, размер (радиус атома) увеличивается.

В следующей таблице приведены основные факторы, влияющие радиус атома:

Фактор	Закон	Возрастает с…	как правило	Влияние на радиус атома
Электронные оболочки	Квантовая механика	Главным и азимутальным квантовым числом	Увеличивает радиус атома	Возрастает сверху вниз в каждой колонке
Атомный заряд	Притяжение электронов протонами ядра атома	Зарядовым числом	Сокращает радиус атома	Сокращается в течение всего периода
Экранирование	Отталкивание внешних электронов внутренними электронами	Количеством электронов во внутренних оболочках	Увеличивает радиус атома	Снижает эффект второго фактора

Лантаноидное сжатие[править | править код]

У химических элементов группы лантаноидов электроны в 4f-подоболочке, которая постепенно заполняется от церия (Z = 58) до лютеция (Z = 71), не особенно эффективны для экранирования увеличивающегося заряда ядра. Элементы, следующие непосредственно за лантаноидами, имеют радиусы атомов, которые меньше, чем можно было бы ожидать, и которые почти идентичны атомным радиусам элементов, находящихся непосредственно над ними^[10]. Следовательно, гафний имеет практически тот же атомный радиус (и химические свойства), что и цирконий, а тантал имеет радиус атома, как у ниобия, и так далее. Эффект лантаноидного сжатия заметен вплоть до платины (Z = 78), после чего он нивелируется релятивистским эффектом, известным как эффект инертной пары^[en].

Лантаноидное сжатие даёт 5 следующих эффектов:

1. Размер ионов Ln3 + регулярно уменьшается с атомным номером. Согласно правилам Фаянса^[en], уменьшение размера ионов Ln³⁺ увеличивает ковалентную связь и уменьшает основную связь между ионами Ln³⁺ и OH⁻ в Ln(OH)₃ до такой степени, что Yb(OH)₃ и Lu(OH)₃ с трудом растворяются в горячем концентрированном NaOH. Отсюда порядок размера ионов Ln³⁺:
   La³⁺ > Ce³⁺ > …, … > Lu³⁺.
2. Наблюдается регулярное уменьшение ионных радиусов.
3. Наблюдается регулярное снижение способности ионов действовать в качестве восстановителя с увеличением атомного номера.
4. Второй и третий ряды переходных элементов d-блока довольно близки по свойствам.
5. Эти элементы встречаются вместе в природных минералах и их трудно разделить.

d-сжатие[править | править код]

d-сжатие^[en] менее выражено, чем лантаноидное сжатие, но возникает по той же причине. В этом случае плохая экранирующая способность 3d-электронов влияет на атомные радиусы и химические свойства элементов, следующих непосредственно за первым рядом переходных металлов, от галлия (Z = 30) до брома (Z = 35)^[10].

Вычисленные радиусы атомов[править | править код]

В таблице приведены значения радиусов атомов, рассчитанные по теоретическим моделям, опубликованные итальянским химиком Энрико Клементи^[en] и другими в 1967 году^[11]. Значения даны в пикометрах (пм).

Группы (столбцы)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

Периоды (строки)

1

H 53

He 31

2

Li 167

Be 122

B 87

C 67

N 56

O 48

F 42

Ne 38

3

Na 190

Mg 145

Al 118

Si 111

P 98

S 88

Cl 79

Ar 71

4

K 243

Ca 194

Sc 184

Ti 176

V 171

Cr 166

Mn 161

Fe 156

Co 152

Ni 149

Cu 145

Zn 142

Ga 136

Ge 125

As 114

Se 103

Br 94

Kr 98

5

Rb 265

Sr 219

Y 212

Zr 206

Nb 198

Mo 190

Tc 183

Ru 178

Rh 173

Pd 169

Ag 165

Cd 161

In 156

Sn 145

Sb 133

Te 123

I 115

Xe 108

6

Cs 298

Ba 253

*

Hf 208

Ta 200

W 193

Re 188

Os 185

Ir 180

Pt 177

Au 174

Hg 171

Tl 156

Pb 154

Bi 143

Po 135

At 127

Rn 120

7

Fr

Ra

**

Rf

Db

Sg

Bh

Hs

Mt

Ds

Rg

Cn

Nh

Fl

Mc

Lv

Ts

Og

Лантаноиды

*

La 226

Ce 210

Pr 247

Nd 206

Pm 205

Sm 238

Eu 231

Gd 233

Tb 225

Dy 228

Ho 226

Er 226

Tm 222

Yb 222

Lu 217

Актиноиды

**

Ac

Th

Pa

U

Np

Pu

Am

Cm

Bk

Cf

Es

Fm

Md

No

Lr

См. также[править | править код]

• Боровский радиус
• Ковалентный радиус
• Радиус Ван-дер-Ваальса
• Ионный радиус
• Химическая связь

Примечания[править | править код]

Литература[править | править код]

• Рабинович В. А., Хавин З.Я. Краткий химический справочник. Изд. 2-е, испр. и доп. — Л.: Химия, 1978. — 392 с.

Теория
Бора водородоподобных атомов.

Нильс
Бор создал теорию строения атома,
способную объяснить опыты Резерфорда
и спектр излучения паров водорода.

Спектр
характеризует распределение интенсивности
излучения по шкале частот (или по шкале
длин волн).

Постулаты
Бора.

1-й
постулат:

электрон
в атоме может двигаться только по
определенным стационарным орбитам,
находясь на которых, он не излучает и
не поглощает энергию. Момент импульса
электрона на этих орбитах кратен
постоянной Планка:

, (1)

m_e
– масса электрона,

– скорость электрона на орбите с номером
n,
r_n
– радиус орбиты с номером n,
n
=1,2,3,….

Дж·с
– постоянная Планка.

2-й
постулат:

при
переходе электрона с одной стационарной
орбиты на другую излучается или
поглощается фотон, энергия которого

.
(2)

E
_n1
и
E
_n2

– энергия электрона в состоянии 1 и 2
(т.е. на орбитах 1 и 2),

– частота электромагнитных волн,
–
постоянная Планка.

Радиус
орбиты электрона в атоме водорода.

1-й
постулат Бора,

.

Выразим
скорость электрона:

.
(3)

Рассмотрим
круговые электронные орбиты. На электрон
с зарядом –e
со стороны ядра с зарядом +e
действует сила Кулона F,
сообщая электрону нормальное ускорение,

.

По
2-му закону Ньютона,

.
(4)

Сократим

и подставим скорость из (3):

.

Отсюда

.

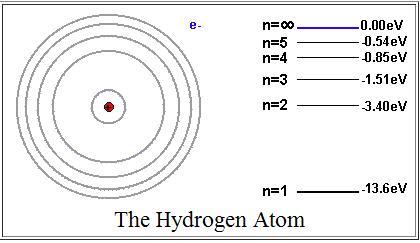
Радиус
первой орбиты электрона (n
= 1), называется радиусом
Бора


,

=

0.53·10^-10

м.

Радиус
орбиты электрона в атоме водорода

,
n
=1,2,3,…. – номер орбиты.

Энергия
электрона в атоме водорода.

Энергия
электрона представляет собой сумму
кинетической энергии
и
потенциальной
.

и

.

Потенциальная
энергия – это энергия электрона с
зарядом

в электрическом поле ядра. Из уравнения
(4) видно, что

.

Тогда
на n
–ой
орбите энергия электрона равна

=

=.

Т.е.
кинетическая энергия электрона равна
полной энергии, взятой со знаком «-».

Также
полную энергию можно записать через
потенциальную:

=
, или

.

Подставим

.
Тогда

=
.

Энергия
на первой орбите (на первом энергетическом
уровне) равна

=

= -13,6 эВ.

Величину

=
13,6 эВ = 2,18∙10^-18
Дж
называют
энергией ионизации
(эта энергия необходима, чтобы перевести
электрон, находящийся на первом уровне,
в свободное состояние, т.е. чтобы
ионизовать атом). Окончательно, энергия
электрона на n
–ом
энергетическом уровне (на n
–ой
орбите) записывается как

=

.

Спектр излучения водорода.

Энергия
излучаемого или поглощаемого кванта:

.

Частота

,

длина волны,

– скорость света в вакууме.

=

+

=

,

=
.

=

–
формула Бальмера,

определяет
длины волн в спектре атома водорода.

=
1,1∙10⁷
м^-1

– постоянная Ридберга.

и

– номера энергетических состояний
(номера орбит) электрона.

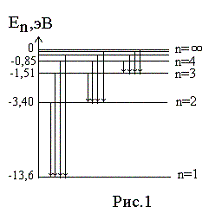
Переходы
электрона с возбужденных энергетических
состояний на основной энергетический
уровень (
= 1) сопровождаются излучением в УФ
области
спектра (серия линий Лаймана),

переходы
на уровень с

= 2 приводят к линиям в
видимой области
(серия Бальмера),

переходы
на уровень с

= 3, 4, 5, … приводят излучению в ИК
области.

Теория
Бора не смогла объяснить строение
сложных атомов. Для объяснения поведения
микрочастиц была развита квантовая
механика.

Она
основана на том, что любая микрочастица,
наряду с корпускулярными, обладает
также волновыми свойствами (гипотеза
де Бройля).

Для
фотона, импульс

.

По
аналогии с фотоном, любую микрочастицу
можно рассматривать как волну с длиной
волны

,

–
длина волны де Бройля.

Гипотеза
де Бройля подтверждена экспериментально
наблюдением дифракции электронов, а
затем и протонов.

Принцип
неопределенностей.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Главная

»

Самолетостроение

»

Физика (3 семестр)

»

Постулаты Бора. Модель атома водорода по Бору.Расчет радиусов электронных орбит и энергии атома.

Постулаты Бора. Модель атома водорода по Бору.Расчет радиусов электронных орбит и энергии атома.

1.В атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии.

Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.

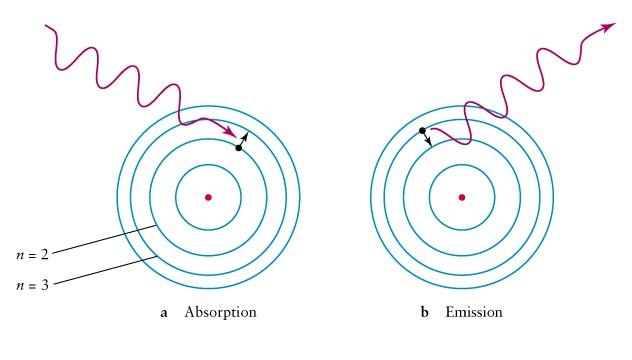
2. При переходе атома из одного стационарного состояния в другое им испускается или поглощается один квант энергии.

Энергия излученного или поглощенного фотона равна разности энергий стационарных состояний: 

где h = 6,63·10^–34 Дж·с – постоянная Планка, ν – частота фотона.

Боровская модель водородоподобного атома (Z — заряд ядра), где отрицательно заряженный электрон заключен в атомной оболочке, окружающей малое, положительно заряженное атомное ядро. Переход электрона с орбиты на орбиту сопровождается излучением или поглощением кванта электромагнитной энергии (hν).
Радиуса n-й стационарной орбиты

где n = 1, 2, 3, … . Из выражения следует, что радиусы орбит растут пропорционально квадратам целых чисел.

Для атома водорода (Z = 1) радиус первой орбиты электрона при n = 1, называемый первым Боровским радиусом (а), равен что соответствует расчетам на основании кинетической теории газов. Так как радиусы стационарных орбит измерить невозможно, то для проверки теории необходимо обратиться к таким величинам, которые могут быть измерены экспериментально. Такой величиной является энергия, излучаемая и поглощаемая атомами водорода.

Полная энергия электрона в водородоподобной системе складывается из его кинетической энергии (m_ev²/2) и потенциальной энергии в электростатическом поле ядра (-Ze²/(4₀r):

Учитывая квантованные для радиуса n-й стационарной орбиты значения , получим, что энергия электрона может принимать только следующие дозволенные дискретные значения:

где знак минус означает, что электрон находится в связанном состоянии.

Энергетическое состояние с n = 1 является основным (нормальным) состоянием; состояния с n > 1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными.

Энергия атома водорода с увеличением n возрастает и энергетические уровни сближаются к границе, соответствующей значению n = . Атом водорода обладает, таким образом, минимальной энергией (E1 = -13,55 эВ) при n =1. максимальной (E_ = 0) при n = . Следовательно, значение E_ = 0 соответствует ионизации атома (отрыву от него электрона). Согласно второму постулату Бора, при переходе атома водорода (Z= 1) из стационарного состояния n в стационарное состояние m с меньшей энергией испускается квант откуда частота излучения.

---

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.