Как найти радиус если известен вписанный угол - Сайт, где вы сможете решить свои вопросы

Все основные формулы для определения длины радиуса окружности

Радиус окружности – отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).

R – радиус окружности (круга)

D – диаметр, D = 2 R

Формула для определения длины радиуса, если известна площадь круга :

Калькулятор для расчета длины радиуса через площадь

Формула для определения длины радиуса, если известна длина окружности :

Калькулятор для расчета длины радиуса через длину окружности

R – радиус окружности (круга)

h – высота сегмента

α – центральный угол

Формула для определения длины радиуса, если известна длина хорды :

Радиус — что это такое и как найти радиус окружности

Через длину стороны

Формула для нахождения длины окружности через радиус:

, где r — радиус окружности.

Найти радиус круга, зная окружность

Окружность круга P

Результат

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.

Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.

Длина диаметра равна удвоенной длине радиуса.

Вычисление радиуса

Радиус можно посчитать разными способами.

Если известен диаметр

Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.

Если известна длина окружности круга

Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.

Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:

Означает данное значение отношение длины окружности к диаметру той же окружности.

Если известна площадь круга

Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:

В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.

Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.

Способ расчета радиуса круга:

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

r — искомый радиус окружности.
a — сторона описанного квадрата.

Как посчитать радиус зная длину окружности

Чему равен радиус (r) если длина окружности C?

Формула

r = C /_2π , где π ≈ 3.14

Свойства радиуса

В отношении радиуса действуют несколько важных правил:

Радиус составляет половину диаметра. Это мы продемонстрировали только что.
У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.

Радиус, который перпендикулярен хорде, делит ее на две равные части.

Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

По площади сектора и центральному углу

Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем

В случае, когда величина α выражена в в радианах , получаем

Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Числовая характеристика	Рисунок	Формула
Площадь круга
Площадь сектора
Площадь сегмента

Площадь круга

где R – радиус круга, D – диаметр круга

Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Центральный угол, вписанный угол и их свойства

Связанные определения

Центральный угол в окружности — это угол , образованный двумя радиусами.
Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .

В случае, когда величина α выражена в градусах , справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах , справедлива пропорция

из которой вытекает равенство:

Уравнение окружности

r 2 = ( x – a ) 2 + ( y – b ) 2

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:

<	x = a + r cos t
y = b + r sin t

Углы между двумя хордами

Случай 1: два секущие пересекаются внутри окружности.

Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности.

Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

r — искомый радиус окружности.
S — площадь треугольника.
p — полупериметр треугольника (равен половине от суммы всех сторон).

Основные свойства касательных к окружности

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

Обобщения

Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

R — искомый радиус окружности.
d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
a, b — стороны вписанного прямоугольника.

Площадь круга, онлайн расчет

Как найти площадь круга по формуле через радиус либо диаметр круга.

Площадь круга, онлайн расчет

Вместо заключения

Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.

Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.

Как зная хорду вычислить радиус окружности

Все основные формулы для определения длины радиуса окружности

Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).

R — радиус окружности (круга)

D — диаметр, D = 2 R

Формула для определения длины радиуса, если известна площадь круга :

Калькулятор для расчета длины радиуса через площадь

Формула для определения длины радиуса, если известна длина окружности :

Калькулятор для расчета длины радиуса через длину окружности

R — радиус окружности (круга)

h — высота сегмента

α — центральный угол

Формула для определения длины радиуса, если известна длина хорды :

Сегмент круга

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Геометрия круга

Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии.

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.

Окружность — линия, ограничивающая круг.
Дуга — часть окружности.
Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
Хорда — отрезок, соединяющий две точки окружности.
Сегмент — часть круга, ограниченная хордой и дугой.
Сектор — часть круга, ограниченная двумя радиусами и дугой.

Интересующие нас величины и их обозначения:

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.

1. Даны диаметр D и длина дуги L

; длина хорды ;
высота сегмента ; центральный угол .

2. Даны диаметр D и длина хорды X

; длина дуги ;
высота сегмента ; центральный угол .

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .

3. Даны диаметр D и центральный угол φ

; длина дуги ;
длина хорды ; высота сегмента .

4. Даны диаметр D и высота сегмента H

; длина дуги ;
длина хорды ; центральный угол .

6. Даны длина дуги L и центральный угол φ

; диаметр ;
длина хорды ; высота сегмента .

8. Даны длина хорды X и центральный угол φ

; длина дуги ;
диаметр ; высота сегмента .

9. Даны длина хорды X и высота сегмента H

; длина дуги ;
диаметр ; центральный угол .

10. Даны центральный угол φ и высота сегмента H

; диаметр ;
длина дуги ; длина хорды .

Внимательный читатель не мог не заметить, что я пропустил два варианта:

5. Даны длина дуги L и длина хорды X

7. Даны длина дуги L и высота сегмента H

Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?

Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.

Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:

длина окружности ;
площадь круга ;
площадь сектора ;
площадь сегмента ;

И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.

[spoiler title=”источники:”]

http://exceltut.ru/radius-chto-eto-takoe-i-kak-najti-radius-okruzhnosti/

http://b4.cooksy.ru/articles/kak-znaya-hordu-vychislit-radius-okruzhnosti

[/spoiler]

Источник

Как найти радиус окружности

Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.

Выбирайте формулу в зависимости от известных величин.

Через площадь круга

Разделите площадь круга на число пи.
Найдите корень из результата.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
π (пи) — константа, равная 3,14.

Через длину окружности

Умножьте число пи на два.
Разделите длину окружности на результат.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
P — длина окружности (периметр круга).
π (пи) — константа, равная 3,14.

Через диаметр окружности

Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
D — диаметр.

Через диагональ вписанного прямоугольника

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
a, b — стороны вписанного прямоугольника.

Через сторону описанного квадрата

Иллюстрация: Лайфхакер

r — искомый радиус окружности.
a — сторона описанного квадрата.

Через стороны и площадь вписанного треугольника

Перемножьте три стороны треугольника.
Разделите результат на четыре площади треугольника.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
a, b, с — стороны вписанного треугольника.
S — площадь треугольника.

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

Иллюстрация: Лайфхакер

r — искомый радиус окружности.
S — площадь треугольника.
p — полупериметр треугольника (равен половине от суммы всех сторон).

Через площадь сектора и его центральный угол

Умножьте площадь сектора на 360 градусов.
Разделите результат на произведение пи и центрального угла.
Найдите корень из полученного числа.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
S — площадь сектора круга.
α — центральный угол.
π (пи) — константа, равная 3,14.

Через сторону вписанного правильного многоугольника

Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Умножьте результат на два.
Разделите сторону многоугольника на результат всех предыдущих действий.

Иллюстрация: Лайфхакер

R — искомый радиус окружности.
a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✂️📌

Как найти периметр прямоугольника
Как научить ребёнка считать играючи
Как перевести обычную дробь в десятичную
6 способов посчитать проценты от суммы с калькулятором и без
9 логических задач, которые по зубам только настоящим интеллектуалам

Источник

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

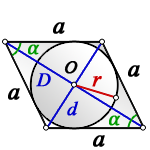
a – сторона ромба

D – большая диагональ

d – меньшая диагональ

α – острый угол

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

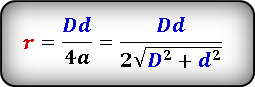
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

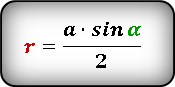
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

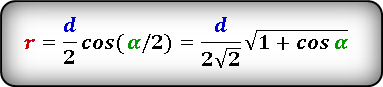
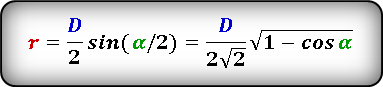
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

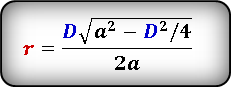
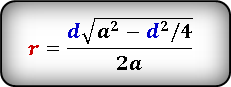
2. Радиус вписанной окружности ромба, равен половине его высоты

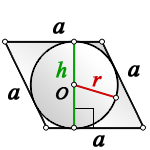
a – сторона ромба

h – высота

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Источник

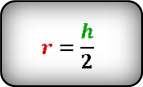
Краткое содержание:

Что такое радиус
Радиус и диаметр
Примеры задач
Формулы для радиуса описанной окружности
Найти радиус описанной окружности треугольника по сторонам
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
Найти радиус описанной окружности равнобедренного треугольника по сторонам
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности трапеции по сторонам и диагонали
Найти радиус описанной окружности около квадрата
Радиус описанной окружности прямоугольника по сторонам
Радиус описанной окружности правильного многоугольника
Радиус описанной окружности правильного шестиугольника
Формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
Радиус вписанной окружности в равносторонний треугольник
Радиус вписанной окружности равнобедренный треугольник
Радиус вписанной окружности в прямоугольный треугольник
Радиус вписанной окружности в равнобочную трапецию
Радиус вписанной окружности в квадрат
Радиус вписанной окружности в ромб
Радиус вписанной окружности в правильный многоугольник
Радиус вписанной окружности в шестиугольник
Примеры задач
Обсуждение

Здравствуйте мои дорогие подписчики и гости сайта 9111.ru!

На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.

Что такое радиус

И действительно:

Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.

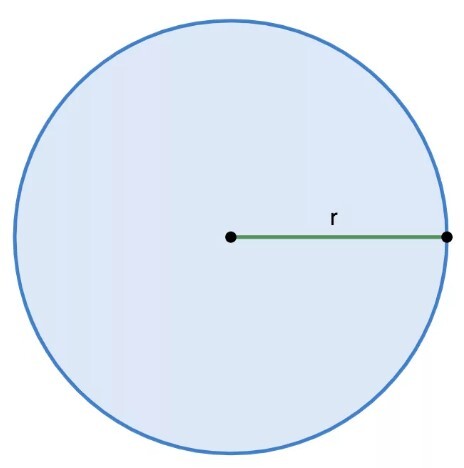
Вот так это выглядит графически.

**************************************

Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.

Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.

Кстати, есть еще несколько значений слова РАДИУС:

Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
В анатомии этим словом обозначают Лучевую кость предплечья.

Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

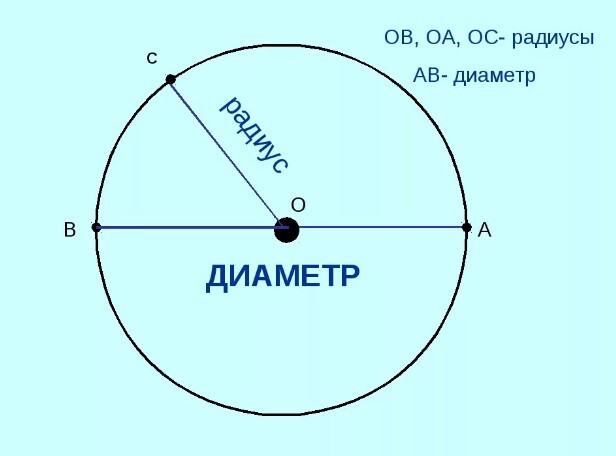
Обозначается диаметр также первой буквой своего слова – D или d.

А именно:

Длина диаметра равна удвоенной длине радиуса.

Примеры задач

Задание 1

Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:

Используем первую формулу (через периметр):

Задание 2

Найдите радиус круга, если его площадь составляет 254,34 см 2.

Решение:

Воспользуемся формулой, выраженной через площадь фигуры:

Формулы для радиуса описанной окружности

Найти радиус описанной окружности треугольника по сторонам

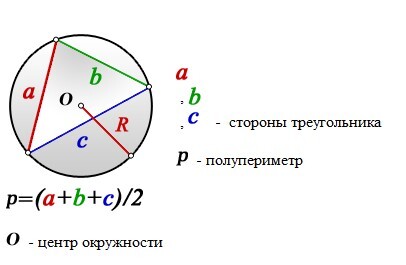
Формула радиуса описанной окружности треугольника (R ) :

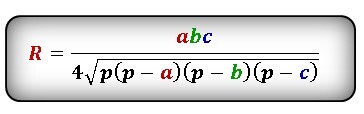
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте

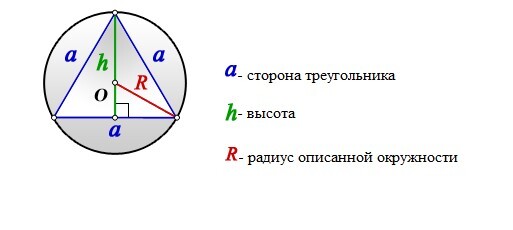
Формула радиуса описанной окружности равностороннего треугольника через его сторону:

Формула радиуса описанной окружности равностороннего треугольника через высоту:

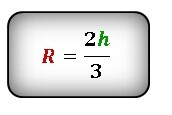
Найти радиус описанной окружности равнобедренного треугольника по сторонам

Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

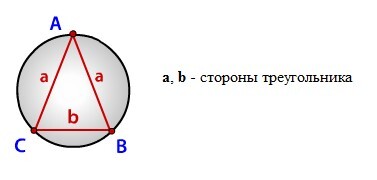
Формула радиуса описанной окружности равнобедренного треугольника (R):

Найти радиус описанной окружности прямоугольного треугольника по катетам

Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.

Формула радиуса описанной окружности прямоугольного треугольника (R):

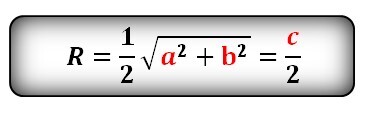
Радиус описанной окружности трапеции по сторонам и диагонали

Формула радиуса описанной окружности равнобокой трапеции, (R)

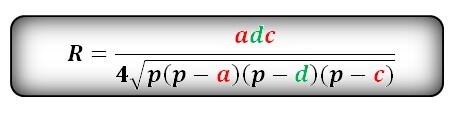
Найти радиус описанной окружности около квадрата

Радиус описанной окружности квадрата равен половине его диагонали

Формула радиуса описанной окружности квадрата (R):

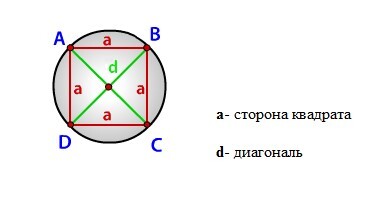
Радиус описанной окружности прямоугольника по сторонам

Радиус описанной окружности прямоугольника равен половине его диагонали

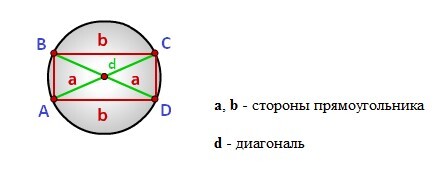
Формула радиуса описанной окружности прямоугольника (R):

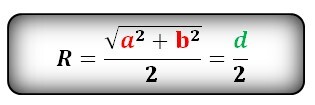
Радиус описанной окружности правильного многоугольника

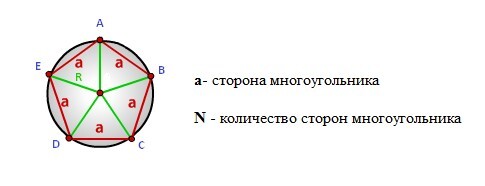
Формула радиуса описанной окружности правильного многоугольника, (R):

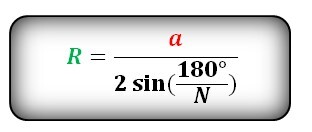
Радиус описанной окружности правильного шестиугольника

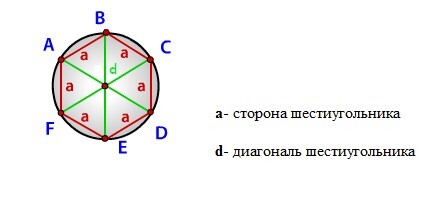
Радиус описанной окружности правильного шестиугольника (R):

Формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

Формула радиуса вписанной окружности в треугольник (r):

Радиус вписанной окружности в равносторонний треугольник

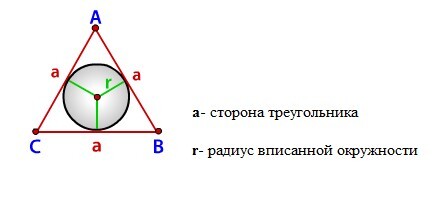
Формула для радиуса вписанной окружности в равносторонний треугольник (r):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны (r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол (r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту (r ) :

Радиус вписанной окружности в прямоугольный треугольник

Формула радиуса вписанной окружности в прямоугольный треугольник (r):

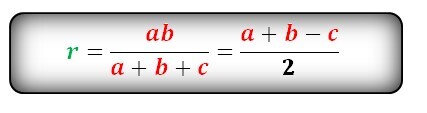
Радиус вписанной окружности в равнобочную трапецию

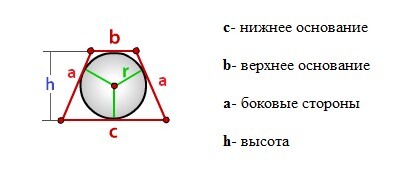
Формула радиуса вписанной окружности равнобочной трапеции (r):

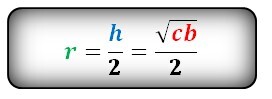
Радиус вписанной окружности в квадрат

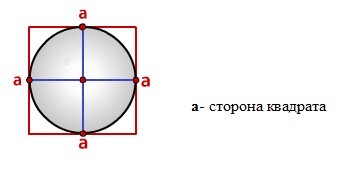
Формула радиуса вписанной окружности в квадрат (r):

Радиус вписанной окружности в ромб

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

Формула радиуса вписанной окружности в ромб через диагонали (r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол (r ) :

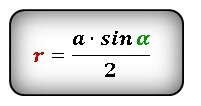
Формула радиуса вписанной окружности в ромб через диагональ и угол (r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону (r ) :

2. Радиус вписанной окружности ромба, равен половине его высоты

Формула радиуса вписанной окружности в ромб (r ) :

Радиус вписанной окружности в правильный многоугольник

Формула радиуса вписанной окружности в правильный многоугольник, (r):

Радиус вписанной окружности в шестиугольник

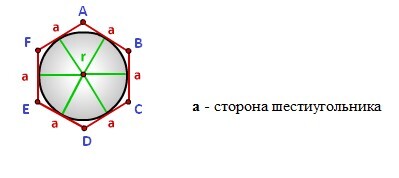
Формула радиуса вписанной окружности в шестиугольник, (r):

Примеры задач

Задание 1

Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.

Решение

Сперва вычислим площадь треугольника. Для этого применим формулу Герона:

Остается только применить соответствующую формулу для вычисления радиуса круга:

Задание 2

Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.

Решение

Воспользуемся подходящей формулой, подставив в нее известные значения:

Всем спасибо и приятного просмотра! Если понравилась публикация подписывайтесь и ставьте палец вверх!

Источники:

https://KtoNaNovenkogo.ru/voprosy-i-otvety/radius-chto-ehto-takoe-kak-najti-radius-okruzhnosti-formula.html
https://MicroExcel.ru/radius-kruga/
https://www-formula.ru/2011-09-24-00-42-22
https://www-formula.ru/2011-09-24-00-40-48
https://MicroExcel.ru/radius-vpisannogo-v-treugolnik-kruga/

Источник

Download Article

The radius of a circle is the distance from the center of the circle to any point on its circumference.^[1] The easiest way to find the radius is by dividing the diameter in half. If you don’t know the diameter but you know other measurements, such as the circle’s circumference () or area ( ${displaystyle A=pi r^{2}}$ ), you can still find the radius by using the formulas and isolating the variable.

1

Write down the circumference formula. The formula is

, where equals the circle’s circumference, and equals its radii^[2]
2

Solve for r. Use algebra to change the circumference formula until r (radius) is alone on one side of the equation:

Example

${frac {C}{2pi }}={frac {2pi r}{2pi }}$
${frac {C}{2pi }}=r$
$r={frac {C}{2pi }}$

Advertisement
3

Plug the circumference into the formula. Whenever a math problem tells you the circumference C of a circle, you can use this equation to find the radius r. Replace C in the equation with the circumference of the circle in your problem:

Example
If the circumference is 15 centimeters, your formula will look like this: $r={frac {15}{2pi }}$ centimeters
4

Round to a decimal answer. Enter your result in a calculator with the button and round the result. If you don’t have a calculator, calculate it by hand, using 3.14 as a close estimate for .

Example
$r={frac {15}{2pi }}=$ about ${frac {7.5}{2*3.14}}=$ approximately 2.39 centimeters

1

Set up the formula for the area of a circle. The formula is

$A=pi r^{{2}}$

, where equals the area of the circle, and equals the radius.^[3]
2

Solve for the radius. Use algebra to get the radius r alone on one side of the equation:

Example
Divide both sides by :
$A=pi r^{{2}}$
${frac {A}{pi }}=r^{{2}}$
Take the square root of both sides:
${sqrt {{frac {A}{pi }}}}=r$
$r={sqrt {{frac {A}{pi }}}}$
3

Plug the area into the formula. Use this formula to find the radius when the problem tells you the area of the circle. Substitute the area of the circle for the variable .

Example
If the area of the circle is 21 square centimeters, the formula will look like this: $r={sqrt {{frac {21}{pi }}}}$
4

Divide the area by . Begin solving the problem by simplifying the portion under the square root ( ${frac {A}{pi }})$ . Use a calculator with a key if possible. If you don’t have a calculator, use 3.14 as an estimate for .

Example
If using 3.14 for , you would calculate:
$r={sqrt {{frac {21}{3.14}}}}$

If your calculator allows you to enter the whole formula on one line, that will give you a more accurate answer.
5

Take the square root.

You will likely need a calculator to do this

, because the number will be a decimal. This value will give you the radius of the circle.

Example
. So, the radius of a circle with an area of 21 square centimeters is about 2.59 centimeters.
Areas always use square units (like square centimeters), but the radius always uses units of length (like centimeters). If you keep track of units in this problem, you’ll notice that ${sqrt {cm^{{2}}}}=cm$ .

1
Check the problem for a diameter. If the problem tells you the diameter of the circle, it’s easy to find the radius. If you are working with an actual circle,

measure the diameter by placing a ruler so its edge passes straight through the circle’s center

, touching the circle on both sides.^[4]
- If you’re not sure where the circle center is, put the ruler down across your best guess. Hold the zero mark of the ruler steady against the circle, and slowly move the other end back and forth around the circle’s edge. The highest measurement you can find is the diameter.
- For example, you might have a circle with a diameter of 4 centimeters.
2
Divide the diameter by two. A circle’s

radius is always half the length of its diameter.

^[5]
- For example, if the diameter is 4 cm, the radius equals 4 cm ÷ 2 = 2 cm.
- In math formulas, the radius is r and the diameter is d. You might see this step in your textbook as $r={frac {d}{2}}$ .

1

Set up the formula for the area of a sector. The formula is

$A_{{sector}}={frac {theta }{360}}(pi )(r^{{2}})$

, where $A_{{sector}}$ equals the area of the sector, equals the central angle of the sector in degrees, and equals the radius of the circle.^[6]
2

Plug the sector’s area and central angle into the formula. This information should be given to you.

Make sure you have the area of the sector, not the area for the circle.

Substitute the area for the variable $A_{{sector}}$ and the angle for the variable .

Example
If the area of the sector is 50 square centimeters, and the central angle is 120 degrees, you would set up the formula like this:
$50={frac {120}{360}}(pi )(r^{{2}})$ .
3

Divide the central angle by 360. This will tell you what fraction of the entire circle the sector represents.

Example
${frac {120}{360}}={frac {1}{3}}$ . This means that the sector is ${frac {1}{3}}$ of the circle.
Your equation should now look like this: $50={frac {1}{3}}(pi )(r^{{2}})$
4

Isolate $(pi )(r^{{2}})$ . To do this, divide both sides of the equation by the fraction or decimal you just calculated.

Example
$50={frac {1}{3}}(pi )(r^{{2}})$
${frac {50}{{frac {1}{3}}}}={frac {{frac {1}{3}}(pi )(r^{{2}})}{{frac {1}{3}}}}$
$150=(pi )(r^{{2}})$
5

Divide both sides of the equation by . This will isolate the variable. For a more precise result, use a calculator. You can also round to 3.14.

Example
$150=(pi )(r^{{2}})$
${frac {150}{pi }}={frac {(pi )(r^{{2}})}{pi }}$
$47.7=r^{{2}}$
6

Take the square root of both sides. This will give you the radius of the circle.

Example
$47.7=r^{{2}}$
${sqrt {47.7}}={sqrt {r^{{2}}}}$

So, the radius of the circle is about 6.91 centimeters.

Practice Problems and Answers

Add New Question

Question

How do I find the radius of a circle when I know the chord length?

It is possible to have quite a few circles, all with different radii, in which one could draw a chord of a given, fixed length. Hence, the chord length by itself cannot determine the radius of the circle.
Question

How do I find the radius of a circle when I know the arc length and the central angle?

Divide the central angle into 360°. Multiply the resulting number by the arc length. That gives you the circumference of the circle. Divide the circumference by pi. That’s the diameter. Half of the diameter is the radius of the circle.
Question

How do I calculate the radius of a circle when no other values are known?

Technically you can’t “calculate” the radius in such a situation. However, it is possible, by construction, to locate the center of such a circle, and then, simply by physically measuring, determine the radius. To do the construction, draw any two chords and construct their perpendicular bisectors; their point of intersection is the center of the circle. Then draw in any radius and measure it with a ruler. Not technically a “calculation.”

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

About This Article

Article SummaryX

To calculate the radius of a circle by using the circumference, take the circumference of the circle and divide it by 2 times π. For a circle with a circumference of 15, you would divide 15 by 2 times 3.14 and round the decimal point to your answer of approximately 2.39. Be sure to include the units in your answer. To learn more, such as how to calculate the radius with the area or diameter, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 3,346,766 times.

Did this article help you?

Источник