Как найти радиус если известна длина хорды

Как найти радиус по хорде

Хорда – это отрезок, соединяющий две точки окружности. Пусть длина хорды известна. Тогда, если также известен угол между радиусами, проведенными в концы хорды, то можно найти и радиус окружности.

Вам понадобится

• Транспортир, линейка.

Инструкция

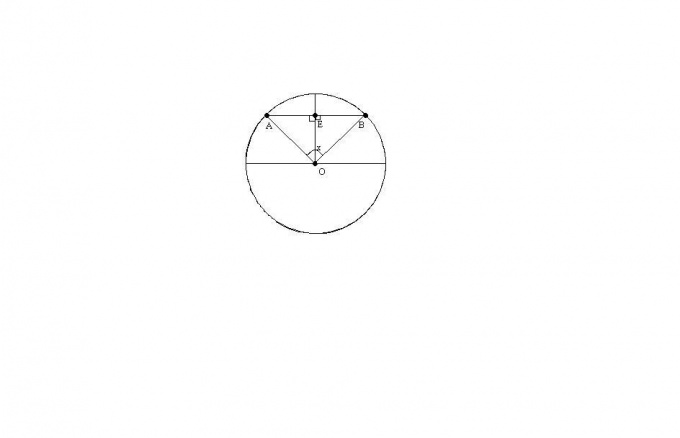
Пусть известны длина хорды AB и угол AOB между радиусами, проведенными в концы хорды. Найдем по этим данным радиус окружности с центром в точке O.

Треугольник AOB – равнобедренный, так как OA = OB = R. По свойству равнобедренного треугольника высота OE одновременно является его медианой и биссектрисой угла AOB. Обозначим угол AOB за х.
Треугольник AEO – прямоугольный с прямым углом AEO. Так как высота ОЕ также является биссектрисой угла AOB, то угол AOE = x/2. Тогда из прямоугольного треугольника AOE имеем: OA = R = (AB/2)/sin(x/2).

Все основные формулы для определения длины радиуса окружности

Радиус окружности – отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).

R – радиус окружности (круга)

D – диаметр, D = 2 R

Формула для определения длины радиуса, если известна площадь круга :

Калькулятор для расчета длины радиуса через площадь

Формула для определения длины радиуса, если известна длина окружности :

Калькулятор для расчета длины радиуса через длину окружности

R – радиус окружности (круга)

h – высота сегмента

α – центральный угол

Формула для определения длины радиуса, если известна длина хорды :

Сегмент круга

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать – как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

[spoiler title=”источники:”]

http://planetcalc.ru/1421/

http://skysmart.ru/articles/mathematic/radius-okruzhnosti

[/spoiler]

Dealing with parts of a circle, such as radius and chord, are tasks that you may face in high school and college trigonometry courses. You also may have to solve these types of equations in career fields such as engineering, design and landscaping. You can find the radius of a circle if you have the length and height of a chord of that circle.

Multiply the height of the chord times four. For instance, if the height is two, multiply two times four to get eight.

Square the length of the chord. If the length is four, for example, multiply four times four to get 16.

Divide your answer from Step 2 by your answer from Step 1. In this example, 16 divided by eight is two.

Add the height of the chord to your answer from Step 3. For example, two plus two equals four.

Divide your answer from Step 4 by two to find the radius. Therefore in this instance, four divided by two equals two. The radius in this example is equal to two.

Things You’ll Need

• Calculator
• Chord length and height measurements