Преподаватель который помогает студентам и школьникам в учёбе.
Кинематический способ определения радиуса кривизны траектории в теоретической механике
Кинематический способ определения радиуса кривизны траектории:
При решении многих технических задач возникает необходимость знать радиус кривизны р (или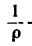
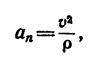
Таким образом, если закон движения точки задан уравнениями 
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:

2. Подставив в (б’) выражения 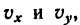 найти
найти 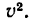
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение 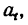 а затем а?.
а затем а?.
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
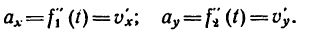
5. Подставив в (г) выражения 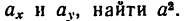
6. Подставить в (в) значения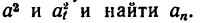
7. Подставив в (а) найденные значения 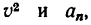 получить радиус кривизны р.
получить радиус кривизны р.
Задача:
Движение точки задано уравнениями 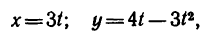
(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.
Решение.
1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим
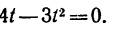
Отсюда [решая уравнение относительно 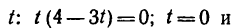
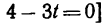 находим, что траектория пересекает ось Ох в моменты времени
находим, что траектория пересекает ось Ох в моменты времени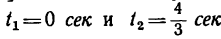
2. Находим выражения проекций скорости:
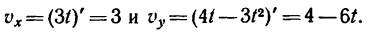
Как видно, проекция скорости на ось Ох – постоянная величина (не зависит от времени).
3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:
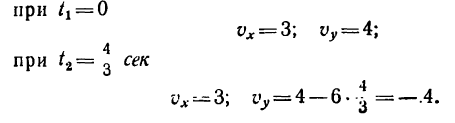
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы
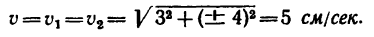
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):
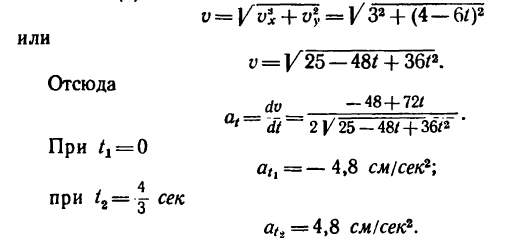
6. Находим проекции полного ускорения точки:
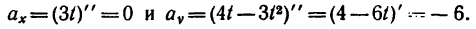
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем
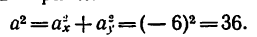
7. Определяем нормальное ускорение точки. Как при 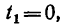
так и при 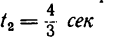
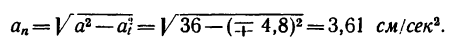
8. Зная, что в моменты пересечения траекторией оси 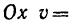 5 см:сек и
5 см:сек и 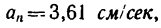 находим радиусы кривизны траектории в этих точках:
находим радиусы кривизны траектории в этих точках:
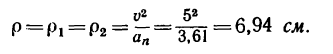
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости 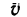 и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы
и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы 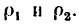
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
Найти центр и радиус окружности
Если окружность задана уравнением вида
найти центр (a;b) и радиус R такой окружности несложно.
Определить по уравнению окружности координаты её центра и радиуса:
Таким образом, центр данной окружности — точка (3;7), радиус R=2.
a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.
Центр окружности — (0;-3), радиус R=3.
Центр — в точке (6;0), радиус R=√5.
Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.
Чтобы найти центр и радиус окружности, заданной уравнением вида
нужно дополнить его до полных квадратов, чтобы привести к привычному виду.
Для этого сначала сгруппируем слагаемые
затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)
При a²+b²-c>0 это уравнение задаёт окружность с радиусом
При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).
При a²+b²-c
Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:
Центром этой окружности является точка (-5;3), радиус R=7.
Центр окружности — точка (2,5;0), радиус R=1,5.
Нахождение центра и радиуса окружности по общему уравнению окружности
Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности
Уравнение НЕ является общим уравнением окружности
Приведение общего уравнения окружности к стандартному виду
Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде
Из этого уравнения достаточно легко найти центр окружности – это будет точка с координатами (a,b), и радиус окружности – это будет квадратный корень из правой части уравнения.
Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:
Это – уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.
Способ решения такого рода задач следующий:
Перегруппируем слагаемые уравнения
Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число – значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.
Для решения обратной задачи – нахождения общего уравнения окружности по координатам центра и радиусу – можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах
Как найти радиус из уравнения окружности
Как найти радиус окружности

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Найти центр и радиус окружности
Если окружность задана уравнением вида
найти центр (a;b) и радиус R такой окружности несложно.
Определить по уравнению окружности координаты её центра и радиуса:
Таким образом, центр данной окружности — точка (3;7), радиус R=2.
a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.
Центр окружности — (0;-3), радиус R=3.
Центр — в точке (6;0), радиус R=√5.
Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.
Чтобы найти центр и радиус окружности, заданной уравнением вида
нужно дополнить его до полных квадратов, чтобы привести к привычному виду.
Для этого сначала сгруппируем слагаемые
затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)
При a²+b²-c>0 это уравнение задаёт окружность с радиусом
При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).
При a²+b²-c
Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:
Центром этой окружности является точка (-5;3), радиус R=7.
Центр окружности — точка (2,5;0), радиус R=1,5.
Нахождение центра и радиуса окружности по общему уравнению окружности
Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности
Уравнение НЕ является общим уравнением окружности
Приведение общего уравнения окружности к стандартному виду
Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде
Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.
Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:
Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.
Способ решения такого рода задач следующий:
Перегруппируем слагаемые уравнения
Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.
Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах
[spoiler title=”источники:”]
http://planetcalc.ru/9507/
http://b4.cooksy.ru/articles/kak-nayti-radius-iz-uravneniya-okruzhnosti
[/spoiler]
Теоретическая механика:
Кинематика точки
Смотрите также решения задач по теме «Кинематика точки» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.
В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.
* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы (§ 31).
В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.
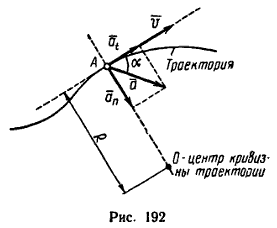
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).
Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.
Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением at – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).
Числовое значение касательного ускорения в общем случае определяется по формуле
at = dv/dt или at = f»(t).
Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением an – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).
Числовое значение нормального ускорения определяется в общем случае по формуле
an = v 2 /R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.
После того как определены касательное и нормальное ускорения, легко определить и ускорение a ( полное ускорение точки ).
Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(at 2 + an 2 ).
Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin α = an/a; cos α = at/a; tg α = an/at.
Но можно сначала определить направление полного ускорения a использовав формулу tg α = an/at,
а затем найти числовое значение a:
a = an/sin α или a = at/cos α.
Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.
Наличие касательного ускорения (at≠0) или его отсутствие (at=0) определяют соответственно неравномерность или равномерность движения точки.
Наличие нормального ускорения (an≠0) или его отсутствие (an=0) определяют криволинейность или прямолинейность движения точки.
Движение точки можно классифицировать так:
а) равномерное прямолинейное (at = 0 и an = 0);
б) равномерное криволинейное (at = 0 и an ≠ 0);
в) неравномерное прямолинейное (at ≠ 0 и an = 0);
г) неравномерное криволинейное (at ≠ 0 и an ≠ 0).
Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.
Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.
§ 27. Равномерное прямолинейное движение точки
Если at=0 и an=0, то вектор скорости остается постоянным (v=const), т. е. не изменяется ни по модулю, ни по направлению. Такое движение называется равномерным прямолинейным .
Уравнение равномерного движения имеет вид
(а) s = s0 + vt
или в частном случае, когда начальное расстояние s0=0,
(б) s = vt.
В уравнение (а) входит всего четыре величины, из них две переменные: s и t и две постоянные: s0 и v. Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.
При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы: расстояние s измеряется в м, время t – в сек, скорость v – в м/сек.
§ 28. Равномерное криволинейное движение точки
Если at = 0 и an ≠ 0, то модуль скорости остается неизменным (точка движется равномерно), но ее направление изменяется и точка движется криволинейно. Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное
an = v 2 /R,
где R – радиус кривизны траектории.
В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:
R = r = const,
а так как и числовое значение скорости постоянно, то
an = v 2 /r = const.
При равномерном движении числовое значение скорости определяется из формулы
v = (s — s0)/t или v = s/t.
Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2πr = πd (d = 2r – диаметр), а время равно периоду, т. е. t = T. Выражение скорости примет вид
v = 2πr/T = πd/T.
§ 29. Равнопеременное движение точки
Если вектор at=const (касательное ускорение постоянно как по модулю, так и по направлению), то an=0. Такое движение называется равнопеременным и прямолинейным .
Если же постоянным остается только числовое значение касательного уравнения
at = dv/dt = f'(t) = const,
то an≠0 и такое движение точки называется равнопеременным криволинейным .
При |at|>0 движение точки называется равноускоренным , а при |at| равнозамедленным .
Уравнение равнопеременного движения независимо от его траектории имеет вид
(1) s = s0 + v0t + att 2 / 2.
Здесь s0 – расстояние точки от исходного положения в момент начала отсчета; v0 – начальная скорость и at – касательное ускорение – величины численно постоянные, a s и t – переменные.
Числовое значение скорости точки в любой момент времени определяется из уравнения
(2) v = v0 + att.
Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s0, v0, at и три переменные: s, v, t.
Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).
Если неизвестные входят в оба основных уравнения, например, неизвестны at и t, то для удобства решения таких задач выведены вспомогательные формулы:
после исключения at из (1) и (2)
(3) s = s0 + (v + v0)t / 2;
после исключения t из (1) и (2)
(4) s = s0 + (v 2 — v0 2 ) / (2at).
В частном случае, когда начальные величины s0=0 и v0=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5) s = att 2 / 2;
(6) v = att;
(7) s = vt / 2;
(8) s = v 2 / (2at).
Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.
Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением . К этому движению применимы формулы (5)–(8), причем
at = g = 9,81 м/сек 2 ≈ 9,8 м/сек 2 .
§ 30. Неравномерное движение точки по любой траектории
§ 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме
Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат (см. § 51, п. 2 в учебнике Е. М. Никитина).
Движение точки в пространстве задается тремя уравнениями:
x = f1(t);
(1) y = f2(t);
z = f3(t);
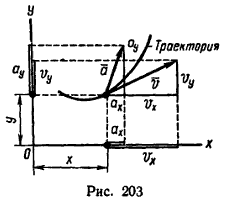
Движение точки в плоскости (рис. 203) задается двумя уравнениями:
(2) x = f1(t);
y = f2(t);
Системы уравнений (1) или (2) называют законом движения точки в координатной форме .
Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).
Если закон движения точки задан в координатной форме, то:
а) траектория плоского движения точки выражается уравнением
y = F(x),
которое образуется из данных уравнений движения после исключения времени t;
б) числовое значение скорости точки находится из формулы
v = sqrt(vx 2 + vy 2 )
после предварительного определения проекции (см. рис. 203) скорости на оси координат
vx = dx/dt и vy = dy/dt;
в) числовое значение ускорения находится из формулы
a = sqrt(ax 2 + ay 2 )
после предварительного определения проекций ускорения на оси координат
ax = dvx/dt и ay = dvy/dt;
г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.
§ 32. Кинематический способ определения радиуса кривизны траектории
При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну ) траектории. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. Используя уравнения движения точки в координатной форме, можно определять радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу
an = v 2 /R,
выражающую числовое значение нормального ускорения.
Скорость v точки определяется по формуле
(б) v = sqrt(vx 2 + vy 2 ).
Числовое значение нормального ускорения an входит в выражение полного ускорения точки
a = sqrt(an 2 + at 2 ),
откуда
(в) an = sqrt(a 2 — at 2 ),
где квадрат полного ускорения
(г) a 2 = ax 2 + ay 2
и касательное ускорение
(д) at = dv/dt.
Таким образом, если закон движения точки задан уравнениями
x = f1(t);
y = f2(t),
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
vx = f1‘(t);
vy = f2‘(t).
2. Подставив в (б’) выражения vx и vy, найти v 2 .
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение at, а затем at 2 .
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
ax = f1»(t) = vx‘;
ay = f2»(t) = vy‘.
5. Подставив в (г) выражения ax и ay, найти a 2 .
6. Подставить в (в) значения a 2 и at 2 и найти an.
7. Подставив в (а) найденные значения v 2 и an, получить радиус кривизны R.
Кинематический способ определения радиуса кривизны траектории в теоретической механике
Кинематический способ определения радиуса кривизны траектории:
При решении многих технических задач возникает необходимость знать радиус кривизны р (или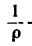
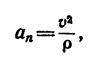
Отсюда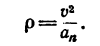
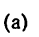
Скорость 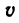 точки определяется по формуле
точки определяется по формуле
Следовательно,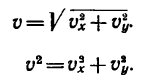
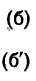
Числовое значение нормального ускорения а„ входит в выражение полного ускорения точки
откуда 
где квадрат полного ускорения 
и касательное ускорение
Таким образом, если закон движения точки задан уравнениями 
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:

2. Подставив в (б’) выражения 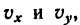 найти
найти 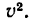
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение 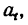 а затем а?.
а затем а?.
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
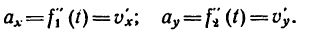
5. Подставив в (г) выражения 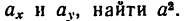
6. Подставить в (в) значения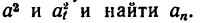
7. Подставив в (а) найденные значения 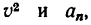 получить радиус кривизны р.
получить радиус кривизны р.
Задача:
Движение точки задано уравнениями 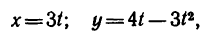
(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.
1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим
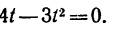
Отсюда [решая уравнение относительно 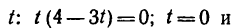
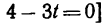 находим, что траектория пересекает ось Ох в моменты времени
находим, что траектория пересекает ось Ох в моменты времени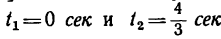
2. Находим выражения проекций скорости:
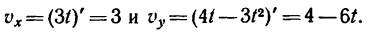
Как видно, проекция скорости на ось Ох — постоянная величина (не зависит от времени).
3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:
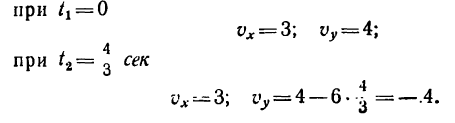
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы
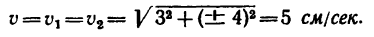
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):
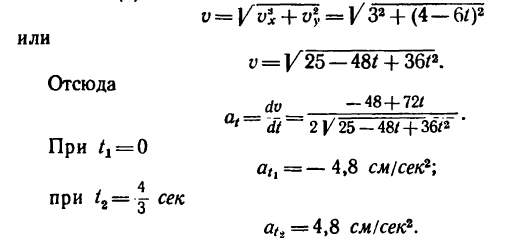
6. Находим проекции полного ускорения точки:
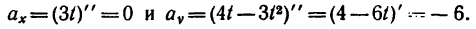
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем
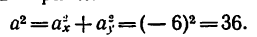
7. Определяем нормальное ускорение точки. Как при 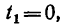
так и при 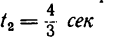
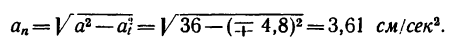
8. Зная, что в моменты пересечения траекторией оси 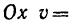 5 см:сек и
5 см:сек и 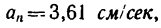 находим радиусы кривизны траектории в этих точках:
находим радиусы кривизны траектории в этих точках:
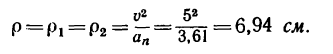
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости 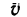 и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы
и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы 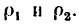
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как найти радиус если задано уравнение движения
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
7.1. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 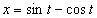 ,
, 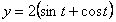 ,
, 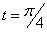 .
.
Решение: Скорости точки :
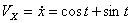 ,
,
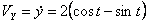 ,
,
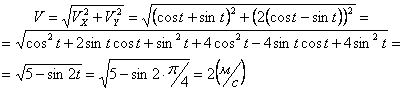
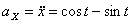 ,
,
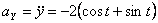 ,
,
Модуль полного ускорения:
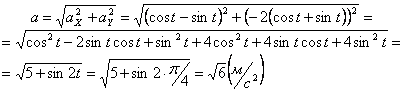
Модуль касательного ускорения точки:
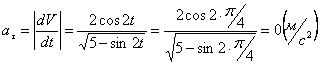 ,
,
А модуль нормального ускорения:
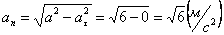 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
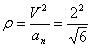 .
.
7.2. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 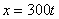 ,
, 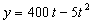 ,
, 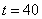 .
.
Решение: Скорости точки :
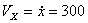 ,
,
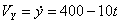 ,
,
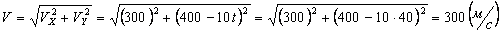
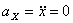 ,
,
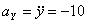 ,
,
Модуль полного ускорения:
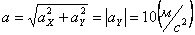
Модуль касательного ускорения точки:
 ,
,
А модуль нормального ускорения:
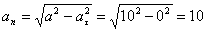 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
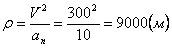 .
.
7.3. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 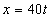 ,
, 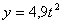 ,
, 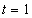 .
.
Решение: Скорости точки:
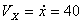 ,
,
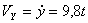 ,
,
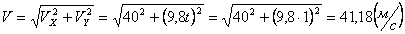 .
.
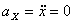 ,
,
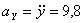 ,
,
Модуль полного ускорения:
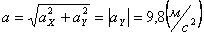 .
.
Модуль касательного ускорения точки:
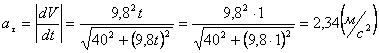 ,
,
А модуль нормального ускорения:
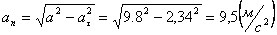 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
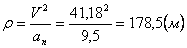 .
.
7.4. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 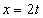 ,
, 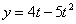 ,
, 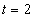 .
.
Решение: Скорости точки :
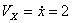 ,
,
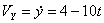 ,
,
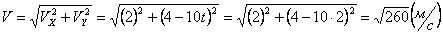
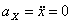 ,
,
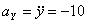 ,
,
Модуль полного ускорения:
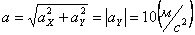
Модуль касательного ускорения точки:
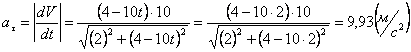 ,
,
А модуль нормального ускорения:
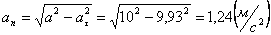 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
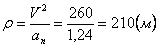 .
.
7.5. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 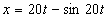 ,
, 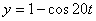 ,
, 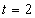 .
.
Решение: Скорости точки по осям :
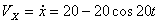 ,
,
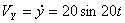 ,
,
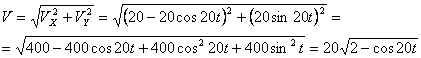
Ускорения точки по осям:
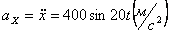 ,
,
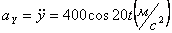 ,
,
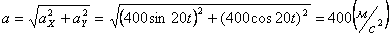 .
.
Модуль касательного ускорения точки:
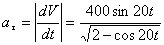 , а модуль нормального ускорения
, а модуль нормального ускорения 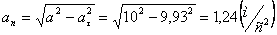 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением 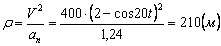 .
.
7.6. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 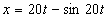 ,
, 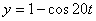 ,
,  .
.
Решение: Скорости точки по осям :
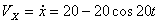 ,
,
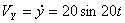 ,
,
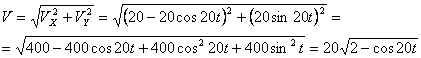
Ускорения точки по осям:
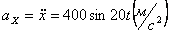 ,
,
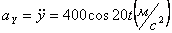 ,
,
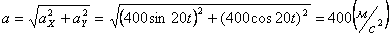 .
.
Модуль касательного ускорения точки:
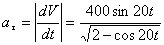 ,
,
а модуль нормального ускорения:
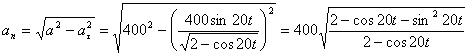 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением 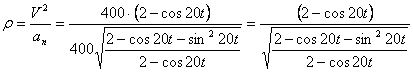 .
.
7.7. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 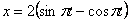 ,
, 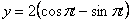 ,
, 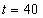 .
.
Решение: Скорости точки :
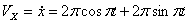 ,
,
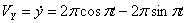 ,
,
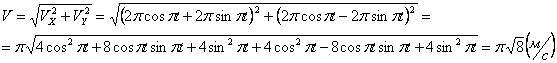
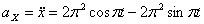 ,
,
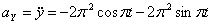 ,
,
Модуль полного ускорения:
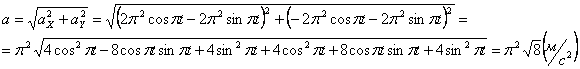
Модуль касательного ускорения точки:
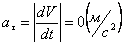 ,
,
А модуль нормального ускорения:
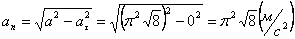 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
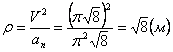 .
.
7.8. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 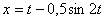 ,
, 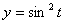 ,
,  .
.
Решение: Скорости точки :
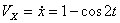 ,
,
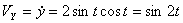 ,
,
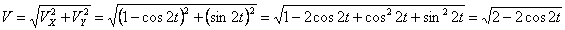 .
.
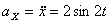 ,
,
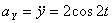 ,
,
Модуль полного ускорения:
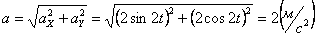 .
.
Модуль касательного ускорения точки:
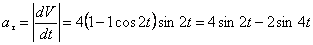 ,
,
А модуль нормального ускорения:
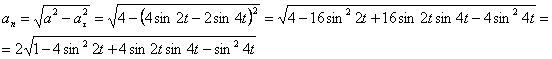 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
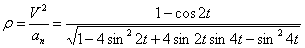 .
.
7.9. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 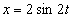 ,
, 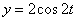 ,
, 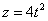 ,
, 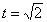 .
.
Решение: Скорости точки :
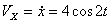 ,
,
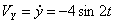 ,
,
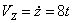
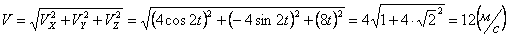 .
.
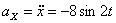 ,
,
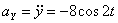 ,
,
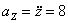
Модуль полного ускорения:
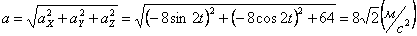 .
.
Модуль касательного ускорения точки:
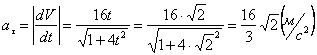 ,
,
А модуль нормального ускорения:
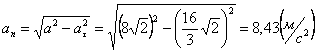 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
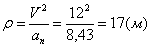 .
.
7.10. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 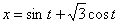 ,
, 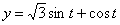 ,
, 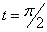 .
.
Решение: Скорости точки :
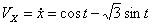 ,
,
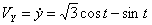 ,
,

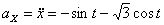 ,
,
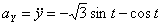 ,
,
Модуль полного ускорения:

Модуль касательного ускорения точки:
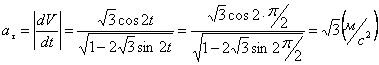 ,
,
А модуль нормального ускорения:
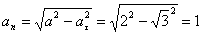 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
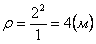 .
.
7.11. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 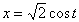 ,
, 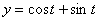 ,
, 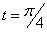 .
.
Решение: Скорости точки :
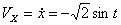 ,
,
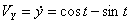 ,
,

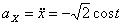 ,
,
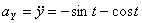 ,
,
Модуль полного ускорения:

Модуль касательного ускорения точки:
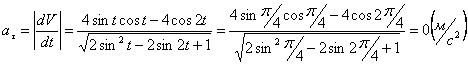 ,
,
А модуль нормального ускорения:
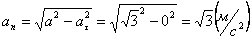 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
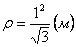 .
.
7.12. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 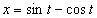 ,
, 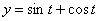 ,
, 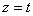 ,
,  .
.
Решение: Скорости точки :
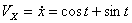 ,
,
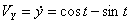 ,
,
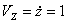

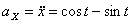 ,
,
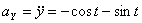 ,
,
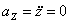
Модуль полного ускорения:

Модуль касательного ускорения точки:
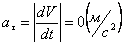 ,
,
А модуль нормального ускорения:
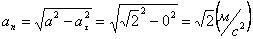 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
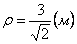 .
.
7.13. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 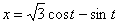 ,
, 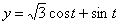 ,
,  .
.
Решение: Скорости точки :
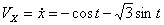 ,
,
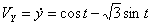 ,
,
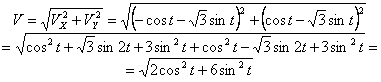
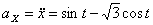 ,
,
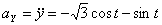 ,
,
Модуль полного ускорения:

Модуль касательного ускорения точки:
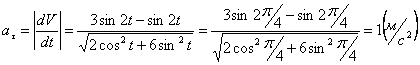 ,
,
А модуль нормального ускорения:
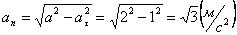 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
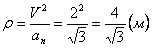 .
.
7.14. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 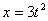 ,
, 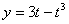 ,
, 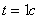 .
.
Найти: 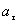 ,
, 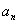 ,
, 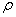 .
.
Решение: Скорости точки по осям :
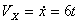 ,
,
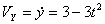 ,
,
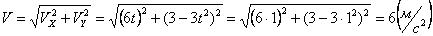 ,
,
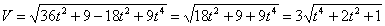
Ускорения точки по осям:
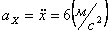 ,
,
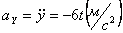 ,
,
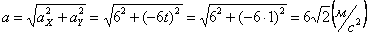
Модуль касательного ускорения точки:
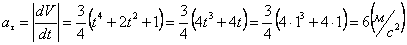 ,
,
А модуль нормального ускорения:
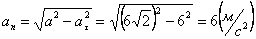 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
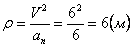 .
.
7.15. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 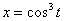 ,
, 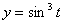 ,
,  .
.
Решение: Скорости точки :
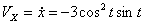 ,
,
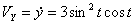 ,
,

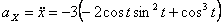 ,
,
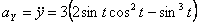 ,
,
Модуль полного ускорения:
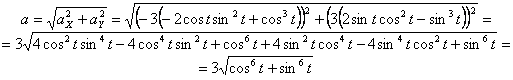
Модуль касательного ускорения точки:
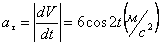 ,
,
А модуль нормального ускорения:
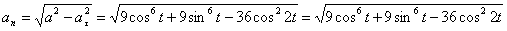 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
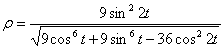 .
.
7.16. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 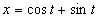 ,
, 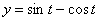 ,
,  .
.
Решение: Скорости точки :
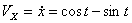 ,
,
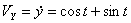 ,
,

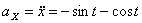 ,
,
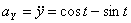 ,
,
Модуль полного ускорения:
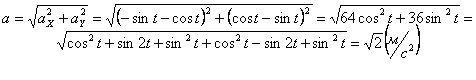
Модуль касательного ускорения точки:
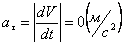 ,
,
А модуль нормального ускорения:
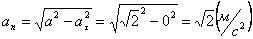 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
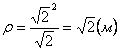 .
.
7.17. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 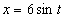 ,
, 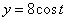 ,
, 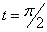 .
.
Решение: Скорости точки :
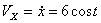 ,
,
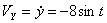 ,
,

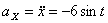 ,
,
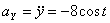 ,
,
Модуль полного ускорения:

Модуль касательного ускорения точки:
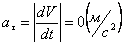 ,
,
А модуль нормального ускорения:
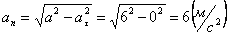 .
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
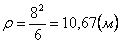 .
.
7.18. Дан закон движения точки по окружности радиусом r . Определить:
1) скорость и ускорение точки при 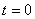 и
и  ;
;
2) моменты остановки точки;
3) путь, пройденный точкой за 10секунд.
Дано: 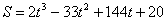 ,
, 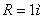 ,
, 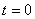 ,
,  .
.
Найти: 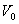 ,
, 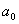 ,
, 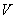 ,
, 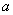 ,
, 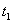 ,
, 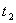 , П.
, П.
Решение: 1. На траектории отметим точку О – начало отсчета координаты s и укажем положительное направление отсчета этой координаты. Отметим положение точки в заданные моменты времени: При 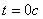 :
:
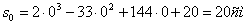 ;
;
При  :
:
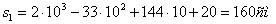 .
.
Проведем из этих точек естественные оси координат.
Определим проекцию скорости на касательную:
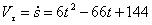 .
.
При 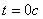 :
: 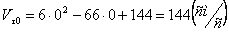 ;
;
При  :
: 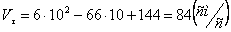 .
.
Векторы 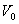 и
и 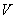 совпадают со своими проекциями. Определим проекции ускорения на естественнее оси координат :
совпадают со своими проекциями. Определим проекции ускорения на естественнее оси координат :
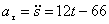 ;
; 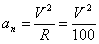 , Полное ускорение точки
, Полное ускорение точки 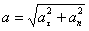 .
.
При 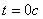 :
:
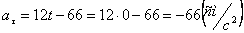 ,
,
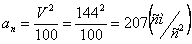 и
и
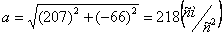 .
.
При 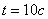 :
:
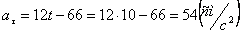 ,
,
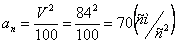 и
и
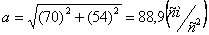 .
.
2. Чтобы найти время остановки надо найти время, когда скорость точки равна нулю:
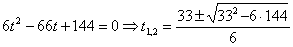 , получим
, получим 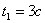 и
и 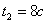 .
.
3. Поскольку за 10 секунд точка сделала две остановки, пройденный ею путь за 10с можно найти как сумму пути, пройденного от начала до первой остановки, от первой до второй остановки и от второй до момента времени  :
:
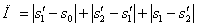 ,
,
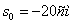 ;
; 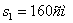 ;
; 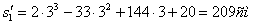 ;
; 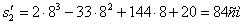 .
.
Путь пройденный точкой за 10 секунд:
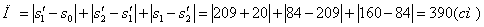 .
.
7.19. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: 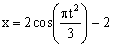 ,
, 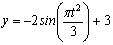 (1)
(1)
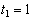 ( x и y – в см , t и t 1 – в с).
( x и y – в см , t и t 1 – в с).
Найти: 1) вид траектории;
2) для t = t 1 положение точки на траектории;
3) 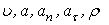 .
.
Решение: 1) Уравнение движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключаем время t из уравнений (1).
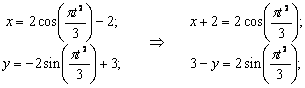
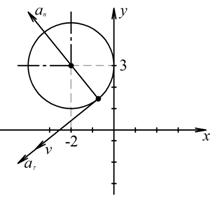
Возводя обе части равенств в квадрат, а затем складывая равенства, получаем 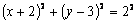 , т.е. траекторией точки М является окружность радиуса 2, показанная на рис.1.
, т.е. траекторией точки М является окружность радиуса 2, показанная на рис.1.
2) Определяем положение точки М в заданный момент времени t =1 с :
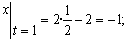
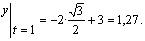
Вектор скорости точки
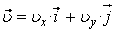 . (2)
. (2)
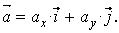 (3)
(3)
Здесь 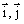 – орты осей
– орты осей 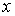 и
и 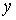 ;
; 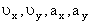 – проекции скорости и ускорения точки на оси координат.
– проекции скорости и ускорения точки на оси координат.
Найдем их, дифференцируя по времени уравнения движения (1):
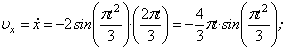
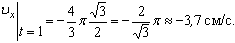
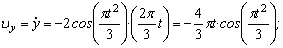
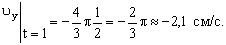
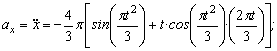
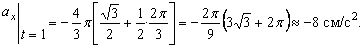
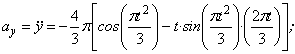
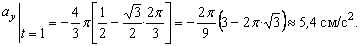
По найденным проекциям определяем модуль скорости:
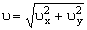 , (4)
, (4)
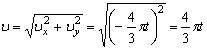 ,
,
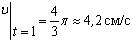 ,
,
и модуль ускорения точки:
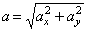 , (5)
, (5)
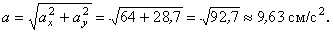
Модуль касательного ускорения точки
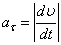 , (6)
, (6)
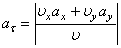 ; (7)
; (7)
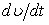 выражает проекцию ускорения точки на направление ее скорости. Знак «+» при
выражает проекцию ускорения точки на направление ее скорости. Знак «+» при 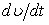 означает, что движение точки ускоренное, направление
означает, что движение точки ускоренное, направление 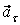 и
и 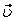 совпадают; знак «–» – что движение замедленное.
совпадают; знак «–» – что движение замедленное.
Вычисляем модуль касательного ускорения для заданного момента времени
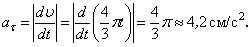
Модуль нормального ускорения точки
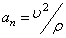 . (8)
. (8)
Если радиус кривизны траектории 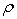 в рассматриваемой точке неизвестен, то нормальное ускорение можно определить по формуле
в рассматриваемой точке неизвестен, то нормальное ускорение можно определить по формуле
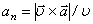 . (9)
. (9)
При движении точки в плоскости формула (9) принимает вид
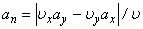 .
.
Модуль нормального ускорения можно определить и следующим образом:
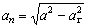 . (10)
. (10)
Воспользуемся в нашем случае формулой (10)
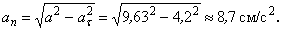
Радиус кривизны траектории в рассматриваемой точке определим из выражения:
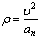 . (11)
. (11)
Тогда 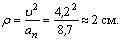
На рис. 1 показано положение точки М в заданный момент времени. Вектор 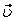 строим по составляющим
строим по составляющим 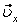 и
и 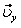 , причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор
, причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор 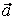 строим по составляющим
строим по составляющим 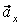 и
и 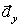 и затем раскладываем на составляющие
и затем раскладываем на составляющие 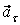 и
и 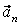 . Совпадение величин
. Совпадение величин 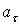 и
и 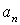 , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
, найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
7.20. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
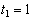 ( x и y – в см , t и t 1 – в с).
( x и y – в см , t и t 1 – в с).
Найти: 1) вид траектории;
2) 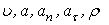 .
.
Указания. Задача — относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени t 1 = 1 с .
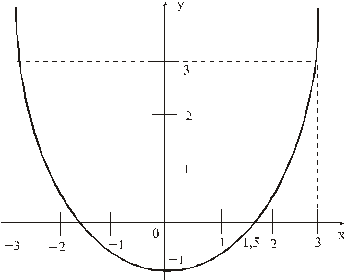
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t :
Отсюда окончательно находим уравнение траектории точки (параболы, см. рисунок):
2. Скорость точки найдем по ее проекциям на координатные оси:
V = 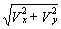 и при t 1 = 1 с,
и при t 1 = 1 с,
3. Аналогично найдем ускорение точки:
а = 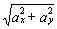
4. Касательное ускорение найдем, дифференцируя по времени равенство:
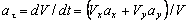 . (3)
. (3)
ч исловые значения всех величин, входящих в правую часть выражения (3), определены и даются равенствами (1) и (2).
Подставив в (3) эти числа, найдем сразу, что при t 1 = 1 с
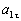 =7,49 см/с 2 .
=7,49 см/с 2 .
5. Нормальное ускорение точки:
a n = 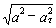 .
.
Подставляя сюда найденные числовые значения a 1 и a 1 τ , получим, что при t 1= 1 с
6. Радиус кривизны траектории ρ = V 2 / a n .
Подставляя сюда числовые значения V 1 и a 1 n , найдем, что при t 1 = 1 с
Ответ: V 1= 8 ,54 см/с, а 1 =8 см/с 2 , 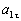 =7,49 см/с 2 , a 1 n =2,81 см/с 2 , ρ1 =25,95 см.
=7,49 см/с 2 , a 1 n =2,81 см/с 2 , ρ1 =25,95 см.
7.21. Точка движется по дуге окружности радиуса R =1 м по закону 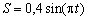 ( s – в метрах, t – в секундах), где s = AM (см. рисунок).
( s – в метрах, t – в секундах), где s = AM (см. рисунок).
Найти: скорость и ускорение точки в момент времени t 1 =1 с .
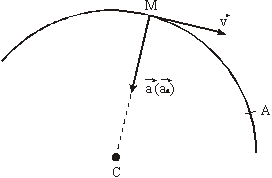
Определяем скорость точки:
V = ds / dt = 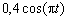 .
.
При t 1 =1 с получим 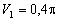 = -1,26 м/ с .
= -1,26 м/ с .
Ускорение находим по его касательной и нормальной составляющим:
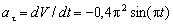 ,
,
п ри t 1 = 1 с получим , учтя, что R = 1 м
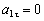 ,
,
тогда ускорение точки при t 1 =1 с будет:
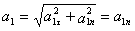 =1,59 м/с 2 .
=1,59 м/с 2 .
Изобразим на рисунке векторы 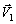 ,
, 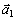 , учитывая знак V 1 и считая положительным направление от А к М.
, учитывая знак V 1 и считая положительным направление от А к М.
7.22. По заданным уравнениям движения точки М установить вид её траектории и для момента времени t = t 1(с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.
Дано: 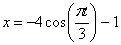 ,
, 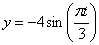 , t 1=1 сек ( x и y – в см , t и t 1 – в с).
, t 1=1 сек ( x и y – в см , t и t 1 – в с).
Найти: 1) вид траектории;
2) 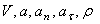 .
.
1) Найдём траекторию движения:
Для этого исключим параметр t .
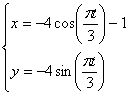
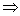
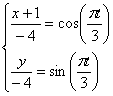
Возведём во вторую степень, получившиеся уравнения, а затем сложим, таким образом, исключится t . Получим:
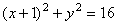
Это окружность с центром в точке с координатами (-1;0) и радиусом 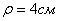
2) Найдём положение точки на траектории в момент времени t = t 1:
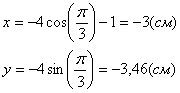
3) Определим скорость токи:
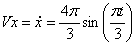
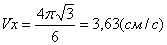
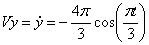
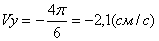
Для нахождения вектора полной скорости необходимо сложить 2 вектора:
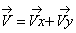
Найдём модуль полной скорости:
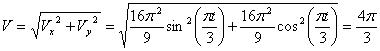
для момента времени t 1:
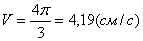
4) Определим ускорение точки:
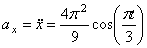
для момента времени t 1:
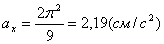
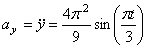
для момента времени t 1:
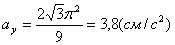
Найдём полное ускорение:
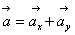
Найдём модуль полного ускорения:
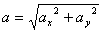
для момента времени t 1:
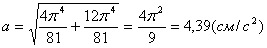
Определим касательное ускорение 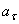 :
:
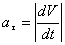 или,
или, 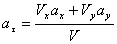
для момента времени t :
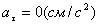
Определим нормальное ускорение an :
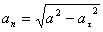
для момента времени t 1:
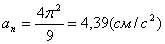

5) Из полученных результатов можно найти радиус кривизны траектории 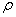 , в момент времени t 1:
, в момент времени t 1:
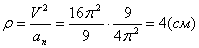
Действительно, этот радиус совпадает с радиусом окружности (траектории).
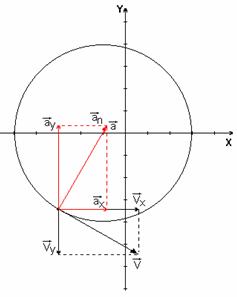
7.23. Точка М движется согласно уравнений 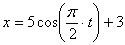 ;
; 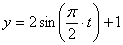 ; ( x , y — в метрах, t — в секундах). Определить уравнение траектории точки, для момента времени t =1с, найти положение точки, а также скорость, полное, касательное, нормальное ускорения точки и радиус кривизны траектории.
; ( x , y — в метрах, t — в секундах). Определить уравнение траектории точки, для момента времени t =1с, найти положение точки, а также скорость, полное, касательное, нормальное ускорения точки и радиус кривизны траектории.
1) Найдем уравнение траектории точки. Для определения уравнения траектории исключим из уравнений движения время  . Из первого уравнения движения точки найдем
. Из первого уравнения движения точки найдем 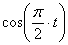
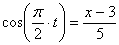
Из второго уравнения движения найдем 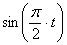
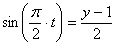
Возведя полученные значения ( правую и левую стороны уравнения ) в квадрат и складывая их находим:
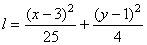 .
.
Следовательно, траекторией точки является эллипс с центром в точке с координатами (3;1).
Вид траектории показан на рисунке.
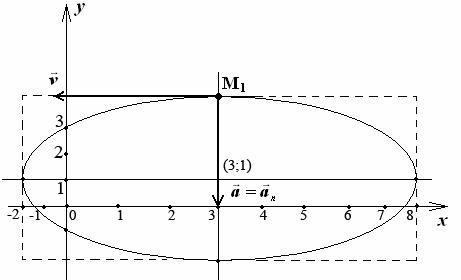
2) Найдем положение точки в момент времени t =1с
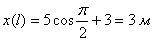 ;
; 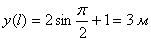 .
.
Положение точки М 1 показано на рисунке.
3) Найдем скорость точки М
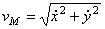 ,
,
Где 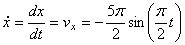 , или в момент времени t1=1c
, или в момент времени t1=1c
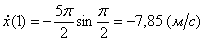
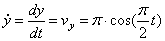 , или в момент времени t1=1c
, или в момент времени t1=1c
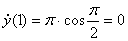
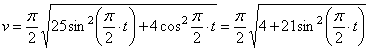
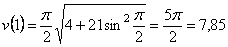

4) Найдём ускорение точки.
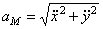 ,
,
где 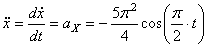 , или
, или 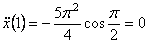 ,
,
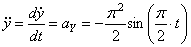 , или
, или 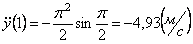

5) Найдем касательное ускорение точки M,
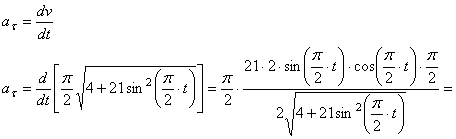
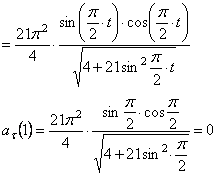
6) Найдём нормальное ускорение точки M ,
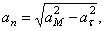
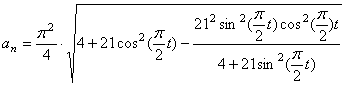
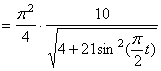
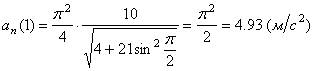
7) Найдем радиус кривизны траектории точки М,
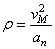 ,
,
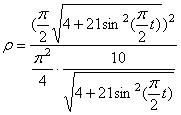
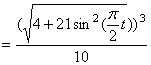
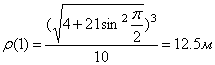
Направление векторов показано на рисунке.
Ответ: 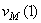 =7.85м/ c ;
=7.85м/ c ; 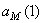 = 4.93 м/ c 2 ;
= 4.93 м/ c 2 ; 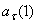 =0;
=0; 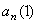 = 4.93 м/ c 2 ;
= 4.93 м/ c 2 ; 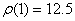 м
м
7.24. Пусть точка М движется в плоскости xOy в соответствии с уравнениями 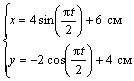 . Для момента времени
. Для момента времени 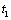 = 0,5 с найти положение точки М на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
= 0,5 с найти положение точки М на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение: Заданный закон движения точки в координатной форме можно рассматривать как параметрические уравнения траектории точки. Исключим время t из уравнений движения и получим уравнение траектории точки в виде:
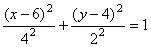 .
.
Таким образом, траекторией точки М является эллипс со смещенным центром, изображенный на рис. Отметим на траектории положение точки М 1 ( x 1, y 1) в момент времени t 1 = 0,5 c
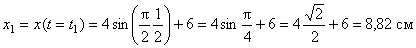 ;
;
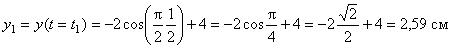 .
.
Вектор скорости точки представим в виде:
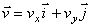 ,
,
где 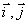 – орты координатных осей О x и О y ;
– орты координатных осей О x и О y ; 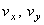 – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от соответствующих координат по времени
– проекции вектора скорости точки на координатные оси, которые равны 1-м производным от соответствующих координат по времени
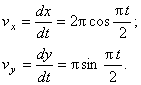
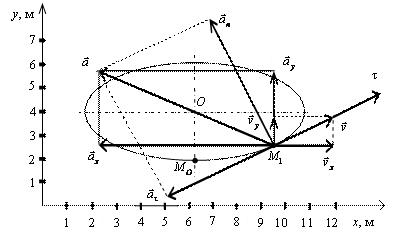
В момент времени t 1 = 0,5 c
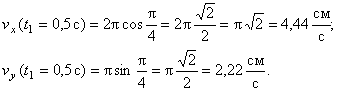
Вектор скорости точки 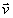 строим по двум взаимно перпендикулярным проекциям
строим по двум взаимно перпендикулярным проекциям 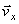 и
и 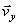 в соответствии с выбранным масштабом
в соответствии с выбранным масштабом
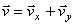 .
.
Полученный вектор должен быть направлен по касательной к траектории точки в сторону движения. Модуль скорости точки определим по уже найденным проекциям
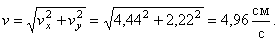
Вектор ускорения точки представим в виде:
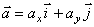 ,
,
где 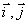 – орты координатных осей О x и О y ;
– орты координатных осей О x и О y ; 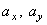 – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от проекций вектора скорости или 2-м производным от соответствующих координат по времени:
– проекции вектора скорости точки на координатные оси, которые равны 1-м производным от проекций вектора скорости или 2-м производным от соответствующих координат по времени:
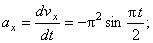
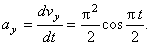
В момент времени t 1 = 0,5 c
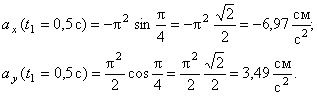
Вектор ускорения точки 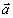 строим по двум взаимно перпендикулярным проекциям
строим по двум взаимно перпендикулярным проекциям 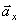 и
и 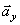 в соответствии с выбранным масштабом
в соответствии с выбранным масштабом
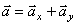 .
.
Полученный вектор ускорения точки в общем случае должен отклоняться от вектора скорости в сторону вогнутости траектории, а при движении по эллипсовидной траектории – проходить через центр эллипса. Модуль ускорения точки определим по уже найденным проекциям
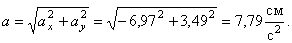
Вектор полного ускорения точки можно также представить в виде геометрической суммы его проекций на оси естественной системы отсчета
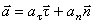 ,
,
где 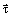 и
и 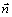 – единичные орты касательной и главной нормали;
– единичные орты касательной и главной нормали; 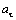 и
и 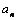 – соответственно проекции вектора ускорения на касательную и главную нормаль. Касательную М 1 t направляем по касательной к траектории в сторону движения точки движения, а главную нормаль М1 n – перпендикулярно касательной в сторону вогнутости траектории. При вычислении касательного ускорения удобно воспользоваться формулой, устанавливающей связь между координатным и естественным способами задания движения точки
– соответственно проекции вектора ускорения на касательную и главную нормаль. Касательную М 1 t направляем по касательной к траектории в сторону движения точки движения, а главную нормаль М1 n – перпендикулярно касательной в сторону вогнутости траектории. При вычислении касательного ускорения удобно воспользоваться формулой, устанавливающей связь между координатным и естественным способами задания движения точки
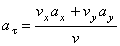 .
.
В момент времени t 1 = 0,5 c
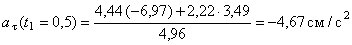 .
.
Значение касательного ускорения 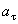 имеет отрицательный знак, следовательно, в данный момент времени движение точки замедленное и вектор касательного ускорения
имеет отрицательный знак, следовательно, в данный момент времени движение точки замедленное и вектор касательного ускорения 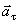 направлен в противоположную сторону направлению вектора скорости точки
направлен в противоположную сторону направлению вектора скорости точки 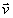 .
.
Нормальное ускорение 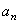 вычислим по формуле
вычислим по формуле 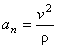 , если известен радиус кривизны траектории. Например, если точка движется по окружности радиусом R, то в любой точке траектории
, если известен радиус кривизны траектории. Например, если точка движется по окружности радиусом R, то в любой точке траектории 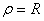 . Если же траекторией движения точки является прямая, то
. Если же траекторией движения точки является прямая, то 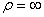 , следовательно,
, следовательно, 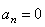 . В данном случае радиус кривизны траектории заранее не известен, поэтому нормальное ускорение определяем по формуле:
. В данном случае радиус кривизны траектории заранее не известен, поэтому нормальное ускорение определяем по формуле:
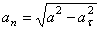 .
.
В момент времени t 1 = 0,5 c
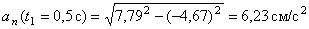 .
.
Построим векторы 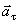 и
и 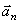 в соответствии с уже выбранным масштабом, а затем сложим их геометрически. В результате получим тот же вектор полного ускорения точки
в соответствии с уже выбранным масштабом, а затем сложим их геометрически. В результате получим тот же вектор полного ускорения точки 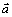 , который ранее уже был получен геометрической суммой составляющих
, который ранее уже был получен геометрической суммой составляющих 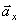 и
и 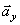 . Этот факт служит контролем правильности решения.
. Этот факт служит контролем правильности решения.
Радиус кривизны траектории в рассматриваемой точке определим по формуле
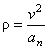 .
.
В момент времени t 1 = 0,5 c
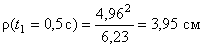 .
.
Ответ: 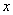 =8,82 см;
=8,82 см; 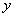 =2,59 см;
=2,59 см; 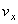 =4,44 см/ c ;
=4,44 см/ c ; 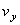 =2,22 см/ c ;
=2,22 см/ c ; 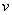 =4,96 см/с;
=4,96 см/с; 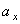 =6,97 см/с 2 ;
=6,97 см/с 2 ; 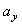 =3,49 см/с 2 ;
=3,49 см/с 2 ; 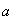 =7,79 см/с 2 ;
=7,79 см/с 2 ; 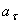 =4,67 см/с 2 ;
=4,67 см/с 2 ; 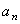 =6,23 см/с 2 ;
=6,23 см/с 2 ; 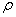 =3,95 см (радиус кривизны траектории в точке
=3,95 см (радиус кривизны траектории в точке 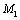 ).
).
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
источники:
http://www.evkova.org/kinematicheskij-sposob-opredeleniya-radiusa-kriviznyi-traektorii-v-teoreticheskoj-mehanike
http://www.teoretmeh.ru/primerkinematika4.htm
Рассмотрим алгоритм решения такой
задачи. Пусть движение точки задано в
координатной форме:
![]()
Для определения радиуса кривизны
траектории необходимо вычислить квадрат
скорости точки и её нормальное ускорение:

Квадрат полного ускорения точки вычисляем
по формуле:
![]()
Учитывая, что нормальная и касательная
составляющие ускорения взаимно
перпендикулярны, находим
![]()
Отсюда:
![]() .
.
Квадрат
скорости точки определяем по формуле:
![]()
Для определения касательного ускорения
продифференцируем по времени последнее
соотношение:
![]()
или
![]()
Здесь
![]() –
–
проекция вектора ускорения на направление
вектора скорости. Заметим, что![]() .
.
Пример 1.7
Движение точки задано уравнениями
![]()
Определить радиус кривизны траектории
для любого момента времени.
Вычислим
квадрат скорость точки:
![]() .
.
Вычислим
квадрат ускорения точки:
![]() .
.
Равенство
![]() принимает вид:
принимает вид:![]() .
.
Отсюда:
 .
.
Нормальное ускорение равно
 .
.
Определяем радиус кривизны траектории

Пример 1.8
Определить радиус кривизны траектории
снаряда, движение которого описано в
примере 1.2.
Применительно
к задаче о движении снаряда получаем:
![]()
Заметим, что направление движения
снаряда по траектории со временем не
изменяется. Направим орт касательной
по направлению вектора скорости. Тогда
проекция вектора скорости на направление
орта касательной к траектории положительна
в любой момент времени.
![]()

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 10.4;
12.1; 12.6; 12.7; 12.9; 12.10.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-17;
СР-18: СР-19.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3
2. Кинематика твёрдого тела
2.1. Простейшие движения твёрдого тела
Пример 2.1
Угол наклона полного ускорения точки
обода махового колеса к радиусу
![]() .
.
Касательное ускорение этой точки в
данный момент времени![]() Найти нормальное ускорение точки,
Найти нормальное ускорение точки,
отстоящей от оси вращения на расстоянии![]() Радиус махового колеса
Радиус махового колеса![]()
|
|
|
Рис. 2.1 |
Нормальное ускорение точки![]() направлено по радиусу (Рис. 2.1),
направлено по радиусу (Рис. 2.1),
следовательно,
 Отсюда:
Отсюда:![]()
Используя формулы,
![]()
![]()
получаем:
![]() ;
;
![]()
Пример 2.2
Вал радиуса
![]() приводится во вращение гирей, прикрепленной
приводится во вращение гирей, прикрепленной
к концу троса, намотанного на вал.
Определить модуль ускорения точки обода
вала, если ускорение гири![]() (Рис.2.2). В начальный момент вал находился
(Рис.2.2). В начальный момент вал находился
в покое.
|
|
|
Рис. 2.2 |
Точки троса, покинув поверхность
вала, движутся прямолинейно равноускоренно:
![]()
Поскольку трос не проскальзывает по
поверхности вала, скорости точек
![]() троса и вала совпадают.
троса и вала совпадают.
Используя формулу Эйлера, находим
угловую скорость вала
![]()
и его угловое ускорение
![]()
Теперь определяем составляющие ускорения
любой точки
![]() обода вала:
обода вала:
![]()
Остается определить модуль ускорения
точки
![]()
![]()
Заметим, что если скорости точек
![]() троса и вала совпадают, то их ускорения
троса и вала совпадают, то их ускорения
различны: точка![]() вала имеет нормальную составляющую
вала имеет нормальную составляющую
ускорения, поскольку движется по
криволинейной траектории.
Пример 2.3
Стрелка гальванометра длиной
![]() колеблется вокруг неподвижной оси по
колеблется вокруг неподвижной оси по
закону![]() Определить ускорение конца стрелки в
Определить ускорение конца стрелки в
ее среднем и крайних положениях, если
период колебаний![]() ,
,
а угловая амплитуда![]()
Прежде всего, зная закон вращения,
определим угловую скорость и угловое
ускорение тела:
![]()
Используя формулы (2.3), определяем
касательное и нормальное ускорения
точки:
![]()
Период
связан с круговой частотой соотношением
2![]() .
.
Для среднего положения стрелки имеем:
![]()
Для крайних положений стрелки имеем:
![]()
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 13.6;
13.14; 13.17; 13.18; 14.4; 14.5; 14.10.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 4-5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2015560.03 Кб15PSY – recommendation.pdf
- #
- #
Как найти радиус кривизны траектории
При рассмотрении движения тел используется ряд характеризующих величин, например тангенциальное и нормальное (центростремительное) ускорение, скорость, а также кривизна траектории. Радиус кривизны – геометрическое понятие, обозначающее радиус окружности R, по которой движется тело. Этот параметр можно найти по соответствующим формулам с помощью заданной траектории движения.

Инструкция
Наиболее часто встречаются задачи на определение радиуса кривизны траектории полета брошенного тела в заданный промежуток времени. Траектория движения в данном случае описывается уравнениями на координатных осях: х = f(t), y = f(t), где t – время, в момент которого требуется найти радиус. Его вычисление будет основываться на применении формулы аn = V²/R. Здесь радиус R выявляется из отношения нормального ускорения аn и мгновенной скорости V движения тела. Узнав данные величины, можно легко найти искомую компоненту R.
Вычислите проекции скорости тела на осях (ОХ, ОY). Математический смысл скорости – это первая производная от уравнения движения. Поэтому они легко находятся взятием производной от заданных уравнений: Vx = x’, Vy = y’. При рассмотрении геометрического отображения данных проекций в координатной системе видно, что они являются катетами прямоугольного треугольника. Причем гипотенуза в нем – искомая мгновенная скорость. Исходя из этого, вычислите величину мгновенной скорости V по теореме Пифагора: V = √( Vx² + Vy²). Подставляя в выражение известное значение времени, найдите числовой показатель V.
Модуль нормального ускорения также легко определить, рассмотрев другой прямоугольный треугольник, образуемый модулем полного ускорения а и касательного ускорения тела ак. Причем здесь нормальное ускорение является катетом и вычисляется так: аn = √( а² – ак²). Для нахождения касательного ускорения продифференцируйте по времени уравнение мгновенной скорости движения: ак = |dV/dt|. Полное же ускорение вычислите по его проекциям на оси, аналогично нахождению мгновенной скорости. Только для этого возьмите от заданных уравнений движения производные второго порядка: ах = х”, аy = y”. Модуль ускорения а = √( ах2 + аy2). Подставляя все найденные величины, определите числовое значение нормального ускорения аn = √( а² – ак²).
Выразите из формулы аn = V²/R искомую переменную радиуса кривизны траектории: R = V²/ аn. Подставьте числовые значения скорости и ускорения, вычислите радиус.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.



