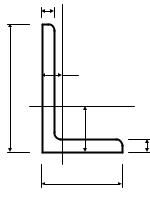
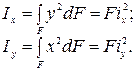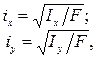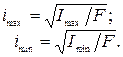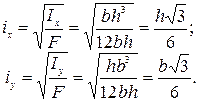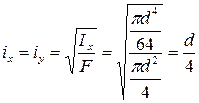Радиусом инерции i называют расстояние от соответствующей оси до точки, концентрация всей площади сечения в которой, даст такой же момент инерции, как и для всей площади рассматриваемой фигуры.
Отсюда:
Здесь:
A — площадь поперечного сечения;
Ix, Iy — осевые моменты инерции.
При расчете относительно главных осей сечения получаем главные радиусы инерции:
где Imax и Imin — соответственно максимальный и минимальный осевые моменты инерции фигуры.
Размерность — метр (либо кратные — см, мм).
Для стандартных прокатных профилей (например: двутавр или швеллер) значения радиусов инерции указаны в соответствующем сортаменте.
Понятие радиуса инерции часто используется в сопромате при расчетах на устойчивость и внецентренное нагружение.
Моменты инерции плоских сечений >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Радиус инерции сечения — геометрическая характеристика сечения, связывающая геометрический момент инерции фигуры 

Отсюда, формула радиуса инерции:
Таким образом, радиус инерции отражает отношение жесткости стержня на изгиб (

В сопротивлении стержней продольному изгибу (потере устойчивости прямолинейной формы при сжатии) основную роль играет гибкость стержня, а значит и величина наименьшего радиуса инерции сечения. Таким образом, большую экономичность будут иметь те сечения, у которых наименьший радиус инерции равен наибольшему, то есть сечения у которых все центральные моменты инерции равны, а эллипс инерции обратился бы в круг.
Единица измерения СИ — м. В строительной литературе чаще записывается в миллиметрах или сантиметрах, ввиду небольшой величины на практике.
Если моменты инерции 



В некоторой литературе радиус инерции обозначается просто 
Литература[править | править код]
- Беляев Н. М. Сопротивление материалов. — 15-е изд., перераб. — М.: Наука, 1976. — 607 с. — 200 000 экз.
Радиус инерции прямоугольного сечения (формула и расчет)
b — ширина сечения в мм; h — высота сечения в мм; y, z — центральные оси сечения.
Введите ширину сечения b в мм:
Введите высоту сечения h в мм:
В результате радиус инерции iy относительно центральной оси y равен:
0.00мм
0.00см
0.00м
В результате радиус инерции iz относительно центральной оси z равен:
0.00мм
0.00см
0.00м
Как найти радиус инерции прямоугольного сечения относительно его центральных осей?
Радиус инерции сечения относительно осей z и y можно рассчитать по формулам:
iy = h/√12 ≈ 0.288675 h,
iz = b/√12 ≈ 0.288675 b,,
где
iy — радиус инерции относительно центральной оси y в мм;
iz -радиус инерции относительно центральной оси z в мм ;
b — ширина сечения в мм (см. на рисунке вверху статьи);
h — высота сечения в мм (см. на рисунке вверху статьи).
Радиус инерции
Момент инерции фигуры относительно координатной оси может быть представлен в виде произведения площади фигуры на квадрат радиуса инерции:
Ввели в рассмотрение еще две геометрические характеристики: радиусы инерции поперечного сечения относительно осей x и y, соответственно. Формула радиуса инерции имеет вид:
Главным центральным осям инерции соответствуют главные радиусы инерции:
Для прямоугольника (см. рис. 4.4, а) главные радиусы инерции равны:
Для круглого сечения формула главных радиусов инерции имеет вид:
2
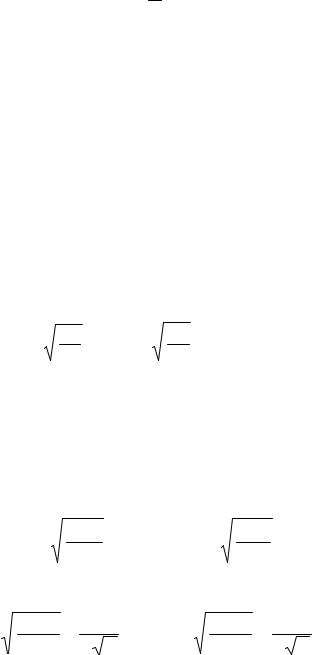
|
25 |
|||||||||||||
|
b h 3 |
b h 2 |
hb 3 |
hb 2 |
||||||||||
|
Wx = |
12 |
= |
; Wy = |
12 |
= |
. |
|||||||
|
h |
6 |
b |
6 |
||||||||||
|
2 |
2 |
Момент сопротивления коробчатого сечения относительно оси х (рис. 2.6):
|
B H 3 −b h 3 |
B H 2 |
b h 3 |
||||||||
|
12 |
||||||||||
|
Wx = |
= |
1 |
− |
. |
||||||
|
H |
6 |
B H 3 |
||||||||
|
2 |
||||||||||
Осевой момент сопротивления круглого сечения:
|
πd 4 |
πd 3 |
|||||
|
Wx =Wy = |
64 |
= |
. |
|||
|
d |
32 |
|||||
2
При решении задач кручения круглых стержней используются полярный момент инерции и полярный момент сопротивления.
|
Полярный момент инерции круга: J p = J x + J y = |
πd 4 |
+ |
πd 4 |
= |
πd 4 |
. |
|||
|
64 |
64 |
32 |
|||||||
|
πd 4 |
πd 3 |
||||||||
|
Полярный момент сопротивления круга: |
Wp = |
32 |
= |
. |
|||||
|
d |
16 |
||||||||
|
2 |
Вводим новую величину, которая определяется следующими формула-
ми
|
ix = |
J |
x , |
i y = |
J y |
. |
(2.13) |
|
A |
||||||
|
A |
Эти величины называются радиусами инерции сечения относительно осей x и y.
Радиусы инерции имеют размерность длины и положительное значе-
ние.
Радиусы инерции относительно главных центральных осей инерции сечения называются, как и моменты инерции, главными центральными радиу-
сами инерции сечения:
|
i |
max |
=i |
= Jmax , |
i |
min |
=i |
2 |
= Jmin . |
(2.14) |
|
1 |
A |
A |
|||||||
Радиусы инерции прямоугольного сечения относительно осей симметрии равны:
|
i x |
= |
b h 3 |
= |
h |
, |
i y = |
h b 3 |
= |
b |
. |
|
12 b h |
12 b h |
2 3 |
||||||||
|
2 |
3 |

26
Радиусы инерции круглого сечения относительно осей симметрии рав-
ны:
|
ix = iy |
= |
πd 4 |
4 |
= |
d |
. |
||
|
64 |
πd 2 |
4 |
||||||
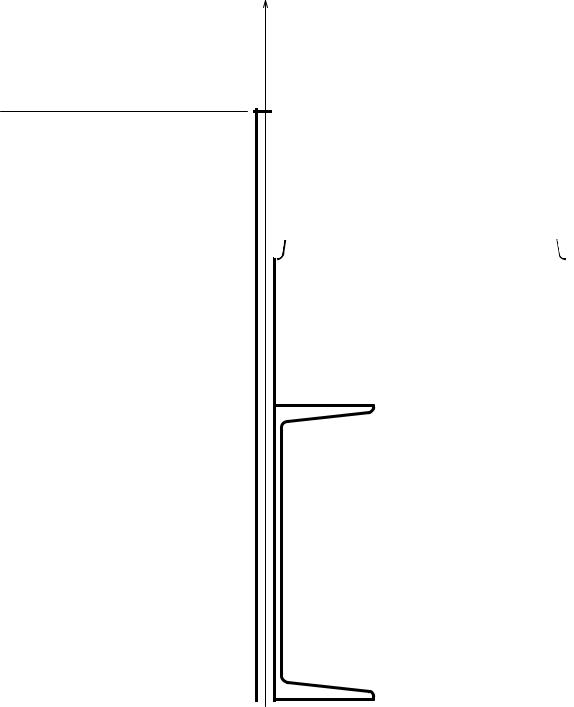
Пример 1. Для заданного поперечного сечения стального стержня, состоящего из следующих элементов (рис. 2.11):
1)вертикального листа 400 х 12 мм;
2)прокатного двутавра №20;
3)прокатного швеллера №20;
4)неравнополочного уголка 100 х 65 х 10 мм, необходимо определить:
–положение центра тяжести поперечного сечения (т. С);
–главные центральные оси поперечного сечения;
–главные центральные моменты инерции поперечного сечения;
–главные центральные радиусы инерции сечения.
Решение. Геометрические характеристики элементов, составляющих заданное сечение:
|
№ эл- |
Площадь в |
Моменты инерции сечения эле- |
|||||||||||||||||||
|
Элементы |
см2 |
ментов в см4 |
|||||||||||||||||||
|
та |
Аi |
||||||||||||||||||||
|
Jx i |
Jy i |
Jx i y i |
|||||||||||||||||||
|
1 |
Вертикальный |
А1 = 48.0 |
Jx 1 |
= 6400 |
Jy 1 |
= 5.76 |
Jx 1 y 1 |
= 0 |
|||||||||||||
|
лист 400х12 |
|||||||||||||||||||||
|
2 |
Двутавр №20 |
А2 = 26.8 |
Jx 2 |
= 115 |
Jy 2 |
= 1840 |
Jx 2 y 2 |
= 0 |
|||||||||||||
|
3 |
Швеллер №20 |
А3 = 23.4 |
Jx 3 |
= 1520 |
Jy 3 |
= 113 |
Jx 3 y 3 |
= 0 |
|||||||||||||
|
4 |
Уголок |
А4 = 15.67 |
Jx 4 |
= 51.68 |
Jy 4 |
= 155.52 |
Jx 4 y 4 |
= 51.18 |
|||||||||||||
|
100х65х10 |
|||||||||||||||||||||
|
1. Общая площадь составного сечения |
|||||||||||||||||||||
|
А = ∑ А i = 48.0 + 26.8 + 23.4 + 15.67 = 113.87 см2. |
|||||||||||||||||||||
|
2. Статические моменты заданного сечения относительно осей х1 и у1 |
|||||||||||||||||||||
|
Sx 1 |
=∑Ai |
yi = 48 · 0 + 26.8 · 15 + 23.4 · (-10) + 15.67 · (-18.36) = – 119.7 см3, |
|||||||||||||||||||
|
Sy 1 |
=∑Ai xi = 48 · 0 + 26.8 · 10.6 + 23.4 · 2.67 + 15.67 · (-3.97) = 284.35 см3. |
||||||||||||||||||||
|
3. Координаты центра тяжести составного сечения |
|||||||||||||||||||||
|
xc = |
Sy 1 |
= |
284.35 |
=2.50 |
см, yc = |
Sx 1 |
= |
−119.7 |
=−1.05см. |
||||||||||||
|
A |
113.87 |
A |
113.87 |
||||||||||||||||||
|
х и у |
4). Координаты центров тяжести элементов сечения относительно осей |
||||||||||||||||||||
|
точка С1: a1 = 1.05 см, |
b1 = – 2.5 см; |
||||||||||||||||||||
|
точка С2: а2 = 15 + 1.05 = 16.05 см, |
b2 = 10.6 – 2.5 = 8.1 см; |
||||||||||||||||||||
|
точка С3: а3 = – (10.0 – 1.05) = – 8.95 см, |
b3 = 2.67 – 2.50 = 0.17 см; |
точка С4: а4 = – (18.36 – 1.05) = – 17.31 см, b4 = – (3.97 + 2.5) = – 6.47 см. 5. Моменты инерции сечения относительно осей х и у

27
Jx =∑(Jx i + Ai ai2 ) = [6400 + 48 · 1.052] + [115 + 26.8 ·16.052] +
|
+ [1520 + 23.4 · (-8.95)2] + [51.68 + 15.67 · (-17.31)2] = 21613.04 |
см4, |
|
Jy =∑( Jy i + Ai bi2 ) = [5.76 + 48 · (-2.5)2] + [1840 + 26.8 · 8.12] + |
см4, |
|
+ [113 + 23.4 · 0.172] |
+ [155.52 + 15.67 · (-6.47)2] = 4829.27 |
|
Jxy =∑(Jx i y i + Ai ai bi ) = [0 |
+ 48 · 1.05 · (-2.5)] + [0 + 26.8 ·16.05 · 8.1] + |
+[0 + 23.4 · (-8.95) · 0.17] + [51.18 + 15.67 · (-17.31) · (-6.47)] = 5128.68 см4.
6.Главные центральные моменты инерции заданного сечения
|
J max = J1,2 |
= |
J x +J y |
± |
1 |
[(J x −J y )2 + 4 J 2xy ]= |
||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||
|
min |
|||||||||||||||||||||||||||||||
|
[(21613.04−4829.27)2 +4 5128.682 ] =13221.16 ± 9834.99. |
|||||||||||||||||||||||||||||||
|
= |
21613.04+4829.27 ± |
1 |
|||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||
|
Jmax = J1 = 23056.15 см4, |
Jmin = J2 = 3386.17 |
см4. |
|||||||||||||||||||||||||||||
|
= 21613.04 + |
|||||||||||||||||||||||||||||||
|
Проверка: Jx + Jy |
4829.27 = 26442.31 см4, |
||||||||||||||||||||||||||||||
|
J1 + J2 = 23056.15 + 3386.17 = 26442.32 см4. |
|||||||||||||||||||||||||||||||
|
7). Углы наклона главных центральных осей инерции сечения |
|||||||||||||||||||||||||||||||
|
tgαmax = |
J xy |
= |
5128.68 |
= −0.28138, |
αmax = −15.72 |
o |
. |
||||||||||||||||||||||||
|
J y −Jmax |
4829.27−23056.15 |
||||||||||||||||||||||||||||||
|
tgαmin = |
J xy |
= |
5128.68 |
= 3.5539325, |
αmax = 74.28 |
o |
. |
||||||||||||||||||||||||
|
J y −Jmin |
4829.27−3386.17 |
||||||||||||||||||||||||||||||
|
Проверка: |
αmax |
+ |
αmin |
=15.72o + 74.28o = 90o. |
|||||||||||||||||||||||||||
|
8). Главные центральные радиусы инерции |
|||||||||||||||||||||||||||||||
|
imax |
= |
Jmax |
= |
23056.15 =14.23 см, |
|||||||||||||||||||||||||||
|
A |
113.87 |
||||||||||||||||||||||||||||||
|
imin |
= |
Jmin |
= |
3386.17 =5.45 см. |
|||||||||||||||||||||||||||
|
A |
113.87 |
5.00 см
15.00 см
|
40.00 см |
см |
|
см |
1.05 |
|
10.00 |
28
|
у4 |
у1 |
у у3 |
у2 |
|
3.97 см |
2.67 см |
min (2) |
|
|
10.60 см |
c2
|
2.50 см |
||||||||
|
O |
||||||||
|
8 |
||||||||
|
.2 |
||||||||
|
4 |
||||||||
|
7 |
||||||||
|
= |
||||||||
|
IN |
||||||||
|
M |
||||||||
|
c |
1 |
х1 |
||||||
|
с |
MAX = – 15. |
72 |
O |
|||||
х3
c3
|
c |
4 |
х4 |
|||
|
20.00 см |
|||||
|
3.37 см |
|||||
|
10.00 см |
1.20 см |
7.60 см |
Рис. 2.11

29
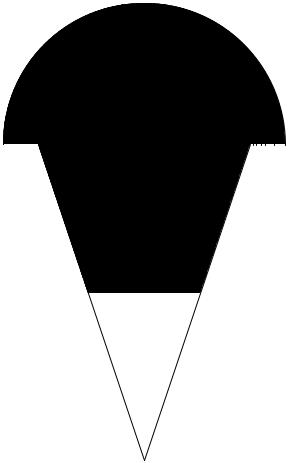
Пример 2. Для заданного поперечного сечения стержня, состоящего из следующих фигур:
1.полукруга с диаметром 8 см;
2.равнобедренного треугольника 6х9 см;
3.прямоугольного отверстия 2х3 см; необходимо определить:
–положение центра тяжести поперечного сечения (т. С);
–главные центральные оси поперечного сечения;
–главные центральные моменты инерции поперечного сечения;
–моменты сопротивления сечения.
Решение. Вычисление геометрических характеристик фигур, составляющих заданное сечение, выполнено и представлено в таблице на стр. 30.
1). Определяем общую площадь заданного сечения
А = А1 + А2 – А3 = 25.13 + 27 – 6 = 46.13 см2.
2). Определяем статический момент сечения относительно оси х1.
Sx1 = y1 A1 + y2 A 2 − y3 A 3 = 0+ (−4.7) 27 − (−3.2) 6 = −107.7см3 . 3). Определяем координаты центра тяжести заданного сечения. Поскольку заданное сечение имеет ось симметрии (ось у), то центр тя-
жести располагается на этой оси, поэтому необходимо определить только координату ус
yc =SAx1 = −46107.13.7 = −2.335 см.
4). Через полученный центр тяжести проводим горизонтальную ось х. Оси х, у является искомыми главными центральными осями инерции
заданного сечения, т.к. ось у – ось симметрии и Jxy = 0.
5). Вычисляем главные центральные моменты инерции сечения
|
Jx = (Jx1 + a12 A1 )+ (Jx 2 |
+ a 22 A 2 )− (Jx 3 + a32 A 3 )= [0.28 100.53 + 2.335 2 25.13 ]+ |
||||||||||||||||||||||||||||||||||||
|
+ [121.5 + (−2.365)2 27]− [4.5 + (−0.865)2 6]= 428.69см4 , |
|||||||||||||||||||||||||||||||||||||
|
Jy = Jy |
1 |
+ |
Jy |
2 |
− Jy |
3 |
=100.53+40.5−2 =139.03см4 , |
Jxy = Jx y |
+ Jx |
2 |
y |
2 |
− Jx |
3 |
y |
3 |
= 0 . |
||||||||||||||||||||
|
1 1 |
|||||||||||||||||||||||||||||||||||||
|
Из полученного решения следует: |
|||||||||||||||||||||||||||||||||||||
|
Jmax = J1 = Jx = 428.69 см4, |
Jmin = J2 = Jy = 139.03 см4 . |
||||||||||||||||||||||||||||||||||||
|
6). Вычисляем осевые моменты сопротивления сечения |
|||||||||||||||||||||||||||||||||||||
|
W |
(1) = |
Jx |
= |
428.69 |
= 92.49см3 , |
W(2) |
= |
Jx |
= |
428.69 |
= 51.25см3 |
, |
|||||||||||||||||||||||||
|
x |
y1 |
4.635 |
x |
y2 |
8.365 |
||||||||||||||||||||||||||||||||
|
W |
= |
Jу |
= |
139.05 |
= 34.76см3 . |
||||||||||||||||||||||||||||||||
|
у |
х |
4 |
30
•
|
2.30 |
3.00 |
1.50 |
|||||||||||||||||||
|
1.70 |
6.00 |
1.50 |
|||||||||||||||||||
|
A1 = |
π 82 |
= |
25.13см |
2 |
A 3 =2 3 =6см2 |
||||||||||||||||
|
8 |
A 2 = |
1 6 |
9 =27 cм2 |
||||||||||||||||||
|
Jx1 |
= |
0.28 |
π |
84 |
=0.28 100.53см |
4 |
Jx3 |
= |
2 33 |
=4.5см |
4 |
||||||||||
|
128 |
2 |
12 |
|||||||||||||||||||
|
6 93 |
|||||||||||||||||||||
|
Jy1 |
= |
π |
8 |
4 |
4 |
Jx2 |
= |
36 |
=121.5 см4 |
Jy3 |
= |
3 23 |
=2см |
4 |
|||||||
|
128 |
=100.53см |
3 |
12 |
||||||||||||||||||
|
9 6 |
|||||||||||||||||||||
|
Jx1y1 =0 |
Jy2 |
= |
=40.5 см4 , Jx2 y2 =0 |
Jx3y3 =0 |
|||||||||||||||||
|
48 |
31
Задание на выполнение расчетно-графической работы №1 по сопротивлению материалов
« ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЙ»
Заданы поперечные сечения стержней.
Сечение первого стержня составлено из прокатных профилей, номера которых определяются по таблице.
Сечение второго стержня составлено из простейших геометрических фигур, у которых размер а =…… см.
Для заданного сечения №……, строка №…… таблицы:
1.Определить положение центра тяжести сечения.
2.Вычислить значения осевых и центробежного моментов инерции относительно центральных осей сечения, параллельных выбранным осям вспомогательной системы координат.
3.Определить значения главных центральных моментов инерции и главных радиусов инерции.
4.Определить положение главных центральных осей инерции сечений.
5.Для сечения, составленного из геометрических фигур, вычислить значения осевых моментов сопротивления.
|
№ |
Равнобо- |
Неравно- |
Вертикаль- |
Горизон- |
Дву- |
Швел- |
|
стро- |
бокий уго- |
ный лист |
тальный |
|||
|
ки |
кий уголок |
лок |
(см) |
лист (см) |
тавр |
лер |
|
1 |
100х100х12 |
100х63х10 |
40х1.2 |
30х1.2 |
20 |
18 |
|
2 |
100х100х16 |
110х70х8 |
40х1.2 |
30х1.2 |
22а |
18а |
|
3 |
110х110х8 |
125х80х10 |
40х1.2 |
30х1.2 |
24 |
20 |
|
4 |
125х125х16 |
125х8012 |
40х1.2 |
30х2.0 |
24а |
20 |
|
5 |
140х140х12 |
140х90х10 |
40х2.0 |
30х2.0 |
27 |
20а |
|
6 |
160х160х14 |
160х100х12 |
50х1.2 |
40х2.0 |
30 |
24 |
|
7 |
160х160х16 |
160х100х14 |
50х1.6 |
40х1.2 |
36 |
24 |
|
8 |
180х180х12 |
180х110х12 |
50х1.6 |
40х1.2 |
40 |
30 |
|
9 |
200х200х16 |
200х125х14 |
60х2.0 |
50х1.2 |
40 |
36 |
|
10 |
200х200х20 |
200х125х16 |
60х2.0 |
50х2.0 |
50 |
40 |
32
33


35
|
Размеры сечения в мм |
Пло- |
Справочные величины для осей |
zo , |
|||||||||||||||||||||||||||||||||||||||||
|
Номер |
щадь |
Масса |
||||||||||||||||||||||||||||||||||||||||||
|
x |
– x |
y |
– y |
|||||||||||||||||||||||||||||||||||||||||
|
швел- |
h |
b |
d |
t |
сече- |
1 метра |
см |
|||||||||||||||||||||||||||||||||||||
|
лера |
ния, |
в кг |
Jx , |
Wx , |
ix , |
Sx , |
Jy , |
Wy , |
iy , |
|||||||||||||||||||||||||||||||||||
|
см2 |
||||||||||||||||||||||||||||||||||||||||||||
|
см4 |
см3 |
см |
см3 |
см4 |
см3 |
см |
||||||||||||||||||||||||||||||||||||||
|
5 |
50 |
32 |
4,4 |
7,0 |
6,16 |
4,84 |
22,8 |
9,1 |
1,92 |
5,59 |
5,61 |
2,75 |
0,95 |
1,16 |
||||||||||||||||||||||||||||||
|
6,5 |
65 |
36 |
4,4 |
7,2 |
7,51 |
5,90 |
48,6 |
15,0 |
2,54 |
9,00 |
8,70 |
3,68 |
1,08 |
1,24 |
||||||||||||||||||||||||||||||
|
8 |
80 |
40 |
4,5 |
7,4 |
8,98 |
7,05 |
89,4 |
22,4 |
3,16 |
13,30 |
12,80 |
4,75 |
1,19 |
1,31 |
||||||||||||||||||||||||||||||
|
10 |
100 |
46 |
4,5 |
7,6 |
10,90 |
8,59 |
174,0 |
34,8 |
3,99 |
20,40 |
20,40 |
6,46 |
1,37 |
1,44 |
||||||||||||||||||||||||||||||
|
12 |
120 |
52 |
4,8 |
7,8 |
13,30 |
10,40 |
304,0 |
50,6 |
4,78 |
29,60 |
31,20 |
8,52 |
1,53 |
1,54 |
||||||||||||||||||||||||||||||
|
14 |
140 |
58 |
4,9 |
8,1 |
15,60 |
12,30 |
491,1 |
70,2 |
5,60 |
40,80 |
45,40 |
11,00 |
1,70 |
1,67 |
||||||||||||||||||||||||||||||
|
14a |
140 |
62 |
4,9 |
8,7 |
17,00 |
13,30 |
545,0 |
77,8 |
5,66 |
45,10 |
57,50 |
13,30 |
1,84 |
1,87 |
||||||||||||||||||||||||||||||
|
16 |
160 |
64 |
5,0 |
8,4 |
18,10 |
14,20 |
747,0 |
93,4 |
6,42 |
54,10 |
63,30 |
13,80 |
1,87 |
1,80 |
||||||||||||||||||||||||||||||
|
16a |
160 |
68 |
5,0 |
9,0 |
19,50 |
15,30 |
823,0 |
103,0 |
6,49 |
59,40 |
78,80 |
16,40 |
2,01 |
2,00 |
||||||||||||||||||||||||||||||
|
18 |
180 |
70 |
5,1 |
8,7 |
20,70 |
16,30 |
1090,0 |
121,0 |
7,24 |
69,80 |
86,00 |
17,00 |
2,04 |
1,94 |
||||||||||||||||||||||||||||||
|
18a |
180 |
74 |
5,1 |
9,3 |
22,20 |
17,40 |
1190,0 |
132,0 |
7,32 |
76,10 |
105,00 |
20,00 |
2,18 |
2,13 |
||||||||||||||||||||||||||||||
|
20 |
200 |
76 |
5,2 |
9,0 |
23,40 |
18,40 |
1520,0 |
152,0 |
8,07 |
87,80 |
113,00 |
20,50 |
2,20 |
2,07 |
||||||||||||||||||||||||||||||
|
20a |
200 |
80 |
5,2 |
9,7 |
25,20 |
19,80 |
1670,0 |
167,0 |
8,15 |
95,90 |
139,00 |
24,20 |
2,35 |
2,28 |
||||||||||||||||||||||||||||||
|
22 |
220 |
82 |
5,4 |
9,5 |
26,70 |
21,00 |
2110,0 |
192,0 |
8,89 |
110,00 |
151,00 |
25,10 |
2,37 |
2,21 |
||||||||||||||||||||||||||||||
|
22a |
220 |
87 |
5,4 |
10,2 |
28,80 |
22,60 |
2330,0 |
212,0 |
8,99 |
121,00 |
187,00 |
30,00 |
2,55 |
2,46 |
||||||||||||||||||||||||||||||
|
24 |
240 |
90 |
5,6 |
10,0 |
30,60 |
24,00 |
2900,0 |
242,0 |
9,73 |
139,00 |
208,00 |
31,60 |
2,60 |
2,42 |
||||||||||||||||||||||||||||||
|
24a |
240 |
95 |
5,6 |
10,7 |
32,90 |
25,80 |
3180,0 |
265,0 |
9,84 |
151,00 |
254,00 |
37,20 |
2,78 |
2,67 |
||||||||||||||||||||||||||||||
|
27 |
270 |
95 |
6,0 |
10,5 |
35,20 |
27,70 |
4160,0 |
308,0 |
10,90 |
178,00 |
262,00 |
37,30 |
2,73 |
2,47 |
||||||||||||||||||||||||||||||
|
30 |
300 |
10 |
6,5 |
11,0 |
40,50 |
31,80 |
5810,0 |
387,0 |
12,00 |
224,00 |
327,00 |
43,60 |
2,84 |
2,52 |
||||||||||||||||||||||||||||||
|
0 |
||||||||||||||||||||||||||||||||||||||||||||
|
33 |
330 |
10 |
7,0 |
11,7 |
46,50 |
36,50 |
7980,0 |
484,0 |
13,10 |
281,0 |
410,00 |
51,80 |
2,97 |
2,59 |
||||||||||||||||||||||||||||||
|
5 |
||||||||||||||||||||||||||||||||||||||||||||
|
36 |
360 |
11 |
7,5 |
12,6 |
53,40 |
41,90 |
10820 |
601,0 |
14,20 |
350,00 |
513,00 |
61,70 |
3,10 |
2,68 |
||||||||||||||||||||||||||||||
|
0 |
||||||||||||||||||||||||||||||||||||||||||||
|
40 |
400 |
11 |
8,0 |
13,5 |
61,50 |
48,30 |
15220 |
761,0 |
15,70 |
444,00 |
642,00 |
73,40 |
3,23 |
2,75 |
||||||||||||||||||||||||||||||
|
5 |
||||||||||||||||||||||||||||||||||||||||||||
36
Т а б л и ц а 2.3
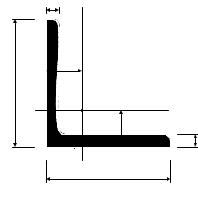
Уголки равнополочные (ГОСТ 8509-86) J – момент инерции;
W – момент сопротивления;
Jxy – центробежный момент инерции; i – радиус инерции;
хо, уо – расстояние от центра тяжести до наружных граней полок
|
Номер |
Размеры сечения |
Пло- |
Справочные величины для осей |
||||||||||||||||||||||||||
|
про- |
в мм |
щадь |
Масса |
||||||||||||||||||||||||||
|
x- x , y – y |
xo = yo , |
||||||||||||||||||||||||||||
|
филя |
сече- |
Jxy , |
1 метра |
||||||||||||||||||||||||||
|
Jx = Jy , |
Wx = Wy, |
ix = iy , |
|||||||||||||||||||||||||||
|
b |
t |
ния, |
см4 |
см |
в кг |
||||||||||||||||||||||||
|
см2 |
см4 |
см3 |
см |
||||||||||||||||||||||||||
|
2 |
20 |
3 |
1,13 |
0.40 |
0,28 |
0,59 |
0,23 |
0,60 |
0,89 |
||||||||||||||||||||
|
4 |
1,46 |
0,50 |
0,37 |
0,58 |
0,28 |
0,64 |
1,15 |
||||||||||||||||||||||
|
2,5 |
25 |
3 |
1,43 |
0,81 |
0,46 |
0,75 |
0,47 |
0,73 |
1,12 |
||||||||||||||||||||
|
4 |
1,86 |
1,03 |
0,59 |
0,74 |
0,59 |
0,76 |
1,46 |
||||||||||||||||||||||
|
2,8 |
28 |
3 |
1,62 |
1,16 |
0,58 |
0,85 |
0,68 |
0,80 |
1,27 |
||||||||||||||||||||
|
3 |
30 |
3 |
1,74 |
1,45 |
0,67 |
0,91 |
0,85 |
0,85 |
1,36 |
||||||||||||||||||||
|
4 |
2,27 |
1,84 |
0,87 |
0,80 |
1,08 |
0,89 |
1,78 |
||||||||||||||||||||||
|
3,2 |
32 |
3 |
1,86 |
1,77 |
0,77 |
0,97 |
1,03 |
0,89 |
1,46 |
||||||||||||||||||||
|
4 |
2,43 |
2,26 |
1,00 |
0,96 |
1,32 |
0,94 |
1,91 |
||||||||||||||||||||||
|
3,5 |
35 |
3 |
2,04 |
2,35 |
0,93 |
1,07 |
1,37 |
0,97 |
1,60 |
||||||||||||||||||||
|
4 |
2,17 |
3,01 |
1,21 |
1,06 |
1,75 |
1,01 |
2,10 |
||||||||||||||||||||||
|
5 |
3,28 |
3,61 |
1,47 |
1,05 |
2,10 |
1,05 |
2,58 |
||||||||||||||||||||||
|
4 |
40 |
3 |
2,35 |
3,55 |
1,22 |
1,23 |
2,08 |
1,09 |
1,85 |
||||||||||||||||||||
|
4 |
3,08 |
4,58 |
1,60 |
1,22 |
2,68 |
1,13 |
2,42 |
||||||||||||||||||||||
|
5 |
3,79 |
5,53 |
1,95 |
1,21 |
3,22 |
1,17 |
2,98 |
||||||||||||||||||||||
|
4,5 |
45 |
3 |
2,65 |
5,13 |
1,56 |
1,39 |
3,00 |
1,21 |
2,08 |
||||||||||||||||||||
|
4 |
3,48 |
6,63 |
2,04 |
1,38 |
3,89 |
1,26 |
2,73 |
||||||||||||||||||||||
|
5 |
4,29 |
8,03 |
2,51 |
1,37 |
4,71 |
1,30 |
3,37 |
||||||||||||||||||||||
|
3 |
2,96 |
7,11 |
1,94 |
1,55 |
4,16 |
1,33 |
2,32 |
||||||||||||||||||||||
|
5 |
50 |
4 |
3,89 |
9,21 |
2,54 |
1,54 |
5,42 |
1,38 |
3,05 |
||||||||||||||||||||
|
5 |
4,80 |
11,20 |
3,13 |
1,53 |
6,57 |
1,42 |
3,77 |
||||||||||||||||||||||
|
6 |
5,69 |
13,07 |
3,69 |
1,52 |
7,65 |
1,46 |
4,47 |
||||||||||||||||||||||
|
5,6 |
56 |
4 |
4,38 |
13,10 |
3,21 |
1,73 |
7,69 |
1,52 |
3,44 |
||||||||||||||||||||
|
5 |
5,41 |
15,97 |
3,96 |
1,72 |
9,41 |
1,57 |
4,25 |
||||||||||||||||||||||
|
4 |
4,72 |
`6,21 |
3,70 |
1,85 |
9,48 |
1,62 |
3,71 |
||||||||||||||||||||||
|
6 |
60 |
5 |
5,83 |
19,79 |
4,56 |
1,84 |
11,61 |
1,66 |
4,58 |
||||||||||||||||||||
|
6 |
6,92 |
23,21 |
5,40 |
1,83 |
13,60 |
1,70 |
5,43 |
||||||||||||||||||||||
|
8 |
9,04 |
29,55 |
7,00 |
1,81 |
17,22 |
1,78 |
7,10 |
||||||||||||||||||||||
|
10 |
11,08 |
35,32 |
8,52 |
1,79 |
20,32 |
1,85 |
8,70 |
||||||||||||||||||||||
|
6,3 |
63 |
4 |
4,96 |
18,86 |
4,09 |
1,95 |
11,00 |
1,69 |
3,90 |
||||||||||||||||||||
|
5 |
6,13 |
23,10 |
5,05 |
1,94 |
13,70 |
1,74 |
4,81 |
||||||||||||||||||||||
|
6 |
7,28 |
27,06 |
5,98 |
1,93 |
15,90 |
1,78 |
5,72 |
||||||||||||||||||||||
|
4,5 |
6,20 |
29,04 |
5,67 |
2,16 |
17,00 |
1,88 |
4,87 |
||||||||||||||||||||||
|
7 |
70 |
5 |
6,86 |
31,94 |
6,27 |
2,16 |
18,70 |
1,90 |
5,38 |
||||||||||||||||||||
|
6 |
8,15 |
37,58 |
7,43 |
2,15 |
22,10 |
1,94 |
6,39 |
||||||||||||||||||||||
|
7 |
9,42 |
42,98 |
8,57 |
2,14 |
25,20 |
1,99 |
7,39 |
||||||||||||||||||||||
|
8 |
10,67 |
48,16 |
9,68 |
2,12 |
28,20 |
2,02 |
8,37 |
||||||||||||||||||||||
|
5 |
7,39 |
39,53 |
7,21 |
2,31 |
23,10 |
2,02 |
5,80 |
||||||||||||||||||||||
|
7,5 |
75 |
6 |
8,78 |
46,57 |
8,57 |
2,30 |
27,30 |
2,06 |
6,89 |
||||||||||||||||||||
|
7 |
10,15 |
53,34 |
9,89 |
2,29 |
31,20 |
2,10 |
7,96 |
||||||||||||||||||||||
|
8 |
11,50 |
59,84 |
11,18 |
2,28 |
35,00 |
2,15 |
9,02 |
||||||||||||||||||||||
|
9 |
12,83 |
66,10 |
12,43 |
2,27 |
38,60 |
2,18 |
10,07 |
|
37 |
||||||||||
|
Номер |
П р о д о л ж е н и е т а б л и ц ы 2.3 |
|||||||||
|
Размеры сечения |
Пло- |
Справочные величины для осей |
Масса |
|||||||
|
про- |
в мм |
щадь |
x- x , y – y |
xo = yo , |
||||||
|
филя |
сече- |
Jxy , |
1 метра |
|||||||
|
Jx = Jy , |
Wx = Wy, |
ix = iy , |
||||||||
|
b |
t |
ния, |
см4 |
см |
в кг |
|||||
|
см2 |
см4 |
см3 |
см |
|||||||
|
5,5 |
8,63 |
52,68 |
9,03 |
2,47 |
30,90 |
2,17 |
6,78 |
|||
|
8 |
80 |
6 |
9,38 |
56,97 |
9,80 |
2,47 |
33,40 |
2,19 |
7,36 |
|
|
7 |
10,85 |
65,31 |
11,32 |
2,45 |
38,30 |
2,23 |
8,51 |
|||
|
8 |
12,30 |
73,36 |
12,80 |
2,44 |
43,00 |
2,27 |
9,65 |
|||
|
6 |
10,61 |
82,10 |
12,49 |
2,78 |
48,10 |
2,43 |
8,33 |
|||
|
9 |
90 |
7 |
12,28 |
94,30 |
14,45 |
2,77 |
55,40 |
2,47 |
9,64 |
|
|
8 |
13,93 |
106,11 |
16,36 |
2,76 |
62,30 |
2,51 |
10,93 |
|||
|
9 |
15,60 |
118,00 |
18,29 |
2,75 |
68,00 |
2,55 |
12,20 |
|||
|
6,5 |
12,82 |
122,10 |
16,69 |
3,09 |
71,40 |
2,68 |
10,06 |
|||
|
7 |
13,75 |
130,59 |
17,90 |
3,08 |
76,40 |
2,71 |
10,79 |
|||
|
10 |
100 |
8 |
15,60 |
147,19 |
20,30 |
3,07 |
86,30 |
2,75 |
12,25 |
|
|
10 |
19,24 |
178,95 |
24,97 |
3,05 |
110,00 |
2,83 |
15,10 |
|||
|
12 |
22,80 |
208,90 |
29,47 |
3,03 |
122,00 |
2,91 |
17,90 |
|||
|
14 |
26,28 |
237,15 |
33,83 |
3,00 |
138,00 |
2,99 |
20,63 |
|||
|
16 |
29,68 |
263,82 |
38,04 |
2,98 |
152,00 |
3,06 |
23,30 |
|||
|
11 |
110 |
7 |
15,15 |
175,61 |
21,83 |
3,40 |
106,00 |
2,96 |
11,89 |
|
|
8 |
17,20 |
198,17 |
24,77 |
3,39 |
116,00 |
3,00 |
13,50 |
|||
|
8 |
19,69 |
294,36 |
32,20 |
3,87 |
172,00 |
3,36 |
15,46 |
|||
|
9 |
22,00 |
327,48 |
36,00 |
3,86 |
192,00 |
3,40 |
17,30 |
|||
|
12,5 |
125 |
10 |
24,33 |
359,82 |
39,74 |
3,85 |
211,00 |
3,45 |
19,10 |
|
|
12 |
28,89 |
422,23 |
47,06 |
3,82 |
248,00 |
3,53 |
22,68 |
|||
|
14 |
33,37 |
481,76 |
54,17 |
3,80 |
282,00 |
3,61 |
26,20 |
|||
|
16 |
37,77 |
538,56 |
61,09 |
3,78 |
315,00 |
3,68 |
29,65 |
|||
|
14 |
140 |
9 |
24,72 |
465,72 |
45,55 |
4,34 |
274,00 |
3,78 |
19,41 |
|
|
10 |
27,33 |
512,29 |
50,32 |
4,33 |
301,00 |
3,82 |
21,45 |
|||
|
12 |
32,49 |
602,49 |
59,66 |
4,31 |
354,00 |
3,90 |
25,50 |
|||
|
10 |
31,43 |
774,24 |
66,19 |
4,96 |
455,00 |
4,30 |
24,67 |
|||
|
11 |
34,42 |
844,21 |
72,44 |
4,95 |
496,00 |
4,35 |
27,02 |
|||
|
16 |
160 |
12 |
37,39 |
912,89 |
78,62 |
4,94 |
537,00 |
4,39 |
28,35 |
|
|
14 |
43,57 |
1046,47 |
90,77 |
4,92 |
615,00 |
4,47 |
33,97 |
|||
|
16 |
49,07 |
1175,19 |
102,64 |
4,89 |
690,00 |
4,55 |
38,52 |
|||
|
18 |
54,79 |
1290,24 |
114,24 |
4,87 |
771,00 |
4,63 |
43,01 |
|||
|
20 |
60,40 |
1418,85 |
125,60 |
4,85 |
830,00 |
4,70 |
47,44 |
|||
|
18 |
180 |
11 |
38,80 |
1216,44 |
92,47 |
5,60 |
716,00 |
4,85 |
30,47 |
|
|
12 |
42,19 |
1316,62 |
100,41 |
5,59 |
776,00 |
4,89 |
33,12 |
|||
|
12 |
47,10 |
1822,78 |
124,64 |
6,22 |
1073,00 |
5,37 |
36,97 |
|||
|
13 |
50,85 |
1960,77 |
134,44 |
6,21 |
1156,00 |
5,42 |
39,92 |
|||
|
20 |
200 |
14 |
54,60 |
2097,00 |
144,17 |
6,20 |
1236,00 |
5,46 |
42,80 |
|
|
16 |
61,98 |
2362,57 |
163,37 |
6,17 |
1393,00 |
5,54 |
48,65 |
|||
|
20 |
76,54 |
2871,47 |
200,73 |
6,12 |
1689,00 |
5,70 |
60,08 |
|||
|
25 |
94,29 |
3466,21 |
245,59 |
6,06 |
2028,00 |
5,89 |
74,02 |
|||
|
30 |
111,54 |
4019,60 |
288,57 |
6,00 |
2332,00 |
6,07 |
87,56 |
|||
|
22 |
220 |
14 |
60,38 |
2814,36 |
175,18 |
6,83 |
1655,00 |
5,91 |
47,40 |
|
|
16 |
68,58 |
3175,44 |
198,71 |
6,80 |
1869,00 |
6,02 |
53,83 |
|||
|
16 |
78,40 |
4717,10 |
258,43 |
7,76 |
2775,00 |
6,75 |
61,55 |
|||
|
18 |
87,72 |
5247,24 |
288,82 |
7,73 |
3089,00 |
6,83 |
68,86 |
|||
|
25 |
250 |
20 |
96,96 |
5764,87 |
318,76 |
7,71 |
3395,00 |
6,91 |
76,11 |
|
|
22 |
106,12 |
6270,32 |
348,20 |
7,09 |
3691,00 |
7,00 |
83,31 |
|||
|
25 |
119,71 |
7006,39 |
391,72 |
7,65 |
4119,00 |
7,11 |
93,97 |
|||
|
28 |
133,12 |
7716,86 |
434,25 |
7,61 |
4527,00 |
7,23 |
104,50 |
|||
|
30 |
141,96 |
8176,52 |
462,11 |
7,59 |
4788,00 |
7,31 |
111,44 |
38
Т а б л и ц а 2.4
Уголки неравнополочные (ГОСТ 8510-86) J – момент инерции;
W – момент сопротивления;
Jxy – центробежный момент инерции; i – радиус инерции;
хо, уо – расстояние от центра тяжести до наружных граней полок
|
Размеры сечения |
Пло- |
Справочные величины для осей |
Масса |
|||||||||||||||||||||||||||||||||||||||||
|
Номер |
щадь |
xo , |
yo , |
Jxy , |
||||||||||||||||||||||||||||||||||||||||
|
в мм |
1 мет- |
|||||||||||||||||||||||||||||||||||||||||||
|
про- |
сече- |
x – x |
y – y |
|||||||||||||||||||||||||||||||||||||||||
|
филя |
B |
b |
t |
ния, |
Jx , |
Wx , |
ix , |
Jy , |
Wy, |
iy , |
см |
см |
см4 |
ра в |
||||||||||||||||||||||||||||||
|
см |
2 |
кг |
||||||||||||||||||||||||||||||||||||||||||
|
см4 |
см3 |
см |
см4 |
см3 |
см |
|||||||||||||||||||||||||||||||||||||||
|
2,5/1,6 |
25 |
16 |
3 |
1,16 |
0,70 |
0,43 |
0,78 |
0,22 |
0,19 |
0,44 |
0,42 |
0,86 |
0,22 |
0,91 |
||||||||||||||||||||||||||||||
|
3,2/2 |
32 |
20 |
3 |
1,49 |
1,52 |
0,72 |
1.01 |
0,46 |
0,30 |
0,55 |
0,49 |
1,08 |
0,47 |
1,17 |
||||||||||||||||||||||||||||||
|
4 |
1,94 |
1,93 |
0,93 |
1,00 |
0,57 |
0,39 |
0,54 |
0,53 |
1,12 |
0,59 |
1,52 |
|||||||||||||||||||||||||||||||||
|
4/2,5 |
40 |
25 |
3 |
1,89 |
3,06 |
1,14 |
1,27 |
0,93 |
0,49 |
0,70 |
0,59 |
1,32 |
0,96 |
1,48 |
||||||||||||||||||||||||||||||
|
4 |
2,47 |
3,93 |
1,49 |
1,26 |
1,18 |
0,63 |
0,69 |
0,63 |
1,37 |
1,22 |
1,94 |
|||||||||||||||||||||||||||||||||
|
5 |
3,03 |
4,73 |
1,82 |
1,25 |
1,41 |
0,77 |
0,68 |
0,66 |
1,41 |
1,44 |
2,37 |
|||||||||||||||||||||||||||||||||
|
4,5/2,8 |
45 |
28 |
3 |
2,14 |
4,41 |
1,45 |
1,43 |
1,32 |
0,61 |
0,79 |
0,64 |
1,47 |
1,38 |
1,68 |
||||||||||||||||||||||||||||||
|
4 |
2,80 |
5,68 |
1,90 |
1,42 |
1,69 |
0,80 |
0,78 |
0,68 |
1,51 |
1,77 |
2,20 |
|||||||||||||||||||||||||||||||||
|
5/3,2 |
50 |
32 |
3 |
2,42 |
6,18 |
1,82 |
1,60 |
1,99 |
0,81 |
0,91 |
0,72 |
1,60 |
2,01 |
1,90 |
||||||||||||||||||||||||||||||
|
4 |
3,17 |
7,98 |
2,38 |
1,59 |
2,56 |
1,05 |
0,90 |
0,76 |
1,65 |
2,59 |
2,49 |
|||||||||||||||||||||||||||||||||
|
5,6/3,6 |
56 |
36 |
4 |
3,58 |
11,37 |
3,01 |
1,78 |
3,70 |
1,34 |
1,02 |
0,84 |
1,82 |
3,71 |
2,81 |
||||||||||||||||||||||||||||||
|
5 |
4,41 |
13,82 |
3,70 |
1,77 |
4,48 |
1,65 |
1,01 |
0,88 |
1,87 |
4,50 |
3,46 |
|||||||||||||||||||||||||||||||||
|
4 |
4,04 |
16,33 |
3,83 |
2,01 |
5,16 |
1,67 |
1,13 |
0,91 |
2,03 |
5,25 |
3,17 |
|||||||||||||||||||||||||||||||||
|
6,3/4,0 |
63 |
40 |
5 |
4,98 |
19,91 |
4,72 |
2,00 |
6,26 |
2,05 |
1,12 |
0,95 |
2,08 |
6,41 |
3,91 |
||||||||||||||||||||||||||||||
|
6 |
5,90 |
23,31 |
5,58 |
1,09 |
7,29 |
2,42 |
1,11 |
0,99 |
2,12 |
7,44 |
4,63 |
|||||||||||||||||||||||||||||||||
|
8 |
7,68 |
29,60 |
7,22 |
1,96 |
9,15 |
3,12 |
1,09 |
1,07 |
2,20 |
9,27 |
6,03 |
|||||||||||||||||||||||||||||||||
|
7/4,5 |
70 |
45 |
5 |
5,59 |
27,76 |
5,88 |
2,23 |
9,05 |
2,62 |
1,27 |
1,05 |
2,28 |
9,12 |
4,39 |
||||||||||||||||||||||||||||||
|
7,5/5 |
75 |
50 |
5 |
6,11 |
34,81 |
6,81 |
2,39 |
12,47 |
3,25 |
1,43 |
1,17 |
2,39 |
12,00 |
4,79 |
||||||||||||||||||||||||||||||
|
6 |
7,25 |
40,92 |
8,08 |
2,38 |
14,60 |
3,85 |
1,42 |
1,21 |
2,44 |
14,10 |
5,69 |
|||||||||||||||||||||||||||||||||
|
8 |
9,47 |
52,38 |
10,52 |
2,35 |
18,52 |
4,99 |
1,40 |
1,29 |
2,52 |
17,80 |
7,43 |
|||||||||||||||||||||||||||||||||
|
8/5 |
80 |
50 |
5 |
6,36 |
41,64 |
7,71 |
2,56 |
12,68 |
3,28 |
1,41 |
1,13 |
2,60 |
13,20 |
4,99 |
||||||||||||||||||||||||||||||
|
6 |
7,55 |
48,98 |
9,15 |
2,55 |
14,85 |
3,88 |
1,40 |
1,17 |
2,65 |
15,50 |
5,92 |
|||||||||||||||||||||||||||||||||
|
9/5,6 |
90 |
56 |
5,5 |
7,86 |
65,28 |
10,74 |
2,88 |
19,67 |
4,53 |
1,58 |
1,26 |
2,92 |
20,51 |
6,17 |
||||||||||||||||||||||||||||||
|
6 |
8,54 |
70,58 |
11,66 |
2,88 |
21,22 |
4,91 |
1.58 |
1,28 |
2,95 |
22,21 |
6,70 |
|||||||||||||||||||||||||||||||||
|
8 |
11,18 |
90,87 |
15,24 |
2,85 |
27,08 |
6,39 |
1,56 |
1,36 |
3,04 |
28,33 |
8,77 |
|||||||||||||||||||||||||||||||||
|
6 |
9,59 |
98,29 |
14,52 |
3,20 |
30,58 |
6,27 |
1,79 |
1,42 |
3,23 |
31,50 |
7,53 |
|||||||||||||||||||||||||||||||||
|
10/6,3 |
100 |
63 |
7 |
11,09 |
112,86 |
16,78 |
3,19 |
34,99 |
7,23 |
1,78 |
1,46 |
3,28 |
36,10 |
8,70 |
||||||||||||||||||||||||||||||
|
8 |
12,57 |
126,96 |
19,01 |
3,18 |
39,21 |
8,17 |
1,77 |
1,50 |
3,32 |
40,50 |
9,87 |
|||||||||||||||||||||||||||||||||
|
10 |
15,47 |
133,83 |
23,32 |
3,15 |
47,13 |
9,99 |
1,75 |
1,58 |
3,40 |
48,60 |
12,14 |
|||||||||||||||||||||||||||||||||
|
11/7 |
110 |
70 |
6,5 |
11.45 |
142,42 |
19,11 |
3,53 |
45,61 |
8,42 |
2,00 |
1,58 |
3,55 |
46,80 |
8,98 |
||||||||||||||||||||||||||||||
|
8 |
13,93 |
171,54 |
23,22 |
3,51 |
54,64 |
10,20 |
1,98 |
1,64 |
3,61 |
55.90 |
10,93 |
|||||||||||||||||||||||||||||||||
|
7 |
14,06 |
226,53 |
26,67 |
4,01 |
73,73 |
11,89 |
2,29 |
1,80 |
4,01 |
74,70 |
11,04 |
|||||||||||||||||||||||||||||||||
|
12,5/8 |
125 |
80 |
8 |
15,96 |
255,62 |
30,26 |
4,00 |
82,95 |
13,47 |
2,28 |
1,84 |
4,05 |
84,10 |
12,53 |
||||||||||||||||||||||||||||||
|
10 |
19,70 |
311,61 |
37,27 |
3,98 |
100,47 |
16,52 |
2,26 |
1,92 |
4,14 |
102,00 |
15,47 |
|||||||||||||||||||||||||||||||||
|
12 |
23,36 |
364,79 |
44,07 |
3,95 |
116,84 |
19,46 |
2,24 |
2,00 |
4,22 |
118,00 |
18,34 |
|||||||||||||||||||||||||||||||||
|
14/9 |
140 |
90 |
8 |
18,00 |
363,68 |
38,25 |
4,49 |
119,79 |
17,19 |
2,58 |
2,03 |
4,49 |
121,00 |
14,13 |
||||||||||||||||||||||||||||||
|
10 |
22,24 |
444,45 |
47,19 |
4,47 |
145,54 |
21,14 |
2,56 |
2,12 |
4,58 |
147,00 |
17,46 |
|||||||||||||||||||||||||||||||||
|
16/10 |
160 |
100 |
9 |
22,87 |
605,97 |
56,04 |
5,15 |
186,03 |
23,96 |
2,85 |
2,24 |
5,19 |
191,00 |
17,96 |
||||||||||||||||||||||||||||||
|
10 |
25,28 |
666,97 |
61,91 |
5,13 |
204,09 |
26,42 |
2,84 |
2,28 |
5,23 |
213,00 |
19,85 |
|||||||||||||||||||||||||||||||||
|
14 |
34,72 |
897,19 |
84,65 |
5,08 |
271,60 |
35,89 |
2,80 |
2,43 |
5,40 |
282,00 |
27,26 |
|||||||||||||||||||||||||||||||||
|
18/11 |
180 |
110 |
10 |
28,33 |
952,28 |
78,59 |
5,80 |
276,37 |
32,27 |
3,12 |
2,44 |
5,88 |
295,00 |
22,24 |
||||||||||||||||||||||||||||||
|
12 |
33,69 |
1122,56 |
93,33 |
5,77 |
324,09 |
38,20 |
3,10 |
2,52 |
5,97 |
318,00 |
26,44 |
|||||||||||||||||||||||||||||||||
|
11 |
34,87 |
1449,02 |
107,31 |
6,45 |
446,36 |
45,98 |
3,58 |
2,79 |
6,50 |
465,00 |
27,37 |
|||||||||||||||||||||||||||||||||
|
20/12,5 |
200 |
125 |
12 |
37,89 |
1568,19 |
116,51 |
6,43 |
481,93 |
49,85 |
3,57 |
2,83 |
6,54 |
503,00 |
29,74 |
||||||||||||||||||||||||||||||
|
14 |
43,87 |
1800,83 |
134,64 |
6,41 |
550,77 |
57,43 |
3,54 |
2,91 |
6,62 |
575,00 |
34,43 |
|||||||||||||||||||||||||||||||||
|
16 |
49,77 |
2026,08 |
152,41 |
6,38 |
616,66 |
64,83 |
3,52 |
2,99 |
6,71 |
643,00 |
39,10 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

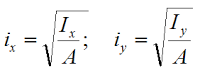
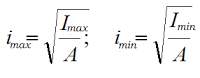


![i_{y}={sqrt[ {}]{{frac {J_{y}}{F}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/366c3061cfb1a62c70e1dcb132026dc76f813b6d)
![i_{z}={sqrt[ {}]{{frac {J_{z}}{F}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/936985f33700a6f05b7e26a71db6d1cf4e7112c8)