Если размер «максимального датчика» объектива составляет 8,8 × 6,6 мм, то круг изображения, проецируемый на датчик, представляет собой всего лишь диагональ датчика, 11 мм (от Пифагора: √ (8,8 ² + 6,6 ²)).
Диагональ датчика 25 мм × 25 мм имеет диагональ 35,4 мм, что в 3,21 раза больше, чем у круга объектива.
Таким образом, вам необходимо «увеличить» фокусное расстояние объектива в 3,21 раза. Или, другими словами, помимо встроенного фокусного расстояния объектива, вам необходимо добавить 2,21, умноженное на фактическое фокусное расстояние. 2,21 × 35 мм = 77,5 мм удлинения .
Это создаст круг изображения с той же степенью виньетирования на сенсоре 25 мм × 25 мм, что и на датчике 8,8 × 6,6 мм (где «степень виньетирования» – это количество остановок потери света в зависимости от процентное расстояние от центра объектива до угла датчика).
Это большое расширение будет иметь существенное влияние на вашу способность фокусироваться. При добавлении расстояния между объективом и корпусом камеры (с удлинительными трубками, сильфоном и т. Д.) Возникают два основных эффекта:
- вы можете сфокусироваться ближе, чем могли бы без расширения (минимальное расстояние фокусировки уменьшается); и
- Вы больше не можете фокусироваться далеко, например, бесконечность (максимальное расстояние фокусировки уменьшается).
Насколько уменьшается максимальное фокусное расстояние?
Давайте сначала сфокусируем объектив с фокусным расстоянием ƒ на бесконечности, которое является «родным» максимальным фокусным расстоянием. Затем, не меняя кольца фокусировки на объективе, давайте установим удлинительную трубку длиной X между объективом и корпусом камеры.
Новое максимальное фокусное расстояние D ‘ определяется по формуле
D ‘ = ƒ * (1 + ƒ / X )
В вашем конкретном случае, X = ƒ × 2,21, поэтому уравнение становится D ‘ = ƒ * (1 + 1 / 2,21) = 1,45 ƒ = 51 мм. (!)
Это означает, что для объектива, который вы пытаетесь использовать, если вы хотите, чтобы он проецировал окружность изображения на датчик, который в 3,21 раза больше, чем он был предназначен, если вы добавите правильное расширение, вы можете фокусировка только до 51 мм перед объективом .
То, что вы хотите сделать, это возможно , но это, вероятно, не практично для любого реального интересного использования.
#ios #swift #uiimageview #uibezierpath #cashapelayer
#iOS #swift #uiimageview #uibezierpath #cashapelayer
Вопрос:
В настоящее время у меня есть представление изображения, которое содержит круглое изображение.
Я настроил это так:
profileImageView.layer.cornerRadius = self.profileImageView.frame.size.width / 2
profileImageView.clipsToBounds = true
Я пытаюсь нарисовать дугу вокруг круга, используя UIBezierPath, и я хотел бы передать радиус изображения для параметра radius.
let circlePath = UIBezierPath(arcCenter: CGPoint(x: profileImageView.frame.size.width/2, y: profileImageView.frame.size.height/2), radius: IMG_VIEW_RADIUS, startAngle: CGFloat(0), endAngle:CGFloat(M_PI * 2), clockwise: true)
Как бы я это сделал?
Комментарии:
1. разве вы не можете использовать границу просмотра изображения
2. Я уже настроил это, но я хотел бы также создать дугу, которая перекрывает границу
3. Просто хак — почему бы не создать другой вид изображения, прозрачный для этого, и просто добавить его границу. Укажите вторую высоту ширины изображения, уменьшенную на 1 от первой, и добавьте поверх первого изображения
4. ооооо, звучит неплохо. Я собираюсь попробовать это
5. Другой способ размещен в качестве ответа
Ответ №1:
Swift 3.0
Другой способ
Я только что добавил изображение, подобное этому
let imageView = UIImageView(frame: CGRect(x: 100, y: 100, width: 200, height: 200))
imageView.backgroundColor = UIColor.green
imageView.layer.cornerRadius = imageView.frame.size.width / 2
imageView.clipsToBounds = true
self.view.addSubview(imageView)
Выполнение кругового пути Безье
let circlePath = UIBezierPath(arcCenter: CGPoint(x: imageView.frame.size.width/2,y: imageView.frame.size.height/2), radius: CGFloat((imageView.frame.size.width/2) - 3.5), startAngle: CGFloat(0), endAngle:CGFloat(M_PI * 2), clockwise: true)
let shapeLayer = CAShapeLayer()
shapeLayer.path = circlePath.cgPath
//fill color
shapeLayer.fillColor = UIColor.clear.cgColor
//stroke color
shapeLayer.strokeColor = UIColor.white.cgColor
//line width
shapeLayer.lineWidth = 2.0
//finally adding the shapeLayer to imageView's layer
imageView.layer.addSublayer(shapeLayer)
Теперь создаем внешнюю границу, используя ту же концепцию
let outerCirclePath = UIBezierPath(arcCenter: CGPoint(x: imageView.frame.size.width/2,y: imageView.frame.size.height/2), radius: CGFloat(imageView.frame.size.width/2 ), startAngle: CGFloat(0), endAngle:CGFloat(M_PI * 2), clockwise: true)
let outerLayer = CAShapeLayer()
outerLayer.path = outerCirclePath.cgPath
//fill color
outerLayer.fillColor = UIColor.clear.cgColor
//stroke color
outerLayer.strokeColor = UIColor.blue.cgColor
//line width
outerLayer.lineWidth = 15.0
imageView.layer.addSublayer(outerLayer)
Теперь измените zPosition слой формы, созданный для внутреннего слоя, поскольку его радиус меньше, чем у внешнего слоя, и его следует добавить сверху, чтобы он был виден
shapeLayer.zPosition = 2
Вам нужно немного изменить радиус первого внутреннего слоя. В моем случае я просто вычел радиус с 3.5

Комментарии:
1. Потрясающе, вы случайно не знаете, есть ли у меня способ добавить этот слой поверх границы?
2. @FaisalSyed Хорошо, я собираюсь изменить код в соответствии с вашими требованиями через 2 минуты
3. @FaisalSyed Проверьте сейчас. Вам нужно один раз немного изменить значения радиуса для внутреннего слоя, а также обязательно изменить
zPositionдобавленный внутренний слой, т. е.shapeLayerв вашем случае, иначе он не будет отображаться4. не знаю, почему это было отклонено ранее, если кто-нибудь проголосует против, пожалуйста, прокомментируйте также, что не так, чтобы можно было сделать предположительное улучшение
Ответ №2:
просто используйте ширину границы и цвет границы
profileImageView?.layer.cornerRadius = 5.0
profileImageView?.layer.borderColor = UIColor.white.cgColor
Комментарии:
1. Я пытаюсь добавить дугу в пределах моей границы. Добавленная таким образом граница скроет дугу
Радиус и диаметр окружности

Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).
Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.
Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.

На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.
Формула радиуса окружности через диаметр:
Формула диаметра окружности через радиус:
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.
Существует радиус вписанной окружности
и радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.
Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.
Как найти радиус окружности

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать – как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Нахождение радиуса круга: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2 π R
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:
S = π R 2
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/radius-okruzhnosti
[/spoiler]
Определение радиуса исходя из картинки
Тарас Г
Ученик
(179),
на голосовании
7 лет назад
Голосование за лучший ответ
♌ Mr.Leo ♌
Мудрец
(16544)
7 лет назад
Циркуль и линейка помогут.
Тарас ГУченик (179)
7 лет назад
Но каким именно образом ?
♌ Mr.Leo ♌
Мудрец
(16544)
Подбираешь раскрыв циркуля по радиусу на картинке, измеряешь линейкой, переносишь на эскиз, обозначаешь. Если эскиз выполняется в масштабе относительно картинки (объекта), применяешь масштаб к выполнению радиусов, в обозначении указываешь реальный размер.
Радиус – это отрезок, который соединяет центр окружности с любой точкой, которая лежит на этой окружности. Диаметр равен двум радиусам.
На чертежах радиусы используются для обозначения внутренних и наружных скруглений, криволинейных элементов.
Нанесение размеров согласно ГОСТу
Любой чертеж строится согласно определенным размерам, с учетом принятого масштаба, а также в процессе оформления все имеющие значения размеры выносятся с точностью до миллиметра. По типу все размеры делятся на линейные и угловые. К первым относятся размеры прямонаправленных участков, а ко вторым – размеры, измеряемые в градусах, секундах и минутах. Радиусы и диаметры также относятся к размерам, которые указываются на чертежах. Поэтому их оформление должно соответствовать требованиям ГОСТа.
До 2012 года на территории Российской Федерации действовал ГОСТ 2 307.608 «Нанесение размеров и предельных отклонений», который был заменен на ГОСТ 2.307.2011. Оба документа имеют схожую структуру, но последняя версия стандарта учитывает изменения, которые произошли с начала цифровизации. Среди определений можно встретить «электронную модель изделия» и «электронный макет». Оба документа определяют правила нанесения размеров и максимальные допуски отклонений.
Оба ГОСТ требуют минимального, но достаточного количества размеров. Например, один из размеров замкнутой цепочке наносится справочно, отмечается с помощью знака *.
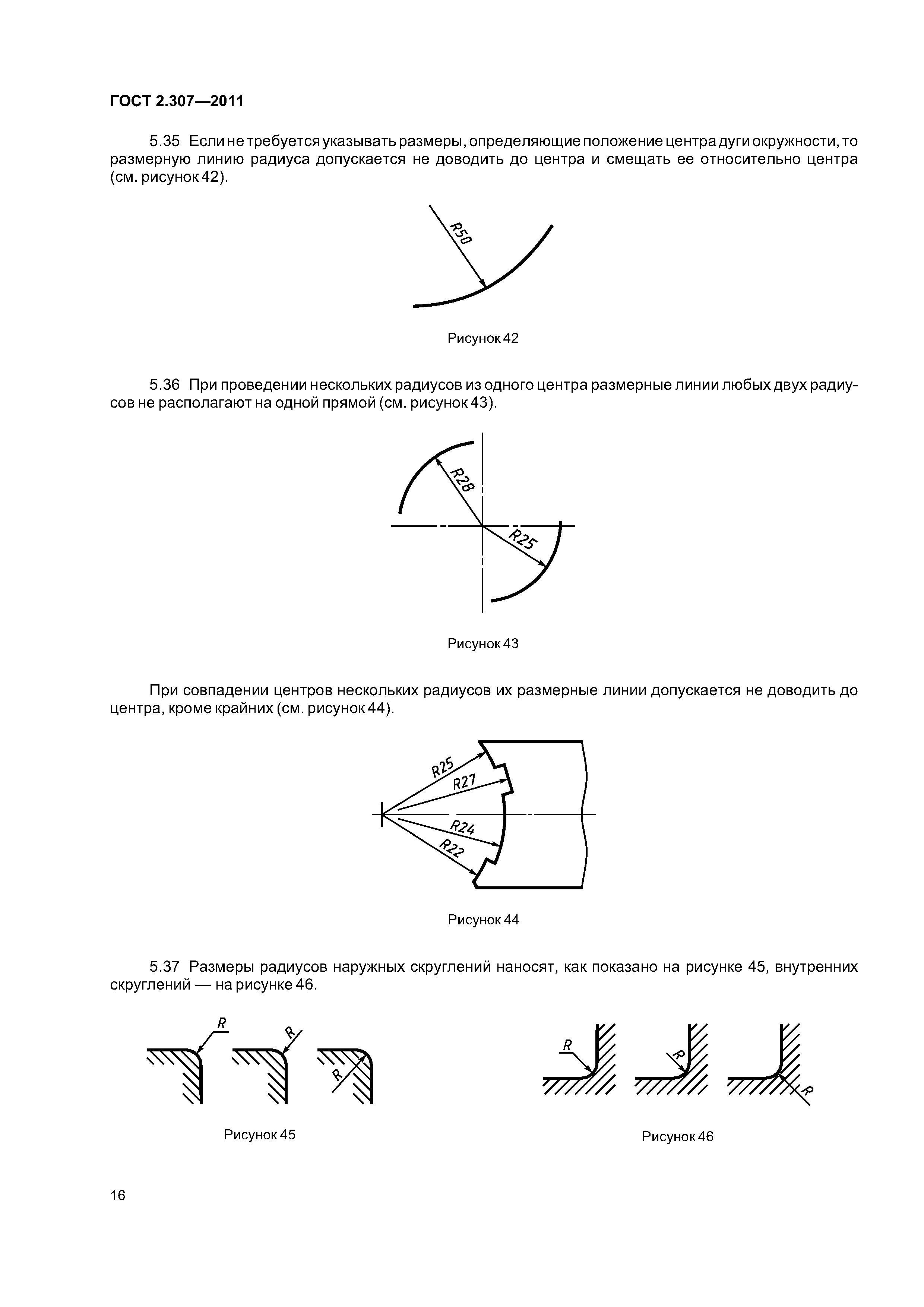
Рисунок 1. ГОСТ 2.307.2011
Радиусы и диаметры на чертеже по ГОСТу
Традиционно, в пояснительных записках и на чертежах используется условное обозначение радиуса латинской буквой R. После этого символа идет размерное число.
Отрезок начинается от центра окружности, на конце отрезка рисуется стрелка, направленная к самой окружности.
Бывают случаи, когда значение радиуса велико и поэтому линию приближают к дуге и показывают с изломом под 90 градусов.
Также зачастую исполнителю нет необходимости показывать центр окружности, особенно если размер очень большой и составляет несколько метров, поэтому сам отрезок не доводят до центра.
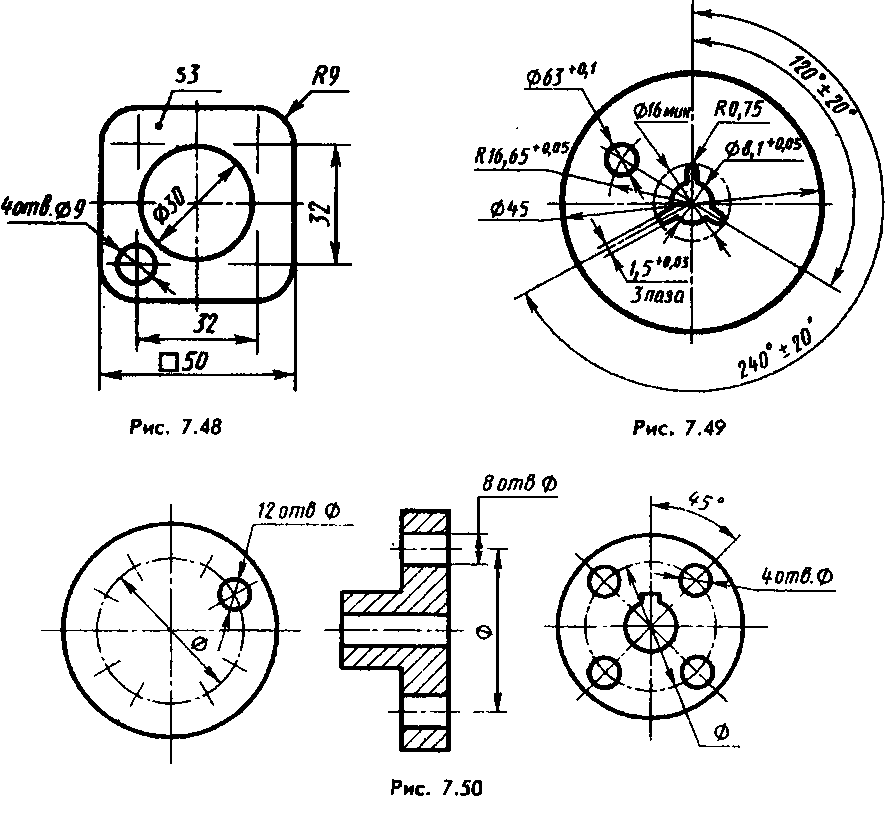
Рисунок 2. Радиусы и диаметры на чертеже по ГОСТу
Как начертить радиус на чертеже
Чтобы начертить радиус на листе необходимо воспользоваться таким инструментом как циркуль. С помощью линейки циркулем отмеряют радиус, размер которого известен заранее. Устанавливают острие циркуля в центр будущей окружности и проводят сектор, часть дуги или окружность целиком в зависимости от условий задачи. Обратным действием можно найти радиус, зная где находится центр окружности. Определить диаметр можно, зная радиус круга, для этого нужно его значение увеличить в два раза. Также, зная длину контура окружности, можно вычислить радиус или диаметр через число Пи.
При построении радиуса на компьютере воспользуемся соответствующим инструментом на панели, обычно можно начертить окружность по заданному центру и значению, начертить сектор или дугу ограничив ее на плоскости. Вводя нужные значения и указав точку на плоскости, программа сама построит окружность по радиусу. Чтобы соединить отрезки с помощью радиуса используется инструмент «Сопряжение». Необходимо выбрать отрезки, а программа сама подберет нужный радиус. Эта функция очень удобна, когда необходимо соединить два элемента, располагающихся под углом, к примеру стены дома на плане или полку и стенку двутавра на чертеже.
Радиусы можно начертить в любой программе векторной графики, начиная от Корел Дро, заканчивая Автокадом, Ревитом, Компасом и Архикадом. Линейный размер наносится после того, как сам элемент вычерчен, через инструмент «Размеры», расположенный в основном меню. Через свойства можно изменить высоту текста, тип оформления концов отрезков, толщину и прочее.

Рисунок 3. Как начертить радиус на чертеже
Как показать несколько радиусов на чертеже
Если из одного центра проводятся несколько радиусов, то согласно принятой практике для простоты прочтения чертежа их не располагают на одной прямой, между ними должен быть угол.
Если необходимо показать несколько линий радиуса, то до центра доводят только крайние радиусы, а остальные остаются укороченными.
В ситуациях, когда применяется большое количество одинаковых радиусов скругления, наносить размеры и показывать условные обозначения не обязательно. В примечаниях указывают всю необходимую информацию, к примеру, что «радиусы скругления составляют 10 мм» или «неуказанные радиусы 7 мм».
Рисунок 4. Несколько радиусов на чертеже
Как показать радиус отверстия
На машиностроительных, строительных, сборочных чертежах зачастую приходиться изображать отверстия, к примеру, отверстия трубопроводов, имеющих внутреннюю резьбу или же болты, которые имеют наружную резьбу. В этом случае также используется радиус, который позволяет определить точный размер элемента. Малый размер может не позволить уместить всю информацию внутри изображения, поэтому все указания и полки размещают снаружи.
На одном листе показывают вид на разные плоскости проекции, на плане трубы показывается ось, на виде справа или слева, отверстие и его радиус или диаметр.
Рисунок 5. Изображение радиуса отверстия на чертеже
Как показать диаметр на чертеже
Диаметр на чертеже обозначается с помощью символа перечеркнутого круга, после которого следует размерное число. Если диаметр элемента меньше 12 мм, то размерное число и стрелка располагаются снаружи. Если размер элемента от 12 до 40 мм, то стрелки, располагают внутри элемента (проходят через центр окружности), а размерные числа выносят наружу. Для диаметра более 40 мм и размерные числа, и стрелки располагают внутри. Чтобы обозначит сферы перед перечёркнутой окружностью наносят еще один круг.
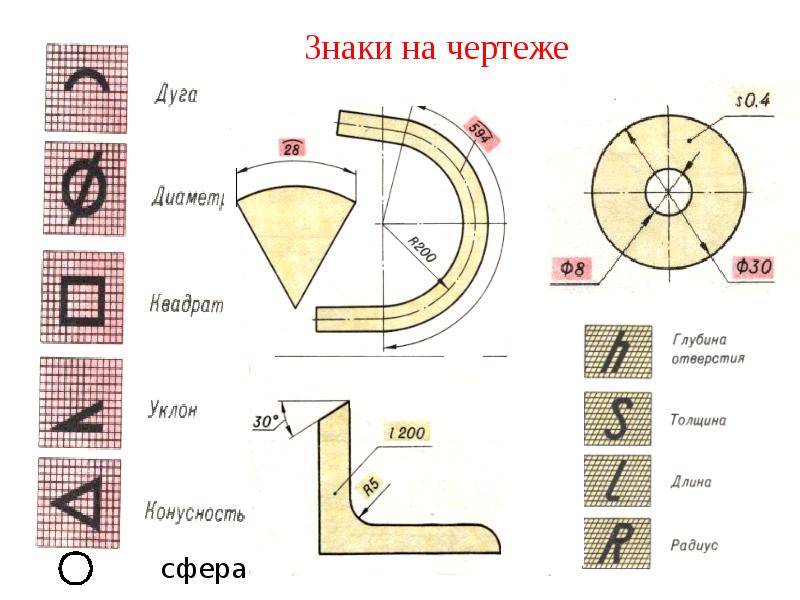
Рисунок 6. Как отметить диаметр на чертеже
Ответы на вопросы
В каком случае допускается не показывать радиус?
Радиус не показывают, если размер скругления в масштабе чертежа равен или менее 1 мм.
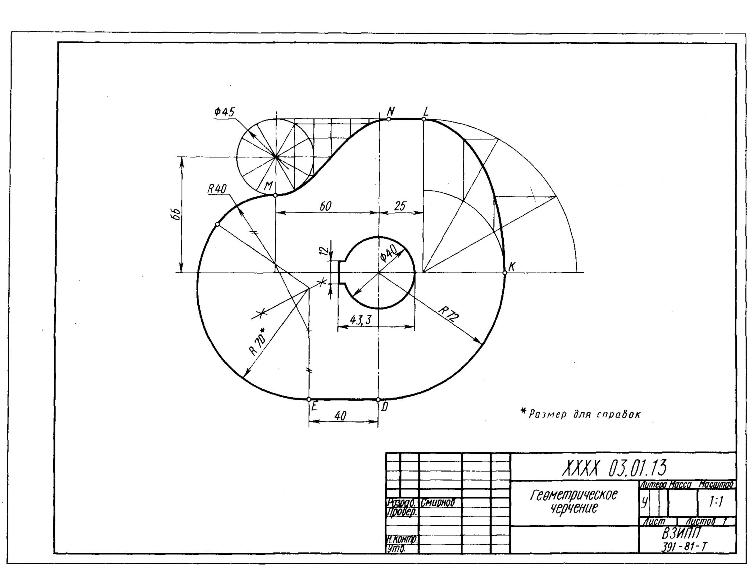
Рисунок 7. Пример обозначения радиусов на чертеже
Как можно упростить обозначение одинаковых радиусов?
Зачастую детали выполняются симметричными, и их скругления имеют одинаковые значения. В этом случае обозначается стрелка для каждого скругления, но все они имеют общую полку, на которой выполняется простановка размерного числа.

Рисунок 8. Одинаковые радиусы
Нужно ли писать единицу измерения после обозначения радиуса?
Радиус, так же, как и ширина, толщина, длина или высота изделия относится к линейным размерам. Согласно требованиям ГОСТа, по умолчанию их наносят в миллиметрах. Соответственно других единицы измерения указывают, если размер определяется в метрах, сантиметрах, дециметрах, футах или иных единицах.
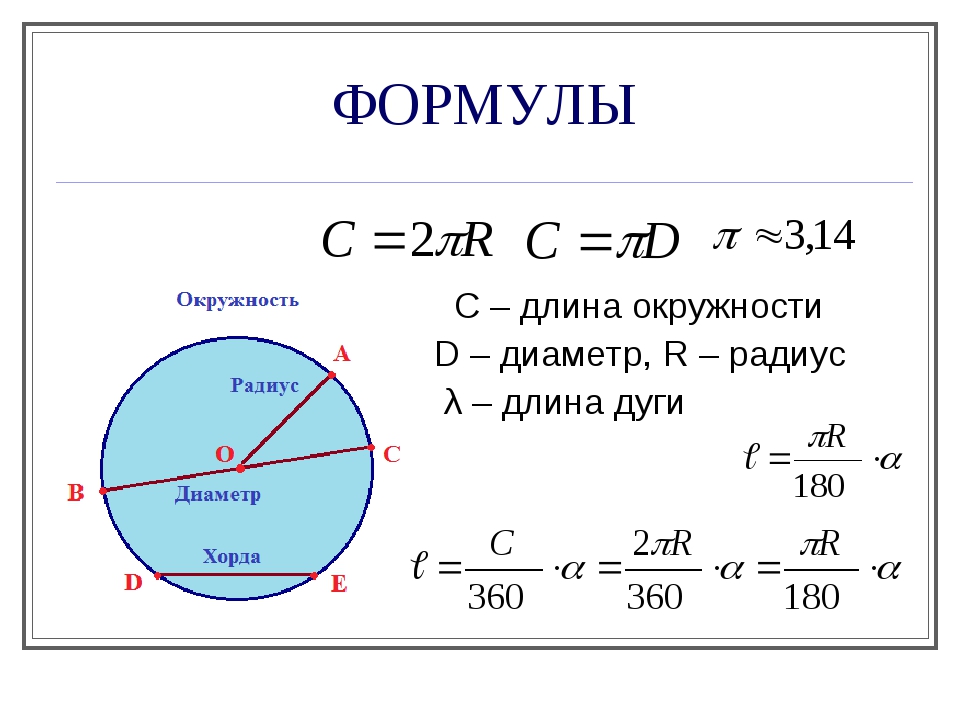
Рисунок 9. Единицы измерения радиуса
