|
|
Макеты страниц
Линзой называют оптическую деталь, ограниченную двумя преломляющими обычно осесимметричными и центрированными поверхностями. Наиболее часто встречающиеся линзы ограничены двумя сферическими поверхностями. Если одна из поверхностей — плоскость, то она должна быть перпендикулярна к оптической оси.
Линзы с осесимметричными и центрированными поверхностями обеспечивают в параксиальной области сохранение гомоцентричности пучка лучей в пространстве изображений.
При отсутствии круговой симметрии хотя бы одной из поверхностей (например, одна из поверхностей линзы цилиндрическая, а вторая плоская) гомоцентричность (в параксиальной области) будет обеспечиваться только в одной из секущих плоскостей, включающих оптическую ось.
Рассмотрим преломляющее действие отдельной лиизы со сферическими поверхностями (рис. 43, а), пользуясь для этой цели нулевыми лучами.
Конструктивными параметрами линзы со сферическими поверхностями (одна из них может быть плоской) будут радиусы сфер  толщина по оптической оси
толщина по оптической оси  и показатель преломления
и показатель преломления  материала линзы
материала линзы  показатели преломления сред соответственно перед и после линзы). Воспользуемся ими для определения фокусных расстояний
показатели преломления сред соответственно перед и после линзы). Воспользуемся ими для определения фокусных расстояний  линзы, ее фокальных отрезков
линзы, ее фокальных отрезков  положения главных плоскостей относительно вершин сферических поверхностей (отрезки
положения главных плоскостей относительно вершин сферических поверхностей (отрезки  и расстояния
и расстояния  между главными плоскостями (главными точками).
между главными плоскостями (главными точками).
Заметим, что последующее изложение в равной мере может быть распространено и на несферические осесимметричные линзы, так как они в параксиальной области действуют как сферические с радиусами, равными радиусам кривизны при вершине несферических поверхностей.
Согласно формулам (85), (82) и (83) имеем:

Последовательная подстановка этих выражений дает следующую формулу для определения заднего фокусного расстояния линзы:

Переднее фокусное расстояние определяют по формуле

Сравнивая формулы (88) и (89), получим  для линзы справедливо такое же соотношение между задним и передним фокусными расстояниями, как и для идеальной оптической системы [формула (34)].
для линзы справедливо такое же соотношение между задним и передним фокусными расстояниями, как и для идеальной оптической системы [формула (34)].
Оптическая сила линзы  является одной из ее основных характеристик. Она является также мерой оптического действия системы, состоящей из комбинации линз.
является одной из ее основных характеристик. Она является также мерой оптического действия системы, состоящей из комбинации линз.
Чем больше (по абсолютному значению) оптическая сила, тем ближе к линзе располагается изображение и тем меньше размер этого изображения [см. формулу (41)].

(кликните для просмотра скана)
Если линза находится в воздухе  то
то 
Единицей оптической силы является диоптрия (дптр), которая равна оптической силе линзы, находящейся в воздухе, с фокусным расстоянием, равным 
Поэтому оптическая сила линзы в диоптриях  где
где  в миллиметрах.
в миллиметрах.
Оценка оптической силы линз в диоптриях принята в офтальмологии.
Заднее и переднее фокусные расстояния каждой из преломляющих поверхностей линзы в соответствии с формулой (76) равны

После подстановки правых частей этих равенств в формулы (88) и (89) получим, что оптическая сила линзы

и окончательно

где  оптическая сила первой преломляющей поверхности линзы;
оптическая сила первой преломляющей поверхности линзы;  оптическая сила второй преломляющей поверхности линзы.
оптическая сила второй преломляющей поверхности линзы.
Формулу (90) полезно сравнить с формулой (56), определяющей оптическую силу двухкомпонентной оптической системы, находящейся в воздухе, между компонентами которой — среда с показателем преломления  Из сравнения следует, что линзу можно представить как двухкомпонентную систему, в которой — оптическая сила 1-й преломляющей поверхности,
Из сравнения следует, что линзу можно представить как двухкомпонентную систему, в которой — оптическая сила 1-й преломляющей поверхности,  -й преломляющей поверхности линзы.
-й преломляющей поверхности линзы.
Задний фокальный отрезок линзы получаем по формуле (86):

При обратном ходе луча находим передний фокальный отрезок

На рис. 43, а показана линза толщиной  с отмеченными значениями фокусных расстояний
с отмеченными значениями фокусных расстояний  и фокальных отрезков
и фокальных отрезков  Найдем отрезки
Найдем отрезки  определяющие положение главных плоскостей относительно вершин преломляющих поверхностей. Из рисунка следует, что
определяющие положение главных плоскостей относительно вершин преломляющих поверхностей. Из рисунка следует, что  Тогда согласно формулам (91) и (92)
Тогда согласно формулам (91) и (92)

Расстояние между главными плоскостями определяется равенством

Пример. Рассчитать двояковыпуклую линзу, с одной стороны которой находится воздух  с другой — вода
с другой — вода  Лннза имеет следующие конструктивные параметры:
Лннза имеет следующие конструктивные параметры: 
При вычислении по формулам (88) и (89) получаем  Фокальные отрезки [формулы (91) и (92)]:
Фокальные отрезки [формулы (91) и (92)]:  Расстояние между главными плоскостями [формула (95)]
Расстояние между главными плоскостями [формула (95)] 
Для расчета линзы, находящейся в воздухе  на основании формул (88)-(95) получим:
на основании формул (88)-(95) получим:

Все линзы можно разделить на три группы:
линзы, поверхности которых имеют разные по знаку радиусы кривизны: двояковыпуклые и двояковогнутые (рис. 43, а и б);
линзы, одна из поверхностей которых плоская: выпуклоплоские и плосковыпуклые, вогнуто-плоские и плосковогиутые (рис. 43, в-е);
линзы, имеющие одинаковые по знаку радиусы кривизны: выпукло-вогнутые и вогнуто-выпуклые толщиной по оси, большей толщины по краю (рис. 43, ж и з), вогнуто-выпуклые и выпукло-вогнутые толщиной по оси, меиьшей толщины по краю (рис. 43, и, к). Такие линзы называются менисками.
Линзы обычно являются осесимметричными деталями. Однако в некоторых случаях используются и цилиндрические линзы (см. гл. XX).
Рассмотрим особенности находящихся в воздухе лииз различных типов со сферическими и плоскими поверхностями.
Двояковогнутая линза (рис. 43, б) имеет  Заднее фокусное расстояние
Заднее фокусное расстояние  отрицательно при любой толщине
отрицательно при любой толщине  линзы, что определяет ее рассеивающее действие. Эта лииза является отрицательной.
линзы, что определяет ее рассеивающее действие. Эта лииза является отрицательной.
Выпукло-плоская линза (рис. 43, в) имеет  Значения фокусных расстояний
Значения фокусных расстояний  фокальных отрезков
фокальных отрезков  отрезков
отрезков  а также расстояние
а также расстояние  между главными плоскостями определяются по формулам, получаемым из (96)- (104):
между главными плоскостями определяются по формулам, получаемым из (96)- (104):

Из формул (105) следует, что, во-первых, фокусные расстояния  не зависят от толщины
не зависят от толщины  линзы, во-вторых, передняя главная плоскость касается выпуклой преломляющей поверхности.
линзы, во-вторых, передняя главная плоскость касается выпуклой преломляющей поверхности.
Плосковыпуклая линза (рис. 43, г) имеет  Расчетные формулы аналогичны предыдущим:
Расчетные формулы аналогичны предыдущим:

Линзы с одной преломляющей поверхностью плоской и другой — выпуклой являются собирательными (положительными).
Вогнуто-плоская линза (см. рис. 43, д) имеет  Формулы для этой линзы следующие:
Формулы для этой линзы следующие:

Из сопоставления полученных формул с формулами (105), относящимися к выпукло-плоской линзе, вытекает их полное соответствие друг с другом.
Плосковогнутая линза (рис. 43, е) с  описывается следующими формулами:
описывается следующими формулами:

Эти формулы полностью совпадают с формулами (106), относящимися к плосковыпуклой линзе.
Выпукло-вогнутый мениск (рис. 43, ж) с  при
при  Это линза является собирательной (положительной), так как
Это линза является собирательной (положительной), так как  Отрезки
Отрезки  отрицательны, следовательно, передняя главная плоскость находится перед линзой.
отрицательны, следовательно, передняя главная плоскость находится перед линзой.
Вогнуто-выпуклый мениск (рис. 43, з)  при
при  также относится к положительным линзам. Задняя главная плоскость всегда располагается за линзой.
также относится к положительным линзам. Задняя главная плоскость всегда располагается за линзой.
Вогнуто-выпуклый мениск (рис. 43, и) с  при
при  относится к отрицательным линзам
относится к отрицательным линзам  Передняя главная плоскость этого мениска находится перед линзой.
Передняя главная плоскость этого мениска находится перед линзой.
Выпукло-вогнутый мениск (рис. 43, к) с  при
при  также относится к отрицательным линзам
также относится к отрицательным линзам  Задняя главная плоскость этого мениска находится за линзой.
Задняя главная плоскость этого мениска находится за линзой.

Рис. 44. Телескопические линзы: а — двояковыпуклая; б – выпукло-вогнутая
В случаях, когда между конструктивными параметрами линзы, входящими в формулу (96), имеет место соотношение  вогнуто-выпуклые и выпукло-вогнутые линзы будут положительными, т. е.
вогнуто-выпуклые и выпукло-вогнутые линзы будут положительными, т. е.  Иными словами, увеличивая толщину
Иными словами, увеличивая толщину  отрицательный мениск можно превратить в положительный.
отрицательный мениск можно превратить в положительный.
Телескопическая линза — линза, преобразующая параллельные лучи, падающие на нее, также в параллельные при их выходе из линзы. Конструктивные параметры этой линзы определяются из соотношения (96) при  В этом случае
В этом случае

Из формулы (76) следует, что заднее фокусное расстояние первой сферической поверхности линзы

а переднее фокусное расстояние второй поверхности линзы

Используя формулы (107)-(109), получаем, что

Два варианта телескопических линз, соответствующие формуле (110), — двояковыпуклая и выпукло-вогнутая линзы показаны на рис. 44.
Линзы с концентрическими сферическими поверхностями (рис. 45) имеют совмещенные главные плоскости, т. е. расстояние

Рис. 45. Лнизы с концентрическими сферическими поверхностями
 между этими плоскостями равно нулю, что следует из формулы (104). При этом
между этими плоскостями равно нулю, что следует из формулы (104). При этом

В равенстве (111) заменим  по формуле (96). Тогда после преобразований получим
по формуле (96). Тогда после преобразований получим  что и определяет конструктивные параметры линзы.
что и определяет конструктивные параметры линзы.
Фокусные расстояния концентрической линзы определяют по следующей формуле:

Линзы со сферическими поверхностями равных радиусов имеют фокусное расстояние, определяемое по формуле (96) с учетом равенства радиусов 

Если при этом толщина линзы  то получим линзу-шар, для которой
то получим линзу-шар, для которой

Линзы с обращенными главными плоскостями показаны на рис. 46. В этих линзах расстояние между главными плоскостями отрицательно, т. е. по ходу луча первой будет задняя главная плоскость, а второй — передняя. Из формулы (104) следует, что рассматриваемый случай имеет место, когда

Подставим в это неравенство значение  найденное по формуле (96), и после преобразований получим, что для линзы с обращенными главными плоскостями должно выполняться следующее условие:
найденное по формуле (96), и после преобразований получим, что для линзы с обращенными главными плоскостями должно выполняться следующее условие:

При этом расстояние  вычисленное по формуле (104), будет отрицательным.
вычисленное по формуле (104), будет отрицательным.
Линзы с несферическими преломляющими поверхностями [11, 27], используемые в качестве оптических деталей приборов, обеспечивают повышение качества оптического изображения, увеличение поля оптической системы и ее относительного отверстия, упрощение оптической системы (уменьшение числа компонентов, а следовательно, габаритных размеров и массы).

Рис. 46. Лннзы с обращенными главными плоскостями

Рис. 47. Сфероэллиптическая линза
Преломляющие поверхности в виде поверхностей второго и высшего порядков используются в линзах осветительных систем, в объективах и окулярах. Например, в осветительной системе микроскопа применяется двояковыпуклая линза, одна из поверхностей которой является параболоидом вращения, в гидрообъективах М. М. Русинова и П. Д. Иванова применяется плосковогнутая линза с параболоидной или эллипсоидной поверхностью. Примером линзы с несферической поверхностью также является сфероэллиптическая линза, обеспечивающая гомоцентрический пучок лучей в пространстве изображений. Эта линза выпуклой эллипсоидной поверхностью обращена к предмету. Вогнутая сферическая поверхность линзы имеет центр в заднем ее фокусе (рис. 47).
Уравнение эллипса, являющегося меридиональным сечением эллипсоида, в этом случае имеет следующий 

где  — координаты меридионального сечения эллипсоида (начало координат в вершине эллипса);
— координаты меридионального сечения эллипсоида (начало координат в вершине эллипса);  задний фокальный отрезок, равный
задний фокальный отрезок, равный  т. е. радиусу сферической поверхности.
т. е. радиусу сферической поверхности.
Конструктивные параметры линзы, определяющие их оптическое действие, находят при расчете оптических систем. К этим параметрам относятся оптические постоянные материала линз (обычно оптического стекла), радиусы сферических поверхностей или уравнения для несферических поверхностей, толщина вдоль оптической оси и световые диаметры.
К линзам предъявляются специальные требования в отношении шероховатости поверхности, качества материала (например, категории стекла), просветляющих покрытий и допусков на конструктивные параметры согласно ГОСТам и нормалям оптической промышленности.
Расчетные радиусы сферических поверхностей должны быть, как правило, согласованы с ГОСТ 1807-75.
Для облегчения изготовления и обеспечения надежного крепления между диаметром линзы  толщиной по оси
толщиной по оси  и толщиной по краю
и толщиной по краю  должны выдерживаться следующие соотношения:
должны выдерживаться следующие соотношения:
1) для положительных линз  при этом толщина по краю
при этом толщина по краю 
2) для отрицательных линз  при этом толщина по оси
при этом толщина по оси 
Диаметр линзы  при вычисленном световом диаметре зависит от способа крепления линзы.
при вычисленном световом диаметре зависит от способа крепления линзы.
Допуски на все конструктивные параметры линз находят расчетным путем (см. п. 127) и округляют до значений, определяемых нормалями [6].
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
- 29. Отражательные призмы
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 37. Оптическое излучение. Поток излучения
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы
ЦЕЛЬ
РАБОТЫ
Изучение
геометрических характеристик линзы и
ознакомление с одним из методов
определения радиуса кривизны и показателя
преломления линзы.
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ РАБОТЫ
Линзой
называется прозрачное тело, ограниченное
сферическими поверхностями (одна из
поверхностей может быть плоской).
Линзы
бывают двояковыпуклые, двояковогнутые,
плоско-выпуклые, плоско-вогнутые,
выпукло-вогнутые, вогнуто-выпуклые.
Выпукло-вогнутые
и вогнуто-выпуклые линзы называют
менисковыми. Их используют, в частности,
в очках.
Линзы
изготавливают из различных материалов
стекла и пластика для видимого излучения,
кварца
для ультрафиолетового, каменной соли
(или сильвинии)
для инфракрасного.
Формула
линзы связывает фокусное расстояние F
с расстоянием от оптического центра
линзы до предмета d
и до изображения f:
![]()
.
(1)
Фокусное
расстояние F
подставляется в эту формулу со знаком
“+”, если линза собирающая, и со
знаком “”,
если линза рассеивающая.
Расстояние
до изображения f
подставляется со знаком “+”, если
изображение действительное, и со знаком
“”,
если оно мнимое.
Величина
называется оптической силой и измеряется
в диоптриях (дптр).
![]()
=
дптр.
Оптическая
сила линзы связана с ее геометрическими
характеристиками формулой:
![]()
,
(2)
где
nл
и nо
показатели преломления линзы и окружающей
среды;
R1
и R2
радиусы кривизны поверхностей линзы,
которые подставляются со знаком “+”
в случае выпуклой поверхности и со
знаком
“”
в случае вогнутой поверхности.
Если
в формуле (2) получается Ф
0, то линза собирающая,
Ф
0
рассеивающая. Это связано со знаками
обеих скобок в правой части. Например,
при R1
0, R2
0 (двояковыпуклая линза) получим собирающую
линзу, если nл
nо
(например, стеклянная линза в воздухе)
и рассеивающую, если nл
nо
(например, воздушная линза в стекле). В
другом случае может быть nл
nо
(воздушная линза в стекле), но R1
0, R2
0, то есть поверхности линзы вогнутые.
Тогда каждая скобка будет иметь знак
“”
, а их произведение даст “+”, и линза
будет собирающей.
Поперечное
увеличение линзы
![]()
, (3)
где
y1
и y2
расстояния соответственно светящейся
точки и ее изображения до главной
оптической оси линзы.
Собирающая
линза может использоваться в качестве
лупы. В этом случае ее увеличение равно ![]()
,
где
D
это расстояние наилучшего зрения; для
нормального глаза
D
= 25 см
один из стандартов для создания оптических
приборов, вооружающих глаз; F
фокусное расстояние лупы.
К
важнейшим оптическим приборам,
изготовленным из линз, относятся
микроскоп и телескоп.
Увеличение
микроскопа
![]()
,
(4)
где
расстояние между фокусами объектива и
окуляра, называемое длиной тубуса
микроскопа; D
расстояние наилучшего зрения; Fоб
и Fок
фокусные расстояния объектива и окуляра,
причем в микроскопе Fоб
Fок.
Увеличение
телескопа ![]()
, (5)
где
Fоб
и Fок
– фокусные расстояния объектива и
окуляра, причем в телескопе Fоб
Fок.
ОПИСАНИЕ
ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
В
данной работе на установке с линзой 3
(рис. 1) определяют расстояние f
от линзы до
действительного изображения нити
лампочки и по формуле (1) определяют
фокусное расстояние плоско-выпуклой
линзы.
![]()
;
![]()
, (6)
г
де
d
= 691 мм для данной установки. Расстояние
f
измеряют по шкале 6, передвигая экран 7
и добиваясь на нем резкого изображения
нити лампочки 1.
Из формулы (2)
получаем для плоско-выпуклой линзы
![]()
,
(7)
где
n
= nл
– показатель преломления линзы;
nо
= nвозд
1 – показатель
преломления воздуха;
R1
= R
– радиус выпуклой поверхности линзы;
R2
=
– радиус плоской поверхности линзы.
Из формулы (7)
получаем показатель преломления:
![]()
; ![]()
;
![]()
. (8)
Радиус
кривизны R
линзы можно измерить с помощью индикатора
2 (рис.1). Если представить сечение линзы
в виде сегмента круга (рис.2), то по теореме
Пифагора получим:
![]()
,
где
а
хорда, h
стрела сегмента.
После
преобразований получаем значение
радиуса:
![]()
.
(9)
П
ередвигая
индикатор в горизонтальном направлении,
измеряют по шкале 4 длину хорды а,
записывая соответствующую стрелу
сегмента h
по показаниям индикатора. Вычислив по
формуле (9) радиус кривизны R,
а по формуле (6) фокусное расстояние
линзы, можно определить показатель
преломления линзы по формуле (8).
Схема
установки приведена на рис.1. Передвигая
руками стойку с индикатором 2, можно
записать показания по шкале 4 (половина
хорды а/2)
и соответствующие показания индикатора
– стрелу сегмента h.
Целое число миллиметров на индикаторе
показывает маленькая стрелка, а десятые
и сотые доли – большая.
ПОРЯДОК
ВЫПОЛНЕНИЯ РАБОТЫ
ПРЕДУПРЕЖДЕНИЕ.
Следите за тем, чтобы оптические
поверхности линзы оставались чистыми
– нельзя касаться их пальцами или
предметами. Индикатор – точный прибор
и все манипуляции с ним необходимо
выполнять плавно, без рывков. Наконечник
сделан из фторопласта для уменьшения
трения. При всех передвижениях руками
стойки с индикатором нужно учесть, что
стойка должна быть всегда прижата к
основанию. В противном случае показания
индикатора будут неточными.
1.
Установка нуля. Получите индикатор и
установите его на место. Для этого
необходимо передвинуть руками стойку
индикатора и установить указатель шкалы
4 на ноль при вертикальном положении
ножки. Вставьте ножку индикатора в паз,
слегка прижмите ее стопорным винтом и
передвижением вверх и вниз самого
индикатора добейтесь нулевого показания
малой и большой стрелок. При этом большая
стрелка должна быть близка к вертикальному
положению. Закрепив индикатор в таком
положении, необходимо найти наивысшую
точку линзы. Для этого передвигайте
стойку на 1 – 2 см влево и вправо и по
стрелке индикатора найдите вершину
сферической поверхности линзы. При этом
нужно учесть, что вблизи вершины есть
мертвая зона протяженностью около 2-х
мм, в пределах которой стрелка неподвижна
– стойку нужно установить посередине
этой зоны. Установив стойку, подведите
шкалу 4 кремальерой 5 точно на ноль и в
дальнейшем кремальеру 5 не трогайте.
Если при этом большая стрелка индикатора
отклонилась от вертикали, вновь установите
индикатор должным образом и закрепите
его. Далее вращением внешнего кольца
индикатора совместите ноль круговой
шкалы с положением большой стрелки.
Учитывая то, что точность установки
нуля определяет точность дальнейших
измерений, еще раз или два повторите
манипуляции пункта 1 с тем, чтобы ноль
шкалы 4 совпадал с нулем индикатора и
это соответствовало вершине сферической
поверхности линзы.
Таблица
1
|
Показания шкалы |
Показания |
Хорда а (мм) |
Стрела сегмента (мм) |
Радиус кривизны |
|
|
При движении |
При движении |
||||
|
20 |
40 |
||||
|
25 |
50 |
||||
|
30 |
60 |
||||
|
35 |
70 |
||||
|
40 |
80 |
||||
|
Среднее значение |
R |
2.
Передвигая стойку вправо, устанавливайте
указатель шкалы 4 на значениях 20, 25, 30,
35, 40 мм (значения, равные половине
соответствующих хорд) и записывайте
показания индикатора h1
(стрела сегмента) в таблицу 1. При этом
целое число миллиметров снимайте по
показаниям маленькой стрелки, а десятые
и сотые доли – по показаниям большой
стрелки.
3.
Передвигая стойку влево от нуля, снимайте
показания индикатора h2
при тех же значениях половины хорды.
4. Передвиньте
стойку с индикатором вправо до упора.
5.
Подключите лампочку к напряжению
12 В.
6.
Слегка вращая “столб” с лампочкой,
добейтесь того, чтобы изображение
лампочки на экране 7 находилось в центре
перекрестия. При этом одновременно
нужно слегка поднять экран рукой и
сфокусировать изображение нити лампочки.
Добившись резкого изображения, запишите
по шкале 6 значение f
в миллиметрах. Повторите измерения f
еще четыре раза.
7. Выключите лампочку
и приступите к расчетам. Все расчеты в
данной работе удобнее проводить с
миллиметрах.
8.
Найдите среднее арифметическое f
результатов наблюдений и определите
полуширину доверительного интервала
f.
Запишите результат измерения f
в виде: f
f.
9.
По формуле 6 вычислите фокусное расстояние
линзы F
в миллиметрах. Для нашей установки d
= 691 мм.
10.
Пренебрегая погрешностью измерения d,
определите полуширину доверительного
интервала F
фокусного расстояния линзы по формуле:
![]()
.
11.
Заполните таблицу 1 и по формуле 9
определите радиус R
кривизны линзы в миллиметрах. Найдите
среднее арифметическое значение R
и полуширину доверительного интервала
R.
12.
По формуле 8 найдите показатель преломления
линзы, а по формуле ![]()
определите полуширину n
доверительного интервала. Запишите
результат измерения показателя
преломления n
в виде: n
n.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Сформулируйте
цель лабораторной работы. -
Что
такое линза? -
Из
каких материалов изготавливают линзы
для ультрафиолетового и инфракрасного
излучений? -
Укажите
формулу линзы. -
Какая
величина называется оптической силой
линзы? -
В
каких единицах измеряется оптическая
сила линзы? -
Укажите
знак фокусного расстояния F
линзы для собирающей и рассеивающей
линз. -
Укажите
знак расстояния f
действительного и мнимого изображений
до линзы. -
Как
оптическая сила линзы зависит от
радиусов поверхностей, ограничивающих
линзу? -
На
стеклянную двояковогнутую линзу в
воздухе падают параллельные лучи света.
Как направлены эти лучи после прохождения
линзы? -
На
воздушную двояковыпуклую линзу в стекле
падают параллельные лучи света. Как
направлены эти лучи после прохождения
линзы? -
Какая
величина называется поперечным
увеличением линзы? -
Напишите
формулу увеличения лупы. -
Линза
для очков изготовлена из стекла крон
с показателем преломления n
= 1,5. Радиус кривизны выпуклой и вогнутой
поверхностей линзы равны соответственно
50 см и 25 см. Определите оптическую силу
линзы. -
Решите
предыдущую задачу для плоско-выпуклой
линзы, если радиус кривизны выпуклой
поверхности равен R
= 50 см. -
Укажите,
какие изображения будут получены в
собирающей линзе при d
= 2F, d
= 3F, F
d
2F. -
Постройте
увеличенное и уменьшенное изображения,
даваемые собирающей линзой. -
Постройте мнимое
изображение, даваемое собирающей
линзой. -
Постройте
изображение, даваемое рассеивающей
линзой. -
Нарисуйте
эскиз экспериментальной установки. -
Укажите
расчетную формулу для определения
фокусного расстояния F
линзы. -
По
какой формуле нужно вычислять полуширину
F
доверительного интервала фокусного
расстояния F линзы? -
Выведите
формулу для определения показателя
преломления n плоско-выпуклой
линзы в данной работе. -
По
какой формуле нужно вычислять полуширину
n
доверительного
интервала показателя преломления n
линзы в данной работе? -
Выведите
формулу для расчета радиуса кривизны
R плоско-выпуклой
линзы в данной работе. -
Определите
показатель преломления плоско-выпуклой
линзы, у которой фокусное расстояние
вдвое больше радиуса кривизны выпуклой
поверхности. -
Найдите
фокусное расстояние линзы F,
если действительное изображение
предмета находится от линзы на расстоянии
вдвое большем расстояния предмета до
линзы, а расстояние между предметом и
его изображением равно 30 см. -
Как
изменится фокусное расстояние собирающей
стеклянной линзы(nЛ
= 1,5), если ее из воздуха (n01
1) поместить в воду
(n02 = 1,33)? -
Меняется
ли расстояние d предмета
до линзы в данной работе? -
Укажите
порядок выполнения данной лабораторной
работы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Линзы:
На уроках природоведения вы. наверное, пользовались микроскопом. Кое-кто из ваших друзей (а может, и вы сами) имеет очки. Вероятнее всего, большинство из вас знакомы с биноклем, зрительной тру бой, телескопом. У всех этих приборов есть общее: их основной частью является линза.
Равные виды линз
Линзой (сферической*) называют прозрачное тело, ограниченное с двух сторон сферическими поверхностями (в частности, одна из поверхностей может быть плоскостью). По форме линзы делятся на выпуклые (рис. 3.50) и вогнутые (рис. 3.51).
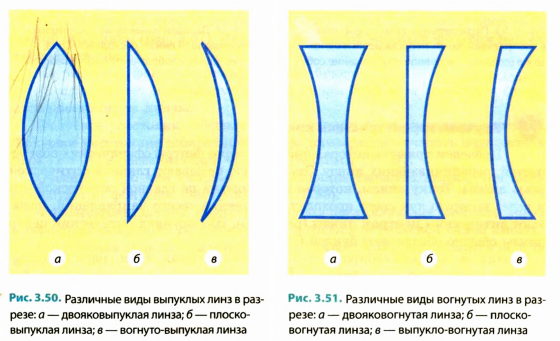
Если толщина линзы d во много раз меньше радиусов 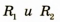
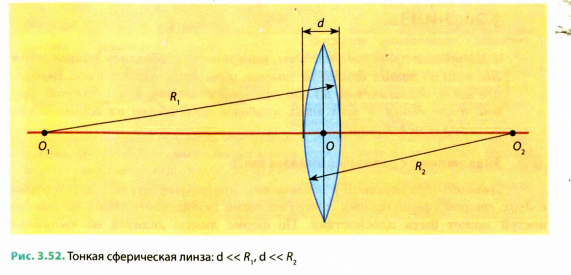
Обычно выпуклые линзы являются собирающими: параллельные лучи, которые падают на собирающую линзу, пройдя сквозь нее, пересекаются в одной точке (рис. 3.53).
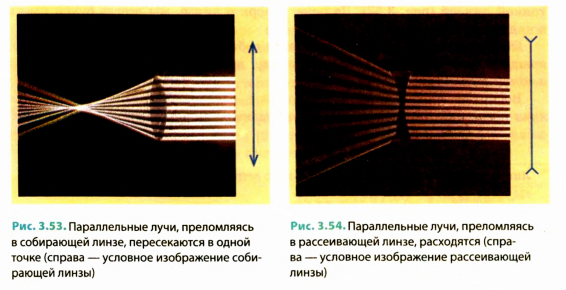
Вогнутые линзы чаще всего бывают рассеивающими: параллельные лучи после прохождения сквозь рассеивающую линзу выходят расходящимся пучком (рис. 3.54).
Линзы также бывают цилиндрическими, но встречаются такие линзы редко.
Характеристики линз
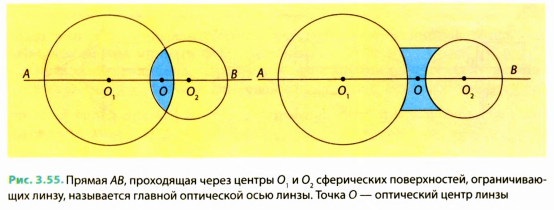
Проведем прямую, которая проходит через центры сферических поверхностей, ограничивающих линзу. Эту прямую называют главной оптической осью линзы. Точку линзы, которая расположена на главной оптической оси и через которую луч света проходит, не изменяя своего направления, называют оптическим центром линзы (рис. 3.55). На рисунках оптический центр линзы обычно обозначают буквой О.
Точку, в которой собираются после преломления лучи, параллельные главной оптической оси собирающей линзы, называют действительным фокусом собирающей линзы (рис. 3.56).
Если пучок лучей, параллельных главной оптической оси, направить на рассеивающую линзу, то после преломления они выйдут расходящимся пучком.
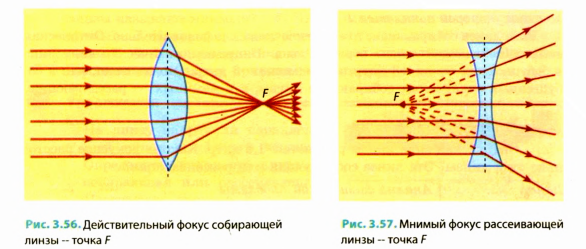
Однако их продолжения соберутся в одной точке на главной оптической оси линзы (рис. 3.57). Эту точку называют мнимым фокусом рассеивающей линзы.
На рисунках фокус линзы обозначают буквой F.
Расстояние от оптического центра линзы до фокуса называют фокусным расстоянием линзы.
Фокусное расстояние обозначается символом F и измеряется в метрах. Фокусное расстояние собирающей линзы договорились считать положительным (F>0), а рассеивающей — отрицательным (F<0).
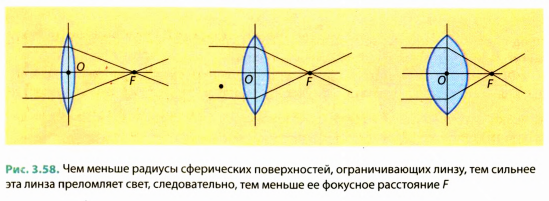
Очевидно, что чем сильнее преломляющие свойства линзы, тем меньшим будет ее фокусное расстояние (рис. 3.58).
Физическая величина, характеризующая преломляющие свойства линзы и обратная фокусному расстоянию, называется оптической силой линзы.
Оптическая сила линзы обозначается символом D и вычисляется по формуле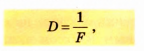
где F — фокусное расстояние линзы.
Единицей оптической силы является диоптрия
1 диоптрия (дптр) — это оптическая сила такой линзы, фокусное рас стояние которой равняется 1 м.
Если линза собирающая, то ее оптическая сила положительна. Оптическая сила рассеивающей линзы отрицательна. Например, оптическая сила линз в бабушкиных очках +3 дптр, а в маминых -3 дптр. Это означает, что в бабушкиных очках стоят собирающие линзы, а в маминых — рассеивающие.
Пример №1
Оптическая сила линзы равняется -1,6 дптр. Каково фокусное расстояние этой линзы? Эта линза собирающая или рассеивающая?
Дано:
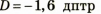
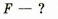
Анализ физической проблемы
Для определения фокусного расстояния этой линзы воспользуемся формулой для вычисления оптической силы линзы. Поскольку 1)< 0, то линза рассеивающая.
Поиск математической модели, решение:
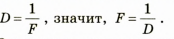
Определим числовое значение искомой величины:
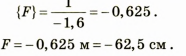
Ответ: F = -62,5 см, линза рассеивающая.
Итоги:
Прозрачное тело, ограниченное с двух сторон сферическими поверхностями, называют линзой. Линзы бывают собирающими и рассеивающими, а по форме — выпуклыми и вогнутыми.
Линза называется собирающей, если пучок параллельных лучей, падающий на нее, после преломления в линзе пересекается в одной точке. Эту точку называют действительным фокусом линзы.
Линза называется рассеивающей, если параллельные лучи, падающие на нее, после преломления в линзе идут расходящимся пучком, однако продолжения этих преломленных лучей пересекаются в одной точке. Эта точка называется мнимым фокусом линзы.
Физическая величина, характеризующая преломляющие свойства линзы и являющаяся обратной фокусному расстоянию линзы, называется оптической силой линзы = Оптическая сила линзы измеряется в диоптриях (дптр).
Формула тонкой линзы
Сейчас никого не удивляет, что можно увидеть бактерии и другие микроорганизмы, рассмотреть невидимые невооруженным глазом детали рельефа поверхности Луны или полюбоваться портретом, нарисованным на маковом зернышке. Все это стало возможным потому, что с по мощью линзы получают разные по размеру изображения предметов.

Изображение предмета, полученное с помощью линзы
Расположив последовательно зажженную свечу, собирающую линзу и экран, получим на экране четкое изображение пламени свечи (рис. 3.59). Изображение может быть как большим, так и меньшим, чем само пламя, или равным ему — в зависимости от расстояния между свечой и экраном. Чтобы выяснить, при каких условиях с помощью линзы образуется то или иное изображение предмета, рассмотрим приемы его построения.
Строим изображение предмета, которое дает тонкая линза
Любой предмет можно представить как совокупность точек. Каждая точка предмета, который светится собственным или
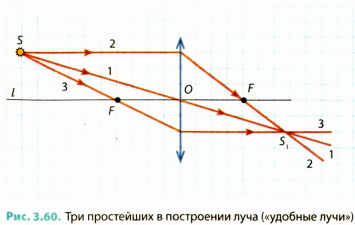
- — луч, проходящий через оптический центр О линзы (не преломляется и не изменяет своего направления);
- — луч, параллельный главной оптической оси / линзы (после преломления в линзе идет через фокус F);
- — луч, проходящий через фокус F (после преломления в линзе идет параллельно главной оптической оси/линзы)
- отраженным светом, испускает лучи во всех направлениях.
Для построения изображения точки S, получаемого с помощью линзы, достаточно найти точку пересечения 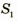 , любых двух лучей, выходящих из точки S и проходящих сквозь линзу (точка
, любых двух лучей, выходящих из точки S и проходящих сквозь линзу (точка 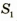 и будет действительным изображением точки S). Кстати, в точке
и будет действительным изображением точки S). Кстати, в точке 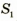 пересекаются все лучи, выходящие из точки S, однако для построения изображения достаточно двух лучей (любых из трех показанных на рис. 3.60).
пересекаются все лучи, выходящие из точки S, однако для построения изображения достаточно двух лучей (любых из трех показанных на рис. 3.60).
Изобразим схематически предмет стрелкой АВ и удалим его от линзы на расстояние, большее, чем 2F (за двойным фокусом) (рис. 3.61, а). Сначала построим изображение 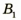 точки В. Для этого воспользуемся двумя «удобными* лучами (луч 1 и луч 2). Эти лучи после преломления в линзе пересекутся в точке
точки В. Для этого воспользуемся двумя «удобными* лучами (луч 1 и луч 2). Эти лучи после преломления в линзе пересекутся в точке 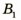 . Значит, точка
. Значит, точка 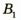 является изображением точки В. Для построения изображения
является изображением точки В. Для построения изображения 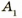 точки А из точки
точки А из точки 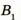 опустим перпендикуляр на главную оптическую ось /. Точка пересечения перпендикуляра и оси / и является точкой
опустим перпендикуляр на главную оптическую ось /. Точка пересечения перпендикуляра и оси / и является точкой 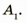
Значит, 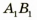 и является изображением предмета АВ, полученное с помощью линзы. Мы видим: если предмет расположен за двойным фокусом собирающей линзы, то его изображение, полученное с помощью линзы, будет уменьшенным, перевернутым, действительным. Такое изображение получается, например, на пленке фотоаппарата (рис. 3.61, б) или сетчатке глаза.
и является изображением предмета АВ, полученное с помощью линзы. Мы видим: если предмет расположен за двойным фокусом собирающей линзы, то его изображение, полученное с помощью линзы, будет уменьшенным, перевернутым, действительным. Такое изображение получается, например, на пленке фотоаппарата (рис. 3.61, б) или сетчатке глаза.
На рис. 3.62, а показано построение изображения предмета АВ, полученного с помощью собирающей линзы, в случае, когда предмет расположен
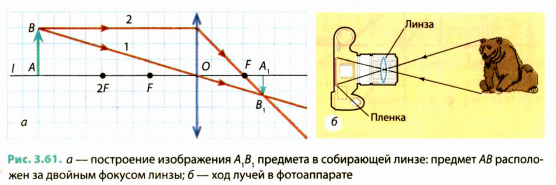
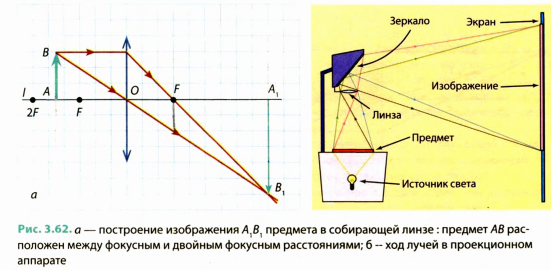
Изображение предмета в этом случае будет увеличенным, перевернутым, действительным. Такое изображение позволяет получить проекционная аппаратура на экране (рис. 3.62, б).
Если поместить предмет между фокусом и линзой, то изображения на экране мы не увидим. Но, посмотрев на предмет сквозь линзу, увидим изображение предмета — оно будет прямое, увеличенное.
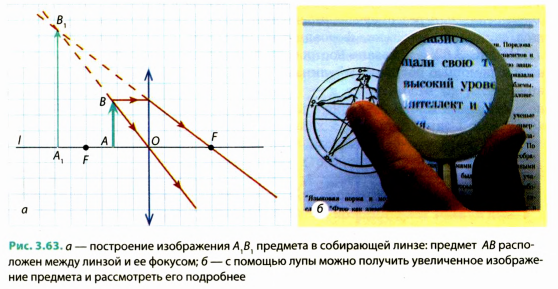
Используя «удобные лучи» (рис. 3.63, а), увидим, что после преломления в линзе реальные лучи, вышедшие из точки В, пойдут расходящимся пучком. Однако их продолжения пересекутся в точке В,. Напоминаем, что в этом случае мы имеем дело с мнимым изображением предмета. То есть если предмет расположен между фокусом и линзой, то его изображение бу дет увеличенным, прямым, мнимым, расположенным с той же стороны от линзы, что и сам предмет. Такое изображение можно получить с помощью лупы (рис. 3.63, б) или микроскопа.
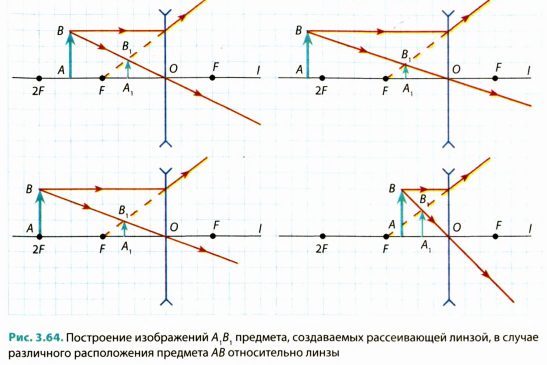
Итак, размеры и вид изображения, полученного с помощью собирающей линзы, зависят от расстояния между предметом и этой линзой.
Внимательно рассмотрите рис. 3.64, на котором показано построение изображения предмета, полученного с помощью рассеивающей линзы. Построение показывает, что рассеивающая линза всегда дает мнимое, уменьшенное, прямое изображение предмета, расположенное с той же стороны от линзы, что и сам предмет.
Мы часто сталкиваемся с ситуацией, когда предмет значительно больше, чем линза (рис. 3.65), или когда часть линзы закрыта непрозрачным экраном (например, линза объектива фотоаппарата). Как создается изображение в этих случаях? На рисунке видно, что лучи 2 и 3 при этом не проходят через линзу. Однако мы, как и раньше, можем использовать эти лучи для построения изображения, получаемого с помощью линзы. Поскольку реальные лучи, вышедшие из точки В, после преломления в линзе пересекаются в одной точке — 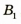 то «удобные лучи*, с помощью которых мы строим изображение, тоже пересеклись бы в точке
то «удобные лучи*, с помощью которых мы строим изображение, тоже пересеклись бы в точке 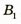
Как выглядит формула тонкой линзы
Существует математическая зависимость между расстоянием d от предмета до линзы, расстоянием f от изображения предмета до линзы и фокусным расстоянием F линзы. Эта зависимость называется формулой тонкой линзы и записывается так:
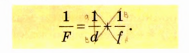
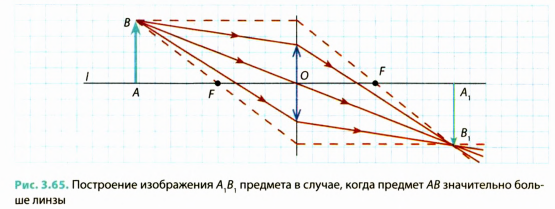
Пользуясь формулой тонкой линзы для решения задач, следует иметь в виду: расстояние f (от изображения предмета до линзы) следует брать со знаком минус, если изображение мнимое, и со знаком плюс, если изображение действительное; фокусное расстояние F собирающей линзы положительное, а рассеивающей — отрицательное.
Пример №2
Рассматривая монету с помощью лупы, оптическая сила которой +5 дптр, мальчик расположил монету на расстоянии 2 см от лупы. Определите, на каком расстоянии от лупы мальчик наблюдал изображение монет
Дано:
d = 2 см = 0,02 м
D = + 5 дптр
f- ?
Анализ физической проблемы, поиск математической модели
Лупу можно считать тонкой линзой, поэтому чтобы найти расстояние от лупы до изображения, воспользуемся
формулой тонкой линзы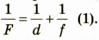 Фокусное расстояние F неизвестно, но мы знаем, что
Фокусное расстояние F неизвестно, но мы знаем, что 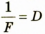 (2), где
(2), где
D — оптическая сила линзы, данная в условии задачи.
Решение и анализ результатов
Подставив формулу (2) в формулу (1), получаем
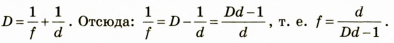
Проверим единицу: 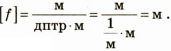
Найдем числовое 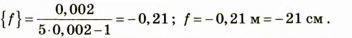
Проанализируем результат: знак ♦-* говорит о том, что изображение является мнимым.
Ответ: f = -21 см, изображение мнимое.
Итоги:
В зависимости от вида линзы (собирающая или рассеивающая) и местоположения предмета относительно этой линзы получают разные изображения предмета с помощью линзы (см.таблицу):
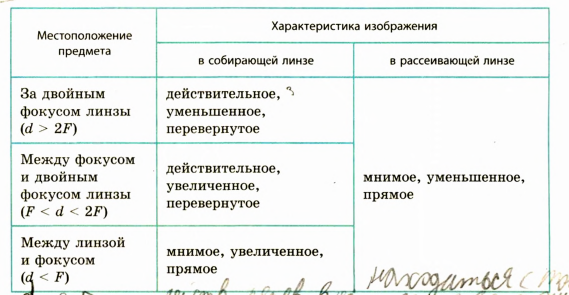
Таким образом, по типу изображения можно судить так и о местоположении предмета относительно нее.
Расстояние d от предмета до линзы, расстояние f от изображения до линзы и фокусное расстояние F связаны формулой тонкой линзы: 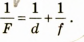
Что такое линза
Многие люди носят очки. А задумывались ли вы над вопросами: что собой представляют стекла очков и какова их роль? Стекла очков есть не что иное, как линзы. Ни один оптический прибор (от простой лупы до сложных телескопов) не обходится без линз. Что же такое линза?
Линза представляет собой прозрачное тело, ограниченное криволинейными (чаще всего сферическими) или криволинейной и плоской поверхностями. Материалом для линз обычно служит оптическое или органическое стекло.
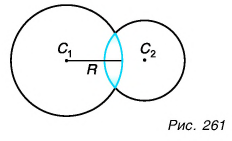
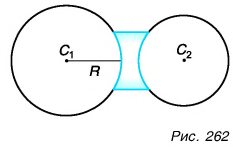
На рисунках 261, 262 представлены сечения линз двух типов: двояковыпуклой (см. рис. 261) и двояковогнутой (см. рис. 262). Одна из поверхностей линзы может быть плоской, как, например, на рисунке 263. Такие линзы называются плосковыпуклая (см. рис. 263, а) и плосковогнутая, (см. рис. 263, б).
Прямая, проходящая через центры 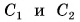 сферических поверхностей (рис. 264), называется главной оптической осью линзы. Радиусы
сферических поверхностей (рис. 264), называется главной оптической осью линзы. Радиусы 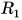 и
и 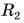 есть радиусы кривизны поверхностей линзы (см. рис. 264).
есть радиусы кривизны поверхностей линзы (см. рис. 264).
Если толщина линзы мала но сравнению с радиусами 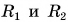 кривизны ее поверхностей (см. рис. 264), то линза называется тонкой. Ее часто изображают
кривизны ее поверхностей (см. рис. 264), то линза называется тонкой. Ее часто изображают 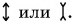 Всякая тонкая линза имеет точку, проходя через которую, луч не меняет своего направления (лучи 1 и 2 на рисунке 264). Эта точка О называется оптическим центром линзы. В дальнейшем мы будем рассматривать только тонкие линзы, изготовленные из вещества, оптически более плотного, чем среда (воздух), в которой они находятся.
Всякая тонкая линза имеет точку, проходя через которую, луч не меняет своего направления (лучи 1 и 2 на рисунке 264). Эта точка О называется оптическим центром линзы. В дальнейшем мы будем рассматривать только тонкие линзы, изготовленные из вещества, оптически более плотного, чем среда (воздух), в которой они находятся.
Как линзы меняют направление падающих на них лучей после преломления? Ответ получим с помощью опыта.
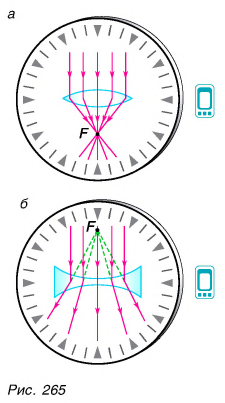
Направим на двояковыпуклую линзу (рис. 265, а) параллельно главной оптической оси лучи света. После преломления в линзе они пересекают главную оптическую ось в одной точке F. Значит, двояковыпуклая линза собирает преломленные лучи, поэтому такая линза называется собирающей. Также превращают параллельный пучок в сходящийся линзы 2, 3, изображенные на рисунке 270. При замене линзы на двояковогнутую (рис. 265, б) лучи после преломления в линзе расходятся, а центральный луч, как и в первом случае, не испытывает преломления. Итак, двояковогнутая линза рассеивает параллельный пучок падающих на нее лучей, поэтому такая линза называется рассеивающей. Рассеивают параллельный пучок и линзы 5, 6 (см. рис. 270).
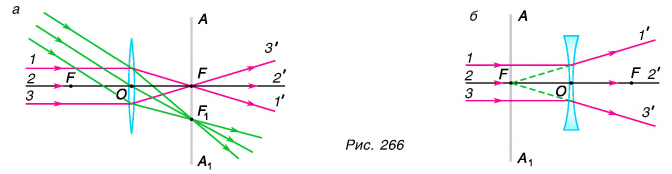
Точка F (см. рис. 265, а, рис. 266, а), в которой пересекаются преломленные линзой лучи, падающие параллельно главной оптической оси, или их продолжения (см. рис. 265, б, рис. 266, б), называется главным фокусом линзы. Так как параллельные лучи можно пустить как с одной, так и с другой стороны линзы, то и главных фокуса у линзы два. Оба фокуса лежат на главной оптической оси симметрично относительно оптического центра линзы (см. рис. 266). А в какой точке собирает линза лучи, идущие под углом к главной оптической оси? Оказывается, в точке 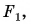 которая находится в плоскости
которая находится в плоскости 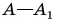 (см. рис. 266, а), проходящей через главный фокус перпендикулярно главной оптической оси. Эта плоскость называется фокальной плоскостью, а точка
(см. рис. 266, а), проходящей через главный фокус перпендикулярно главной оптической оси. Эта плоскость называется фокальной плоскостью, а точка 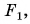 в отличие от главного фокуса, называется фокусом.
в отличие от главного фокуса, называется фокусом.
Обратите внимание, что у собирающей линзы в фокусе пересекаются сами преломленные лучи, несущие энергию, поэтому фокус называется действительным. У рассеивающей линзы в фокусе пересекаются продолжения преломленных лучей. Такой фокус называют мнимым.
Расстояние от оптического центра до главного фокуса называется фокусным расстоянием. Его тоже принято обозначать буквой F.
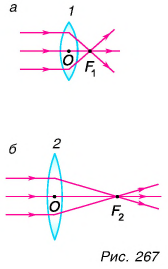
Линза, имеющая более выпуклые поверхности, преломляет лучи сильнее. Линза 1 (рис. 267, а) преломляет лучи сильнее, чем линза 2 (рис. 267, 6). Фокусное расстояние 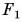 у линзы 1 меньше, чем
у линзы 1 меньше, чем 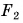 у линзы 2.
у линзы 2.
Чтобы количественно оценить преломляющую способность линзы, введем величину, обратную фокусному расстоянию, и назовем ее оптической силой линзы (обозначается буквой D):
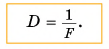
Оптическая сила измеряется в диоптриях (сокращенно дптр). Очевидно, что D = 1 дптр, если фокусное расстояние линзы F = 1 м.
А как оценивается оптическая сила рассеивающей линзы, у которой фокус мнимый? В этом случае фокусное расстояние считается отрицательным, а следовательно, и оптическая сила — отрицательной величиной.
Например, если F = -0,5 м, то оптическая сила
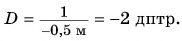
Теперь для вас не будет загадкой рекомендация врача-окулиста: «Вам нужны очки со стеклами +1,5 диоптрии или -2 диоптрии».
Для любознательных:
Не следует думать, что любая линза с выпуклой поверхностью будет обязательно собирающей, а с вогнутой — рассеивающей. Собирающей является всякая линза, у которой середина толще краев (например, линзы 2, 2, 3 на рисунке 270), а рассеивающей — линза, у которой середина тоньше краев (см. рис. 270, линзы 4, 5, 6). И не забывайте, что все наши рассуждения справедливы, если вещество линзы (стекло) имеет большую оптическую плотность, чем окружающая среда (воздух).
В природе собирающими линзами являются капельки росы, в быту — наполненные водой прозрачные сосуды — кувшин, пластиковая бутылка. Подумайте и ответьте, какие это линзы.
Главные выводы:
- Линзы меняют направление падающих на них лучей после преломления, за исключением тех, которые проходят через оптический центр линзы.
- Собирающая линза после преломления делает параллельный пучок лучей сходящимся, рассеивающая линза — расходящимся.
- Лучи, идущие параллельно главной оптической оси, после преломления в собирающей линзе пересекаются в главном фокусе. В рассеивающей линзе в главном фокусе пересекаются продолжения преломленных лучей.
- Величина, обратная фокусному расстоянию, определяет оптическую силу линзы.
Построение изображений в тонких линзах
Глядя в окуляр микроскопа на уроках биологии, задумывались ли вы, как получается увеличенное изображение клеток? Главными частями микроскопа являются линзы. Именно они позволяют получать увеличенное или уменьшенное (например, в фотоаппарате) изображение предмета.
Какие изображения предмета создает линза?
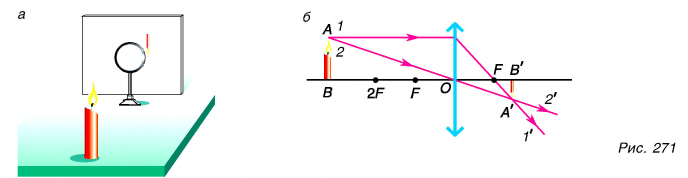
Проведем опыт. На столе расположим экран, собирающую линзу и зажженную свечу (рис. 271, а), удаленную от линзы на расстояние б/, большее, чем удвоенное фокусное, т. е. d > 2F. Будем передвигать экран до тех пор, пока не увидим на нем четкое изображение пламени свечи. Чем оно отличается от изображения, которое мы увидим в зеркале, поместив перед ним эту же свечу? Во-первых, оно уменьшенное, во-вторых, перевернутое. Ио самое главное, что это изображение, в отличие от мнимого изображения в зеркале, реально существует. На экране концентрируется энергия света. Чувствительный термометр, помещенный в изображение пламени свечи, покажет повышение температуры. Поэтому полученное в линзе изображение называют действительным, в отличие от мнимых изображений, наблюдаемых в плоском зеркале.
Подтвердим сказанное построением (рис. 271, б). Для получения изображения точки А достаточно использовать два луча, ход которых после преломления в линзе известен. Луч 1 идет параллельно главной оптической оси и после преломления в линзе проходит через главный фокус. Луч 2 идет через оптический центр и не меняет своего направления после прохождения сквозь линзу. Точка А’, являющаяся пересечением прошедших линзу лучей  и 2′, есть действительное изображение точки А. Заметим, что через точку А пройдет и любой другой преломленный луч идущий от точки А, благодаря чему энергия, излученная точкой А пламени свечи, будет сконцентрирована в точке А’.
и 2′, есть действительное изображение точки А. Заметим, что через точку А пройдет и любой другой преломленный луч идущий от точки А, благодаря чему энергия, излученная точкой А пламени свечи, будет сконцентрирована в точке А’.
Продолжим опыт. Поставим свечу на расстоянии d = 2F. Перемещая экран, мы увидим на нем действительное, перевернутое изображение пламени свечи, но размер его будет равен размеру пламени самой свечи (рис. 272). Сделайте сами построение изображения для этого случая.
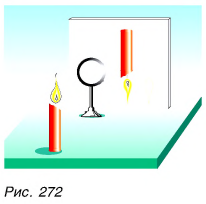
Передвигая свечу ближе к линзе (F < d < 2F) и удаляя экран, мы увидим на нем действительное, перевернутое, увеличенное изображение пламени свечи (построение сделайте сами).
Наконец поставим свечу на расстоянии d от линзы, меньше фокусного, т. е. d
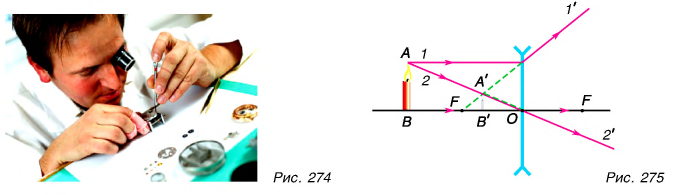
А какие изображения предмета дает рассеивающая линза? Пусть параллельно главной оптической оси надает луч 1 (рис. 275). После линзы преломленный луч 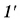 идет так, что только его продолжение проходит через фокус. Луч 2 не испытывает преломления. Видно, что лучи
идет так, что только его продолжение проходит через фокус. Луч 2 не испытывает преломления. Видно, что лучи 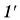 и 2′ не пересекаются. В точке А’ пересекаются их продолжения. Тогда изображение точки А, а значит, и всего предмета АВ — мнимое. Как все мнимые изображения, оно прямое, но уменьшенное. Даст ли рассеивающая линза действительное изображение, если менять положение предмета? Может ли оно быть увеличенным? Ответьте на эти вопросы сами, сделав соответствующие построения изображений предмета в тетради.
и 2′ не пересекаются. В точке А’ пересекаются их продолжения. Тогда изображение точки А, а значит, и всего предмета АВ — мнимое. Как все мнимые изображения, оно прямое, но уменьшенное. Даст ли рассеивающая линза действительное изображение, если менять положение предмета? Может ли оно быть увеличенным? Ответьте на эти вопросы сами, сделав соответствующие построения изображений предмета в тетради.
Главные выводы:
- Собирающая линза дает как действительные, так и мнимые изображения, рассеивающая — только мнимые.
- Все мнимые изображения — прямые, все действительные — перевернутые.
- Для нахождения изображения точки наиболее целесообразно использовать луч, идущий параллельно главной оптической оси линзы, и луч, идущий через ее оптический центр.
Пример №3
С помощью стеклянной линзы на экране, удаленном от линзы на расстояние f = 36 см, получено увеличенное в 3 раза изображение предмета. Определите расстояние от предмета до линзы и оптическую силу линзы.
Дано:
Н = Зh
f = 36 см
d — ?
D — ?
Решение
Построим изображение предмета в линзе (рис. 276).
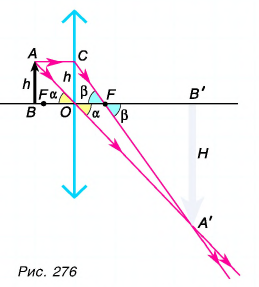
Поскольку изображение есть на экране, то оно действительное. Кроме того, оно увеличенное, значит, предмет находится между фокусом и двойным фокусом, а линза собирающая.
По условию размер предмета АВ в 3 раза меньше размера изображения А’В’. Из подобия треугольников АОВ и А’ОВ’ следует, что таким же будет и соотношение их сторон ВО и OB’, Значит, искомое расстояние d будет в 3 раза меньше заданного расстояния f. Это дает первый ответ: 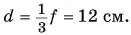 Для ответа на второй вопрос используем подобие другой нары треугольников — CFO и A’FB’. И здесь подобные стороны треугольников различаются в 3 раза.
Для ответа на второй вопрос используем подобие другой нары треугольников — CFO и A’FB’. И здесь подобные стороны треугольников различаются в 3 раза.
Так как одна из них — OF равна фокусному расстоянию F линзы, а другая — FB’ равна разности f – F, то их связь можно записать так: 3F = f – F, или 4F = f = 36 см. Вычислив значение фокусного расстояния 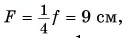 найдем и искомое значение оптической силы D линзы:
найдем и искомое значение оптической силы D линзы: 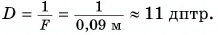
Ответ: 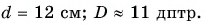
Оптическая сила и фокусное расстояние линзы
Граница разделения двух, прозрачных для света, тел может быть искривленной. Если прозрачное тело ограничить искривленными поверхностями, получим линзу (нем. linse – «чечевица»).
Линза — это прозрачное тело, ограниченное двумя выпуклыми или вво-гнутыми прозрачными поверхностями, преломляющими лучи света.
Одна из поверхностей линз может быть плоской. Линзы изготавливают из какого-либо прозрачного для света вещества: стекла, кварца, разных пластмасс, каменной соли, но чаще всего – из специальных сортов стекла.
Наибольшее распространение получили линзы, ограниченные сферическими поверхностями. В зависимости от взаимного размещения сферических поверхностей, ограничивающих линзу, различают 6 типов линз: двояковыпуклая, плоско-выпуклая, вогнуто-выпуклая (рис. 165, а, б, в); двояковогнутая, плоско-вогнутая, выпукло-ввогнутая (рис. 165, г, д, е).
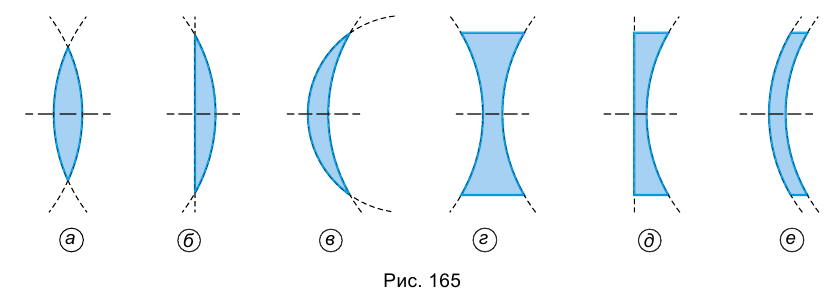
Любая линза имеет характерные точки и линии. Выясним, какие именно.
1. Прямую, проходящую через центры 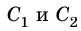 сферических поверхностей, которые ограничивают линзу, называют ее главной оптической осью (рис. 166).
сферических поверхностей, которые ограничивают линзу, называют ее главной оптической осью (рис. 166).
2. Точку О, которая лежит на главной оптической оси в центре линзы, называют оптическим центром линзы (рис. 166).
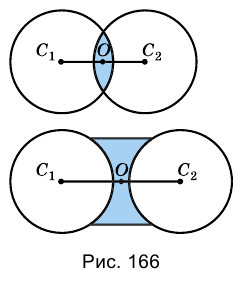
Опыт 1. Направим на линзу пучок лучей, параллельных ее главной оптической оси. Проходя через линзу, световые лучи преломляются и пересекаются в одной точке, лежащей на главной оптической оси линзы (рис. 167).
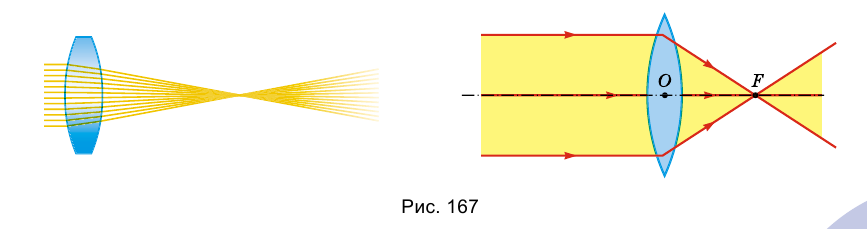
Эту точку называют главным фокусом линзы F.
3. Главный фокус линзы F – точка, в которой сходятся все, параллельные главной оптической оси, лучи после их преломления в линзе.
4. Фокусное расстояние f – расстояние от оптического центра линзы О до главного фокуса F.
Каждая линза имеет два главных фокуса.
Любая тонкая линза характеризуется двумя основными параметрами -фокусным расстоянием и оптической силой. Оптическую силу линзы обозначают большой буквой D и определяют по формуле:
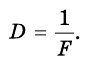
Единицей оптической силы является одна диоптрия (1 дптр), 1 дптр = 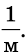 .
.
Как видно из опыта, линза преобразует пучок параллельных лучей в сходящийся, то есть собирает его в одну точку. Такую линзу называют собирательной.
Собирательная линза — это линза, которая световые лучи, падающие на нее параллельно ее главной оптической оси, после преломления собирает на этой оси в одну точку.
Опыт 2. Возьмем линзу другого типа и направим на нее параллельный главной оптической оси пучок лучей света. Лучи, преломившись на границе воздух-стекло, выходят из линзы расходящимся пучком, или рассеиваются (рис. 168).

Такую линзу называют рассеивающей.
Рассеивающая линза — это линза, которая световые лучи, падающие на нее параллельно ее главной оптической оси, после преломления отклоняет от этой оси.
Если пучок лучей, выходящий из рассеивающей линзы, продолжить в противоположном направлении, то продолжения лучей пересекутся в точке F, которая лежит на оптической оси с той же стороны, с которой свет падает на линзу. Эту точку F называют мнимым главным фокусом рассеивающей линзы (рис. 169).
Опыт 3. Пропустим световые лучи только через оптические центры линз. В результате опыта убеждаемся (рис. 170), что световые лучи, проходящие через оптический центр линзы, не преломляются, то есть не изменяют своего направления.
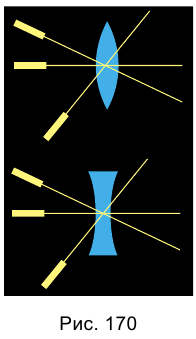
С помощью линз можно не только собирать или рассеивать световые лучи, но и строить изображение предметов. Как раз благодаря этому свойству линзы широко используют в практических целях.
Каким же образом строятся изображения предметов с помощью линз?
Изображение предмета — это воссоздание вида, формы и цвета предмета световыми лучами, проходящими через оптическую систему линз, которые имеют одну общую оптическую ось.
Если изображение предмета образовано пересечением самих лучей, то его называют действительным, если их продолжением – мнимым.
Определить ход лучей, отраженных всеми точками поверхности тела, невозможно. Поэтому для построения изображения будем использовать такие лучи, ход которых известен:
- 1. Луч, проходящий через оптический центр линзы, не преломляется (рис. 171, а).
- 2. Луч, параллельный главной оптической оси линзы, после преломления в линзе проходит через главный фокус линзы (рис. 171, б).
- 3. Луч, проходящий через главный фокус линзы, после преломления в ней, проходит параллельно главной оптической оси (рис. 171, в).
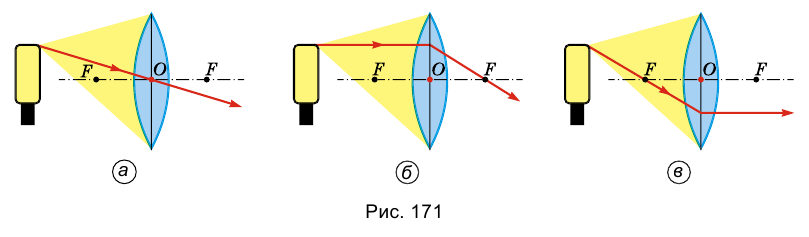
Рассмотрим случаи, при которых получается то или другое изображение, и особенности этих изображений.
1. Предмет АВ размещен между линзой и ее фокусом F.

Построим изображение точки А, использовав для этого упомянутые лучи. Луч АС (рис. 172), параллельный главной оси линзы, преломившись в линзе, пройдет через главный фокус, а луч АО не изменит своего направления. Как видно на рисунке, эти лучи расходятся. Чтобы построить изображение точки А, следует продолжить лучи в противоположном направлении до пересечения, это будет точка 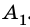 Это изображение точки есть мнимым. Такое же построение хода лучей можно выполнить для всех точек предмета, находящихся между точками А и В. Изображение этих промежуточных точек будут лежать между
Это изображение точки есть мнимым. Такое же построение хода лучей можно выполнить для всех точек предмета, находящихся между точками А и В. Изображение этих промежуточных точек будут лежать между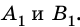 . Таким образом,
. Таким образом, 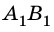 – изображение предмета АВ.
– изображение предмета АВ.
Если предмет находится между линзой и ее фокусом, то получают увеличенное, прямое, мнимое его изображение, размещенное дальше от линзы, чем сам предмет.
Такое изображение получают, когда пользуются лупой – прибором для рассматривания мелких предметов (например, чтения мелкого текста).
2. Предмет размещен в главном фокусе линзы F.
Для построения изображения предмета АВ снова воспользуемся лучами АС и АО (рис. 173). После прохождения лучей сквозь линзу мы увидим, что они параллельны между собой. Следовательно, изображение предмета АВ мы не получим.
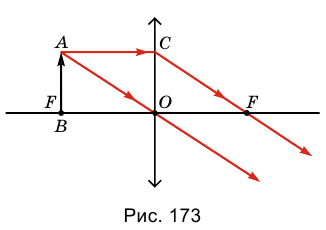
Если в главном фокусе разместить источник света, то мы превратим пучок расходящихся лучей на пучок параллельных лучей, который хорошо освещает отдаленные предметы.
Если предмет размещен в главном фокусе линзы F, изображение предмета получить нельзя.
3. Предмет размещен между главным фокусом линзы F и двойным фокусом линзы 2F.
Во время построения изображения (рис. 174) мы видим, что лучи АС и АО после прохождения линзы пересекаются в точке 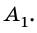 . В этой точке образуется действительное изображение точки А. Изображение
. В этой точке образуется действительное изображение точки А. Изображение 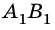 предмета АВ также будет действительным.
предмета АВ также будет действительным.
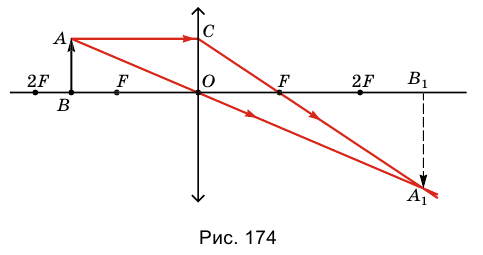
Если предмет находится между фокусом F и двойным фокусом 2F линзы, то образуется увеличенное, перевернутое и действительное изображение предмета; оно размещено с противоположной относительно предмета стороны линзы на расстоянии, больше двойного фокусного расстояния.
Такое изображение используют в проекционном аппарате, киноаппарате. Чтобы изображение на экране было прямым, диапозитивы или киноленту устанавливают в аппарат в перевернутом виде.
4. Предмет находится в двойном фокусе линзы. 2F.
В этом случае линза дает (рис. 175) перевернутое, действительное изображение предмета такого же размера, как и он сам. Это изображение размещено в ее двойном фокусе 2F с противоположной относительно предмета стороны линзы.
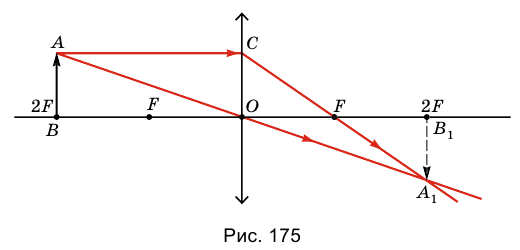
5. Если предмет находится за двойным фокусом линзы 2F (рис. 176), линза дает уменьшенное, перевернутое и действительное изображение предмета, которое размещено между ее главным фокусом F и двойным фокусом 2F с противоположной относительно предмета стороны линзы.
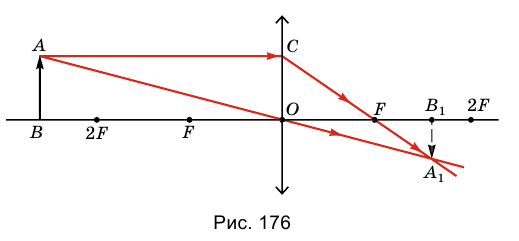
Такое изображение используют в фотоаппарате.
Пример №4
Почему не рекомендуется поливать растения днем, когда они освещены солнечными лучами, особенно те, на листьях которых остаются капельки воды?
Ответ: потому что капельки играют роль линз, фокусирующих солнечные лучи, и растения получают ожоги.
Пример №5
На рисунке 177 показан ход лучей в линзах. Какие это линзы?
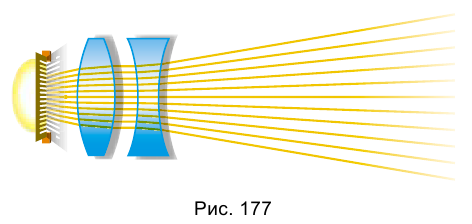
Ответ: (слева направо) источник света, собирательная линза, рассеивающая линза.
Простые оптические приборы
Знания законов отражения и преломления света в зеркалах и линзах дали возможность создать ряд оптических приборов, имеющих важное значение для современной науки и техники. Их используют специалисты разных отраслей. Это микроскоп биолога и фотоаппарат журналиста, кинокамера оператора и телескоп астронома, перископ подводника и т. п. Кроме того, оптическими приборами являются очки миллионов людей разного возраста и специальностей.
Самый простой оптический прибор – лупа.
Лупа (франц. loupe – «нарост») – оптический прибор, являющийся собирательной линзой, применяется для рассматривания мелких деталей, плохо заметных невооруженным глазом.
Общий вид луп разного вида представлен на рисунке 181, а.
Чтобы увидеть изображение предмета увеличенным, лупу следует разместить так, чтобы данный предмет был между лупой и ее фокусом (рис. 181, б).
Лучи, падающие на лупу от крайних точек предмета, преломляются в линзе и сходятся.
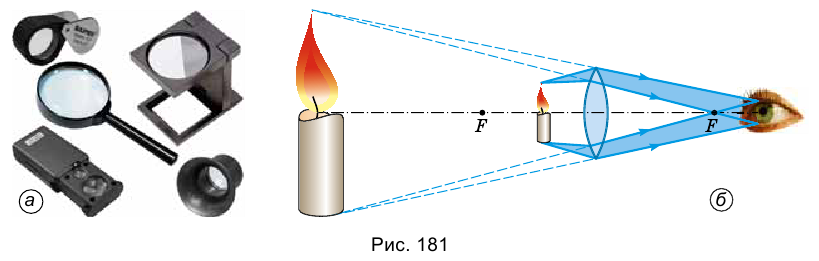
Каким же образом все это видит наш глаз?
Оказывается, наш глаз не замечает преломления лучей. Лучи, идущие от предмета сквозь линзу, воспринимаются глазом как прямолинейные. Нам кажется, что лучи, идущие от лупы к глазу, продолжаются после лупы, не преломляясь. Благодаря этому мы видим предмет увеличенным по сравнению с его действительными размерами.
Лупа дает увеличение в 10-40 раз.
Значительное увеличение изображения предметов можно получить с помощью двух линз, размещенных в металлической трубе на определенном расстоянии друг от друга. Такой прибор называют микроскопом.
Микроскоп (греч. mikro – «маленький», skopeo – «смотрю») – оптический прибор для рассматривания мелких предметов и их деталей (рис. 182, а).
Ход лучей в микроскопе показан на рисунке 182, б. Линзу, размещенную со стороны глаза, называют окуляром (лат. oculus – «глаз»), а линзу, размещенную со стороны данного предмета, называют объективом (лат. objectivus – «предметный»).
Первое увеличение изображения предмета дает объектив. Предмет в микроскопе размещается немного дальше от фокуса обьектива. В результате этого выходит увеличенное и перевернутое изображение предмета.
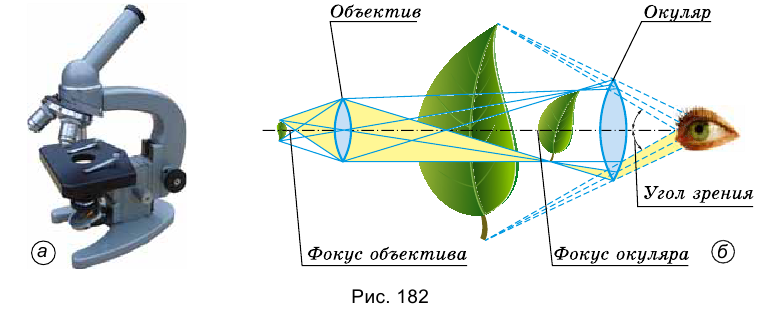
Это изображение увеличивается еще раз линзой-окуляром: оно будто служит для окуляра предметом. Окуляр, подобно лупе, размещают на расстоянии (меньше фокусного) от промежуточного изображения. В итоге мы получаем новое, более увеличенное изображение.
Если, например, объектив микроскопа дает изображение предмета, увеличенное в 20 раз, а окуляр увеличивает это изображение в 15 раз, то общее увеличение, которое дает микроскоп, будет уже 20*15 = 300 раз.
Современные электронные микроскопы дают увеличение в десятки тысяч раз. Например, так выглядят под микроскопом бактерии, увеличенные в 25 000 раз (рис. 183).
Посмотрите еще раз на схему микроскопа (рис. 182, б). Объектив микроскопа – линза – имеет меньшее фокусное расстояние, чем окуляр этого прибора. А что будет, если мы возьмем объектив, который имеет большее фокусное расстояние, чем окуляр?
В этом случае мы получим новый прибор, который называют телескопом, или рефрактором (лат. refringo – «преломляю»). Такой телескоп создал еще в 1611 г. немецкий астроном Иоганн Кеплер. А вообще первый телескоп на основе зрительной трубы построил в 1609 г. Галилео Галилей.
Телескоп (греч. tele – «далеко», skopeo – «смотреть») – оптический прибор для астрономических исследований космических объектов (рис. 184).
Прохождение в телескопе лучей от небесного тела показано на рисунке 185.

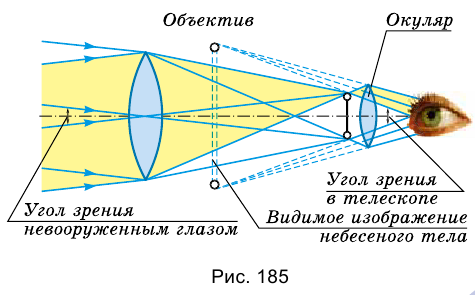
Как следует из рисунка, изображение небесного тела в телескопе мы видим под большим углом зрения, в отличие от невооруженного глаза. Окуляр телескопа, как и окуляр микроскопа, действует как обычная лупа.
Следует отметить, что, рассматривая с помощью телескопа отдаленные предметы на Земле, мы видим их перевернутыми. Однако для наблюдения за небесными телами это обстоятельство не столь важно.
Самый большой телескоп-рефрактор установлен в Йеркской обсерватории университета в Чикаго (США). Его объектив в диаметре достигает 102 см.
Другой тип – это телескопы-рефлекторы (лат. reflecto – «отображаю»). В таких телескопах, кроме преломления лучей света, используют другое их свойство – способность отражаться от зеркальных поверхностей.
Изображение небесного тела отражается с помощью маленького плоского зеркальца и рассматривается с помощью окуляра (рис. 186), который увеличивает отраженное изображение.
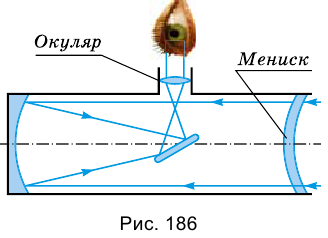
Первый рефлектор с диаметром зеркала 2,5 см и фокусным расстоянием 16,5 см построил в 1668 г. Исаак Ньютон. Сегодня самым большим в мире является зеркальный телескоп HESS II, установленный в Намибии, его площадь достигает 600 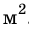 . Устройство предназначено для изучения происхождения космических лучей.
. Устройство предназначено для изучения происхождения космических лучей.
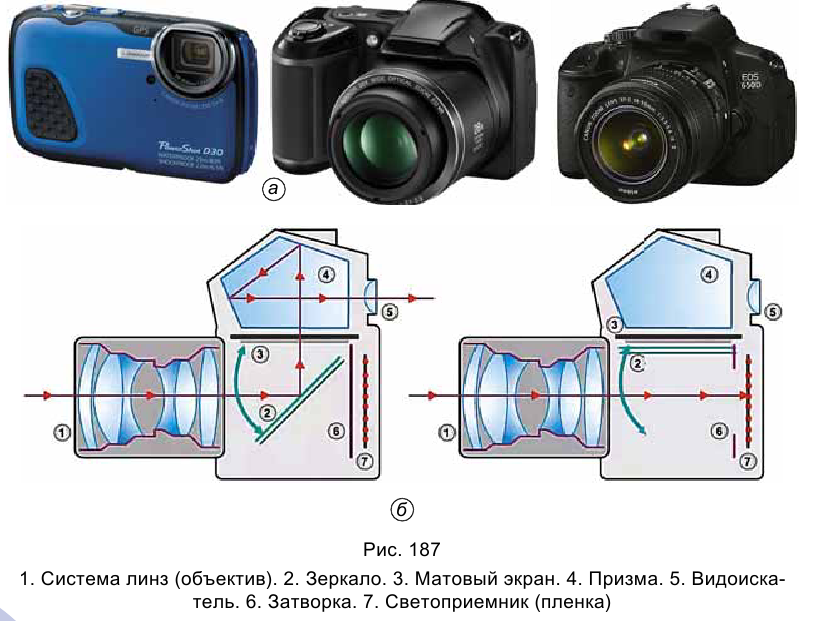
Фотоаппарат – это оптический прибор, с помощью которого на цифровом устройстве (англ, digital device – «техническое устройство или приспособление, предназначенное для получения и обработки информации в цифровой форме, используя цифровые технологии»), фотопленке, фотопластинке, фотобумаге получают изображение предмета.
Сегодня существует много различных типов фотоаппаратов (рис. 187, а). Они отличаются формой и размерами, но их строение и основные части одинаковы. Ход лучей в фотоаппарате изображен на рисунке 187, б.
- Заказать решение задач по физике
Подробное объяснение формулы тонкой линзы
Линза называется собирающей, если после преломления в ней параллельный пучок становится сходящимся. Если же после преломления в линзе параллельный пучок становится расходящимся, то линза называется рассеивающей (рис. 58).
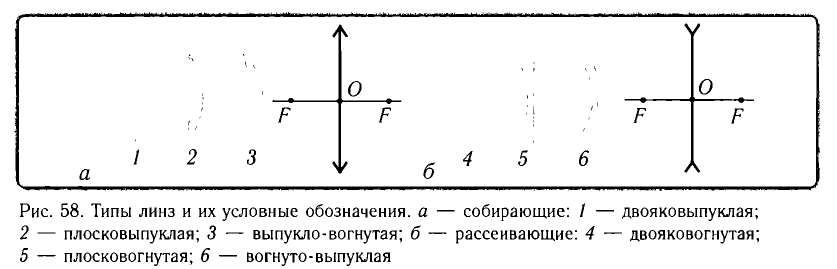
Основные типы линз и лучи, используемые для построения изображений в них, даны на рисунках 59, 60.
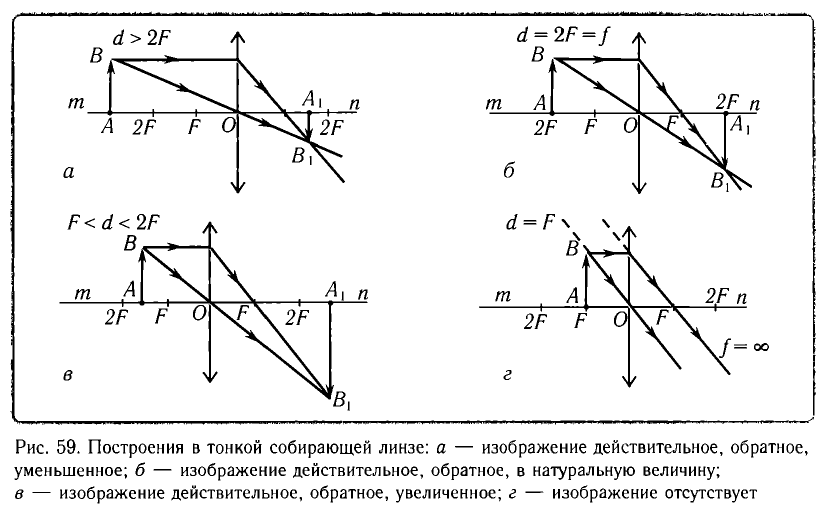
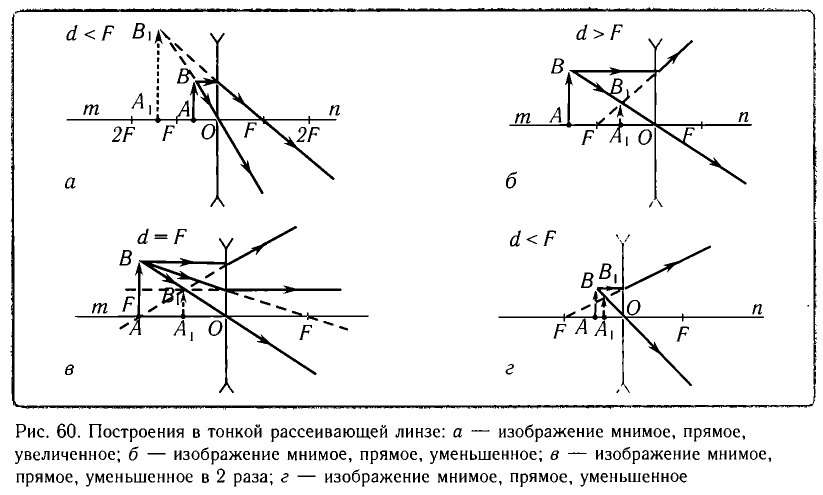
Величина, обратная фокусному расстоянию линзы, выраженному в метрах, называется ее оптической силой:
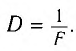
Единица оптической силы — диоптрия (1 дптр).
1 дптр соответствует оптической силе линзы с фокусным расстоянием I м: 1 дптр= 1 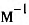 .
.
Между фокусным расстоянием F тонкой линзы, расстоянием от предмета до линзы d и расстоянием от линзы до изображения f существует определенная количественная зависимость, называемая формулой линзы.
Выведем формулу тонкой линзы, рассматривая ход характерных лучей (рис. 61).
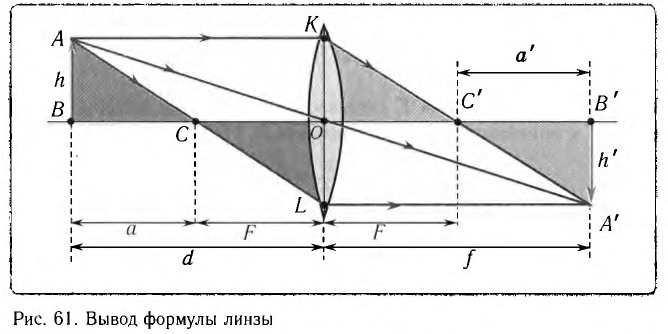
Пусть расстояние от предмета до линзы d, расстояние от линзы до изображения f, фокусное расстояние линзы F, расстояние от предмета до переднего главного фокуса а, расстояние от заднего главного фокуса до изображения а’.
Из рисунка 61 видно, что 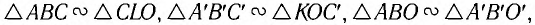 следовательно
следовательно

Из формул (1) и (2) следует формула Ньютона:
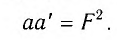
С учетом того, что d = а + F, f = а’ + F, получаем формулу тонкой линзы:
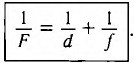
Поперечным увеличением Г называется отношение линейного размера изображения h’ к линейному размеру предмета h. Из выражения (3) находим
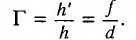
В 1604 г. в исследовании «Дополнения к Вителло» Кеплер изучал преломление света в линзах различной конфигурации и для малых углов падения пришел к формуле линзы.
Для практического использования формулы тонкой линзы следует запомнить правило знаков:
- для собирающей линзы, действительных источника и изображения величины F, d, f считают положительными;
- для рассеивающей линзы, мнимых источника и изображения величины F, d,f считают отрицательными.
Заметим, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей.
Таким образом, линза с F>0 является собирающей (положительной), а с F< 0 — рассеивающей (отрицательной).
Оптическая сила линзы зависит от свойств окружающей среды.
В современных оптических приборах используются системы линз для улучшения качества изображений. Оптическая сила D системы тонких линз, сложенных вместе, равна сумме их оптических сил 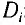 :
:
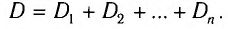
Пример №6
Предмет расположен на расстоянии d = 0,15 м от рассеивающей линзы с фокусным расстоянием F=-0,30 м. На каком расстоянии f от линзы получается изображение данного предмета?
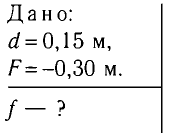
Решение
Из формулы тонкой линзы
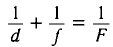
находим
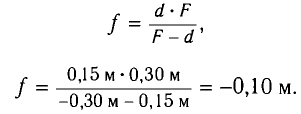
Отрицательное значение f соответствует мнимому изображению предмета.
Ответ: f =-0,10 м, изображение мнимое.
Пример №7
На каком расстоянии d от рассеивающей линзы с оптической силой D = -4 дптр надо поместить предмет, чтобы его мнимое изображение получилось в k = b раз меньше (Г = 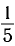 ) самого предмета?
) самого предмета?
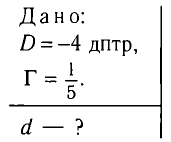
Решение
Из формулы для увеличения
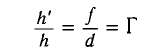
находим
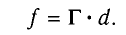
Из формулы линзы
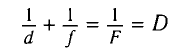
с учетом выражения для f получаем
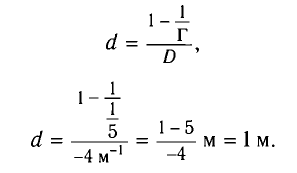
Ответ: d= 1 м.
Пример №8
Определите фокусное расстояние F собирающей линзы, дающей мнимое изображение предмета, помещенного перед ней на расстоянии d- 0,4 м, если расстояние от линзы до изображения f =-1,2 м.
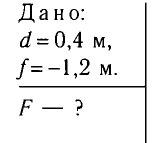
Решение
Из формулы тонкой линзы
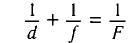
находим
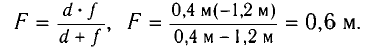
Ответ: F= 0,6 м.
Разбираем формулу тонкой линзы
Линза называется собирающей, если после преломления в ней параллельный пучок становится сходящимся. Если же после преломления в линзе параллельный пучок становится расходящимся, то линза называется рассеивающей (рис. 80).
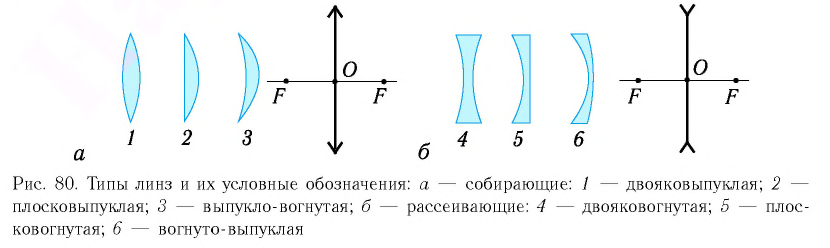
Величина, обратная фокусному расстоянию линзы, выраженному в метрах, называется ее оптической силой:
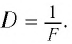
Единица оптической силы — 1 диоптрия (1 дптр).
1 дптр соответствует оптической силе линзы с фокусным расстоянием
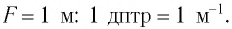
Линзы можно представить в виде совокупности частей трехгранных призм. На рисунке 81, а изображена модель двояковыпуклой линзы, собранной из частей призм, повернутых основаниями к центру линзы. Соответственно, модель двояковогнутой линзы будет представлена частями призм, повернутых основаниями от центра линзы (рис. 81, б).
Преломляющие углы этих призм можно подобрать таким образом, чтобы падающие на нее параллельные лучи после преломления в призмах собрались в одной точке 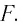
Линза считается тонкой, если ее толщина в центре намного меньше радиусов ограничивающих ее поверхностей. Тонкая линза дает неискаженное изображение только в том случае, если свет монохроматический и предмет достаточно мал, следовательно, лучи распространяются вблизи главной оптической оси. Такие лучи получили название параксиальных.
Отметим условия, при одновременном выполнении которых линза является собирающей:
- толщина в центре больше толщины у краев,
- ее показатель преломления больше показателя преломления окружающей среды.
При невыполнении (или выполнении) только одного из этих условий линза является рассеивающей.
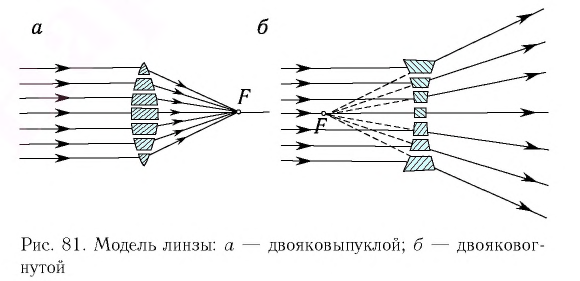
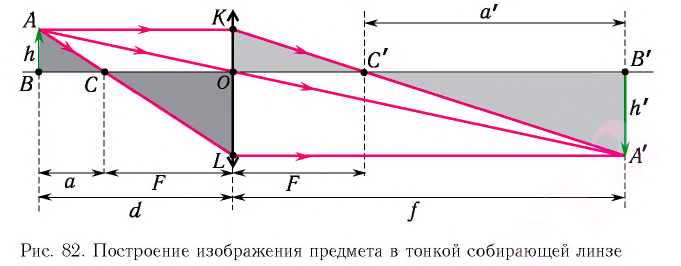
Между фокусным расстоянием тонкой линзы, расстоянием от предмета до линзы и от линзы до изображения существует определенная количественная зависимость, называемая формулой линзы.
Выведем формулу тонкой линзы из геометрических соображений, рассматривая ход характерных лучей. Обратим внимание на луч, идущий через оптический центр 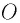 линзы, луч, параллельный главной оптической оси линзы, и луч, проходящий через главный фокус линзы.
линзы, луч, параллельный главной оптической оси линзы, и луч, проходящий через главный фокус линзы.
Построим изображение предмета 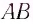 в тонкой собирающей линзе (рис. 82). Пусть расстояние от предмета до линзы
в тонкой собирающей линзе (рис. 82). Пусть расстояние от предмета до линзы 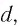 расстояние от линзы до изображения
расстояние от линзы до изображения 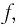 фокусное расстояние линзы
фокусное расстояние линзы 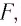 расстояние от предмета до переднего главного фокуса
расстояние от предмета до переднего главного фокуса 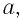 расстояние от заднего главного фокуса до изображения
расстояние от заднего главного фокуса до изображения 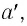 высота предмета
высота предмета 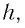 высота его изображения
высота его изображения 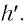
Из рисунка 82 видно, что 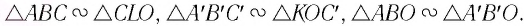 Из подобия треугольников следует:
Из подобия треугольников следует:
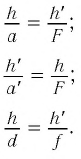
Используя соотношения (1) и (2), получим:
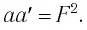
Соотношение 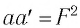 называется формулой Ньютона.
называется формулой Ньютона.
С учетом того, что 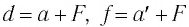 (см. рис. 82), находим:
(см. рис. 82), находим: 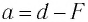 и подставляем в формулу (4):
и подставляем в формулу (4):
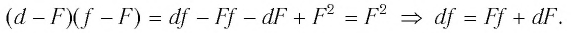
Разделив обе части последнего выражения на 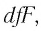 получаем формулу тонкой линзы:
получаем формулу тонкой линзы:
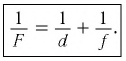
Линейным (поперечным) увеличением Г называется отношение линейного размера изображения 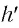 к линейному размеру предмета
к линейному размеру предмета 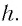 Из соотношения (3) находим линейное увеличение тонкой линзы:
Из соотношения (3) находим линейное увеличение тонкой линзы:
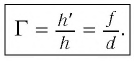
В 1604 г. в исследовании «Дополнения к Вителло» И. Кеплер изучал преломление света в линзах различной конфигурации и для малых углов падения пришел к формуле линзы.
Для практического использования формулы линзы следует твердо запомнить правило знаков:
Заметим, что предмет или источник является мнимым, только в том случае, если на линзу падает пучок сходящихся лучей.
Таким образом, линза с 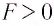 является собирающей (положительной), а с
является собирающей (положительной), а с 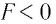 — рассеивающей (отрицательной).
— рассеивающей (отрицательной).
Оптическая сила линзы зависит от свойств окружающей среды (вспомните, как плохо мы видим под водой без плавательных очков).
В современных оптических приборах для улучшения качества изображений используются системы линз. Оптическая сила 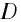 системы тонких линз, сложенных вместе, равна сумме их оптических сил
системы тонких линз, сложенных вместе, равна сумме их оптических сил 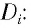
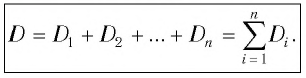
Пример №9
На каком расстоянии 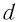 от рассеивающей линзы с оптической силой
от рассеивающей линзы с оптической силой 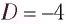 дптр надо поместить предмет, чтобы его мнимое изображение получилось в
дптр надо поместить предмет, чтобы его мнимое изображение получилось в 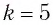 раз меньше
раз меньше 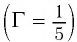 самого предмета? Постройте изображение предмета.
самого предмета? Постройте изображение предмета.
Дано:
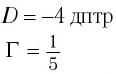
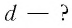
Решение
Из формулы для линейного увеличения
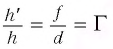
находим:
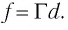
По формуле тонкой линзы ( рис. 83) с учетом правила знаков:
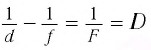
и с учетом выражения для 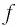 получаем:
получаем:
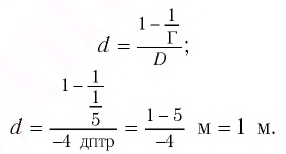
Ответ: 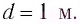
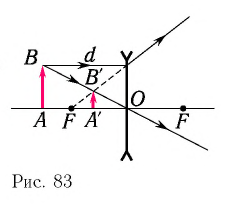
Изучаем линзы
Скорее всего, вы пользовались фотоаппаратом, знакомы с биноклем, подзорной трубой, телескопом, на уроках биологии работали с микроскопом. Некоторые из вас носят очки. Все эти устройства имеют общее — их основной частью является линза. О том, какое значение имеют данные устройства в жизни человека, вы можете рассказать и сами, а вот о том, что такое линза, какие существуют виды линз и каковы их свойства, вы узнаете из этого параграфа.
Линза — прозрачное тело, ограниченное с двух сторон сферическими поверхностями*.
 Одна из поверхностей линзы может быть плоскостью, поскольку плоскость можно рассматривать как сферу бесконечного радиуса. Линзы также бывают цилиндрическими, но встречаются такие линзы редко.
Одна из поверхностей линзы может быть плоскостью, поскольку плоскость можно рассматривать как сферу бесконечного радиуса. Линзы также бывают цилиндрическими, но встречаются такие линзы редко.
По форме линзы делят на выпуклые (рис. 14.1) и вогнутые (рис. 14.2).
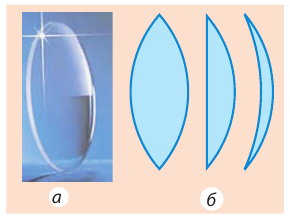
Рис. 14.1. Толщина выпуклой линзы посредине больше, чем у краев: а — вид; б — разные выпуклые линзы в разрезе
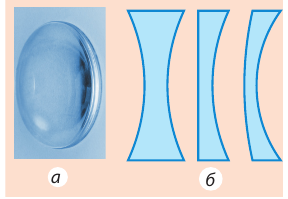
Рис. 14.2. Толщина вогнутой линзы посредине меньше, чем у краев: а — вид; б — разные вогнутые линзы в разрезе
Если толщина 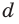 линзы во много раз меньше радиусов сферических поверхностей, ограничивающих линзу, такую линзу называют тонкой. Далее мы будем рассматривать только тонкие линзы. Прямую, которая проходит через центры сферических поверхностей, ограничивающих линзу, называют главной оптической осью линзы (рис. 14.3).
линзы во много раз меньше радиусов сферических поверхностей, ограничивающих линзу, такую линзу называют тонкой. Далее мы будем рассматривать только тонкие линзы. Прямую, которая проходит через центры сферических поверхностей, ограничивающих линзу, называют главной оптической осью линзы (рис. 14.3).
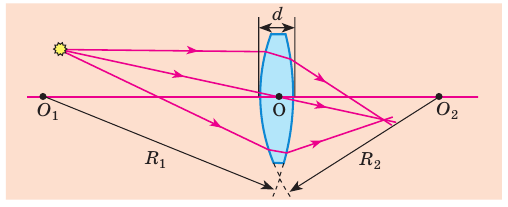
Рис. 14.3. Тонкая сферическая линза: 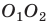 — главная оптическая ось линзы;
— главная оптическая ось линзы; 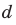 — толщина линзы;
— толщина линзы; 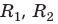 — радиусы сферических поверхностей, ограничивающих линзу;
— радиусы сферических поверхностей, ограничивающих линзу; 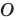 — оптический центр линзы
— оптический центр линзы
Если на линзу направить пучок световых лучей, они преломятся на ее поверхностях и изменят свое направление. В то же время на главной оптической оси линзы есть точка, которую луч света проходит практически не изменяя своего направления. Эту точку называют оптическим центром линзы (см. рис. 14.3).
Направим на линзу пучок лучей, параллельных ее главной оптической оси. Если лучи, пройдя сквозь линзу, идут сходящимся пучком, такая линза — собирающая. Точка F, в которой пересекаются преломленные лучи, — действительный главный фокус линзы (рис. 14.4).
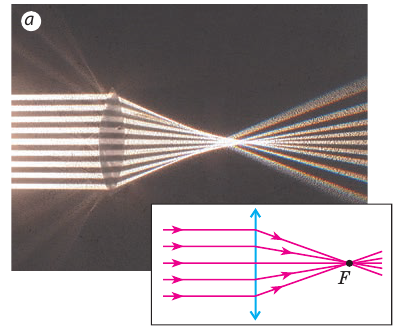
Рис. 14.4. Ход лучей после преломления в собирающей линзе. Точка F — действительный главный фокус линзы
Линза является рассеивающей, если лучи, параллельные ее главной оптической оси, пройдя сквозь линзу, идут расходящимся пучком. Точку F, в которой пересекаются продолжения преломленных лучей, называют мнимым главным фокусом линзы (рис. 14.5).
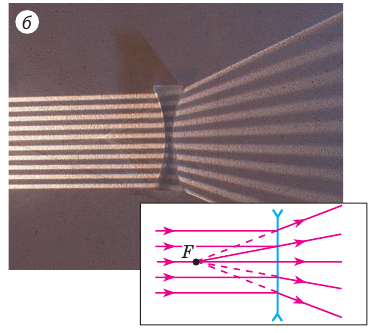
Рис. 14.5. Ход лучей после преломления в рассеивающей линзе. Точка F — мнимый главный фокус линзы
Обратите внимание: любой пучок параллельных лучей, даже если эти лучи не параллельны главной оптической оси, после преломления в собирающей линзе всегда пересекаются в одной точке (рис. 14.6) (если линза рассеивающая, в одной точке пересекаются продолжения преломленных лучей).
Рис. 14.6. Ход параллельных лучей после преломления в собирающей линзе
Если оптическая плотность материала, из которого изготовлена линза, больше оптической плотности среды 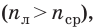 то выпуклая линза будет собирать лучи (будет собирающей), а вогнутая линза будет рассеивать лучи (будет рассеивающей) (см. рис. 14.4, 14.5).
то выпуклая линза будет собирать лучи (будет собирающей), а вогнутая линза будет рассеивать лучи (будет рассеивающей) (см. рис. 14.4, 14.5).
Если оптическая плотность материала, из которого изготовлена линза, меньше оптической плотности среды 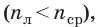 то выпуклая линза будет рассеивающей (рис. 14.7, а), а вогнутая линза — собирающей (рис. 14.7, б).
то выпуклая линза будет рассеивающей (рис. 14.7, а), а вогнутая линза — собирающей (рис. 14.7, б).
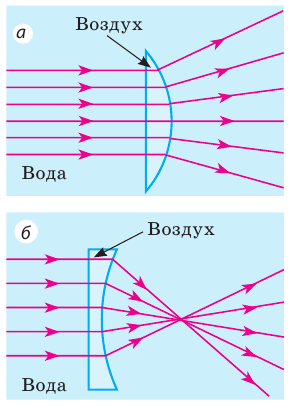
Рис. 14.7. Выпуклая (а) и вогнутая (б) воздушные линзы в воде
Определение оптической силы линзы
Любая линза имеет два главных фокуса*, расположенных на одинаковом расстоянии от оптического центра линзы (см. рис. 14.8).
 Далее главный фокус линзы, как правило, будем называть фокусом линзы.
Далее главный фокус линзы, как правило, будем называть фокусом линзы.
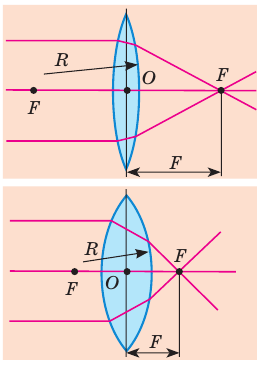
Рис. 14.8. Чем меньше радиусы R сферических поверхностей, ограничивающих линзу, тем сильнее эта линза преломляет свет, а значит, тем меньше ее фокусное расстояние F
Расстояние от оптического центра линзы до главного фокуса называют фокусным расстоянием линзы.
Фокусное расстояние, как и фокус, обозначают символом F. Единица фокусного расстояния в СИ — метр:
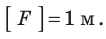
Фокусное расстояние собирающей линзы договорились считать положительным, а рассеивающей — отрицательным. Очевидно, что чем сильнее преломляющие свойства линзы, тем меньше по модулю ее фокусное расстояние (рис. 14.8).
Физическую величину, которая характеризует линзу и является обратной фокусному расстоянию линзы, называют оптической силой линзы.
Оптическую силу линзы обозначают символом D и вычисляют по формуле:
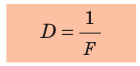
Единица оптической силы — диоптрия: 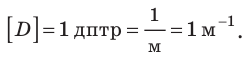
1 диоптрия — это оптическая сила линзы, фокусное расстояние которой равно 1 м. Оптическая сила собирающей линзы положительна, а рассеивающей линзы — отрицательна.
Подводим итоги:
Прозрачное тело, ограниченное с двух сторон сферическими поверхностями, называют линзой. Линза является собирающей, если пучок параллельных лучей, падающий на нее, после преломления в линзе пересекается в одной точке (эта точка — действительный фокус линзы). Линза является рассеивающей, если параллельные лучи, падающие на нее, после преломления идут расходящимся пучком, а продолжения преломленных лучей пересекаются в одной точке (эта точка — мнимый фокус линзы).
Физическую величину, которая характеризует преломляющие свойства линзы и обратна ее фокусному расстоянию, называют оптической силой линзы: 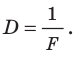 Единица оптической силы линзы — диоптрия
Единица оптической силы линзы — диоптрия 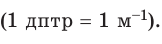
Построение изображений в линзах
Основное свойство линз заключается в том, что линзы дают изображение точки, а соответственно, и предмета (как совокупности точек) (рис. 15.1). В зависимости от расстояния между предметом и линзой изображение предмета может быть больше или меньше, чем сам предмет, мнимым или действительным. Выясним, при каких условиях с помощью линзы образуются те или иные изображения, и рассмотрим приемы их построения.

Рис. 15.1. Получение изображения пламени свечи с помощью собирающей линзы
Любой предмет можно представить как совокупность точек. Каждая точка предмета излучает (или отражает) свет во всех направлениях. В создании изображения участвует множество лучей, однако для построения изображения некоторой точки S достаточно найти точку пересечения любых двух лучей, выходящих из точки S и проходящих через линзу. Обычно для этого выбирают два из трех «удобных лучей» (рис. 15.2).
Точка S1 будет действительным изображением точки S, если в точке пересекаются сами преломленные лучи (рис. 15.2, а). Точка будет мнимым изображением точки S, если в точке пересекаются продолжения преломленных лучей (рис. 15.2, б).
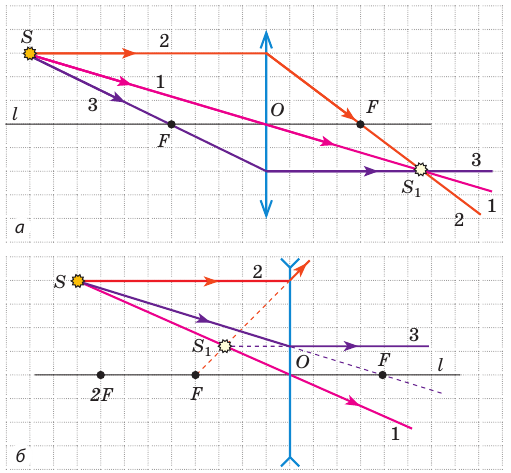
Рис. 15.2. Три самых простых в построении луча («удобные лучи»):
- луч, проходящий через оптический центр О линзы, не преломляется и не изменяет своего направления;
- луч, параллельный главной оптической оси
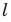 линзы, после преломления в линзе идет через фокус
линзы, после преломления в линзе идет через фокус 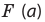 или через фокус
или через фокус 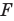 идет его продолжение (б);
идет его продолжение (б); - луч, проходящий через фокус
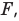 после преломления в линзе идет параллельно главной оптической оси
после преломления в линзе идет параллельно главной оптической оси 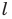 линзы (а, б)
линзы (а, б)
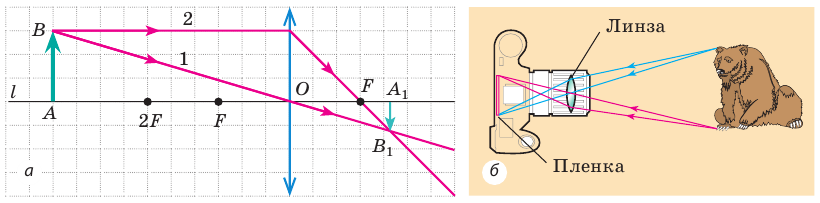
Рис. 15.3. а — построение изображения 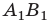 предмета
предмета 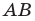 в собирающей линзе: предмет
в собирающей линзе: предмет 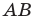 расположен за двойным фокусом линзы; б — ход лучей в фотоаппарате
расположен за двойным фокусом линзы; б — ход лучей в фотоаппарате
Строим изображение предмета, которое даёт линза:
Рассмотрим все возможные случаи расположения предмета АВ относительно собирающей линзы и докажем, что размеры и вид изображения зависят от расстояния между предметом и линзой.
1. Предмет расположен за двойным фокусом собирающей линзы (рис. 15.3, а). Сначала построим изображение точки 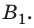 Для этого воспользуемся двумя лучами — 1 и 2. После преломления в линзе они пересекутся в точке
Для этого воспользуемся двумя лучами — 1 и 2. После преломления в линзе они пересекутся в точке 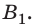 Значит, точка
Значит, точка 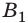 является действительным изображением точки
является действительным изображением точки 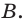 Для построения изображения точки
Для построения изображения точки 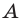 опустим из точки
опустим из точки 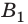 перпендикуляр на главную оптическую ось
перпендикуляр на главную оптическую ось 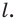 Точка
Точка 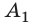 пересечения перпендикуляра и оси I является изображением точки
пересечения перпендикуляра и оси I является изображением точки 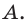
Итак, 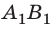 — изображение предмета
— изображение предмета 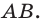 Это изображение действительное, уменьшенное, перевернутое. Такое изображение получается, например, на сетчатке глаза или пленке фотоаппарата (рис. 15.3, б).
Это изображение действительное, уменьшенное, перевернутое. Такое изображение получается, например, на сетчатке глаза или пленке фотоаппарата (рис. 15.3, б).
2. Предмет расположен между фокусом и двойным фокусом собирающей линзы (рис. 15.4, а). Изображение предмета действительное, увеличенное, перевернутое. Такое изображение позволяет получить на экране проекционная аппаратура (рис. 15.4, б).
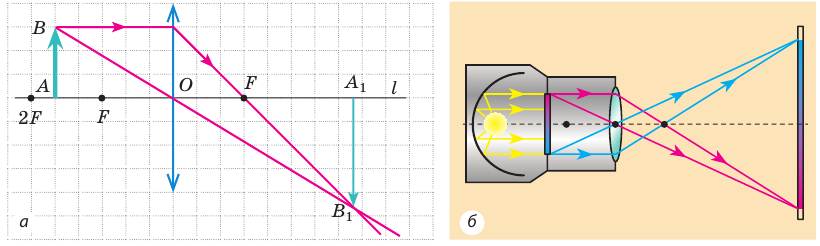
Рис. 15.4. а — построение изображения 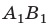 предмета
предмета 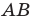 в собирающей линзе: предмет
в собирающей линзе: предмет 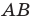 расположен между фокусом и двойным фокусом линзы; б — ход лучей в проекционном аппарате
расположен между фокусом и двойным фокусом линзы; б — ход лучей в проекционном аппарате
3. Предмет расположен между фокусом и собирающей линзой (рис. 15.5, а). Лучи, вышедшие из точки 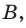 после преломления в линзе идут расходящимся пучком. Однако их продолжения пересекаются в точке
после преломления в линзе идут расходящимся пучком. Однако их продолжения пересекаются в точке 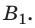
В данном случае изображение предмета является мнимым, увеличенным, прямым. Изображение расположено по ту же сторону от линзы, что и предмет, поэтому мы не можем увидеть изображение предмета на экране, но видим его, когда смотрим на предмет через линзу. Именно такое изображение дает короткофокусная собирающая линза — лупа (рис. 15.5, б).
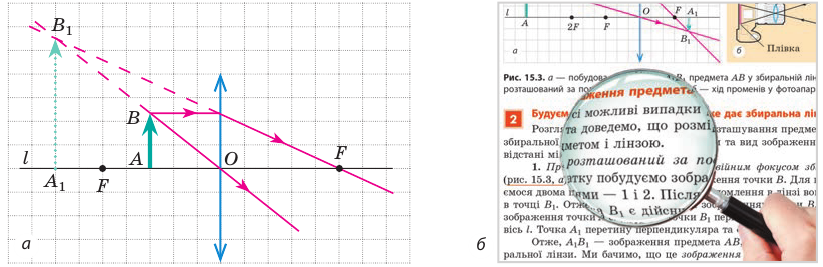
Рис. 15.5. а – построение изображения 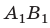 предмета
предмета 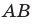 в собирающей линзе: предмет
в собирающей линзе: предмет 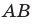 расположен между линзой и ее фокусом; б – с помощью
расположен между линзой и ее фокусом; б – с помощью
4. Предмет расположен на фокусном расстоянии от собирающей линзы. После преломления все лучи идут параллельным пучком (рис. 15.6), следовательно, в данном случае ни действительного, ни мнимого изображения мы не получим.

Рис. 15.6. Если предмет расположен в фокусе собирающей линзы, мы не получим его изображения
Внимательно рассмотрите рис. 15.7, на котором показано построение изображений предмета, полученных с помощью рассеивающей линзы. Видим, что рассеивающая линза всегда дает мнимое, уменьшенное, прямое изображение, расположенное по ту же сторону от линзы, что и сам предмет.
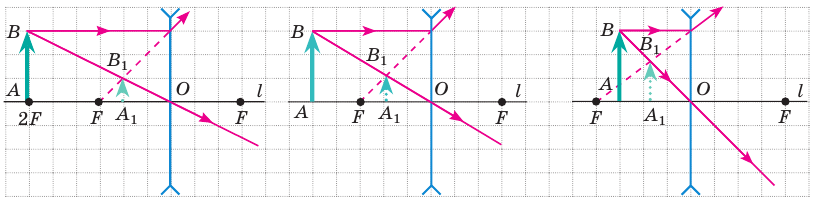
Рис. 15.7. Рассеивающая линза всегда дает мнимое, уменьшенное, прямое изображение
Чаще всего предмет больше, чем линза, или часть линзы закрыта непрозрачным экраном (как, например, линза в объективе фотоаппарата). Изменяется ли при этом внешний вид изображения? Конечно же нет. Ведь от каждой точки предмета на линзу падает множество лучей, и все они собираются в соответствующей точке изображения. Если закрыть часть линзы, это приведет лишь к тому, что энергия, попадающая в каждую точку изображения, уменьшится. Изображение будет менее ярким, однако ни его вид, ни месторасположение не изменятся. Именно поэтому, строя изображение, мы можем использовать все «удобные лучи», даже те, которые не проходят через линзу (рис. 15.8).
Формула тонкой линзы:
Построим изображение предмета в собирающей линзе (рис. 15.9).
Рассмотрим прямоугольные треугольники 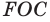 и
и 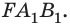 Эти треугольники подобны
Эти треугольники подобны 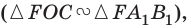 поэтому
поэтому 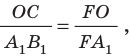 или
или 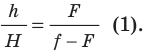
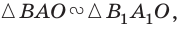 поэтому
поэтому 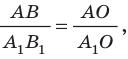 или
или 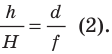
Приравняв правые части равенств (1) и (2), имеем 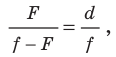 то есть
то есть 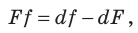 или
или 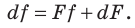 Разделив обе части последнего равенства на
Разделив обе части последнего равенства на 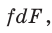 получим формулу тонкой линзы:
получим формулу тонкой линзы:
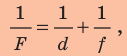 или
или 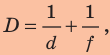
где 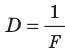 – оптическая сила линзы.
– оптическая сила линзы.
При решении задач следует иметь в виду:
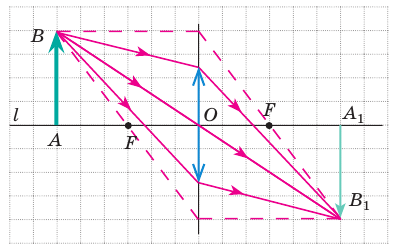
Рис. 15.8. Построение изображения предмета в случае, когда предмет значительно больше линзы
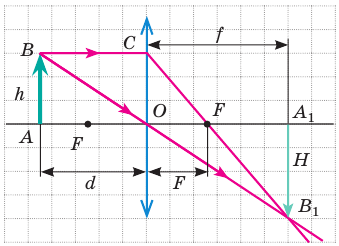
Рис. 15.9. К выведению формулы тонкой линзы: h — высота предмета; Н — высота изображения; d — расстояние от предмета до линзы; f — расстояние от линзы до изображения; F — фокусное расстояние
Пример №10
Рассматривая монету с помощью лупы, оптическая сила которой +10 дптр, мальчик расположил монету на расстоянии 6 см от лупы. Определите: 1) фокусное расстояние линзы; 2) на каком расстоянии от лупы находится изображение монеты; 3) какое изображение дает лупа — действительное или мнимое; 4) какое увеличение дает лупа.
Анализ физической проблемы. Лупу можно считать тонкой линзой, поэтому воспользуемся формулой тонкой линзы. Фокусное расстояние найдем, воспользовавшись определением оптической силы линзы.
Дано:
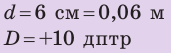
Найти:
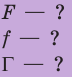
Поиск математической модели, решение
По определению 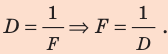
По формуле тонкой линзы: 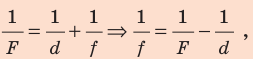 или
или 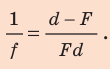 Следовательно,
Следовательно, 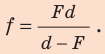
Зная расстояние 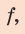 определим увеличение
определим увеличение 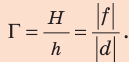
Найдем значения искомых величин:
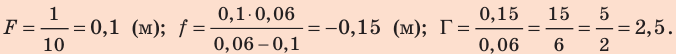
Знак «-» перед значением 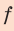 говорит о том, что изображение мнимое.
говорит о том, что изображение мнимое.
Ответ: 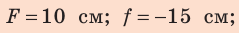 изображение мнимое;
изображение мнимое; 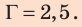
Подводим итоги:
В зависимости от типа линзы (собирающая или рассеивающая) и месторасположения предмета относительно данной линзы получают разные изображения предмета:
| Расположение предмета | Характеристика изображения в линзе | |
| собирающей | рассеивающей | |
За двойным фокусом линзы 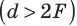 |
действительное, уменьшенное, перевернутое | мнимое, уменьшенное, прямое |
В двойном фокусе линзы 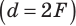 |
действительное, равное, перевернутое | |
Между фокусом и двойным фокусом линзы 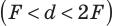 |
действительное, увеличенное, перевернутое | |
В фокусе линзы 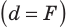 |
изображения нет | |
Между линзой и фокусом 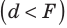 |
мнимое, увеличенное, прямое |
Расстояние 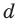 от предмета до линзы, расстояние
от предмета до линзы, расстояние 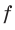 от линзы до изображения и фокусное расстояние
от линзы до изображения и фокусное расстояние 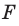 связаны формулой тонкой линзы:
связаны формулой тонкой линзы: 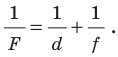
- Глаз как оптическая система
- Звук в физике и его характеристики
- Звуковые и ультразвуковые колебания
- Инерция в физике
- Дифракция света
- Принцип Гюйгенса — Френеля
- Прохождение света через плоскопараллельные пластинки и призмы
- Поляризация света
Линза – это прозрачный оптический компонент, используемый для фокусировки или дефокусировки излучения, излучаемого периферийным объектом. Световые лучи, прошедшие линзу, формируют действительное или мнимое изображение.
Изображения, формируемые линзами, возникают из-за преломления света. Выпуклая линза еще называется собирающей или положительной. Она фокусирует лучи, исходящие от точечного объекта, в определенной точке; следовательно, сформированное изображение считается действительным.
Двояковыпуклая линза – это линза с двумя выпуклыми поверхностями, оптические центры которых совпадают.
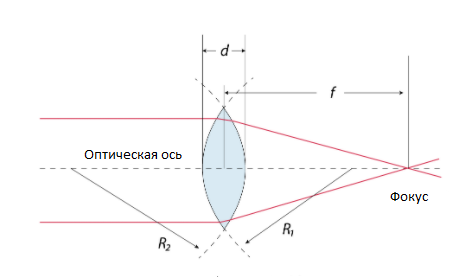
Рисунок 1 – Схема ДВЛ
Когда излучение попадает на края линзы, оптические лучи становятся параллельны друг другу.
Типы линз
По кривизне двух оптических плоскостей линзы бывают двух типов: двояковыпуклые, выпукло-вогнутые
и с одной плоской стороной. Элемент является двояковыпуклым, если обе плоскости выпуклые.
Двояковыпуклые линзы (ДВЛ) применяются как увеличительные или конденсирующие компоненты. Они также находят применение во многих системах формирования изображений, таких как телескопы, монокуляры, микроскопы, бинокли, камеры, проекторы и т. д.
ДВЛ представляют собой простые симметричные элементы, которые содержат две выпуклые линзы со сферической формой, каждая из которых имеет одинаковый радиус кривизны (см. рис 1).
Формула ДВЛ
Для расчета фокусного расстояния сферической линзы можно применить уравнение для толстой линзы, приведенное ниже. В этом выражении n – показатель преломления материала, R1 и R2 – радиусы кривизны, а d – толщина.
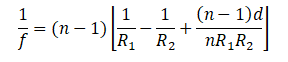
Для двояковыпуклых линз, у которых передний и задний радиусы кривизны равны по величине и противоположны по знаку, R1 = -R2 = R, имеем

Типовые материалы и параметры линз
BK7, вероятно, представляет собой наиболее распространенное оптическое стекло, из которого производят высококачественные оптические компоненты видимого и ближнего инфракрасного диапазона. Его обычно выбирают всякий раз, когда дополнительные преимущества УФ плавленого кварца (то есть хорошее пропускание в УФ и более низкий коэффициент теплового расширения) не являются необходимыми. Его высокая однородность, низкое содержание пузырьков и включений, а также простота изготовления делают его хорошим выбором для пропускающей оптики. BK7 также относительно твердый материал, он показывает хорошую устойчивость к царапинам.
CaF2 обычно используется для приложений, требующих высокого пропускания в инфракрасном и ультрафиолетовом спектральных диапазонах. Его чрезвычайно высокий порог лазерного повреждения делает CaF2 полезным для использования с эксимерными лазерами. Материал демонстрирует низкий показатель преломления, варьирующийся от 1,35 до 1,51 в диапазоне его использования от 180 нм до 8,0 мкм. Фторид кальция также довольно химически инертен и обладает превосходной твердостью.
Линзы из ZnSe особенно хорошо подходят для использования с мощными CO2-лазерами.
|
Материал
|
|
|
BK7 |
350 нм – 2.0 мкм |
|
УФ Плавленый кварц |
185 нм – 2.1 мкм |
|
CaF2 |
0.18 – 8.0 мкм |
|
ZnSe |
0.6 – 21.0 мкм, обычно используется AR покрытие 7 мкм – 12 мкм |
Так как данные оптические элементы применяются в высокоточных оптических установках, необходимо тщательно подбирать изделие под конкретную задачу, ориентируясь на допуски.
- Допуск диаметра: критический механический допуск, который необходимо учитывать при установке оптики. Отклонения от номинального диаметра могут помешать правильной посадке линз в их монтажном приспособлении, что приведет к децентрализации или наклону внутри оптического узла.
- Центрирование: точное выравнивание оптической оси гарантирует, что линзы могут использоваться в сложных приложениях для обработки изображений. В сочетании с упомянутыми выше прецизионными допусками на диаметр, строгие допуски на центровку обеспечивают минимальное биение изображения в оптической сборке.
- Качество поверхности: даже незначительные царапины или ямки на оптической плоскости элемента могут привести к рассеянию лучей, что может быть вредным для лазерных приложений. Данный параметр также влияет на порог лазерного повреждения. Объективы с плохим допуском на данный параметр могут выйти из строя при воздействии излучения даже средней мощности. Царапины и углубления на линзе также могут привести к тому, что лазерный свет будет рассеиваться взад и вперед, разрушая покрытие.
Пример важности допусков
В расширителях луча ошибки центрирования могут привести к дрейфу луча, в результате чего выходной луч не параллелен входному лучу. Дрейф луча усложняет юстировку лазерных систем, поскольку требует наклона механического корпуса для компенсации несоосности входной и выходной осей.
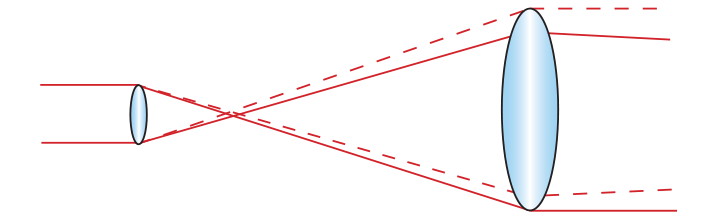
Рисунок 2 – Влияние ошибок центрирования на расширитель луча
Типичные характеристики линз приведены в таблице ниже.
|
Параметр
|
|
|
Неравномерность поверхности |
λ/4 |
|
Качество поверхности |
40-20 S-D |
|
Допуск на толщину |
±0.1 мм |
|
Допуск на диаметр |
+0.0 / -0.1 мм |
|
Центровка |
<3 угловых минут |
|
Световой диаметр |
>90% от диаметра линзы |
|
Допуск на фокусное расстояние |
±1% |
Многие линзы имеют антиотражающие покрытия на своих плоскостях, которые существенно уменьшают отражения, вызванные изменением показателя преломления. Обратите внимание, однако, что это работает только в ограниченном диапазоне длин волн. Существует компромисс между сильным подавлением отражений и широкой полосой пропускания.
ДВЛ работают лучше всего, когда объект и изображение находятся на противоположных сторонах линзы, а отношение объекта к расстоянию до изображения (сопряженное соотношение) составляет от 0,2 до 5.
ДВЛ исправляют следующие проблемы, возникающие в оптических системах:
- Кома
- Искажение
- Хроматические и сферические аберрации
Благодаря своим особенностям, ДВЛ применяются для фокусировки лучей в объективах и конденсорах. Они обеспечивают меньший фокус по сравнению с аналогичными плоско-выпуклыми линзами. ДВЛ также применяются как расширители пучка и в комбинациях с другими оптическими элементами в проекционных системах.
Применение
Ниже приведены самые распространенные сферы использования ДВЛ:
- в очках
У человека могут быть такие проблемы, как дальнозоркость или близорукость, поскольку хрусталик глаза не может правильно фокусировать лучи на сетчатке. У человека, страдающего дальнозоркостью, изображение, формируемое хрусталиком, находится далеко за сетчаткой. ДВЛ, установленная перед глазом, может скорректировать эту проблему. Она уменьшает длину фокусировки, и излучение должным образом фокусируется на сетчатке.
- в фотоаппаратах
В фотоаппаратах ДВЛ используется для фокусировки на изображении, а также для увеличения изображения объекта. Кроме того, объектив камеры состоит из комбинации выпуклой и вогнутой линз, за которыми следует вторая выпуклая линза.
- в микроскопах
В микроскопе ДВЛ увеличивают изображения. Микроскопы создают увеличенные изображения очень маленьких объектов, для этого очень полезны выпуклые линзы. Более того, простые микроскопы в большинстве своем состоят из трех линз.
У этого термина существуют и другие значения, см. Линза (значения).
![]()
Ли́нза (нем. Linse, от лат. lens — чечевица) — деталь из прозрачного однородного материала , имеющая две преломляющие полированные поверхности, например, обе сферические или же одну плоскую, а другую — сферическую. В настоящее время всё чаще применяются и «асферические линзы», форма поверхности которых отличается от сферы. В качестве материала линз обычно используются оптические материалы, такие как стекло, оптическое стекло, кристаллы, оптически прозрачные пластмассы и другие материалы[1].
Термин «линза» используют также применительно к другим приборам и явлениям, действие которых на излучение подобно действию линзы, например:
- плоские «линзы», изготовленные из материала с переменным показателем преломления, изменяющимся в зависимости от расстояния от центра;
- линзы Френеля;
- зонная пластинка Френеля, использующая явление дифракции;
- «линзы» воздуха в атмосфере — неоднородность свойств, в частности показателя преломления (проявляется в виде мерцания изображения звёзд в ночном небе);
- гравитационная линза — наблюдаемый на межгалактических расстояниях эффект отклонения электромагнитных волн массивными объектами;
- магнитная линза — устройство, использующее постоянное магнитное поле для фокусирования пучка заряженных частиц (ионов или электронов) и применяющееся в электронных и ионных микроскопах;
- изображение линзы, сформированное оптической системой или частью оптической системы. Используется при расчёте сложных оптических систем.
История[править | править код]
Свет преломляется сферическим стеклянным сосудом, наполненным водой. Роджер Бэкон, XIII век

Объектив для LSST, планируемого телескопа для обзора неба
Слово линза происходит от lēns, латинского названия чечевицы, потому что двояковыпуклая линза имеет форму чечевицы. Линзой также называется геометрическая фигура[2].
Некоторые учёные утверждают, что археологические свидетельства указывают на широкое использование линз в древности на протяжении нескольких тысячелетий[3]. Так называемая линза Нимруда — артефакт из горного хрусталя, датируемый VIII веком (750—710 гг.) до нашей эры, который, возможно, использовался в качестве увеличительного или зажигательного стекла либо предназначался для других целей[4][5][6]. Другие предположили, что некоторые египетские иероглифы изображают «простые стеклянные менисковые линзы»[7].
Самый древний литературный источник, в котором упоминается об использовании линз, а именно зажигательного стекла, — пьеса Аристофана «Облака» (424 г. до н. э.)[8]. Плиний Старший (I век н. э.) подтверждает, что зажигательные стёкла были известны в античности, а именно в римский период[9]. В работах Плиния содержится также самая ранняя из известных ссылок на использование корректирующих линз: он упоминает, что Нерон, как говорят, смотрел гладиаторские игры, используя изумруд (предположительно вогнутый, чтобы исправить близорукость, хотя отсылка не точна)[10]. И Плиний, и Сенека Младший (3 г. до н. э. — 65 г. н. э.) описали увеличивающий эффект стеклянного шара, наполненного водой.
Птолемей (II век) написал книгу по оптике, которая, однако, сохранилась только в латинском переводе с неполного и очень плохого арабского перевода. Однако книга была принята средневековыми учёными в исламском мире и прокомментирована Ибн Салом (X век), чей вклад, в свою очередь, был улучшен Альхазеном (Книга об оптике, XI век). Арабский перевод Оптики Птолемея стал доступен в латинском переводе в XII веке (Евгений Палермский, 1154 г.). Между XI и XIII веками были изобретены «камни для чтения». Это были примитивные плоско-выпуклые линзы, изначально сделанные путем разрезания стеклянной сферы пополам. Средневековые (XI или XII век) линзы Висбю из горного хрусталя могли быть предназначены для использования в качестве зажигательных стёкол, однако возможно, что их изготовили для каких -то иных целей[11].
Очки были изобретены как усовершенствование «камней для чтения» периода Высокого Средневековья в Северной Италии во второй половине XIII века[12]. Это стало началом развития оптической индустрии шлифовки и полировки линз для очков — сначала в Венеции и Флоренции в конце XIII века[13], а затем в центрах производства очков в Нидерландах и Германии[14]. Создатели очков сделали улучшенные типы линз для коррекции зрения, основанные больше на эмпирических знаниях, полученных при наблюдении за эффектами линз (вероятно, без знания элементарной оптической теории того времени)[15][16]. Практические разработки и эксперименты с линзами привели к изобретению составного оптического микроскопа около 1595 года и телескопа-рефрактора в 1608 году — и тот и другой появились в центрах изготовления очков в Нидерландах[17][18].
С изобретением телескопа в XVII веке и микроскопа в начале XVIII было проведено множество экспериментов с формами линз в стремлении исправить наблюдаемые в последних хроматические ошибки. Оптики пытались конструировать линзы различной формы кривизны, ошибочно полагая, что ошибки возникли из-за дефектов сферической формы их поверхностей[19]. Оптическая теория преломления и эксперименты показали, что ни один одноэлементный объектив не может сфокусировать все цвета. Это привело к изобретению составной ахроматической линзы Честером Муром Холлом в Англии в 1733 году, изобретение также было заявлено англичанином Джоном Доллондом в патенте 1758 года.

Растение, видимое через двояковыпуклую линзу
Характеристики простых линз[править | править код]
В зависимости от форм различают собирающие (положительные) и рассеивающие (отрицательные) линзы. К группе собирающих линз обычно относят линзы, у которых середина толще их краёв, а к группе рассеивающих — линзы, края которых толще середины. Следует отметить, что это верно только если показатель преломления у материала линзы больше, чем у окружающей среды. Если показатель преломления линзы меньше, ситуация будет обратной. Например пузырёк воздуха в воде — двояковыпуклая рассеивающая линза.
Линзы характеризуются, как правило, своей оптической силой (измеряется в диоптриях), и фокусным расстоянием.
Для построения оптических приборов с исправленной оптической аберрацией (прежде всего — хроматической, обусловленной дисперсией света, — ахроматы и апохроматы) важны и иные свойства линз и их материалов, например, показатель преломления, коэффициент дисперсии, показатель поглощения и показатель рассеяния материала в выбранном оптическом диапазоне.
Иногда линзы/линзовые оптические системы (рефракторы) специально рассчитываются на использование в средах с относительно высоким показателем преломления (см. иммерсионный микроскоп, иммерсионные жидкости).
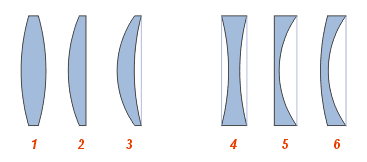
Виды линз: собирающие: 1 — двояковыпуклая; 2 — плоско-выпуклая; 3 — вогнуто-выпуклая (положительный (выпуклый) мениск); рассеивающие: 4 — двояковогнутая; 5 — плоско-вогнутая; 6 — выпукло-вогнутая (отрицательный (вогнутый) мениск)

Использование линзы для изменения формы волнового фронта. Здесь плоский волновой фронт становится сферическим при прохождении через линзу
Выпукло-вогнутая линза называется мениском и может быть собирательной (утолщается к середине), рассеивающей (утолщается к краям) или телескопической (фокусное расстояние равно бесконечности). Так, например линзы очков для близоруких — как правило, отрицательные мениски.
Вопреки распространённому заблуждению, оптическая сила мениска с одинаковыми радиусами не равна нулю, а положительна, и зависит от показателя преломления стекла и от толщины линзы. Мениск, центры кривизны поверхностей которого находятся в одной точке называется концентрической линзой (оптическая сила всегда отрицательна).
Отличительным свойством собирательной линзы является способность собирать падающие на её поверхность лучи в одной точке, расположенной по другую сторону линзы.
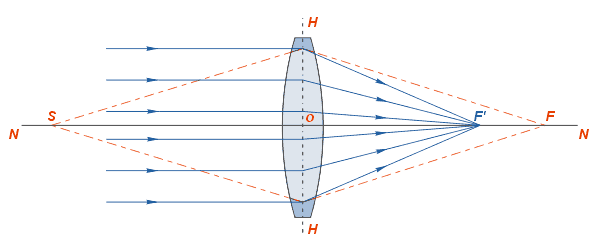
Основные элементы линзы: NN — оптическая ось — прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу; O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре)[20].
Если на некотором расстоянии перед собирательной линзой поместить светящуюся точку S, то луч света, направленный по оси, пройдёт через линзу не преломившись, а лучи, проходящие не через центр, будут преломляться в сторону оптической оси и пересекутся на ней в некоторой точке F, которая и будет изображением точки S. Эта точка носит название сопряжённого фокуса, или просто фокуса.
Если на линзу будет падать свет от очень удалённого источника, лучи которого можно представить идущими параллельным пучком, то на выходе из неё лучи преломляются под бо́льшим углом, и точка F переместится на оптической оси ближе к линзе. При данных условиях точка пересечения лучей, вышедших из линзы, называется фокусом F’, а расстояние от центра линзы до фокуса — фокусным расстоянием.
Лучи, падающие на рассеивающую линзу, на выходе из неё будут преломляться в сторону краёв линзы, то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая и будет фокусом этой линзы. Этот фокус будет мнимым.
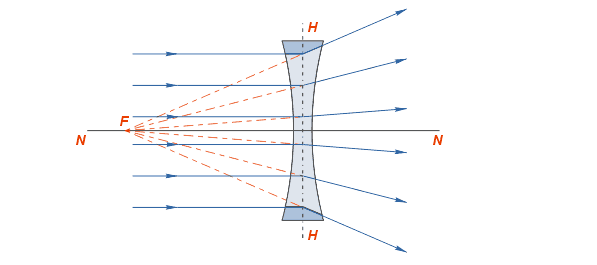
Мнимый фокус рассеивающей линзы

Сходящиеся лучи слева от линзы являются лучами, отраженными от поверхности линзы, и не связаны с положением мнимого фокуса
Сказанное о фокусе на оптической оси в равной степени относится и к тем случаям, когда изображение точки находится на наклонной линии, проходящей через центр линзы под углом к оптической оси. Плоскость, перпендикулярная оптической оси, расположенная в фокусе линзы, называется фокальной плоскостью.
Собирающие линзы могут быть направлены к предмету любой стороной, вследствие чего лучи при прохождении через линзу могут собираться как с одной, так и с другой её стороны. Таким образом, линза имеет два фокуса — передний и задний. Расположены они на оптической оси по обе стороны линзы на фокусном расстоянии от главных точек линзы.
Часто в технике применяется понятие увеличение линзы (лупы) и обозначается как 2×, 3× и т. д. В данном случае увеличение определяется по формуле 


Ход лучей в тонкой линзе[править | править код]
Линза, для которой толщина принята равной нулю, в оптике называется «тонкой». Для такой линзы показывают не две главных плоскости, а одну, в которой как бы сливаются вместе передняя и задняя.
Рассмотрим построение хода луча произвольного направления в тонкой собирающей линзе. Для этого воспользуемся двумя свойствами тонкой линзы:
- луч, прошедший через оптический центр линзы, не меняет своего направления;
- параллельные лучи, проходящие через линзу, сходятся в фокальной плоскости.

Рассмотрим луч SA произвольного направления, падающий на линзу в точке A. Построим линию его распространения после преломления в линзе. Для этого построим луч OB, параллельный SA и проходящий через оптический центр O линзы. По первому свойству линзы луч OB не изменит своего направления и пересечёт фокальную плоскость в точке B. По второму свойству линзы параллельный ему луч SA после преломления должен пересечь фокальную плоскость в той же точке. Таким образом, после прохождения через линзу луч SA пойдёт по пути AB.
Аналогичным образом можно построить другие лучи, например луч SPQ.
Обозначим расстояние SO от линзы до источника света через u, расстояние OD от линзы до точки фокусировки лучей через v, фокусное расстояние OF через f. Выведем формулу, связывающую эти величины.
Рассмотрим две пары подобных треугольников: 



Разделив первую пропорцию на вторую, получим
После деления обеих частей выражения на v и перегруппировки членов, приходим к окончательной формуле
где 
Ход лучей в системе линз[править | править код]
Ход лучей в системе линз строится теми же методами, что и для одиночной линзы.
Рассмотрим систему из двух линз, одна из которых имеет фокусное расстояние OF, а вторая O2F2. Строим путь SAB для первой линзы и продолжаем отрезок AB до вхождения во вторую линзу в точке C.

Из точки O2 строим луч O2E, параллельный AB. При пересечении с фокальной плоскостью второй линзы этот луч даст точку E. Согласно второму свойству тонкой линзы луч AB после прохождения через вторую линзу пойдёт по пути CE. Пересечение этой линии с оптической осью второй линзы даст точку D, где сфокусируются все лучи, вышедшие из источника S и прошедшие через обе линзы.
Построение изображения тонкой собирающей линзой[править | править код]
При изложении характеристики линз был рассмотрен принцип построения изображения светящейся точки в фокусе линзы. Лучи, падающие на линзу слева, проходят через её задний фокус, а падающие справа — через передний фокус. Следует учесть, что у рассеивающих линз, наоборот, задний фокус расположен спереди линзы, а передний позади.

Построение линзой изображения предметов, имеющих определённую форму и размеры, получается следующим образом: допустим, линия AB представляет собой объект, находящийся на некотором расстоянии от линзы, значительно превышающем её фокусное расстояние. От каждой точки предмета через линзу пройдёт бесчисленное количество лучей, из которых, для наглядности, на рисунке схематически изображён ход только трёх лучей.
Три луча, исходящие из точки A, пройдут через линзу и пересекутся в соответствующих точках схода на A1B1, образуя изображение. Полученное изображение является действительным и перевёрнутым.
В данном случае изображение получено в сопряжённом фокусе в некоторой фокальной плоскости FF, несколько удалённой от главной фокальной плоскости F’F’, проходящей параллельно ей через главный фокус.
Далее приведены различные случаи построения изображений предмета, помещённого на различных расстояниях от линзы.
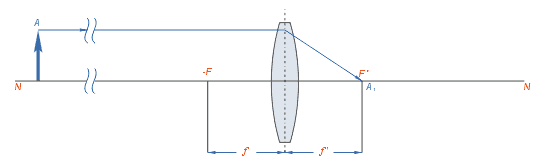
Если предмет находится на бесконечно далёком от линзы расстоянии, то его изображение получается в заднем фокусе линзы F’ действительным, перевёрнутым и уменьшенным до подобия точки.
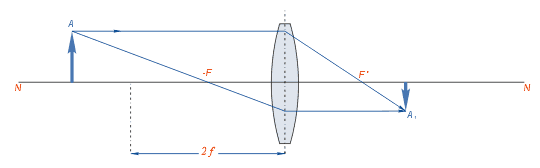
Если предмет приближён к линзе и находится на расстоянии, превышающем двойное фокусное расстояние линзы, то изображение его будет действительным, перевёрнутым и уменьшенным и расположится за главным фокусом на отрезке между ним и двойным фокусным расстоянием.
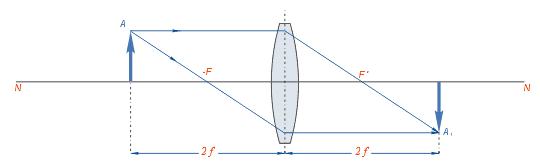
Если предмет помещён на двойном фокусном расстоянии от линзы, то полученное изображение находится по другую сторону линзы на двойном фокусном расстоянии от неё. Изображение получается действительным, перевёрнутым и равным по величине предмету.

Если предмет помещён между передним фокусом и двойным фокусным расстоянием, то изображение будет получено за двойным фокусным расстоянием и будет действительным, перевёрнутым и увеличенным.
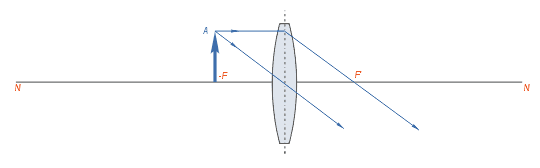
Если предмет находится в плоскости переднего главного фокуса линзы, то лучи, пройдя через линзу, пойдут параллельно, и изображение может получиться лишь в бесконечности.
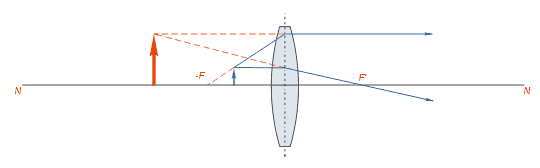
Если предмет поместить на расстоянии, меньшем главного фокусного расстояния, то лучи выйдут из линзы расходящимся пучком, нигде не пересекаясь. Изображение при этом получается мнимое, прямое и увеличенное, то есть в данном случае линза работает как лупа.
Нетрудно заметить, что при приближении предмета из бесконечности к переднему фокусу линзы изображение удаляется от заднего фокуса и по достижении предметом плоскости переднего фокуса оказывается в бесконечности от него.
Эта закономерность имеет большое значение в практике различных видов фотографических работ, поэтому для определения зависимости между расстоянием от предмета до линзы и от линзы до плоскости изображения необходимо знать основную формулу линзы.
Формула тонкой линзы[править | править код]
Расстояния от точки предмета до центра линзы и от точки изображения до центра линзы называются сопряжёнными фокусными расстояниями.

Эти величины находятся в зависимости между собой и определяются формулой, называемой формулой тонкой линзы (впервые полученной Исааком Барроу):
где 


Для нахождения той или иной неизвестной величины при двух известных пользуются следующими уравнениями:
Следует отметить, что знаки величин 



Изображения чёрных букв через тонкую выпуклую линзу с фокусным расстоянием f (красным цветом). Показаны лучи для букв E, I и K (синим, зелёным и оранжевым соответственно). Изображение буквы E (находящейся на расстоянии 2f) действительное и перевернутое, такого же размера. Изображение I (на f) — в бесконечности. Изображение К (на f/2) мнимое, прямое, увеличенное в 2 раза
Линейное увеличение[править | править код]
Линейным увеличением 



Здесь 
В практике вычислений гораздо удобнее это соотношение выражать в значениях 



Расчёт фокусного расстояния и оптической силы линзы[править | править код]
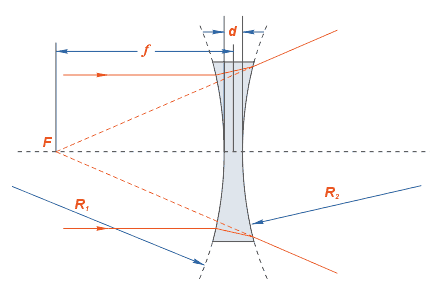
Значение фокусного расстояния для линзы может быть рассчитано по следующей формуле:
, где





Для 


Эту формулу также называют формулой тонкой линзы. Величина фокусного расстояния положительна для собирающих линз, и отрицательна для рассеивающих. Величина 

Указанные формулы могут быть получены аккуратным рассмотрением процесса построения изображения в линзе с использованием закона Снелла, если перейти от общих тригонометрических формул к параксиальному приближению. Кроме того, для вывода формулы тонкой линзы удобно заменить её треугольной призмой и затем использовать формулу угла отклонения этой призмы[23].
Линзы симметричны, то есть они имеют одинаковое фокусное расстояние независимо от направления света — слева или справа, что, однако, не относится к другим характеристикам, например, аберрациям, величина которых зависит от того, какой стороной линза повёрнута к свету.
Комбинация нескольких линз (центрированная система)[править | править код]
Линзы могут комбинироваться друг с другом для построения сложных оптических систем. Оптическая сила системы из двух линз может быть найдена как простая сумма оптических сил каждой линзы (при условии, что обе линзы можно считать тонкими и они расположены вплотную друг к другу на одной оси):
.
Если линзы расположены на некотором расстоянии друг от друга и их оси совпадают (система из произвольного числа линз, обладающих таким свойством, называется центрированной системой), то их общую оптическую силу с достаточной степенью точности можно найти из следующего выражения:
,
где 
Недостатки простой линзы[править | править код]
В современных оптических приборах к качеству изображения предъявляются высокие требования.
Изображение, даваемое простой линзой, в силу целого ряда недостатков не удовлетворяет этим требованиям. Устранение большинства недостатков достигается соответствующим подбором ряда линз в центрированную оптическую систему — объектив. Недостатки оптических систем называются аберрациями, которые делятся на следующие виды:
- геометрические аберрации:
- сферическая аберрация;
- кома;
- астигматизм;
- дисторсия;
- кривизна поля изображения;
- хроматическая аберрация;
- дифракционная аберрация (эта аберрация вызывается другими элементами оптической системы, и к самой линзе отношения не имеет).
Линзы со специальными свойствами[править | править код]
Линзы из органических полимеров[править | править код]
Полимеры дают возможность создавать недорогие асферические линзы с помощью литья.
В области офтальмологии созданы мягкие контактные линзы. Их производство основано на применении материалов, имеющих бифазную природу, сочетающих фрагменты кремний-органического или кремний-фторорганического полимера силикона и гидрофильного полимера гидрогеля. Работа в течение более 20 лет привела к созданию в конце 1990-х годов силикон-гидрогелевых линз, которые благодаря сочетанию гидрофильных свойств и высокой кислородопроницаемости могут непрерывно использоваться в течение 30 дней круглосуточно.[24]
Линзы из кварцевого стекла[править | править код]
Кварцевое стекло — однокомпонентное стекло, состоящее из диоксида кремния, с незначительным (около 0,01 % и меньше) содержанием примесей Al2О3, СаО и MgO. Оно отличается высокой термостойкостью и инертностью ко многим химическим реактивам за исключением плавиковой кислоты.
Прозрачное кварцевое стекло хорошо пропускает ультрафиолетовые и видимые лучи света.
Линзы из кремния[править | править код]
Кремний хорошо пропускает инфракрасное излучение с длинами волн от 1 до 9 мкм, имеет большой показатель преломления (n = 3,42 при 
Кроме того, свойства кремния и современные технологии его обработки позволяют создать линзы для рентгеновского диапазона электромагнитных волн[26].
Просветлённые линзы[править | править код]
Путём нанесения на поверхность линзы многослойных диэлектрических покрытий можно добиться значительного уменьшения отражения света и, вследствие этого, увеличения коэффициента пропускания.Такие линзы легко узнать по фиолетовым бликам: они не отражают зелёный цвет, отражая красный и синий, что в сумме даёт фиолетовый. Подавляющее большинство линз для фототехники производства СССР, в том числе для бытовых объективов, изготавливалось просветлёнными.
Применение линз[править | править код]
Линзы являются широко распространённым оптическим элементом большинства оптических систем.
Традиционное применение линз — бинокли, телескопы, оптические прицелы, теодолиты, микроскопы, фото- и видеотехника. Одиночные собирающие линзы используются как увеличительные стёкла.
Другая важная сфера применения линз — офтальмология, где без них невозможно исправление недостатков зрения — близорукости, дальнозоркости, неправильной аккомодации, астигматизма и других заболеваний. Линзы используют в таких приспособлениях, как очки и контактные линзы. Также существует подвид линз, ночные линзы. Они имеют более жесткую основу и используются исключительно во время сна, для временной коррекции зрения в дневное время.
В радиоастрономии и радарах часто используются диэлектрические линзы, собирающие поток радиоволн в приёмную антенну, либо фокусирующие их на цели.
В конструкции плутониевых ядерных бомб для преобразования сферической расходящейся ударной волны от точечного источника (детонатора) в сферическую сходящуюся, применялись линзовые системы, изготовленные из взрывчатки с разной скоростью детонации (то есть с разным показателем преломления).
См. также[править | править код]
- Лентикулярный растр
- Линза Френеля
- Линза Люнеберга
- Билинза Бийе
- Цейс, Карл
- Контактные линзы
- Лупа
- Магнитная линза
- Фокус (физика)
- Оптические системы
- Оптические приборы
- Оптические материалы
- Аберрации оптических систем
Примечания[править | править код]
- ↑ Ананьев Ю. А. Линза // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 591—592. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ The variant spelling lense is sometimes seen. While it is listed as an alternative spelling in some dictionaries, most mainstream dictionaries do not list it as acceptable.
- ↑ Sines, George (1987). “Lenses in antiquity”. American Journal of Archaeology. 91 (2): 191—196. DOI:10.2307/505216.
- ↑ Whitehouse. World’s oldest telescope?, BBC News (1 July 1999). Архивировано 1 февраля 2009 года. Дата обращения: 10 мая 2008.
- ↑ The Nimrud lens/The Layard lens. Collection database. The British Museum. Дата обращения: 25 ноября 2012. Архивировано 19 октября 2012 года.
- ↑ D. Brewster. On an account of a rock-crystal lens and decomposed glass found in Niniveh // Die Fortschritte der Physik : [нем.]. — Deutsche Physikalische Gesellschaft, 1852. — P. 355.
- ↑ Kriss, Timothy C. (April 1998). “History of the Operating Microscope: From Magnifying Glass to Microneurosurgery”. Neurosurgery. 42 (4): 899—907. DOI:10.1097/00006123-199804000-00116. PMID 9574655.
- ↑ Aristophanes. The Clouds. — Project Gutenberg, 22 Jan 2013. — ISBN EBook #2562.
- ↑ Pliny the Elder, The Natural History (trans. John Bostock) Book XXXVII, Chap. 10 Архивная копия от 4 октября 2008 на Wayback Machine.
- ↑ Pliny the Elder, The Natural History (trans. John Bostock) Book XXXVII, Chap. 16 Архивная копия от 28 сентября 2008 на Wayback Machine
- ↑ Tilton, Buck. [[1] в «Книгах Google» The Complete Book of Fire: Building Campfires for Warmth, Light, Cooking, and Survival]. — Menasha Ridge Press, 2005. — P. 25. — ISBN 978-0-89732-633-9.
- ↑ Glick, Thomas F. [[2] в «Книгах Google» Medieval science, technology, and medicine: an encyclopedia]. — Routledge, 2005. — P. 167. — ISBN 978-0-415-96930-7.
- ↑ Al Van Helden. The Galileo Project > Science > The Telescope Архивная копия от 3 августа 2017 на Wayback Machine. Galileo.rice.edu. Retrieved on 6 June 2012.
- ↑ Henry C. King. [[3] в «Книгах Google» The History of the Telescope]. — Courier Dover Publications. — P. 27. — ISBN 978-0-486-43265-6.
- ↑ Paul S. Agutter. [[4] в «Книгах Google» Thinking about Life: The History and Philosophy of Biology and Other Sciences]. — Springer. — P. 17. — ISBN 978-1-4020-8865-0.
- ↑ Vincent Ilardi. [[5] в «Книгах Google» Renaissance Vision from Spectacles to Telescopes]. — American Philosophical Society, 2007. — P. 210. — ISBN 978-0-87169-259-7.
- ↑ Microscopes: Time Line Архивная копия от 9 января 2010 на Wayback Machine, Nobel Foundation. Retrieved 3 April 2009
- ↑ Fred Watson. [[6] в «Книгах Google» Stargazer: The Life and Times of the Telescope]. — Allen & Unwin. — P. 55. — ISBN 978-1-74175-383-7.
- ↑ This paragraph is adapted from the 1888 edition of the Encyclopædia Britannica.
- ↑ Ход лучей показан, как в идеализированной (тонкой) линзе, без указания на преломление на реальной границе раздела сред. Дополнительно показан несколько утрированный образ двояковыпуклой линзы.
- ↑ Хендель А. Основные законы физики. — М.: Физматгиз, 1959. — 284 с. Архивировано 21 января 2015 года.
- ↑ [psychology_pedagogy.academic.ru/14495/РАССТОЯНИЕ_НАИЛУЧШЕГО_ЗРЕНИЯ Расстояние наилучшего зрения на academic.ru]
- ↑ Ландсберг Г.С. §88. Преломление в линзе. Фокусы линзы // Элементарный учебник физики. — 13-е изд. — М.: Физматлит, 2003. — Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика. — С. 236—242. — 656 с. — ISBN 5922103512.
- ↑ Наука в Сибири. Дата обращения: 15 ноября 2007. Архивировано 20 января 2009 года.
- ↑ Физическая энциклопедия. В 5-ти томах. / А. М. Прохоров. — М.: Советская энциклопедия, 1988.
- ↑ Аристов В. В., Шабельников Л. Г. Современные достижения рентгеновской оптики преломления // УФН. — 2008. — Т. 178. — С. 61–83. — doi:10.3367/UFNr.0178.200801c.0061.
Литература[править | править код]
- Краткий фотографический справочник / Под общей редакцией д.т.н. В. В. Пуськова. — 2-е изд. — М.: Искусство, 1953.
- Ландсберг Г. С. Оптика. — 5-ое изд. — М.: Наука, 1976.
- Политехнический словарь / глав. ред. А. Ю. Ишлинский. — 3-е изд. — М.: Советская Энциклопедия, 1989.
- Линза // Фотокинотехника: Энциклопедия / Гл. ред. Е. А. Иофис. — М.: Советская энциклопедия, 1981. — 447 с.
Ссылки[править | править код]
- Как изготавливаются линзы для фотоаппаратов и видеокамер. Discovery (видео)
{{спам-ссылки|1=
- psychology_pedagogy.academic.ru
|2=1}











