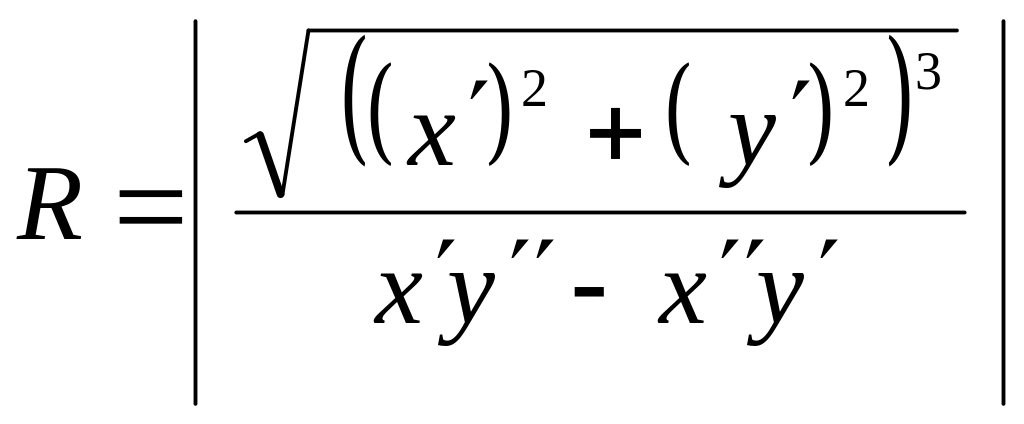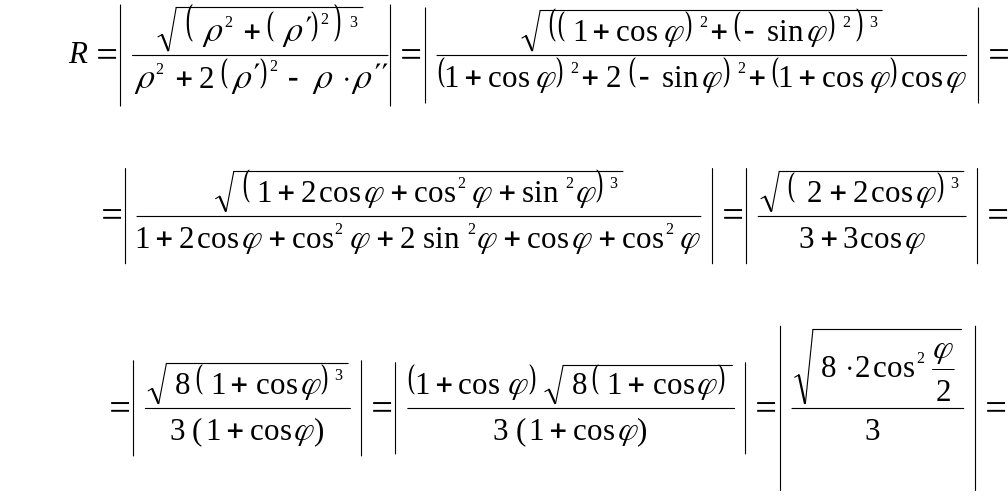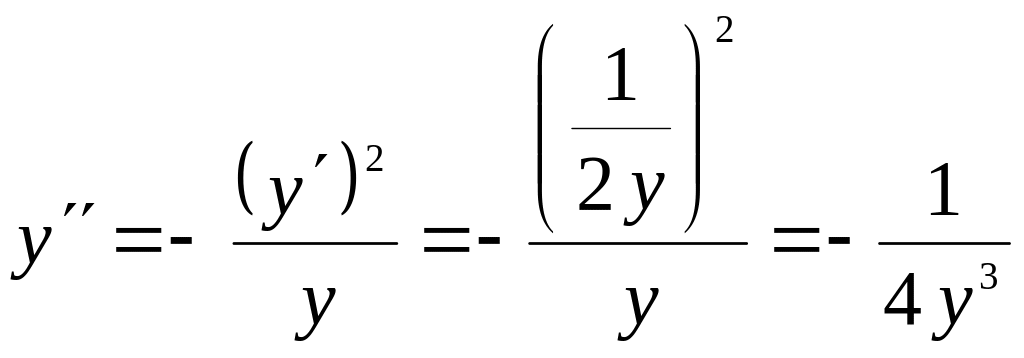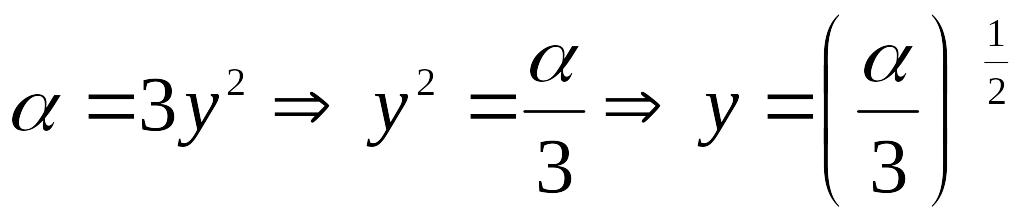Как найти радиус кривизны функции в точке

Радиус, центр и круг кривизны. Эволюта и эвольвента

Радиусом
кривизны называется величина, обратная
кривизне, т. е.

.

Если
плоская кривая отнесена к прямоугольной
системе координат и задана уравнением

,
то радиус кривизны

выражается формулой

Eсли
плоская кривая отнесена к прямоугольной
системе координат и задана параметрически
системой уравнений

, то радиус кривизны

выражается формулой

где

,

,

Если
плоская кривая отнесена к полярной
системе координат и задана уравнением

,
то радиус кривизны

выражается формулой

где

Окружностью
кривизны данной линии её точке А
называется
предельное положение окружности,
проходящей через три точки A,
B,
C
кривой, когда

и

.

Радиус
окружности кривизны равен радиусу
кривизны. Центр окружности кривизны
называется центром кривизны и находится
на нормали к линии, проведенной в точке
А
в сторону вогнутости этой линии.

Координаты

и

центра кривизны линии

вычисляются по формулам:

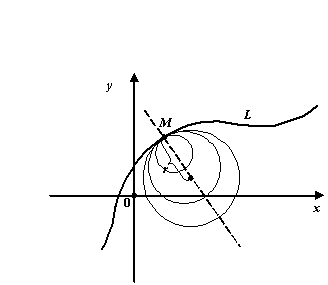
Эволютой
линии называется множество её центров
кривизны, а сама линия относительно
своей эволюты называется эвольвентой.

Формулы
для координат центра кривизны можно
рассматривать как параметрические
уравнения эволюты, где параметром
является абсцисса х
исходной линии.

Данная
линия может иметь лишь одну эволюту, но
у данной эволюты существует бесконечное
множество эвольвент.

Пример.
Найти
радиус кривизны линии

в
точке с абсциссой

Решение.
Найдем значения производных первого и
второго порядков функции

в точке с абсциссой

Подставим
найденные значения

в
формулу

Следовательно,
радиус кривизны
линии

в
точке с абсциссой

Пример.
Найти
радиус кривизны линии

в
точке

.

Решение.
Дифференцируя по t,
получим

Вычислим
значения производных в
точке

Подставляя
найденные значения

в
формулу

имеем

Следовательно,
радиус кривизны
линии

в
точке с абсциссой

Пример.
Найти
радиус кривизны кардиоиды

в
любой её точке.

Решение.
Найдем

Подставим
найденные выражения в формулу

Следовательно,
радиус кривизны
кардиоиды

в
любой её точке

Пример.
Найти
координаты

центра кривизны линии

в
точке

.

Решение.
Найдем значения производных первого
и второго порядков функции

в точке с абсциссой

Подставим
значения

и найденные
значения

в
формулы

Следовательно,
координаты
центра кривизны линии

в
точке

Пример.
Составить
уравнение эволюты кривой

.

Решение.
Продифференцируем дважды уравнение
параболы:

;

Так
как

,
то

Найдем
координаты

центра кривизны линии ,
предварительно выразив х
из уравнения

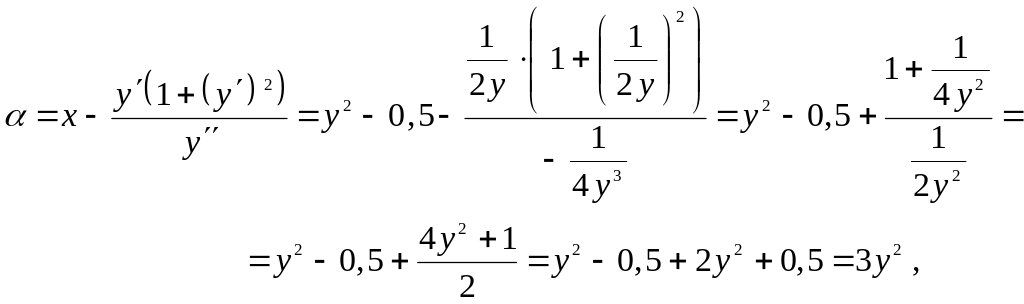
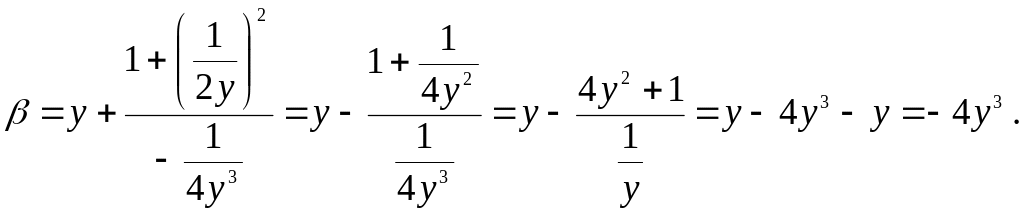
Имеем

–
уравнение эволюты в параметрической
форме. Выразим параметр у
из

и

;

Окончательно
получаем,

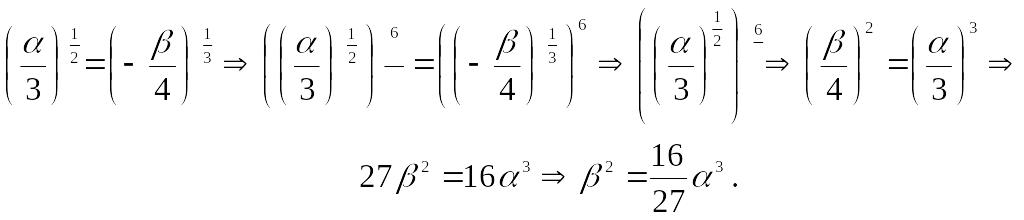
Следовательно,
уравнение
эволюты кривой

имеет вид

(уравнение
полукубической параболы).

Упражнения

1.
Найти радиус кривизны линии

в
точке A:

а)

,
A
(
2; 2 ), б)

,
A
(
0; 1 ) .

2.
Найти радиус кривизны трехлепестковой
розы

, при

.

3.
Найти координаты

центра кривизны линии

в
точке A:

а)

,
A
(
1; 1 ), б)

,
A
(
1; 0 ) .

4.
Составить уравнение эволюты кривой

а)

,
б)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как узнать радиус кривизны

Пусть задана функция, определенная уравнением y = f(x) и соответствующим графиком. Требуется найти радиус ее кривизны, то есть измерить степень искривленности графика этой функции в некоторой точке x0.

Инструкция

Кривизна любой линии определяется скоростью поворота ее касательной в точке x при движении этой точки по кривой. Поскольку тангенс угла наклона касательной равен значению производной от f(x) в этой точке, то скорость изменения этого угла должна зависеть от второй производной.

Эталоном кривизны логично принять окружность, поскольку она равномерно искривлена на всем своем протяжении. Радиус такой окружности есть мера ее кривизны.

По аналогии, радиусом кривизны заданной линии в точке x0 называется радиус окружности, которая наиболее точно измеряет степень ее искривленности в этой точке.

Требуемая окружность должна соприкасаться с заданной кривой в точке x0, то есть располагаться со стороны ее вогнутости так, чтобы касательная к кривой в этой точке была также и касательной к окружности. Это значит, что если F(x) — уравнение окружности, то должны выполняться равенства:

F(x0) = f(x0),
F′(x0) = f′(x0).

Таких окружностей, очевидно, существует бесконечно много. Но для измерения кривизны необходимо выбрать ту, которая наиболее точно соответствует заданной кривой в этой точке. Поскольку кривизна измеряется второй производной, то к этим двум равенствам необходимо добавить еще и третье:

F′′(x0) = f′′(x0).

Исходя из этих соотношений, радиус кривизны вычисляется по формуле:

R = ((1 + f′(x0)^2)^(3/2))/(|f′′(x0)|).

Величина, обратная радиусу кривизны, называется кривизной линии в данной точке.

Если f′′(x0) = 0, то радиус кривизны равен бесконечности, то есть линия в этой точке не искривлена. Это всегда верно для прямых, а также для любых линий в точках перегиба. Кривизна в таких точках, соответственно, равна нулю.

Центр окружности, измеряющей кривизну линии в заданной точке, называется центром кривизны. Линия, являющаяся геометрическим местом для всех центров кривизны заданной линии, называется ее эволютой.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

From Wikipedia, the free encyclopedia

This article is about the general mathematical concept. For its optical applications, see Radius of curvature (optics).

In differential geometry, the radius of curvature (Rc), R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.^[1]^[2]^[3]

Definition[edit]

In the case of a space curve, the radius of curvature is the length of the curvature vector.

In the case of a plane curve, then R is the absolute value of^[3]

${displaystyle Requiv left|{frac {ds}{dvarphi }}right|={frac {1}{kappa }},}$

where s is the arc length from a fixed point on the curve, φ is the tangential angle and κ is the curvature.

Formula[edit]

In 2D[edit]

If the curve is given in Cartesian coordinates as y(x), i.e., as the graph of a function, then the radius of curvature is (assuming the curve is differentiable up to order 2):

${displaystyle R=left|{frac {left(1+y'^{,2}right)^{frac {3}{2}}}{y''}}right|,qquad {mbox{where}}quad y'={frac {dy}{dx}},quad y''={frac {d^{2}y}{dx^{2}}},}$

and |z| denotes the absolute value of z.
Also in Classical mechanics branch of Physics Radius of curvature is given by (Net Velocity)²/Acceleration Perpendicular

If the curve is given parametrically by functions x(t) and y(t), then the radius of curvature is

${displaystyle R=left|{frac {ds}{dvarphi }}right|=left|{frac {left({{dot {x}}^{2}+{dot {y}}^{2}}right)^{frac {3}{2}}}{{dot {x}}{ddot {y}}-{dot {y}}{ddot {x}}}}right|,qquad {mbox{where}}quad {dot {x}}={frac {dx}{dt}},quad {ddot {x}}={frac {d^{2}x}{dt^{2}}},quad {dot {y}}={frac {dy}{dt}},quad {ddot {y}}={frac {d^{2}y}{dt^{2}}}.}$

Heuristically, this result can be interpreted as^[2]

${displaystyle R={frac {left|mathbf {v} right|^{3}}{left|mathbf {v} times mathbf {dot {v}} right|}},qquad {mbox{where}}quad left|mathbf {v} right|={big |}({dot {x}},{dot {y}}){big |}=R{frac {dvarphi }{dt}}.}$

In n dimensions[edit]

If γ : ℝ → ℝⁿ is a parametrized curve in ℝⁿ then the radius of curvature at each point of the curve, ρ : ℝ → ℝ, is given by^[3]

${displaystyle rho ={frac {left|{boldsymbol {gamma }}'right|^{3}}{sqrt {left|{boldsymbol {gamma }}'right|^{2},left|{boldsymbol {gamma }}''right|^{2}-left({boldsymbol {gamma }}'cdot {boldsymbol {gamma }}''right)^{2}}}}}$

As a special case, if f(t) is a function from ℝ to ℝ, then the radius of curvature of its graph, γ(t) = (t, f(t)), is

${displaystyle rho (t)={frac {left|1+f'^{,2}(t)right|^{frac {3}{2}}}{left|f''(t)right|}}.}$

Derivation[edit]

Let γ be as above, and fix t. We want to find the radius ρ of a parametrized circle which matches γ in its zeroth, first, and second derivatives at t. Clearly the radius will not depend on the position γ(t), only on the velocity γ′(t) and acceleration γ″(t). There are only three independent scalars that can be obtained from two vectors v and w, namely v · v, v · w, and w · w. Thus the radius of curvature must be a function of the three scalars |γ′(t)|², |γ″(t)|² and γ′(t) · γ″(t).^[3]

The general equation for a parametrized circle in ℝⁿ is

{displaystyle mathbf {g} (u)=mathbf {a} cos(h(u))+mathbf {b} sin(h(u))+mathbf {c} }

where c ∈ ℝⁿ is the center of the circle (irrelevant since it disappears in the derivatives), a,b ∈ ℝⁿ are perpendicular vectors of length ρ (that is, a · a = b · b = ρ² and a · b = 0), and h : ℝ → ℝ is an arbitrary function which is twice differentiable at t.

The relevant derivatives of g work out to be

${displaystyle {begin{aligned}|mathbf {g} '|^{2}&=rho ^{2}(h')^{2}\mathbf {g} 'cdot mathbf {g} ''&=rho ^{2}h'h''\|mathbf {g} ''|^{2}&=rho ^{2}left((h')^{4}+(h'')^{2}right)end{aligned}}}$

If we now equate these derivatives of g to the corresponding derivatives of γ at t we obtain

${displaystyle {begin{aligned}|{boldsymbol {gamma }}'(t)|^{2}&=rho ^{2}h'^{,2}(t)\{boldsymbol {gamma }}'(t)cdot {boldsymbol {gamma }}''(t)&=rho ^{2}h'(t)h''(t)\|{boldsymbol {gamma }}''(t)|^{2}&=rho ^{2}left(h'^{,4}(t)+h''^{,2}(t)right)end{aligned}}}$

These three equations in three unknowns (ρ, h′(t) and h″(t)) can be solved for ρ, giving the formula for the radius of curvature:

${displaystyle rho (t)={frac {left|{boldsymbol {gamma }}'(t)right|^{3}}{sqrt {left|{boldsymbol {gamma }}'(t)right|^{2},left|{boldsymbol {gamma }}''(t)right|^{2}-{big (}{boldsymbol {gamma }}'(t)cdot {boldsymbol {gamma }}''(t){big )}^{2}}}}}$

or, omitting the parameter t for readability,

${displaystyle rho ={frac {left|{boldsymbol {gamma }}'right|^{3}}{sqrt {left|{boldsymbol {gamma }}'right|^{2};left|{boldsymbol {gamma }}''right|^{2}-left({boldsymbol {gamma }}'cdot {boldsymbol {gamma }}''right)^{2}}}}.}$

Examples[edit]

Semicircles and circles[edit]

For a semi-circle of radius a in the upper half-plane

${displaystyle y={sqrt {a^{2}-x^{2}}},quad y'={frac {-x}{sqrt {a^{2}-x^{2}}}},quad y''={frac {-a^{2}}{left(a^{2}-x^{2}right)^{frac {3}{2}}}},quad R=|-a|=a.}$

An ellipse (red) and its evolute (blue). The dots are the vertices of the ellipse, at the points of greatest and least curvature.

For a semi-circle of radius a in the lower half-plane

${displaystyle y=-{sqrt {a^{2}-x^{2}}},quad R=|a|=a.}$

The circle of radius a has a radius of curvature equal to a.

Ellipses[edit]

In an ellipse with major axis 2a and minor axis 2b, the vertices on the major axis have the smallest radius of curvature of any points, R = b²/a; and the vertices on the minor axis have the largest radius of curvature of any points, R = a²/b.

The ellipse’s radius of curvature, as a function of parameter t

${displaystyle R(t)={frac {(b^{2}cos ^{2}t+a^{2}sin ^{2}t)^{3/2}}{ab}};,;;{text{where}};;theta =tan ^{-1}{Big (}{frac {y}{x}}{Big )}=tan ^{-1}{Big (}{frac {b}{a}};tan ;t{Big )}}$

^[4]

And as a function of θ

${displaystyle R(theta )={frac {a^{2}}{b}}{biggl (}{frac {1-e^{2}(2-e^{2})(cos theta )^{2})}{1-e^{2}(cos theta )^{2}}}{biggr )}^{3/2}}$

Where e is the eccentricity of the ellipse and is given by:

${displaystyle e^{2}=1-{frac {b^{2}}{a^{2}}}}$

Applications[edit]

For the use in differential geometry, see Cesàro equation.
For the radius of curvature of the earth (approximated by an oblate ellipsoid); see also: arc measurement
Radius of curvature is also used in a three part equation for bending of beams.
Radius of curvature (optics)
Thin films technologies
Printed electronics
Minimum railway curve radius
AFM probe

Stress in semiconductor structures[edit]

Stress in the semiconductor structure involving evaporated thin films usually results from the thermal expansion (thermal stress) during the manufacturing process. Thermal stress occurs because film depositions are usually made above room temperature. Upon cooling from the deposition temperature to room temperature, the difference in the thermal expansion coefficients of the substrate and the film cause thermal stress.^[5]

Intrinsic stress results from the microstructure created in the film as atoms are deposited on the substrate. Tensile stress results from microvoids (small holes, considered to be defects) in the thin film, because of the attractive interaction of atoms across the voids.

The stress in thin film semiconductor structures results in the buckling of the wafers. The radius of the curvature of the stressed structure is related to stress tensor in the structure, and can be described by modified Stoney formula.^[6] The topography of the stressed structure including radii of curvature can be measured using optical scanner methods. The modern scanner tools have capability to measure full topography of the substrate and to measure both principal radii of curvature, while providing the accuracy of the order of 0.1% for radii of curvature of 90 meters and more.^[7]

References[edit]

^ Weisstien, Eric. “Radius of Curvature”. Wolfram Mathworld. Retrieved 15 August 2016.
^ ^a ^b Kishan, Hari (2007). Differential Calculus. Atlantic Publishers & Dist. ISBN 9788126908202.
^ ^a ^b ^c ^d Love, Clyde E.; Rainville, Earl D. (1962). Differential and Integral Calculus (Sixth ed.). New York: MacMillan.
^ Weisstein, Eric W. “Ellipse”. mathworld.wolfram.com. Retrieved 2022-02-23.
^ “Controlling Stress in Thin Films”. Flipchips.com. Retrieved 2016-04-22.
^ “On the determination of film stress from substrate bending : Stoney’s formula and its limits” (PDF). Qucosa.de. Retrieved 2016-04-22.
^ Peter Walecki. “Model X”. Zebraoptical.com. Retrieved 2016-04-22.

External links[edit]

The Geometry Center: Principal Curvatures
15.3 Curvature and Radius of Curvature
Weisstein, Eric W. “Principal Curvatures”. MathWorld.
Weisstein, Eric W. “Principal Radius of Curvature”. MathWorld.

Источник

‹– Назад

Радиус кривизны

Определение 8.3 Радиусом кривизны кривой в точке называется число , где — кривизна линии в точке . Если кривизна в точке равна 0, то радиус кривизны формально полагаем равным .

Заметим, что для окружности это определение даёт значение радиуса кривизны, совпадающее с радиусом окружности (постоянное во всех точках окружности).

Без доказательства сообщим, что из всех окружностей, касающихся линии в фиксированной точке , наиболее плотно прилегает²⁴ к линии та окружность, которая имеет радиус, равный радиусу кривизны кривой в точке , и выпуклость в ту же сторону, что кривая . Эта окружность называется окружностью кривизны линии в точке .

Рис.8.6.Окружности, касающиеся линии , и окружность кривизны

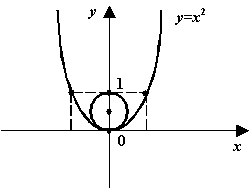
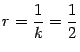
Пример 8.7 Радиус кривизны параболы в её вершине равен . Значит, окружность радиуса с центром в точке наилучшим образом приближает параболу в окрестности её вершины, то есть является для параболы окружностью кривизны в вершине параболы.

Рис.8.7.Окружность кривизны для параболы в вершине

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Источник

Радиус, центр и круг кривизны. Эволюта и эвольвента

Как узнать радиус кривизны

Definition[edit]