From Wikipedia, the free encyclopedia
This article is about the general mathematical concept. For its optical applications, see Radius of curvature (optics).

In differential geometry, the radius of curvature (Rc), R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.[1][2][3]
Definition[edit]
In the case of a space curve, the radius of curvature is the length of the curvature vector.
In the case of a plane curve, then R is the absolute value of[3]
where s is the arc length from a fixed point on the curve, φ is the tangential angle and κ is the curvature.
Formula[edit]
In 2D[edit]
If the curve is given in Cartesian coordinates as y(x), i.e., as the graph of a function, then the radius of curvature is (assuming the curve is differentiable up to order 2):
and |z| denotes the absolute value of z.
Also in Classical mechanics branch of Physics Radius of curvature is given by (Net Velocity)²/Acceleration Perpendicular
If the curve is given parametrically by functions x(t) and y(t), then the radius of curvature is
Heuristically, this result can be interpreted as[2]
In n dimensions[edit]
If γ : ℝ → ℝn is a parametrized curve in ℝn then the radius of curvature at each point of the curve, ρ : ℝ → ℝ, is given by[3]
.
As a special case, if f(t) is a function from ℝ to ℝ, then the radius of curvature of its graph, γ(t) = (t, f(t)), is
Derivation[edit]
Let γ be as above, and fix t. We want to find the radius ρ of a parametrized circle which matches γ in its zeroth, first, and second derivatives at t. Clearly the radius will not depend on the position γ(t), only on the velocity γ′(t) and acceleration γ″(t). There are only three independent scalars that can be obtained from two vectors v and w, namely v · v, v · w, and w · w. Thus the radius of curvature must be a function of the three scalars |γ′(t)|2, |γ″(t)|2 and γ′(t) · γ″(t).[3]
The general equation for a parametrized circle in ℝn is
where c ∈ ℝn is the center of the circle (irrelevant since it disappears in the derivatives), a,b ∈ ℝn are perpendicular vectors of length ρ (that is, a · a = b · b = ρ2 and a · b = 0), and h : ℝ → ℝ is an arbitrary function which is twice differentiable at t.
The relevant derivatives of g work out to be
If we now equate these derivatives of g to the corresponding derivatives of γ at t we obtain
These three equations in three unknowns (ρ, h′(t) and h″(t)) can be solved for ρ, giving the formula for the radius of curvature:
or, omitting the parameter t for readability,
Examples[edit]
Semicircles and circles[edit]
For a semi-circle of radius a in the upper half-plane

An ellipse (red) and its evolute (blue). The dots are the vertices of the ellipse, at the points of greatest and least curvature.
For a semi-circle of radius a in the lower half-plane
The circle of radius a has a radius of curvature equal to a.
Ellipses[edit]
In an ellipse with major axis 2a and minor axis 2b, the vertices on the major axis have the smallest radius of curvature of any points, R = b2/a; and the vertices on the minor axis have the largest radius of curvature of any points, R = a2/b.
The ellipse’s radius of curvature, as a function of parameter t
[4]
And as a function of θ
Where e is the eccentricity of the ellipse and is given by:

Applications[edit]
- For the use in differential geometry, see Cesàro equation.
- For the radius of curvature of the earth (approximated by an oblate ellipsoid); see also: arc measurement
- Radius of curvature is also used in a three part equation for bending of beams.
- Radius of curvature (optics)
- Thin films technologies
- Printed electronics
- Minimum railway curve radius
- AFM probe
Stress in semiconductor structures[edit]
Stress in the semiconductor structure involving evaporated thin films usually results from the thermal expansion (thermal stress) during the manufacturing process. Thermal stress occurs because film depositions are usually made above room temperature. Upon cooling from the deposition temperature to room temperature, the difference in the thermal expansion coefficients of the substrate and the film cause thermal stress.[5]
Intrinsic stress results from the microstructure created in the film as atoms are deposited on the substrate. Tensile stress results from microvoids (small holes, considered to be defects) in the thin film, because of the attractive interaction of atoms across the voids.
The stress in thin film semiconductor structures results in the buckling of the wafers. The radius of the curvature of the stressed structure is related to stress tensor in the structure, and can be described by modified Stoney formula.[6] The topography of the stressed structure including radii of curvature can be measured using optical scanner methods. The modern scanner tools have capability to measure full topography of the substrate and to measure both principal radii of curvature, while providing the accuracy of the order of 0.1% for radii of curvature of 90 meters and more.[7]
See also[edit]
- Base curve radius
- Bend radius
- Degree of curvature (civil engineering)
- Osculating circle
- Track transition curve
References[edit]
- ^ Weisstien, Eric. “Radius of Curvature”. Wolfram Mathworld. Retrieved 15 August 2016.
- ^ a b Kishan, Hari (2007). Differential Calculus. Atlantic Publishers & Dist. ISBN 9788126908202.
- ^ a b c d Love, Clyde E.; Rainville, Earl D. (1962). Differential and Integral Calculus (Sixth ed.). New York: MacMillan.
- ^ Weisstein, Eric W. “Ellipse”. mathworld.wolfram.com. Retrieved 2022-02-23.
- ^ “Controlling Stress in Thin Films”. Flipchips.com. Retrieved 2016-04-22.
- ^ “On the determination of film stress from substrate bending : Stoney’s formula and its limits” (PDF). Qucosa.de. Retrieved 2016-04-22.
- ^ Peter Walecki. “Model X”. Zebraoptical.com. Retrieved 2016-04-22.
Further reading[edit]
- do Carmo, Manfredo (1976). Differential Geometry of Curves and Surfaces. ISBN 0-13-212589-7.
External links[edit]
- The Geometry Center: Principal Curvatures
- 15.3 Curvature and Radius of Curvature
- Weisstein, Eric W. “Principal Curvatures”. MathWorld.
- Weisstein, Eric W. “Principal Radius of Curvature”. MathWorld.
Радиус кривизны окружности как найти
Рассмотрим плоскую кривую, заданную уравнением (y = fleft( x right).) Пусть в точке (Mleft( right)) проведена касательная к данной кривой, которая образует угол (alpha) с осью абсцисс (рисунок (1)). При смещении (Delta s) вдоль дуги кривой точка (M) переходит в точку (.) При этом положение касательной также изменяется: угол наклона касательной к оси (Ox) в точке () будет составлять (alpha + Deltaalpha.) Таким образом, при смещении точки кривой на расстояние (Delta s) касательная поворачивается на угол (Deltaalpha.) (Будем считать, что угол (alpha) возрастает при вращении против часовой стрелки.)
Абсолютное значение отношения (largefrac<<Delta alpha >><<Delta s>>normalsize) называется средней кривизной дуги (M.) В пределе, при (Delta s to 0,) мы получаем кривизну кривой в точке (M:) [K = limlimits_ <Delta s to 0>left| <frac<<Delta alpha >><<Delta s>>> right|.] Из приведенного определения следует, что кривизна в какой-либо точке кривой характеризует скорость вращения касательной в этой точке.
Для плоской кривой (y = fleft( x right)) кривизна в точке (Mleft( right)) выражается через первую и вторую производные функции (fleft( x right)) по формуле [K = frac <<left| right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] Если кривая задана в параметрической форме уравнениями (x = xleft( t right),) (y = yleft( t right),) то ее кривизна в произвольной точке (Mleft( right)) равна [K = frac <<left| right|>> <<<<left[ <<<left( right)>^2> + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] В случае, если кривая задана полярным уравнением (r = rleft( theta right),) кривизна находится по формуле [K = frac <<left| <+ 2 <<left( right)>^2> – rr”> right|>> <<<<left[ <+ <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>>.] Радиусом кривизны кривой в точке (Mleft( right)) называется величина, обратная кривизне (K) данной кривой в рассматриваемой точке: [R = frac<1>.] Следовательно, для плоских кривых, заданных явным уравнением (y = fleft( x right),) радиус кривизны в точке (Mleft( right)) будет определяться выражением [R = frac <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>> <<left| right|>>.]
Очевидно, достаточно найти кривизну эллипса в точках (Aleft( right)) и (Bleft( <0,b>right)) (рисунок (2)), поскольку в силу симметрии кривой кривизна в двух противоположных вершинах эллипса будет такой же.
Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме : [x = acos t,;;;y = bsin t.] где (t) − параметр. В точке (Aleft( right)) параметр имеет значение (t = 0,) а в точке (Bleft( <0,b>right)) его значение равно (t = largefrac<pi ><2>normalsize.)
Данная функция достигает максимума в точках (x = largefrac<<2pi n>>normalsize,;n in Z.) В силу периодичности кривизна во всех точках максимума одинакова, поэтому достаточно рассмотреть лишь точку (x = 0).
В данном случае точка (x = 0) является точкой перегиба функции (y = arctan x.) Поскольку в точке перегиба вторая производная равна нулю, то кривизна здесь также должна быть равна нулю, что и показывает полученное решение.
Экспоненциальная функция (y = ) − это единственная уникальная функция, у которой производные любого порядка равны самой функции. Поэтому для кривизны данной кривой можно сразу написать следующую формулу: [ right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefrac<3><2>normalsize>>>> > = <frac<<>><<<<left( <1 + >> right)>^<largefrac<3><2>normalsize>>>>.> ] Знак модуля в числителе опущен, поскольку экспоненциальная функция всегда положительна.
Радиус кривизны плоской кривой
Любая линия является кривой, даже прямая. Поэтому к любой линии применимы такие характеристики как кривизна или радиус кривизны. Как правило кривизна обозначается латинской литерой k, а радиус кривизны греческой литерой ρ.
Между собой эти характеристики кривой связаны следующим образом:
k = 1/ρ (542.1)
Т.е. чем больше радиус кривой, тем меньше ее кривизна.
А теперь рассмотрим несколько частных случаев кривых.
Радиус кривизны окружности
Окружность – это плоская кривая с постоянным радиусом кривизны. Т.е. радиус окружности это и есть радиус кривизны окружности:
Как определить радиус окружности, мы рассмотрим ниже.
Кривизна дуги
Любая дуга – это часть окружности. Соответственно радиус дуги равен радиусу окружности:
Рисунок 542.1. Дуга – часть окружности
На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.
Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.
Понятие кривизны дуги формулируется так:
Кривизна дуги – это отношение угла между касательными, проведенными в начале и конце дуги, к длине дуги
Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:
А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:
то, подставив значение длины дуги в уравнение (542.3), получим:
Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:
но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью
Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.
И еще одно интересное свойство дуги: Если соединить точки А и В прямой линией, то угол между этой линией и касательными будет равен α/2, а сама прямая линия – это и есть расстояние между точками А и В. Если дуга расположена в плоскости соответствующим образом, например так, как показано на рисунке 542.2:
Рисунок 542.2. Дуга из точки начала координат.
то расстояние между точками – это проекция l дуги на ось х. А максимальное расстояние между дугой и осью х – это стрела дуги h.
Радиус кривизны прямой линии
Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.
Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:
kп.л = 1/∞ = 0 (542.6)
Про до сих пор неразрешенный парадокс, возникающий при подобных подходах к прямой линии и к окружности, я уже упоминал в статье “Основы геометрии. Определения основных элементов, пятый элемент”. Здесь лишь добавлю, что через прямую линию можно провести бесконечное множество плоскостей и в любой из этих плоскостей радиус кривизны прямой линии будет равен бесконечности. При этом через окружность можно провести две взаимно перпендикулярные плоскости, в одной из которых окружность будет окружностью, а в другой – прямой линией конечной длины. Поэтому
все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими
Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:
1. Из уравнения (542.1) можно сделать вывод, что:
kp = 1 (542.7)
Соответственно для прямой линии:
0·∞ = 1 (542.7.2)
Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.
2. Если прямая – это дуга с бесконечно большим радиусом, соответственно касательные, проведенные в концах такой дуги, совпадают с прямой, а угол, образованный касательными, равен нулю.
Это означает, что радиусы проведенные в концах дуги – прямой линии, являются параллельными прямыми и не могут пересекаться. А между тем по определению это радиусы, которые обязательно должны сходиться в некоторой точке – центре окружности.
Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.
Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.
Радиус кривизны точки
Точка – это самый простой и самый сложный элемент геометрии. Одни считают, что точка не имеет размеров, а значит и определить кривизну или радиус кривизны точки не возможно. Другие, в частности Евклид, считают, что точка не имеет частей, а каковы при этом размеры точки – не совсем понятно. Я же считаю, что точка – это начальный, далее не делимый элемент геометрии, размеры которого пренебрежимо малы по сравнению с остальными рассматриваемыми элементами. В этом случае для точки будут справедливыми следующие уравнения кривизны и радиуса кривизны:
kт. = 1/0 = ∞ (542.9)
И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что “деление на ноль невозможно”, тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.
Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.
Примечание: На мой взгляд большинство из описанных выше парадоксов возникают из-за неправильного толкования понятия “бесконечность”. Бесконечность как некая абсолютная величина не имеет пределов, а значит и никакому измерению не поддается. Кроме того бесконечность – это даже не постоянная, а переменная величина. Например луч – это прямая линия с началом в некоторой точке. Длина луча может быть бесконечно большой. При этом прямая линия тоже может быть бесконечно длинной при этом не иметь ни начала ни конца. Получается, что с одной стороны бесконечно длинный луч вроде бы в 2 раза короче, чем бесконечно длинная прямая. А с другой стороны длины их бесконечны и поэтому равны.
Возможным выходом из этой ситуации является принятие понятия “бесконечность”, как относительного. Например, кривизна прямой линии является пренебрежимо малой величиной по отношению к радиусу кривизны. Или радиус кривизны прямой линии несопоставимо больше кривизны. Подобные толкования допускают и наличие кривизны прямой и некое конечное значение радиуса кривизны прямой и многое другое. Я бы назвал такой относительный подход к рассмотрению проблемы реалистичным, а подходы, использующие абсолютные понятия – идеализированными. Впрочем прямого отношения к теме данной статьи это не имеет. Продолжим рассмотрение плоских кривых.
И окружность и прямая линия являются плоскими кривыми с постоянным радиусом кривизны. При этом радиус кривизны прямой линии всегда известен, так как равен бесконечности, а для окружности всегда можно определить радиус, воспользовавшись теоремой Пифагора. Так в частном случае, если центр окружности совпадает с началом координат рассматриваемой плоскости (u = 0; v = 0 – координаты центра окружности), то:
Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.
R 2 = x 2 + y 2 (541.1.2)
А в общем случае, когда координаты центра окружности не совпадают с началом координат:
Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.
R 2 = (x – u) 2 + (y – v) 2 (542.10)
Но в жизни достаточно часто приходится сталкиваться с кривыми, радиус кривизны которых – не постоянная величина. Более того, этот радиус может изменяться в двух плоскостях измерения. Тем не менее так далеко углубляться в геометрию и алгебру мы не будем и далее рассмотрим, как можно определить радиус плоской кривой в некоторой точке.
Плоские кривые с изменяющимся радиусом кривизны
Примеров плоских кривых с изменяющимся радиусом кривизны очень много, это и гиперболы, и параболы, и синусоиды и т.п. Определение радиуса кривизны таких кривых основано на следующих теоретических предпосылках:
1. Любую окружность можно рассматривать как некоторое множество дуг.
2. Если количество дуг, составляющих окружность, стремится к бесконечности, то соответственно длина таких дуг стремится к нулю (m → 0).
3. Если мы обозначим длину такой очень короткой дуги как приращение функции длины окружности (m = Δl), то уравнение кривизны (542.3) примет следующий вид:
(542.3.1)
4. Тогда любую плоскую кривую с изменяющимся радиусом можно рассматривать как стремящееся к бесконечности множество дуг с постоянным радиусом. Другими словами в пределах любой кривой, описываемой параметрическими уравнениями, всегда можно выделить дугу, пусть даже и очень малой длины, стремящейся к точке и определить для нее кривизну и радиус кривизны в рассматриваемой точке.
Это означает, что самый точный способ определения радиуса кривизны в таком случае – это использование дифференциальных исчислений. В общем случае для этого нужно два раза продифференцировать уравнение радиуса окружности (542.10) по аргументу функции х, а затем извлечь квадратный корень из полученного результата. В итоге (полный вывод уравнения здесь не привожу из-за повышенной сложности записи, а для особо заинтересованных есть справочники и другие сайты) мы получим следующую формулу для определения радиуса кривизны:
(542.11)
Соответственно кривизна плоской кривой в рассматриваемой точке будет равна:
(542.12)
В частном случае, когда тангенс угла между касательными – первая производная от функции – является относительно малой величиной, например, tg2° = 0.035 соответственно (tg2°) 2 = 0.0012, то влиянием куба суммы первой производной и единицы на кривизну можно пренебречь (значение знаменателя дроби сводится к единице) и тогда:
k = y” = d 2 y/dx 2 (542.12.2)
Т.е. формально в таких случаях кривизной считается не отношение угла наклона между касательными к длине дуги, а некоторая величина, примерно соответствующая высоте h на рисунке 542.2.
Эта особенность второй производной очень активно используется в частности для упрощения определения прогиба элементов строительных конструкций.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье “Записаться на прием к доктору”
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины – номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Категории:
- Расчет конструкций . Основы прикладной геометрии
Оценка пользователей:
10.0 (голосов: 1)
Переходов на сайт:
6701
Комментарии:
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье “Записаться на прием к доктору” (ссылка в шапке сайта).
Радиус, круг и центр кривизны
Вы будете перенаправлены на Автор24
Смысл понятий радиуса, круга и центра кривизны
В технических приложениях часто оказывается удобным использовать окружности для приближенной замены кривой в окрестностях рассматриваемых точек. Это существенно упрощает решение целого ряда задач за счет применения более удобных выражений.
Наиболее употребительными характеристиками любой кривой являются касательная и нормаль. Касательная — предельное положение секущей $MN$ при неограниченном приближении точки $N$ к точке $M$ вдоль кривой. Нормаль — прямая, проходящая через точку касания перпендикулярно касательной.
Уравнение касательной в точке $Mleft(x_ <0>,y_ <0>right)$ к кривой $y=fleft(xright)$ имет вид $y-y_ <0>=y’left(x_ <0>right)cdot left(x-x_ <0>right)$, уравнение нормали $y-y_ <0>=-frac<1> right)> cdot left(x-x_ <0>right)$.
Записать уравнения касательной и нормали к кривой $y=3cdot x^ <2>-x+2$ в заданной точке $x_ <0>=1$.
Значение функции в заданной точке: $y_ <0>=yleft(x_ <0>right)=yleft(1right)=3cdot 1^ <2>-1+2=4$.
Значение производной в заданной точке:
[y’=left(3cdot x^ <2>-x+2right)^ <<‘>> =6cdot x-1; y’left(x_ <0>right)=y’left(1right)=6cdot 1-1=5.]
Уравнение касательной: $y-4=5cdot left(x-1right)$ или $5cdot x-y-1=0$.
Уравнение нормали: $y-4=-frac<1> <5>cdot left(x-1right)$ или $x+5cdot y-21=0$.
Радиус кривизны — это параметр кривой, значение которого обратно значению кривизны $R=frac<1> $. Следовательно, это такая же переменная величина, как и кривизна.
Если в данной точке $M$ построить нормаль к кривой и отложить на ней в сторону вогнутости кривой отрезок, равный по длине радиусу кривизны кривой в этой точке, то получим точку — центр кривизны. Окружность с центром в полученной точке и радиусом, равным радиусу кривизны — это круг кривизны. Так как данная кривая и её круг кривизны касаются в данной точке, то они имеют в данной точке общую касательную. Кроме того, значения кривизны кривой и круга кривизны в данной точке совпадают.
Важным свойством круга кривизны является то, что он является соприкасающимся кругом, то есть предельным положением круга, проходящего через три точки кривой, стремящимся к совпадению в данной.
Если некоторая точка перемещается вдоль кривой, то и соответствующий ей центр кривизны также описывает некоторую кривую. Геометрическое место центров кривизны данной кривой называется её эволютой. При этом данная кривая по отношению к своей эволюте называется её эвольвентой.
Вычисление радиуса и определение центра круга кривизны
Формулы для радиуса кривизны получить легко, если известны формулы для вычисления кривизны кривой.
При произвольном параметрическом задании кривой $x=xleft(tright)$ и $y=yleft(tright)$ имеем $R=frac <sqrt<left(left(x’_right)^ <2>+left(y’_ right)^ <2>right)^ <3>> > cdot x’_ -x”_ cdot y’_ > $.
Если кривая задана в явном виде $y=fleft(xright)$, то $R=frac <sqrt<left(1+left(y’right)^<2>right)^ <3>> > $.
Если кривая задана в полярных координатах $rho =rho left(phi right)$, то $R=frac <sqrt<left(rho ^<2>+left(rho ‘_ <phi >right)^ <2>right)^ <3>> > <rho ^<2>+2cdot left(rho ‘_ <phi >right)^ <2>-rho cdot rho ”_ <phi phi >> $.
Готовые работы на аналогичную тему
Найти радиус кривизны экспоненты $y=e^ $ при $x=0$.
Находим производные: $y’=e^ $; $y”=e^ $.
По формуле для радиуса кривизны получаем:
Вычисляем радиус кривизны экспоненты при $x=0$:
Найти радиус кривизны кардиоиды $rho =1+cos phi $.
Находим производные: $rho ‘=-sin phi $; $rho ”=-cos phi $.
[rho ^ <2>+rho ‘^ <2>=left(1+cos phi right)^ <2>+left(-sin phi right)^ <2>=2cdot left(1+cos phi right);] [rho ^ <2>+2cdot rho ‘^ <2>-rho cdot rho ”=left(1+cos phi right)^ <2>+2cdot left(-sin phi right)^ <2>-left(1+cos phi right)cdot left(-cos phi right)=] [=3cdot left(1+cos phi right).]
По формуле для радиуса кривизны получаем:
Найдем координаты центра кривизны $Pleft(x_ ;y_ right)$ кривой $y=fleft(xright)$.
Координаты центра кривизны для точки $Mleft(x;yright)$ удовлетворяют уравнению нормали $y_ -y=-frac<1> cdot left(x_ -xright)$.
Уравнение круга кривизны: $left(x-x_ right)^ <2>+left(y-y_ right)^ <2>=R^ <2>$.
Координаты центра кривизны по существу являются параметрическими уравнения эволюты.
Найти эволюту параболы $y=x^ <2>$. Результаты представить графически.
Находим производные: $y’=2cdot x$; $y”=2$.
По формулам $left<begin =x-frac right)> > \ =y+frac <1+y’^<2>> > endright. $ находим координаты центра кривизны для произвольной точки $Mleft(x;yright)$.
Полученные выражения фактически представляют собой параметрические уравнения эволюты, в которых $x$ является параметром. Если исключить параметр $x$ из этих уравнений, то может быть получено уравнение вида $Fleft(x_ ;y_ right)=0$, которое непосредственно связывает координаты эволюты.
Совмещенный график эвольвенты $y=x^ <2>$ и её эволюты:
На графике синей линией изображена парабола $y=x^ <2>$, а красной линией — её эволюта. Эволюта представляет собой полукубическую параболу.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 30 11 2022
[spoiler title=”источники:”]
http://doctorlom.com/item542.html
http://spravochnick.ru/matematika/krivizna_krivoy/radius_krug_i_centr_krivizny/
[/spoiler]
Макеты страниц
Мы видели, что кривизна к окружности есть величина, обратная ее радиусу 

Чем больше радиус окружности, тем меньше ее кривизна. По аналогии вводится понятие радиуса кривизны кривой в данной точке.
Определение. Радиусом кривизны R в данной точке кривой называется величина, обратная кривизне 

Так как кривизна кривой, вообще говоря, изменяется при переходе от данной ее точки к другой, то и радиус кривизны является переменной величиной.
Если кривая задана уравнением  то ее радиус кривизны
то ее радиус кривизны  как величина, обратная кривизне, определяется следующей формулой:
как величина, обратная кривизне, определяется следующей формулой:

Если же кривая задана параметрически, то ее радиус кривизны выражается формулой

Пример. Найти радиус кривизны кривой  в точке М (1; 0).
в точке М (1; 0).
Решение. Находим  . По формуле (78) получим
. По формуле (78) получим

Построим теперь в данной точке М кривой отрезок МР, направленный по нормали к кривой в сторону ее вогнутости и равный по величине радиусу кривизны кривой в точке М:

(рис. 201). Окружность с центром в точке Р и радиусом, равным радиусу кривизны кривой в данной точке  , называется кругом кривизны. Центр Р этого круга называется центром кривизны. Очевидно, данная кривая и ее круг кривизны в точке М имеют общую касательную (рис. 201).
, называется кругом кривизны. Центр Р этого круга называется центром кривизны. Очевидно, данная кривая и ее круг кривизны в точке М имеют общую касательную (рис. 201).

Рис. 201

Рис. 202
Покажем, как найти координаты центра кривизны кривой, заданной уравнением  .
.
Пусть  – точка данной кривой и
– точка данной кривой и  – соответствующий ее центр кривизны (рис. 202). Уравнение нормали к кривой в точке
– соответствующий ее центр кривизны (рис. 202). Уравнение нормали к кривой в точке  имеет вид
имеет вид

Так как точка  лежит на нормали, то ее координаты удовлетворяют этому уравнению:
лежит на нормали, то ее координаты удовлетворяют этому уравнению:

Кроме того, расстояние между точками  равно радиусу кривизны R кривой:
равно радиусу кривизны R кривой:

откуда

Решая совместно систему уравнений

и заменяя R его выражением по формуле (78), найдем

Предположим для определенности, что  . Тогда кривая вогнута и
. Тогда кривая вогнута и  (см. рис. 202), т. е. в правой части формулы (80) для
(см. рис. 202), т. е. в правой части формулы (80) для  следует взять знак «плюс», и, следовательно, в правой части формулы для
следует взять знак «плюс», и, следовательно, в правой части формулы для  – знак «минус». При этом, поскольку
– знак «минус». При этом, поскольку  для координат
для координат  центра кривизны мы получим следующие формулы:
центра кривизны мы получим следующие формулы:

Можно показать, что в случае  формулы (81) сохраняют свой вид.
формулы (81) сохраняют свой вид.
-
Радиус, центр и круг кривизны. Эволюта и эвольвента
Радиусом
кривизны называется величина, обратная
кривизне, т. е.
![]()
.
Если
плоская кривая отнесена к прямоугольной
системе координат и задана уравнением
,
то радиус кривизны
![]()
выражается формулой

.
Eсли
плоская кривая отнесена к прямоугольной
системе координат и задана параметрически
системой уравнений
, то радиус кривизны
выражается формулой
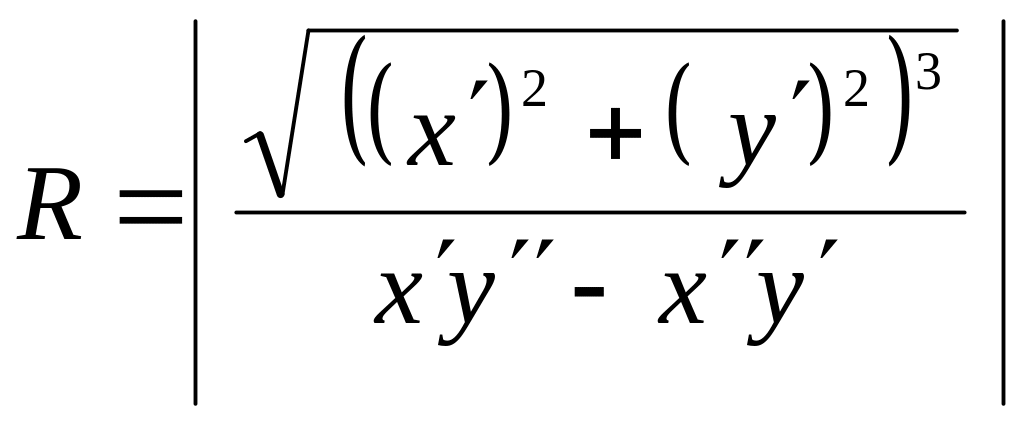
,
где
,
![]()
,
,
.
Если
плоская кривая отнесена к полярной
системе координат и задана уравнением
,
то радиус кривизны
выражается формулой

,
где
,
.
Окружностью
кривизны данной линии её точке А
называется
предельное положение окружности,
проходящей через три точки A,
B,
C
кривой, когда
![]()
и
![]()
.
Радиус
окружности кривизны равен радиусу
кривизны. Центр окружности кривизны
называется центром кривизны и находится
на нормали к линии, проведенной в точке
А
в сторону вогнутости этой линии.
Координаты
![]()
и
![]()
центра кривизны линии
вычисляются по формулам:
![]()
,
![]()
.
Эволютой
линии называется множество её центров
кривизны, а сама линия относительно
своей эволюты называется эвольвентой.
Формулы
для координат центра кривизны можно
рассматривать как параметрические
уравнения эволюты, где параметром
является абсцисса х
исходной линии.
Данная
линия может иметь лишь одну эволюту, но
у данной эволюты существует бесконечное
множество эвольвент.
Пример.
Найти
радиус кривизны линии
![]()
в
точке с абсциссой
.
Решение.
Найдем значения производных первого и
второго порядков функции
в точке с абсциссой
:
![]()
,
![]()
.
Подставим
найденные значения
![]()
и
![]()
в
формулу
:
![]()
.
Следовательно,
радиус кривизны
линии
в
точке с абсциссой
![]()
.
Пример.
Найти
радиус кривизны линии
![]()
в
точке
![]()
.
Решение.
Дифференцируя по t,
получим
![]()
,
![]()
,
![]()
,
![]()
.
Вычислим
значения производных в
точке
:
![]()
![]()
![]()
,
![]()
.
Подставляя
найденные значения
![]()
![]()
![]()
,
![]()
в
формулу
,
имеем

Следовательно,
радиус кривизны
линии
в
точке с абсциссой
![]()
Пример.
Найти
радиус кривизны кардиоиды
![]()
в
любой её точке.
Решение.
Найдем
и
:
![]()
![]()
.
Подставим
найденные выражения в формулу
:
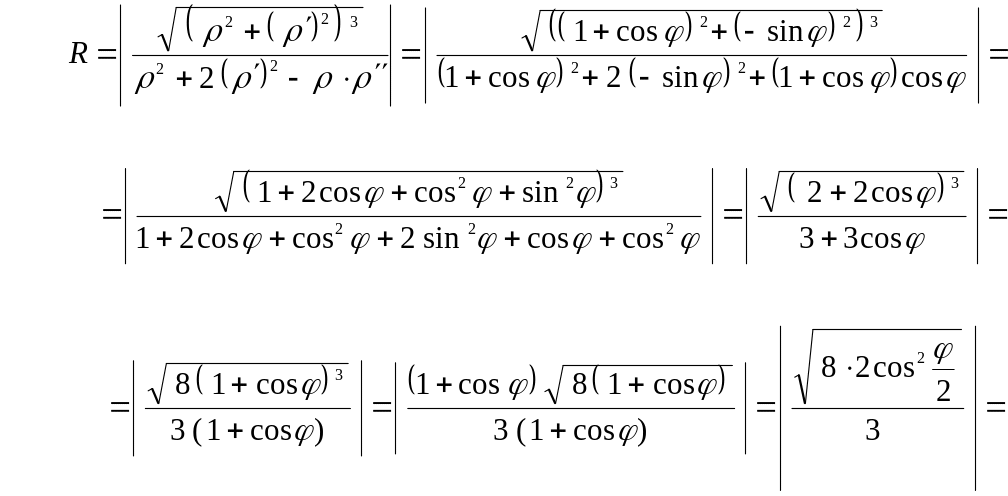

Следовательно,
радиус кривизны
кардиоиды
в
любой её точке
![]()
Пример.
Найти
координаты
и
центра кривизны линии
![]()
в
точке
![]()
.
Решение.
Найдем значения производных первого
и второго порядков функции
в точке с абсциссой
:
![]()
,
![]()
.
Подставим
значения
,
![]()
и найденные
значения
![]()
и
в
формулы
,
:
![]()
,
![]()
Следовательно,
координаты
центра кривизны линии
в
точке
![]()
и
![]()
Пример.
Составить
уравнение эволюты кривой
![]()
.
Решение.
Продифференцируем дважды уравнение
параболы:
![]()
;
![]()
.
Так
как
![]()
,
то
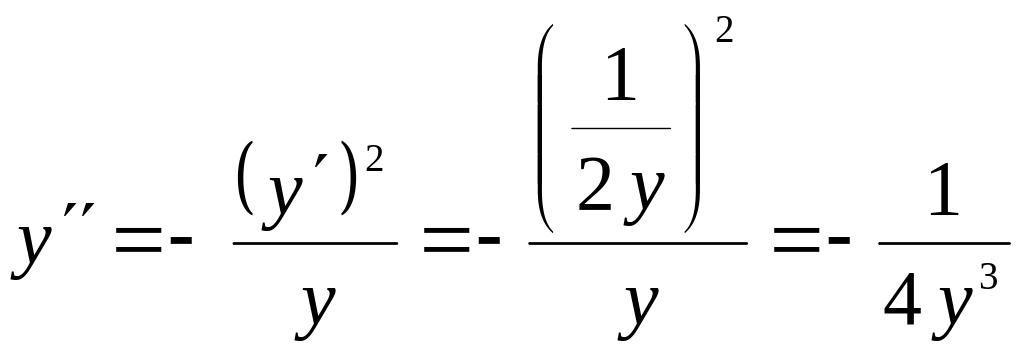
.
Найдем
координаты
и
центра кривизны линии ,
предварительно выразив х
из уравнения
:
![]()
.
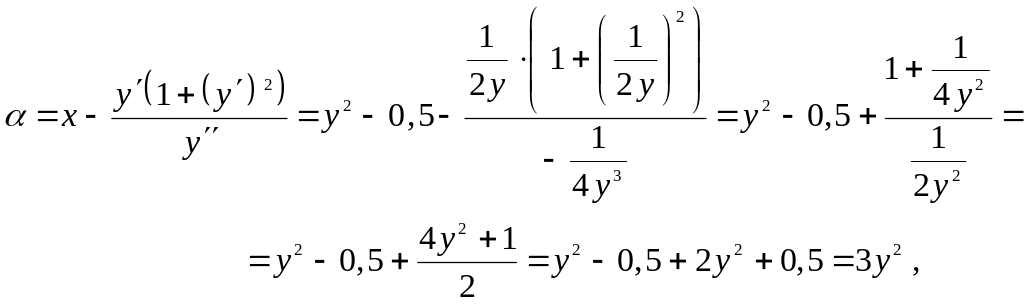
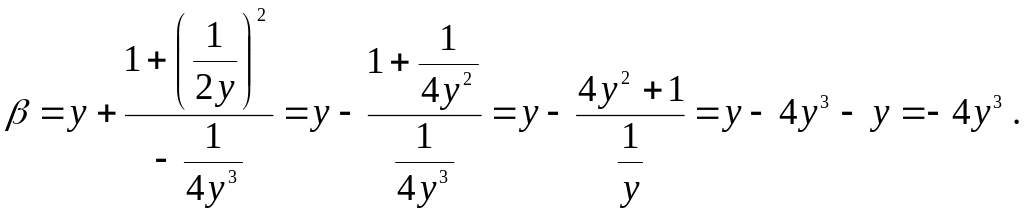
Имеем
![]()
![]()
–
уравнение эволюты в параметрической
форме. Выразим параметр у
из
![]()
и
:
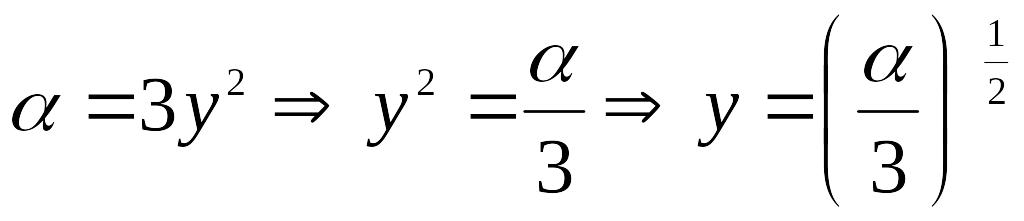
;

.
Окончательно
получаем,
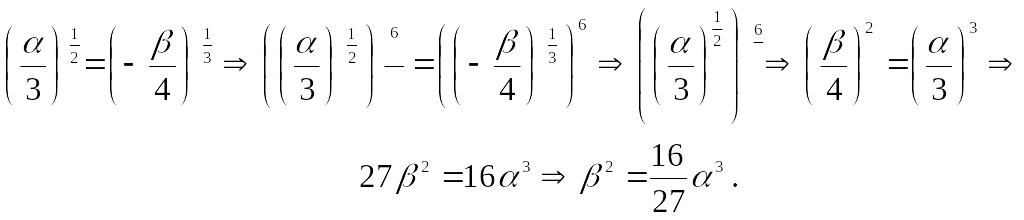
Следовательно,
уравнение
эволюты кривой
![]()
имеет вид
![]()
(уравнение
полукубической параболы).
Упражнения
1.
Найти радиус кривизны линии
![]()
в
точке A:
а)
![]()
,
A
(
2; 2 ), б)
![]()
,
A
(
0; 1 ) .
2.
Найти радиус кривизны трехлепестковой
розы
![]()
, при
![]()
.
3.
Найти координаты
![]()
и
![]()
центра кривизны линии
в
точке A:
а)
![]()
,
A
(
1; 1 ), б)
![]()
,
A
(
1; 0 ) .
4.
Составить уравнение эволюты кривой
:
а)
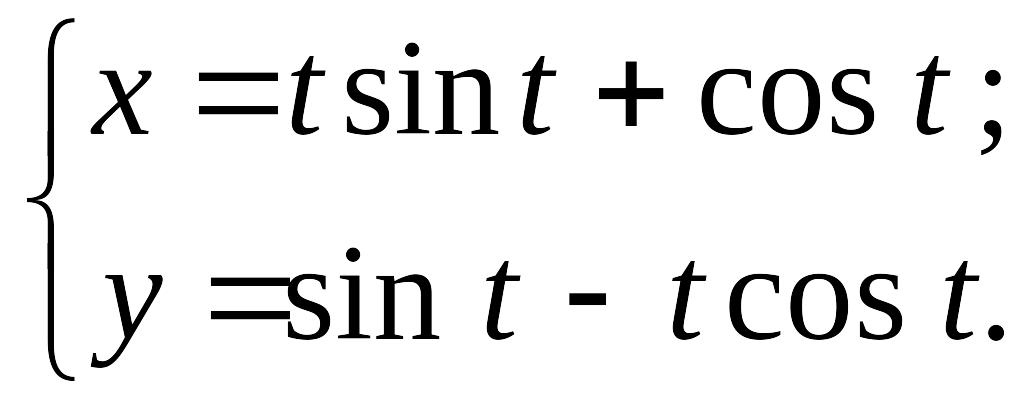
,
б)
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Смысл понятий радиуса, круга и центра кривизны
В технических приложениях часто оказывается удобным использовать окружности для приближенной замены кривой в окрестностях рассматриваемых точек. Это существенно упрощает решение целого ряда задач за счет применения более удобных выражений.
Наиболее употребительными характеристиками любой кривой являются касательная и нормаль. Касательная — предельное положение секущей $MN$ при неограниченном приближении точки $N$ к точке $M$ вдоль кривой. Нормаль — прямая, проходящая через точку касания перпендикулярно касательной.
Уравнение касательной в точке $Mleft(x_{0} ,y_{0} right)$ к кривой $y=fleft(xright)$ имет вид $y-y_{0} =y’left(x_{0} right)cdot left(x-x_{0} right)$, уравнение нормали $y-y_{0} =-frac{1}{y’left(x_{0} right)} cdot left(x-x_{0} right)$.
Задача 1
Записать уравнения касательной и нормали к кривой $y=3cdot x^{2} -x+2$ в заданной точке $x_{0} =1$.
Значение функции в заданной точке: $y_{0} =yleft(x_{0} right)=yleft(1right)=3cdot 1^{2} -1+2=4$.
Значение производной в заданной точке:
[y’=left(3cdot x^{2} -x+2right)^{{‘} } =6cdot x-1; y’left(x_{0} right)=y’left(1right)=6cdot 1-1=5.]
Уравнение касательной: $y-4=5cdot left(x-1right)$ или $5cdot x-y-1=0$.
Уравнение нормали: $y-4=-frac{1}{5} cdot left(x-1right)$ или $x+5cdot y-21=0$.
Определение
Радиус кривизны — это параметр кривой, значение которого обратно значению кривизны $R=frac{1}{K} $. Следовательно, это такая же переменная величина, как и кривизна.
Если в данной точке $M$ построить нормаль к кривой и отложить на ней в сторону вогнутости кривой отрезок, равный по длине радиусу кривизны кривой в этой точке, то получим точку — центр кривизны. Окружность с центром в полученной точке и радиусом, равным радиусу кривизны — это круг кривизны. Так как данная кривая и её круг кривизны касаются в данной точке, то они имеют в данной точке общую касательную. Кроме того, значения кривизны кривой и круга кривизны в данной точке совпадают.
Важным свойством круга кривизны является то, что он является соприкасающимся кругом, то есть предельным положением круга, проходящего через три точки кривой, стремящимся к совпадению в данной.
Если некоторая точка перемещается вдоль кривой, то и соответствующий ей центр кривизны также описывает некоторую кривую. Геометрическое место центров кривизны данной кривой называется её эволютой. При этом данная кривая по отношению к своей эволюте называется её эвольвентой.
Вычисление радиуса и определение центра круга кривизны
Формулы для радиуса кривизны получить легко, если известны формулы для вычисления кривизны кривой.
При произвольном параметрическом задании кривой $x=xleft(tright)$ и $y=yleft(tright)$ имеем $R=frac{sqrt{left(left(x’_{t} right)^{2} +left(y’_{t} right)^{2} right)^{3} } }{y”_{tt} cdot x’_{t} -x”_{tt} cdot y’_{t} } $.
Если кривая задана в явном виде $y=fleft(xright)$, то $R=frac{sqrt{left(1+left(y’right)^{2} right)^{3} } }{y”} $.
Если кривая задана в полярных координатах $rho =rho left(phi right)$, то $R=frac{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } }{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot rho ”_{phi phi } } $.
«Радиус, круг и центр кривизны» 👇
Задача 2
Найти радиус кривизны экспоненты $y=e^{x} $ при $x=0$.
Находим производные: $y’=e^{x} $; $y”=e^{x} $.
По формуле для радиуса кривизны получаем:
[R=frac{sqrt{left(1+left(y’right)^{2} right)^{3} } }{y”} =frac{sqrt{left(1+left(e^{x} right)^{2} right)^{3} } }{e^{x} } =frac{sqrt{left(1+e^{2cdot x} right)^{3} } }{e^{x} } .]
Вычисляем радиус кривизны экспоненты при $x=0$:
[Rleft(0right)=frac{sqrt{left(1+e^{2cdot 0} right)^{3} } }{e^{0} } =2cdot sqrt{2} . ]
Задача 3
Найти радиус кривизны кардиоиды $rho =1+cos phi $.
Находим производные: $rho ‘=-sin phi $; $rho ”=-cos phi $.
Вычисляем:
[rho ^{2} +rho ‘^{2} =left(1+cos phi right)^{2} +left(-sin phi right)^{2} =2cdot left(1+cos phi right);]
[rho ^{2} +2cdot rho ‘^{2} -rho cdot rho ”=left(1+cos phi right)^{2} +2cdot left(-sin phi right)^{2} -left(1+cos phi right)cdot left(-cos phi right)=]
[=3cdot left(1+cos phi right).]
По формуле для радиуса кривизны получаем:
[R=frac{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } }{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot rho ”_{phi phi } } =frac{sqrt{left(2cdot left(1+cos phi right)right)^{3} } }{3cdot left(1+cos phi right)} =frac{2}{3} cdot sqrt{2cdot left(1+cos phi right)} =frac{4}{3} cdot cos frac{phi }{2} .]
Найдем координаты центра кривизны $Pleft(x_{C} ;y_{C} right)$ кривой $y=fleft(xright)$.
Координаты центра кривизны для точки $Mleft(x;yright)$ удовлетворяют уравнению нормали $y_{C} -y=-frac{1}{y’left(xright)} cdot left(x_{C} -xright)$.
Уравнение круга кривизны: $left(x-x_{C} right)^{2} +left(y-y_{C} right)^{2} =R^{2} $.
Решив систему $left{begin{array}{c} {y_{C} -y=-frac{1}{y’left(xright)} cdot left(x_{C} -xright)} \ {left(x-x_{C} right)^{2} +left(y-y_{C} right)^{2} =R^{2} } end{array}right. $, получим искомые координаты центра кривизны: $left{begin{array}{c} {x_{C} =x-frac{y’cdot left(1+y’^{2} right)}{y”} } \ {y_{C} =y+frac{1+y’^{2} }{y”} } end{array}right. $.
Координаты центра кривизны по существу являются параметрическими уравнения эволюты.
Задача 4
Найти эволюту параболы $y=x^{2} $. Результаты представить графически.
Находим производные: $y’=2cdot x$; $y”=2$.
По формулам $left{begin{array}{c} {x_{C} =x-frac{y’cdot left(1+y’^{2} right)}{y”} } \ {y_{C} =y+frac{1+y’^{2} }{y”} } end{array}right. $ находим координаты центра кривизны для произвольной точки $Mleft(x;yright)$.
Получаем:
[x_{C} =x-frac{2cdot xcdot left(1+left(2cdot xright)^{2} right)}{2} =-4cdot x^{3} ;]
[y_{C} =y+frac{1+left(2cdot xright)^{2} }{2} =3cdot x^{2} +frac{1}{2} .]
Полученные выражения фактически представляют собой параметрические уравнения эволюты, в которых $x$ является параметром. Если исключить параметр $x$ из этих уравнений, то может быть получено уравнение вида $Fleft(x_{C} ;y_{C} right)=0$, которое непосредственно связывает координаты эволюты.
Совмещенный график эвольвенты $y=x^{2} $ и её эволюты:
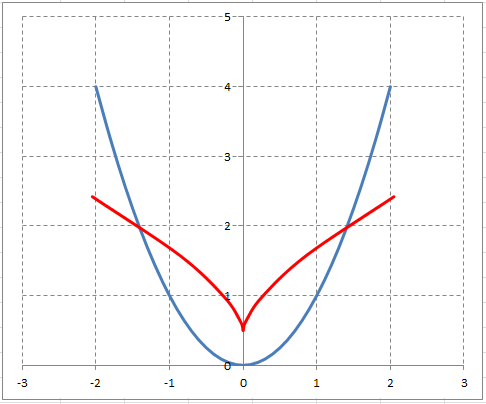
На графике синей линией изображена парабола $y=x^{2} $, а красной линией — её эволюта. Эволюта представляет собой полукубическую параболу.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме














