Сообщения без ответов | Активные темы | Избранное
|
|
Геометрическая оптика(Найти радиус кривизны поверхностей)
|
|
26/09/09 |
Здравствуйте! Возникла проблема с задачей: Две тонкие, симметричные линзы с одинаковыми радиусами кривизны: одна – собирающая (n1 =1.7), другая – рассеивающая (n2 =1.5) сложили и погрузили в воду (n3 = 4/3). Фокусное расстояние системы оказалось равным 33.3 см. Найдите (в сантиметрах) радиус кривизны поверхностей. Заранее спасибо!
|
|
|
|
|
Парджеттер |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
||
07/10/07 |
Во-первых, есть схожая задача у Иродова. Во-вторых, есть волшебная формула про оптическую силу линзы, которая естественным образом связана с фокусным расстоянием
|
||
|
|
|||
|
hellen |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
|
26/09/09 |
решаю, R1=R2=R( для удобства)
|
|
|
|
|
Парджеттер |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
|||||
07/10/07 |
это правильно или тема не усвоена? Неправильно.
|
|||||
|
|
||||||
|
hellen |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
|
26/09/09 |
|
|
|
|
|
Парджеттер |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
||
07/10/07 |
🙁 ща рыдать буду.. Рыдать не надо. Надо исправить формулы и продолжить конструктивный диалог )
|
||
|
|
|||
|
hellen |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
|
26/09/09 |
|
|
|
|
|
Парджеттер |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
||
07/10/07 |
примерно так? Не совсем.
|
||
|
|
|||
|
hellen |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
|
26/09/09 |
а как тогда эти силы искать если только коэффициенты преломлений есть?
|
|
|
|
|
Парджеттер |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
||
07/10/07 |
а как тогда эти силы искать если только коэффициенты преломлений есть? А этого разве недостаточно? Получите уравнение на — 28 сен 2009, 19:39 — Просто запишите указанные выражения чисто формально для двух линз, затем сложите. Получите суммарную оптическую силу. Выразите оптическую силу через фокус (как я писал выше) и останется найти из этого уравнения радиусы линз. — 28 сен 2009, 19:40 — если это подставлять, то 8,88 получается Такие штуки вообще вредно проделывать. Угадывание в физических задачах вредно без должной подготовки. А с нею это называется “интуиция”
|
||
|
|
|||
|
hellen |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
|
26/09/09 |
|
|
|
|
|
Парджеттер |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
||
07/10/07 |
а теперь правильно? Да не совсем.
|
||
|
|
|||
|
hellen |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
|
26/09/09 |
первые два уравнения рассматривают каждую линзу поотдельности, там двойки быть не может, потому что линза одна в одном уравнении, другая в другом
|
|
|
|
|
Парджеттер |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
||
07/10/07 |
первые два уравнения рассматривают каждую линзу поотдельности, там двойки быть не может, потому что линза одна в одном уравнении, другая в другом Вы лучше не спорьте, а книжку почитайте, если сомневаетесь. минус чтоли перед Хотите ставьте минус, а можете учесть знаки радиусов кривизны. Но мне, кажется, что Вам еще до этого далеко )
Среда. Только у вас не стоит
|
||
|
|
|||
|
hellen |
Re: Геометрическая оптика(Найти радиус кривизны поверхностей)
|
|
26/09/09 |
мозг опух… — Пн сен 28, 2009 20:49:06 — голова предмет тяжелый — Пн сен 28, 2009 20:54:28 —
|
|
|
|
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Страницы работы
Содержание работы
Министерство образования и науки
Российской Федерации
Федеральное агентство по образованию
Государственное
образовательное учреждение высшего профессионального образования
« ИНСТИТУТ ЦВЕТНЫХ МЕТАЛЛОВ И ЗОЛОТА»СФУ
Кафедра физики
Лабораторная работа № 6
Определение радиуса кривизны линзы
с помощью колец Ньютона
Выполнил: Проверил:
Красноярск 2010 г.
Цель работы: Определение радиуса
кривизны линзы R, входящей в устройство колец Ньютона, а также оценка
доверительного интервала и относительной погрешности в определении величины R.
Оборудование:
Оптическая скамья, осветитель, диафрагма, прибор Ньютона, линза-объектив,
экран, светофильтр.
Теоретическое введение.
Кольца Ньютона наблюдаются в
случае соприкосновении выпуклой поверхности плоско-выпуклой линзы малой
кривизны с плоско-параллельной поверхностью. Воздушная прослойка между
плоскостью и линзой имеет переменную толщину, разность хода интерферирующих их
лучей зависит от толщины этой прослойки. Чем больше толщина воздушной
прослойки, тем больше число наблюдаемых колец.
Кольца Ньютона могут
наблюдаться в отраженном и проходящем свете.
В отраженном свете оптическая
разность хода для колец Ньютона определяют, учитывая λ/2,условием:
![]() ,
,
В отраженном свете по условию
образовании максимума:
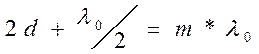 ,
,
Для минимумов в отраженном
свете:
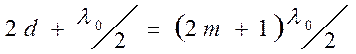 .
.
Так как на экране получаются
увеличенные интерференционные кольца, то вначале надо рассчитать радиусы
действительных колец:
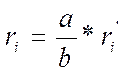 ,
,
Радиусы действительных колец
рассчитывают для опыта с проходящим и отраженным светом. В первом случае берут
радиусы колец определенного цвета, во втором – радиусы темных колец при
условии, что в опыте с отраженным светом использовали фильтр того же цвета.
Радиус кривизны линзы, входящей
в устройство колец Ньютона, определяется теоретически по формуле:
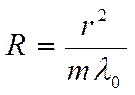 ,
,
Так как практически трудно добиться
идеального контакта сферической поверхности линзы и плоской пластинки в одной
точке вследствие упругой деформации стекла и падения в место соприкосновения
пылинки, то формулу использовать непосредственно нельзя: кольцу с номером m в действительности может
соответствовать номер (m+p), где p – неизвестное целое число, одинаковое для всех колец. Для
исключения числа p вычисление
радиуса кривизны надо делать по разности квадратов радиуса двух колец:
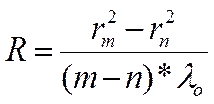 .
.
Ход работы:
Измеряем радиусы полученных колец:
![]() ;
; ![]() ;
;
![]() .
.
Вычисляем радиусы действительных колец по формуле:
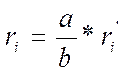 ,
,
где ![]() =155
=155
мм=0,155 м; ![]() =445мм=0,445м.
=445мм=0,445м.
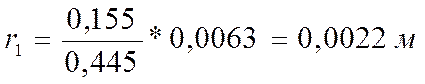 ;
;
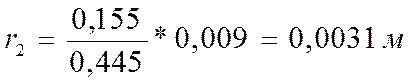 ;
;
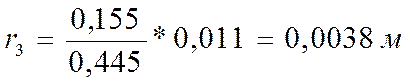 ;
;
После того как мы вычислили действительные радиусы колец, вычисляем
радиус кривизны линзы по формуле:
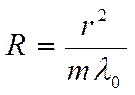 ,
,
Где ![]() =435
=435
Нм=![]() м,
м,
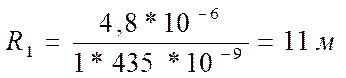 ;
;
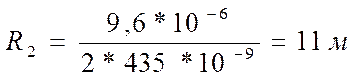 ;
;
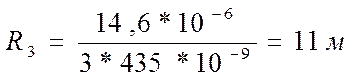 .
.
Найдем среднее значение:
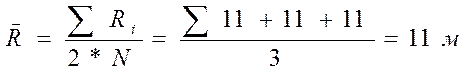 ;
;
Найдем средне квадратичную
погрешность:
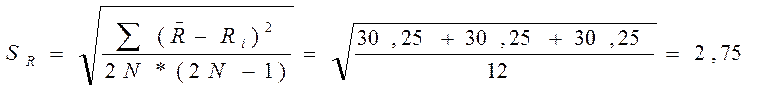 ;
;
Доверительный интервал найдем
по формуле:
![]() ;
; ![]() ;
;
Найдем относительную
погрешность:
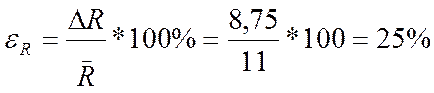 .
.
Вывод: Мы определили радиусы
кривизны линзы R, входящей в устройство колец Ньютона, а также
оценили доверительный интервал и относительную погрешность в определении
величины R.
Похожие материалы
- Изучение гармонических колебаний пружинного маятника
- Изучение законов кинематики и динамики поступательного движения на машине Атвуда
- Изучение основных законов внешнего фотоэлектрического эффекта
Информация о работе
Тип:
Отчеты по лабораторным работам
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Содержание:
Линзы:
На уроках природоведения вы. наверное, пользовались микроскопом. Кое-кто из ваших друзей (а может, и вы сами) имеет очки. Вероятнее всего, большинство из вас знакомы с биноклем, зрительной тру бой, телескопом. У всех этих приборов есть общее: их основной частью является линза.
Равные виды линз
Линзой (сферической*) называют прозрачное тело, ограниченное с двух сторон сферическими поверхностями (в частности, одна из поверхностей может быть плоскостью). По форме линзы делятся на выпуклые (рис. 3.50) и вогнутые (рис. 3.51).
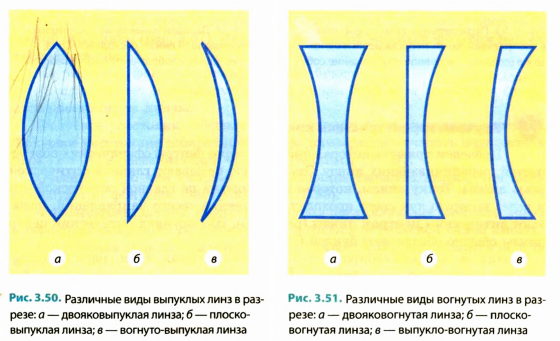
Если толщина линзы d во много раз меньше радиусов 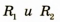
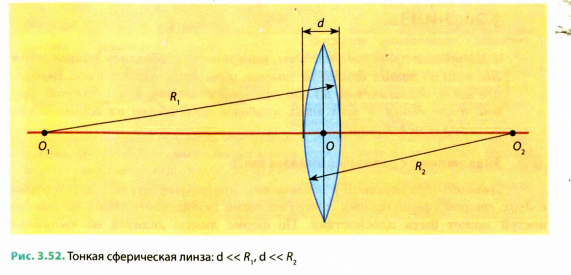
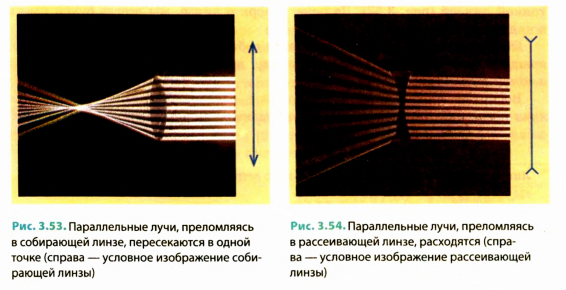
Обычно выпуклые линзы являются собирающими: параллельные лучи, которые падают на собирающую линзу, пройдя сквозь нее, пересекаются в одной точке (рис. 3.53).
Вогнутые линзы чаще всего бывают рассеивающими: параллельные лучи после прохождения сквозь рассеивающую линзу выходят расходящимся пучком (рис. 3.54).
Линзы также бывают цилиндрическими, но встречаются такие линзы редко.
Характеристики линз
Проведем прямую, которая проходит через центры сферических поверхностей, ограничивающих линзу. Эту прямую называют главной оптической осью линзы. Точку линзы, которая расположена на главной оптической оси и через которую луч света проходит, не изменяя своего направления, называют оптическим центром линзы (рис. 3.55). На рисунках оптический центр линзы обычно обозначают буквой О.
Точку, в которой собираются после преломления лучи, параллельные главной оптической оси собирающей линзы, называют действительным фокусом собирающей линзы (рис. 3.56).
Если пучок лучей, параллельных главной оптической оси, направить на рассеивающую линзу, то после преломления они выйдут расходящимся пучком.
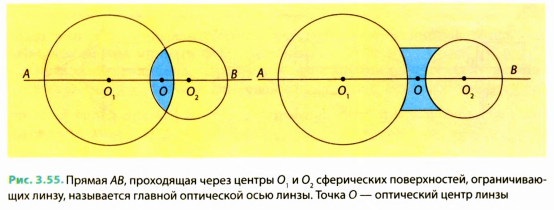
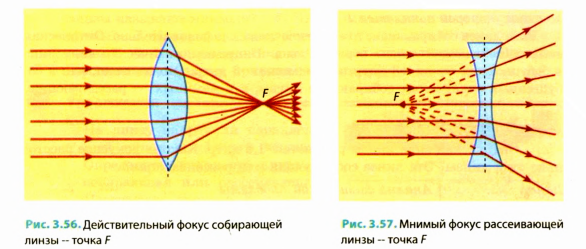
Однако их продолжения соберутся в одной точке на главной оптической оси линзы (рис. 3.57). Эту точку называют мнимым фокусом рассеивающей линзы.
На рисунках фокус линзы обозначают буквой F.
Расстояние от оптического центра линзы до фокуса называют фокусным расстоянием линзы.
Фокусное расстояние обозначается символом F и измеряется в метрах. Фокусное расстояние собирающей линзы договорились считать положительным (F>0), а рассеивающей — отрицательным (F<0).
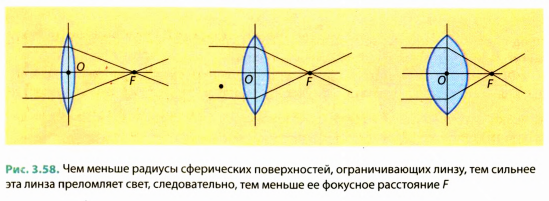
Очевидно, что чем сильнее преломляющие свойства линзы, тем меньшим будет ее фокусное расстояние (рис. 3.58).
Физическая величина, характеризующая преломляющие свойства линзы и обратная фокусному расстоянию, называется оптической силой линзы.
Оптическая сила линзы обозначается символом D и вычисляется по формуле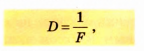
где F — фокусное расстояние линзы.
Единицей оптической силы является диоптрия
1 диоптрия (дптр) — это оптическая сила такой линзы, фокусное рас стояние которой равняется 1 м.
Если линза собирающая, то ее оптическая сила положительна. Оптическая сила рассеивающей линзы отрицательна. Например, оптическая сила линз в бабушкиных очках +3 дптр, а в маминых -3 дптр. Это означает, что в бабушкиных очках стоят собирающие линзы, а в маминых — рассеивающие.
Пример №1
Оптическая сила линзы равняется -1,6 дптр. Каково фокусное расстояние этой линзы? Эта линза собирающая или рассеивающая?
Дано:
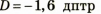
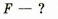
Анализ физической проблемы
Для определения фокусного расстояния этой линзы воспользуемся формулой для вычисления оптической силы линзы. Поскольку 1)< 0, то линза рассеивающая.
Поиск математической модели, решение:
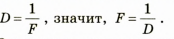
Определим числовое значение искомой величины:
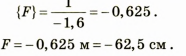
Ответ: F = -62,5 см, линза рассеивающая.
Итоги:
Прозрачное тело, ограниченное с двух сторон сферическими поверхностями, называют линзой. Линзы бывают собирающими и рассеивающими, а по форме — выпуклыми и вогнутыми.
Линза называется собирающей, если пучок параллельных лучей, падающий на нее, после преломления в линзе пересекается в одной точке. Эту точку называют действительным фокусом линзы.
Линза называется рассеивающей, если параллельные лучи, падающие на нее, после преломления в линзе идут расходящимся пучком, однако продолжения этих преломленных лучей пересекаются в одной точке. Эта точка называется мнимым фокусом линзы.
Физическая величина, характеризующая преломляющие свойства линзы и являющаяся обратной фокусному расстоянию линзы, называется оптической силой линзы = Оптическая сила линзы измеряется в диоптриях (дптр).
Формула тонкой линзы
Сейчас никого не удивляет, что можно увидеть бактерии и другие микроорганизмы, рассмотреть невидимые невооруженным глазом детали рельефа поверхности Луны или полюбоваться портретом, нарисованным на маковом зернышке. Все это стало возможным потому, что с по мощью линзы получают разные по размеру изображения предметов.

Изображение предмета, полученное с помощью линзы
Расположив последовательно зажженную свечу, собирающую линзу и экран, получим на экране четкое изображение пламени свечи (рис. 3.59). Изображение может быть как большим, так и меньшим, чем само пламя, или равным ему — в зависимости от расстояния между свечой и экраном. Чтобы выяснить, при каких условиях с помощью линзы образуется то или иное изображение предмета, рассмотрим приемы его построения.
Строим изображение предмета, которое дает тонкая линза
Любой предмет можно представить как совокупность точек. Каждая точка предмета, который светится собственным или
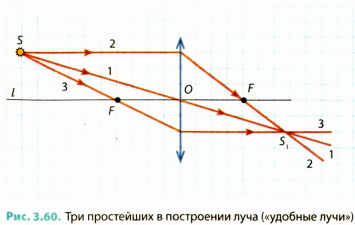
- — луч, проходящий через оптический центр О линзы (не преломляется и не изменяет своего направления);
- — луч, параллельный главной оптической оси / линзы (после преломления в линзе идет через фокус F);
- — луч, проходящий через фокус F (после преломления в линзе идет параллельно главной оптической оси/линзы)
- отраженным светом, испускает лучи во всех направлениях.
Для построения изображения точки S, получаемого с помощью линзы, достаточно найти точку пересечения 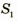 , любых двух лучей, выходящих из точки S и проходящих сквозь линзу (точка
, любых двух лучей, выходящих из точки S и проходящих сквозь линзу (точка 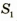 и будет действительным изображением точки S). Кстати, в точке
и будет действительным изображением точки S). Кстати, в точке 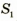 пересекаются все лучи, выходящие из точки S, однако для построения изображения достаточно двух лучей (любых из трех показанных на рис. 3.60).
пересекаются все лучи, выходящие из точки S, однако для построения изображения достаточно двух лучей (любых из трех показанных на рис. 3.60).
Изобразим схематически предмет стрелкой АВ и удалим его от линзы на расстояние, большее, чем 2F (за двойным фокусом) (рис. 3.61, а). Сначала построим изображение 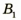 точки В. Для этого воспользуемся двумя «удобными* лучами (луч 1 и луч 2). Эти лучи после преломления в линзе пересекутся в точке
точки В. Для этого воспользуемся двумя «удобными* лучами (луч 1 и луч 2). Эти лучи после преломления в линзе пересекутся в точке 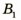 . Значит, точка
. Значит, точка 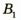 является изображением точки В. Для построения изображения
является изображением точки В. Для построения изображения 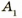 точки А из точки
точки А из точки 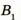 опустим перпендикуляр на главную оптическую ось /. Точка пересечения перпендикуляра и оси / и является точкой
опустим перпендикуляр на главную оптическую ось /. Точка пересечения перпендикуляра и оси / и является точкой 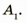
Значит, 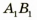 и является изображением предмета АВ, полученное с помощью линзы. Мы видим: если предмет расположен за двойным фокусом собирающей линзы, то его изображение, полученное с помощью линзы, будет уменьшенным, перевернутым, действительным. Такое изображение получается, например, на пленке фотоаппарата (рис. 3.61, б) или сетчатке глаза.
и является изображением предмета АВ, полученное с помощью линзы. Мы видим: если предмет расположен за двойным фокусом собирающей линзы, то его изображение, полученное с помощью линзы, будет уменьшенным, перевернутым, действительным. Такое изображение получается, например, на пленке фотоаппарата (рис. 3.61, б) или сетчатке глаза.
На рис. 3.62, а показано построение изображения предмета АВ, полученного с помощью собирающей линзы, в случае, когда предмет расположен
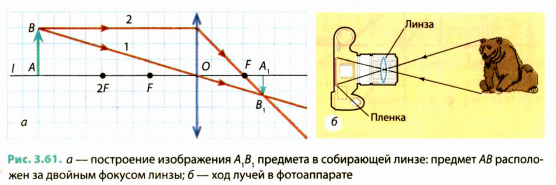
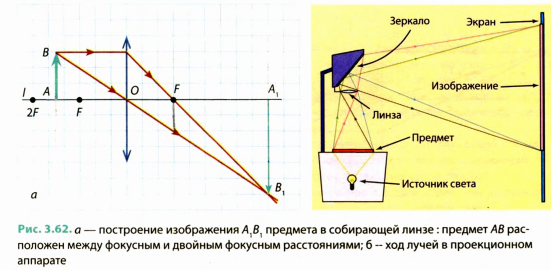
Изображение предмета в этом случае будет увеличенным, перевернутым, действительным. Такое изображение позволяет получить проекционная аппаратура на экране (рис. 3.62, б).
Если поместить предмет между фокусом и линзой, то изображения на экране мы не увидим. Но, посмотрев на предмет сквозь линзу, увидим изображение предмета — оно будет прямое, увеличенное.
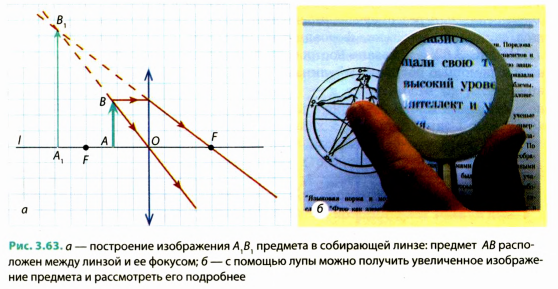
Используя «удобные лучи» (рис. 3.63, а), увидим, что после преломления в линзе реальные лучи, вышедшие из точки В, пойдут расходящимся пучком. Однако их продолжения пересекутся в точке В,. Напоминаем, что в этом случае мы имеем дело с мнимым изображением предмета. То есть если предмет расположен между фокусом и линзой, то его изображение бу дет увеличенным, прямым, мнимым, расположенным с той же стороны от линзы, что и сам предмет. Такое изображение можно получить с помощью лупы (рис. 3.63, б) или микроскопа.
Итак, размеры и вид изображения, полученного с помощью собирающей линзы, зависят от расстояния между предметом и этой линзой.
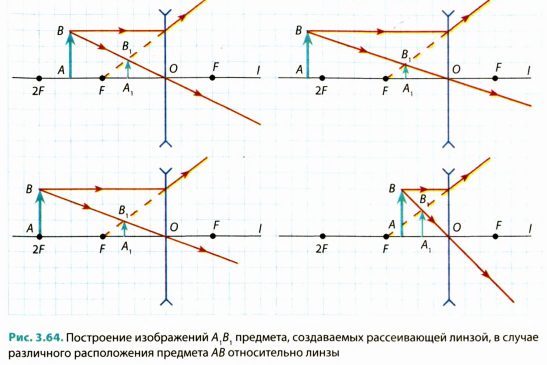
Внимательно рассмотрите рис. 3.64, на котором показано построение изображения предмета, полученного с помощью рассеивающей линзы. Построение показывает, что рассеивающая линза всегда дает мнимое, уменьшенное, прямое изображение предмета, расположенное с той же стороны от линзы, что и сам предмет.
Мы часто сталкиваемся с ситуацией, когда предмет значительно больше, чем линза (рис. 3.65), или когда часть линзы закрыта непрозрачным экраном (например, линза объектива фотоаппарата). Как создается изображение в этих случаях? На рисунке видно, что лучи 2 и 3 при этом не проходят через линзу. Однако мы, как и раньше, можем использовать эти лучи для построения изображения, получаемого с помощью линзы. Поскольку реальные лучи, вышедшие из точки В, после преломления в линзе пересекаются в одной точке —  то «удобные лучи*, с помощью которых мы строим изображение, тоже пересеклись бы в точке
то «удобные лучи*, с помощью которых мы строим изображение, тоже пересеклись бы в точке 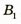
Как выглядит формула тонкой линзы
Существует математическая зависимость между расстоянием d от предмета до линзы, расстоянием f от изображения предмета до линзы и фокусным расстоянием F линзы. Эта зависимость называется формулой тонкой линзы и записывается так:
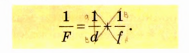
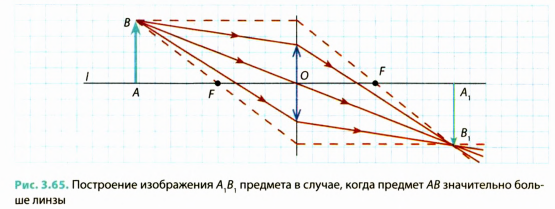
Пользуясь формулой тонкой линзы для решения задач, следует иметь в виду: расстояние f (от изображения предмета до линзы) следует брать со знаком минус, если изображение мнимое, и со знаком плюс, если изображение действительное; фокусное расстояние F собирающей линзы положительное, а рассеивающей — отрицательное.
Пример №2
Рассматривая монету с помощью лупы, оптическая сила которой +5 дптр, мальчик расположил монету на расстоянии 2 см от лупы. Определите, на каком расстоянии от лупы мальчик наблюдал изображение монет
Дано:
d = 2 см = 0,02 м
D = + 5 дптр
f- ?
Анализ физической проблемы, поиск математической модели
Лупу можно считать тонкой линзой, поэтому чтобы найти расстояние от лупы до изображения, воспользуемся
формулой тонкой линзы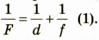 Фокусное расстояние F неизвестно, но мы знаем, что
Фокусное расстояние F неизвестно, но мы знаем, что 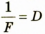 (2), где
(2), где
D — оптическая сила линзы, данная в условии задачи.
Решение и анализ результатов
Подставив формулу (2) в формулу (1), получаем
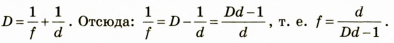
Проверим единицу: 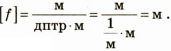
Найдем числовое 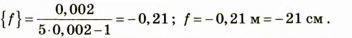
Проанализируем результат: знак ♦-* говорит о том, что изображение является мнимым.
Ответ: f = -21 см, изображение мнимое.
Итоги:
В зависимости от вида линзы (собирающая или рассеивающая) и местоположения предмета относительно этой линзы получают разные изображения предмета с помощью линзы (см.таблицу):
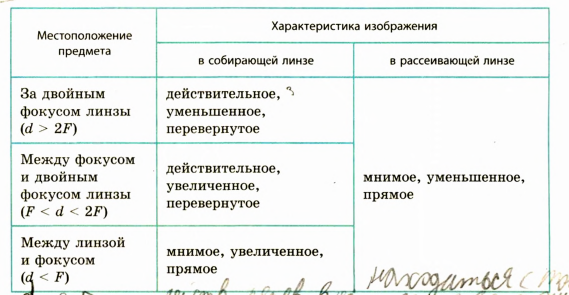
Таким образом, по типу изображения можно судить так и о местоположении предмета относительно нее.
Расстояние d от предмета до линзы, расстояние f от изображения до линзы и фокусное расстояние F связаны формулой тонкой линзы: 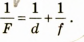
Что такое линза
Многие люди носят очки. А задумывались ли вы над вопросами: что собой представляют стекла очков и какова их роль? Стекла очков есть не что иное, как линзы. Ни один оптический прибор (от простой лупы до сложных телескопов) не обходится без линз. Что же такое линза?
Линза представляет собой прозрачное тело, ограниченное криволинейными (чаще всего сферическими) или криволинейной и плоской поверхностями. Материалом для линз обычно служит оптическое или органическое стекло.
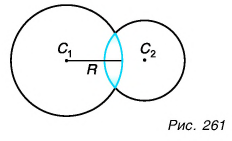
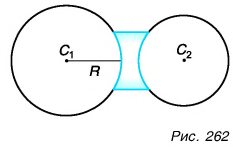
На рисунках 261, 262 представлены сечения линз двух типов: двояковыпуклой (см. рис. 261) и двояковогнутой (см. рис. 262). Одна из поверхностей линзы может быть плоской, как, например, на рисунке 263. Такие линзы называются плосковыпуклая (см. рис. 263, а) и плосковогнутая, (см. рис. 263, б).
Прямая, проходящая через центры 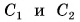 сферических поверхностей (рис. 264), называется главной оптической осью линзы. Радиусы
сферических поверхностей (рис. 264), называется главной оптической осью линзы. Радиусы 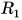 и
и 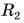 есть радиусы кривизны поверхностей линзы (см. рис. 264).
есть радиусы кривизны поверхностей линзы (см. рис. 264).
Если толщина линзы мала но сравнению с радиусами 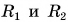 кривизны ее поверхностей (см. рис. 264), то линза называется тонкой. Ее часто изображают
кривизны ее поверхностей (см. рис. 264), то линза называется тонкой. Ее часто изображают 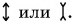 Всякая тонкая линза имеет точку, проходя через которую, луч не меняет своего направления (лучи 1 и 2 на рисунке 264). Эта точка О называется оптическим центром линзы. В дальнейшем мы будем рассматривать только тонкие линзы, изготовленные из вещества, оптически более плотного, чем среда (воздух), в которой они находятся.
Всякая тонкая линза имеет точку, проходя через которую, луч не меняет своего направления (лучи 1 и 2 на рисунке 264). Эта точка О называется оптическим центром линзы. В дальнейшем мы будем рассматривать только тонкие линзы, изготовленные из вещества, оптически более плотного, чем среда (воздух), в которой они находятся.
Как линзы меняют направление падающих на них лучей после преломления? Ответ получим с помощью опыта.
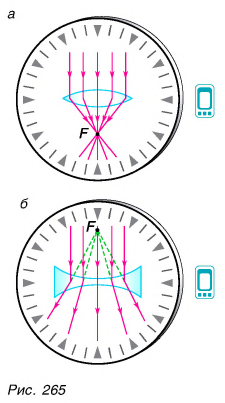
Направим на двояковыпуклую линзу (рис. 265, а) параллельно главной оптической оси лучи света. После преломления в линзе они пересекают главную оптическую ось в одной точке F. Значит, двояковыпуклая линза собирает преломленные лучи, поэтому такая линза называется собирающей. Также превращают параллельный пучок в сходящийся линзы 2, 3, изображенные на рисунке 270. При замене линзы на двояковогнутую (рис. 265, б) лучи после преломления в линзе расходятся, а центральный луч, как и в первом случае, не испытывает преломления. Итак, двояковогнутая линза рассеивает параллельный пучок падающих на нее лучей, поэтому такая линза называется рассеивающей. Рассеивают параллельный пучок и линзы 5, 6 (см. рис. 270).
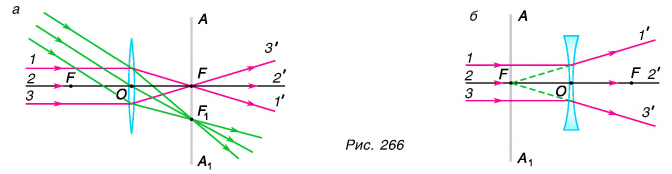
Точка F (см. рис. 265, а, рис. 266, а), в которой пересекаются преломленные линзой лучи, падающие параллельно главной оптической оси, или их продолжения (см. рис. 265, б, рис. 266, б), называется главным фокусом линзы. Так как параллельные лучи можно пустить как с одной, так и с другой стороны линзы, то и главных фокуса у линзы два. Оба фокуса лежат на главной оптической оси симметрично относительно оптического центра линзы (см. рис. 266). А в какой точке собирает линза лучи, идущие под углом к главной оптической оси? Оказывается, в точке 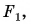 которая находится в плоскости
которая находится в плоскости 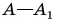 (см. рис. 266, а), проходящей через главный фокус перпендикулярно главной оптической оси. Эта плоскость называется фокальной плоскостью, а точка
(см. рис. 266, а), проходящей через главный фокус перпендикулярно главной оптической оси. Эта плоскость называется фокальной плоскостью, а точка 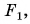 в отличие от главного фокуса, называется фокусом.
в отличие от главного фокуса, называется фокусом.
Обратите внимание, что у собирающей линзы в фокусе пересекаются сами преломленные лучи, несущие энергию, поэтому фокус называется действительным. У рассеивающей линзы в фокусе пересекаются продолжения преломленных лучей. Такой фокус называют мнимым.
Расстояние от оптического центра до главного фокуса называется фокусным расстоянием. Его тоже принято обозначать буквой F.
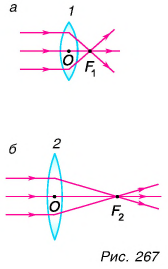
Линза, имеющая более выпуклые поверхности, преломляет лучи сильнее. Линза 1 (рис. 267, а) преломляет лучи сильнее, чем линза 2 (рис. 267, 6). Фокусное расстояние 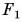 у линзы 1 меньше, чем
у линзы 1 меньше, чем 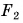 у линзы 2.
у линзы 2.
Чтобы количественно оценить преломляющую способность линзы, введем величину, обратную фокусному расстоянию, и назовем ее оптической силой линзы (обозначается буквой D):
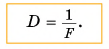
Оптическая сила измеряется в диоптриях (сокращенно дптр). Очевидно, что D = 1 дптр, если фокусное расстояние линзы F = 1 м.
А как оценивается оптическая сила рассеивающей линзы, у которой фокус мнимый? В этом случае фокусное расстояние считается отрицательным, а следовательно, и оптическая сила — отрицательной величиной.
Например, если F = -0,5 м, то оптическая сила
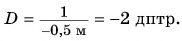
Теперь для вас не будет загадкой рекомендация врача-окулиста: «Вам нужны очки со стеклами +1,5 диоптрии или -2 диоптрии».
Для любознательных:
Не следует думать, что любая линза с выпуклой поверхностью будет обязательно собирающей, а с вогнутой — рассеивающей. Собирающей является всякая линза, у которой середина толще краев (например, линзы 2, 2, 3 на рисунке 270), а рассеивающей — линза, у которой середина тоньше краев (см. рис. 270, линзы 4, 5, 6). И не забывайте, что все наши рассуждения справедливы, если вещество линзы (стекло) имеет большую оптическую плотность, чем окружающая среда (воздух).
В природе собирающими линзами являются капельки росы, в быту — наполненные водой прозрачные сосуды — кувшин, пластиковая бутылка. Подумайте и ответьте, какие это линзы.
Главные выводы:
- Линзы меняют направление падающих на них лучей после преломления, за исключением тех, которые проходят через оптический центр линзы.
- Собирающая линза после преломления делает параллельный пучок лучей сходящимся, рассеивающая линза — расходящимся.
- Лучи, идущие параллельно главной оптической оси, после преломления в собирающей линзе пересекаются в главном фокусе. В рассеивающей линзе в главном фокусе пересекаются продолжения преломленных лучей.
- Величина, обратная фокусному расстоянию, определяет оптическую силу линзы.
Построение изображений в тонких линзах
Глядя в окуляр микроскопа на уроках биологии, задумывались ли вы, как получается увеличенное изображение клеток? Главными частями микроскопа являются линзы. Именно они позволяют получать увеличенное или уменьшенное (например, в фотоаппарате) изображение предмета.
Какие изображения предмета создает линза?
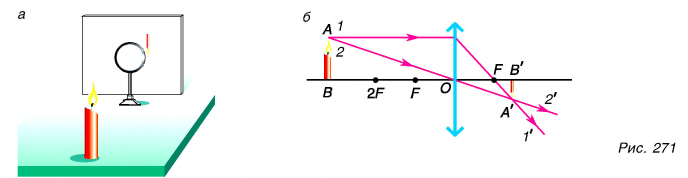
Проведем опыт. На столе расположим экран, собирающую линзу и зажженную свечу (рис. 271, а), удаленную от линзы на расстояние б/, большее, чем удвоенное фокусное, т. е. d > 2F. Будем передвигать экран до тех пор, пока не увидим на нем четкое изображение пламени свечи. Чем оно отличается от изображения, которое мы увидим в зеркале, поместив перед ним эту же свечу? Во-первых, оно уменьшенное, во-вторых, перевернутое. Ио самое главное, что это изображение, в отличие от мнимого изображения в зеркале, реально существует. На экране концентрируется энергия света. Чувствительный термометр, помещенный в изображение пламени свечи, покажет повышение температуры. Поэтому полученное в линзе изображение называют действительным, в отличие от мнимых изображений, наблюдаемых в плоском зеркале.
Подтвердим сказанное построением (рис. 271, б). Для получения изображения точки А достаточно использовать два луча, ход которых после преломления в линзе известен. Луч 1 идет параллельно главной оптической оси и после преломления в линзе проходит через главный фокус. Луч 2 идет через оптический центр и не меняет своего направления после прохождения сквозь линзу. Точка А’, являющаяся пересечением прошедших линзу лучей 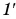 и 2′, есть действительное изображение точки А. Заметим, что через точку А пройдет и любой другой преломленный луч идущий от точки А, благодаря чему энергия, излученная точкой А пламени свечи, будет сконцентрирована в точке А’.
и 2′, есть действительное изображение точки А. Заметим, что через точку А пройдет и любой другой преломленный луч идущий от точки А, благодаря чему энергия, излученная точкой А пламени свечи, будет сконцентрирована в точке А’.
Продолжим опыт. Поставим свечу на расстоянии d = 2F. Перемещая экран, мы увидим на нем действительное, перевернутое изображение пламени свечи, но размер его будет равен размеру пламени самой свечи (рис. 272). Сделайте сами построение изображения для этого случая.
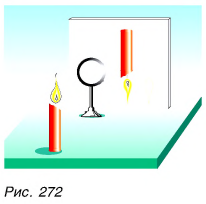
Передвигая свечу ближе к линзе (F < d < 2F) и удаляя экран, мы увидим на нем действительное, перевернутое, увеличенное изображение пламени свечи (построение сделайте сами).
Наконец поставим свечу на расстоянии d от линзы, меньше фокусного, т. е. d
А какие изображения предмета дает рассеивающая линза? Пусть параллельно главной оптической оси надает луч 1 (рис. 275). После линзы преломленный луч 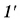 идет так, что только его продолжение проходит через фокус. Луч 2 не испытывает преломления. Видно, что лучи
идет так, что только его продолжение проходит через фокус. Луч 2 не испытывает преломления. Видно, что лучи 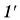 и 2′ не пересекаются. В точке А’ пересекаются их продолжения. Тогда изображение точки А, а значит, и всего предмета АВ — мнимое. Как все мнимые изображения, оно прямое, но уменьшенное. Даст ли рассеивающая линза действительное изображение, если менять положение предмета? Может ли оно быть увеличенным? Ответьте на эти вопросы сами, сделав соответствующие построения изображений предмета в тетради.
и 2′ не пересекаются. В точке А’ пересекаются их продолжения. Тогда изображение точки А, а значит, и всего предмета АВ — мнимое. Как все мнимые изображения, оно прямое, но уменьшенное. Даст ли рассеивающая линза действительное изображение, если менять положение предмета? Может ли оно быть увеличенным? Ответьте на эти вопросы сами, сделав соответствующие построения изображений предмета в тетради.
Главные выводы:
- Собирающая линза дает как действительные, так и мнимые изображения, рассеивающая — только мнимые.
- Все мнимые изображения — прямые, все действительные — перевернутые.
- Для нахождения изображения точки наиболее целесообразно использовать луч, идущий параллельно главной оптической оси линзы, и луч, идущий через ее оптический центр.
Пример №3
С помощью стеклянной линзы на экране, удаленном от линзы на расстояние f = 36 см, получено увеличенное в 3 раза изображение предмета. Определите расстояние от предмета до линзы и оптическую силу линзы.
Дано:
Н = Зh
f = 36 см
d — ?
D — ?
Решение
Построим изображение предмета в линзе (рис. 276).
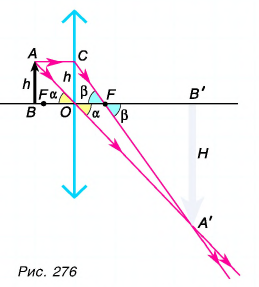
Поскольку изображение есть на экране, то оно действительное. Кроме того, оно увеличенное, значит, предмет находится между фокусом и двойным фокусом, а линза собирающая.
По условию размер предмета АВ в 3 раза меньше размера изображения А’В’. Из подобия треугольников АОВ и А’ОВ’ следует, что таким же будет и соотношение их сторон ВО и OB’, Значит, искомое расстояние d будет в 3 раза меньше заданного расстояния f. Это дает первый ответ: 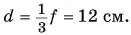 Для ответа на второй вопрос используем подобие другой нары треугольников — CFO и A’FB’. И здесь подобные стороны треугольников различаются в 3 раза.
Для ответа на второй вопрос используем подобие другой нары треугольников — CFO и A’FB’. И здесь подобные стороны треугольников различаются в 3 раза.
Так как одна из них — OF равна фокусному расстоянию F линзы, а другая — FB’ равна разности f – F, то их связь можно записать так: 3F = f – F, или 4F = f = 36 см. Вычислив значение фокусного расстояния 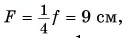 найдем и искомое значение оптической силы D линзы:
найдем и искомое значение оптической силы D линзы: 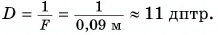
Ответ: 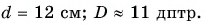
Оптическая сила и фокусное расстояние линзы
Граница разделения двух, прозрачных для света, тел может быть искривленной. Если прозрачное тело ограничить искривленными поверхностями, получим линзу (нем. linse – «чечевица»).
Линза — это прозрачное тело, ограниченное двумя выпуклыми или вво-гнутыми прозрачными поверхностями, преломляющими лучи света.
Одна из поверхностей линз может быть плоской. Линзы изготавливают из какого-либо прозрачного для света вещества: стекла, кварца, разных пластмасс, каменной соли, но чаще всего – из специальных сортов стекла.
Наибольшее распространение получили линзы, ограниченные сферическими поверхностями. В зависимости от взаимного размещения сферических поверхностей, ограничивающих линзу, различают 6 типов линз: двояковыпуклая, плоско-выпуклая, вогнуто-выпуклая (рис. 165, а, б, в); двояковогнутая, плоско-вогнутая, выпукло-ввогнутая (рис. 165, г, д, е).
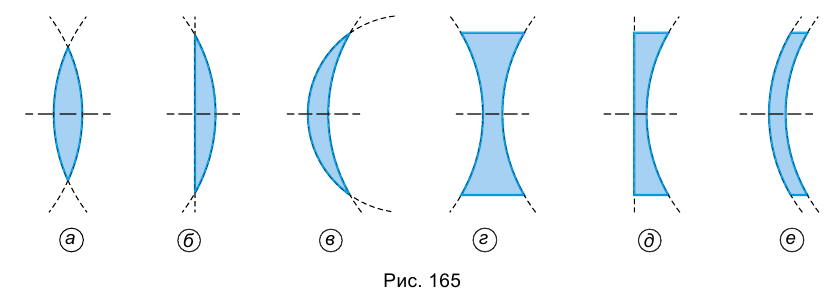
Любая линза имеет характерные точки и линии. Выясним, какие именно.
1. Прямую, проходящую через центры 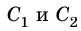 сферических поверхностей, которые ограничивают линзу, называют ее главной оптической осью (рис. 166).
сферических поверхностей, которые ограничивают линзу, называют ее главной оптической осью (рис. 166).
2. Точку О, которая лежит на главной оптической оси в центре линзы, называют оптическим центром линзы (рис. 166).
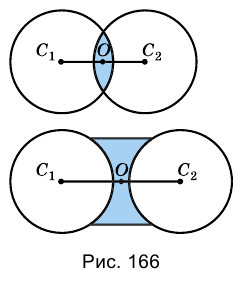
Опыт 1. Направим на линзу пучок лучей, параллельных ее главной оптической оси. Проходя через линзу, световые лучи преломляются и пересекаются в одной точке, лежащей на главной оптической оси линзы (рис. 167).
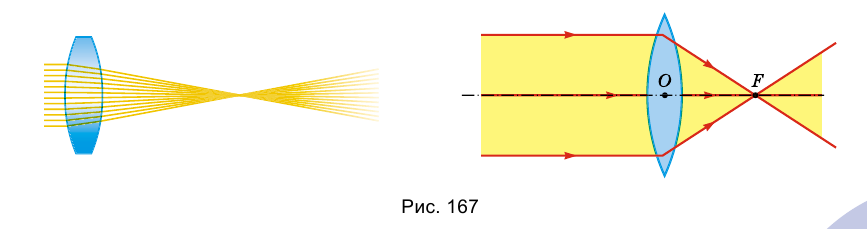
Эту точку называют главным фокусом линзы F.
3. Главный фокус линзы F – точка, в которой сходятся все, параллельные главной оптической оси, лучи после их преломления в линзе.
4. Фокусное расстояние f – расстояние от оптического центра линзы О до главного фокуса F.
Каждая линза имеет два главных фокуса.
Любая тонкая линза характеризуется двумя основными параметрами -фокусным расстоянием и оптической силой. Оптическую силу линзы обозначают большой буквой D и определяют по формуле:
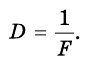
Единицей оптической силы является одна диоптрия (1 дптр), 1 дптр = 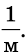 .
.
Как видно из опыта, линза преобразует пучок параллельных лучей в сходящийся, то есть собирает его в одну точку. Такую линзу называют собирательной.
Собирательная линза — это линза, которая световые лучи, падающие на нее параллельно ее главной оптической оси, после преломления собирает на этой оси в одну точку.
Опыт 2. Возьмем линзу другого типа и направим на нее параллельный главной оптической оси пучок лучей света. Лучи, преломившись на границе воздух-стекло, выходят из линзы расходящимся пучком, или рассеиваются (рис. 168).

Такую линзу называют рассеивающей.
Рассеивающая линза — это линза, которая световые лучи, падающие на нее параллельно ее главной оптической оси, после преломления отклоняет от этой оси.
Если пучок лучей, выходящий из рассеивающей линзы, продолжить в противоположном направлении, то продолжения лучей пересекутся в точке F, которая лежит на оптической оси с той же стороны, с которой свет падает на линзу. Эту точку F называют мнимым главным фокусом рассеивающей линзы (рис. 169).
Опыт 3. Пропустим световые лучи только через оптические центры линз. В результате опыта убеждаемся (рис. 170), что световые лучи, проходящие через оптический центр линзы, не преломляются, то есть не изменяют своего направления.
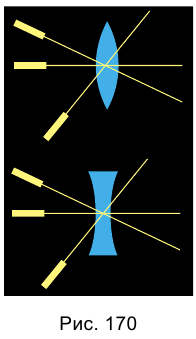
С помощью линз можно не только собирать или рассеивать световые лучи, но и строить изображение предметов. Как раз благодаря этому свойству линзы широко используют в практических целях.
Каким же образом строятся изображения предметов с помощью линз?
Изображение предмета — это воссоздание вида, формы и цвета предмета световыми лучами, проходящими через оптическую систему линз, которые имеют одну общую оптическую ось.
Если изображение предмета образовано пересечением самих лучей, то его называют действительным, если их продолжением – мнимым.
Определить ход лучей, отраженных всеми точками поверхности тела, невозможно. Поэтому для построения изображения будем использовать такие лучи, ход которых известен:
- 1. Луч, проходящий через оптический центр линзы, не преломляется (рис. 171, а).
- 2. Луч, параллельный главной оптической оси линзы, после преломления в линзе проходит через главный фокус линзы (рис. 171, б).
- 3. Луч, проходящий через главный фокус линзы, после преломления в ней, проходит параллельно главной оптической оси (рис. 171, в).
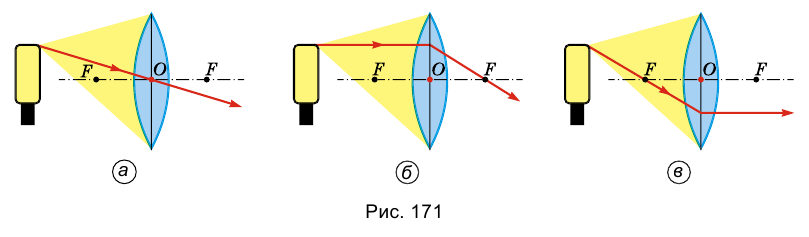
Рассмотрим случаи, при которых получается то или другое изображение, и особенности этих изображений.
1. Предмет АВ размещен между линзой и ее фокусом F.

Построим изображение точки А, использовав для этого упомянутые лучи. Луч АС (рис. 172), параллельный главной оси линзы, преломившись в линзе, пройдет через главный фокус, а луч АО не изменит своего направления. Как видно на рисунке, эти лучи расходятся. Чтобы построить изображение точки А, следует продолжить лучи в противоположном направлении до пересечения, это будет точка 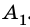 Это изображение точки есть мнимым. Такое же построение хода лучей можно выполнить для всех точек предмета, находящихся между точками А и В. Изображение этих промежуточных точек будут лежать между
Это изображение точки есть мнимым. Такое же построение хода лучей можно выполнить для всех точек предмета, находящихся между точками А и В. Изображение этих промежуточных точек будут лежать между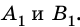 . Таким образом,
. Таким образом, 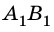 – изображение предмета АВ.
– изображение предмета АВ.
Если предмет находится между линзой и ее фокусом, то получают увеличенное, прямое, мнимое его изображение, размещенное дальше от линзы, чем сам предмет.
Такое изображение получают, когда пользуются лупой – прибором для рассматривания мелких предметов (например, чтения мелкого текста).
2. Предмет размещен в главном фокусе линзы F.
Для построения изображения предмета АВ снова воспользуемся лучами АС и АО (рис. 173). После прохождения лучей сквозь линзу мы увидим, что они параллельны между собой. Следовательно, изображение предмета АВ мы не получим.
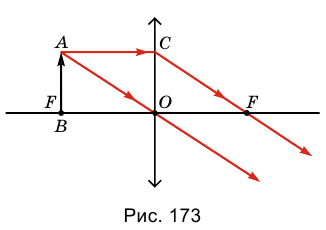
Если в главном фокусе разместить источник света, то мы превратим пучок расходящихся лучей на пучок параллельных лучей, который хорошо освещает отдаленные предметы.
Если предмет размещен в главном фокусе линзы F, изображение предмета получить нельзя.
3. Предмет размещен между главным фокусом линзы F и двойным фокусом линзы 2F.
Во время построения изображения (рис. 174) мы видим, что лучи АС и АО после прохождения линзы пересекаются в точке 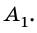 . В этой точке образуется действительное изображение точки А. Изображение
. В этой точке образуется действительное изображение точки А. Изображение 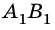 предмета АВ также будет действительным.
предмета АВ также будет действительным.
Если предмет находится между фокусом F и двойным фокусом 2F линзы, то образуется увеличенное, перевернутое и действительное изображение предмета; оно размещено с противоположной относительно предмета стороны линзы на расстоянии, больше двойного фокусного расстояния.
Такое изображение используют в проекционном аппарате, киноаппарате. Чтобы изображение на экране было прямым, диапозитивы или киноленту устанавливают в аппарат в перевернутом виде.
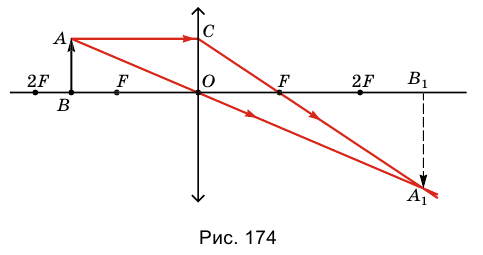
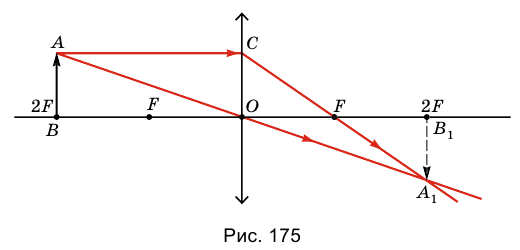
4. Предмет находится в двойном фокусе линзы. 2F.
В этом случае линза дает (рис. 175) перевернутое, действительное изображение предмета такого же размера, как и он сам. Это изображение размещено в ее двойном фокусе 2F с противоположной относительно предмета стороны линзы.
5. Если предмет находится за двойным фокусом линзы 2F (рис. 176), линза дает уменьшенное, перевернутое и действительное изображение предмета, которое размещено между ее главным фокусом F и двойным фокусом 2F с противоположной относительно предмета стороны линзы.
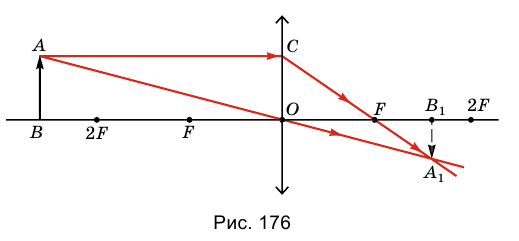
Такое изображение используют в фотоаппарате.
Пример №4
Почему не рекомендуется поливать растения днем, когда они освещены солнечными лучами, особенно те, на листьях которых остаются капельки воды?
Ответ: потому что капельки играют роль линз, фокусирующих солнечные лучи, и растения получают ожоги.
Пример №5
На рисунке 177 показан ход лучей в линзах. Какие это линзы?
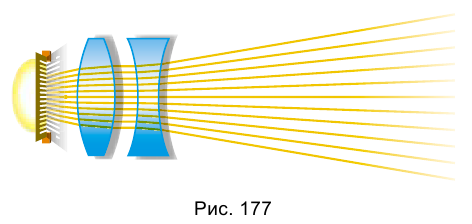
Ответ: (слева направо) источник света, собирательная линза, рассеивающая линза.
Простые оптические приборы
Знания законов отражения и преломления света в зеркалах и линзах дали возможность создать ряд оптических приборов, имеющих важное значение для современной науки и техники. Их используют специалисты разных отраслей. Это микроскоп биолога и фотоаппарат журналиста, кинокамера оператора и телескоп астронома, перископ подводника и т. п. Кроме того, оптическими приборами являются очки миллионов людей разного возраста и специальностей.
Самый простой оптический прибор – лупа.
Лупа (франц. loupe – «нарост») – оптический прибор, являющийся собирательной линзой, применяется для рассматривания мелких деталей, плохо заметных невооруженным глазом.
Общий вид луп разного вида представлен на рисунке 181, а.
Чтобы увидеть изображение предмета увеличенным, лупу следует разместить так, чтобы данный предмет был между лупой и ее фокусом (рис. 181, б).
Лучи, падающие на лупу от крайних точек предмета, преломляются в линзе и сходятся.
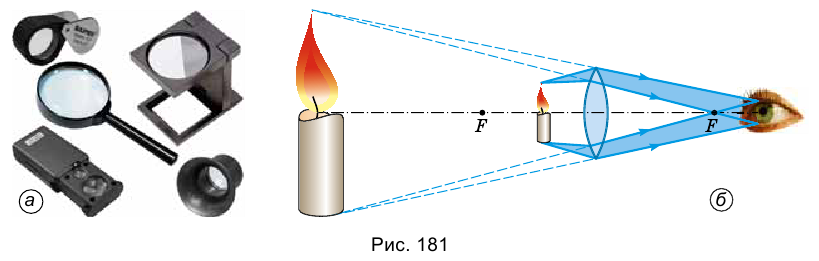
Каким же образом все это видит наш глаз?
Оказывается, наш глаз не замечает преломления лучей. Лучи, идущие от предмета сквозь линзу, воспринимаются глазом как прямолинейные. Нам кажется, что лучи, идущие от лупы к глазу, продолжаются после лупы, не преломляясь. Благодаря этому мы видим предмет увеличенным по сравнению с его действительными размерами.
Лупа дает увеличение в 10-40 раз.
Значительное увеличение изображения предметов можно получить с помощью двух линз, размещенных в металлической трубе на определенном расстоянии друг от друга. Такой прибор называют микроскопом.
Микроскоп (греч. mikro – «маленький», skopeo – «смотрю») – оптический прибор для рассматривания мелких предметов и их деталей (рис. 182, а).
Ход лучей в микроскопе показан на рисунке 182, б. Линзу, размещенную со стороны глаза, называют окуляром (лат. oculus – «глаз»), а линзу, размещенную со стороны данного предмета, называют объективом (лат. objectivus – «предметный»).
Первое увеличение изображения предмета дает объектив. Предмет в микроскопе размещается немного дальше от фокуса обьектива. В результате этого выходит увеличенное и перевернутое изображение предмета.
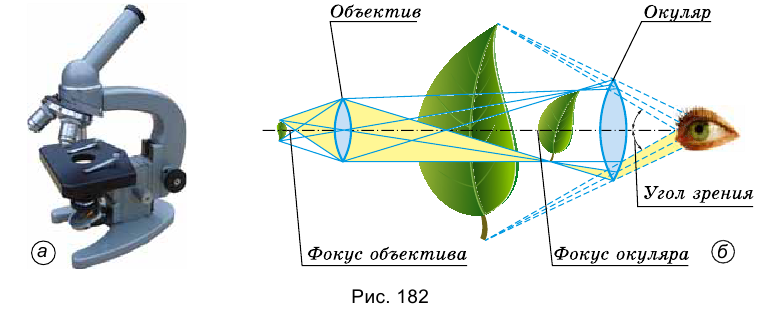
Это изображение увеличивается еще раз линзой-окуляром: оно будто служит для окуляра предметом. Окуляр, подобно лупе, размещают на расстоянии (меньше фокусного) от промежуточного изображения. В итоге мы получаем новое, более увеличенное изображение.
Если, например, объектив микроскопа дает изображение предмета, увеличенное в 20 раз, а окуляр увеличивает это изображение в 15 раз, то общее увеличение, которое дает микроскоп, будет уже 20*15 = 300 раз.
Современные электронные микроскопы дают увеличение в десятки тысяч раз. Например, так выглядят под микроскопом бактерии, увеличенные в 25 000 раз (рис. 183).
Посмотрите еще раз на схему микроскопа (рис. 182, б). Объектив микроскопа – линза – имеет меньшее фокусное расстояние, чем окуляр этого прибора. А что будет, если мы возьмем объектив, который имеет большее фокусное расстояние, чем окуляр?
В этом случае мы получим новый прибор, который называют телескопом, или рефрактором (лат. refringo – «преломляю»). Такой телескоп создал еще в 1611 г. немецкий астроном Иоганн Кеплер. А вообще первый телескоп на основе зрительной трубы построил в 1609 г. Галилео Галилей.
Телескоп (греч. tele – «далеко», skopeo – «смотреть») – оптический прибор для астрономических исследований космических объектов (рис. 184).
Прохождение в телескопе лучей от небесного тела показано на рисунке 185.

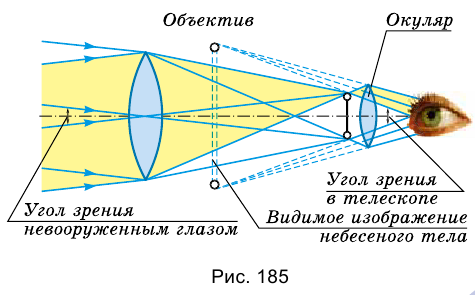
Как следует из рисунка, изображение небесного тела в телескопе мы видим под большим углом зрения, в отличие от невооруженного глаза. Окуляр телескопа, как и окуляр микроскопа, действует как обычная лупа.
Следует отметить, что, рассматривая с помощью телескопа отдаленные предметы на Земле, мы видим их перевернутыми. Однако для наблюдения за небесными телами это обстоятельство не столь важно.
Самый большой телескоп-рефрактор установлен в Йеркской обсерватории университета в Чикаго (США). Его объектив в диаметре достигает 102 см.
Другой тип – это телескопы-рефлекторы (лат. reflecto – «отображаю»). В таких телескопах, кроме преломления лучей света, используют другое их свойство – способность отражаться от зеркальных поверхностей.
Изображение небесного тела отражается с помощью маленького плоского зеркальца и рассматривается с помощью окуляра (рис. 186), который увеличивает отраженное изображение.
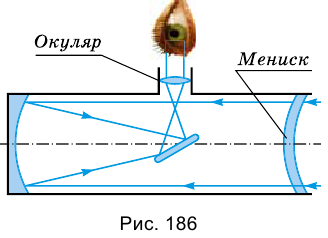
Первый рефлектор с диаметром зеркала 2,5 см и фокусным расстоянием 16,5 см построил в 1668 г. Исаак Ньютон. Сегодня самым большим в мире является зеркальный телескоп HESS II, установленный в Намибии, его площадь достигает 600 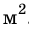 . Устройство предназначено для изучения происхождения космических лучей.
. Устройство предназначено для изучения происхождения космических лучей.
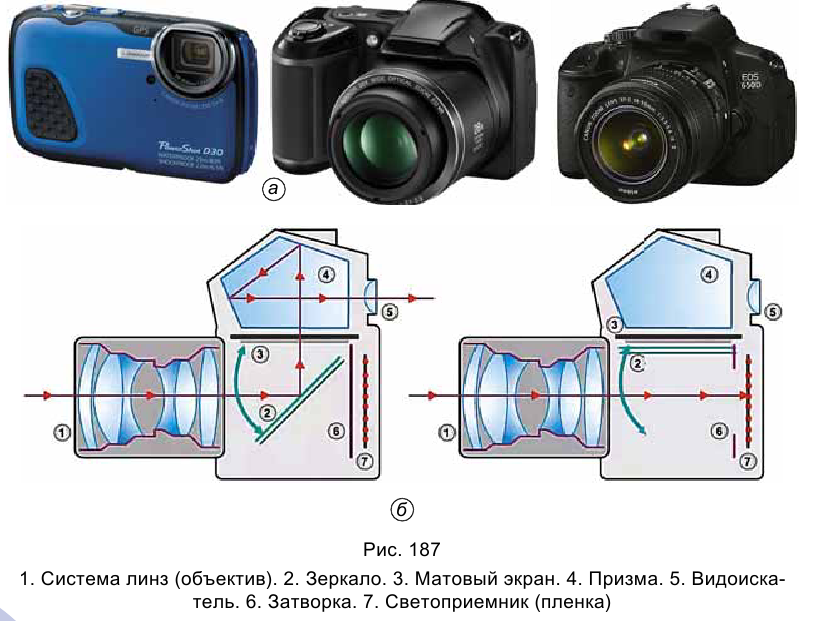
Фотоаппарат – это оптический прибор, с помощью которого на цифровом устройстве (англ, digital device – «техническое устройство или приспособление, предназначенное для получения и обработки информации в цифровой форме, используя цифровые технологии»), фотопленке, фотопластинке, фотобумаге получают изображение предмета.
Сегодня существует много различных типов фотоаппаратов (рис. 187, а). Они отличаются формой и размерами, но их строение и основные части одинаковы. Ход лучей в фотоаппарате изображен на рисунке 187, б.
- Заказать решение задач по физике
Подробное объяснение формулы тонкой линзы
Линза называется собирающей, если после преломления в ней параллельный пучок становится сходящимся. Если же после преломления в линзе параллельный пучок становится расходящимся, то линза называется рассеивающей (рис. 58).
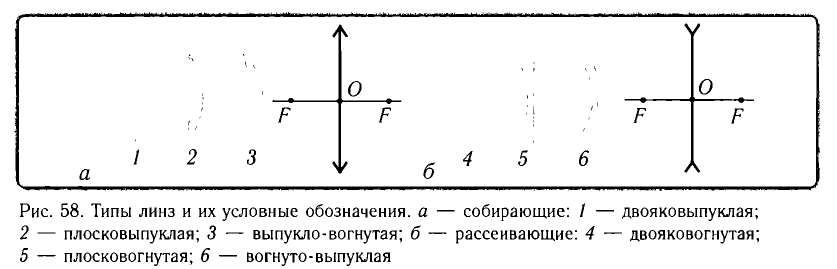
Основные типы линз и лучи, используемые для построения изображений в них, даны на рисунках 59, 60.
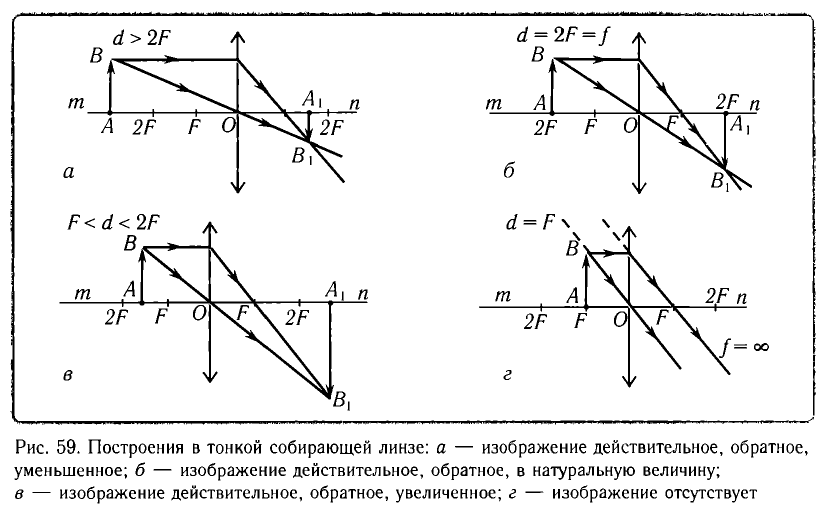
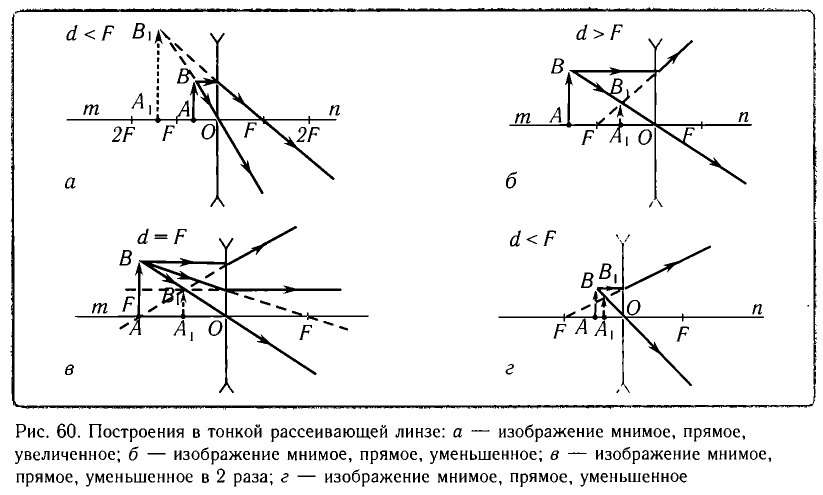
Величина, обратная фокусному расстоянию линзы, выраженному в метрах, называется ее оптической силой:
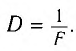
Единица оптической силы — диоптрия (1 дптр).
1 дптр соответствует оптической силе линзы с фокусным расстоянием I м: 1 дптр= 1 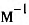 .
.
Между фокусным расстоянием F тонкой линзы, расстоянием от предмета до линзы d и расстоянием от линзы до изображения f существует определенная количественная зависимость, называемая формулой линзы.
Выведем формулу тонкой линзы, рассматривая ход характерных лучей (рис. 61).
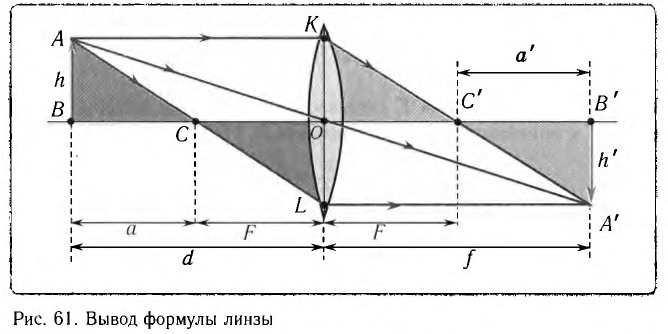
Пусть расстояние от предмета до линзы d, расстояние от линзы до изображения f, фокусное расстояние линзы F, расстояние от предмета до переднего главного фокуса а, расстояние от заднего главного фокуса до изображения а’.
Из рисунка 61 видно, что 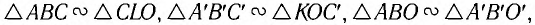 следовательно
следовательно

Из формул (1) и (2) следует формула Ньютона:
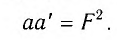
С учетом того, что d = а + F, f = а’ + F, получаем формулу тонкой линзы:
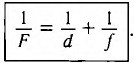
Поперечным увеличением Г называется отношение линейного размера изображения h’ к линейному размеру предмета h. Из выражения (3) находим
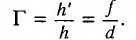
В 1604 г. в исследовании «Дополнения к Вителло» Кеплер изучал преломление света в линзах различной конфигурации и для малых углов падения пришел к формуле линзы.
Для практического использования формулы тонкой линзы следует запомнить правило знаков:
- для собирающей линзы, действительных источника и изображения величины F, d, f считают положительными;
- для рассеивающей линзы, мнимых источника и изображения величины F, d,f считают отрицательными.
Заметим, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей.
Таким образом, линза с F>0 является собирающей (положительной), а с F< 0 — рассеивающей (отрицательной).
Оптическая сила линзы зависит от свойств окружающей среды.
В современных оптических приборах используются системы линз для улучшения качества изображений. Оптическая сила D системы тонких линз, сложенных вместе, равна сумме их оптических сил 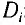 :
:
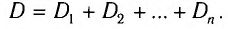
Пример №6
Предмет расположен на расстоянии d = 0,15 м от рассеивающей линзы с фокусным расстоянием F=-0,30 м. На каком расстоянии f от линзы получается изображение данного предмета?
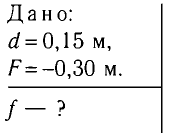
Решение
Из формулы тонкой линзы
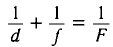
находим
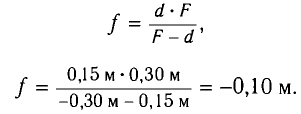
Отрицательное значение f соответствует мнимому изображению предмета.
Ответ: f =-0,10 м, изображение мнимое.
Пример №7
На каком расстоянии d от рассеивающей линзы с оптической силой D = -4 дптр надо поместить предмет, чтобы его мнимое изображение получилось в k = b раз меньше (Г = 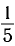 ) самого предмета?
) самого предмета?
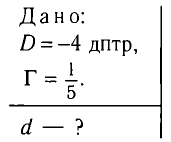
Решение
Из формулы для увеличения
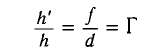
находим
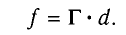
Из формулы линзы
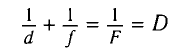
с учетом выражения для f получаем
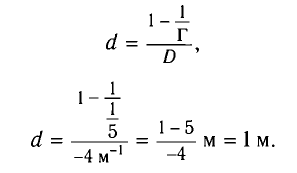
Ответ: d= 1 м.
Пример №8
Определите фокусное расстояние F собирающей линзы, дающей мнимое изображение предмета, помещенного перед ней на расстоянии d- 0,4 м, если расстояние от линзы до изображения f =-1,2 м.
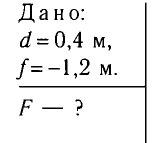
Решение
Из формулы тонкой линзы
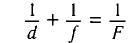
находим
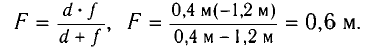
Ответ: F= 0,6 м.
Разбираем формулу тонкой линзы
Линза называется собирающей, если после преломления в ней параллельный пучок становится сходящимся. Если же после преломления в линзе параллельный пучок становится расходящимся, то линза называется рассеивающей (рис. 80).
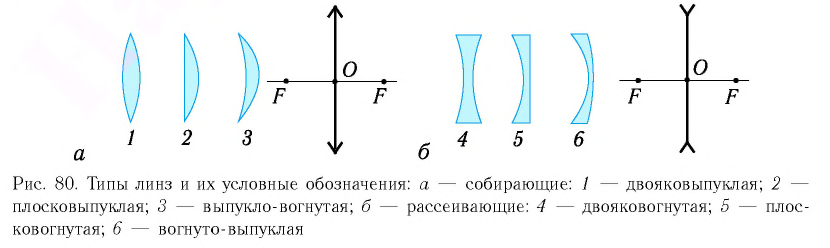
Величина, обратная фокусному расстоянию линзы, выраженному в метрах, называется ее оптической силой:
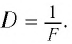
Единица оптической силы — 1 диоптрия (1 дптр).
1 дптр соответствует оптической силе линзы с фокусным расстоянием
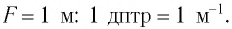
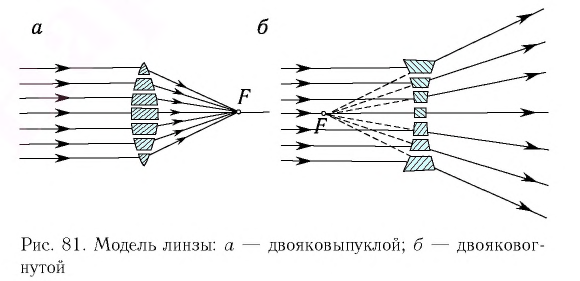
Линзы можно представить в виде совокупности частей трехгранных призм. На рисунке 81, а изображена модель двояковыпуклой линзы, собранной из частей призм, повернутых основаниями к центру линзы. Соответственно, модель двояковогнутой линзы будет представлена частями призм, повернутых основаниями от центра линзы (рис. 81, б).
Преломляющие углы этих призм можно подобрать таким образом, чтобы падающие на нее параллельные лучи после преломления в призмах собрались в одной точке 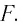
Линза считается тонкой, если ее толщина в центре намного меньше радиусов ограничивающих ее поверхностей. Тонкая линза дает неискаженное изображение только в том случае, если свет монохроматический и предмет достаточно мал, следовательно, лучи распространяются вблизи главной оптической оси. Такие лучи получили название параксиальных.
Отметим условия, при одновременном выполнении которых линза является собирающей:
- толщина в центре больше толщины у краев,
- ее показатель преломления больше показателя преломления окружающей среды.
При невыполнении (или выполнении) только одного из этих условий линза является рассеивающей.
Между фокусным расстоянием тонкой линзы, расстоянием от предмета до линзы и от линзы до изображения существует определенная количественная зависимость, называемая формулой линзы.
Выведем формулу тонкой линзы из геометрических соображений, рассматривая ход характерных лучей. Обратим внимание на луч, идущий через оптический центр 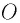 линзы, луч, параллельный главной оптической оси линзы, и луч, проходящий через главный фокус линзы.
линзы, луч, параллельный главной оптической оси линзы, и луч, проходящий через главный фокус линзы.
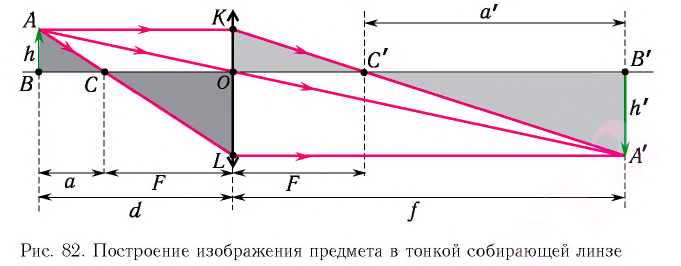
Построим изображение предмета 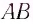 в тонкой собирающей линзе (рис. 82). Пусть расстояние от предмета до линзы
в тонкой собирающей линзе (рис. 82). Пусть расстояние от предмета до линзы 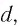 расстояние от линзы до изображения
расстояние от линзы до изображения 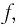 фокусное расстояние линзы
фокусное расстояние линзы 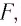 расстояние от предмета до переднего главного фокуса
расстояние от предмета до переднего главного фокуса 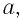 расстояние от заднего главного фокуса до изображения
расстояние от заднего главного фокуса до изображения 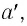 высота предмета
высота предмета 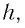 высота его изображения
высота его изображения 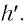
Из рисунка 82 видно, что 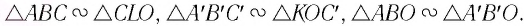 Из подобия треугольников следует:
Из подобия треугольников следует:
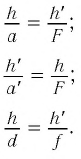
Используя соотношения (1) и (2), получим:
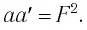
Соотношение 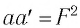 называется формулой Ньютона.
называется формулой Ньютона.
С учетом того, что 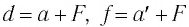 (см. рис. 82), находим:
(см. рис. 82), находим: 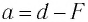 и подставляем в формулу (4):
и подставляем в формулу (4):
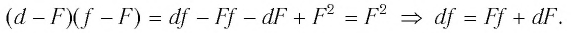
Разделив обе части последнего выражения на 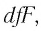 получаем формулу тонкой линзы:
получаем формулу тонкой линзы:
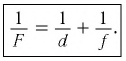
Линейным (поперечным) увеличением Г называется отношение линейного размера изображения 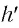 к линейному размеру предмета
к линейному размеру предмета 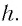 Из соотношения (3) находим линейное увеличение тонкой линзы:
Из соотношения (3) находим линейное увеличение тонкой линзы:
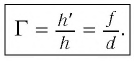
В 1604 г. в исследовании «Дополнения к Вителло» И. Кеплер изучал преломление света в линзах различной конфигурации и для малых углов падения пришел к формуле линзы.
Для практического использования формулы линзы следует твердо запомнить правило знаков:
Заметим, что предмет или источник является мнимым, только в том случае, если на линзу падает пучок сходящихся лучей.
Таким образом, линза с 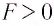 является собирающей (положительной), а с
является собирающей (положительной), а с 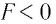 — рассеивающей (отрицательной).
— рассеивающей (отрицательной).
Оптическая сила линзы зависит от свойств окружающей среды (вспомните, как плохо мы видим под водой без плавательных очков).
В современных оптических приборах для улучшения качества изображений используются системы линз. Оптическая сила 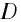 системы тонких линз, сложенных вместе, равна сумме их оптических сил
системы тонких линз, сложенных вместе, равна сумме их оптических сил 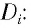
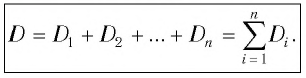
Пример №9
На каком расстоянии 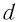 от рассеивающей линзы с оптической силой
от рассеивающей линзы с оптической силой 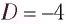 дптр надо поместить предмет, чтобы его мнимое изображение получилось в
дптр надо поместить предмет, чтобы его мнимое изображение получилось в 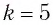 раз меньше
раз меньше 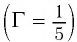 самого предмета? Постройте изображение предмета.
самого предмета? Постройте изображение предмета.
Дано:
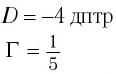
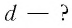
Решение
Из формулы для линейного увеличения
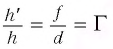
находим:
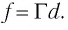
По формуле тонкой линзы ( рис. 83) с учетом правила знаков:
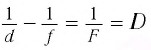
и с учетом выражения для 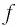 получаем:
получаем:
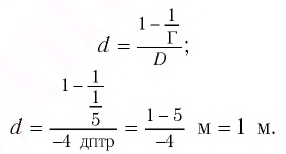
Ответ: 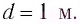
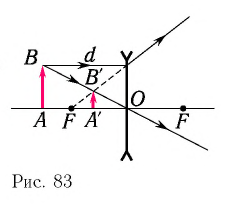
Изучаем линзы
Скорее всего, вы пользовались фотоаппаратом, знакомы с биноклем, подзорной трубой, телескопом, на уроках биологии работали с микроскопом. Некоторые из вас носят очки. Все эти устройства имеют общее — их основной частью является линза. О том, какое значение имеют данные устройства в жизни человека, вы можете рассказать и сами, а вот о том, что такое линза, какие существуют виды линз и каковы их свойства, вы узнаете из этого параграфа.
Линза — прозрачное тело, ограниченное с двух сторон сферическими поверхностями*.
 Одна из поверхностей линзы может быть плоскостью, поскольку плоскость можно рассматривать как сферу бесконечного радиуса. Линзы также бывают цилиндрическими, но встречаются такие линзы редко.
Одна из поверхностей линзы может быть плоскостью, поскольку плоскость можно рассматривать как сферу бесконечного радиуса. Линзы также бывают цилиндрическими, но встречаются такие линзы редко.
По форме линзы делят на выпуклые (рис. 14.1) и вогнутые (рис. 14.2).
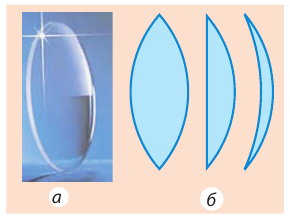
Рис. 14.1. Толщина выпуклой линзы посредине больше, чем у краев: а — вид; б — разные выпуклые линзы в разрезе
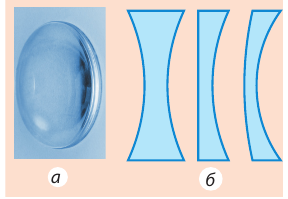
Рис. 14.2. Толщина вогнутой линзы посредине меньше, чем у краев: а — вид; б — разные вогнутые линзы в разрезе
Если толщина 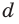 линзы во много раз меньше радиусов сферических поверхностей, ограничивающих линзу, такую линзу называют тонкой. Далее мы будем рассматривать только тонкие линзы. Прямую, которая проходит через центры сферических поверхностей, ограничивающих линзу, называют главной оптической осью линзы (рис. 14.3).
линзы во много раз меньше радиусов сферических поверхностей, ограничивающих линзу, такую линзу называют тонкой. Далее мы будем рассматривать только тонкие линзы. Прямую, которая проходит через центры сферических поверхностей, ограничивающих линзу, называют главной оптической осью линзы (рис. 14.3).
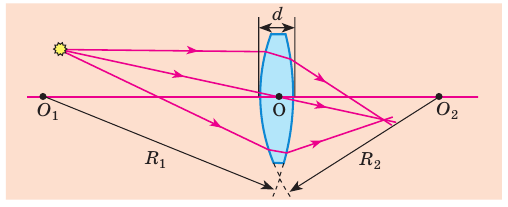
Рис. 14.3. Тонкая сферическая линза: 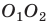 — главная оптическая ось линзы;
— главная оптическая ось линзы; 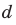 — толщина линзы;
— толщина линзы; 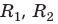 — радиусы сферических поверхностей, ограничивающих линзу;
— радиусы сферических поверхностей, ограничивающих линзу; 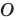 — оптический центр линзы
— оптический центр линзы
Если на линзу направить пучок световых лучей, они преломятся на ее поверхностях и изменят свое направление. В то же время на главной оптической оси линзы есть точка, которую луч света проходит практически не изменяя своего направления. Эту точку называют оптическим центром линзы (см. рис. 14.3).
Направим на линзу пучок лучей, параллельных ее главной оптической оси. Если лучи, пройдя сквозь линзу, идут сходящимся пучком, такая линза — собирающая. Точка F, в которой пересекаются преломленные лучи, — действительный главный фокус линзы (рис. 14.4).
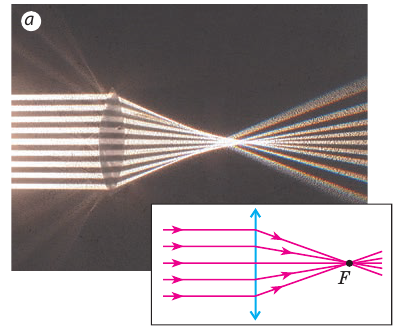
Рис. 14.4. Ход лучей после преломления в собирающей линзе. Точка F — действительный главный фокус линзы
Линза является рассеивающей, если лучи, параллельные ее главной оптической оси, пройдя сквозь линзу, идут расходящимся пучком. Точку F, в которой пересекаются продолжения преломленных лучей, называют мнимым главным фокусом линзы (рис. 14.5).
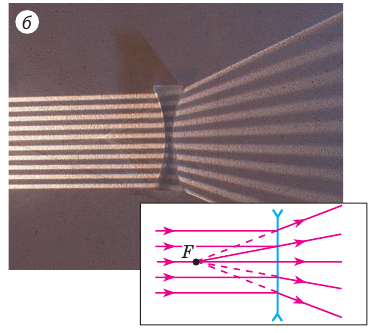
Рис. 14.5. Ход лучей после преломления в рассеивающей линзе. Точка F — мнимый главный фокус линзы
Обратите внимание: любой пучок параллельных лучей, даже если эти лучи не параллельны главной оптической оси, после преломления в собирающей линзе всегда пересекаются в одной точке (рис. 14.6) (если линза рассеивающая, в одной точке пересекаются продолжения преломленных лучей).
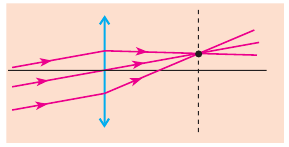
Рис. 14.6. Ход параллельных лучей после преломления в собирающей линзе
Если оптическая плотность материала, из которого изготовлена линза, больше оптической плотности среды 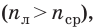 то выпуклая линза будет собирать лучи (будет собирающей), а вогнутая линза будет рассеивать лучи (будет рассеивающей) (см. рис. 14.4, 14.5).
то выпуклая линза будет собирать лучи (будет собирающей), а вогнутая линза будет рассеивать лучи (будет рассеивающей) (см. рис. 14.4, 14.5).
Если оптическая плотность материала, из которого изготовлена линза, меньше оптической плотности среды 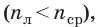 то выпуклая линза будет рассеивающей (рис. 14.7, а), а вогнутая линза — собирающей (рис. 14.7, б).
то выпуклая линза будет рассеивающей (рис. 14.7, а), а вогнутая линза — собирающей (рис. 14.7, б).
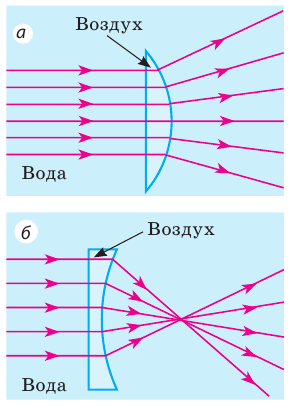
Рис. 14.7. Выпуклая (а) и вогнутая (б) воздушные линзы в воде
Определение оптической силы линзы
Любая линза имеет два главных фокуса*, расположенных на одинаковом расстоянии от оптического центра линзы (см. рис. 14.8).
 Далее главный фокус линзы, как правило, будем называть фокусом линзы.
Далее главный фокус линзы, как правило, будем называть фокусом линзы.
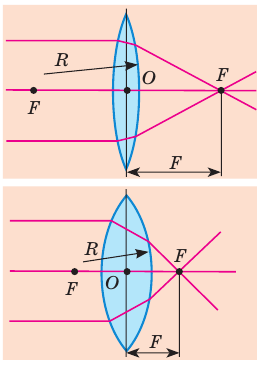
Рис. 14.8. Чем меньше радиусы R сферических поверхностей, ограничивающих линзу, тем сильнее эта линза преломляет свет, а значит, тем меньше ее фокусное расстояние F
Расстояние от оптического центра линзы до главного фокуса называют фокусным расстоянием линзы.
Фокусное расстояние, как и фокус, обозначают символом F. Единица фокусного расстояния в СИ — метр:
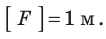
Фокусное расстояние собирающей линзы договорились считать положительным, а рассеивающей — отрицательным. Очевидно, что чем сильнее преломляющие свойства линзы, тем меньше по модулю ее фокусное расстояние (рис. 14.8).
Физическую величину, которая характеризует линзу и является обратной фокусному расстоянию линзы, называют оптической силой линзы.
Оптическую силу линзы обозначают символом D и вычисляют по формуле:
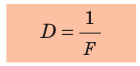
Единица оптической силы — диоптрия: 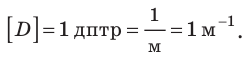
1 диоптрия — это оптическая сила линзы, фокусное расстояние которой равно 1 м. Оптическая сила собирающей линзы положительна, а рассеивающей линзы — отрицательна.
Подводим итоги:
Прозрачное тело, ограниченное с двух сторон сферическими поверхностями, называют линзой. Линза является собирающей, если пучок параллельных лучей, падающий на нее, после преломления в линзе пересекается в одной точке (эта точка — действительный фокус линзы). Линза является рассеивающей, если параллельные лучи, падающие на нее, после преломления идут расходящимся пучком, а продолжения преломленных лучей пересекаются в одной точке (эта точка — мнимый фокус линзы).
Физическую величину, которая характеризует преломляющие свойства линзы и обратна ее фокусному расстоянию, называют оптической силой линзы: 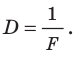 Единица оптической силы линзы — диоптрия
Единица оптической силы линзы — диоптрия 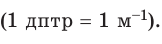
Построение изображений в линзах
Основное свойство линз заключается в том, что линзы дают изображение точки, а соответственно, и предмета (как совокупности точек) (рис. 15.1). В зависимости от расстояния между предметом и линзой изображение предмета может быть больше или меньше, чем сам предмет, мнимым или действительным. Выясним, при каких условиях с помощью линзы образуются те или иные изображения, и рассмотрим приемы их построения.

Рис. 15.1. Получение изображения пламени свечи с помощью собирающей линзы
Любой предмет можно представить как совокупность точек. Каждая точка предмета излучает (или отражает) свет во всех направлениях. В создании изображения участвует множество лучей, однако для построения изображения некоторой точки S достаточно найти точку пересечения любых двух лучей, выходящих из точки S и проходящих через линзу. Обычно для этого выбирают два из трех «удобных лучей» (рис. 15.2).
Точка S1 будет действительным изображением точки S, если в точке пересекаются сами преломленные лучи (рис. 15.2, а). Точка будет мнимым изображением точки S, если в точке пересекаются продолжения преломленных лучей (рис. 15.2, б).
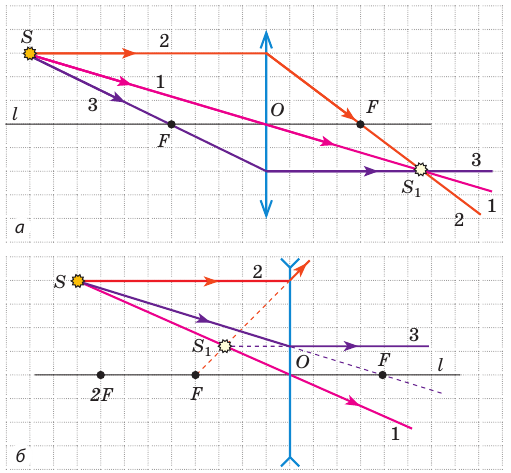
Рис. 15.2. Три самых простых в построении луча («удобные лучи»):
- луч, проходящий через оптический центр О линзы, не преломляется и не изменяет своего направления;
- луч, параллельный главной оптической оси
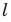 линзы, после преломления в линзе идет через фокус
линзы, после преломления в линзе идет через фокус 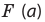 или через фокус
или через фокус 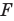 идет его продолжение (б);
идет его продолжение (б); - луч, проходящий через фокус
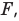 после преломления в линзе идет параллельно главной оптической оси
после преломления в линзе идет параллельно главной оптической оси 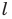 линзы (а, б)
линзы (а, б)
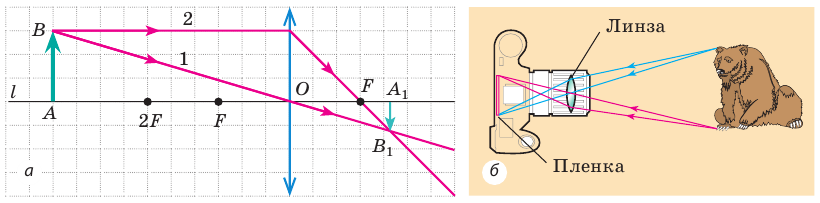
Рис. 15.3. а — построение изображения 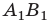 предмета
предмета 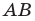 в собирающей линзе: предмет
в собирающей линзе: предмет 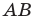 расположен за двойным фокусом линзы; б — ход лучей в фотоаппарате
расположен за двойным фокусом линзы; б — ход лучей в фотоаппарате
Строим изображение предмета, которое даёт линза:
Рассмотрим все возможные случаи расположения предмета АВ относительно собирающей линзы и докажем, что размеры и вид изображения зависят от расстояния между предметом и линзой.
1. Предмет расположен за двойным фокусом собирающей линзы (рис. 15.3, а). Сначала построим изображение точки 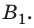 Для этого воспользуемся двумя лучами — 1 и 2. После преломления в линзе они пересекутся в точке
Для этого воспользуемся двумя лучами — 1 и 2. После преломления в линзе они пересекутся в точке 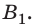 Значит, точка
Значит, точка 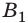 является действительным изображением точки
является действительным изображением точки 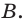 Для построения изображения точки
Для построения изображения точки 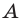 опустим из точки
опустим из точки 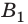 перпендикуляр на главную оптическую ось
перпендикуляр на главную оптическую ось 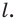 Точка
Точка 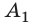 пересечения перпендикуляра и оси I является изображением точки
пересечения перпендикуляра и оси I является изображением точки 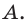
Итак, 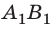 — изображение предмета
— изображение предмета 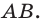 Это изображение действительное, уменьшенное, перевернутое. Такое изображение получается, например, на сетчатке глаза или пленке фотоаппарата (рис. 15.3, б).
Это изображение действительное, уменьшенное, перевернутое. Такое изображение получается, например, на сетчатке глаза или пленке фотоаппарата (рис. 15.3, б).
2. Предмет расположен между фокусом и двойным фокусом собирающей линзы (рис. 15.4, а). Изображение предмета действительное, увеличенное, перевернутое. Такое изображение позволяет получить на экране проекционная аппаратура (рис. 15.4, б).
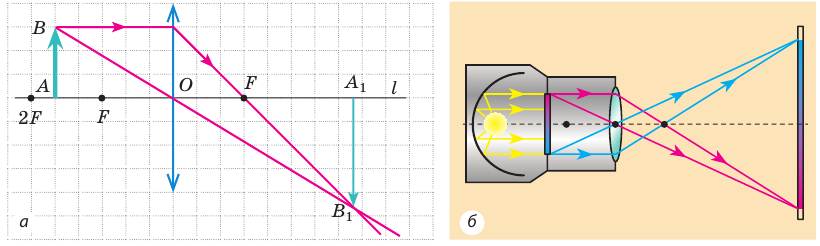
Рис. 15.4. а — построение изображения 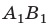 предмета
предмета 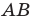 в собирающей линзе: предмет
в собирающей линзе: предмет 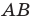 расположен между фокусом и двойным фокусом линзы; б — ход лучей в проекционном аппарате
расположен между фокусом и двойным фокусом линзы; б — ход лучей в проекционном аппарате
3. Предмет расположен между фокусом и собирающей линзой (рис. 15.5, а). Лучи, вышедшие из точки 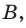 после преломления в линзе идут расходящимся пучком. Однако их продолжения пересекаются в точке
после преломления в линзе идут расходящимся пучком. Однако их продолжения пересекаются в точке 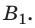
В данном случае изображение предмета является мнимым, увеличенным, прямым. Изображение расположено по ту же сторону от линзы, что и предмет, поэтому мы не можем увидеть изображение предмета на экране, но видим его, когда смотрим на предмет через линзу. Именно такое изображение дает короткофокусная собирающая линза — лупа (рис. 15.5, б).
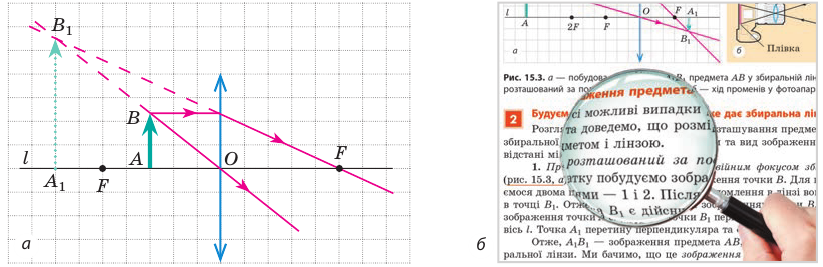
Рис. 15.5. а – построение изображения 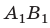 предмета
предмета 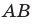 в собирающей линзе: предмет
в собирающей линзе: предмет 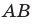 расположен между линзой и ее фокусом; б – с помощью
расположен между линзой и ее фокусом; б – с помощью
4. Предмет расположен на фокусном расстоянии от собирающей линзы. После преломления все лучи идут параллельным пучком (рис. 15.6), следовательно, в данном случае ни действительного, ни мнимого изображения мы не получим.

Рис. 15.6. Если предмет расположен в фокусе собирающей линзы, мы не получим его изображения
Внимательно рассмотрите рис. 15.7, на котором показано построение изображений предмета, полученных с помощью рассеивающей линзы. Видим, что рассеивающая линза всегда дает мнимое, уменьшенное, прямое изображение, расположенное по ту же сторону от линзы, что и сам предмет.
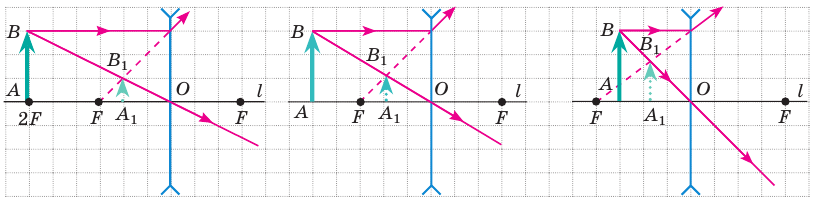
Рис. 15.7. Рассеивающая линза всегда дает мнимое, уменьшенное, прямое изображение
Чаще всего предмет больше, чем линза, или часть линзы закрыта непрозрачным экраном (как, например, линза в объективе фотоаппарата). Изменяется ли при этом внешний вид изображения? Конечно же нет. Ведь от каждой точки предмета на линзу падает множество лучей, и все они собираются в соответствующей точке изображения. Если закрыть часть линзы, это приведет лишь к тому, что энергия, попадающая в каждую точку изображения, уменьшится. Изображение будет менее ярким, однако ни его вид, ни месторасположение не изменятся. Именно поэтому, строя изображение, мы можем использовать все «удобные лучи», даже те, которые не проходят через линзу (рис. 15.8).
Формула тонкой линзы:
Построим изображение предмета в собирающей линзе (рис. 15.9).
Рассмотрим прямоугольные треугольники 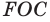 и
и 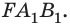 Эти треугольники подобны
Эти треугольники подобны 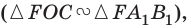 поэтому
поэтому 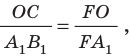 или
или 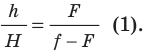
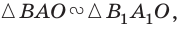 поэтому
поэтому 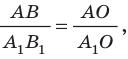 или
или 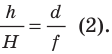
Приравняв правые части равенств (1) и (2), имеем 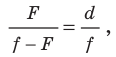 то есть
то есть 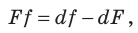 или
или 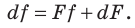 Разделив обе части последнего равенства на
Разделив обе части последнего равенства на 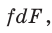 получим формулу тонкой линзы:
получим формулу тонкой линзы:
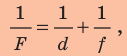 или
или 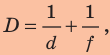
где 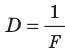 – оптическая сила линзы.
– оптическая сила линзы.
При решении задач следует иметь в виду:
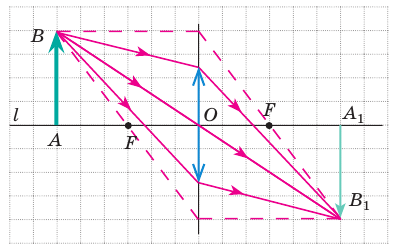
Рис. 15.8. Построение изображения предмета в случае, когда предмет значительно больше линзы
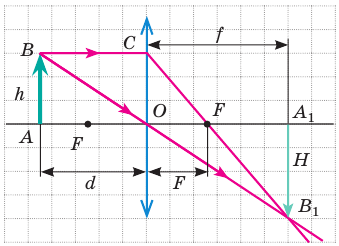
Рис. 15.9. К выведению формулы тонкой линзы: h — высота предмета; Н — высота изображения; d — расстояние от предмета до линзы; f — расстояние от линзы до изображения; F — фокусное расстояние
Пример №10
Рассматривая монету с помощью лупы, оптическая сила которой +10 дптр, мальчик расположил монету на расстоянии 6 см от лупы. Определите: 1) фокусное расстояние линзы; 2) на каком расстоянии от лупы находится изображение монеты; 3) какое изображение дает лупа — действительное или мнимое; 4) какое увеличение дает лупа.
Анализ физической проблемы. Лупу можно считать тонкой линзой, поэтому воспользуемся формулой тонкой линзы. Фокусное расстояние найдем, воспользовавшись определением оптической силы линзы.
Дано:
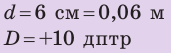
Найти:
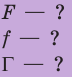
Поиск математической модели, решение
По определению 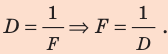
По формуле тонкой линзы: 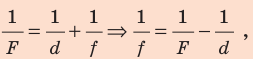 или
или 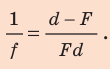 Следовательно,
Следовательно, 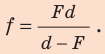
Зная расстояние 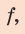 определим увеличение
определим увеличение 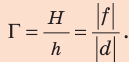
Найдем значения искомых величин:
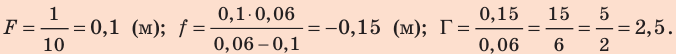
Знак «-» перед значением 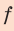 говорит о том, что изображение мнимое.
говорит о том, что изображение мнимое.
Ответ: 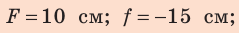 изображение мнимое;
изображение мнимое; 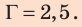
Подводим итоги:
В зависимости от типа линзы (собирающая или рассеивающая) и месторасположения предмета относительно данной линзы получают разные изображения предмета:
| Расположение предмета | Характеристика изображения в линзе | |
| собирающей | рассеивающей | |
За двойным фокусом линзы 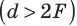 |
действительное, уменьшенное, перевернутое | мнимое, уменьшенное, прямое |
В двойном фокусе линзы 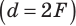 |
действительное, равное, перевернутое | |
Между фокусом и двойным фокусом линзы 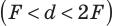 |
действительное, увеличенное, перевернутое | |
В фокусе линзы 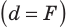 |
изображения нет | |
Между линзой и фокусом 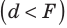 |
мнимое, увеличенное, прямое |
Расстояние 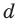 от предмета до линзы, расстояние
от предмета до линзы, расстояние 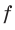 от линзы до изображения и фокусное расстояние
от линзы до изображения и фокусное расстояние 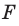 связаны формулой тонкой линзы:
связаны формулой тонкой линзы: 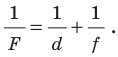
- Глаз как оптическая система
- Звук в физике и его характеристики
- Звуковые и ультразвуковые колебания
- Инерция в физике
- Дифракция света
- Принцип Гюйгенса — Френеля
- Прохождение света через плоскопараллельные пластинки и призмы
- Поляризация света
ЦЕЛЬ
РАБОТЫ
Изучение
геометрических характеристик линзы и
ознакомление с одним из методов
определения радиуса кривизны и показателя
преломления линзы.
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ РАБОТЫ
Линзой
называется прозрачное тело, ограниченное
сферическими поверхностями (одна из
поверхностей может быть плоской).
Линзы
бывают двояковыпуклые, двояковогнутые,
плоско-выпуклые, плоско-вогнутые,
выпукло-вогнутые, вогнуто-выпуклые.
Выпукло-вогнутые
и вогнуто-выпуклые линзы называют
менисковыми. Их используют, в частности,
в очках.
Линзы
изготавливают из различных материалов
стекла и пластика для видимого излучения,
кварца
для ультрафиолетового, каменной соли
(или сильвинии)
для инфракрасного.
Формула
линзы связывает фокусное расстояние F
с расстоянием от оптического центра
линзы до предмета d
и до изображения f:
![]()
.
(1)
Фокусное
расстояние F
подставляется в эту формулу со знаком
“+”, если линза собирающая, и со
знаком “”,
если линза рассеивающая.
Расстояние
до изображения f
подставляется со знаком “+”, если
изображение действительное, и со знаком
“”,
если оно мнимое.
Величина
называется оптической силой и измеряется
в диоптриях (дптр).
![]()
=
дптр.
Оптическая
сила линзы связана с ее геометрическими
характеристиками формулой:
![]()
,
(2)
где
nл
и nо
показатели преломления линзы и окружающей
среды;
R1
и R2
радиусы кривизны поверхностей линзы,
которые подставляются со знаком “+”
в случае выпуклой поверхности и со
знаком
“”
в случае вогнутой поверхности.
Если
в формуле (2) получается Ф
0, то линза собирающая,
Ф
0
рассеивающая. Это связано со знаками
обеих скобок в правой части. Например,
при R1
0, R2
0 (двояковыпуклая линза) получим собирающую
линзу, если nл
nо
(например, стеклянная линза в воздухе)
и рассеивающую, если nл
nо
(например, воздушная линза в стекле). В
другом случае может быть nл
nо
(воздушная линза в стекле), но R1
0, R2
0, то есть поверхности линзы вогнутые.
Тогда каждая скобка будет иметь знак
“”
, а их произведение даст “+”, и линза
будет собирающей.
Поперечное
увеличение линзы
![]()
, (3)
где
y1
и y2
расстояния соответственно светящейся
точки и ее изображения до главной
оптической оси линзы.
Собирающая
линза может использоваться в качестве
лупы. В этом случае ее увеличение равно ![]()
,
где
D
это расстояние наилучшего зрения; для
нормального глаза
D
= 25 см
один из стандартов для создания оптических
приборов, вооружающих глаз; F
фокусное расстояние лупы.
К
важнейшим оптическим приборам,
изготовленным из линз, относятся
микроскоп и телескоп.
Увеличение
микроскопа
![]()
,
(4)
где
расстояние между фокусами объектива и
окуляра, называемое длиной тубуса
микроскопа; D
расстояние наилучшего зрения; Fоб
и Fок
фокусные расстояния объектива и окуляра,
причем в микроскопе Fоб
Fок.
Увеличение
телескопа ![]()
, (5)
где
Fоб
и Fок
– фокусные расстояния объектива и
окуляра, причем в телескопе Fоб
Fок.
ОПИСАНИЕ
ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
В
данной работе на установке с линзой 3
(рис. 1) определяют расстояние f
от линзы до
действительного изображения нити
лампочки и по формуле (1) определяют
фокусное расстояние плоско-выпуклой
линзы.
![]()
;
![]()
, (6)
г
де
d
= 691 мм для данной установки. Расстояние
f
измеряют по шкале 6, передвигая экран 7
и добиваясь на нем резкого изображения
нити лампочки 1.
Из формулы (2)
получаем для плоско-выпуклой линзы
![]()
,
(7)
где
n
= nл
– показатель преломления линзы;
nо
= nвозд
1 – показатель
преломления воздуха;
R1
= R
– радиус выпуклой поверхности линзы;
R2
=
– радиус плоской поверхности линзы.
Из формулы (7)
получаем показатель преломления:
![]()
; ![]()
;
![]()
. (8)
Радиус
кривизны R
линзы можно измерить с помощью индикатора
2 (рис.1). Если представить сечение линзы
в виде сегмента круга (рис.2), то по теореме
Пифагора получим:
![]()
,
где
а
хорда, h
стрела сегмента.
После
преобразований получаем значение
радиуса:
![]()
.
(9)
П
ередвигая
индикатор в горизонтальном направлении,
измеряют по шкале 4 длину хорды а,
записывая соответствующую стрелу
сегмента h
по показаниям индикатора. Вычислив по
формуле (9) радиус кривизны R,
а по формуле (6) фокусное расстояние
линзы, можно определить показатель
преломления линзы по формуле (8).
Схема
установки приведена на рис.1. Передвигая
руками стойку с индикатором 2, можно
записать показания по шкале 4 (половина
хорды а/2)
и соответствующие показания индикатора
– стрелу сегмента h.
Целое число миллиметров на индикаторе
показывает маленькая стрелка, а десятые
и сотые доли – большая.
ПОРЯДОК
ВЫПОЛНЕНИЯ РАБОТЫ
ПРЕДУПРЕЖДЕНИЕ.
Следите за тем, чтобы оптические
поверхности линзы оставались чистыми
– нельзя касаться их пальцами или
предметами. Индикатор – точный прибор
и все манипуляции с ним необходимо
выполнять плавно, без рывков. Наконечник
сделан из фторопласта для уменьшения
трения. При всех передвижениях руками
стойки с индикатором нужно учесть, что
стойка должна быть всегда прижата к
основанию. В противном случае показания
индикатора будут неточными.
1.
Установка нуля. Получите индикатор и
установите его на место. Для этого
необходимо передвинуть руками стойку
индикатора и установить указатель шкалы
4 на ноль при вертикальном положении
ножки. Вставьте ножку индикатора в паз,
слегка прижмите ее стопорным винтом и
передвижением вверх и вниз самого
индикатора добейтесь нулевого показания
малой и большой стрелок. При этом большая
стрелка должна быть близка к вертикальному
положению. Закрепив индикатор в таком
положении, необходимо найти наивысшую
точку линзы. Для этого передвигайте
стойку на 1 – 2 см влево и вправо и по
стрелке индикатора найдите вершину
сферической поверхности линзы. При этом
нужно учесть, что вблизи вершины есть
мертвая зона протяженностью около 2-х
мм, в пределах которой стрелка неподвижна
– стойку нужно установить посередине
этой зоны. Установив стойку, подведите
шкалу 4 кремальерой 5 точно на ноль и в
дальнейшем кремальеру 5 не трогайте.
Если при этом большая стрелка индикатора
отклонилась от вертикали, вновь установите
индикатор должным образом и закрепите
его. Далее вращением внешнего кольца
индикатора совместите ноль круговой
шкалы с положением большой стрелки.
Учитывая то, что точность установки
нуля определяет точность дальнейших
измерений, еще раз или два повторите
манипуляции пункта 1 с тем, чтобы ноль
шкалы 4 совпадал с нулем индикатора и
это соответствовало вершине сферической
поверхности линзы.
Таблица
1
|
Показания шкалы |
Показания |
Хорда а (мм) |
Стрела сегмента (мм) |
Радиус кривизны |
|
|
При движении |
При движении |
||||
|
20 |
40 |
||||
|
25 |
50 |
||||
|
30 |
60 |
||||
|
35 |
70 |
||||
|
40 |
80 |
||||
|
Среднее значение |
R |
2.
Передвигая стойку вправо, устанавливайте
указатель шкалы 4 на значениях 20, 25, 30,
35, 40 мм (значения, равные половине
соответствующих хорд) и записывайте
показания индикатора h1
(стрела сегмента) в таблицу 1. При этом
целое число миллиметров снимайте по
показаниям маленькой стрелки, а десятые
и сотые доли – по показаниям большой
стрелки.
3.
Передвигая стойку влево от нуля, снимайте
показания индикатора h2
при тех же значениях половины хорды.
4. Передвиньте
стойку с индикатором вправо до упора.
5.
Подключите лампочку к напряжению
12 В.
6.
Слегка вращая “столб” с лампочкой,
добейтесь того, чтобы изображение
лампочки на экране 7 находилось в центре
перекрестия. При этом одновременно
нужно слегка поднять экран рукой и
сфокусировать изображение нити лампочки.
Добившись резкого изображения, запишите
по шкале 6 значение f
в миллиметрах. Повторите измерения f
еще четыре раза.
7. Выключите лампочку
и приступите к расчетам. Все расчеты в
данной работе удобнее проводить с
миллиметрах.
8.
Найдите среднее арифметическое f
результатов наблюдений и определите
полуширину доверительного интервала
f.
Запишите результат измерения f
в виде: f
f.
9.
По формуле 6 вычислите фокусное расстояние
линзы F
в миллиметрах. Для нашей установки d
= 691 мм.
10.
Пренебрегая погрешностью измерения d,
определите полуширину доверительного
интервала F
фокусного расстояния линзы по формуле:
![]()
.
11.
Заполните таблицу 1 и по формуле 9
определите радиус R
кривизны линзы в миллиметрах. Найдите
среднее арифметическое значение R
и полуширину доверительного интервала
R.
12.
По формуле 8 найдите показатель преломления
линзы, а по формуле ![]()
определите полуширину n
доверительного интервала. Запишите
результат измерения показателя
преломления n
в виде: n
n.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Сформулируйте
цель лабораторной работы. -
Что
такое линза? -
Из
каких материалов изготавливают линзы
для ультрафиолетового и инфракрасного
излучений? -
Укажите
формулу линзы. -
Какая
величина называется оптической силой
линзы? -
В
каких единицах измеряется оптическая
сила линзы? -
Укажите
знак фокусного расстояния F
линзы для собирающей и рассеивающей
линз. -
Укажите
знак расстояния f
действительного и мнимого изображений
до линзы. -
Как
оптическая сила линзы зависит от
радиусов поверхностей, ограничивающих
линзу? -
На
стеклянную двояковогнутую линзу в
воздухе падают параллельные лучи света.
Как направлены эти лучи после прохождения
линзы? -
На
воздушную двояковыпуклую линзу в стекле
падают параллельные лучи света. Как
направлены эти лучи после прохождения
линзы? -
Какая
величина называется поперечным
увеличением линзы? -
Напишите
формулу увеличения лупы. -
Линза
для очков изготовлена из стекла крон
с показателем преломления n
= 1,5. Радиус кривизны выпуклой и вогнутой
поверхностей линзы равны соответственно
50 см и 25 см. Определите оптическую силу
линзы. -
Решите
предыдущую задачу для плоско-выпуклой
линзы, если радиус кривизны выпуклой
поверхности равен R
= 50 см. -
Укажите,
какие изображения будут получены в
собирающей линзе при d
= 2F, d
= 3F, F
d
2F. -
Постройте
увеличенное и уменьшенное изображения,
даваемые собирающей линзой. -
Постройте мнимое
изображение, даваемое собирающей
линзой. -
Постройте
изображение, даваемое рассеивающей
линзой. -
Нарисуйте
эскиз экспериментальной установки. -
Укажите
расчетную формулу для определения
фокусного расстояния F
линзы. -
По
какой формуле нужно вычислять полуширину
F
доверительного интервала фокусного
расстояния F линзы? -
Выведите
формулу для определения показателя
преломления n плоско-выпуклой
линзы в данной работе. -
По
какой формуле нужно вычислять полуширину
n
доверительного
интервала показателя преломления n
линзы в данной работе? -
Выведите
формулу для расчета радиуса кривизны
R плоско-выпуклой
линзы в данной работе. -
Определите
показатель преломления плоско-выпуклой
линзы, у которой фокусное расстояние
вдвое больше радиуса кривизны выпуклой
поверхности. -
Найдите
фокусное расстояние линзы F,
если действительное изображение
предмета находится от линзы на расстоянии
вдвое большем расстояния предмета до
линзы, а расстояние между предметом и
его изображением равно 30 см. -
Как
изменится фокусное расстояние собирающей
стеклянной линзы(nЛ
= 1,5), если ее из воздуха (n01
1) поместить в воду
(n02 = 1,33)? -
Меняется
ли расстояние d предмета
до линзы в данной работе? -
Укажите
порядок выполнения данной лабораторной
работы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5

 . Это
. Это  .
.
 в результате.
в результате. . У Вас два радиуса одинаковые, но почему-то двойка отсутствует.
. У Вас два радиуса одинаковые, но почему-то двойка отсутствует. поставить?
поставить? – это что не среда?!?..
– это что не среда?!?..


