Сила Лоренца
Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
[ е = – 1.602 cdot 10^{-19} enspace Кл. ]
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
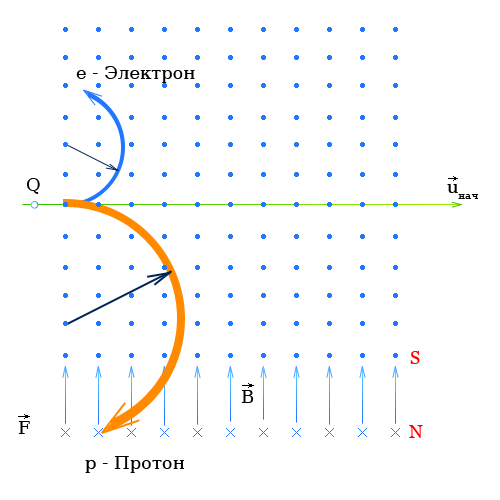
Сила Лоренца действующая на электрон и протон
Величина и направление силы Лоренца определяются соотношением
[ vector{F_{L}}= e vector{v} × vector{B} ]
где $vector{v}$, $vector{B}$ и $vector{F}$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
[ F_{L} = e v B ]
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины.
Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
Если
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10-31 кг — масса электрона, | кг |
| e | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
[ evB = frac{m_{e} v^{2}}{r} ]
и, следовательно,
[ r = frac{m_{e} v}{eB} ]
Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
[ p = + 1.602 cdot 10^{-19} enspace Кл. ]
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
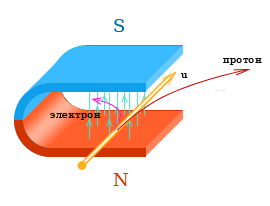
Сила Лоренца действующая на протон
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
Если
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10-27 кг — масса протона, | кг |
| p | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
[ r = frac{m_{p} v}{p B} ]
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Сила Лоренца |
стр. 667 |
|---|
Найти радиус кривизны протона в поле
NickNameUser
Знаток
(490),
на голосовании
2 года назад
Помогите, пожалуйста, найти радиус кривизны протона.
U = 1,9 килоВ
B = 203 милиТл
Табличные данные протона (используйте без сокращений, пожалуйста):
q = 1,6022 * 10^-19 Кл
m = 1,672621777 * 10^-27 Кг
Если можно, то с решением, пожалуйста
Голосование за лучший ответ
Sceptic Ratio
Оракул
(84830)
2 года назад
У протона нет радиуса кривизны, это вам не мячик.
Если речь о радиусе кривизны траектории, то не хватает:
1. скорости протона
2. ориентации линий магнитного поля B
3. ориентации линий электрического поля U
Тадасана
Просветленный
(32233)
2 года назад
Радиус кривизны бывает у извилины мозга в точке, если мозг плоский. Если мозг объемный, то главных кривизн в точке на поверхности извилины уже две штуки.
А что такое радиус кривизны протона, да еще в поле, я даже затрудняюсь себе представить.
-
- 0
-
Определите радиус кривезны R траектории пратона ,который двигается в магнитном поле индукцией B=0,5 То со скоростью v=50 км/с
-
Комментариев (0)
-
- 0
-
M=1.67*10^-27 кг q=1.6*10^-19 Кл B=0.5 Тл v=5*10^4 м/с R=?
===
q*B=m*v/R
R=m*v/(q*B)=1.67*10^-27*5*10^4/(1.6*10^-19*0.5)=1.043*10^-3 м
============================
-
Комментариев (0)
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Вначале определим от каких параметров зависит радиус кривизны заряженной частицы в магнитном поле.
В задаче описано два процесса. 1 процесс — частица с зарядом q разгоняется в электрическом поле. При этом Aэл = ΔWk, где Aэл = q⋅(φ1 – φ2) — работа электрического поля по разгону частицы, ΔWk = W2 – W1 — изменение кинетической энергии, W2 = m⋅υ2/2, W1 = 0 — кинетические энергии частицы массой m в конечном положение (на вылете из электрического поля) и в начальном (по умолчанию начальная скорость равна 0). Тогда
[
q cdot left(varphi_1 – varphi_2 right) = frac{m cdot upsilon^2}{2}.
] (1)
2 процесс — частица движется в магнитном поле по криволинейной траектории, следовательно, ее скорость перпендикулярна вектору магнитной индукции, т.е. α = 90°. При движении заряженной частицы по окружности, можно записать m⋅aц = Fл, где Fл = q⋅B⋅υ⋅sin α — сила Лоренца, aц = υ2/R — центростремительное ускорение. Тогда
[
frac{m cdot upsilon^2}{R} = q cdot upsilon cdot B,, , , ,
frac{m cdot upsilon}{R} = qcdot B.
] (2)
Решим систему уравнений (1) и (2). Например, из уравнения (1) находим скорость
[
upsilon = sqrt{frac{2q cdot left(varphi_1 – varphi_2 right)}{m}}
]
и подставляем ее в уравнение (2)
[
R= frac{m cdot upsilon}{q cdot B} = frac{m}{q cdot B} cdot
sqrt{frac{2q cdot left(varphi_1 – varphi_2 right)}{m}} =
frac{1}{B} cdot sqrt{frac{2m cdot left(varphi_1 – varphi_2 right)}{q}}.
]
Полученное уравнение распишем для двух частиц: протона и электрона. Эти частицы ускорялись «одинаковой разностью потенциалов» (т.е. у них равны φ1 – φ2), они влетают в одно и то же магнитное поле (у них равные индукции B). Кроме того они имеют численно равные заряды (но противоположные по знаку). Массы протона и электрона найдем в справочнике. С учетом этого получаем
[
frac{R_p}{R_e} = frac{1}{B} cdot sqrt{frac{2m_p cdot
left(varphi_1 – varphi_2 right)}{q}} cdot B cdot
sqrt{frac{q}{2m_e cdot left(varphi_1 – varphi_2 right)}} =
sqrt{frac{m_p}{m_e}},
]
Rp/Re ≈ 43.
Придирка к условию: если электрон и протон ускорять в одном и том же электрическом поле, то они полетят в разные стороны. Да и в магнитном поле они будут вращаться в разные стороны.
