Как найти радиус кривизны в физике

Радиус кривизны траектории

В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.

Задача 1.

Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:

Откуда :

То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.

К задаче 1

Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому

Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и . Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:

Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:

Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :

Определим полную скорость тела в момент времени :

Угол наклона вектора скорости к горизонту в этот момент равен:

А можно было сразу и косинус найти:

Тогда искомый радиус кривизны траектории равен:

Ответ: м, м, м.

Задача 2.

Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б).
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:

По условию :

б) Мы уже определили , осталась максимальная высота подъема.

Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:

Приравниваем и :

Откуда .

Ответ: а) , б) .

2 комментария

Есин из Хотам и ПВ
✉️
17.02.2022 15:20:44

Thank you very much

Jahongir
✉️
12.04.2022 19:14:12

Спасибо огромное! Полностью разобрался 🙂 Успехов вам!

Источник

Определение радиуса кривизны траектории точки

В том случае, когда
движение задано координатным способом,
радиус кривизны траектории определяется
следующим образом:

 по формулам
координатного способа задания движения
(1.1) определяются скорость и полное
ускорение точки:

;

 по формулам
траекторного способа задания движения
(1.2) определяются нормальное и касательное
ускорения:

и далее 
радиус кривизны траектории по формуле
(1.3):

. (1.4)

Порядок выполнения задания

Движение точки
задано кинематическими уравнениями в
соответствии с номером варианта задачи
(см. таблицу «Исходные данные» с. 10-14).

1. Определить
траекторию точки и изобразить ее на
чертеже. Указать на ней положение точки
в заданные моменты времени, обозначив
их М₀
и М₁
(М₀
– в момент
времени t = 0;
М₁

в момент t = t₁).

2. Определить
алгебраические величины проекций
скорости точки в общем виде, а затем
для момента времена
t = t₁.
По найденным алгебраическим величинам
проекций скорости построить вектор на
чертеже и вычислить его величину.

3. Определить
алгебраические величины
проекций ускорений точки на оси координат
в общем
виде, а затем для
момента времени
t = t₁_.
Построить вектор ускорения на чертеже
и вычислить его величину.

4. Для
определения касательного ускорения
необходимо иметь проекцию вектора
скорости точки на касательную в виде
функции времени:
,
тогда касательное ускорение точки
опреде-ляется по формуле.
Определитьдля момента време-ни
t = t₁
и построить этот вектор на чертеже.

5. Установить
характер движения точки в момент времени
t = t₁
(по направлениям векторов
и).
Если векторы сонаправлены, то движение
точки ускоренное, если они противоположны
по направлению, то – замедленное.

6. Нормальное
ускорение точки в момент времени
определяется из равенства

в котором
каждый из векторов
ивычислен в этот момент времени. Векторпостроить на чертеже.

7. Радиус
кривизны траектории точки в момент
времени t = t₁
определить по формуле (1.4).

Исходные данные

№ вар.	x =x(t)	y =y(t)	z =z(t)	t₁, с
м
1			0
0
	0
2			0	1
	0
0

№ вар.	x = x(t)	y = y(t)	z = z(t)	t₁, с
м
3			0	0
		0
0
4	0
	0		1
0
5			2	1
	0
2
6			3
	0
		6	1
7			0
	0		1
0

№ вар.	x =x(t)	y =y(t)	z =z(t)	t₁, с
м
8	0
		0	1
	0
9			0
	0
0
10			0
	0
		0
11	0
	0
		0
12		0		1
		0	1
	0

№ вар.	x =x(t)	y =y(t)	z =z(t)	t₁, с
м
13			0
0			1
	0
14		0
0
		0
15			0	1
	0		2
0
16	0
	0
		0
17			0	20
0
t	0		1
18			0
	0
0			1

№ вар.	x =x(t)	y =y(t)	z =z(t)	t₁, с
м
19	0
		0
	0
20			0
	0		1
0			1

П р и м е р. Движение
точки задано кинематическими урав-нениями:
;;;,
гдеx
и y
в м,
а t

в с.

1. Определить
траекторию точки и построить её на
чертеже. Указать на ней положения точки
в заданные моменты времени, обозначить
их
и(–
в момент времени;–
в моментс)
pис. 1.4.
Исключив параметр
из уравнений, получим

Так как
,
то
это уравнение окруж-ности с радиусом

.

При

Рис.
1.4

При
с,

а
(м),

;,
так как.

2. Для
момента времени
определить и построить на чертеже:

 скорость точки
:

(м/с),

 модуль вектора
скорости.

Направляющие
косинусы вектора скорости:

 ускорение
точки
:

Модуль вектора
ускорения точки
:

Направляющие
косинусы вектора ускорения точки:

3. Определить
касательное и нормальное ускорения
точки

постоянные
величины;

Полное ускорение
точки
равно нормальному ускорению, так как
скорость по величине постоянна:.

4. Определить
характер движения точки: точка
движется по окружности равномерно!

5. Определить
радиус кривизны траектории точки в
момент
:

нормальное ускорение;

отсюда


радиус окружности
траектории точки
.

Соседние файлы в предмете Физика

Источник

From Wikipedia, the free encyclopedia

This article is about the general mathematical concept. For its optical applications, see Radius of curvature (optics).

In differential geometry, the radius of curvature (Rc), R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.^[1]^[2]^[3]

Definition[edit]

In the case of a space curve, the radius of curvature is the length of the curvature vector.

In the case of a plane curve, then R is the absolute value of^[3]

${displaystyle Requiv left|{frac {ds}{dvarphi }}right|={frac {1}{kappa }},}$

where s is the arc length from a fixed point on the curve, φ is the tangential angle and κ is the curvature.

Formula[edit]

In 2D[edit]

If the curve is given in Cartesian coordinates as y(x), i.e., as the graph of a function, then the radius of curvature is (assuming the curve is differentiable up to order 2):

${displaystyle R=left|{frac {left(1+y'^{,2}right)^{frac {3}{2}}}{y''}}right|,qquad {mbox{where}}quad y'={frac {dy}{dx}},quad y''={frac {d^{2}y}{dx^{2}}},}$

and |z| denotes the absolute value of z.
Also in Classical mechanics branch of Physics Radius of curvature is given by (Net Velocity)²/Acceleration Perpendicular

If the curve is given parametrically by functions x(t) and y(t), then the radius of curvature is

${displaystyle R=left|{frac {ds}{dvarphi }}right|=left|{frac {left({{dot {x}}^{2}+{dot {y}}^{2}}right)^{frac {3}{2}}}{{dot {x}}{ddot {y}}-{dot {y}}{ddot {x}}}}right|,qquad {mbox{where}}quad {dot {x}}={frac {dx}{dt}},quad {ddot {x}}={frac {d^{2}x}{dt^{2}}},quad {dot {y}}={frac {dy}{dt}},quad {ddot {y}}={frac {d^{2}y}{dt^{2}}}.}$

Heuristically, this result can be interpreted as^[2]

${displaystyle R={frac {left|mathbf {v} right|^{3}}{left|mathbf {v} times mathbf {dot {v}} right|}},qquad {mbox{where}}quad left|mathbf {v} right|={big |}({dot {x}},{dot {y}}){big |}=R{frac {dvarphi }{dt}}.}$

In n dimensions[edit]

If γ : ℝ → ℝⁿ is a parametrized curve in ℝⁿ then the radius of curvature at each point of the curve, ρ : ℝ → ℝ, is given by^[3]

${displaystyle rho ={frac {left|{boldsymbol {gamma }}'right|^{3}}{sqrt {left|{boldsymbol {gamma }}'right|^{2},left|{boldsymbol {gamma }}''right|^{2}-left({boldsymbol {gamma }}'cdot {boldsymbol {gamma }}''right)^{2}}}}}$

As a special case, if f(t) is a function from ℝ to ℝ, then the radius of curvature of its graph, γ(t) = (t, f(t)), is

${displaystyle rho (t)={frac {left|1+f'^{,2}(t)right|^{frac {3}{2}}}{left|f''(t)right|}}.}$

Derivation[edit]

Let γ be as above, and fix t. We want to find the radius ρ of a parametrized circle which matches γ in its zeroth, first, and second derivatives at t. Clearly the radius will not depend on the position γ(t), only on the velocity γ′(t) and acceleration γ″(t). There are only three independent scalars that can be obtained from two vectors v and w, namely v · v, v · w, and w · w. Thus the radius of curvature must be a function of the three scalars |γ′(t)|², |γ″(t)|² and γ′(t) · γ″(t).^[3]

The general equation for a parametrized circle in ℝⁿ is

{displaystyle mathbf {g} (u)=mathbf {a} cos(h(u))+mathbf {b} sin(h(u))+mathbf {c} }

where c ∈ ℝⁿ is the center of the circle (irrelevant since it disappears in the derivatives), a,b ∈ ℝⁿ are perpendicular vectors of length ρ (that is, a · a = b · b = ρ² and a · b = 0), and h : ℝ → ℝ is an arbitrary function which is twice differentiable at t.

The relevant derivatives of g work out to be

${displaystyle {begin{aligned}|mathbf {g} '|^{2}&=rho ^{2}(h')^{2}\mathbf {g} 'cdot mathbf {g} ''&=rho ^{2}h'h''\|mathbf {g} ''|^{2}&=rho ^{2}left((h')^{4}+(h'')^{2}right)end{aligned}}}$

If we now equate these derivatives of g to the corresponding derivatives of γ at t we obtain

${displaystyle {begin{aligned}|{boldsymbol {gamma }}'(t)|^{2}&=rho ^{2}h'^{,2}(t)\{boldsymbol {gamma }}'(t)cdot {boldsymbol {gamma }}''(t)&=rho ^{2}h'(t)h''(t)\|{boldsymbol {gamma }}''(t)|^{2}&=rho ^{2}left(h'^{,4}(t)+h''^{,2}(t)right)end{aligned}}}$

These three equations in three unknowns (ρ, h′(t) and h″(t)) can be solved for ρ, giving the formula for the radius of curvature:

${displaystyle rho (t)={frac {left|{boldsymbol {gamma }}'(t)right|^{3}}{sqrt {left|{boldsymbol {gamma }}'(t)right|^{2},left|{boldsymbol {gamma }}''(t)right|^{2}-{big (}{boldsymbol {gamma }}'(t)cdot {boldsymbol {gamma }}''(t){big )}^{2}}}}}$

or, omitting the parameter t for readability,

${displaystyle rho ={frac {left|{boldsymbol {gamma }}'right|^{3}}{sqrt {left|{boldsymbol {gamma }}'right|^{2};left|{boldsymbol {gamma }}''right|^{2}-left({boldsymbol {gamma }}'cdot {boldsymbol {gamma }}''right)^{2}}}}.}$

Examples[edit]

Semicircles and circles[edit]

For a semi-circle of radius a in the upper half-plane

${displaystyle y={sqrt {a^{2}-x^{2}}},quad y'={frac {-x}{sqrt {a^{2}-x^{2}}}},quad y''={frac {-a^{2}}{left(a^{2}-x^{2}right)^{frac {3}{2}}}},quad R=|-a|=a.}$

An ellipse (red) and its evolute (blue). The dots are the vertices of the ellipse, at the points of greatest and least curvature.

For a semi-circle of radius a in the lower half-plane

${displaystyle y=-{sqrt {a^{2}-x^{2}}},quad R=|a|=a.}$

The circle of radius a has a radius of curvature equal to a.

Ellipses[edit]

In an ellipse with major axis 2a and minor axis 2b, the vertices on the major axis have the smallest radius of curvature of any points, R = b²/a; and the vertices on the minor axis have the largest radius of curvature of any points, R = a²/b.

The ellipse’s radius of curvature, as a function of parameter t

${displaystyle R(t)={frac {(b^{2}cos ^{2}t+a^{2}sin ^{2}t)^{3/2}}{ab}};,;;{text{where}};;theta =tan ^{-1}{Big (}{frac {y}{x}}{Big )}=tan ^{-1}{Big (}{frac {b}{a}};tan ;t{Big )}}$

^[4]

And as a function of θ

${displaystyle R(theta )={frac {a^{2}}{b}}{biggl (}{frac {1-e^{2}(2-e^{2})(cos theta )^{2})}{1-e^{2}(cos theta )^{2}}}{biggr )}^{3/2}}$

Where e is the eccentricity of the ellipse and is given by:

${displaystyle e^{2}=1-{frac {b^{2}}{a^{2}}}}$

Applications[edit]

For the use in differential geometry, see Cesàro equation.
For the radius of curvature of the earth (approximated by an oblate ellipsoid); see also: arc measurement
Radius of curvature is also used in a three part equation for bending of beams.
Radius of curvature (optics)
Thin films technologies
Printed electronics
Minimum railway curve radius
AFM probe

Stress in semiconductor structures[edit]

Stress in the semiconductor structure involving evaporated thin films usually results from the thermal expansion (thermal stress) during the manufacturing process. Thermal stress occurs because film depositions are usually made above room temperature. Upon cooling from the deposition temperature to room temperature, the difference in the thermal expansion coefficients of the substrate and the film cause thermal stress.^[5]

Intrinsic stress results from the microstructure created in the film as atoms are deposited on the substrate. Tensile stress results from microvoids (small holes, considered to be defects) in the thin film, because of the attractive interaction of atoms across the voids.

The stress in thin film semiconductor structures results in the buckling of the wafers. The radius of the curvature of the stressed structure is related to stress tensor in the structure, and can be described by modified Stoney formula.^[6] The topography of the stressed structure including radii of curvature can be measured using optical scanner methods. The modern scanner tools have capability to measure full topography of the substrate and to measure both principal radii of curvature, while providing the accuracy of the order of 0.1% for radii of curvature of 90 meters and more.^[7]

References[edit]

^ Weisstien, Eric. “Radius of Curvature”. Wolfram Mathworld. Retrieved 15 August 2016.
^ ^a ^b Kishan, Hari (2007). Differential Calculus. Atlantic Publishers & Dist. ISBN 9788126908202.
^ ^a ^b ^c ^d Love, Clyde E.; Rainville, Earl D. (1962). Differential and Integral Calculus (Sixth ed.). New York: MacMillan.
^ Weisstein, Eric W. “Ellipse”. mathworld.wolfram.com. Retrieved 2022-02-23.
^ “Controlling Stress in Thin Films”. Flipchips.com. Retrieved 2016-04-22.
^ “On the determination of film stress from substrate bending : Stoney’s formula and its limits” (PDF). Qucosa.de. Retrieved 2016-04-22.
^ Peter Walecki. “Model X”. Zebraoptical.com. Retrieved 2016-04-22.

External links[edit]

The Geometry Center: Principal Curvatures
15.3 Curvature and Radius of Curvature
Weisstein, Eric W. “Principal Curvatures”. MathWorld.
Weisstein, Eric W. “Principal Radius of Curvature”. MathWorld.

Источник

Как найти радиус кривизны траектории

При рассмотрении движения тел используется ряд характеризующих величин, например тангенциальное и нормальное (центростремительное) ускорение, скорость, а также кривизна траектории. Радиус кривизны – геометрическое понятие, обозначающее радиус окружности R, по которой движется тело. Этот параметр можно найти по соответствующим формулам с помощью заданной траектории движения.

Инструкция

Наиболее часто встречаются задачи на определение радиуса кривизны траектории полета брошенного тела в заданный промежуток времени. Траектория движения в данном случае описывается уравнениями на координатных осях: х = f(t), y = f(t), где t – время, в момент которого требуется найти радиус. Его вычисление будет основываться на применении формулы аn = V²/R. Здесь радиус R выявляется из отношения нормального ускорения аn и мгновенной скорости V движения тела. Узнав данные величины, можно легко найти искомую компоненту R.

Вычислите проекции скорости тела на осях (ОХ, ОY). Математический смысл скорости – это первая производная от уравнения движения. Поэтому они легко находятся взятием производной от заданных уравнений: Vx = x’, Vy = y’. При рассмотрении геометрического отображения данных проекций в координатной системе видно, что они являются катетами прямоугольного треугольника. Причем гипотенуза в нем – искомая мгновенная скорость. Исходя из этого, вычислите величину мгновенной скорости V по теореме Пифагора: V = √( Vx² + Vy²). Подставляя в выражение известное значение времени, найдите числовой показатель V.

Модуль нормального ускорения также легко определить, рассмотрев другой прямоугольный треугольник, образуемый модулем полного ускорения а и касательного ускорения тела ак. Причем здесь нормальное ускорение является катетом и вычисляется так: аn = √( а² – ак²). Для нахождения касательного ускорения продифференцируйте по времени уравнение мгновенной скорости движения: ак = |dV/dt|. Полное же ускорение вычислите по его проекциям на оси, аналогично нахождению мгновенной скорости. Только для этого возьмите от заданных уравнений движения производные второго порядка: ах = х”, аy = y”. Модуль ускорения а = √( ах2 + аy2). Подставляя все найденные величины, определите числовое значение нормального ускорения аn = √( а² – ак²).

Выразите из формулы аn = V²/R искомую переменную радиуса кривизны траектории: R = V²/ аn. Подставьте числовые значения скорости и ускорения, вычислите радиус.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Кинематический способ определения радиуса кривизны траектории в теоретической механике

Кинематический способ определения радиуса кривизны траектории:

При решении многих технических задач возникает необходимость знать радиус кривизны р (или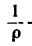

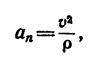
Таким образом, если закон движения точки задан уравнениями

то при определении радиуса кривизны траектории рекомендуется произвести следующее:

1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:

2. Подставив в (б’) выражения 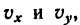найти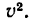

3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение 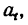а затем а?.

4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения

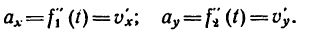
5. Подставив в (г) выражения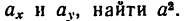

6. Подставить в (в) значения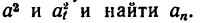

7. Подставив в (а) найденные значения 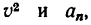получить радиус кривизны р.

Задача:

Движение точки задано уравнениями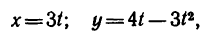

(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.

Решение.

1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим

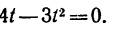
Отсюда [решая уравнение относительно 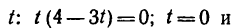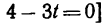находим, что траектория пересекает ось Ох в моменты времени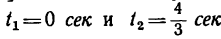

2. Находим выражения проекций скорости:

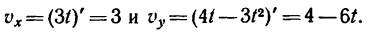
Как видно, проекция скорости на ось Ох – постоянная величина (не зависит от времени).

3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:

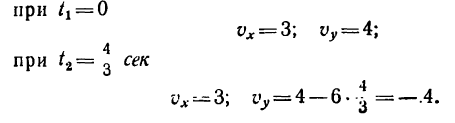
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы

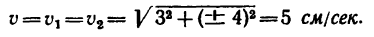
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):

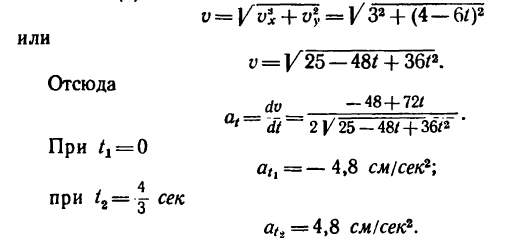
6. Находим проекции полного ускорения точки:

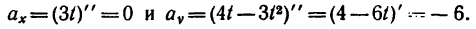
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем

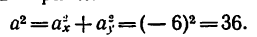
7. Определяем нормальное ускорение точки. Как при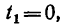

так и при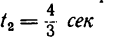

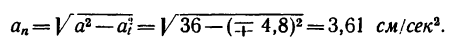
8. Зная, что в моменты пересечения траекторией оси 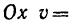5 см:сек и 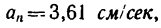находим радиусы кривизны траектории в этих точках:

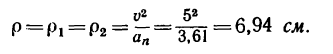
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости 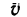и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы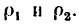

Равномерное вращательное движение
Равнопеременное вращательное движение
Неравномерное вращательное движение
Плоскопараллельное движение тела
Равномерное криволинейное движение точки
Равнопеременное движение точки
Неравномерное движение точки по любой траектории
Определение траектории, скорости и ускорения точки

Источник

Радиус кривизны траектории

2 комментария

Определение радиуса кривизны траектории точки

Порядок выполнения задания

Исходные данные

Definition[edit]

Formula[edit]

In 2D[edit]

In n dimensions[edit]

Derivation[edit]

Examples[edit]

Semicircles and circles[edit]

Ellipses[edit]

Applications[edit]

Stress in semiconductor structures[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

Как найти радиус кривизны траектории

Кинематический способ определения радиуса кривизны траектории в теоретической механике

Добавить комментарий Отменить ответ

Радиус кривизны траектории

2 комментария

Определение радиуса кривизны траектории точки

Порядок выполнения задания

Исходные данные

Definition[edit]

Formula[edit]

In 2D[edit]

In n dimensions[edit]

Derivation[edit]

Examples[edit]

Semicircles and circles[edit]

Ellipses[edit]

Applications[edit]

Stress in semiconductor structures[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

Как найти радиус кривизны траектории

Кинематический способ определения радиуса кривизны траектории в теоретической механике

Вам также может понравиться

Как найти фото для рекламы

Как найти телефон по аккаунту самостоятельно

Как найти сложное числительное

Добавить комментарий Отменить ответ