Вогнутое зеркало — это часть внутренней гладко отполированной поверхности сферы, эллипсоида или другого вращающегося тела, обычно сделанная из металла или стекла, покрытая тонким слоем металла.
Вы знаете, как выглядит ваше отражение в зеркале, но как бы оно выглядело, если бы вы стояли перед большим зеркалом, отражающая поверхность которого является внутренней частью сферы? Сможете ли вы геометрически построить полученное изображение, как мы это делали с плоским зеркалом?
Вогнутое зеркало представляет особый тип зеркала, которое отражает свет особым образом. Он имеет очень широкий спектр применения и является ключевым компонентом многих различных устройств. Они используются, например, в автомобильных фарах (определенной формы) для получения сфокусированного пучка света.
Если внимательно рассмотреть внутреннюю поверхность металлической ложки или ковша или стеклянный отражатель фонаря, то можно увидеть, что они вогнуты и хорошо отражают падающие лучи света. Они являются примерами вогнутых зеркал.
Поверхность вогнутых зеркал является частью внутренней поверхности сферы или другого вращающегося твердого тела. Зеркала фонарей и автомобильных фар обычно имеют форму параболических поверхностей.
Когда вы начинаете вращать круг вокруг его диаметра, вы получаете сферу (поверхность шара). Если отрезать его часть и заставить внутреннюю часть очень хорошо отражать свет, то получится вогнутое сферическое зеркало (см. рисунок 2).
Чтобы обсудить характеристики вогнутых зеркал, ход лучей и научиться строить изображения в вогнутых зеркалах, мы будем использовать параболическое зеркало, поскольку в таком зеркале лучи, отраженные от зеркала, концентрируются в фокусной точке F (фокусе).
Характеристики, описывающие вогнутое сферическое зеркало
Вогнутое сферическое зеркало — это зеркало, отражающая поверхность которого является внутренней поверхностью части сферы.
Чтобы описать и объяснить формирование изображения с помощью вогнутого сферического зеркала, нам потребуется понимание и знание определенных понятий, которые описывают её оптическую систему. Их иллюстрацию можно увидеть на рисунке 3 ниже:
Оптическая ось — это прямая линия, проходящая через центр кривизны зеркала (O) и совпадающая с его осью симметрии.
Радиус кривизны зеркала r — это также отрезок между центром кривизны зеркала O и точкой, где оптическая ось пересекает поверхность зеркала (которую иногда называют вершиной зеркала).
Фокусная точка зеркала (F) — это геометрическая точка, в которой пересекаются все лучи света, идущие параллельно оптической оси зеркала до отражения от поверхности вогнутого зеркала. Фокусная точка находится точно посередине радиуса кривизны зеркала r (см. рисунок 4).
Поскольку точка F называется фокусом зеркала, длина отрезка, соединяющего эту точку с поверхностью зеркала (W) вдоль оптической оси, называется фокусным расстоянием зеркала f.
Между фокусным расстоянием (f) и радиусом кривизны (r) вогнутого сферического зеркала существует следующая зависимость: f = r / 2. Единицей СИ фокусного расстояния f является метр.
Формирование изображения в вогнутых зеркалах
Как формируется изображение в вогнутом сферическом зеркале? Изменяя расстояние между зеркалом и предметами, вы получаете различные изображения — перевернутые, прямые, уменьшенные, увеличенные… или иногда вообще не удается получить никакого изображения.
Помните! Луч света — это линия, вдоль которой распространяется свет. Для геометрического построения изображения, помимо прочего в зеркалах, используются так называемые характерные лучи.
В случае вогнутого сферического зеркала это будут:
- луч, параллельный оптической оси, который после отражения проходит через фокус зеркала F. Ход этого луча следует из определения фокуса;
- луч, соответствующий радиусу кривизны зеркала r и проходящий через центр кривизны зеркала O, проходит тот же путь после отражения. Это связано с тем, что угол падения на поверхность зеркала равен нулю;
- луч, проходящий через фокус зеркала F после отражения, идет параллельно оптической оси. Как и в 1), это следует из определения фокуса.
На рисунках 5-7 ниже вы можете наблюдать некоторые примеры построения изображений в вогнутых зеркалах.
| Положение объекта (x) | Положение изображения (y) | Характеристики изображения, получаемого в вогнутом зеркале |
| Расстояние до объекта меньше фокусного расстояния, x < f | Изображение за зеркалом | Мнимое, прямое, увеличенное |
| Расстояние до объекта равно фокусному расстоянию, x = f | При отражении лучи света идут параллельно друг другу | Без изображения |
| Расстояние до объекта больше фокусного расстояния и меньше двойного фокусного расстояния, f < x < 2f или f < x < r | y > r | Действительное, перевернутое, увеличенное |
| Расстояние до объекта равно удвоенному фокусному расстоянию, x = 2f или x = r | y = r | Действительное, перевернутое, имеет те же размеры, что и объект |
| Расстояние до объекта, превышающее двойное фокусное расстояние, x > 2f или x > r | f < y < r | Действительное, перевернутое, уменьшенное |
Оптическое увеличение.
Изображение, полученное с помощью вогнутого зеркала, может быть меньше объекта, больше его или быть одинакового размера. Мы говорим, что изображение может иметь разное увеличение.
Мы определяем оптическое увеличение p как отношение высоты полученного изображения h2 на высоту объекта h1, то есть p = h2 / h1 . Оно называется линейным увеличением и является безразмерной величиной.
Увеличенное изображение имеет оптическое увеличение p > 1, уменьшенное изображение имеет оптическое увеличение p < 1.
Пример задачи. Рассчитайте высоту объекта, если его изображение, сформированное в вогнутом сферическом зеркале, имеет высоту 5 см и увеличение 0,5?
Решение задачи. Мы знаем формулу для увеличения p = h2 / h1 . У нас p = 0,5 и h2 = 5 cм. Тогда h1 = 5 / 0,5 = 10 см. Итак, высота объекта h1 = 10 см.
Подведем итог.
Как видите, в зависимости от положения объекта, существуют различные его изображения, наблюдаемые в вогнутом сферическом зеркале. Это может быть видимое изображение (сформированное за зеркальной поверхностью) или реальное изображение (сформированное перед зеркальной поверхностью), уменьшенное или увеличенное, прямое или перевернутое.
Изображение точки формируется там, где пересекаются лучи после отражения от зеркала (реальное изображение) или где пересекаются продолжения отраженных лучей (мнимое изображение — как в плоском зеркале).
Примеры применения вогнутых зеркал
Вогнутые зеркала используются в качестве отражателей в автомобильных лампах, фонариках, антеннах, станциях метро, на перекрестках улиц для обзора окрестности и астрономических телескопах.
Интересный факт! В странах, где нет электричества или доступ к нему затруднен, а доступ к солнечной энергии практически неограничен, для приготовления пищи используются вогнутые зеркала.
Пользуясь тем, что солнечные лучи, идущие параллельно оптической оси, пересекаются после отражения от зеркала в одной точке — его фокусе, мы можем использовать их энергию для приготовления пищи. Достаточно поместить в фокус зеркала кастрюлю, покрытую темной эмалью, и она будет поглощать энергию светового излучения и нагревать пищу. Такой плиты достаточно, чтобы вскипятить воду и приготовить любую пищу. Вблизи экватора энергия солнечных лучей достаточно высока, и мы, конечно, можем даже испечь что-нибудь.
Без вогнутых зеркал мы не смогли бы вести наблюдения за небом и изучать небесные тела, удаленные на миллионы световых лет.
Вогнутые зеркала используются там, где необходимо сконцентрировать световую энергию, например в зеркальном телескопе. С его помощью можно наблюдать даже неяркие далекие звезды.
Задачами телескопов являются:
- собирает больше света — площадь поверхности хрусталика во много раз больше площади зрачка глаза, что позволяет видеть очень далекие тела, от которых исходит очень мало света;
- увеличение углового расстояния между объектами или частями объектов, что позволяет увидеть их структуру.
Зеркальный телескоп — инструмент, разработанный Исааком Ньютоном и используемый до сих пор, — состоит из вогнутого зеркала, которое фокусирует попадающие на него лучи света. Затем они попадают на другое (плоское) зеркало, которое изменяет направление световых лучей к окуляру и затем к глазу. Телескопы этого типа используются как астрономами-любителями, так и в крупнейших астрономических обсерваториях мира.
Самые большие однозеркальные телескопы в мире имеют диаметр чуть более 8 метров. Более крупные телескопы имеют диаметр более 10 метров, но состоят из множества сегментов. Чрезвычайно большой телескоп, строительство которого ведется в настоящее время, будет иметь диаметр 39 метров и состоять почти из 800 зеркал.
Плоское зеркало представляет собой простейшее способное создавать изображение предмета оптическое устройство. Получаемое с помощью него изображение некоторого объекта формируется за счет отражаемых от зеркальной поверхности лучей.
По причине его образования вследствие пересечения «мнимых» продолжений, а не непосредственно самих лучей подобные изображения носят название мнимых (рис 3.2.1).
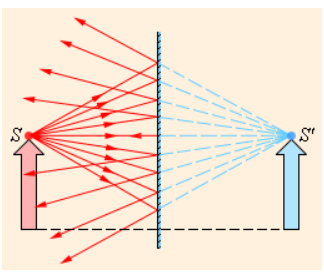
Рисунок 3.2.1. Ход лучей при отражении от плоского зеркала. Точка S’ является мнимым изображением точки S.
Мнимое изображение предмета расположено симметрично относительно плоскости зеркальной поверхности вследствие закона отражения света. Размер изображения эквивалентен размеру отражаемого объекта.
Виды зеркал
Обладающую формой сферического сегмента зеркально отражающую поверхность называют сферическим зеркалом.
Оптическим центром зеркала называют использованный в процессе вырезания в качестве необходимого материала центр сферы.
Полюсом является вершина сферического сегмента.
Проходящая через оптический центр и полюс зеркала прямая, называется главной оптической осью сферического зеркала.
Главная оптическая ось выделена из всех других проходящих через оптический центр прямых только тем, что она является осью симметрии зеркала.
Сферические зеркала делятся на вогнутые и выпуклые.
Если на вогнутое сферическое зеркало падает параллельный главной оптической оси пучок лучей, то, отразившись от зеркала, лучи пересекутся в точке, которая носит название главного фокуса F зеркала.
Типы изображений в зеркалах
Расстояние от фокуса до полюса зеркала называют фокусным расстоянием. Оно, как главный фокус, обозначается буквой F.
У вогнутого сферического зеркала главный фокус является действительным. Он расположен в середине между центром и полюсом зеркала, как это проиллюстрировано на рисунке зеркала 3.2.2.
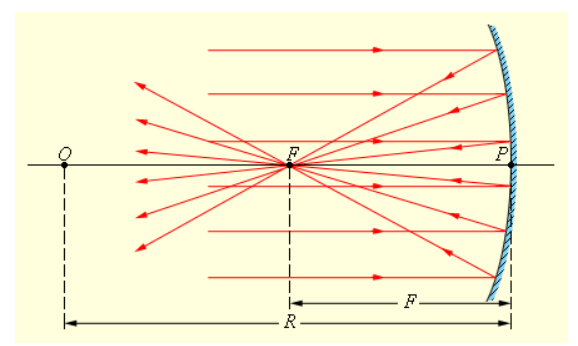
Рисунок 3.2.2. Отражение параллельного пучка лучей от вогнутого сферического зеркала. Точки O – оптический центр, P – полюс, F – главный фокус зеркала; OP – главная оптическая ось, R – радиус кривизны зеркала.
Стоит учитывать, что отраженные лучи пересекаются примерно в одной точке только тогда, когда падающий параллельный пучок, так называемый параксиальный пучок, достаточно узок.
Главный фокус выпуклого зеркала мнимый. В случае, если на выпуклое зеркало падает параллельный главной оптической оси пучок лучей, то, отразившись в фокусе, пересекаются продолжения лучей (рисунок 3.2.3).
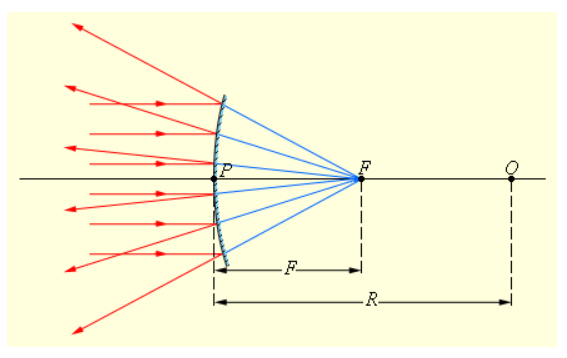
Рисунок 3.2.3. Отражение параллельного пучка лучей от выпуклого зеркала. F – мнимый фокус зеркала, O – оптический центр, OP – главная оптическая ось.
Фокусные расстояния сферических зеркал характеризуются определенным знаком: в случае вогнутого зеркала F=R2, выпуклого же – F=-R2, где R представляет собой радиус кривизны зеркала.
Изображение каждой конкретной точки A предмета в сферическом зеркале может быть построено благодаря любой паре стандартных лучей:
- Луч AOC, который проходит сквозь оптический центр зеркала. Отраженный луч COA идет по этой же прямой;
- Луч AFD, проходящий через фокус зеркала. Отраженный луч параллелен главной оптической оси;
- Луч AP, падающий на полюс зеркала. Отраженный луч относительно главной оптической оси симметричен с падающим.
- Параллельный главной оптической оси луч AE. Отраженный луч EFA1 проходит через принадлежащий зеркалу фокус.
Приведенные в списке выше стандартные лучи на рисунке 3.2.4 проиллюстрированы для случая вогнутого зеркала. Данные лучи проходят через являющуюся изображением точки A точку A’. Оставшиеся отраженные лучи тоже проходят через точку A’.
Такой ход лучей, при котором все вышедшие из одной точки лучи пересекаются в другой точке, называется стигматическим.
Отрезок A’B’ представляет собой изображение объекта AB. Аналогичны построения и для случая с выпуклым зеркалом.
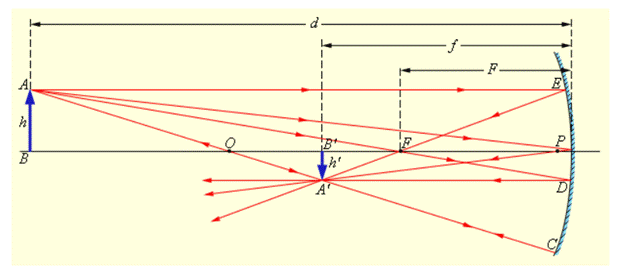
Рисунок 3.2.4. Построение изображения в вогнутом сферическом зеркале.
С помощью формулы сферического зеркала могут быть определены размер и положение изображения объекта:
1d+1f=1F.
В данном соотношении d играет роль расстояния от предмета до зеркала, а f представляет собой расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:
- d>0 и f>0 – для действительных изображений и предметов;
- d<0 и f<0 – для мнимых изображений и предметов.
Для проиллюстрированного на рисунке 3.2.4 случая мы имеем: F>0, то есть зеркало вогнутое; d=3F>0 (действительный предмет).
Из формулы сферического зеркала получаем: f=32F>0, соответственно, изображение является действительным.
Если вместо вогнутого зеркала взять выпуклое, с аналогичным по модулю фокусным расстоянием, мы получим приведенный ниже результат:
F<0, d=–3F>0, f=34F<0 – изображение мнимое.
Величина линейного увеличения, принадлежащая сферическому зеркалу, может быть определена в виде отношения линейных размеров предмета h и изображения h’.
В зависимости от того, является ли изображение перевернутым или прямым, h’ приписывают определенный знак, (h'<0) минус в первом случае и плюс во втором (h’>0). Величина h всегда считается положительной. В случае подобного определения линейное увеличение сферического зеркала выражается в виде формулы, легко получаемой из рисунка 3.2.4:
Г=h’h=-fd.
В первом из рассмотренных ранее примеров Г=-12<0 – соответственно, изображение является перевернутым, уменьшенным в 2 раза. Во втором Г=14>0 – то есть изображение прямое и уменьшенное в 4 раза.
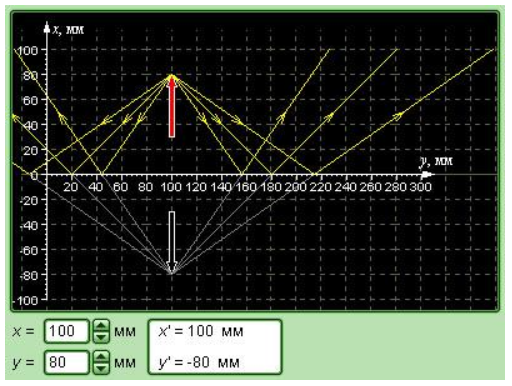
Рисунок 3.2.5. Модель изображения в плоском зеркале.
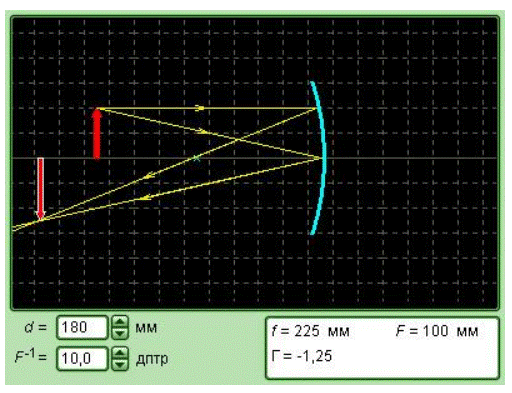
Рисунок 3.2.6. Модель сферического зеркала.
21
Задача 4 Радиус кривизны вогнутого зеркала 40см. Найти по-
ложение объекта, при котором его изображение – действительное и увеличенное в два раза. Найти такое положение, при котором изображение – мнимое и увеличенное в два раза.
Решение:
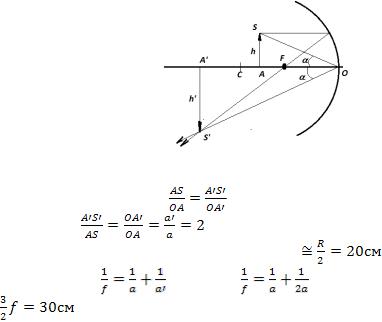
Оптическая схема задачи представлена на рис.9
|
Рис.9 |
|||
|
Рассмотрим AOS и |
A’OS’. Они –подобны. Из подобия |
||
|
треугольников следует: |
. Обозначим |
OA =a, OA’ |
|
|
=a’. Тогда |
. OF = f является фокусным |
||
|
расстоянием зеркала и определяется как f |
. |
Из |
|
|
соотношения |
следует |
и a=ОА |
= |
Задача 5.
Пучок параллельных лучей проходит сквозь круглое отверстие в листе бумаги. На расстоянии a = 45 см от листа расположен экран, плоскость которого парал-
22
лельна плоскости листа. На экране прошедшие сквозь отверстие лучи образуют светлый круг диаметром d = 6,0 см. Когда экран заменили выпуклым зеркалом, то на листе бумаги появился светлый круг диаметром D = 33 см. Определите радиус кривизны R зеркала.
Решение:
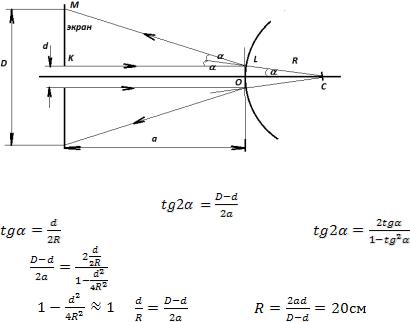
Графически задача изображена на рис.10
|
Рис.10 |
|||
|
Из |
KLM следует |
. Из |
COL следует |
|
. Из тригонометрии известно, что |
|||
|
или |
. Принимая во внимание, что |
d <<R, полу- |
|
|
чаем |
и |
, откуда |
ОПТИЧЕСКИЕ ПРИБОРЫ.
Приборами, где реализуются основные законы геометрической оптики, является линза и призмы. Оптическая линза — это обычно диск из прозрачного однородного материала, ограниченный двумя полированными поверхно-
23
стями — сферическими или плоской и сферической. В настоящее время всё чаще применяются и так называемые «асферические линзы», форма поверхности которых отличается от сферы. В качестве материала линз обычно используются оптические материалы, такие как стекло, оптическое стекло, оптически прозрачные пластмассы и другие материалы.
Характеристики тонких линз
В зависимости от форм различают собирающие (положительные) и рассеивающие (отрицательные) линзы. К группе собирающих линз обычно относят линзы, у которых середина толще их краёв, а к группе рассеивающих — линзы, края которых толще середины (рис.6). Это верно только если показатель преломления у материала линзы больше, чем у окружающей среды. Если показатель преломления линзы меньше, ситуация будет обратной. Например пузырёк воздуха в воде — двояковыпуклая рассеивающая линза.
Для построения оптических приборов с исправленной оптической аберрацией (прежде всего — хроматической, обусловленной дисперсией света, — ахроматы и апохроматы) важны и иные свойства линз и их материалов, например, коэффициент преломления, коэффициент дисперсии, коэффициент пропускания материала в выбранном оптиче-
|
ском |
диапазоне. |
|
Иногда линзовые оптические системы |
(рефракторы) |
специально рассчитываются на использование в средах с относительно высоким коэффициентом преломления . Выпукло-вогнутая линза может быть собирательной (утолщается к середине) или рассеивающей (утолщается к краям). Линза, у которой радиусы поверхностей равны, имеет оптическую силу, равную нулю (применяется для коррекции дисперсии или как покровная линза). Так, линзы
24
очков для близоруких — как правило, отрицательные, а для дальнозорких – положительные
Рис. 6. Виды линз: Собирающие:1 — двояковыпуклая; 2 — плоско-выпуклая; 3 — вогнуто-выпуклая (положительный мениск);Рассеивающие: 4 — двояковогнутая; 5 — плосковогнутая; 6 — выпукло-вогнутая (отрицательный мениск)
Отличительным свойством собирательной линзы является способность собирать падающие на её поверхность параллельные лучи в одной точке, расположенной по другую сторону линзы.
Рис.7.Основные элементы линзы.
На рис.7 представлены следующие элементы линзы:
25
NN — главная оптическая ось — прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу; O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре). Ход лучей на рис.7 показан, как в идеализированной (плоской) линзе, без указания на преломление на реальной границе раздела фаз и несколько утрированный образ двояковыпуклой линзы
Если на некотором расстоянии перед собирательной линзой поместить светящуюся точку S, то луч света, направленный по оси, пройдёт через линзу не преломившись, а лучи, проходящие не через центр, будут преломляться в сторону оптической оси и пересекутся на ней в некоторой точке F, которая и будет изображением точки S. Эта точка носит название сопряжённого фокуса, или про-
|
сто |
фокуса. |
|
Если на линзу будет падать свет от очень удалённого |
источника, лучи которого можно представить идущими параллельным пучком, то по выходе из неё лучи преломятся под большим углом и точка F переместится на оптической оси ближе к линзе. При данных условиях точка пересечения лучей, вышедших из линзы, называется главным фокусом F’( для собирающей линзы этот фокус действительный), а расстояние от центра линзы до главного фокуса — главным фокусным расстоянием.
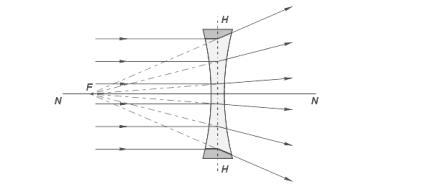
Лучи, падающие на рассеивающую линзу, по выходе из неё будут преломляться в сторону краёв линзы, то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая и будет ф о- кусом этой линзы (рис.8). Этот фокус будет мнимым.
Сказанное о фокусе на главной оптической оси в равной степени относится и к тем случаям, когда изображение
26
точки находится на побочной или наклонной оптической оси, т. е. линии, проходящей через центр линзы под углом к главной оптической оси. Плоскость, перпендикулярная главной оптической оси, расположенная в главном фокусе линзы, называется главной фокальной плоскостью, а в сопряжённом фокусе — просто фокальной плоскостью.
Собирающие линзы могут быть направлены к предмету любой стороной, вследствие чего лучи по прохождении через линзу могут собираться как с одной, так и с другой её стороны. Таким образом, линза имеет два фокуса — передний и задний. Расположены они на оптической оси по обе стороны линзы на фокусном расстоянии от центра линзы. Если с двух сторон линзы показатели преломления сред равны, то и фокусные расстояния для переднего и заднего фокуса будут равными.
Рис.8. Мнимый фокус рассеивающей линзы.
Построение изображения в тонкой собирающей линзе.
При изложении характеристики линз был рассмотрен принцип построения изображения светящейся точки в фокусе линзы. Лучи, падающие на линзу слева, проходят через её задний фокус, а падающие справа — через передний фокус (рис. 9). Следует учесть, что у рассеивающих линз, наоборот, задний фокус расположен спереди линзы, а пе-
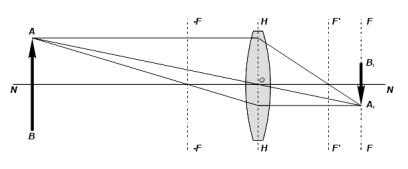
Построение линзой изображения предметов, имеющих определённую форму и размеры, получается следующим образом: допустим, линия AB представляет собой объект, находящийся на некотором расстоянии от линзы, значительно превышающем её фокусное расстояние. От каждой точки предмета через линзу пройдёт бесчисленное количество лучей, из которых, для наглядности, на рисунке схематически изображён ход только трёх лучей (рис.9).
Три луча, исходящие из точки A (рис.9), пройдут через линзу и пересекутся в соответствующих точках схода на A1B1, образуя изображение. Полученное изображение яв-
|
ляется |
действительным |
и |
перевёрнутым. |
|
В данном случае изображение |
получено в сопряжён- |
ном фокусе в некоторой фокальной плоскости FF, несколько удалённой от главной фокальной плоскости F’F’, проходящей параллельно ей через главный фокус.
Рис.9. Построение изображения в собирающей линзе.
На рис.10 и рис.11 приведены различные случаи построения изображений предмета, помещённого на различных расстояниях от линзы.
28
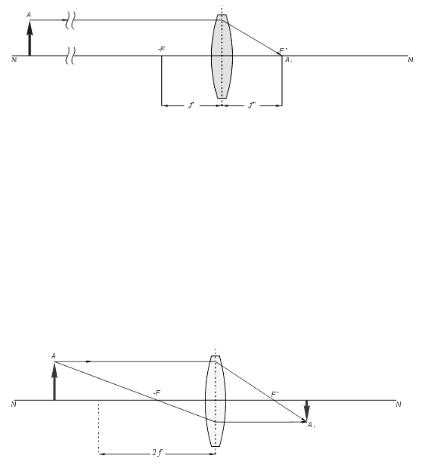
Рис.10. Предмет находится на бесконечном расстоянии.
Если предмет находится на бесконечно далёком от линзы расстоянии, то его изображение получается в заднем фокусе линзы F’ действительным, перевёрнутым и уменьшенным до подобия точки (рис.11).
Если предмет приближён к линзе и находится на расстоянии, превышающем двойное фокусное расстояние линзы, то изображение его будет действительным, перевёрнутым и уменьшенным и расположится за главным фокусом на отрезке между ним и двойным фокусным расстоянием ( рис.11).
|
Рис.11. Построение изображения предмета за двой- |
||
|
ным |
фокусным |
расстоянием. |
29
Рис.12. Предмет находится на двойном фокусном расстоянии.
Если предмет помещён на двойном фокусном расстоянии от линзы, то полученное изображение находится по другую сторону линзы на двойном фокусном расстоянии от неё. Изображение получается действительным, перевёрнутым и равным по величине предмету (рис.12).
Рис.13.Предмет находится между фокусным и двойным фокусным расстоянием.
Если предмет помещён между передним фокусом и двойным фокусным расстоянием, то изображение будет получено за двойным фокусным расстоянием и будет действительным, перевёрнутым и увеличенным (рис.13).
30
Рис. 14. Предмет находится в фокусе.
Если предмет находится в плоскости переднего главного фокуса линзы, то лучи, пройдя через линзу, пойдут параллельно, и изображение может получиться лишь в бесконечности (рис.14).
Если предмет поместить на расстоянии, меньшем главного фокусного расстояния, то лучи выйдут из линзы расходящимся пучком, нигде не пересекаясь. Изображение при этом получается мнимое, прямое и увеличенное, т. е. в данном случае линза работает как лупа (рис.15).
Рис.15. Предмет находится между фокусом и линзой.
Нетрудно заметить, что при приближении предмета из бесконечности к переднему фокусу линзы изображение удаляется от заднего фокуса и по достижении предметом плоскости переднего фокуса оказывается в бесконечности от него.
Эта закономерность имеет большое значение в практике различных видов фотографических работ, поэтому для
Соседние файлы в предмете Оптика
- #
- #
- #
Вогнутые зеркала
Закон отражения справедлив также для искривленных поверхностей,
однако в этом случае в разных точках поверхности зеркала перпендикуляр имеет различные направления.
Вогнутые зеркала представляют собой или часть сферы (сферическое зеркало) или часть параболоида вращения (параболическое зеркало).
Лучи, падающие на поверхность вогнутого зеркала параллельно оптической оси, после отражения собираются в фокусе F.
Расстояние от фокуса F до вершины зеркала S называется фокусным расстоянием f.
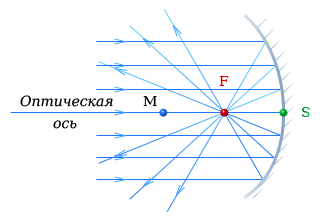
вогнутые зеркала
Если
| f | фокусное расстояние вогнутого зеркала, | метр |
|---|---|---|
| r | радиус кривизны поверхности зеркала, | метр |
то
[ f = frac{r}{2} ]
Фокальная точка делит пополам отрезок, соединяющий центр кривизны M и вершину зеркала S.
Вогнутые зеркала |
стр. 590 |
|---|
Зеркала, поверхность которых составляет часть поверхности шара, называют сферическими; они бывают вогнутые (рис. 29.9, а) и выпуклые (29.9, б). На рис. 29.9 R — радиус кривизны зеркала. Диаметр 
окружности, ограничивающей зеркало, называют отверстием зеркала, а самую удаленную от него точку О зеркальной поверхности называют вершиной зеркала. Прямую, проходящую через сферический центр зеркала С и его вершину О, называют главной оптической осью зеркала, а любую другую прямую, проходящую через точку С и поверхность зеркала, называют побочной оптической осью зеркала.
Рис. 29.9,
Когда луч света идет по какой-либо оптической оси, то угол его падения на поверхность зеркала равен нулю, поэтому такой луч после отражения идет по той же оптической оси в обратную сторону.
Если на вогнутое зеркало падает пучок лучей, параллельных его главной оптической оси, то после отражения от зеркала эти лучи проходят через точку Ф, лежащую на главной оптической
оси (рис. 29.10, а), которую называют главным фокусом зеркала. После отражения от выпуклогозеркала такие лучи идут расходящимся пучком (рис. 29.10, б), но так, что их продолжения тоже сходятся в одной точке Ф (за зеркалом) — главном фокусе зеркала.
Таким образом, вогнутые зеркала являются собирающими. Главный фокус у них действительный. Выпуклые зеркала — рассеивающие, главный фокус у них мнимый.
Рис. 29.10.
Расстояние от главного фокуса до вершины зеркала 
называют главным фокусным расстоянием 
Когда лучи падают на зеркало параллельно одной из его побочных оптических осей, например 
(рис. 29.11), то после отражения от зеркала они собираются в одной точке на этой же оси — в фокусе зеркала.
Рис. 29.11.
Если побочные оси составляют небольшой угол с главной оптической осью, то все фокусы зеркала располагаются в фокальной плоскости 
проходящей через главный фокус Ф перпендикулярно главной оптической оси.
Выясним, как связано главное фокусное расстояние 
с радиусом кривизны зеркала 
Луч 
параллельный главной оптической оси зеркала, после отражения идет по пути 
(рис. 29.10, а). Соединим точку 
со сферическим центром зеркала С. Из законов отражения следует, что 
Так как 
то 
Следовательно, 
равнобедренный, т. е. 
Поскольку поверхность зеркала всегда составляет малую
часть сферы, приближенно можно считать 
Таким образом, 
Это означает, что точка Ф делит радиус зеркала 
пополам, т. е.
Из законов отражения следует, что падающий и отраженный лучи в сферических зеркалах обладают обратимостью. Поэтому, если источник света поместить в главный фокус вогнутого зеркала, то после отражения от зеркала лучи практически пойдут параллельно главной оптической оси зеркала (рис. 29.12).
Рис. 29.12.
Для получения параллельных пучков света на практике вместо сферического зеркала используют параболическое зеркало, отражающая поверхность которого является частью поверхности параболоида вращения. Параболическое зеркало дает более направленный пучок света. На этом свойстве зеркал основано устройство прожекторов и рефлекторов (отражателей) различного рода.
