Окружность
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ 
:
О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.
Хорда AB стягивает дуги AFB и AJB.
Как найти радиус окружности применяя циркуль
Добрый день коллеги. Что бы найти радиус окружности с помощью линейки и циркуля много времени не нужно. Вспомним школьные годы. Для тех, кто запамятовал или прогуливал будет полезен этот урок.
Все легко. Но случается, когда очевидное произносишь вслух, тогда вдруг понимаешь: «- Я так и думал. Что такое диаметр окружности я знал. Просто не помню…».
Существуют разные подходы.
- Можно найти диаметр круга через вычисления.
- Найти цент окружности с помощью угольника.
- Решить с помощью листа ватмана (важно, чтобы был лист с 90 градусными углами).
- А можно применив циркуль и линейку.
Рассмотрим простой способ (один из…), как найти диаметр окружности с помощью линейки и циркуля.
Здесь чистая геометрия. А эта наука идет рядом с живописью, с архитектурой.
Для чего это художникам?
Работа с цветным стеклом. В церквях окна с раскрашенными кусочками стекла составляют картины. Делая такие витражи без точных вычислений не обойтись. Каждый из кусочков нужно точно вырезать и поставить в определенную ячейку. Поэтому и здесь пригодиться наш метод.
Представим, что мы расписываем стену, у нас имеется круглый трафарет, но вот центра нет. А нам жизненно необходимо его определить и точно прикладывать к определенным точкам нашей композиции на стене.
Может мы мастера по дереву. Делаем резной круглый стул или стол. В средине необходимо просверлить или нарисовать узор.
Очень тяжелая работа роспись на потолке. Формы разные. Когда начинаем с начала, то средина будет. Когда панно переделываем, то круг имеется, но центр нужно найти. С размерами необходимо будет повозиться, но это второй вопрос.
Возможно найти радиус круга, центр путем подбора, но это долго и не эффективно.
На видео ниже детально описано как найти центр.
Как найти центр окружности
Рассмотрим в картинках, как найти радиус окружности
Что такое диаметр окружности многие знают.
Линия, нарисованная через центр окружности и будет диаметр. Радиус круга — это его половина (для того, кто не помнит).
Дана окружность зеленый цвет.
На теле зеленого круга ставим случайно точку A, и вокруг нее описываем круг фиолетового цвета.
Ставим еще одну точку B. Описываем второй круг.
Проведя через пересечения фиолетовых окружностей прямую, получаем диаметр зеленого круга C D.
Эту же процедуру проводим с желтыми объектами. Только их центрами будут точки C D.
Проведя через пересечения желтых объектов прямую, получим очередной диаметр перпендикулярный первому. Их пересечение будет центром зеленого с точкой O. 
Важно, чтобы фиолетовые круги были одинаковы, а по размеру чуть больше зеленого.
К желтым окружностям это тоже относится.
Этим не хитрым способом получим центр, что поможет без задержек выполнить заказ.
Человек на рисунке часто окружен архитектурными объектами. Без точных вычислений определить геометрию окружения, уходящую в перспективу, не выйдет. В такие моменты и нужны знания геометрии.
Построить среду обитания не сложно. Имея знания, подобная задача не будет трудной.
Все художники (без исключения) пользуются построением.
В уроках рисования на нашем сайте можно онлайн узнать ответы на разные вопросы.
В курсе по рисунку собраны уроки перспективы, тона, построения, композиции и разные хитрости.
Посмотреть заметки о делении круга на семь частей, на пять, двенадцать…
Круг. Окружность (центр, радиус, диаметр)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.
[spoiler title=”источники:”]
http://artatac.ru/uroki_risovaniia/risovanie/nayti-radius-okruzhnosti.html
http://interneturok.ru/lesson/matematika/3-klass/tema-umnozhenie-i-delenie/krug-okruzhnost-tsentr-radius-diametr
[/spoiler]
Окружность
- Построение окружности циркулем
- Радиус, хорда и диаметр
- Дуга
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
D = 2r.
Дуга
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ :
О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.
Хорда AB стягивает дуги AFB и AJB.
Полезно знать математический способ, позволяющий рассчитать радиус дуги. Он особенно удобен, когда требуется точно разметить плавную дугу с помощью большого импровизированного циркуля, а не гибкого лекала, после того как вам стали известны три опорные точки или два главных размера.
Как видно на рисунке справа, требуется знать лишь высоту и длину дуги. Подставьте эти размеры в простую формулу и вычислите радиус. Получив результат, настройте циркуль на этот размер и начертите идеальную дугу требуемого радиуса.
Например, если нужно построить дугу длиной 240 и высотой 30 мм, следует действовать так:
Сначала подставьте эти размеры в формулу. В нашем случае L=120, Н=30, поэтому (1202+302): (2×30) = (14400+900): 60= 153000:60 = 255.
Теперь сделайте для этого радиуса циркуль, как показано на фото внизу. Выровняйте один конец с серединой дуги на заготовке. Проведите из этой точки под прямым углом по линейке прямую линию и поставьте на нее второй конец циркуля. Теперь вы можете начертить идеальную дугу, которая соединит все три опорные точки.
Простая формула для определения радиуса дуги, 2.5 out of 5 based on 22 ratings
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Окружность
Окружность – это замкнутая кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Заданная точка является центром окружности. На Рис.1 точка О – центр окружности.
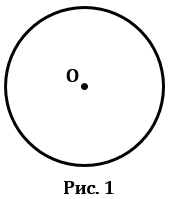
Основные характеристики окружности
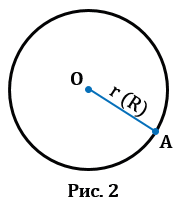
1. Радиус – это отрезок, соединяющий центр с какой-либо точкой окружности. У любой окружности можно провести бесконечно много радиусов, которые будут иметь одну и ту же длину. Обозначают радиус r или R. На Рис.2 представлена окружность с центром в точке О радиусом ОА.
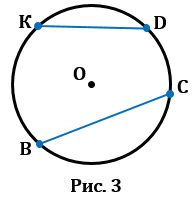
2. Хорда – это отрезок, соединяющий две точки окружности. У любой окружности можно провести бесконечно много хорд. На Рис.3 ВС и KD – хорды окружности с центром в точке О.
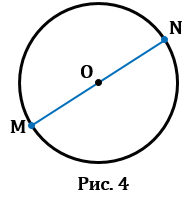
3. Диаметр – это отрезок, соединяющий две точки окружности и проходящий через ее центр (т.е. диаметр – это частный случай хорды). У любой окружности можно провести бесконечно много диаметров, которые будут иметь одну и ту же длину. На Рис.4 МN – диаметр окружности с центром в точке О. Обозначают диаметр d или D. Диаметр в два раза больше радиуса, т.е. d = 2r (D = 2R), откуда r = d : 2 (R = D : 2), следовательно, центр окружности (точка О) является серединой диаметра.
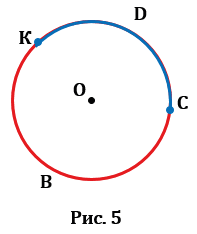
4. Дуга – это часть окружности, ограниченная двумя точками. На Рис.5 KDC и KBC – дуги, ограниченные точками К и С.
Построение окружности
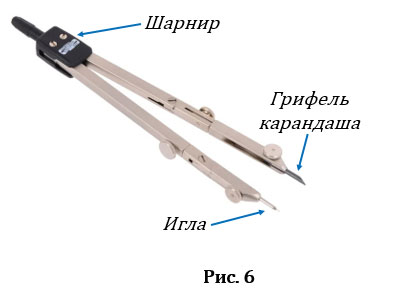
Для того, чтобы построить окружность используют специальный прибор, который называется циркулем (Рис.6). Циркуль состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет, например грифель карандаша.
Выполнение построения:
- отмечаем точку, которая будет центром окружности;
- делаем нужный раствор циркуля (расстояние между иглой и грифелем карандаша), т.е. определяем радиус окружности, которую нам нужно построить (Рис.7);
- ставим иглу циркуля в точку, которая определяет центр окружности;
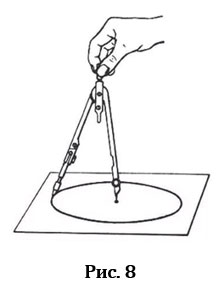
- проводим окружность данного радиуса (Рис.8).
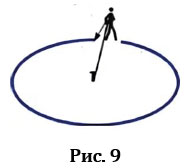
Для того, чтобы построить окружность на местности используют веревку. Сначала отмечаем место, которое будет определять центр окружности, вбиваем в это место колышек, привязываем к нему один конец веревки и отходим, держа другой конец веревки на расстояние равное радиусу окружности, которую мы хотим получить, отмечаем линию окружности (Рис.9).
Часть плоскости, которая ограничена окружностью (выделена черным цветом), называется кругом (выделен голубым цветом) (Рис.10).
Советуем посмотреть:
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 183,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 677,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 25,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 892,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1109,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1110,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1125,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1289,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
