Радиус кривизны траектории
В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.
Задача 1.
Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:
Откуда :
То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.

К задаче 1
Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому
Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и
. Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:
Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:
Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :
Определим полную скорость тела в момент времени :
Угол наклона вектора скорости к горизонту в этот момент равен:
А можно было сразу и косинус найти:
Тогда искомый радиус кривизны траектории равен:
Ответ: м,
м,
м.
Задача 2.
Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б)
.
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:
По условию :
б) Мы уже определили , осталась максимальная высота подъема.
Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:
Приравниваем и
:
Откуда .
Ответ: а) , б)
.
2 комментария
Есин из Хотам и ПВ
✉️
17.02.2022 15:20:44
Thank you very much
Jahongir
✉️
12.04.2022 19:14:12
Спасибо огромное! Полностью разобрался 🙂 Успехов вам!
Как найти радиус окружности траектории
Как найти радиус окружности

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Как найти радиус окружности траектории
Рассмотрим плоскую кривую, заданную уравнением (y = fleft( x right).) Пусть в точке (Mleft( right)) проведена касательная к данной кривой, которая образует угол (alpha) с осью абсцисс (рисунок (1)). При смещении (Delta s) вдоль дуги кривой точка (M) переходит в точку ( .) При этом положение касательной также изменяется: угол наклона касательной к оси (Ox) в точке ( ) будет составлять (alpha + Deltaalpha.) Таким образом, при смещении точки кривой на расстояние (Delta s) касательная поворачивается на угол (Deltaalpha.) (Будем считать, что угол (alpha) возрастает при вращении против часовой стрелки.)
Абсолютное значение отношения (largefrac > >normalsize) называется средней кривизной дуги (M .) В пределе, при (Delta s to 0,) мы получаем кривизну кривой в точке (M:) [K = limlimits_ left| > >> right|.] Из приведенного определения следует, что кривизна в какой-либо точке кривой характеризует скорость вращения касательной в этой точке.
Для плоской кривой (y = fleft( x right)) кривизна в точке (Mleft( right)) выражается через первую и вторую производные функции (fleft( x right)) по формуле [K = frac right|>> right)>^2>> right]>^ normalsize>>>>.] Если кривая задана в параметрической форме уравнениями (x = xleft( t right),) (y = yleft( t right),) то ее кривизна в произвольной точке (Mleft( right)) равна [K = frac right|>> right)>^2> + right)>^2>> right]>^ normalsize>>>>.] В случае, если кривая задана полярным уравнением (r = rleft( theta right),) кривизна находится по формуле [K = frac + 2 right)>^2> — rr»> right|>> + right)>^2>> right]>^ normalsize>>>>.] Радиусом кривизны кривой в точке (Mleft( right)) называется величина, обратная кривизне (K) данной кривой в рассматриваемой точке: [R = frac .] Следовательно, для плоских кривых, заданных явным уравнением (y = fleft( x right),) радиус кривизны в точке (Mleft( right)) будет определяться выражением [R = frac right)>^2>> right]>^ normalsize>>>> right|>>.]
Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме : [x = acos t,;;;y = bsin t.] где (t) − параметр. В точке (Aleft( right)) параметр имеет значение (t = 0,) а в точке (Bleft( right)) его значение равно (t = largefrac normalsize.)
Данная функция достигает максимума в точках (x = largefrac > normalsize,;n in Z.) В силу периодичности кривизна во всех точках максимума одинакова, поэтому достаточно рассмотреть лишь точку (x = 0).
В данном случае точка (x = 0) является точкой перегиба функции (y = arctan x.) Поскольку в точке перегиба вторая производная равна нулю, то кривизна здесь также должна быть равна нулю, что и показывает полученное решение.
Экспоненциальная функция (y = ) − это единственная уникальная функция, у которой производные любого порядка равны самой функции. Поэтому для кривизны данной кривой можно сразу написать следующую формулу: [ right|>> right)>^2>> right]>^ normalsize>>>> > = >> >> right)>^ normalsize>>>>.> ] Знак модуля в числителе опущен, поскольку экспоненциальная функция всегда положительна.
Радиус кривизны плоской кривой
Любая линия является кривой, даже прямая. Поэтому к любой линии применимы такие характеристики как кривизна или радиус кривизны. Как правило кривизна обозначается латинской литерой k, а радиус кривизны греческой литерой ρ.
Между собой эти характеристики кривой связаны следующим образом:
k = 1/ρ (542.1)
Т.е. чем больше радиус кривой, тем меньше ее кривизна.
А теперь рассмотрим несколько частных случаев кривых.
Радиус кривизны окружности
Окружность — это плоская кривая с постоянным радиусом кривизны. Т.е. радиус окружности это и есть радиус кривизны окружности:
Как определить радиус окружности, мы рассмотрим ниже.
Кривизна дуги
Любая дуга — это часть окружности. Соответственно радиус дуги равен радиусу окружности:
Рисунок 542.1. Дуга — часть окружности
На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.
Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.
Понятие кривизны дуги формулируется так:
Кривизна дуги — это отношение угла между касательными, проведенными в начале и конце дуги, к длине дуги
Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:
А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:
то, подставив значение длины дуги в уравнение (542.3), получим:
Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:
но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью
Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.
И еще одно интересное свойство дуги: Если соединить точки А и В прямой линией, то угол между этой линией и касательными будет равен α/2, а сама прямая линия — это и есть расстояние между точками А и В. Если дуга расположена в плоскости соответствующим образом, например так, как показано на рисунке 542.2:
Рисунок 542.2. Дуга из точки начала координат.
то расстояние между точками — это проекция l дуги на ось х. А максимальное расстояние между дугой и осью х — это стрела дуги h.
Радиус кривизны прямой линии
Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.
Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:
kп.л = 1/∞ = 0 (542.6)
Про до сих пор неразрешенный парадокс, возникающий при подобных подходах к прямой линии и к окружности, я уже упоминал в статье «Основы геометрии. Определения основных элементов, пятый элемент». Здесь лишь добавлю, что через прямую линию можно провести бесконечное множество плоскостей и в любой из этих плоскостей радиус кривизны прямой линии будет равен бесконечности. При этом через окружность можно провести две взаимно перпендикулярные плоскости, в одной из которых окружность будет окружностью, а в другой — прямой линией конечной длины. Поэтому
все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими
Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:
1. Из уравнения (542.1) можно сделать вывод, что:
kp = 1 (542.7)
Соответственно для прямой линии:
0·∞ = 1 (542.7.2)
Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.
2. Если прямая — это дуга с бесконечно большим радиусом, соответственно касательные, проведенные в концах такой дуги, совпадают с прямой, а угол, образованный касательными, равен нулю.
Это означает, что радиусы проведенные в концах дуги — прямой линии, являются параллельными прямыми и не могут пересекаться. А между тем по определению это радиусы, которые обязательно должны сходиться в некоторой точке — центре окружности.
Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.
Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.
Радиус кривизны точки
Точка — это самый простой и самый сложный элемент геометрии. Одни считают, что точка не имеет размеров, а значит и определить кривизну или радиус кривизны точки не возможно. Другие, в частности Евклид, считают, что точка не имеет частей, а каковы при этом размеры точки — не совсем понятно. Я же считаю, что точка — это начальный, далее не делимый элемент геометрии, размеры которого пренебрежимо малы по сравнению с остальными рассматриваемыми элементами. В этом случае для точки будут справедливыми следующие уравнения кривизны и радиуса кривизны:
kт. = 1/0 = ∞ (542.9)
И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что «деление на ноль невозможно», тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.
Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.
Примечание: На мой взгляд большинство из описанных выше парадоксов возникают из-за неправильного толкования понятия «бесконечность». Бесконечность как некая абсолютная величина не имеет пределов, а значит и никакому измерению не поддается. Кроме того бесконечность — это даже не постоянная, а переменная величина. Например луч — это прямая линия с началом в некоторой точке. Длина луча может быть бесконечно большой. При этом прямая линия тоже может быть бесконечно длинной при этом не иметь ни начала ни конца. Получается, что с одной стороны бесконечно длинный луч вроде бы в 2 раза короче, чем бесконечно длинная прямая. А с другой стороны длины их бесконечны и поэтому равны.
Возможным выходом из этой ситуации является принятие понятия «бесконечность», как относительного. Например, кривизна прямой линии является пренебрежимо малой величиной по отношению к радиусу кривизны. Или радиус кривизны прямой линии несопоставимо больше кривизны. Подобные толкования допускают и наличие кривизны прямой и некое конечное значение радиуса кривизны прямой и многое другое. Я бы назвал такой относительный подход к рассмотрению проблемы реалистичным, а подходы, использующие абсолютные понятия — идеализированными. Впрочем прямого отношения к теме данной статьи это не имеет. Продолжим рассмотрение плоских кривых.
И окружность и прямая линия являются плоскими кривыми с постоянным радиусом кривизны. При этом радиус кривизны прямой линии всегда известен, так как равен бесконечности, а для окружности всегда можно определить радиус, воспользовавшись теоремой Пифагора. Так в частном случае, если центр окружности совпадает с началом координат рассматриваемой плоскости (u = 0; v = 0 — координаты центра окружности), то:
Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.
R 2 = x 2 + y 2 (541.1.2)
А в общем случае, когда координаты центра окружности не совпадают с началом координат:
Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.
R 2 = (x — u) 2 + (y — v) 2 (542.10)
Но в жизни достаточно часто приходится сталкиваться с кривыми, радиус кривизны которых — не постоянная величина. Более того, этот радиус может изменяться в двух плоскостях измерения. Тем не менее так далеко углубляться в геометрию и алгебру мы не будем и далее рассмотрим, как можно определить радиус плоской кривой в некоторой точке.
Плоские кривые с изменяющимся радиусом кривизны
Примеров плоских кривых с изменяющимся радиусом кривизны очень много, это и гиперболы, и параболы, и синусоиды и т.п. Определение радиуса кривизны таких кривых основано на следующих теоретических предпосылках:
1. Любую окружность можно рассматривать как некоторое множество дуг.
2. Если количество дуг, составляющих окружность, стремится к бесконечности, то соответственно длина таких дуг стремится к нулю (m → 0).
3. Если мы обозначим длину такой очень короткой дуги как приращение функции длины окружности (m = Δl), то уравнение кривизны (542.3) примет следующий вид:
(542.3.1)
4. Тогда любую плоскую кривую с изменяющимся радиусом можно рассматривать как стремящееся к бесконечности множество дуг с постоянным радиусом. Другими словами в пределах любой кривой, описываемой параметрическими уравнениями, всегда можно выделить дугу, пусть даже и очень малой длины, стремящейся к точке и определить для нее кривизну и радиус кривизны в рассматриваемой точке.
Это означает, что самый точный способ определения радиуса кривизны в таком случае — это использование дифференциальных исчислений. В общем случае для этого нужно два раза продифференцировать уравнение радиуса окружности (542.10) по аргументу функции х, а затем извлечь квадратный корень из полученного результата. В итоге (полный вывод уравнения здесь не привожу из-за повышенной сложности записи, а для особо заинтересованных есть справочники и другие сайты) мы получим следующую формулу для определения радиуса кривизны:
(542.11)
Соответственно кривизна плоской кривой в рассматриваемой точке будет равна:
(542.12)
В частном случае, когда тангенс угла между касательными — первая производная от функции — является относительно малой величиной, например, tg2° = 0.035 соответственно (tg2°) 2 = 0.0012, то влиянием куба суммы первой производной и единицы на кривизну можно пренебречь (значение знаменателя дроби сводится к единице) и тогда:
k = y» = d 2 y/dx 2 (542.12.2)
Т.е. формально в таких случаях кривизной считается не отношение угла наклона между касательными к длине дуги, а некоторая величина, примерно соответствующая высоте h на рисунке 542.2.
Эта особенность второй производной очень активно используется в частности для упрощения определения прогиба элементов строительных конструкций.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Категории:
- Расчет конструкций . Основы прикладной геометрии
Оценка пользователей:
10.0 (голосов: 1)
Переходов на сайт:
6701
Комментарии:
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Радиус кривизны плоской кривой
Любая линия является кривой, даже прямая. Поэтому к любой линии применимы такие характеристики как кривизна или радиус кривизны. Как правило кривизна обозначается латинской литерой k, а радиус кривизны греческой литерой ρ.
Между собой эти характеристики кривой связаны следующим образом:
k = 1/ρ (542.1)
Т.е. чем больше радиус кривой, тем меньше ее кривизна.
А теперь рассмотрим несколько частных случаев кривых.
Радиус кривизны окружности
Окружность – это плоская кривая с постоянным радиусом кривизны. Т.е. радиус окружности это и есть радиус кривизны окружности:
Как определить радиус окружности, мы рассмотрим ниже.
Кривизна дуги
Любая дуга – это часть окружности. Соответственно радиус дуги равен радиусу окружности:
Рисунок 542.1. Дуга – часть окружности
На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.
Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.
Понятие кривизны дуги формулируется так:
Кривизна дуги – это отношение угла между касательными, проведенными в начале и конце дуги, к длине дуги
Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:
А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:
то, подставив значение длины дуги в уравнение (542.3), получим:
Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:
но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью
Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.
И еще одно интересное свойство дуги: Если соединить точки А и В прямой линией, то угол между этой линией и касательными будет равен α/2, а сама прямая линия – это и есть расстояние между точками А и В. Если дуга расположена в плоскости соответствующим образом, например так, как показано на рисунке 542.2:
Рисунок 542.2. Дуга из точки начала координат.
то расстояние между точками – это проекция l дуги на ось х. А максимальное расстояние между дугой и осью х – это стрела дуги h.
Радиус кривизны прямой линии
Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.
Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:
kп.л = 1/∞ = 0 (542.6)
Про до сих пор неразрешенный парадокс, возникающий при подобных подходах к прямой линии и к окружности, я уже упоминал в статье “Основы геометрии. Определения основных элементов, пятый элемент”. Здесь лишь добавлю, что через прямую линию можно провести бесконечное множество плоскостей и в любой из этих плоскостей радиус кривизны прямой линии будет равен бесконечности. При этом через окружность можно провести две взаимно перпендикулярные плоскости, в одной из которых окружность будет окружностью, а в другой – прямой линией конечной длины. Поэтому
все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими
Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:
1. Из уравнения (542.1) можно сделать вывод, что:
kp = 1 (542.7)
Соответственно для прямой линии:
0·∞ = 1 (542.7.2)
Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.
2. Если прямая – это дуга с бесконечно большим радиусом, соответственно касательные, проведенные в концах такой дуги, совпадают с прямой, а угол, образованный касательными, равен нулю.
Это означает, что радиусы проведенные в концах дуги – прямой линии, являются параллельными прямыми и не могут пересекаться. А между тем по определению это радиусы, которые обязательно должны сходиться в некоторой точке – центре окружности.
Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.
Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.
Радиус кривизны точки
Точка – это самый простой и самый сложный элемент геометрии. Одни считают, что точка не имеет размеров, а значит и определить кривизну или радиус кривизны точки не возможно. Другие, в частности Евклид, считают, что точка не имеет частей, а каковы при этом размеры точки – не совсем понятно. Я же считаю, что точка – это начальный, далее не делимый элемент геометрии, размеры которого пренебрежимо малы по сравнению с остальными рассматриваемыми элементами. В этом случае для точки будут справедливыми следующие уравнения кривизны и радиуса кривизны:
kт. = 1/0 = ∞ (542.9)
И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что “деление на ноль невозможно”, тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.
Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.
Примечание: На мой взгляд большинство из описанных выше парадоксов возникают из-за неправильного толкования понятия “бесконечность”. Бесконечность как некая абсолютная величина не имеет пределов, а значит и никакому измерению не поддается. Кроме того бесконечность – это даже не постоянная, а переменная величина. Например луч – это прямая линия с началом в некоторой точке. Длина луча может быть бесконечно большой. При этом прямая линия тоже может быть бесконечно длинной при этом не иметь ни начала ни конца. Получается, что с одной стороны бесконечно длинный луч вроде бы в 2 раза короче, чем бесконечно длинная прямая. А с другой стороны длины их бесконечны и поэтому равны.
Возможным выходом из этой ситуации является принятие понятия “бесконечность”, как относительного. Например, кривизна прямой линии является пренебрежимо малой величиной по отношению к радиусу кривизны. Или радиус кривизны прямой линии несопоставимо больше кривизны. Подобные толкования допускают и наличие кривизны прямой и некое конечное значение радиуса кривизны прямой и многое другое. Я бы назвал такой относительный подход к рассмотрению проблемы реалистичным, а подходы, использующие абсолютные понятия – идеализированными. Впрочем прямого отношения к теме данной статьи это не имеет. Продолжим рассмотрение плоских кривых.
И окружность и прямая линия являются плоскими кривыми с постоянным радиусом кривизны. При этом радиус кривизны прямой линии всегда известен, так как равен бесконечности, а для окружности всегда можно определить радиус, воспользовавшись теоремой Пифагора. Так в частном случае, если центр окружности совпадает с началом координат рассматриваемой плоскости (u = 0; v = 0 – координаты центра окружности), то:
Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.
R 2 = x 2 + y 2 (541.1.2)
А в общем случае, когда координаты центра окружности не совпадают с началом координат:
Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.
R 2 = (x – u) 2 + (y – v) 2 (542.10)
Но в жизни достаточно часто приходится сталкиваться с кривыми, радиус кривизны которых – не постоянная величина. Более того, этот радиус может изменяться в двух плоскостях измерения. Тем не менее так далеко углубляться в геометрию и алгебру мы не будем и далее рассмотрим, как можно определить радиус плоской кривой в некоторой точке.
Плоские кривые с изменяющимся радиусом кривизны
Примеров плоских кривых с изменяющимся радиусом кривизны очень много, это и гиперболы, и параболы, и синусоиды и т.п. Определение радиуса кривизны таких кривых основано на следующих теоретических предпосылках:
1. Любую окружность можно рассматривать как некоторое множество дуг.
2. Если количество дуг, составляющих окружность, стремится к бесконечности, то соответственно длина таких дуг стремится к нулю (m → 0).
3. Если мы обозначим длину такой очень короткой дуги как приращение функции длины окружности (m = Δl), то уравнение кривизны (542.3) примет следующий вид:
(542.3.1)
4. Тогда любую плоскую кривую с изменяющимся радиусом можно рассматривать как стремящееся к бесконечности множество дуг с постоянным радиусом. Другими словами в пределах любой кривой, описываемой параметрическими уравнениями, всегда можно выделить дугу, пусть даже и очень малой длины, стремящейся к точке и определить для нее кривизну и радиус кривизны в рассматриваемой точке.
Это означает, что самый точный способ определения радиуса кривизны в таком случае – это использование дифференциальных исчислений. В общем случае для этого нужно два раза продифференцировать уравнение радиуса окружности (542.10) по аргументу функции х, а затем извлечь квадратный корень из полученного результата. В итоге (полный вывод уравнения здесь не привожу из-за повышенной сложности записи, а для особо заинтересованных есть справочники и другие сайты) мы получим следующую формулу для определения радиуса кривизны:
(542.11)
Соответственно кривизна плоской кривой в рассматриваемой точке будет равна:
(542.12)
В частном случае, когда тангенс угла между касательными – первая производная от функции – является относительно малой величиной, например, tg2° = 0.035 соответственно (tg2°) 2 = 0.0012, то влиянием куба суммы первой производной и единицы на кривизну можно пренебречь (значение знаменателя дроби сводится к единице) и тогда:
k = y” = d 2 y/dx 2 (542.12.2)
Т.е. формально в таких случаях кривизной считается не отношение угла наклона между касательными к длине дуги, а некоторая величина, примерно соответствующая высоте h на рисунке 542.2.
Эта особенность второй производной очень активно используется в частности для упрощения определения прогиба элементов строительных конструкций.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье “Записаться на прием к доктору”
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины – номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Категории:
- Расчет конструкций . Основы прикладной геометрии
Оценка пользователей:
10.0 (голосов: 1)
Переходов на сайт:
6701
Комментарии:
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье “Записаться на прием к доктору” (ссылка в шапке сайта).
Найти радиус траектории в точке окружность
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
7.1. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.2. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.3. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки:
,
,
.
,
,
Модуль полного ускорения:
.
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.4. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.5. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки по осям :
,
,
Ускорения точки по осям:
,
,
.
Модуль касательного ускорения точки:
, а модуль нормального ускорения .
Нормальное ускорение и радиус кривизны траектории связаны соотношением .
7.6. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки по осям :
,
,
Ускорения точки по осям:
,
,
.
Модуль касательного ускорения точки:
,
а модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением .
7.7. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.8. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
.
,
,
Модуль полного ускорения:
.
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.9. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , , .
Решение: Скорости точки :
,
,
.
,
,
Модуль полного ускорения:
.
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.10. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.11. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.12. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.13. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.14. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Найти: , , .
Решение: Скорости точки по осям :
,
,
,
Ускорения точки по осям:
,
,
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.15. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.16. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.17. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , , .
Решение: Скорости точки :
,
,
,
,
Модуль полного ускорения:
Модуль касательного ускорения точки:
,
А модуль нормального ускорения:
.
Нормальное ускорение и радиус кривизны траектории связаны соотношением:
.
7.18. Дан закон движения точки по окружности радиусом r . Определить:
1) скорость и ускорение точки при и ;
2) моменты остановки точки;
3) путь, пройденный точкой за 10секунд.
Дано: , , , .
Найти: , , , , , , П.
Решение: 1. На траектории отметим точку О – начало отсчета координаты s и укажем положительное направление отсчета этой координаты. Отметим положение точки в заданные моменты времени: При :
;
При :
.
Проведем из этих точек естественные оси координат.
Определим проекцию скорости на касательную:
.
При : ;
При : .
Векторы и совпадают со своими проекциями. Определим проекции ускорения на естественнее оси координат :
; , Полное ускорение точки .
При :
,
и
.
При :
,
и
.
2. Чтобы найти время остановки надо найти время, когда скорость точки равна нулю:
, получим и .
3. Поскольку за 10 секунд точка сделала две остановки, пройденный ею путь за 10с можно найти как сумму пути, пройденного от начала до первой остановки, от первой до второй остановки и от второй до момента времени :
,
; ; ; .
Путь пройденный точкой за 10 секунд:
.
7.19. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Дано: , (1)
( x и y – в см , t и t 1 – в с).
Найти: 1) вид траектории;
2) для t = t 1 положение точки на траектории;
3) .
Решение: 1) Уравнение движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключаем время t из уравнений (1).
Возводя обе части равенств в квадрат, а затем складывая равенства, получаем , т.е. траекторией точки М является окружность радиуса 2, показанная на рис.1.
2) Определяем положение точки М в заданный момент времени t =1 с :
Вектор скорости точки
. (2)
(3)
Здесь – орты осей и ; – проекции скорости и ускорения точки на оси координат.
Найдем их, дифференцируя по времени уравнения движения (1):
По найденным проекциям определяем модуль скорости:
, (4)
,
,
и модуль ускорения точки:
, (5)
Модуль касательного ускорения точки
, (6)
; (7)
выражает проекцию ускорения точки на направление ее скорости. Знак «+» при означает, что движение точки ускоренное, направление и совпадают; знак «–» – что движение замедленное.
Вычисляем модуль касательного ускорения для заданного момента времени
Модуль нормального ускорения точки
. (8)
Если радиус кривизны траектории в рассматриваемой точке неизвестен, то нормальное ускорение можно определить по формуле
. (9)
При движении точки в плоскости формула (9) принимает вид
.
Модуль нормального ускорения можно определить и следующим образом:
. (10)
Воспользуемся в нашем случае формулой (10)
Радиус кривизны траектории в рассматриваемой точке определим из выражения:
. (11)
Тогда
На рис. 1 показано положение точки М в заданный момент времени. Вектор строим по составляющим и , причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор строим по составляющим и и затем раскладываем на составляющие и . Совпадение величин и , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
7.20. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
( x и y – в см , t и t 1 – в с).
Найти: 1) вид траектории;
2) .
Указания. Задача – относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени t 1 = 1 с .
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t :
Отсюда окончательно находим уравнение траектории точки (параболы, см. рисунок):
2. Скорость точки найдем по ее проекциям на координатные оси:
V = и при t 1 = 1 с,
3. Аналогично найдем ускорение точки:
а =
4. Касательное ускорение найдем, дифференцируя по времени равенство:
. (3)
ч исловые значения всех величин, входящих в правую часть выражения (3), определены и даются равенствами (1) и (2).
Подставив в (3) эти числа, найдем сразу, что при t 1 = 1 с
=7,49 см/с 2 .
5. Нормальное ускорение точки:
a n = .
Подставляя сюда найденные числовые значения a 1 и a 1 τ , получим, что при t 1= 1 с
6. Радиус кривизны траектории ρ = V 2 / a n .
Подставляя сюда числовые значения V 1 и a 1 n , найдем, что при t 1 = 1 с
Ответ: V 1= 8 ,54 см/с, а 1 =8 см/с 2 , =7,49 см/с 2 , a 1 n =2,81 см/с 2 , ρ1 =25,95 см.
7.21. Точка движется по дуге окружности радиуса R =1 м по закону ( s – в метрах, t – в секундах), где s = AM (см. рисунок).
Найти: скорость и ускорение точки в момент времени t 1 =1 с .
Определяем скорость точки:
V = ds / dt = .
При t 1 =1 с получим = -1,26 м/ с .
Ускорение находим по его касательной и нормальной составляющим:
,
п ри t 1 = 1 с получим , учтя, что R = 1 м
,
тогда ускорение точки при t 1 =1 с будет:
=1,59 м/с 2 .
Изобразим на рисунке векторы , , учитывая знак V 1 и считая положительным направление от А к М.
7.22. По заданным уравнениям движения точки М установить вид её траектории и для момента времени t = t 1(с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.
Дано: , , t 1=1 сек ( x и y – в см , t и t 1 – в с).
Найти: 1) вид траектории;
2) .
1) Найдём траекторию движения:
Для этого исключим параметр t .
Возведём во вторую степень, получившиеся уравнения, а затем сложим, таким образом, исключится t . Получим:
Это окружность с центром в точке с координатами (-1;0) и радиусом
2) Найдём положение точки на траектории в момент времени t = t 1:
3) Определим скорость токи:
Для нахождения вектора полной скорости необходимо сложить 2 вектора:
Найдём модуль полной скорости:
для момента времени t 1:
4) Определим ускорение точки:
для момента времени t 1:
для момента времени t 1:
Найдём полное ускорение:
Найдём модуль полного ускорения:
для момента времени t 1:
Определим касательное ускорение :
или,
для момента времени t :
Определим нормальное ускорение an :
для момента времени t 1:
5) Из полученных результатов можно найти радиус кривизны траектории , в момент времени t 1:
Действительно, этот радиус совпадает с радиусом окружности (траектории).
7.23. Точка М движется согласно уравнений ; ; ( x , y – в метрах, t – в секундах). Определить уравнение траектории точки, для момента времени t =1с, найти положение точки, а также скорость, полное, касательное, нормальное ускорения точки и радиус кривизны траектории.
1) Найдем уравнение траектории точки. Для определения уравнения траектории исключим из уравнений движения время . Из первого уравнения движения точки найдем
Из второго уравнения движения найдем
Возведя полученные значения ( правую и левую стороны уравнения ) в квадрат и складывая их находим:
.
Следовательно, траекторией точки является эллипс с центром в точке с координатами (3;1).
Вид траектории показан на рисунке.
2) Найдем положение точки в момент времени t =1с
; .
Положение точки М 1 показано на рисунке.
3) Найдем скорость точки М
,
Где , или в момент времени t1=1c
, или в момент времени t1=1c
4) Найдём ускорение точки.
,
где , или ,
, или
5) Найдем касательное ускорение точки M,
6) Найдём нормальное ускорение точки M ,
7) Найдем радиус кривизны траектории точки М,
,
Направление векторов показано на рисунке.
Ответ: =7.85м/ c ; = 4.93 м/ c 2 ; =0; = 4.93 м/ c 2 ; м
7.24. Пусть точка М движется в плоскости xOy в соответствии с уравнениями . Для момента времени = 0,5 с найти положение точки М на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение: Заданный закон движения точки в координатной форме можно рассматривать как параметрические уравнения траектории точки. Исключим время t из уравнений движения и получим уравнение траектории точки в виде:
.
Таким образом, траекторией точки М является эллипс со смещенным центром, изображенный на рис. Отметим на траектории положение точки М 1 ( x 1, y 1) в момент времени t 1 = 0,5 c
;
.
Вектор скорости точки представим в виде:
,
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от соответствующих координат по времени
В момент времени t 1 = 0,5 c
Вектор скорости точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом
.
Полученный вектор должен быть направлен по касательной к траектории точки в сторону движения. Модуль скорости точки определим по уже найденным проекциям
Вектор ускорения точки представим в виде:
,
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от проекций вектора скорости или 2-м производным от соответствующих координат по времени:
В момент времени t 1 = 0,5 c
Вектор ускорения точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом
.
Полученный вектор ускорения точки в общем случае должен отклоняться от вектора скорости в сторону вогнутости траектории, а при движении по эллипсовидной траектории – проходить через центр эллипса. Модуль ускорения точки определим по уже найденным проекциям
Вектор полного ускорения точки можно также представить в виде геометрической суммы его проекций на оси естественной системы отсчета
,
где и – единичные орты касательной и главной нормали; и – соответственно проекции вектора ускорения на касательную и главную нормаль. Касательную М 1 t направляем по касательной к траектории в сторону движения точки движения, а главную нормаль М1 n – перпендикулярно касательной в сторону вогнутости траектории. При вычислении касательного ускорения удобно воспользоваться формулой, устанавливающей связь между координатным и естественным способами задания движения точки
.
В момент времени t 1 = 0,5 c
.
Значение касательного ускорения имеет отрицательный знак, следовательно, в данный момент времени движение точки замедленное и вектор касательного ускорения направлен в противоположную сторону направлению вектора скорости точки .
Нормальное ускорение вычислим по формуле , если известен радиус кривизны траектории. Например, если точка движется по окружности радиусом R, то в любой точке траектории . Если же траекторией движения точки является прямая, то , следовательно, . В данном случае радиус кривизны траектории заранее не известен, поэтому нормальное ускорение определяем по формуле:
.
В момент времени t 1 = 0,5 c
.
Построим векторы и в соответствии с уже выбранным масштабом, а затем сложим их геометрически. В результате получим тот же вектор полного ускорения точки , который ранее уже был получен геометрической суммой составляющих и . Этот факт служит контролем правильности решения.
Радиус кривизны траектории в рассматриваемой точке определим по формуле
.
В момент времени t 1 = 0,5 c
.
Ответ: =8,82 см; =2,59 см; =4,44 см/ c ; =2,22 см/ c ; =4,96 см/с; =6,97 см/с 2 ; =3,49 см/с 2 ; =7,79 см/с 2 ; =4,67 см/с 2 ; =6,23 см/с 2 ; =3,95 см (радиус кривизны траектории в точке ).
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
[spoiler title=”источники:”]
http://doctorlom.com/item542.html
http://www.teoretmeh.ru/primerkinematika4.htm
[/spoiler]
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 ноября 2016 года; проверки требуют 5 правок.
- О разновидности перекрёстков: см. Круговой перекрёсток.
В физике кругово́е движе́ние — это вращательное движение материальной точки или тела, когда ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела. В этом случае траектория точки или тела является окружностью, круговой орбитой. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение.
Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма.
Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона.
Формулы для равномерного кругового движения[править | править код]
Для движения по кругу радиуса R длина окружности будет C = 2π R. Если период вращения есть T, то угловая скорость вращения ω будет равна:
Скорость движения объекта равна
Угол поворота θ за время t равен:
Ускорение, вызванное изменением направления скорости, можно найти, если заметить, что скорость совершает полное изменение направления за то же самое время T, за которое объект делает один оборот. Тогда вектор скорости проходит путь длиной 2π v каждые T секунд, или:
и направлено радиально к центру.
Взаимосвязи векторов показаны на рис. 1. Ось вращения изображена вектором Ω, перпендикулярно плоскости орбиты и имеет величину ω = dθ / dt. Направление вектора Ω выбрано в соответствии с правилом правой руки. По этому соглашению скорость это векторное произведение вида:
и есть вектор, перпендикулярный как Ω так и r ( t ), направленный по касательной к орбите и имеющий величину ω R. Аналогично, ускорение определяется как:
Оно представляет собой вектор, перпендикулярный как Ω так и v ( t ), имеющий величину ω |v| = ω2 R и направление строго противоположно к r ( t ).
Постоянная скорость[править | править код]
В простейшем случае скорость, масса и радиус являются постоянными.
Рассмотрим тело массой один килограмм, движущееся по кругу радиуса один метр с угловой скоростью один радиан в секунду.
Теперь рассмотрим тело массы 


Переменная скорость[править | править код]
В круговом движении полную силу, приложенную к объекту, можно разложить на две составляющие: центростремительную, удерживающую тело на круговой орбите (т. е. меняющую направление вектора скорости), и тангенциальную, направленную по касательной к окружности и вызывающую изменение длины вектора скорости (т. е. меняющую скорость вращения тела по орбите). Величина центростремительной составляющей зависит от мгновенной скорости.
Для примера, когда камень привязан к концу верёвки, то он подвергается воздействию некоторой силы, которую мы можем разложить на радиальную и боковую составляющие. Радиальная направлена к центру (вовнутрь) окружности и вызвана тем, что веревка сопротивляется удлинению. А боковая составляющая определяет будет вращение камня ускоряться или замедляться.
Описание кругового движения в полярных координатах[править | править код]
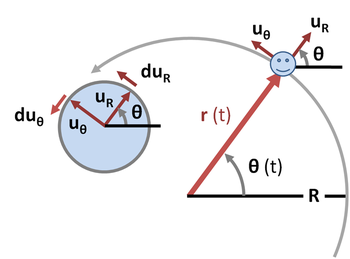
Траектория кругового движения тела может быть описана в полярной системе координат значениями фиксированного расстояние R от центра орбиты, являющейся точкой отсчёта, и угла ориентации θ (t) от некоторого фиксированного направления (рис. 2). Вектор перемещения 
где 


Скорость является производной перемещения по времени:
Поскольку радиус окружности является константой, радиальная составляющая скорости равна нулю. Единичный вектор 


где направление изменения должно быть перпендикулярно к 






Следовательно, скорость становится:
Ускорение тела также можно разложить на радиальную и тангенциальную составляющие. Ускорение есть производная скорости по времени:
Производная по времени от 






где отрицательный знак необходим, чтобы сохранить 



Центростремительное ускорение — это радиальная составляющая, направленная по радиусу вовнутрь:
тогда как тангенциальная составляющая изменяет значение скорости:
Описание кругового движения в комплексных числах[править | править код]
Круговое движение можно описать с использованием комплексных чисел. Пусть 


где 
есть угол комплексного вектора по отношению к вещественной оси как функция времени t.
Поскольку радиус есть константа:
где точка означает дифференциал по времени.
В этих обозначениях скорость имеет вид :
а ускорение:
Первое слагаемое направлено против вектора перемещения, а второе — перпендикулярно ему, как и в предыдущих результатах.
Ссылки[править | править код]
- BIGS animation (англ.) Круговое движение
- Circular Motion (англ.) – глава из онлайн-учебника
См. также[править | править код]
- Момент импульса
- Уравнения движения
- Математический маятник
- Центростремительная сила
- Сила инерции
Как найти радиус кривизны траектории
При рассмотрении движения тел используется ряд характеризующих величин, например тангенциальное и нормальное (центростремительное) ускорение, скорость, а также кривизна траектории. Радиус кривизны – геометрическое понятие, обозначающее радиус окружности R, по которой движется тело. Этот параметр можно найти по соответствующим формулам с помощью заданной траектории движения.

Инструкция
Наиболее часто встречаются задачи на определение радиуса кривизны траектории полета брошенного тела в заданный промежуток времени. Траектория движения в данном случае описывается уравнениями на координатных осях: х = f(t), y = f(t), где t – время, в момент которого требуется найти радиус. Его вычисление будет основываться на применении формулы аn = V²/R. Здесь радиус R выявляется из отношения нормального ускорения аn и мгновенной скорости V движения тела. Узнав данные величины, можно легко найти искомую компоненту R.
Вычислите проекции скорости тела на осях (ОХ, ОY). Математический смысл скорости – это первая производная от уравнения движения. Поэтому они легко находятся взятием производной от заданных уравнений: Vx = x’, Vy = y’. При рассмотрении геометрического отображения данных проекций в координатной системе видно, что они являются катетами прямоугольного треугольника. Причем гипотенуза в нем – искомая мгновенная скорость. Исходя из этого, вычислите величину мгновенной скорости V по теореме Пифагора: V = √( Vx² + Vy²). Подставляя в выражение известное значение времени, найдите числовой показатель V.
Модуль нормального ускорения также легко определить, рассмотрев другой прямоугольный треугольник, образуемый модулем полного ускорения а и касательного ускорения тела ак. Причем здесь нормальное ускорение является катетом и вычисляется так: аn = √( а² – ак²). Для нахождения касательного ускорения продифференцируйте по времени уравнение мгновенной скорости движения: ак = |dV/dt|. Полное же ускорение вычислите по его проекциям на оси, аналогично нахождению мгновенной скорости. Только для этого возьмите от заданных уравнений движения производные второго порядка: ах = х”, аy = y”. Модуль ускорения а = √( ах2 + аy2). Подставляя все найденные величины, определите числовое значение нормального ускорения аn = √( а² – ак²).
Выразите из формулы аn = V²/R искомую переменную радиуса кривизны траектории: R = V²/ аn. Подставьте числовые значения скорости и ускорения, вычислите радиус.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Преподаватель который помогает студентам и школьникам в учёбе.
Кинематический способ определения радиуса кривизны траектории в теоретической механике
Кинематический способ определения радиуса кривизны траектории:
При решении многих технических задач возникает необходимость знать радиус кривизны р (или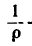
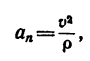
Таким образом, если закон движения точки задан уравнениями 
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:

2. Подставив в (б’) выражения  найти
найти 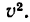
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение 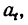 а затем а?.
а затем а?.
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
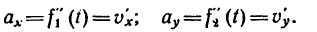
5. Подставив в (г) выражения 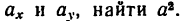
6. Подставить в (в) значения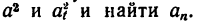
7. Подставив в (а) найденные значения 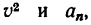 получить радиус кривизны р.
получить радиус кривизны р.
Задача:
Движение точки задано уравнениями 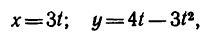
(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.
Решение.
1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим
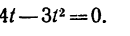
Отсюда [решая уравнение относительно 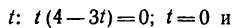
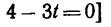 находим, что траектория пересекает ось Ох в моменты времени
находим, что траектория пересекает ось Ох в моменты времени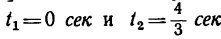
2. Находим выражения проекций скорости:
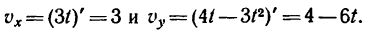
Как видно, проекция скорости на ось Ох – постоянная величина (не зависит от времени).
3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:
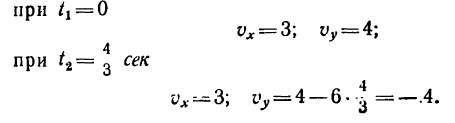
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы
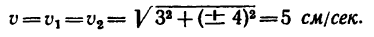
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):
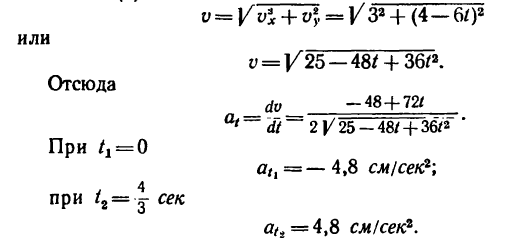
6. Находим проекции полного ускорения точки:
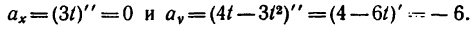
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем
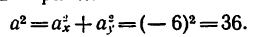
7. Определяем нормальное ускорение точки. Как при 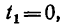
так и при 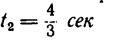
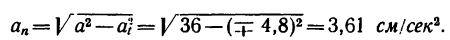
8. Зная, что в моменты пересечения траекторией оси 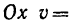 5 см:сек и
5 см:сек и 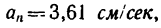 находим радиусы кривизны траектории в этих точках:
находим радиусы кривизны траектории в этих точках:
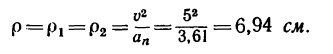
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости 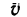 и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы
и ускорения а в местах пересечения траектории с осью Ох (эти векторы легко построить при помощи найденных проекций), а также радиусы 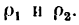
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки