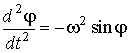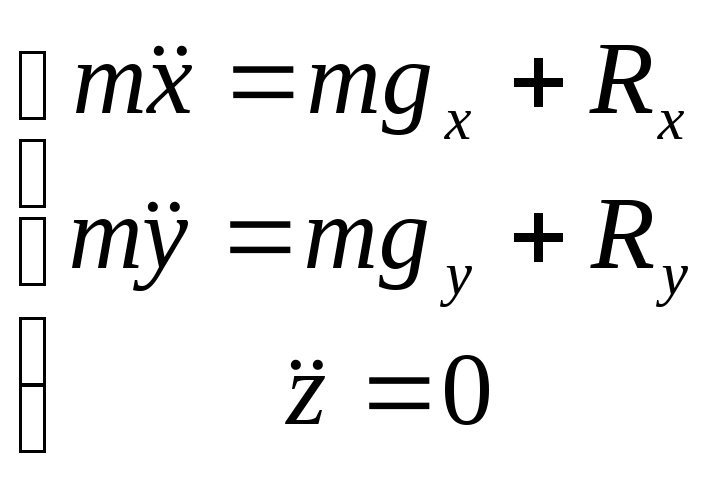Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 февраля 2023 года; проверки требует 1 правка.
Математический маятник. Чёрный пунктир — положение равновесия, 
— угол отклонения от вертикали в некоторый момент
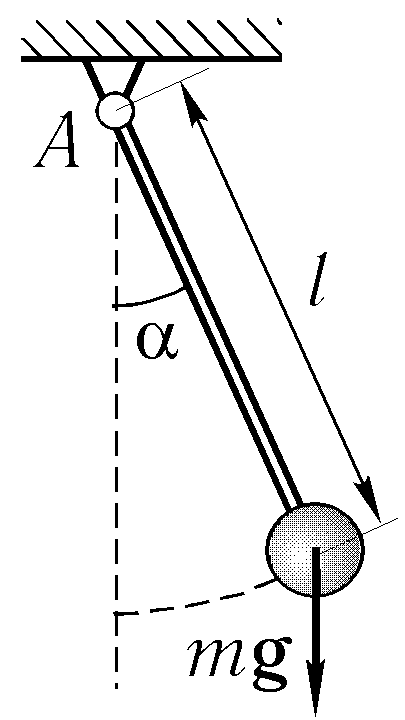
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения[1]. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен
и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.
Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.
Характер движения маятника[править | править код]
Математический маятник со стержнем способен колебаться только в какой-то одной плоскости (вдоль какого-то выделенного горизонтального направления) и, следовательно, является системой с одной степенью свободы. Если же стержень заменить на нерастяжимую нить, получится система с двумя степенями свободы (так как становятся возможными колебания по двум горизонтальным координатам).
При колебаниях в одной плоскости маятник движется по дуге окружности радиуса 
, а при наличии двух степеней свободы может описывать кривые на сфере того же радиуса[1]. Нередко, в том числе в случае нити, ограничиваются анализом плоского движения; оно и рассматривается далее.
Уравнение колебаний маятника[править | править код]
Маятник (схема с обозначениями)
Если в записи второго закона Ньютона 
для математического маятника выделить тангенциальную составляющую (
, получится выражение
,
так как 
, а из действующих на точку сил тяжести и натяжения ненулевую компоненту 
даёт только первая. Следовательно, колебания маятника описываются обыкновенным дифференциальным уравнением (ДУ) вида
- ,
где неизвестная функция 
― это угол отклонения маятника в момент 
от нижнего положения равновесия, выраженный в радианах, ― длина подвеса, 
― ускорение свободного падения. Предполагается, что потерь энергии в системе нет. В области малых углов 
это уравнение превращается в
- .
Для решения ДУ второго порядка, то есть для определения закона движения маятника, необходимо задать два начальных условия — угол и его производную 
при 
.
Решения уравнения движения[править | править код]
Возможные типы решений[править | править код]
В общем случае решение ДУ с начальными условиями для маятника может быть получено численно. Варианты движения (в случае, если маятник — это материальная точка на лёгком стержне), качественно, представлены на анимации. В каждом окне вверху показана зависимость угловой скорости от угла . По мере нарастания размаха поведение маятника всё сильнее отклоняется от режима гармонических колебаний.
-
Маятник висит
-
Малые колебания (размах 45°)
-
Колебания с размахом 90°
-
Колебания с размахом 135°
-
Колебания с размахом 170°
-
Фиксация в верхнем положении
-
Движение близкое к сепаратрисе
-
Вращение маятника
Гармонические колебания[править | править код]
Уравнение малых колебаний маятника около нижнего положения равновесия, когда уместна замена , называется гармоническим уравнением:
- ,
где 
― положительная константа, определяемая только из параметров маятника и имеющая смысл собственной частоты колебаний. Кроме того, может быть осуществлён переход к переменной «горизонтальная координата» 
(ось 
лежит в плоскости качания и ортогональна нити в нижней точке):
- .
Малые колебания маятника являются гармоническими. Это означает, что смещение маятника от положения равновесия изменяется во времени по синусоидальному закону[2]:
- ,
где 
— амплитуда колебаний маятника, 
— начальная фаза колебаний.
Если пользоваться переменной , то при необходимо задать координату 
и скорость 
, что позволит найти две независимые константы , из соотношений 
и 
.
Случай нелинейных колебаний[править | править код]
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 
— это синус Якоби. Для 
он является периодической функцией, при малых 
совпадает с обычным тригонометрическим синусом.
Параметр определяется выражением
- .
Период колебаний нелинейного маятника составляет
- ,
где K — эллиптический интеграл первого рода.
Для вычислений практически удобно разлагать эллиптический интеграл в ряд:
![{displaystyle T=T_{0}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {theta _{0}}{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {theta _{0}}{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {theta _{0}}{2}}right)+dots right}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5346cf06ad62d5c061cf5527d53a86e61cf89478)
где 
— период малых колебаний, 
— максимальный угол отклонения маятника от вертикали.
При углах до 1 радиана (≈ 60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:
- .
Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах сентябрьского выпуска журнала «Заметки американского математического общества» 2012 года[3]:
- ,
где 
— арифметико-геометрическое среднее чисел 1 и 
.
Движение по сепаратрисе[править | править код]
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, а затем останавливается, возвратившись в исходное положение.
Факты[править | править код]
Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.
- Если амплитуда колебания маятника близка к , то есть движение маятника на фазовой плоскости близко к сепаратрисе, то под действием малой периодической вынуждающей силы система демонстрирует хаотическое поведение. Это одна из простейших механических систем, в которой хаос возникает под действием периодического возмущения[4].
- Если точка подвеса не неподвижна, а совершает колебания, то у маятника может появиться новое положение равновесия. Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками». Такая система называется маятником Капицы.
- В условиях вращения Земли при достаточно длинной нити подвеса плоскость, в которой маятник совершает колебания, будет медленно поворачиваться относительно земной поверхности в сторону, противоположную направлению вращения Земли (маятник Фуко).
См. также[править | править код]
- Физический маятник
- Маятник Фуко
- Маятник Дубошинского
Примечания[править | править код]
- ↑ 1 2 Главный редактор А. М. Прохоров. Маятник // Физический энциклопедический словарь. — М.: Советская энциклопедия. — 1983. — Статья в Физическом энциклопедическом словаре
- ↑ Скорость и ускорение маятника при гармонических колебаниях также изменяются во времени по синусоидальному закону.
- ↑ Adlaj S. An Eloquent Formula for the Perimeter of an Ellipse (англ.) // Notices of the AMS. — 2012. — Vol. 59, no. 8. — P. 1096—1097. — ISSN 1088-9477.
- ↑ В. В. Вечеславов. Хаотический слой маятника при низких и средних частотах возмущений // Журнал технической физики. — 2004. — Т. 74, № 5. — С. 1—5. Архивировано 14 февраля 2017 года.
Ссылки[править | править код]
- Коллекция Java-апплетов, моделирующая поведение математических маятников, в частности маятника Капицы.
- Java-апплет, моделирующий колебание математического маятника при наличии вязкого трения с черчением фазовой траектории.
- Учебный фильм «Математический и физический маятник», производство СССР
Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Уравнение движения математического маятника
Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.
Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
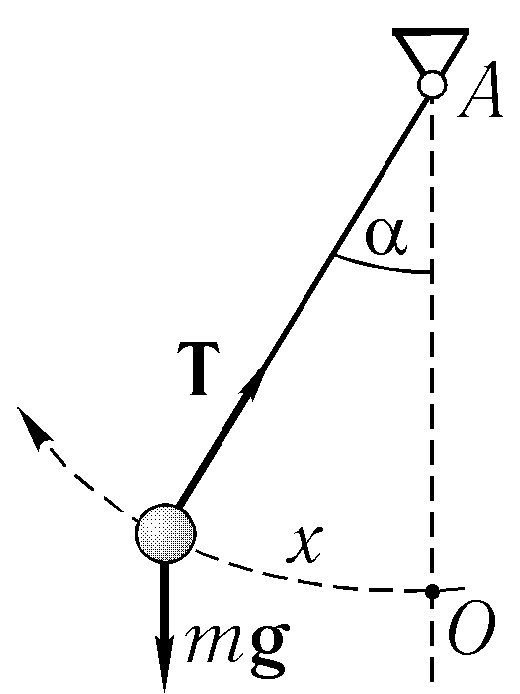
где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Лекция
9
Теория
колебаний.
Колебания
бываю различной природы
Механические,
электромагнитные, звуковые.
Последовательные
периодические изменения параметров
системы называются колебаниями.
Время,
за которое система возвращается в
начальное состояние после вывода ее из
положения равновесия, называется
периодом -Т.
Количество
колебаний, совершаемых за единицу
времени, называется частотой.
–
частота [Гц]
Колебания,
подчиняющиеся тригонометрическим
законам, называются гармоническими.
Математический маятник
Сейчас уже невозможно
проверить легенду о том, как Галилей,
стоя на молитве в соборе, внимательно
наблюдал за качанием бронзовых люстр.
Наблюдал и определял время, затраченное
люстрой на движение туда и обратно. Это
время потом назвали периодом колебаний.
Часов у Галилея не было, и, чтобы сравнить
период колебаний люстр, подвешенных на
цепях разной длины, он использовал
частоту биения своего пульса.
Маятники используют
для регулировки хода часов, поскольку
любой маятник имеет вполне определённый
период колебаний. Маятник находит также
важное применение в геологической
разведке. Известно, что в разных местах
земного шара значения g различны. Различны
они потому, что Земля — не вполне
правильный шар. Кроме того, в тех местах,
где залегают плотные породы, например,
некоторые металлические руды, значение
g аномально высоко. Точные измерения g
с помощью математического маятника
иногда позволяют обнаружить такие
месторождения.
Уравнение движения
математического маятника
Математическим
маятником называется тяжёлая материальная
точка, которая двигается или по
вертикальной окружности (плоский
математический маятник), или по сфере
(сферический маятник). В первом приближении
математическим маятником можно считать
груз малых размеров, подвешенный на
нерастяжимой гибкой нити.
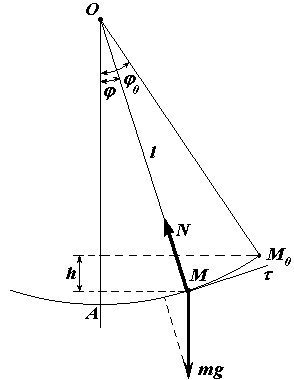
Рассмотрим движение
плоского математического маятника по
окружности радиуса l с центром в точке
О (рис. 1). Будем определять положение
точки М (маятника) углом отклонения φ
радиуса ОМ от вертикали. Направляя
касательную M t в сторону положительного
отсчёта угла φ , составим естественное
уравнение движения. Это уравнение
образуется из уравнения движения
mа
= F + N, (1)
где F — действующая
на точку активная сила, а N — реакция
связи.
Рис.1
Уравнение (1) мы
получили по второму закону Ньютона,
который является основным законом
динамики и гласит, что производная по
времени от количества движения
материальной точки равна действующей
на неё силе, т. е.
(2).
Считая массу
постоянной, можно представить предыдущее
уравнение в виде
или
,
где W есть ускорение
точки.
Итак, уравнение
(1) в проекции на ось t даст нам одно из
естественных уравнений движения точки
по заданной неподвижной гладкой кривой:
или
.
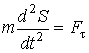
В нашем случае
получим в проекции на ось t,
где m есть
масса маятника.
Так как
или
,
отсюда находим
.
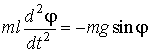
Сокращая
на m будем окончательно иметь:
,
,
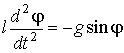
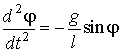
(4).
Рассмотрим сначала
случай малых колебаний. Пусть в начальный
момент маятник отклонён от вертикали
на угол φ и опущен без начальной скорости.
Тогда начальные условия будут:
при t = 0,
(5).
Из интеграла
энергии:
(6),
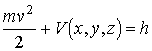
где
V — потенциальная энергия, а h — постоянная
интегрирования, следует, что при этих
условиях в любой момент времени угол φ
< φ 0. Значение постоянной h
определяется по начальным данным.
Допустим, что угол φ 0 мал (φ 0
<< 1); тогда угол φ будет также мал, и
можно приближённо положить sin φ -» φ. При
этом уравнение (4) примет вид
(7).
1)
Колебания груза за счет сжатой пружины
Закон
Гука: сила, действующая со стороны
пружины, пропорциональна деформации
(сжатию).
F = – kx
Второй
закон Ньютона
Подставляя
выражение для ускорения через производную
Алгебраические
преобразования
Каноническое
уравнение колебаний
,
x
– смещение груза относительно положения
равновесия;
-собственная
частота колебаний
2)Математический
маятник(груз точечный, нить жесткая,
отклонения малы)
Координатное
описание с использованием равновесия
сил
Векторная
запись
Запись
в проекциях на оси
Представление
через вращательное движение
Угловая
скорость
Угловое
ускорение
Закон
вращательного движения
(произведение
момента инерции на угловое ускорение
равняется моменту силы)
Расписывая
момент инерции, угловое ускорение и
момент силы, перепишем
при
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
13.03.20163.54 Mб24Фелдман Л. Основы анализа поверхности.djvu
- #
- #
- #
- #
- #
- #
- #
- #
Маятник Максвелла. Внешний вид и параметры лабораторной установки. Определение момента инерции маятника Максвелла
Страницы работы
Фрагмент текста работы
Санкт-Петербургский государственный университет
аэрокосмического приборостроения
Рейтинг за работу
Преподаватель
Отчёт по лабораторной работе №3
по курсу общая физика
«Маятник Максвелла»
ОФ43.2205_1.03_ЛР
Работу выполнил студент
группы 1564 кс
Санкт-Петербург
2005
1. Цель работы: определение момента инерции маятника Максвелла.
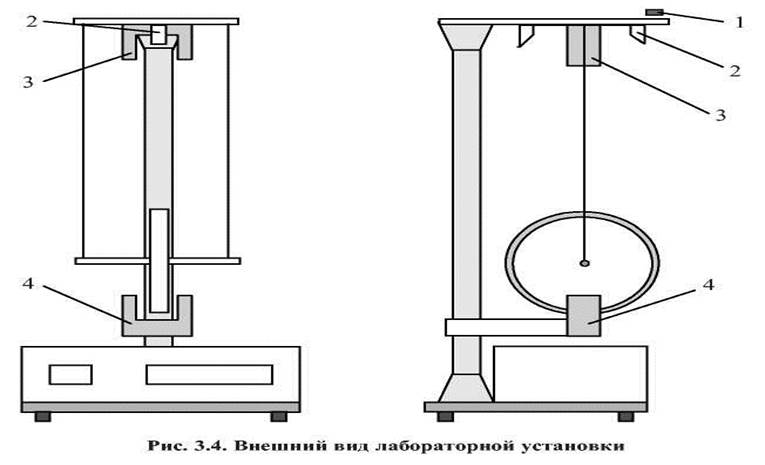
2. Описание
лабораторной установки.
На вертикальной
стойке крепятся два кронштейна. Верхний неподвижный кронштейн снабжён воротком 1
для крепления и регулировки бифилярного подвеса, электромагнитом 2 для
фиксирования маятника в верхнем положении и фотодатчиком 3, включающий
секундомер. На подвижном кронштейне закреплён фотодатчик 4, включающий
секундомер. Шкала секундомера 5 вынесена на лицевую панель прибора.
Кнопка «Сеть»
включает питание установки, кнопка «сброс» производит обнуление показаний
секундомера. При нажатии на кнопку «Пуск» отключается электромагнит, и маятник
приходит в движение.
Массу и момент
инерции маятника можно менять при помощи сменных колец, надеваемых на диск.
Длина нити должна быть такой, чтобы нижняя кромка маятника была на 1-2 мм ниже
оптической оси нижнего фотодатчика. Ось маятника должна быть горизонтальной.
Длина нити (высота падения) определяется по шкале, нанесённой на вертикальной
стойке.
Параметры установки:
радиус оси Rоси = 5 мм, радиус нити Rнити = 0,6 мм, радиус диска R1 = 42,5 мм, внешний радиус кольца R2 = 52,5 мм, масса диска mD
= 125 г, масса первого кольца m1 = 390 г, масса второго кольца m2 = 264 г.
Таблица технических характеристик приборов.
|
Прибор |
Тип |
Предел |
Цена |
Класс |
|
Секундомер |
МК-2 |
99,999 |
0,001 |
1 |
|
Линейка |
– |
44 мм |
1 мм |
0,5 |
θh = 2 мм.
θt = 0,001 с.
3. Рабочие формулы.
1.) tср. = (t1 + t2 + … +
tN)/N,
где tср. – среднее
значение времени падения; t1 – время падения при первом измерении; tN – время падения при последнем измерении; N
– количество измерений.
2.) I = m·(r + rн)2·[(g·t2/2·h0) – 1], где I – момент инерции маятника Максвелла; m –
масса маятника; r – радиус оси маятника; rн – радиус нити; g – ускорение свободного падения; t – время
падения маятника; h0 – высота падения маятника.
3.) Iср.взв.
= I1 + I2 + … + IN/N, где Iср.взв. – среднее взвешенное значение момента инерции.
4.) ID = mD·RD2/2, где ID
– момент инерции диска; mD
– масса диска; RD – радиус диска.
5.) IК = mК·(RК12 + RК22)/2, где IК – момент инерции кольца; mК – масса кольца; RК1 – внутренний радиус кольца; RК2 – внешний радиус кольца.
6.) Iтеор. = [mD·R12 + mК·(R12 + R22)]/2, где I – теоретическое выражение для
маятника Максвелла; R1 – радиус диска; R2 – внешний радиус кольца.
4. Результаты
измерений и вычислений.
Таблица 1. m =
33 + 125 = 158 г, h = 20 + 1 = 21 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
0,909 |
0,912 |
0,898 |
0,92 |
0,901 |
0,915 |
0,914 |
0,899 |
0,916 |
0,915 |
|
tср., с |
0,91 |
|||||||||
|
I, кг·м2 |
9,08·10-5 |
|||||||||
|
St, с |
0,008 |
|||||||||
|
St, с |
0,0025 |
|||||||||
|
Δt, с |
0,007 |
|||||||||
|
ID, кг·м2 |
11,289·10–5 |
Таблица 2. m =
33 + 125 + 390 = 548 г, h = 20 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
1,401 |
1,394 |
1,504 |
1,414 |
1,394 |
1,395 |
1,425 |
1,468 |
1,422 |
1,417 |
|
tср., с |
1,423 |
|||||||||
|
I, |
83,539·10-5 |
|||||||||
|
St, с |
0,036 |
|||||||||
|
St, с |
0,0114 |
|||||||||
|
Δt, с |
0,027 |
|||||||||
|
ID, кг·м2 |
11,289·10–5 |
|||||||||
|
IК, кг·м2 |
88,969·10-5 |
|||||||||
|
Iтеор., кг·м2 |
100,258·10-5 |
Таблица 3. m =
33 + 125 + 264 = 422 г, h = 20 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
1,362 |
1,496 |
1,358 |
1,345 |
1,356 |
1,363 |
1,383 |
1,37 |
1,352 |
1,383 |
|
tср., с |
1,377 |
|||||||||
|
I, |
60,155·10-5 |
|||||||||
|
St, с |
0,044 |
|||||||||
|
St, с |
0,014 |
|||||||||
|
Δt, с |
0,033 |
|||||||||
|
ID, кг·м2 |
11,289·10–5 |
|||||||||
|
IК, кг·м2 |
60,225·10-5 |
|||||||||
|
Iтеор., кг·м2 |
71,514·10-5 |
Таблица 4. m =
33 + 125 + 264 = 422 г, h = 18 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
1,301 |
1,282 |
1,301 |
1,3 |
1,295 |
1,294 |
1,301 |
1,304 |
1,294 |
1,293 |
|
tср., с |
1,297 |
|||||||||
|
I, |
59,297·10-5 |
|||||||||
|
St, с |
0,006 |
|||||||||
|
St, с |
0,0019 |
|||||||||
|
Δt, с |
0,005 |
|||||||||
|
ID, кг·м2 |
11,289·10–5 |
|||||||||
|
Iтеор., кг·м2 |
71,514·10-5 |
Таблица 5. m =
33 + 125 + 264 = 422 г, h = 15 см.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
t, |
1,144 |
1,152 |
1,149 |
1,148 |
1,173 |
1,148 |
1,142 |
1,145 |
1,145 |
1,168 |
|
tср., с |
1,151 |
|||||||||
|
I, |
55,949·10-5 |
|||||||||
|
St, с |
0,011 |
|||||||||
|
St, с |
0,0035 |
|||||||||
|
Δt, с |
0,009 |
|||||||||
|
ID, кг·м2 |
11,289·10–5 |
|||||||||
|
Iтеор., кг·м2 |
71,514·10-5 |
Iср.взв.
= 58,467·10-5 (кг·м2).
5. Примеры
вычислений.
1.) tср. = (t1 + t2 + t3 + t4 + t5 + t6 + t7 + t8 + t9 + + t10)/10 = (0,909 + 0,912 + 0,898 + 0,92 + 0,901 + + 0,915 + 0,914 +
0,899 + 0,916 + 0,915)/10 =9,099/10 = = 0,91 (с).
2.) I = m·(r + rн)2·[(g·t2/2·h0) – 1] =
158·10-3·(5·10-3 + + 0,6·10-3)2·[(9,8·0,912/2·21·10-2)
– 1] = 9,08·10-5 (кг·м2).
3.) Iср.взв. = I3
+ I4 +I5/3 = 60,155·10-5 + 59,297·10-5
+ + 55,949·10-5/3 = 58,467·10-5 (кг·м2).
4.) ID = mD·RD2/2 = 125·10-3·(42,5·10-3)2/2 = =
0,125·1806,25·10–6/2 = 11,289·10–5 (кг·м2).
5.) IК = mК·(RК12 + RК22)/2=
390·10-3·[(42,5·10-3)2 + + (52,5·10-3)2]/2
= 0,39·[1806,25·10-6 + 2756,25·10-6]/2= = 0,39·4562,5·10-6/2
= 88,969·10-5 (кг·м2).
6.) Iтеор. = [mD·R12
+ mК·(R12 + R22)]/2=[125·10-3·(42,5·10-3)2
+ + 390·10-3·[(42,5·10-3)2 + (52,5·10-3)2]]/2
= [0,125 x x 1806,25·10-6 + 0,39·[1806,25·10-6 +
2756,25·10-6]]/2 = = [225,781·10-6 + 0,39·4562,5·10-6]/2
= = [225,781·10-6 + 1779,375·10-6]/2 =
2005,156·10-6/2 = = 1002,578·10-6 = 100,258·10-5
(кг·м2).
6. Вычисление
погрешностей.
1.) St = √((t1–tср.)2 + (tN–tср.)2/N-1), где St – средняя квадратичная погрешность значения времени.
2.) St = St/√N, где St – случайная погрешность
удельного сопротивления.
3.) Δt = θt + kSt, где Δt – полная
погрешность удельного сопротивления.
Примеры вычислений:
1.) St = √((t1-tср.)2 + (tN-tср.)2/N-1) = √((0,909 – 0,91)2 + + (0,912 – 0,91)2(0,898
– 0,91)2 + (0,92 – 0,91)2 + + (0,901 – 0,91)2
+ (0,915 – 0,91)2 + (0,914 – 0,91)2 + + (0,899 – 0,91)2
+ (0,916–0,91)2 + (0,915 – 0,91)2/10 — 1 = √(0,000001 + 0,000004
+ 0,000144 + 0,0001 + + 0,000081 + 0,000025 + 0,000016 + 0,000121 + 0,000036+
+ 0,000025/9 = √0,000553/9 = √0,0000614 = 0,0078358 = = 0,008 (с).
2.) St = St/√N = 0,008/√10 = 0,008/3,162 = 0,0025 (с).
3.) Δt = θt
+ kSt = 0,001 + 2,3·0,0025 = 0,007 (с).
8. Окончательные
результаты, их обсуждение или несовпадение.
В данной лабораторной работе были
проведены исследования маятника Максвелла; рассчитаны среднее время падения
маятника, и по нему момент инерции, проведена обработка результатов измерений;
было произведено исследование зависимости момента инерции маятника от высоты, с
которой происходит падение маятника.
Из проделанных опытов и вычислений видно,
что момент инерции маятника не зависит от высоты падения маятника, так как чем
больше высота, тем больше время падения маятника. А на момент инерции маятника
влияет масса маятника, радиус оси и радиус нити. Также из формулы для момента
инерции маятника Максвелла:
I = m·(r + rн)2·[(g·t2/2·h0) – 1] следует, что при изменении высоты
меняется и время падения, но соотношение остаётся прежним, поэтому высота не
влияет на момент инерции маятника Максвелла.
В лабораторной работе мы рассчитываем
момент инерции по двум формулам:
1.) Экспериментальное значение момента
инерции:
I = m·(r + rн)2·[(g·t2/2·h0) – 1];
2.) Теоретическое
выражение для момента инерции маятника:
Iтеор. = [mD·R12 + mК·(R12 + R22)]/2.
Моменты инерции,
посчитанные по этим формулам, различаются между собой
Похожие материалы
- Отчет по лабораторной работе №1 Бипризма Френеля
- Определение электрического сопротивления. Экспериментальная проверка закона Ома. Определение удельного сопротивления нихрома
- Столкновение шаров. Проверка законов сохранения импульса и энергии, определение деформации шаров и силы удара
Информация о работе
Тип:
Отчеты по лабораторным работам
