Как найти радиус нижнего основания усеченного конуса

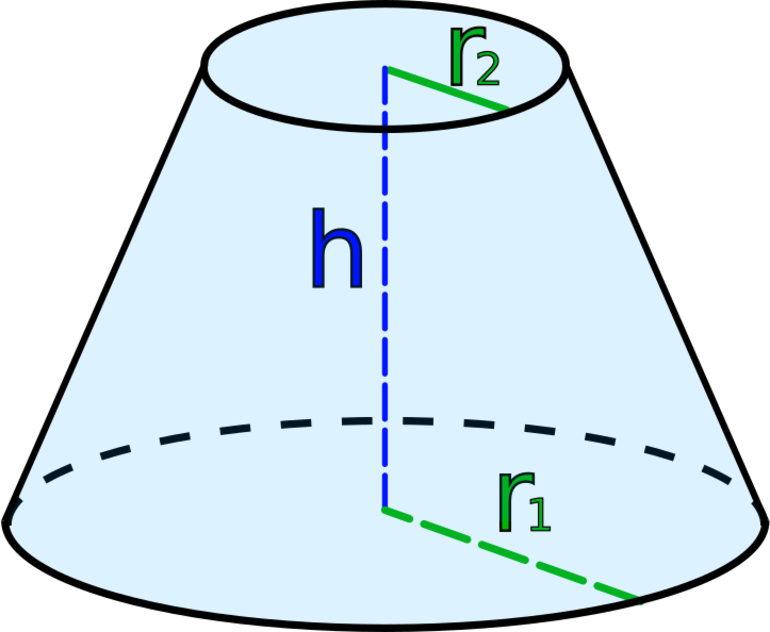
Радиус и высота усеченного конуса

Свойства

Радиусы оснований усеченного конуса позволяют вычислить диаметры оснований, их периметр и площадь по стандартным формулам для окружности с учетом двух различных радиусов усеченного конуса. d=2r D=2R p=2πr P=2πR S_r=πr^2 S_R=πR^2

Поскольку нам известна высота усеченного конуса, но для дальнейших вычислений нужна также и образующая, то нужно построить трапецию во внутреннем пространстве усеченного конуса таким образом, чтобы она соединяла указанные величины через радиусы. В такой трапеции, поскольку она прямоугольная, можно построить дополнительный прямоугольный треугольник и найти в нем апофему по теореме Пифагора, а также углы при основаниях и апофеме, через тригонометрические отношения l=√(h^2+(R-r)^2 ) tan⁡β=h/(R-r) α=180°-β

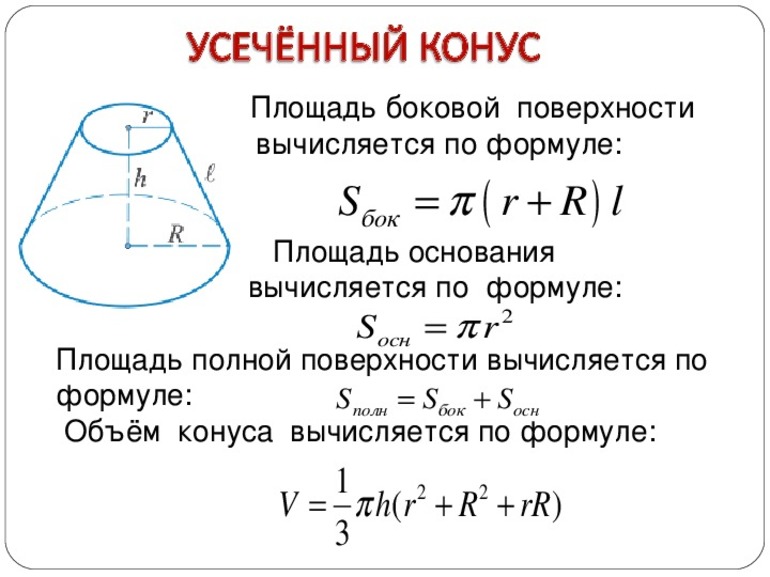
Площадь боковой поверхности усеченного конуса зависит от радиусов оснований конуса и от апофемы, которую можно найти, зная высоту, по формуле приведенной выше. Площадь полной поверхности состоит из площади боковой поверхности и площади двух оснований усеченного конуса. S_(б.п.)=πl(R+r) S_(п.п.)=S_(б.п.)+S_r+S_R=πl(R+r)+πr^2+πR^2

Найти объем усеченного конуса, зная высоту и радиусы оснований, достаточно просто, поскольку стандартная формула не предполагает других элементов расчета. V=πh/3(R^2+rR+r^2)

Усеченный конус – построение фигуры, формулы и задачи

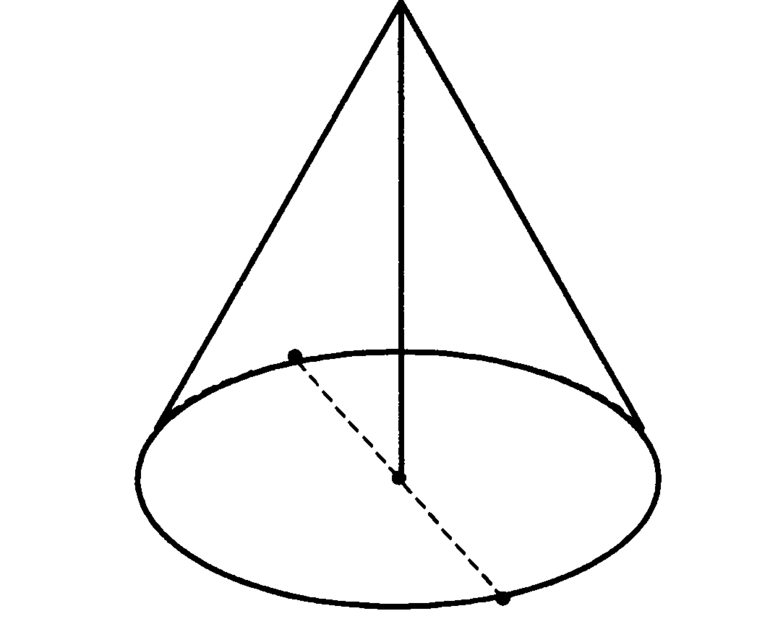
Исходный полный конус

Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.

Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.

Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:

1. Вершина — зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
2. Коническая поверхность, образованная в результате перемещения отрезка — образующей, или генератрисы.
3. Основание — часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.

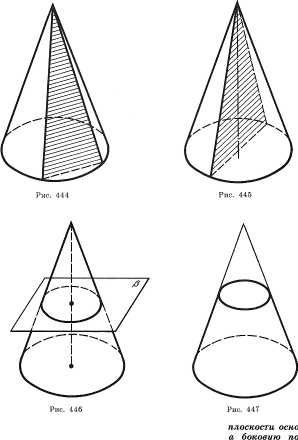
Существующие виды

В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:

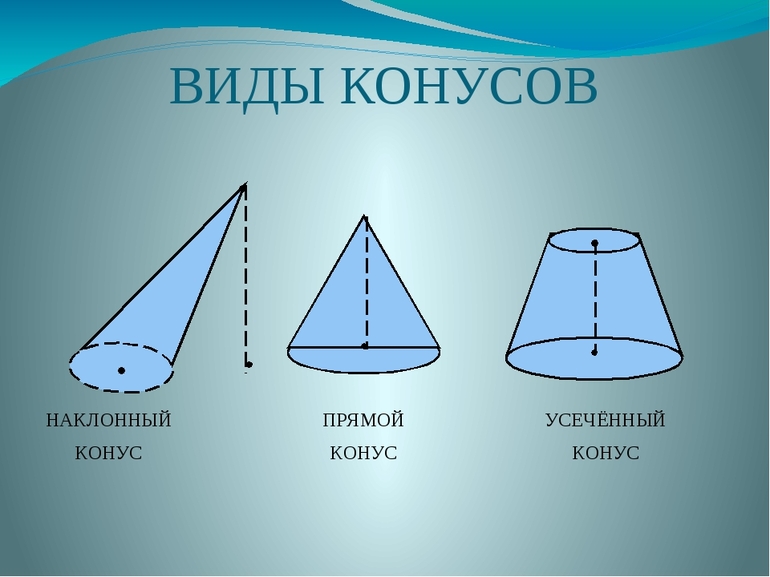
1. Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
2. Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
3. Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.

Круглая прямая фигура

Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.

С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.

Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r 2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.

Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r 2 *h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.

Усеченный геометрический объект

Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.

Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.

Способы построения

Можно выделить два основных способа построения усеченного круглого геометрического объекта:

• из круглого прямого конуса;
• с помощью трапеции.

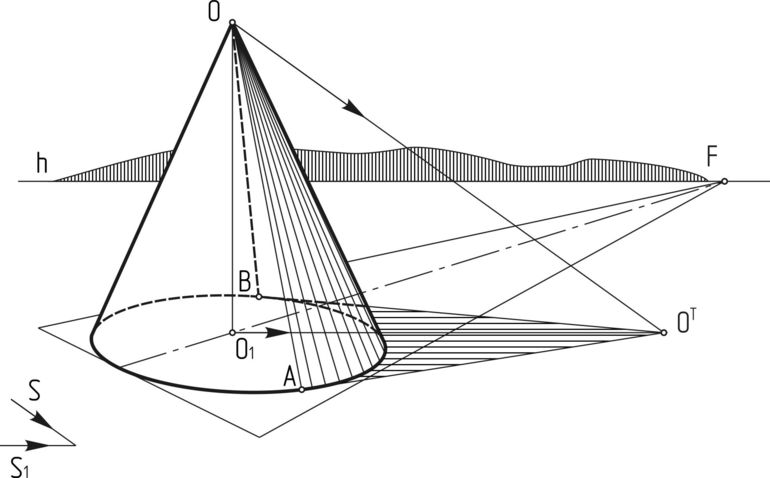
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.

Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.

Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.

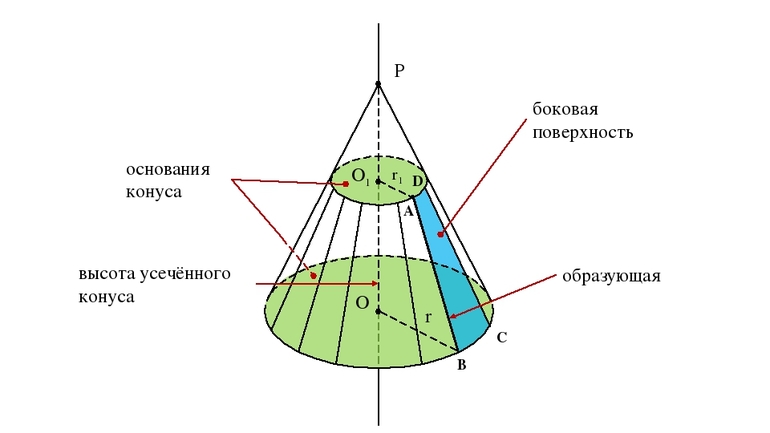
Площадь поверхности

Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r 2 . Для боковой поверхности следует выполнить следующие действия:

1. Разрезать ее вдоль образующей и развернуть на плоскости.
2. Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
3. Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
4. Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:

S = S1 + S2 + Sb = pi*r1 2 + pi*r2 2 + pi*g*(r1 + r2).

Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.

Формула объема

Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:

V = 1/3*pi*r1 2 *H — 1/3*pi*r2 2 *(H-h).

Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:

V = 1/3*pi*h*(r1 2 + r2 2 + r1*r2).

Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:

V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).

Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.

Пример решения задачи

Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см 2 . При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.

Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:

S = S1 + S2 = pi*r1 2 + pi*r2 2 = 4*pi*r2 2 + pi*r2 2 = 5*pi*r2 2 .

Откуда получается:

r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.

Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.

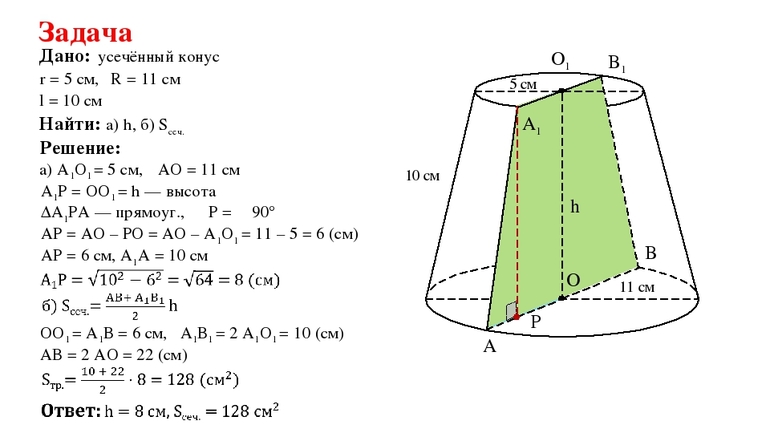
Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:

g = ((r1-r2)^2 + h 2 )^0,5 = (2,52 2 + 15 2 )^0,5 = 15,21 см.

Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:

Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см 2 .

Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.

Калькуляторы расчета размеров развертки конуса

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

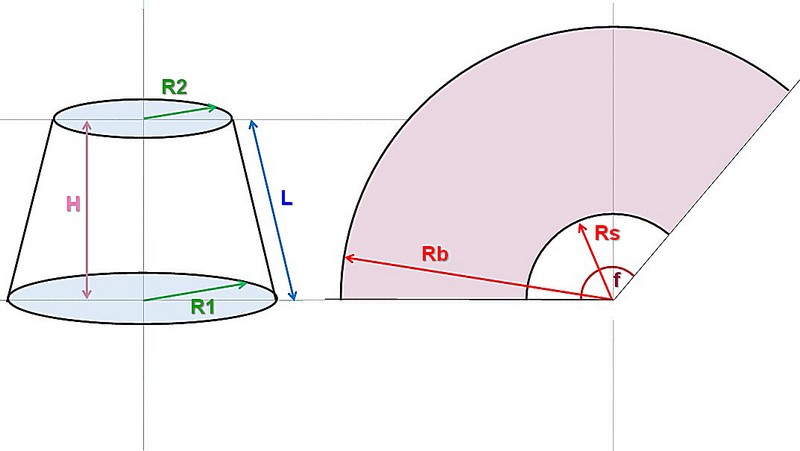Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Шаг 1 – определение длины образующей L

(Если она уже известна – шаг пропускается)

Шаг 2 – определение радиусов внутренней и внешней дуги развертки

Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.

[spoiler title=”источники:”]

http://nauka.club/matematika/geometriya/usechennyy-konus.html

http://stroyday.ru/kalkulyatory/obshhestroitelnye-voprosy/kalkulyatory-rascheta-razmerov-razvertki-konusa.html

[/spoiler]

• Радиус и высота усеченного конуса

  Радиусы оснований усеченного конуса позволяют вычислить диаметры оснований, их периметр и площадь по стандартным формулам для окружности с учетом двух различных радиусов усеченного конуса.
  d=2r
  D=2R
  p=2πr
  P=2πR
  S_r=πr^2
  S_R=πR^2

  Поскольку нам известна высота усеченного конуса, но для дальнейших вычислений нужна также и образующая, то нужно построить трапецию во внутреннем пространстве усеченного конуса таким образом, чтобы она соединяла указанные величины через радиусы. В такой трапеции, поскольку она прямоугольная, можно построить дополнительный прямоугольный треугольник и найти в нем апофему по теореме Пифагора, а также углы при основаниях и апофеме, через тригонометрические отношения
  l=√(h^2+(R-r)^2 )
  tan⁡β=h/(R-r)
  α=180°-β

  Площадь боковой поверхности усеченного конуса зависит от радиусов оснований конуса и от апофемы, которую можно найти, зная высоту, по формуле приведенной выше. Площадь полной поверхности состоит из площади боковой поверхности и площади двух оснований усеченного конуса.
  S_(б.п.)=πl(R+r)
  S_(п.п.)=S_(б.п.)+S_r+S_R=πl(R+r)+πr^2+πR^2

  Найти объем усеченного конуса, зная высоту и радиусы оснований, достаточно просто, поскольку стандартная формула не предполагает других элементов расчета.
  V=πh/3(R^2+rR+r^2)

Frustum of a cone is a special shape that is formed when we cut the cone with a plane parallel to its base. The cone is a three-dimensional shape having a circular base and a vertex. So the frustum of a cone is a solid volume that is formed by removing a part of the cone with a plane parallel to circular base. The frustum is not only defined for cones but can be also defined for the different types of pyramids (square pyramid, triangular pyramid, etc.).

Some of the common shapes of a frustum of cone which we discover in our daily life are buckets, lamp shade, and others. Let us learn more about the frustum of cones in this article.

What is Frustum of Cone?

Frustum is a Latin word, which means pieces, therefore frustum of cone is a solid piece of the cone. When a right circular cone is cut by a plane parallel to the base of the cone the shape so obtained is called frustum of the cone. The figure given below shows us how a plane cuts the cone parallel to its base to form the frustum of the cone.

Now, the frustum of the cone is easily defined as,

If a right circular cone is cut off by a plane parallel to it’s base, the shape of the portion between the cutting plane and the base plane is called frustum of cone. 

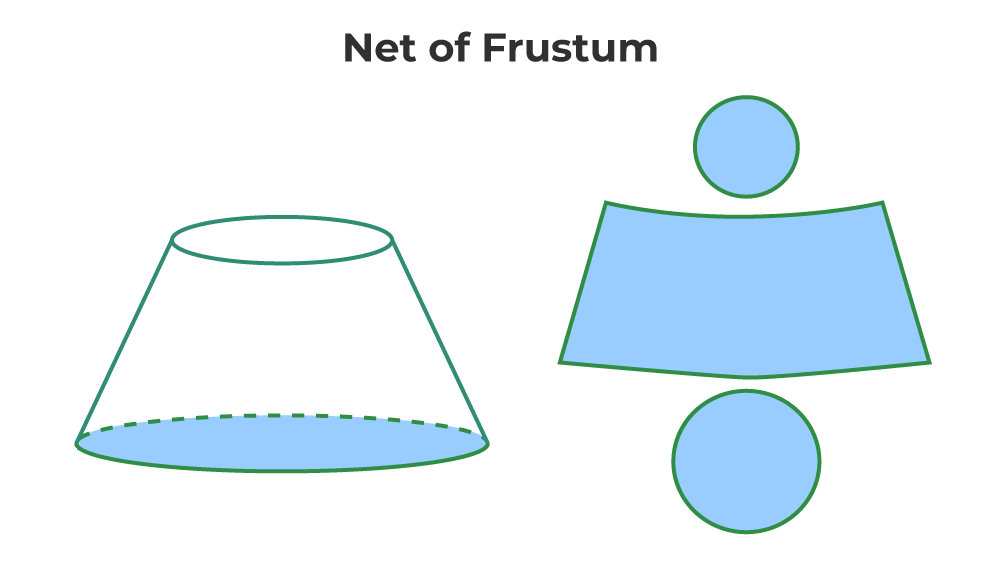
Net of Frustum of Cone

If a three-dimensional (3D) shape is cut open and made a two-dimensional shape the shape so obtained is called the net. One can assume that when the net of the figure is folded properly in a correct manner it forms the desired 3D shape. The image given below shows the net of the frustum of the cone.

Properties of Frustum of Cone

Properties of a Frustum of a cone are very similar to the cone, some of the important properties of frustum of cone are,

• Base of the cone the original cone is contained in the frustum of a cone but its vertex is not contained in the frustum.
• Formulas of frustum of a cone are dependent on its height and two radii (corresponding to the top and bottom bases).
• Height of the frustum of the cone is the perpendicular distance between the centers of its two bases.

Formulas of Frustum of Cone

Frustum of Cone is such a shape that is frequently seen in our daily life, for example, table lamps, buckets, etc. The important formulas for the frustum of a cone are,

• Volume of Frustum of Cone
• Surface Area of Frustum of Cone

Let’s learn about these formulas in detail below,

Volume of Frustum of Cone

Frustum of cone is a sliced part of a cone, where a small cone is removed from the larger cone. Therefore, to calculate the volume of the frustum of cone, one just needs to calculate the difference between the volume of the larger and smaller cone. 

Let’s assume,

• Total height of the cone is to be H + h
• Total slant height to be l’ + L
• The radius of a complete cone is r
• The radius of the sliced cone is r’

Since the volume of the cone is given as V = 1/3πr²h

Volume of complete cone V₁ = 1/3πr²(H+h)

Volume of smaller cone V₂ =1/3πr’²(h)

Now the volume of the frustum of cone (V) can be calculated using the formula,

V = V₁ – V₂

V = 1/3πr²(H+h) – 1/3πr’²(h)

V= 1/3π[r²(H+h) – r’²(h)]…(1)

Using the property of similarity of the triangles of △OCD and △OAB, one can write, 

r / (H + h) = r’ / h

r / r’ = (H + h) / h

H + h = hr / r’

Substitute this value of (H+h) in equation (1), and simplify,

 V  = 1/3π[r²(rh / r’) – r’²(h)}

   = 1/3π[{hr³ – hr’³} / r’]…(2)

Using the similar triangle’s property again in △OCD and △OAB, we will find out the value of h

r / (H + h) = r’ / h

r / r’ = (H + h) / h

rh = (H + h)r’

rh = Hr’ + hr’

(r -r’)h = Hr’

h = Hr’ / (r -r’)

Substituting these values in equation (2),

V = 1/3π[{r³h – r³h} / r’]

   = 1/3π[{r³ – r’³}h / r’]

   = 1/3π[{r³ – r’³}{Hr’ / (r – r’)} / r’]

   = 1/3πH(r² + r’² +rr’)

Thus,

Volume of the frustum of cone = 1/3 πH(r² + r’² + rr’)

Surface Area of Frustum of Cone

The surface area of frustum of cone can be calculated by the difference between the surface area of the complete cone and the smaller cone (removed from the complete cone). The surface area of the frustum of cone can be calculated using the below diagram, where one needs to sum up the surface areas of the curved surfaces, and the surface areas of the top and bottom surfaces of the frustum of cone.

Similar to the Volume of the frustum of cone, the curved surface area will be also equal to the difference between the surface areas of the bigger cone and the smaller cone. 

In the figure given above, triangles OAB and OCD are similar. Therefore, using the similarity criteria, one can write,

l’ / l = r’ / r…(1)

Since, l’ = l – L, therefore, from equation (1),

(l – L) / l = r’ / r

After cross-multiplication, 

lr – Lr = lr’

l(r – r’) = Lr

l = Lr / (r – r’)…(2)

The curved surface area of a complete cone = πrl

The curved surface area of the smaller cone = πr’l’

Difference between the curved surface areas of complete cone and smaller cone = π (rl – r’l’)

Thus, the curved surface area (CSA) of the frustum of cone = πl (r – r’l’/l)

Use equation (1) to substitute the value of l’/l in the above equation, and simplify,

CSA of the frustum of cone = πl (r – r’×r’/r) = πl (r² – r’²)/r

Now, substitute the value of l from equation (2), and simplify,

CSA of the frustum of cone = πlr/(r – r’)× (r² – r’²)/r = πl (r + r’)

Thus, one can write,

Curved surface area of frustum of cone = πl (r + r’)

Now, let’s calculate the surface area of the top and bottom bases of the frustum of the cone, such that, 

The surface area of the top base of the frustum of cone having a radius r’ = πr’²

The surface area of the bottom base of the frustum of cone having a radius r = πr²

So,

Total surface area of the frustum of cone = Curved surface area of the frustum of cone + surface area of the top base + surface area of the bottom base

Therefore,

The total surface area of the frustum of cone = πl (r + r’) + πr’² + πr² = πl (r + r’) + π (r² + r’²) 

 Thus, the total surface area of the frustum of cone is = πl (r + r’) + π (r² + r’²) 

This formula can be also written as, 

The total surface area of the frustum of cone is = πl (r² – r’²)/r + π (r² + r’²) 

So, one can write,

Total surface area of frustum of cone = πl(r + r’) + π (r² + r’²) 

or

Total surface area of frustum of cone = πl (r² – r’²)/r  + π (r² + r’²) 

Note that, l is the slant height of the smaller cone that can be given as 

L = √ [H² + (r – r’)²]

Read, More

• Volume of  Cone
• Volume of Cylinder
• Volume of Sphere

Solved Examples on Frustum of Cone

Example 1: Find out the Volume of a frustum of a cone that is 15 cm high and the radii for both the bases are 5 cm and 8 cm. 

Solution: 

Using the formula studied above, one can write,

V = 1/3 πH(r² + r’² + rr’)

Given, 

H = 15 cm
r’= 5 cm
r = 8 cm

V = 1/3 π15(8² + 5² + 40)

V = 5π(129)

V = 645π cm³

Example 2: Find out the surface area and total surface area of a frustum of a cone which is 10 cm high and the radii for both the bases are 4 cm and 8 cm. 

Solution: 

We know the formula for surface area and total surface area of the frustum. We need to plug in the required values. 

Curved Surface area of the frustum = πl(r+r’)

where,
L = √ [H² + (R – r)²]

Given,
H = 10 cm
r = 4 cm
R = 8 cm 

Calculating the value of L, 

L = √ [10² + (8 – 4)²]

  =  √(100+16) =  √(116)

Curved Surface Area of Frustum = πL(R+r)

= π√(116)×(8+4)

= 48π√(29)

Total Surface Area = Curved Surface Area of Frustum + Area of Both Bases

= 48π√(29) + π(8)² + π(4)² 

= 48π√(29) + 64π + 16π

= 48π√(29) + 80π cm²

Example 3: Let’s say we have an open metal bucket whose height is 50cm and the radii of the bases are 10cm and 20cm. Find the area of the metallic sheet used to make the bucket.

Solution: 

Bucket is in the form of frustum which closed from the bottom. We need to calculate the total surface area of this frustum. 

Given
H = 50 cm
r ‘= 10 cm
r = 20 cm

Curved Surface Area of Frustum = πL(R+r)

L = √ [H² + (r – r’)²]

L = √ [50² + (20 – 10)²]

  = √(2500+100) =  √(2600)

  = √100(26) = 10√(26)

Curved Surface Area of Frustum = πL(R+r)

= π10√(26)×(20+10)

= 300π√(26)

Total Surface Area = Curved Surface Area of Frustum + Area of Both Bases

= 300π√(26) + π(20)² + π(10)² 

= 300π√(26) + 400π + 100π

= (300π√(26) + 500π) cm²

Example 4: Find out the expression of the volume for a frustum if its height is 6y, and its radii are y and 2y respectively.

Solution: 

Using the formula studied above, 

V = 1/3 πH(r² + r’² + rr’)

Given, 

H = 6y
r’= y
r = 2y

V = 1/3 π6[(2y)² + (y)² + (y)(2y)]

V = 2πy(7y²)

V = 14πy³ unit³

FAQs on Frustum of Cone

Question 1: What is the Frustum of a Cone?

Answer:

When we cut a cone in such a way that the plane of cutting is parallel to the base of the cone. The resultant figure so obtained is called the Frustum of the Cone.

Question 2: What are the Frustum of Cone Formulas?

Answer:

The formulas of the frustum of a cone are discussed below. Let’s take a frustum of base radius ‘R’ and top radius ‘r’, height ‘H’, and slant height then,

• Volume of frustum of a cone (V) = 1/3πH(r² + rr’ + r’²)
• Total surface area of frustum of a cone = πl (r + r’) + π (r’² + r²).

Question 3: What is the CSA of a frustum?

Answer:

The curved surface area of the frustum of a cone is calculated using the formula,

CSA = πl (r + r’)

where,
r’ is the radius of the upper circle of frustum
r is the radius base
l is the slant height

Question 4: What is the Surface Area of Frustum of Cone?

Answer:

The surface area of the frustum of a cone is calculated using the formula,

• CSA of frustum of cone = πl [ (r² – r’²) / r’ ]
• TSA of frustum of cone = π (r² + r’²) + πl [ (r² – r’²) / r’]

Question 5: What is the Volume of the Frustum of Cone?

Answer:

The volume of the frustum of a cone is calculated using the formula,

• V = 1/3πh[ (r³ – r’³) / r’]
• V = 1/3πH(r² + rr’ + r’²)

ГОУ СПО «Московский издательский
полиграфический колледж им. Ивана
Федорова»

Исследовательская
работа по теме:

«Конус. Усеченный
конус.»

Выполнили:

Студентка
группы 1КТ2

Асташкина
Валентина, Фролова Дарья

Проверила:

Епихина Е.В.

Москва

2012

Содержание:

1. Конус.
Элементы

2. Усеченный
конус

3. Элементы

4. Свойства

5. Свойства
усеченного конуса

6. Формулы

5. Теоремы

5. Решение
задач

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Конус.

Ко́нус (от др.-греч.
κώνος
«шишка») — тело,
полученное объединением всех лучей,
исходящих из одной точки (вершины
конуса) и проходящих через плоскую
поверхность. Иногда конусом называют
часть такого тела, полученную объединением
всех отрезков, соединяющих вершину и
точки плоской поверхности (последнюю
в таком случае называют основанием
конуса, а конус называют опирающимся
на данное основание). Также можно сказать,
что это тело, полученное при вращении
прямоугольного треугольника вокруг
одного из его катетов. Далее будет
рассматриваться именно этот случай,
если не оговорено обратное. Если основание
конуса представляет собой многоугольник,
такой конус является пирамидой.

рисунок 1     рисунок 2

Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга,— вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания (рис. 1) Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности. Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом. Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси (рис.2). Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.

рисунок 3                                   рисунок 4   рисунок 5                                 рисунок 6

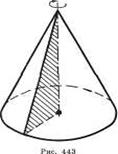
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 3). В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса (рис. 4).

Усеченный конус.

Усечённый
конус — часть конуса,
заключенная между его основанием и
сечением, параллельным основанию.
Усеченный конус можно рассматривать
как результат вращения равнобедренной
трапеции вокруг её симметрии. При
вращении основания трапеции описывают
круги – основания усеченного конуса.
Высота усеченного конуса – расстояние
между основаниями.

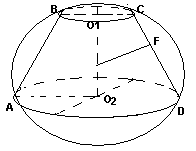
Круги с центрами О1 и О2 – верхнее и
нижнее основания усеченного конуса, R
r – радиусы оснований, АВ= L образующая
,α угол наклона образующе и плоскости
нижнего основания.

Отрезок О1О2-высота. Трапеция АВСD –
осевое сечение.

Боковая сторона трапеции называется
образующей усеченного конуса; круги,
полученные при вращении оснований
трапеции, – основаниями усеченного
конуса.

Развертка усеченного конуса представляет
собой объединение части кругового
кольца и двух кругов.

Свойства:

• Если площадь основания конечна, то
  объём конуса также конечен и равен
  трети произведения высоты на площадь
  основания. Таким образом, все конусы,
  опирающиеся на данное основание и
  имеющие вершину, находящуюся на данной
  плоскости, параллельной основанию,
  имеют равный объём, поскольку их высоты
  равны.

• Центр
  тяжести любого конуса с конечным
  объёмом лежит на четверти высоты от
  основания.

• Телесный
  угол при вершине прямого
  кругового конуса равен

где

 —
угол раствора конуса (то есть угол
между двумя противоположными образующими).

• Площадь
  боковой поверхности такого конуса
  равна

где

 —
радиус основания,

 —
длина образующей.

• Объем
  кругового конуса равен

• Пересечение плоскости с прямым круговым
  конусом является одним из конических
  сечений (в невырожденных
  случаях — эллипсом, параболой или
  гиперболой, в зависимости от положения
  секущей плоскости).

Св-ва усеченного
конуса:

1)       
В усеченный конус можно вписать шар
тогда и только тогда, когда образующая
равна сумме радиусов оснований.

2)       
Вокруг усеченного конуса всегда
можно описать шар.

Формулы:
  Конус (рис. 1.19)

     Площадь боковой
поверхности:

     Площадь полной
поверхности:

     Объем:

     Усеченный конус
(рис. 1.20)

     

     

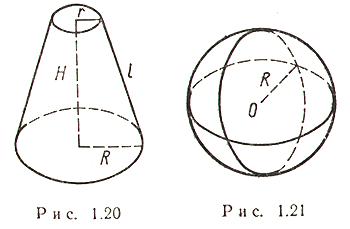
Боковая площадь
поверхности круглого конуса, формула.

Боковая площадь поверхности круглого
конуса равна произведению половины
окружности основания (C) на образующую
(l):

1.	S= 1 2  C l=π r l

(r – радиус вращения конуса; l – образующая
конуса)

Полная площадь
поверхности круглого конуса, формула.

Полная площадь поверхности круглого
конуса равна сумме площадей боковой
поверхности конуса и его основания.
Основание конуса есть круг
и его площадь вычисляется по формуле
площади круга:

2.	S=π r l+π r2=π r (r+ l)

(r – радиус вращения конуса; l – образующая
конуса)

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

План урока:

Понятие цилиндра

Понятие конуса

Усеченный конус

Понятие цилиндра

Построим на некоторой плоскости α окружность L, центр которой находится в точке О, а ее радиус обозначим как r. Далее через каждую точку этой окруж-ти проведем прямую, которая будет перпендикулярна к α. Все вместе эти прямые образуют поверхность, которую принято называть цилиндрической поверхностью (может использоваться сокращение поверх-ть). Введем несколько понятий:

• Окружность, построенная в плос-ти α, именуется основанием цилиндрической поверх-ти;
• Каждая прямая, проходящая через эту окруж-ть L и перпендикулярная α – это образующая цилиндрической поверх-ти;
• Прямая, проходящая через точку О и также перпендикулярная α, именуется осью цилиндрической поверх-ти.

Примечание. Заметьте, что в стереометрии при изображении окружности на плос-ти она выглядит как эллипс (овал).

Заметим, что так как все образующие и ось цилиндрической поверх-ти перпендикулярны одной и той же плос-ти α, то они будут параллельны друг другу.

Далее проведем плос-ть β, параллельную α. Так как образующие и ось пересекали α, то они должны пересекать и β. В результате они образуют в плос-ти β какую-то плоскую линию L₁. Докажем, что L₁ – это также окружность.

Действительно, пусть ось цилиндрической поверх-ти пересекает плос-ти α и β в точках О и О₁ соответственно. Произвольная образующая пересекает эти же плос-ти в точках А и А₁:

Так как ОО₁||АА₁, то ОО₁А₁А – это плоский четырехугольник. ОО₁⊥α и ОО₁⊥β, поэтому углы ∠АОО₁ и ∠А₁О₁О – прямые. АА₁⊥α и АА₁⊥β, поэтому прямыми будут и углы ∠ОАА₁ и ∠О₁А₁А. Получается, что ОО₁А₁А – это прямоугольник, и поэтому отрезки ОА и О₁А₁ одинаковы:

Итак, точка А₁ находится на расстоянии r от О₁. Аналогично и для любой другой точки на линии L₁ можно показать, что она находится на расстоянии r от О₁. То есть все точки L₁ равноудалены от О₁, и поэтому L₁ – это окруж-ть с центром в точке О₁, ч. т. д.

Обратите внимание, что окруж-ти L и L₁ имеют одинаковые радиусы, то есть это одинаковые окруж-ти.

Объемная фигура, образованная окруж-тями L и L₁, именуется цилиндром. Рассмотрим его основные элементы:

• круги L₁ и L – это основания цилиндра;
• отрезок ОО₁ – ось цилиндра;
• отрезки образующих, заключенные между основаниями, именуются образующими цилиндра;
• часть цилиндрической поверх-ти, заключенную между основаниями цилиндра, именуют боковой поверхностью цилиндра.

Напомним, что отрезки параллельных прямых, заключенные между параллельными плос-тями, имеют одинаковую длину. Отсюда вытекает тот факт, что образующие цилиндра одинаковы.

Введем ещё два термина:

• длина образующей именуется высотой цилиндра;
• радиус оснований цилиндра именуется радиусом цилиндра.

Отметим, что на самом деле мы рассмотрели только частный случай цилиндра – так называемый прямой круговой цилиндр. Его основания – это круги (поэтому он именуется круговым), а его образующие образуют с основаниями прямой угол(поэтому он именуется прямым). Можно построить наклонный цилиндр (его также называют косым), у которого образующие не перпендикулярны основанию. Также существуют и цилиндры, у которых основаниями являются не окруж-ти, а другие фигуры, например параболы:

В принципе любую призму (а значит и любой параллелепипед) можно считать цилиндром. Однако в дальнейшем в курсе школьной стереометрии под цилиндром будет подразумеваться исключительно прямой круговой цилиндр, если специально не оговорено иное.

В реальной жизни очень многие предметы имеют форму цилиндра. Колонны в зданиях, ножки стульев, бочки, рулоны бумаги представляют собой цилиндры. Даже дерево можно условно считать цилиндром.

Рассмотрим сечение цилиндра плос-тью, перпендикулярной его основаниям.

Пусть сечение пересекает нижнее основание цилиндра в точках А₁ и В₁. Тогда перпендикуляры к основанию, проходящие через эти точки, будут принадлежать этому сечению. Но эти перпендикуляры – одновременно и образующие цилиндра А₁А и В₁В. Значит, сечение проходит и через точки А и В. Раз АА₁ и ВВ₁ – перпендикуляры к обоим основаниям цилиндра, то

Итак, в четырехугольнике АВВ₁А₁ все углы прямые, то есть он представляет собой прямоугольник. Более того, можно утверждать, что любое сечение, проходящее через образующую цилиндра, будет прямоугольником, ведь такое сечение будет перпендикулярно основаниям, так как оно содержит перпендикуляр к ним. Сечение, проходящее через цилиндрическую ось, именуется осевым сечением. Оно также имеет форму прямоугольника.

Далее рассмотрим сечение цилиндра плос-тью, параллельной основаниям:

Пусть секущей будет плос-ть γ, а нижнее основание располагается в плос-ти α. Тогда по определению фигура, «зажатая» между этими двумя плос-тями – это цилиндр, а потому сечение должно иметь форму круга. Получается, что сечение γ разбивает цилиндр на два цилиндра.

Рассмотрим боковую поверх-ть цилиндра. Она представляет собой замкнутую поверхность. Если ее условно «разрезать» по образующей цилиндра и развернуть, то получится прямоугольник:

Длина одной стороны такого прямоугольника (он называется разверткой боковой поверх-ти цилиндра) – это длина образующей цилиндра, то есть его высота. Длина второй стороны совпадает с длиной окруж-ти, лежащей в основании цилиндра. Если радиус цилиндра обозначен как r, то длина этой окруж-ти составляет 2πr. Тогда площадь боковой поверх-ти можно рассчитать как площадь прямоугольника:

Площадь полной поверх-ти цилиндра – это сумма площадей его оснований и его боковой поверх-ти. Так как площадь круга рассчитывается по формуле

Рассмотрим ещё несколько важных понятий. В цилиндр может быть вписана прямая призма. В таком случае основания призмы находятся в тех же плос-тях, что и основания цилиндра, а её боковые грани – это образующие цилиндра.

Если плос-ть содержит образующую цилиндра, но не пересекает его основания, то такая плос-ть именуется касательной к цилиндру. Можно сказать, что касательная плос-ть – это такая плос-ть, которая имеет ровно по одной общей точке с каждым основанием цилиндром.

Если каждая боковая грань призмы – это касательная к цилиндру, а основания призмы находятся в тех же плос-тях, что и основания цилиндра, то говорят, что цилиндр вписан в призму.

Естественно, что если цилиндр вписан в призму, то его основания оказываются вписанными в те многоугольники, которые являются основаниями призмы. Если же призма вписана в цилиндр, то основания цилиндра – это уже окруж-ти, описанные около этих многоугольников.

Рассмотрим несколько задач, в которых фигурируют цилиндры.

Задание. Найдите боковую и полную площади цилиндра, если его радиус составляет 2 м, а высота – 3 м.

Задание. Какова длина диагонали осевого сечения цилиндра, с высотой 4 м и радиусом 1,5 м?

Решение. Осевое сечение цилиндра – это прямоугольник, обозначим его как АВСD. Сторона АВ – это высота цилиндра, а AD – это диаметр нижнего основания, ведь AD проходит через центр окруж-ти О. Тогда длина AD вдвое больше радиуса цилиндра:

Задание. Осевое сечение цилиндра – это квадрат, площадь которого обозначена буквой Q. Какова площадь основания цилиндра?

Решение. Обозначим сторону сечения-квадрата буквой а. Зная площадь сечения, легко найдем и сторону:

Задание. Высота цилиндра составляет 8 см, а его радиус – 5 см. Через его образующую проведено сечение, которое имеет форму квадрата. Каково расстояние между этим сечением и осью цилиндра?

Решение. Обозначим сечение как АВСD. Так как и это сечение, и ось цилиндра перпендикулярны основаниям цилиндра, то они должны быть параллельны друг другу. Расстояние между ними – это длина перпендикуляра О₁К, опущенного из центра основания на сторону ВС:

Отрезок АВ имеет длину 8 см, ведь это высота цилиндра. Так как АВСD – квадрат, то и ВС имеет такую же длину. ВС – это хорда в окруж-ти с центром в точке О₁. Напомним, что перпендикуляр к хорде, опущенный из центра окруж-ти, делит ее пополам, поэтому

 

Задание. Диаметр цилиндра равен его высоте. На верхнем основании, центр которого находится в точке О, отмечены точки А и В так, что ∠АОВ составляет 60°. Отрезок АА₁ – образующая цилиндра. Найдите тангенс угла ∠ВА₁А.

Решение. Рассмотрим ∆АОВ. Он равнобедренный, ведь радиусы АО и ОВ одинаковы. Но если в равнобедренном треугольнике один из углов составляет 60°, то и все углы будут также будут по 60°, то есть это равносторонний треугольник. Тогда, если радиус цилиндра обозначен как r, то

Понятие конуса

Построим на плос-ти α окруж-ть L с центром в точке О. Далее через О проведем перпендикуляр к α и отметим на нем точку Р. Если мы отрезками соединим точку Р с каждой точкой окруж-ти L, то получим поверх-ть, которая именуется конической поверхностью. При этом:

• прямая ОР – это ось конической поверх-ти;
• прямые, соединяющие Р с точками на окруж-ти L, именуются образующими конической поверх-ти;
• сама точка Р – это вершина конической поверх-ти.

Объемное тело, ограниченное окруж-тью L и конической поверх-тью, именуется конусом. Соответственно вершина конической поверх-ти, её ось и образующие будут одновременно являться вершиной, осью и образующими конуса. Окруж-ть L – это основание конуса.

Ещё несколько терминов:

• коническая поверх-ть конуса именуется его боковой поверх-тью;
• если же к этой площади прибавить ещё и площадь основания, то в итоге получится полная площадь конуса;
• отрезок ОР – это не только ось конуса, но и высота конуса.

Как и в случае с цилиндром, мы в данном случае рассматриваем особый случай конуса – прямой круговой конус. В более общем случае ось конуса может не быть перпендикуляром к плос-ти основания (так называемый косой конус). Также в его основании может находиться не окруж-ть, а другая плоская фигура.

В общем случае любая пирамида может рассматриваться как частный случай конуса. Однако в рамках школьного курса под конусом подразумевается исключительно прямой круговой конус, если только не обговорено иное.

Докажем важное утверждение:

Действительно, рассмотрим две произвольные образующие РА и РВ у конуса с вершиной Р, у которой О – центр основания:

Так как ось ОР перпендикулярна основанию, то ∆РОА и ∆РОВ – прямоугольные. У них общий катет РО, а катеты АО и ОВ одинаковы как радиусы окруж-ти. Тогда ∆РОА и ∆РОВ равны, поэтому одинаковы и образующие РА и РВ, ч. т. д.

Заметим, что конус получается при вращении прямоугольного треуг-ка вокруг его катета. Так, на следующем рисунке конус получается при вращении ∆РОА с прямым углом О относительно катета РО:

Если сечение конуса проходит через его ось, то оно именуется осевым сечением. Ясно, что это сечение будет являться треуг-ком, причем две его стороны – это образующие конуса, а третья сторона диаметр основания. Образующие конуса одинаковы, поэтому осевое сечение будет равнобедренным треуг-ком.

Теперь рассмотрим сечение, параллельное плос-ти основания. Пусть оно пересекает ось РО в какой-то точке О₁. Также пусть А₁ – точка пересечения образующей АР исходного конуса с секущей плос-тью α:

Заметим, что раз ось РО перпендикулярна основанию, то она также будет перпендикулярна и секущей плос-ти, ведь основание и плос-ть α параллельны. Тогда ∠РО₁А₁ будет прямым.

Теперь рассмотрим ∠РОА и ∠РО₁А₁. Они прямоугольные и у них есть общие угол ∠АРО. Значит, это подобные треуг-ки. Обозначим радиус ОА как r, а длину А₁О₁ как r₁. Тогда из подобия получаем:

Рассмотрим теперь другую образующую ВР, которая пересекает секущую плос-ть в точке В₁. Отрезки АО и ОВ одинаковы. Повторяя предыдущие рассуждения, легко доказать подобие ∆РОВ и ∆РО₁В₁, откуда можно вычислить длину О₁В₁:

Получили, что точки А₁и В₁ находятся на одинаковом расстоянии r₁ от точки О₁. Мы выбрали точки А и В произвольно, поэтому для любых двух точек, принадлежащих сечению конуса, можно утверждать, что они равноудалены от точки О₁. Это значит, что все точки сечения лежат на окруж-ти с центром в точке О₁ и радиусом r₁, то есть сечение имеет форму окруж-ти.

Как определить площадь боковой поверхности конуса? Для этого ее надо «разрезать» вдоль одной из образующих и развернуть на плос-ти. В результате получится круговой сектор.

Напомним, что площадь сектора может быть рассчитана по формуле

Теперь обозначим длину образующей буквой l, а радиус основания конуса как r. Тогда

Для вычисления полной площади конуса к боковой поверх-ти необходимо добавить ещё и площадь основания:

Усеченный конус

Ранее мы уже изучали сечение конуса плос-тью, параллельной его основанию. Такое сечение разбивает конус на две фигуры. Одна из них – это конус меньших размеров, а вторая именуется усеченным конусом:

Введем несколько понятий и отметим очевидные факты:

• боковая поверхность усеченного конуса – это коническая поверх-ть;
• у усеченного конуса есть два основания, имеющих форму окруж-ти;
• те отрезки образующих конической поверх-ти, которые заключены между основаниями усеченного конуса, именуются образующими усеченного конуса;
• отрезок, соединяющий центры оснований, именуется высотой усеченного конуса, или его осью.

В предыдущем параграфе мы уже выяснили, что радиусы оснований усеченного конуса связаны с высотами исходного конуса и того конуса, который получается при проведении секущей плос-ти:

Заметим, что любые две образующие усеченного конуса одинаковы. Действительно, пусть усеченный конус с образующими АА₁ и ВВ₁ получен их исходного конуса с образующими АР и ВР:

Заметим, что осевое сечение усеченного конуса – это равнобедренная трапеция:

Действительно, построим осевое сечение исходного конуса, которое пройдет через образующие РА и РВ. Пусть эти образующие пересекают плос-ть верхнего основания усеченного конуса в точках А₁ и В₁ соответственно. Тогда АА₁В₁В будет осевым сечением усеченного конуса. Точки А, А₁, В₁ и В располагаются в одной плос-ти РАВ, то есть АА₁В₁В – плоский четырехугольник. Его стороны АВ и А₁В₁ не могут пересекаться, ведь они принадлежат параллельным основаниям, поэтому АВ||А₁В₁. Стороны АА₁ и ВВ₁ одинаковы как образующие, при этом прямые АА₁ и ВВ₁ непараллельны, ведь они пересекаются в точке Р. В итоге получается, что АА₁В₁В – равнобедренная трапеция. Отдельно отметим, что ось ОО₁ делит эту равнобедренную трапецию на две прямоугольных трапеции.

Теперь выведем формулы для рассчета площади боковой поверх-ти усеченного конуса. Ясно, что развертка усеченного конуса – это часть развертки поверх-ти исходного конуса:

Нам надо найти площадь фигуры АА₁А₁’А’ (показана желтым цветом). Ее можно найти как разность площадей секторов РАА’и РА₁А₁’. Но эти площади можно вычислить по формуле боковых поверх-тей конусов:

Обозначим длину образующей АА₁ как l. Далее выразим А₁P через r, r₁ и l. ∆АОР и ∆РА₁О₁ подобны, поэтому можно записать:

Подставляем полученное выражение в (1) и получаем:

Чтобы посчитать полную площадь поверх-ти усеченного конуса, необходимо к боковой поверх-ти добавить площади верхнего и нижнего основания:

Рассмотрим несколько задач про конусы.

Задание. Высота конуса составляет 15 см, а его радиус – 8 см. Вычислите длину его образующей.

Решение. Обозначим вершину конуса буквой Р, буквой О – центр основания, а буквой А – произвольную точку на окруж-ти. Тогда высотой конуса будет отрезок ОР, радиусом – отрезок ОА, а образующей окажется отрезок АР:

Высота ОР перпендикулярна плос-ти основания, поэтому ∠РОА – прямой, а ∆РОА – прямоугольный. Тогда АР можно найти по теореме Пифагора:

Задание. Угол между образующей конуса и плос-тью основания составляет 30°, а длина образующей – 12 см. Какова площадь основания конуса?

Решение. Обозначим образующую как АР, а высоту конуса как ОР. Тогда радиус ОА будет проекцией АР на плос-ть основания, то именно ∠РАО будет составлять 30°:

Для вычисления площади основания надо найти радиус АО. Это можно сделать через прямоугольный ∆РОА:

Задание. Осевое сечение конуса имеет площадь 6, а площадь основания равна 8. Вычислите его высоту.

Решение. Пусть осевым сечением будет ∆РАВ, а РО – искомая высота:

Зная площадь основания, легко найдем радиус конуса ОА, а потом и диаметр АВ:

Так как РО – высота для ∆РАВ, то площадь этого треуг-ка может быть рассчитана так:

Задание. Найдите площадь боковой и полной поверх-ти конуса, если образующая имеет длину 8, а радиус основания составляет 5.

Решение. В этой задаче надо просто применить формулу для вычисления площадей:

Задание. Дан конус. Развертка его конической поверх-ти – это сектор, чья дуга составляет 60°. Р – вершина конуса, а РAB – осевое сечение. Вычислите ∠АРВ.

Решение. Длину образующих РА и РВ обозначим как L. Сначала находим длину дуги АА’:

Теперь искомый нами ∠АРВ можно найти с помощью теоремы косинусов, записанной для ∆АРВ:

Задание. Найдите длину образующей усеченного конуса, если радиусы его оснований составляют 6 см и 3 см, а его высота – 4 см.

Решение. Обозначим искомую образующую как АВ, а буквами О и О₁ обозначим центры нижнего и верхнего оснований соответственно:

При изучении осевого сечения усеченного конуса мы уже выяснили, что АВО₁О – прямоугольная трапеция. Опустим в ней высоту ВН, которая будет иметь ту же длину, что и высота конуса ОО₁:

Ответ: 5 см.

Задание. Радиусы оснований усеченного конуса обозначены буквами R и r (R > r). Образующая конуса образует с нижним основанием угол 45°. Составьте формулу, по которой можно найти площадь осевого сечения этого конуса.

Решение. Осевым сечением будет равнобедренная трапеция А₁АВВ₁:

Проведем высоту А₁Н. Вычислим АН:

Теперь площадь трапеции А₁АВВ₁ можно посчитать по формуле:

Задание. Основания усеченного конуса – окружности с радиусами 6 и 7 см. Длина образующей – 5 см. Вычислите площадь его боковой и полной поверх-ти.

Решение. Здесь надо просто подставить данные из условия в формулы для вычисления площадей:

Ответ: 65π см², 150π см².

Сегодня мы узнали две новые объемные фигуры – цилиндр и конус. Эти фигуры иногда называют телами вращения, ведь они получаются вращением плоских фигур вокруг одной из их сторон. Важно помнить, что у всех тел вращения есть такие элементы, как основание (иногда не одно), ось и образующие.