Как найти радиус обьем шара

В данной публикации мы рассмотрим, как можно вычислить радиус шара и разберем примеры решения задач для закрепления материала.

Формулы вычисления радиуса шара
- 1. Через объем
- 2. Через площадь поверхности
Примеры задач

Формулы вычисления радиуса шара

1. Через объем

Радиус шара вычисляется по формуле:

V – объем шара; равен трем четвертым произведения его радиуса в кубе и числа π.

π – число, приближенное значение которого равняется 3,14.

2. Через площадь поверхности

Радиус шара рассчитывается таким образом:

S – площадь поверхности шара; равна четырем его радиусам в квадрате, умноженным на число π.

S = 4πR²

Примеры задач

Задание 1
Объем шара составляет 904,32 см³. Найдите его радиус.

Решение:
Воспользовавшись первой формулой получаем:

Задание 2
Вычислите радиус шара, если площадь его поверхности равна 314 см².

Решение:
В данном случае рассчитать радиус шара можно, применив 2-ю формулу (через площадь поверхности):

Источник

Как вычислить радиус шара по объему?

Для вычисления параметров шара существуют формулы.

В частности, чтобы вычислить радиус шара при известном объеме, следует использовать такую формулу:

Где R – радиус шара (искомое значение), V – объем (известное значение), пи – константа, значение которой принимается как 3,14, при этом для более точных вычислений следует брать большее количество знаков после запятой.

автор вопроса выбрал этот ответ лучшим

Ксарфакс
[156K]

5 лет назад

Радиус шара по объему

Шар представляет собой геометрическое тело, являющееся совокупностью всех точек пространства, которые находятся от центра шара на расстоянии не больше заданного. Данное расстояние называется радиусом шара.

Для того, чтобы выразить радиус шара через объём, нужно вспомнить формулу:

Объём шара V равен произведению 4/3 на число π (которое является константой и равно 3,14) и на радиус в кубе.

Из этой формулы можно сначала выразить куб радиуса:

Конечная формула получится такой:

Радиус шара будет равен кубическому корню из дроби; числитель дроби – объем, умноженный на 3; знаменатель дроби – число π, умноженное на 4.

Пример

Предположим, объем шара равен 9 кубическим метрам.

Радиус шара находим по формуле, приведенной выше:

R ≈ ³√((3 * 9) / (4 * 3,14)) ≈ ³√(27 / 12,56) ≈ 3 / ³√12,56 ≈ 3 / 2,29 ≈ 1,31 метр.

Таким образом, если объём шара составляет 9 куб. метров, то его радиус будет равен приблизительно 1,31 метра.

Бархатные лапки
[382K]

более года назад

Такие задания иногда встречаются на ЕГЭ, с одной стороны вроде ничего сложного, но все же извилины придется напрячь, чтобы ее решить. Лично мне такие задачки давались с трудом, так как я не сильно любила геометрию, но все же формулы приходилось заучивать, чтобы решать задачки.

Давайте для начала вспомним по какой формуле мы находим объем шара.

Итак, эта формула выглядит следующим образом:

Значит радиус шара мы можем вычислить по такой формуле:

В данном случае мы выражаем одну величину через другую.

Так что все оказалось не так уж и запутанно и ученикам вполне под силу справится с такой заковыристой задачкой.

bezdelnik
[34.1K]

5 лет назад

Радиус шара по известному объёму вычисляется по формуле R равен корню кубическому из 3*V}/4*pi, где V – объём шара, pi- трансцендентное число равное отношению длины половины окружности к её радиусу. Поэтому точно вычислить радиус не возможно, а только с определённой погрешностью. Некоторую сложность представляет извлечение кубического корня. Для этого можно воспользоваться таблицей кубов. Например, при V=1000 куб.мм. и pi=3,14 подкоренное выражение равно 238,8535… и по таблице находим R равен примерно 6,2 мм.

Марина Вологда
[295K]

более года назад

Надо вспомнить формулу и проблем с вычислением радиуса шара не возникнет.

Итак, сначала укажем формулу:

R – это как раз искомый нами радиус.

3 и корень – это кубический корень из полученной дроби.

? – это пи (оно всегда едино и составляет 3.14).

V – объем шара, который нам известен.

Ну а теперь не сложно высчитать радиус, зная его объем, подставляя в формулу известные нам данные.

Simple Ein
[191K]

3 года назад

Найти радиус шара, зная объем очень легко.

Объем шара находится по формуле:

Выразим из данной формулы значение радиуса шара. Для этого необходимо объем разделить на число «Пи», умножив на ¾. Из полученного числа необходимо найти кубический корень.

-Александр–
[31K]

5 лет назад

Формула объема шара:

V=4/3*п*(R в степени 3)

отсюда

R = корень третей степени из (3/4*V/п)

Лара Изюминка
[59.8K]

2 года назад

Достаточно простая задача для тех, кто помнит, чему равен обьем шара. А он равен четыре третьх умножить на пи умножить на радиус в кубе.

Далее нужно уметь просто выражать одну величину через другую.

В итоге у нас радиус равен корень кубический из ( 3 умножить на обьем и это разделить на 4 пи.) Итак еще нужно вспомнить, что пи это 3,14 приблизительно. Если нужна большая точность, берут больше знаков после запятой в числе пи. Это имеет смысл при нахождении радиуса в больших сооружениях, в архитектуре. Обычно хватает точности два знака после запятой. Эта формула нужна при решении задач по стереометрии .

Vodila
[16.6K]

более года назад

Зная, что обьем шара равен 43 пи умножить на радиус в квадрате совсем нетрудно выразить радиус. Очевидно, что он будет равен корень кубический из три четвертых обьема, деленного на пи. Вот собственно и вся формула. Такая задача иногда встречается в ЕГЭ по математике.

Hamster1337
[28.6K]

2 года назад

Для того, что бы найти радиус шара при наличии объёма, следует воспользоваться следующей формулой:

Где число “П” равно 3,14. Так же существуют другие формулы для поиска радиуса шара (из данной формулы можно вывести другую формулу).

Для того, чтобы отыскать радиус шара при том, что объем известен воспользуйтесь формулой, а именно, в качестве основной применима такая.

R является искомым значением, а также радиусом шара. V отображает значение, являющееся известным, объем. Пи является константа, у которой значение = 3,14. Так, когда делаются точные расчеты следует брать большее количество знаков, которые находятся после запятой.

Знаете ответ?

Источник

У этого термина существуют и другие значения, см. Шар (значения).

Поверхность шара — сфера
r — радиус шара

Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

Связанные определения[править | править код]

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие плоские сечения шара называются малыми кругами. Площадь этих сечений вычисляется по формуле πR².

Основные геометрические формулы[править | править код]

Площадь поверхности и объём шара радиуса (и диаметром d = 2r ) определяются формулами:

$S= 4pi r^{2}$

$S= pi d^{2}$

$V={frac {4}{3}}pi r^{3}$

Доказательство

Возьмём четверть круга радиуса R с центром в точке . Уравнение окружности этого круга : $x^{2}+y^{2}=R^{2}$ , откуда $y^{2}=R^{2}-x^{2}$ .

Функция $y={sqrt {R^{2}-x^{2}}},xin (0;R)$ непрерывная, убывающая, неотрицательная. При вращении четверти круга вокруг оси Ox образуется полушар, следовательно:

${1 over 2}V=pi int limits _{0}^{R}(R^{2}-x^{2})dx=pi cdot {Bigl .}left(R^{2}x-{frac {x^{3}}{3}}right){Bigr |}_{0}^{R}=pi cdot (R^{3}-{frac {R^{3}}{3}})={frac {2}{3}}pi R^{3}$

Откуда $V={frac {4}{3}}pi R^{3}$ Ч. т. д.

$V={frac {pi d^{3}}{6}}$

Доказательство

$d=2r, V={4 over 3} pi r^3 = {4 over 3} pi left ( {d over 2} right )^3 = {4 over 3} pi frac {d^3} {8} = frac {pi d^3} {6}$ Ч. т. д.

Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии.

Определения[править | править код]

Пусть дано метрическое пространство (X,rho) . Тогда

$B_{r}(x_{0})={xin Xmid rho (x,x_{0})<r}.$

$D_{r}(x_{0})={xin Xmid rho (x,x_{0})leqslant r}.$

Замечания[править | править код]

Шар радиуса с центром $x_{0}$ также называют -окрестностью точки $x_{0}$ .

Свойства[править | править код]

$B_{1}(x)={x},;overline {B_{1}(x)}={x},;D_{1}(x)=X.$

Объём[править | править код]

Объём n-мерного шара радиуса R в n-мерном евклидовом пространстве:^[1]

${displaystyle V_{n}(R)={frac {pi ^{n/2}}{Gamma ({frac {n}{2}}+1)}}R^{n},}$

где Γ — это эйлеровская гамма-функция (которая является расширением факториала на поле действительных и комплексных чисел). Используя частные представления гамма-функции для целых и полуцелых значений, можно получить формулы объёма n-мерного шара, которые не требуют гамма-функции:

${displaystyle V_{2k}(R)={frac {pi ^{k}}{k!}}R^{2k}}$

${displaystyle V_{2k+1}(R)={frac {2^{k+1}pi ^{k}}{(2k+1)!!}}R^{2k+1}={frac {2(k!)(4pi )^{k}}{(2k+1)!}}R^{2k+1}}$

Знаком !! здесь обозначен двойной факториал.

Эти формулы также можно свести в одну общую:

${displaystyle V_{n}(R)={frac {2^{left[{frac {n+1}{2}}right]}pi ^{left[{frac {n}{2}}right]}}{n!!}}R^{n}}$

Обратная функция для выражения зависимости радиуса от объёма:

${displaystyle R_{n}(V)={frac {Gamma (n/2+1)^{1/n}}{sqrt {pi }}}V^{1/n}}$

Эта формула также может быть разделена на две: для пространств с чётным и нечётным количеством размерностей, используя факториал и двойной факториал вместо гамма-функции:

${displaystyle R_{2k}(V)={frac {(k!V)^{1/2k}}{sqrt {pi }}}}$

${displaystyle R_{2k+1}(V)=left({frac {(2k+1)!!V}{2^{k+1}pi ^{k}}}right)^{1/(2k+1)}}$

Рекурсия[править | править код]

Формулу объёма также можно выразить в виде рекурсивной функции. Эти формулы могут быть доказаны непосредственно или выведены из основной формулы, представленной выше. Проще всего выразить объём n-мерного шара через объём шара размерности n-2 (при условии, что они имеют одинаковый радиус):

${displaystyle V_{n}(R)={frac {2pi R^{2}}{n}}V_{n-2}(R)}$

Также существует формула объёма n-мерного шара в зависимости от объёма (n−1)-мерного шара того же радиуса:

${displaystyle V_{n}(R)=R{sqrt {pi }}{frac {Gamma ({frac {n+1}{2}})}{Gamma ({frac {n}{2}}+1)}}V_{n-1}(R)}$

То же без гамма-функции:

${displaystyle {begin{aligned}V_{2k}(R)&=Rpi {frac {(2k-1)!!}{2^{k}k!}}V_{2k-1}(R)=Rpi {frac {(2k-1)(2k-3)cdots 5cdot 3cdot 1}{(2k)(2k-2)cdots 6cdot 4cdot 2}}V_{2k-1}(R),\V_{2k+1}(R)&=2R{frac {2^{k}k!}{(2k+1)!!}}V_{2k}(R)=2R{frac {(2k)(2k-2)cdots 6cdot 4cdot 2}{(2k+1)(2k-1)cdots 5cdot 3cdot 1}}V_{2k}(R).end{aligned}}}$

Пространства младших размерностей[править | править код]

Формулы объёма для некоторых пространств младших размерностей:

Кол-во измерений	Объём шара радиуса R	Радиус шара объёма V
1
2	$pi R^{2}$	${displaystyle {frac {V^{1/2}}{sqrt {pi }}}}$
3	${displaystyle {frac {4pi }{3}}R^{3}}$	${displaystyle left({frac {3V}{4pi }}right)^{1/3}}$
4	${displaystyle {frac {pi ^{2}}{2}}R^{4}}$	${displaystyle {frac {(2V)^{1/4}}{sqrt {pi }}}}$
5	${displaystyle {frac {8pi ^{2}}{15}}R^{5}}$	${displaystyle left({frac {15V}{8pi ^{2}}}right)^{1/5}}$
6	${displaystyle {frac {pi ^{3}}{6}}R^{6}}$	${displaystyle {frac {(6V)^{1/6}}{sqrt {pi }}}}$
7	${displaystyle {frac {16pi ^{3}}{105}}R^{7}}$	${displaystyle left({frac {105V}{16pi ^{3}}}right)^{1/7}}$
8	${displaystyle {frac {pi ^{4}}{24}}R^{8}}$	${displaystyle {frac {(24V)^{1/8}}{sqrt {pi }}}}$
9	${displaystyle {frac {32pi ^{4}}{945}}R^{9}}$	${displaystyle left({frac {945V}{32pi ^{4}}}right)^{1/9}}$
10	${displaystyle {frac {pi ^{5}}{120}}R^{10}}$	${displaystyle {frac {(120V)^{1/10}}{sqrt {pi }}}}$

Пространства старших размерностей[править | править код]

Объём гипершара размерности n единичного радиуса в зависимости от n.

При стремлении количества размерностей к бесконечности объём шара единичного радиуса стремится к нулю. Это может быть выведено из рекурсивного представления формулы объёма.

Примеры[править | править код]

Пусть $mathbb{R}^d$ — евклидово пространство с обычным евклидовым расстоянием. Тогда

если (пространство — прямая), то

${displaystyle B_{r}(x_{0})={xin mathbb {R} mid |x-x_{0}|<r}=left(x_{0}-{r},x_{0}+{r}right),}$

${displaystyle D_{r}(x_{0})={xin mathbb {R} mid |x-x_{0}|leq r}=left[x_{0}-{r},x_{0}+{r}right].}$

— открытый и замкнутый отрезок соответственно.

— открытый и замкнутый диск соответственно.

— открытый и замкнутый стереометрический шар соответственно.

Тогда

См. также[править | править код]

Шаровой слой
Гиперсфера
Сферический слой

Примечания[править | править код]

↑ Equation 5.19.4, NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/, Release 1.0.6 of 2013-05-06.

Литература[править | править код]

Шар, геометрическое тело // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Ссылки на онлайн калькуляторы[править | править код]

Вычисление объема и площади шара. Дата обращения: 12 марта 2012. Архивировано из оригинала 8 августа 2011 года.
Онлайн-калькуляторы. Дата обращения: 2 июля 2019. Архивировано из оригинала 9 января 2019 года.
Математические этюды. Дата обращения: 20 октября 2011. Архивировано из оригинала 18 октября 2011 года. Мультфильм про объём шара

Источник

Радиус шара

Радиус

Отрезок, соединяющий центр шара с любой точкой на его поверхности, является радиусом шара, обозначается как r или R. В зависимости от исходных данных радиус шара можно вычислить:

— по диаметру. Как известно, радиус шара равен половине его диаметра:

г = D/2,

где г — радиус, D — диаметр шара.

— по длине окружности.
Длина окружности © равна произведению пи на диаметр (D), через радиус шара — удвоенному произведению пи на радиус ^®:

C = πD = 2πr

r = С / 2π

π — величина постоянная, равна отношению длины окружности к диаметру. Число Пи, равное 3,141592653… обычно округляется до 3,14.

— по площади шара.
Площадь шара равна произведению четырех пи на квадрат радиуса:

S=4πr²,

где S — площадь шара, r — радиус.
Из этой формулы выводим форму радиуса:

r = √S / 4π,

т.е. радиус равен корню квадратному из площади шара деленной на четыре пи.

— по объему шара.
Объем шара равен произведению четырех третьих на число пи и на радиус шара в кубе:

V = 4/3 πr³,

где V — объем, r — радиус шара.
Отсюда, радиус шара равен корню кубическому из объема шара деленного на три четвертых Пи:

r = ∛(V / (¾π))

Рассчитать радиус шара через объем

Источник

Загрузить PDF

Радиус шара (обозначается как r или R) – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Как и в случае круга, радиус шара является важной величиной, которая необходима для нахождения диаметра шара, длины окружности, площади поверхности и/или объема. Но радиус шара можно найти и по данному значению диаметра, длины окружности и другой величины. Используйте формулу, в которую можно подставить данные значения.

1
Вычислите радиус по диаметру. Радиус равен половине диаметра, поэтому используйте формулу г = D/2. Эта такая же формула, которая используется при вычислении радиуса и диаметра круга.^[1]
- Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см. Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).
2
Вычислите радиус по длине окружности. Используйте формулу: r = C/2π. Так как длина окружности C = πD = 2πr, то разделите формулу для вычисления длины окружности на 2π и получите формулу для нахождения радиуса.^[2]
- Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см.
- Такая же формула используется при вычислении радиуса и длины окружности круга.
3
Вычислите радиус по объему шара. Используйте формулу: r = ((V/π)(3/4))^1/3.^[3] Объем шара вычисляется по формуле V = (4/3)πr³. Обособив r на одной стороне уравнения, вы получите формулу ((V/π)(3/4))³ = г, то есть для вычисления радиуса объем шара делим на π, результат умножаем на 3/4, а полученный результат возводим в степень 1/3 (или извлекаем кубический корень).^[4]
- Например, дан шар с объемом 100 см³. Радиус этого шара вычисляется так:
  - ((V/π)(3/4))^1/3 = r
  - ((100/π)(3/4))^1/3 = r
  - ((31,83)(3/4))^1/3 = r
  - (23,87)^1/3 = r
  - 2,88 см = r
4
Вычислите радиус по площади поверхности. Используйте формулу: г = √(A/(4 π)). Площадь поверхности шара вычисляется по формуле А = 4πr². Обособив r на одной стороне уравнения, вы получите формулу √(A/(4π)) = r, то есть, чтобы вычислить радиус, нужно извлечь квадратный корень из площади поверхности, деленной на 4π. Вместо того чтобы извлекать корень, выражение (A/(4π)) можно возвести в степень 1/2.^[5]
- Например, дан шар с площадью поверхности 1200 см³. Радиус этого шара вычисляется так:
  - √(A/(4π)) = r
  - √(1200/(4π)) = r
  - √(300/(π)) = r
  - √(95,49) = r
  - 9,77 см = r
Реклама

1
Запомните основные величины, которые имеют отношение к вычислению радиуса шара. Радиус шара – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Радиус шара можно вычислить по данным значениям диаметра, длины окружности, объема или площади поверхности.
- Диаметр (D) – это отрезок, который соединяет две точки на поверхности шара и проходит через его центр (то есть это наибольшее расстояние между противоположными точками, лежащими на поверхности шара). Диаметр равен удвоенному радиусу.
- Длина окружности (С) представляет собой длину окружности большого круга, то есть круга, который образует секущая плоскость, проходящая через центр шара.
- Объем (V) – это значение трехмерного пространства, занимаемого шаром.^[6]
- Площадь поверхности (А) – это значение двумерного (плоского) пространства, ограниченного поверхностью шара.
- Пи (π) – это постоянная, которая равна отношению длины окружности к ее диаметру. Первыми десятью цифрами этой постоянной являются 3,141592653, но зачастую число Пи округляется до 3,14.
2
Воспользуйтесь значениями данных величин, чтобы найти радиус. Радиус можно вычислить по данным значениям диаметра, длины окружности, объема и площади поверхности. Более того, указанные величины можно найти по данному значению радиуса. Чтобы вычислить радиус, просто преобразуйте формулы для нахождения указанных величин. Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности.
- D = 2г. Как и в случае круга, диаметр шара в два раза больше его радиуса.
- C = πD = 2πr. Как и в случае круга, длина окружности шара равна произведению π на диаметр шара. Так как диаметр вдвое больше радиуса, то длина окружности шара равна удвоенному произведению π на радиус шара.
- V = (4/3)πr³. Объем шара равен произведению 4/3 на π и на радиус в кубе.^[7]
- А = 4πr². Площадь поверхности шара равна учетверенному произведению π на радиус в квадрате. Так как площадь круга равна πr², то площадь поверхности шара в четыре раза больше площади круга, который образует секущая плоскость, проходящая через центр шара.
Реклама

1
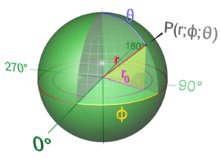
Найдите координаты (х,у,z) центра шара. Радиус шара равен расстоянию между его центром и любой точкой, лежащей на поверхности шара. Если известны координаты центра шара и любой точки, лежащей на его поверхности, можно найти радиус шара по специальной формуле, вычислив расстояние между двумя точками. Сначала найдите координаты центра шара. Имейте в виду, что так как шар является трехмерной фигурой, то точка будет иметь три координаты (х,у,z), а не две (х,у).
- Рассмотрим пример. Дан шар с центром с координатами (4,-1,12). Воспользуйтесь этими координатами, чтобы найти радиус шара.
2
Найдите координаты точки, лежащей на поверхности шара. Теперь нужно найти координаты (х,у,z) любой точки, лежащей на поверхности шара. Так как все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара, для вычисления радиуса шара можно выбрать любую точку.
- В нашем примере допустим, что некоторая точка, лежащая на поверхности шара, имеет координаты (3,3,0). Вычислив расстояние между этой точкой и центром шара, вы найдете радиус.
3
Вычислите радиус по формуле d = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²). Узнав координаты центра шара и точки, лежащей на его поверхности, вы можете найти расстояние между ними, которое равно радиусу шара. Расстояние между двумя точками вычисляется по формуле d = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²), где d – расстояние между точками, (x₁,y₁,z₁) – координаты центра шара, (x₂,y₂,z₂) – координаты точки, лежащей на поверхности шара.
- В рассматриваемом примере вместо (x₁,y₁,z₁) подставьте (4,-1,12), а вместо (x₂,y₂,z₂) подставьте (3,3,0):
  - d = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²)
  - d = √((3 – 4)² + (3 – -1)² + (0 – 12)²)
  - d = √((-1)² + (4)² + (-12)²)
  - d = √(1 + 16 + 144)
  - d = √(161)
  - d = 12,69. Это искомый радиус шара.
4
Имейте в виду, что в общих случаях r = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²). Все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара. Если в формуле для нахождения расстояния между двумя точками “d” заменить на “r”, получится формула для вычисления радиуса шара по известным координатам (x₁,y₁,z₁) центра шара и координатам (x₂,y₂,z₂) любой точки, лежащей на поверхности шара.
- Возведите обе стороны этого уравнения в квадрат, и получите r² = (x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)². Отметьте, что это уравнение соответствует уравнению сферы r² = x² + y² + z² с центром с координатами (0,0,0).
Реклама

Советы

Не забывайте про порядок выполнения математических операций. Если вы не помните этот порядок, а ваш калькулятор умеет работать с круглыми скобками, пользуйтесь ими.
В этой статье рассказывается о вычислении радиуса шара. Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса.
π (Пи) – это буква греческого алфавита, которая обозначает постоянную, равную отношению диаметра круга к длине его окружности. Число Пи является иррациональным числом, которое не записывается как отношение действительных чисел. Существует множество приближений, например, отношение 333/106 позволит найти число Пи с точностью до четырех цифр после десятичной запятой. Как правило, пользуются приблизительным значением числа Пи, которое равно 3,14.

Об этой статье

Эту страницу просматривали 114 745 раз.

Была ли эта статья полезной?

Источник

Формулы вычисления радиуса шара

1. Через объем

2. Через площадь поверхности

Примеры задач

Связанные определения[править | править код]

Основные геометрические формулы[править | править код]

Определения[править | править код]

Замечания[править | править код]

Свойства[править | править код]

Объём[править | править код]

Рекурсия[править | править код]

Пространства младших размерностей[править | править код]

Пространства старших размерностей[править | править код]

Примеры[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки на онлайн калькуляторы[править | править код]

Радиус шара

г = D/2,

C = πD = 2πr

r = С / 2π

S=4πr²,

r = √S / 4π,

V = 4/3 πr³,

r = ∛(V / (¾π))

Рассчитать радиус шара через объем

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Добавить комментарий Отменить ответ

Формулы вычисления радиуса шара

1. Через объем

2. Через площадь поверхности

Примеры задач

Связанные определения[править | править код]

Основные геометрические формулы[править | править код]

Определения[править | править код]

Замечания[править | править код]

Свойства[править | править код]

Объём[править | править код]

Рекурсия[править | править код]

Пространства младших размерностей[править | править код]

Пространства старших размерностей[править | править код]

Примеры[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки на онлайн калькуляторы[править | править код]

Радиус шара

г = D/2,

C = πD = 2πr

r = С / 2π

S=4πr2,

r = √S / 4π,

V = 4/3 πr3,

r = ∛(V / (¾π))

Рассчитать радиус шара через объем

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Прикол как найти мужчину

Как найти переписку в ватсапе которую удалили

Как найти сторону вписанного многоугольника зная радиус

Добавить комментарий Отменить ответ

S=4πr²,

V = 4/3 πr³,