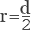В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
-
Формулы вычисления радиуса круга
- 1. Через длину окружности/периметр круга
- 2. Через площадь круга
-
Примеры задач
Формулы вычисления радиуса круга
1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:
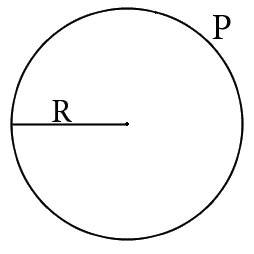
C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2πR
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:
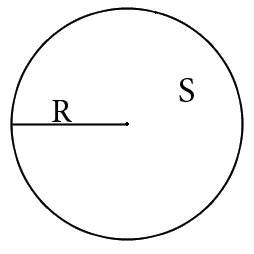
S – это площадь круга; равна числу π, умноженному на квадрат его радиуса:
S = πR2
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см2.
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
Как посчитать радиус окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать радиус окружности
Чтобы посчитать радиус окружности (круга) воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы узнать какой радиус у окружности вам необходимо знать либо её диаметр, либо её площадь, либо длину окружности. Зная один из этих параметров, просто введите его в соответствующие поле и узнаете, чему равен радиус.
Как посчитать радиус зная длину окружности
Чему равен радиус если длина окружности ?
Ответ:
0
Чему равен радиус (r) если длина окружности C?
Формула
r = C/2π, где π ≈ 3.14
Пример
Если длина круга равна 3 см, то его радиус примерно равен 0.477 см.
Как посчитать радиус окружности зная её площадь
Чему равен радиус окружности если
её площадь ?
Ответ:
0
Чему равен радиус окружности (r) если её площадь S?
Формула
r = √S/π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см2, то его радиус примерно равен 1.26 см.
Как посчитать радиус окружности зная диаметр
Чему равен радиус окружности если
её диаметр ?
Ответ:
0
Чему равен радиус окружности (r) если её диаметр d?
Формула
r = d/2
Пример
Если диаметр круга равен 3 см, то его радиус = 1.5 см.
См. также
При помощи нашего калькулятора вы легко сможете узнать радиус круга или окружности.
Для того что бы вычислить радиус круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить радиус круга.
Радиус круга рассчитывается по следующим формулам:
- Если нам известна длина:
Формула для расчета радиуса круга через его длину:
R=P/(2π)
- Если нам известна площадь:
Формула для расчета радиус круга через площадь:
R=√
S/π
- Если нам известен диаметр:
Формула для расчета радиус круга через диаметр:
R=D/2
Где R – радиус круга, S – площадь круга, P – длина круга, D – диаметр, π – число Пи которое всегда примерно равно 3,14.
Радиус круга (окружности) – отрезок, который соединяет центр плоской геометрической фигуры с ее граничной линией. Онлайн калькулятор позволяет найти радиус круга по исходному значению длины окружности.
Размер любой окружности зависит от одного единственного параметра, которым руководствуются при ее начертании – это радиус. Радиус окружности по определению является расстоянием от центра окружности до каждой точки, находящейся на ней. Радиус окружности находится в прямо пропорциональной зависимости от длины окружности и диаметра. Радиус окружностей, вписанных и описанных вокруг многоугольников, также связан и с другими измерениями.
Радиус круга представляет собой равноудаленность всех точек окружности от ее центра. Вне зависимости от размера окружности, радиус представляет собой отношение длины окружности к удвоенному числу π, приблизительно равному 3,14.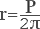 
Также значение радиуса можно рассчитать, опираясь на площадь круга. Для этого надо извлечь квадратный корень из отношения площади круга к числу π.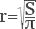 
Самый простой способ определит радиус круга – через диаметр. Диаметр является удвоенным радиусом, значит, для нахождения радиуса нужно диаметр разделить на два: 
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
