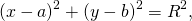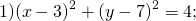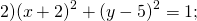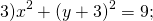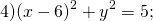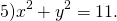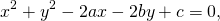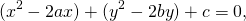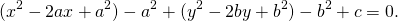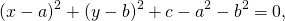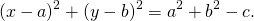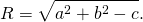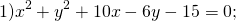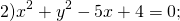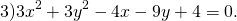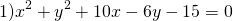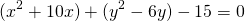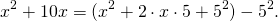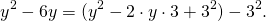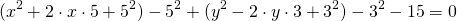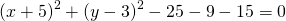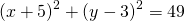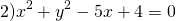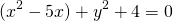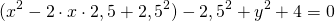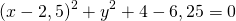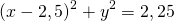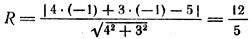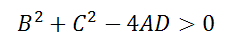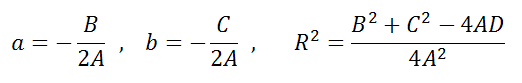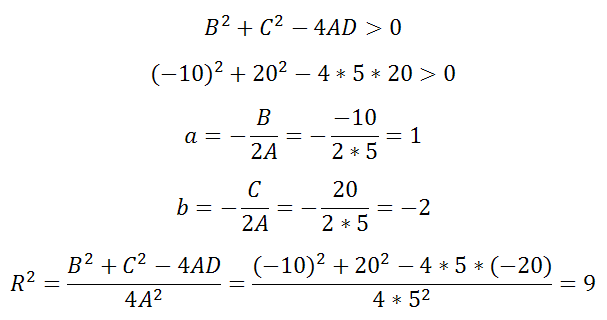Как найти радиус окружности через уравнение окружности - Сайт, где вы сможете решить свои вопросы

Если окружность задана уравнением вида

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

найти центр (a;b) и радиус R такой окружности несложно.

Примеры.

Определить по уравнению окружности координаты её центра и радиуса:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

$[3){x^2} + {(y + 3)^2} = 9;]$

$[4){(x - 6)^2} + {y^2} = 5;]$

$[5){x^2} + {y^2} = 11.]$

Решение:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

a=3, b=7, R²=4.

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

$[3){x^2} + {(y + 3)^2} = 9;]$

a=0, b=-3, R²=9.

Центр окружности — (0;-3), радиус R=3.

$[4){(x - 6)^2} + {y^2} = 5;]$

a=6, b=0, R²=5.

Центр — в точке (6;0), радиус R=√5.

$[5){x^2} + {y^2} = 11.]$

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

$[{x^2} + {y^2} - 2ax - 2by + c = 0,]$

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

$[({x^2} - 2ax) + ({y^2} - 2by) + c = 0,]$

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

$[({x^2} - 2ax + {a^2}) - {a^2} + ({y^2} - 2by + {b^2}) - {b^2} + c = 0.]$

Отсюда

$[{(x - a)^2} + {(y - b)^2} + c - {a^2} - {b^2} = 0,]$

$[{(x - a)^2} + {(y - b)^2} = {a^2} + {b^2} - c.]$

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

$[R = sqrt {{a^2} + {b^2} - c} .]$

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.

Примеры.

Найти координаты центра и радиус окружности:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0;]$

$[2){x^2} + {y^2} - 5x + 4 = 0;]$

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0.]$

Решение:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0]$

Группируем слагаемые

$[({x^2} + 10x) + ({y^2} - 6y) - 15 = 0]$

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

$[{x^2} + 10x = ({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2}.]$

Аналогично

$[{y^2} - 6y = ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2}.]$

Таким образом,

$[({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2} + ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2} - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} - 25 - 9 - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} = 49]$

Центром этой окружности является точка (-5;3), радиус R=7.

$[2){x^2} + {y^2} - 5x + 4 = 0]$

$[({x^2} - 5x) + {y^2} + 4 = 0]$

$[({x^2} - 2 cdot x cdot 2,5 + {2,5^2}) - {2,5^2} + {y^2} + 4 = 0]$

$[{(x - 2,5)^2} + {y^2} + 4 - 6,25 = 0]$

$[{(x - 2,5)^2} + {y^2} = 2,25]$

Центр окружности — точка (2,5;0), радиус R=1,5.

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0]$

Разделим обе части уравнения на 3:

$[{x^2} + {y^2} - frac{4}{3}x - 3y + frac{4}{3} = 0]$

Далее — аналогично

$[({x^2} - frac{4}{3}x) + ({y^2} - 3y) + frac{4}{3} = 0]$

$[({x^2} - 2 cdot x cdot frac{2}{3} + {(frac{2}{3})^2}) - {(frac{2}{3})^2} + ({y^2} - 2 cdot y cdot frac{3}{2} + {(frac{3}{2})^2}) - ]$

$[ - {(frac{3}{2})^2} + frac{4}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} - frac{{{4^{backslash 4}}}}{9} - frac{{{9^{backslash 9}}}}{4} + frac{{{4^{backslash 12}}}}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} = frac{{49}}{{36}}]$

Центр этой окружности лежит в точке

$[(frac{2}{3};frac{3}{2}),R = frac{7}{6}.]$

Источник

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Для каждой скобки применим метод выделения полного квадрата (подробнее смотри тут — Метод выделения полного квадрата), то есть заменим выражение вида на выражение вида . С учетом того, что коэффициенты при квадратах равны единице, а свободный член можно принять за ноль, формула для вычисления h и k упрощаются.

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

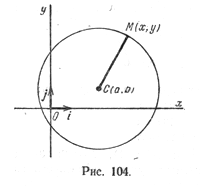
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = ( sqrt <(x — a)^2 + (у — b)^2>), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

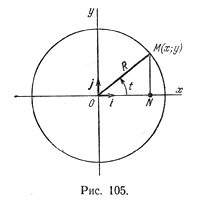
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

источники:

http://planetcalc.ru/9507/

http://razdupli.ru/teor/31_uravnenie-okruzhnosti.php

Источник

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать – как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Как определить радиус окружности через уравнение

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Как найти радиус окружности

О чем эта статья:

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Если известна площадь круга

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

Нахождение радиуса круга: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:

C = 2 π R

π – число, приближенное значение которого равно 3,14.

2. Через площадь круга

Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:

S = π R 2

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/radius-okruzhnosti

http://b4.cooksy.ru/articles/kak-opredelit-radius-okruzhnosti-cherez-uravnenie

[/spoiler]

Источник

Нахождение центра и радиуса окружности по общему уравнению окружности

Коэффициенты a, b, c, d, e уравнения

Введите коэффициенты a, b, c, d, e в указанном порядке ax² + by² + cx + dy + e = 0

Точность вычисления

Знаков после запятой: 2

Уравнение после выделения полного квадрата

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности – это будет точка с координатами (a,b), и радиус окружности – это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это – уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения
Для каждой скобки применим метод выделения полного квадрата (подробнее смотри тут – Метод выделения полного квадрата), то есть заменим выражение вида на выражение вида . С учетом того, что коэффициенты при квадратах равны единице, а свободный член можно принять за ноль, формула для вычисления h и k упрощаются.

Для x^2+cx :
$h_x=-frac{c}{2}\k_x=-frac{c^2}{4}$

Для y^2+dy :
$h_y=-frac{d}{2}\k_y=-frac{d^2}{4}$

Тогда
$(x^2+cx) + (y^2+dy)+e=0 \ to (x-h_x)^2+k_x + (y-h_y)^2+k_y + e=0 \ to (x-h_x)^2 + (y-h_y)^2=-e - k_x - k_y$

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число – значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи – нахождения общего уравнения окружности по координатам центра и радиусу – можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Источник

Как найти радиус и центр окружности

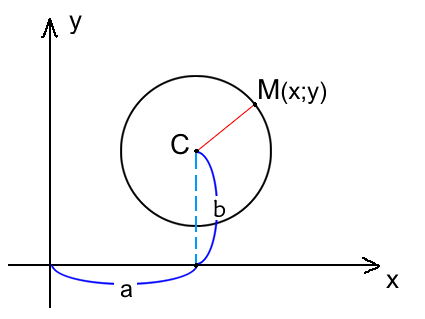
Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x² и y² были равны в уравнение вида:

3. Если выполняется неравенство

Как найти радиус и центр окружности

Уравнение Ax²+Bx+Ay²+Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x²-10x+5y²+20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x²+4xy+y²=1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x²+9y²=36 не представляет окружность, так как в нём коэффициенты при x² и y² не равны.

7974

Источник

Найти центр и радиус окружности

Нахождение центра и радиуса окружности по общему уравнению окружности

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Уравнение окружности

Найти центр и радиус окружности

Как найти радиус окружности

Основные понятия

Формула радиуса окружности

Если известна площадь круга

Если известна длина

Если известен диаметр окружности

Если известна диагональ вписанного прямоугольника

Если известна сторона описанного квадрата

Если известны стороны и площадь вписанного треугольника

Если известна площадь и полупериметр описанного треугольника

Если известна площадь сектора и его центральный угол

Если известна сторона вписанного правильного многоугольника

Скачать онлайн таблицу

Как определить радиус окружности через уравнение

Нахождение центра и радиуса окружности по общему уравнению окружности

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Как найти радиус окружности

Основные понятия

Формула радиуса окружности

Если известна площадь круга

Если известна длина

Если известен диаметр окружности

Если известна диагональ вписанного прямоугольника

Если известна сторона описанного квадрата

Если известны стороны и площадь вписанного треугольника

Если известна площадь и полупериметр описанного треугольника

Если известна площадь сектора и его центральный угол

Если известна сторона вписанного правильного многоугольника

Скачать онлайн таблицу

Нахождение радиуса круга: формула и примеры

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

2. Через площадь круга

Примеры задач

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Как найти радиус и центр окружности

Окружность радиуса R с центром в начале координат представляется уравнением:

Как найти радиус и центр окружности

Вам также может понравиться

Как найти людей которым нужен сайт

Путь в любую секунду как найти

Ошибка файловой системы 2147416359 windows 10 как исправить фото

Добавить комментарий Отменить ответ