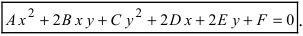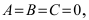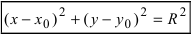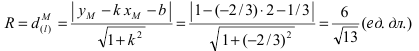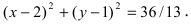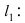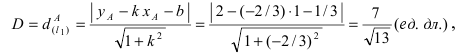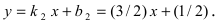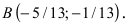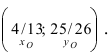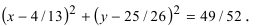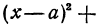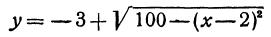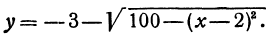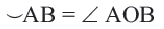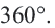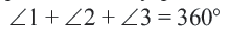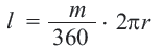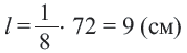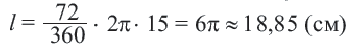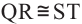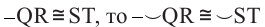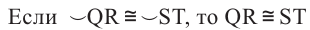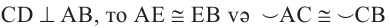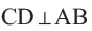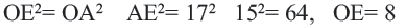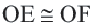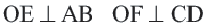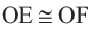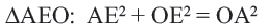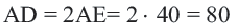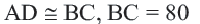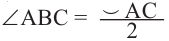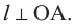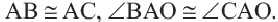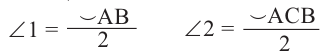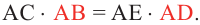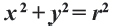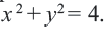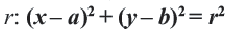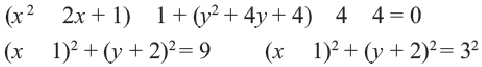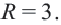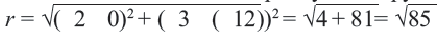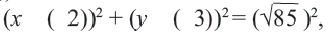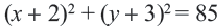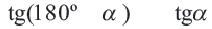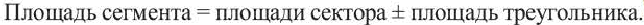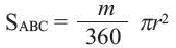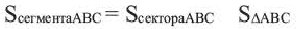Как найти радиус окружности лежащей на прямой

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

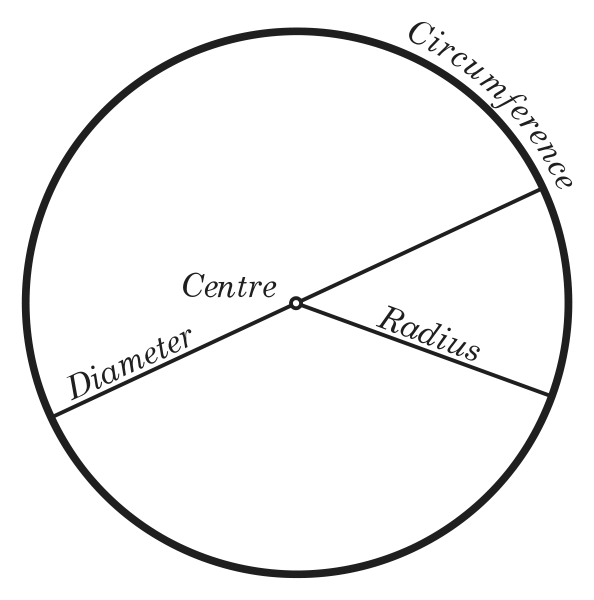
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать – как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

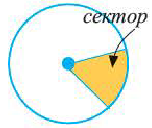
Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Нахождение радиуса круга: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:

C = 2 π R

π – число, приближенное значение которого равно 3,14.

2. Через площадь круга

Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:

S = π R 2

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Радиус — что это такое и как найти радиус окружности

Через длину стороны

Формула для нахождения длины окружности через радиус:

, где r — радиус окружности.

Найти радиус круга, зная окружность

Окружность круга P

Результат

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.

Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.

Длина диаметра равна удвоенной длине радиуса.

Вычисление радиуса

Радиус можно посчитать разными способами.

Если известен диаметр

Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.

Если известна длина окружности круга

Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.

Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:

Означает данное значение отношение длины окружности к диаметру той же окружности.

Если известна площадь круга

Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:

В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.

Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.

Способ расчета радиуса круга:

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

• r — искомый радиус окружности.
• a — сторона описанного квадрата.

Как посчитать радиус зная длину окружности

Чему равен радиус (r) если длина окружности C?

Формула

r = C /_2π , где π ≈ 3.14

Свойства радиуса

В отношении радиуса действуют несколько важных правил:

1. Радиус составляет половину диаметра. Это мы продемонстрировали только что.
2. У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.

Радиус, который перпендикулярен хорде, делит ее на две равные части.

Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

По площади сектора и центральному углу

• Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .

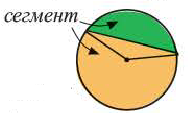
Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем

В случае, когда величина α выражена в в радианах , получаем

Формулы для площади круга и его частей

,

где R – радиус круга, D – диаметр круга

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Числовая характеристика	Рисунок	Формула
Площадь круга
Площадь сектора
Площадь сегмента

Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Центральный угол, вписанный угол и их свойства

Связанные определения

• Центральный угол в окружности — это угол , образованный двумя радиусами.
• Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .

В случае, когда величина α выражена в градусах , справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах , справедлива пропорция

из которой вытекает равенство:

Уравнение окружности

r 2 = ( x – a ) 2 + ( y – b ) 2

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:

<	x = a + r cos t
y = b + r sin t

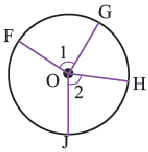
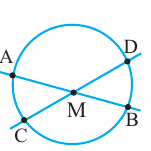
Углы между двумя хордами

Случай 1: два секущие пересекаются внутри окружности.

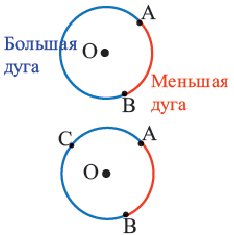
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности.

Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

• r — искомый радиус окружности.
• S — площадь треугольника.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

Основные свойства касательных к окружности

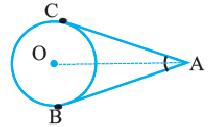
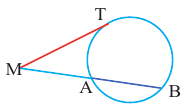
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

Обобщения

Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

• R — искомый радиус окружности.
• d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
• a, b — стороны вписанного прямоугольника.

Площадь круга, онлайн расчет

Как найти площадь круга по формуле через радиус либо диаметр круга.

Площадь круга, онлайн расчет

Вместо заключения

Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.

Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.

[spoiler title=”источники:”]

http://exceltut.ru/radius-chto-eto-takoe-i-kak-najti-radius-okruzhnosti/

[/spoiler]

Как найти радиус окружности

Слово радиус переводится с латинского radius как “спица колеса, луч”. Радиусом называется любой отрезок прямой, который соединяет центр окружности или сферы с любой из точек, лежащих на этой окружности или на поверхности данной сферы, также и длина этого отрезка является радиусом. Для обозначения радиуса в вычислениях и математических выражения используется латинская буква R.

Инструкция

Диаметр окружности представляет собой отрезок прямой, который проходит через центр окружности и соединяет две наиболее удаленные между собой точки, лежащие на окружности. Длина этого отрезка тоже называется диаметром окружности. Радиус равен половине диаметра окружности, поэтому если известен диаметр данной окружности, чтобы найти ее радиус достаточно разделить его пополам. R = D/2, где D – диаметр окружности.

Длина кривой, образующей окружность на плоскости является длиной окружности. В случае если известна длина окружности вы можете воспользоваться формулой: R = L/2?, где L – длина окружности, ? – это постоянная величина, равная 3,14159… Постоянная ? равна отношению длины окружности к диаметру, эта величина является одинаковой для всех окружностей.

Круг – это геометрическая фигура, представляющая собой часть плоскости, ограниченная кривой являющейся окружностью. Если известна площадь круга, то найти радиус окружности можно из следующей формулы: R = v(S/?), где v — корень квадратный, S – площадь круга.

Обратите внимание

Радиус окружности – это положительная величина не равная нулю.

Источники:

• как найти окружность радиуса

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Содержание:

Окружность:

Определение: Кривой второго порядка называется линия, описываемая уравнением

Замечание: Если коэффициенты

При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.

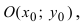
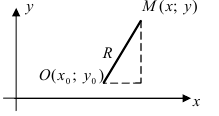
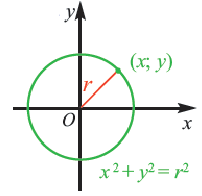
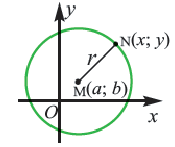
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки называемой центром окружности, на расстояние R, которое называется радиусом окружности.

Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:

Рис. 27. Вывод уравнения окружности.

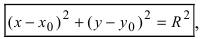
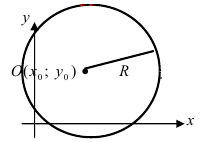
Из рисунка видно, что по теореме Пифагора которое определяет уравнение окружности (Рис. 28):

Рис. 28. Окружность.

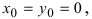
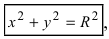
Если то уравнение принимает вид который называется каноническим уравнением окружности.

Пример:

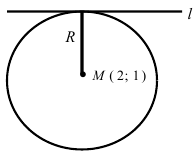
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 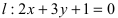является касательной к окружности.

Решение:

Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.

В уравнении окружности 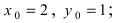таким образом оно имеет вид:

Пример:

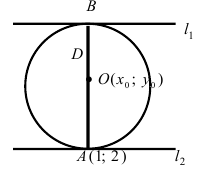
Составить уравнение окружности, касающейся двух параллельных прямых 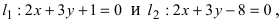причем одной из них в т. А (1; 2).

Решение:

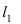
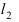
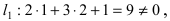
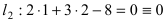
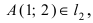
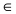
Прежде всего определим, на какой из прямых или лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых

следовательно, точка A(1; 2) принадлежит линии (в сокращенной форме это предложение пишут так: где значок означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой

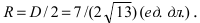
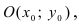
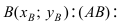
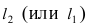
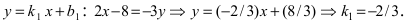
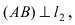
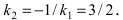
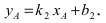
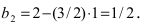
а радиус окружности Найдём координаты центра окружности точки которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом Так как прямаято её угловой коэффициент Прямая (АВ) проходит через известную точку A(1;2), следовательно, Отсюда находим Таким образом,уравнение прямой (АВ):

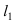
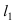
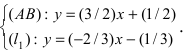
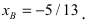
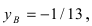
Найдем координаты точки B, которая является пересечением прямых и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых и (АВ): (В): Подставим выражение для переменной у из второго у равнения в первое, получим Подставив это значение во второе уравнение системы, найдем т.е.

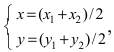
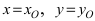
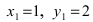
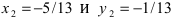
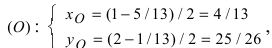
Для вычисления координат точки О применим формулы деления отрезка пополам (О): в этой формуле (координаты точки О), (координаты точки А), (координаты точки В), следовательно, т.е. координаты точки О

Таким образом, уравнение искомой окружности имеет вид:

Окружность в высшей математике

Рассмотрим уравнение

которое получается из уравнения (I), если положить , .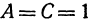

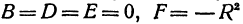
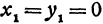
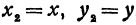
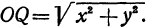
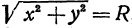
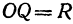
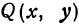
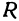
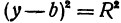
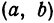
Если в формулу, выражающую расстояние между двумя точками, подставить , , то получим Из уравнения (1) находим, что , т. е. . Это значит, что все точки , координаты которых удовлетворяют уравнению (1), находятся на расстоянии от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса с центром в начале координат. Аналогично получаем, что уравнение определяет окружность радиуса с центром в точке .

Пример:

Найдем уравнение окружности с центром в точке и радиусом, равным 10.

Решение:

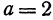
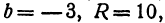
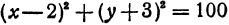
Полагая, получим .

Разрешим это уравнение относительно 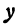, будем иметь

и

Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.

Центральный угол. Градусная мера дуги

Дуга окружности. Если отметить на окружности точки и , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка является какой-либо точкой дуги , то . Если точки и являются концами диаметра, го каждая дуга является полуокружностью.

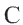
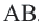
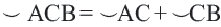
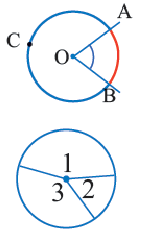
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла:

Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна

Дуги окружности и их величины

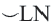
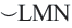
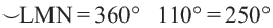
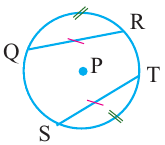
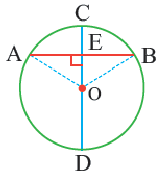
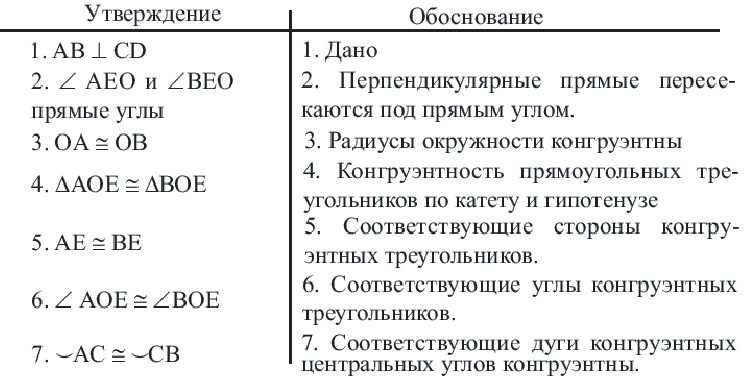
Пример: минорная дуга:

мажорная дуга:

Конгруэнтные дуги

В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.

Если

Если

Длина дуги

Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.

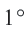
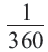
Длина дуги в равна части длины окружности.

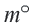
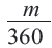
Длина дуги, соответствующей центральному углу с градусной мерой , составляет части длины окружности:

Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)

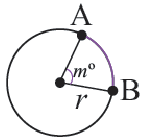
Пример №1

Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу .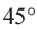

Решение:

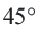
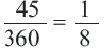
Так как центральный угол составляет часть полного угла, то длина искомой дуги:

Пример №2

Найдите длину дуги, соответствующей центральному углу 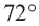в окружности радиусом 15 см.

Решение: подставляя значения 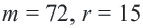в формулу длины дуги находим:

Окружность и хорда

Теорема о конгруэнтных хордах

Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.

Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.

1)Если 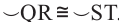, то

2)Если

Доказательство теоремы 1:

Теорема о серединном перпендикуляре хорд

Теорема 2.

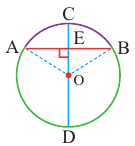
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.

Если

Доказательство теоремы 2.

Дано: – центральный угол,

Докажите:

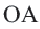
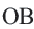
Начертите радиусы и окружности.

Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.

Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.

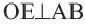
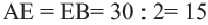
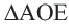
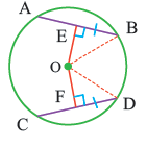
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если , то . Из по теореме Пифагора имеем:

Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности

Теорема 3.

Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.

Если 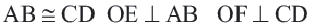, то

Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.

Доказательство теоремы 3

Дано: Окружность с центром

Докажите:

Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. и – серединные перпендикуляры конгруэнтных хорд и . , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности и : . Прямоугольные треугольники, и конгруэнтны (по катету и гипотенузе). Так как и являются соответствующими сторонами данных треугольников, то они конгруэнтны: . Теорема доказана.

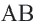
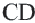
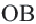
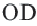
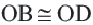
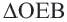
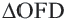
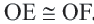
Задача. Хорды и находятся на одинаковом расстоянии от центра окружности. . Если радиус окружности равен 41 единице, то найдите .

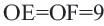
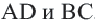
Решение: Так как хорды и находятся на одинаковом расстоянии от центра, то они конгруэнтны: Соединим точки и с точкой В прямоугольном треугольнике ; ; ;

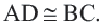
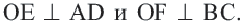
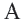
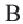
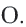
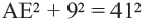
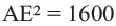
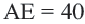
Так как

Угол, вписанный в окружность

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.

является углом вписанным в окружность с центром , а дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.

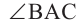
Угол, вписанный в окружность:

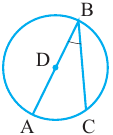
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается.

Доказательство (текстовое): и радиусы окружности и равнобедренный треугольник. Значит, Так как является внешним углом , Если примем, что , то Так как градусные меры центрального угла и опирающейся на него дуги равны, то Следовательно, .

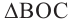
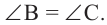
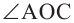
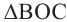
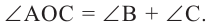
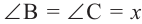
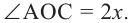
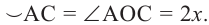
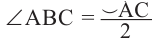
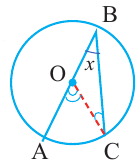
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.

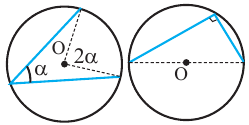
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.

Конгруэнтные углы, вписанные в окружность

Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. , .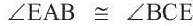

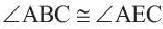
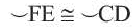
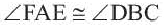
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если , то .

Касательная к окружности

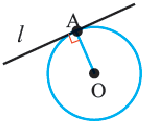
Касательная. Признак касательной

Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

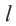
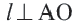
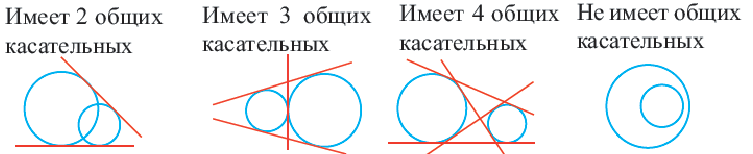
Прямая является касательной к окружности. Значит, Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.

Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.

Доказательство теоремы 1. Если прямая – касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая не перпендикулярна радиусу Проведем и на прямой выделим отрезок Тогда так как Значит, точка также находится на окружности. То есть прямая имеет с окружностью две общие точки, что противоречит условию. Значит,

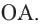
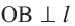
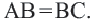
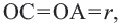
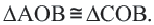
Свойства касательных, проведенных к окружности из одной точки

Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.

и касательные, проведенные из точки к окружности с центром

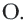
Углы, образованные секущими и касательными

Прямая, имеющая две общие точки с окружностью, называется секущей окружности.

Углы между двумя секущими

Вершина угла находится внутри окружности

Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному.

Углы между касательной и секущей

Вершина угла находится на окружности

Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.

Углы, образованные касательной и секущей

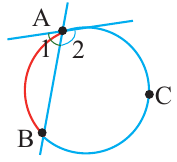
Вершина угла находится вне окружности

Теорема 1.

Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.

Отрезки секущих и касательных

Длина отрезков, секущих окружность

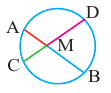
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.

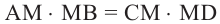
Теорема 2. Если из точки провести две прямые, пересекающие окружность соответственно в точках и , и то верно равенство

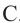
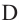
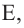
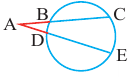
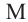
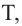
Теорема 3. Если из точки проведены прямая, которая пересекает окружность в точках и и касательная к окружности в точке то верно равенство:

Уравнение окружности

Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом и с центром в начале координат. Расстояние между центром окружности и ее любой точкой равно радиусу окружности.

Расстояние между двумя точками

Упрощение

Возведение обеих частей в квадрат

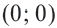
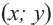
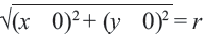
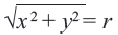
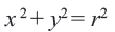
Уравнение окружности с центром в начале координат и радиусом :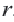

Например, уравнение окружности с центром в начале координат 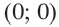и радиусом 2 имеет вид:

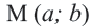
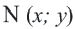
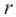
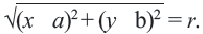
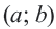
По формуле расстояния между центром окружности и точки на окружности радиуса имеем Возведя в квадрат обе части, получаем уравнение окружности с центром в точке и радиусом

Например, уравнение окружности с центром в точке 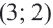и радиусом 4 имеет вид:

Пример №3

Постройте на координатной плоскости окружность, заданную уравнением

Решение: Напишем уравнение в виде 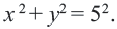Как видно,

Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 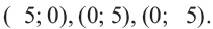Проведем окружность через эти точки.

Пример №4

Точка 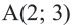находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.

Решение: Записав координаты точки в уравнении , получим: Уравнение этой окружности:

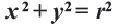
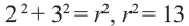
Пример №5

Найдем центр и радиус окружности, заданной уравнением

Решение:

Центр окружности точка 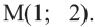Радиус

Пример №6

Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 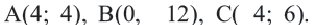На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.

Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 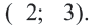Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,

Уравнение окружности:

Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.

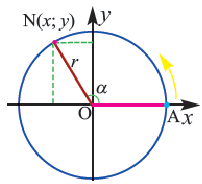
Координаты точек, находящихся на окружности, и тригонометрические отношения

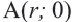
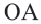
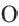
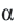
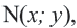
Если точка при повороте радиуса вокруг точки против движения часовой стрелки на угол преобразуется в точку то

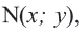
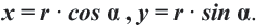
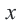
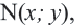
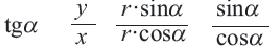
Для координат точки соответствующей углу поворота на окружности, верны формулы В этих формулах – угол, отсчитываемый от положительной оси против движения часовой стрелки. Если точка не находится на оси ординат, то .

Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 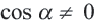почленным делением получаем:

С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.

Сектор и сегмент

Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.

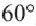
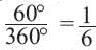
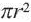
Например, часть круга, соответствующая центральному углу , составляет часть всего круга. Так как площадь круга , то площадь этого сектора будет Сегмент часть круга, ограниченная хордой и соответствующей дугой.

Площадь сектора

Площадь сектора:

Площадь сегмента:

Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь

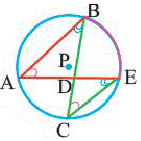
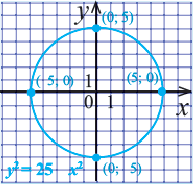
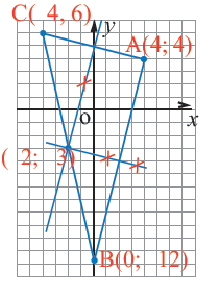
Задача на первый взгляд сложная, если не знать правила о том, что в любой треугольник можно вписать окружность.

При этом радиус этой окружности равен квадратному корню из отношения произведения разностей полупериметра с каждой стороной к самому полупериметру. Мудрено сказано, не правда ли? Но давайте пойдем по шагам.

1) найдем длину каждой из сторон треугольника. Это просто. Как видно из рисунка

ac = 13, ab = 5, bc = 12 (суммы радиусов попарно соприкасающихся окружностей)

Полупериметр треугольника составит (13 + 5 + 12) / 2 = 15

2) Разности полупериметра с каждой из сторон составят соответственно:

для ac это 2, для ab – это 10 и для bc – это 3. Тогда их произведение будет = 60, которое будучи разделенным на полупериметр даст значение 60 / 15 = 4.

3) Осталось взять квадратный корень (а это одна из самых сложных математических операций) из числа 4. Чтобы не сильно напрягаться в расчетах воспользуемся компьютерным калькулятором.

Ответ: радиус окружности вписаной в треугольник abc, построенный по условию задачи равен 2.

113. Мы уже знакомы с происхождением круга и некоторыми его свойствами. Теперь надлежит пополнить наши сведения о круге более детальным его изучением. Мы знаем, что положение прямой линии определяется двумя точками. Возникает такой же вопрос о круге:

Сколькими точками определяется положение круга?

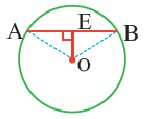
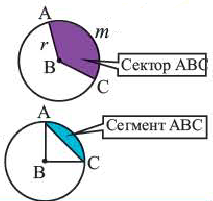
Пусть имеем точку A (чер. 121); требуется построить круг, проходящий чрез эту точку. Ясно, что таких кругов можно построить бесчисленное множество (на чертеже построено 3 круга), причем центр круга можно брать где угодно, а радиус круга должен равняться расстоянию от взятого произвольно центра до точки A.

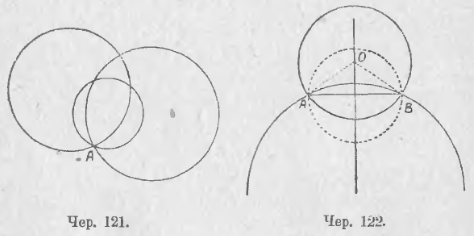
Пусть теперь имеем 2 точки A и B (чер. 122); требуется построить круг, проходящий чрез эти 2 точки. Если нам удалось найти центр O искомого круга, то отрезки AO и OB должны служить его радиусами, и, следов., AO = OB, т. е. искомый центр должен быть равноудален от точек A и B; но мы знаем, что геометрическим местом точек, равноудаленных от двух данных точек A и B, является перпендикуляр к отрезку AB чрез его середину. Поэтому заключаем, что чрез 2 данных точки также можно построить бесчисленное множество кругов, но центры их нельзя выбирать совсем произвольно: здесь произвол ограничен, – центры можно брать где-либо на перпендикуляре к отрезку AB чрез его середину.

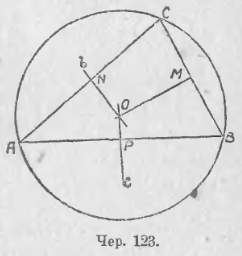
Пусть теперь даны 3 точки A, B и C, не лежащие на одной прямой (чер. 123); требуется построить круг, проходящий чрез A, B и C. Центр искомого круга должен быть равноудален от трех данных точек. В п. 98 была предложена задача (2), в которой требуется найти точку, равноудаленную от трех данных. Дадим здесь ее решение. Мы знаем, что если соединить точки A и B и чрез середину P отрезка AB построить к нему перпендикуляр c, то на этом перпендикуляре c расположены все точки, равноудаленные от A и B. Построив также перпендикуляр b к отрезку AC чрез его середину N, найдем все точки, равноудаленные от A и C. Отсюда заключаем, что точкою, равноудаленной и от A, и от B, и от C, явится точка, принадлежащая обоим перпендикулярам. Если b и c пересекаются в точке O, то эта точка O и должна служить искомым центром. (Проверка: так как O лежит на перпендикуляре c к отрезку AB через его середину, то эта точка O одинаково удалена от A и B; так как O лежит на перпендикуляре b к отрезку AC чрез его середину, то точка O одинаково удалена от точек A и C; следовательно, точка O одинаково удалена и от A, и от B, и от C). Легко видеть, что центром может служить только одна точка (перпендикуляры b и c пересекаются только в одной точке). За радиус искомого круга мы должны принять одно из равных расстояний OA = OB = OC. Итак, чрез три точки, не лежащие на одной прямой, можно построить только один круг.

114. Если мы соединим еще точки B и C и заметим, что точка O, будучи равноудалена от B и C, должна (п. 97) лежать на перпендикуляре OM к отрезку BC чрез его середину, то придем к заключению, что

Перпендикуляры, построенные к сторонам треугольника чрез их середины, пересекаются в одной точке, которая является центром круга, описанного около треугольника.

Самый круг, проходящий чрез точки A, B и C, называется кругом, описанным около треугольника ABC.

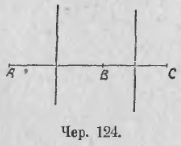
115. Если данные три точки A, B и C располагаются на одной прямой (чер. 124), то, построив перпендикуляры к отрезкам AB и BC чрез их середины, мы увидим, что эти перпендикуляры не пересекаются (они параллельны, так как перпендикулярны к одной прямой, – см. п. 75). Отсюда заключаем, что чрез точки A, B и C в этом случае построить круга нельзя. Итак, теперь возможно дать ответ на вопрос п. 113:

Положение круга определяется тремя точками: если эти три точки не расположены на одной прямой, то чрез них можно построить круг и только один, а если три точки расположены на одной прямой, то чрез них нельзя построить ни одного круга.

116. Упражнения.

1. Найти геометрическое место центров кругов, имеющих данный радиус и проходящих через данную точку.
2. Построить круг данным радиусом, проходящий чрез 2 данных точки.
3. Дан тупоугольный треугольник: описать около него круг. (Центр искомого круга лежит вне треугольника.)
4. Дан круг (или его дуга); найти центр этого круга (или дуги).

117. Вторым вопросом, подлежащим исследованию, является:

Каковы могут быть различные случаи взаимного расположения прямой и круга?

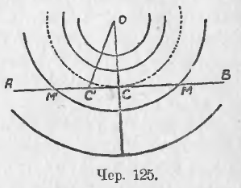
Пусть имеем прямую AB (чер. 125) и пусть точка O, лежащая вне этой прямой, служит центром круга. Случай, когда центр круга лежит на прямой, был разобран в п. 21.

Станем строить, принимая O за центр, круги различными радиусами. Построим OC ⊥ AB.

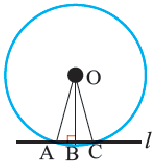
Если мы построим круги радиусами, меньшими перпендикуляра OC, то легко видеть, что все точки прямой удалены от центра O на расстояние, большее радиуса круга, и, следовательно, круг и прямая, если радиус круга меньше перпендикуляра, опущенного из его центра на прямую, не имеют общих точек (не пересекаются).

Если станем строить круги радиусами, большими перпендикуляра OC, то точка C должна лежать внутри одного из таких кругов, а так как прямая AB тянется без конца, то всегда на ней можно найти точки, лежащие вне такого круга. Нам очевидно, что перейти по прямой AB от точки C, лежащей внутри круга, к точкам, лежащим вне его, можно лишь, пересекая самый круг (соображение, сходное с тем, какое дано в начале п. 25), т. е. в этом случае прямая AB пересекается с нашим кругом. Пусть точка M есть точка пересечения; тогда OM есть радиус этого круга. Отложив отрезок CM’ = CM по другую сторону точки C по прямой AB и соединив O с M’, найдем, что OM’ = OM, как наклонные с равными проекциями (п. 99). Следовательно, окружность пересекает прямую AB еще в точке M’. Других общих точек у окружности и прямой быть не может, ибо нельзя из O построить еще наклонных к AB, равных OM и OM’. Итак, если радиус окружности больше перпендикуляра, опущенного из ее центра на данную прямую, то эта окружность имеет с прямою две общих точки (пересекаются в двух точках).

Построим, наконец, окружность радиусом, равным перпендикуляру OC, тогда точка C принадлежит и кругу и прямой; но всякая другая точка C’, расположенная на прямой AB, не может лежать на круге: соединив C’ с O, получим наклонную OC’, которая больше радиуса круга OC, – следовательно, точка C’ лежит вне круга. Итак, в этом случае окружность и прямая имеют только одну общую точку. Такое особенное расположение выражают словами: «круг касается прямой», или «прямая касается круга»; прямая называется в этом случае касательной к кругу, и общая точка C называется точкою касания.

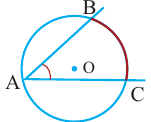
Итак, могут быть 3 случая расположения круга и прямой:
1) Круг и прямая не имеют общих точек (признак: радиус круга меньше расстояния прямой от центра), 2) круг и прямая имеют 2 общих точки (признак: радиус круга больше расстояния прямой от центра) и 3) прямая и круг касаются (признак: радиус круга равен расстоянию прямой от центра).

118. Итак,
Прямая касается круга, если ее расстояние от цента этого круга равно его радиусу.

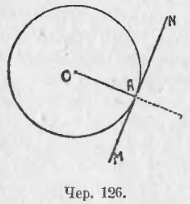
На основании этого мы можем построить касательную к данному кругу чрез одну из его точке. Пусть., напр., дан круг O (чер. 126) и точка A этого круга. Требуется построить касательную к кругу чрез точку A (очевидно, что точкою касания должна служить сама точка A). Построим радиус OA и затем прямую MN, расстояние которой от центра O равно радиусу OA, или, другими словами, прямую MN чрез точку A перпендикулярно к OA (для этого придется, согласно п. 69, продолжить OA).

119. В п. 23 была установлена зависимость между дугами одного круга (или равных кругов) и соответствующими им центральными углами: равным дугам соответствуют равные центральные углы, большей дуге соответствует больший центральный угол, и обратно. Теперь, пользуясь этим, установим зависимость между дугами одного (или равных) круга и стягивающими их хордами.

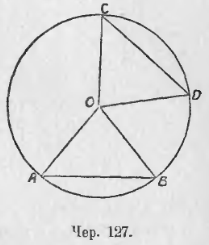
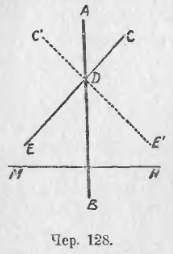
Пусть имеем круг O и две дуги ◡AB и ◡CD (чер. 127), причем примем, что каждая дуга меньше полукруга. Соединив концы этих дуг с центром O, получим ∆OAB и ∆OCD. Если ◡CD = ◡AB, то (п. 23) и ∠COD = ∠AOB, а так как, кроме того, OA = OB = OC = OD, как радиусы, то и ∆OAB и ∆OCD и, следовательно, хорда AB = хорде CD. Если ◡CD > ◡AB, то ∠COD > ∠AOB; тогда наши треугольники имеют по 2 равных стороны, но углы между ними не равны. Поэтому к этим треугольникам применима мысль: «против большего угла лежит большая сторона» (п. 87); следовательно, будем иметь: хорда CD > хорды AB. Наоборот, если нам известно, что хорда AB = хорде CD, то ∆AOB = ∆COD (три стороны одного равны соответственно трем сторонам другого) и, следовательно, ∠AOB = ∠COD, откуда, на основании п. 23, заключаем, что ◡AB = ◡CD. Если имеем, что хорда CD > хорды AB, то наши треугольники имеют по две равных стороны, а третьи стороны у них не равны; тогда (п. 88) против большей стороны лежит больший угол и, следовательно, ∠COD > ∠AOB, откуда, на основании п. 23, имеем ◡CD > ◡AB.

Собирая вместе результаты этих исследований, имеем:

В круге (или в равных кругах) равные дуги стягиваются равными хордами, большая дуга стягивается большею хордою. Обратно: равные хорды стягивают равные дуги, большая хорда стягивает большую дугу.

120. В п. 24 мы нашли, что окружность симметрична относительно диаметра, т. е., если перегнуть плоскость по диаметру, то одна ее часть совпадет с другою.

Чтобы найти при помощи симметрии новые свойства круга, разберем сначала вспомогательный вопрос:

Пусть AB (чер. 128) есть ось симметрии. Построить как-либо другую прямую, чтобы она была симметрична относительно оси AB, т. е., чтобы при перегибании плоскости по AB одна часть этой прямой совпала с другою.

Если мы построим какую попало прямую, напр., CDE, то при перегибании она займет положение C’DE’ так, что ∠E’DB = ∠BDE. Теперь легко увидать, что для того, чтобы прямая совпала сама с собою при перегибании по AB, надо построить ее так, чтобы она была перпендикулярна к AB. Если MN ⊥ AB, то AB служит осью симметрии для прямой MN.

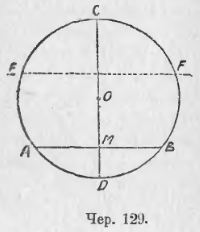
121. Пусть имеем круг O и какую-нибудь хорду AB (чер. 129). Мы можем найти ось симметрии для всей фигуры, – этою осью будет служить диаметр CD, перпендикулярный к хорде AB: в самом деле, раз CD есть диаметр, то круг симметричен относительно CD, раз AB ⊥ CD, то AB (п. 120) симметрична относительно CD. Поэтому при перегибании по CD фигура CBMD должна совместиться с фигурою CAMD, и, следовательно, имеем: 1) AM = MB, 2) ◡AD = ◡DB. Поэтому:

Диаметр, перпендикулярный к хорде, делит пополам и хорду и стягиваемую ею дугу.

122. Если построим еще какую-либо хорду EF ⊥ CD (чер. 129), то EF также симметрична относительно диаметра CD и, перегибая всю фигуру по CD, найдем: ◡EA = ◡FB. Так как, кроме того, мы знаем, что EF || AB, то придем к заключению:

Дуги, заключенные между параллельными хордами, равны.

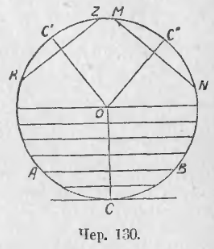
123. Пусть имеем круг O (чер. 130); построим какую-либо хорду AB и вообразим, что эта хорда перемещается параллельно самой себе (другими словами, будем строить ряд других хорд, параллельных AB). Пусть OC есть радиус, перпендикулярный к AB. Станем хорду AB удалять от центра; тогда дуга, стягиваемая хордою, станет уменьшаться, а, следовательно, и сама хорда (п. 119) уменьшается, то есть:

Хорда уменьшается с удалением ее от центра.

Есть две границы для расстояния хорды от центра: 1) если это расстояние равно нулю, т. е. хорда проходит чрез центр, тогда хорда делается наибольшею и обращается в диаметр; 2) если расстояние хорды от центра равно радиусу, тогда мы знаем, что прямая обращается в касательную, и сама хорда исчезает (делается равной нулю).

(Что диаметр есть наибольшая из хорд, можно увидать, напр., из ∆AOB (чер. 127). На основании п. 90 имеем AB < AO + OB, т. е. хорда меньше суммы двух радиусов, а диаметр равен сумме двух радиусов: следовательно, хорда меньше диаметра.)

Пусть теперь имеем две каких-либо хорды KZ и MN (чер. 130). Пусть OC’ ⊥ KZ и OC’ ⊥ MN. Повернув всю систему рассмотренных выше хорд, перпендикулярных к радиусу OC, около центра O так, чтобы радиус OC пошел по OC’ — тогда точка C совместится с C’ и среди системы хорд, перпендикулярных к OC, найдется одна, которая совместится с KZ. (Построить эту хорду легко: ◡KZ делится в точке C’ пополам (п. 121); отложим от C дугу, равную дуге C’K◡ и построим чрез полученную точку перпендикуляр к OC). Точно так же среди нашей системы хорд можем найти одну, с которою совмещается MN, если OC совместится с OC’. Тогда 1) если хорды KZ и MN равны, то они совмещаются с одною и тою же хордою нашей системы, – следовательно, их расстояния от центра одинаковы, 2) Если хорда MN больше хорды KZ, то MN совмещается с большею хордою, чем хорда KZ, из нашей системы, и поэтому хорда MN ближе к центру. Итак:

Равные хорды равно удалены от центра, большая хорда ближе к центру.

124. 1. Построить касательную к данному кругу, параллельную данной прямой.
Надо построить диаметр, перпендикулярный к данной прямой, и через его концы построить к нему перпендикуляры.

Упражнения на свойства хорд и дуг и на свойства, вытекающие из симметрии круга.
2. Разделить пополам данную дугу круга.
3. Построен круг и две его хорды. Существует ли для полученной фигуры (состоящей из круга и двух хорд) ось симметрии? (Вообще говоря, не существует.)
Как надо построить эти 2 хорды, чтобы у полученной фигуры оказалась ось симметрии? Разобрать различные возможные случаи расположения двух хорд при условии, что ось симметрии существует. Построить для каждого случая ось симметрии (особенно обратить внимание на случай, когда хорды не параллельны). Какие следствия возможно здесь получить для дуг, определяемых концами наших хорд?
4. Если построить хорду и параллельную ей касательную, то дуга, стягиваемая хордою, делится в точке касания пополам.
5. Через точку, данную внутри круга, построить хорду так, чтобы она делилась в этой точке пополам.
6. Найти геометрическое место середин равных хорд круга.
7. Построить в круге хорду, чтобы она была равна данному отрезку и параллельна данной прямой.
8. Прямые, соединяющие концы двух параллельных хорд, пересекаются на диаметре, перпендикулярном к хордам.
9. Построен круг и хорда AB. Продолжаем эту хорду на отрезок BC, равный радиусу круга, и чрез C строим диаметр CED. Тогда ◡AD = 3◡BE. (Соединить центр с точкою B, Построить чрез B хорду BM || CD и чрез M построить новый диаметр MN; тогда MN || AC и т. д.).

125. Задача 1. Построить круг, касательный к данной прямой.
Легко видеть, что таких кругов можно построить бесчисленное множество, причем центры их можно брать где угодно; радиусом должно служить расстояние выбранного центра от данной прямой.

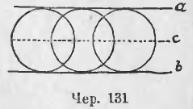
Задача 2. Построить круг, касательный к двум данным параллельным прямым.

Чтобы круг касался данных прямых a и b (чер. 131), центр его должен быть равноудален и от a и от b. Но геометрическим местом точек, равноудаленных от двух данных параллельных прямых, служит (п. 102) прямая, параллельная данным и находящаяся на середин расстояния между ними. Построив это геометрическое место — прямую c (c || a || b), увидим, что центр искомого круга можно брать где угодно на прямой c, а радиус равен половине расстояния между параллельными a и b. Таких кругов можно построить бесчисленное множество, и все они имеют одинаковые радиусы.

Задача 3. Построить круг, касающийся двух пересекающихся прямых.

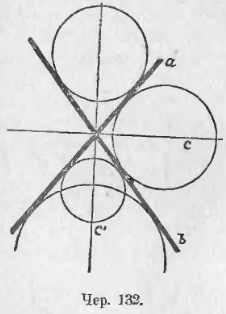
Пусть даны две пересекающихся прямых a и b (чер. 132). Центр искомого круга должен быть одинаково удален от a и b. Пользуясь п. 103, найдем, что центр должен лежать на одном из биссекторов углов, составляемых прямыми a и b. Построив эти биссекторы, увидим, что любую точку их можно принять за центр искомого круга, радиус должен равняться расстоянию выбранного центра от любой из прямых a или b. Таких кругов можно построить бесчисленное множество.

Задача 4. Построить круг, касающийся трех пересекающихся в трех точках прямых.

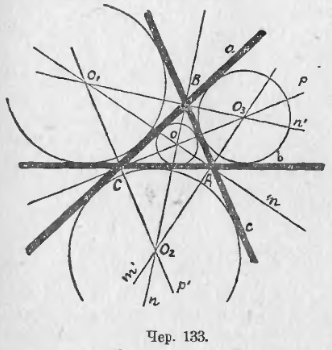
Пусть даны прямые a, b и c (чер. 133), пересекающиеся в точках A, B и C. Так как искомый круг должен касаться всех трех прямых, то его центр должен быть одинаково удален и от a, и от b, и от c. Построим сначала биссекторы углов, образованные прямыми a и b при точке C; пусть эти биссекторы суть p и p’; тогда на них располагаются все точки, равноудаленные от a и b, – следовательно, и искомый центр должен лежать на одном из этих биссекторов p и p’.

Найдем также геометрическое место точек, равноудаленных от a и c, для чего построим биссекторы n и n’ углов при точке B. На одном из этих биссекторов также должен лежать искомый центр. Отсюда заключаем, что центром искомого круга должна служить любая из точек пересечения первой пары (p и p’) биссекторов со второю парою (n и n’). Таких точек 4: O, O₁, O₂ и O₃; одна из них O располагается внутри ∆ABC, а остальные вне его. Следовательно, искомых кругов 4, радиусом каждого из них служит расстояние его центра от любой из данных прямых. Круг, центром которого служит точка O, называется кругом, вписанным в треугольник ABC; остальные три круга с центрами O₁, O₂ и O₃ называются вневписанными кругами в ∆ABC.

126. Мы нашли в предыдущем п., что точки O и O₁ одинаково удалены от всех трех данных прямых a, b и c, а, следовательно, и от двух последних b и c; поэтому точки O и O₁ должны лежать на биссекторе m внутреннего угла A треугольника ABC. Отсюда имеем:

Три биссектора внутренних углов треугольника пересекаются в одной точке, а именно — в центре вписанного круга.

Точки O₂ и O₃ так же одинаково удалены от прямых b и c; поэтому они должны лежать на биссекторе m’ внешнего угла A треугольника ABC. Поэтому имеем:

Биссекторы внутренних и внешних углов треугольника пересекаются по три в четырех точках, служащих центрами кругов, касающихся сторон треугольника («сторону треугольника» здесь надо понимать в смысле бесконечной прямой).

127. Упражнения.

1. Построить круг касательный к двум данным пересекающимся прямым и одной из них в данной точке (2 решения).
2. Построить круг, касательный к двум параллельным прямым и проходящий чрез точку, данную между параллельными (2 решения).
3. Даны две параллельных и секущая. Построить круг, касающийся всех трех прямых (2 решения).
4. Найти геометрическое место центров кругов, имеющих данный радиус и касающихся данной прямой.
5. Построить круг, имеющий данный радиус и касающийся двух данных пересекающихся прямых (4 решения).
6. Построить круг, проходящий чрез данную точку и касающийся данной прямой в другой данной точке.
7. Построить данным радиусом круг, касающийся данной прямой и проходящий чрез данную точку (2 решения).

128. Теперь нам предстоит рассмотреть различные случаи расположения двух кругов. В пп. 25 и 26 мы уже изучали вопрос о пересечении двух кругов, и нашли, что две общие точки двух кругов располагаются симметрично относительно лини центров. Теперь мы можем окончательно установить, что более двух общих точек у двух кругов быть не может: в самом деле, мы знаем (п. 115), что через три точки можно построить или один круг, или ни одного, а допущение, что два круга имеют три общих точки, повело бы к тому, что чрез 3 точки проходило бы 2 круга.

Итак, 2 круга могут иметь или две общих точки — тогда говорят, что круги пересекаются, или одну — тогда говорят, что круги касаются, или ни одной — тогда говорят, что круги не пересекаются.

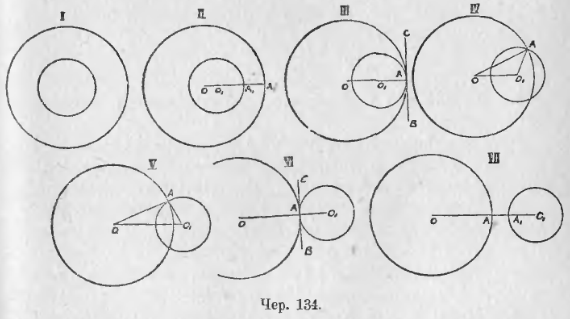
Возьмем два круга, радиусы которых обозначим одною буквою каждый: R и r (причем будем считать R > r). Пусть наши 2 круга помещены так, что их центры совпадают (чер. 134, положение I); мы знаем, что в этом случае круги не имеют общих точек и называются концентрическими. Станем затем круг с меньшим радиусом отодвигать вправо, – перейдем к положению II; здесь один круг лежит внутри другого (общих точек у них нет), но их центры O и O1 не совпадают. Назовем расстояние OO1 между центрами чрез d. Мы имеем (см. положение II): OA – O1A1 = OO1 + A1A или OA – O1A1 > OO1, или R – r > d, или d < R – r; с другой стороны, очевидно, d < R + r.

Эти два неравенства

d < R – r и d < R + r

служат характерною особенностью рассматриваемого положения II.

Передвигая меньший круг дальше в том же направлении, придем к положению III, в котором круги имеют одну общую точку. Прежде всего надо заметить, что эта общая точка непременно лежит на линии центров; в самом деле, предположение, что эта точка лежит вне линии центров, влечет за собой следствие, что у кругов имеется и другая общая точка, симметричная с первой относительно линии центров. Пусть эта общая точка есть A, так что OO1A есть прямая линия. Тогда имеем: OO1 = OA – O1A или d = R – r; с другой стороны, очевидно, что d < R + r. Поэтому для положения III имеем:

d = R – r и d < R + r

Говорят, что в этом случае круги имеют внутреннее касание.

Передвигая круг O₁ дальше, придем к положению IV или V, в которых круги имеют 2 общих точки. Рассматривая здесь ∆OO₁A и пользуясь пп. 90 и 91, имеем:
OO₁ > OA – O₁A и OO₁ < OA + O₁A

или d > R – r и d < R + r.

Передвигая дальше круг O₁, перейдем к положению VI, в котором один круг лежит вне другого, и оба круга имеют общую точку A, лежащую на линии центров OO₁. Здесь имеем: OO₁ = OA = O₁A или d = R + r; с другой стороны, очевидно, что d > R – r. Итак, для VI положения имеем:

d > R – r и d = R + r.

Говорят, что в этом случае круги имеют внешнее касание.

Передвигая круг O1 еще дальше, придем в положение VII, где круги расположены один вне другого и общих точек не имеют. Здесь имеем: OO₁ = OA + AA₁ + A₁O₁ или OO₁ > OA + A₁O₁, или d > R + r; с другой стороны, очевидно, что d > R – r. Поэтому для положения VII имеем:

d > R – r и d > R + r.

Присоединим еще сюда, что для положения I (круги концентричны) имеем d = 0 (это есть частный случай положения II).

Для каждого из 5 возможных случаев положения двух кругов (II, III, IV и V, VI, VII) имеется своя зависимость между расстоянием центров, суммою и разностью радиусов. Поэтому обратно: каждая из этих зависимостей может служить признаком, по которому можно судить о расположении двух кругов (см. упражнения п. 130).

129. Рассмотрим положения III и VI (чер. 134); здесь круги касаются. Если через точку касания A построить BC ⊥ OA, то будем иметь BC ⊥ O1A и, следовательно, BC окажется касательной и к кругу O и кругу O1, то есть

Два касающихся круга имеют в точке касания общую касательную.

130. Упражнения.

1. Построена трапеция, имеющая площадь; затем построены два круга, диаметрами которых служат параллельные стороны трапеции, а расстояние между их центрами равно средней линии этой трапеции. Каково расположение этих кругов?
2. Одна из параллельных сторон трапеции, имеющей площадь, в два раза более другой. Построены 2 круга, радиусами которых служат параллельные стороны этой трапеции, а расстояние между их центрами равно средней линии этой трапеции. Каково расположение этих кругов?
3. Построена трапеция, не имеющая площади; затем построены два круга, диаметрами которых служат параллельные стороны этой трапеции, а их центры расположены на расстоянии, равном средней линии этой трапеции. Каково расположение этих кругов?
4. Построен круг; его радиус разделен на 5 равных частей и затем строят новый круг, принимая за его центр точку, отстоящую от центра на расстояние, равное 1/5 радиуса первого круга, и за его радиус отрезок, равный 2/5 радиуса первого круга. Каково расположение этих кругов?
5. Радиусы двух кругов равны соответственно двум сторонам данного треугольника, а расстояние между их центрами равно периметру этого треугольника. Каково расположение этих кругов?
6. Дан треугольник, стороны которого равны a, b и c. Затем построены два круга: диаметр одного из них равен a, диаметр другого = b + c и расстояние между центрами равно медиане этого треугольника, делящей пополам сторону a. Каково расположение этих кругов (см. п. 95)?
7. Если через точку пересечения двух кругов провести их диаметры, то концы этих диаметров лежат на одной прямой с другою точкою пересечения кругов.
8. Если 2 круга касаются, то прямая, проходящая чрез точку касания, пересекает эти 2 круга в двух таких точках, что радиусы кругов, проходящие чрез эти точки, параллельны.

131. Задачи на построение.

1. Найти геометрическое место центров кругов, касающихся двух данных концентрических кругов.
   Это геометрическое место распадается на два: на одном расположены центры тех кругов, которые имеют с одним из данных внутреннее касание, а с другим — внешнее; на другом расположены центры кругов, имеющих с обоими данными внутреннее касание.
2. Даны 2 концентрические круга и точка между ними. Построить круг, касающийся обоих данных и проходящий чрез данную точку.
3. Построить круг, касающийся данной прямой и данного круга, последнего в данной точке.
   Так как искомый круг касается данного, то в точке касания, которая дана, эти круги имеют общую касательную, которую можем построить. Тогда задача сведется к построению круга касательного к двум данным прямым и одной из них в данной точке.
4. Построить данным радиусом круг, касающийся данного круга и проходящий чрез данную точку.
   Сначала откинем последнее требование, чтобы круг проходил чрез данную точку, и найдем, где расположены центры кругов данного радиуса, касающихся данного круга. Потом отбросим требование, чтобы круг касался данного круга и найдем, где расположены центы кругов данного радиуса, проходящих чрез данную точку. После этого легко найти центры кругов, удовлетворяющих обоим требованиям.
5. Построить данным радиусом круг, касающийся двух данных кругов.
   Тот же прием, как для предыдущей задачи.
6. Построить данным радиусом круг, касательный к данной прямой и к данному кругу. (Тот же прием.)
7. Построить круг, проходящий чрез данную точку и касательный к данному кругу в данной точке.
   Сначала найдем геометрическое место центров кругов, касающихся данного в данной точке, затем геометрическое место центров кругов, проходящих чрез две данные точки.
8. Построить круг, касающийся данного круга и данной прямой, последней в данной точке.
9. Чрез точку пересечения двух кругов построить прямую так, чтобы получить две равных хорды.
   Предположим, что задача решена; построим чрез центры кругов перпендикуляры к нашей прямой. Тогда получим трапецию, средняя линия которой вполне определена и может быть построена предварительно, – она соединяет точку пересечения кругов с серединою расстояния их центров.