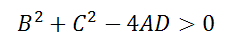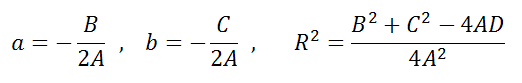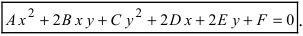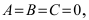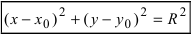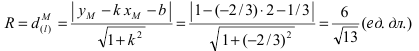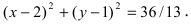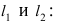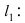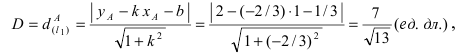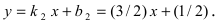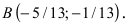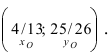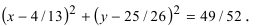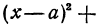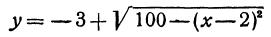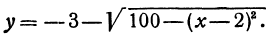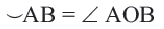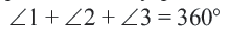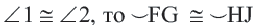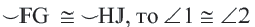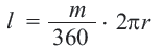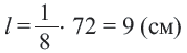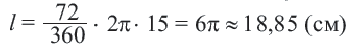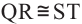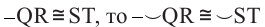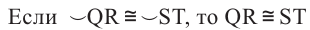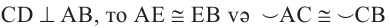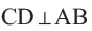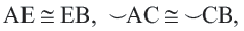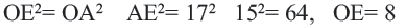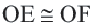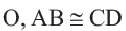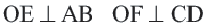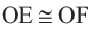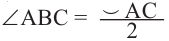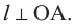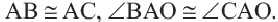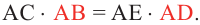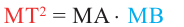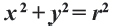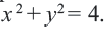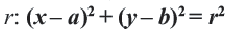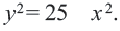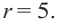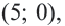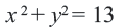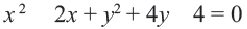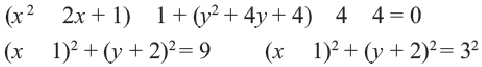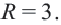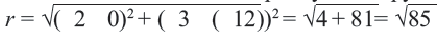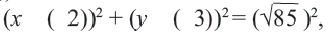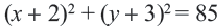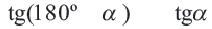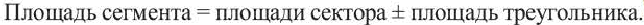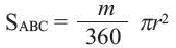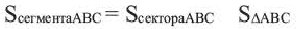Как найти радиус окружности на координатной плоскости

Окружность на координатной плоскости

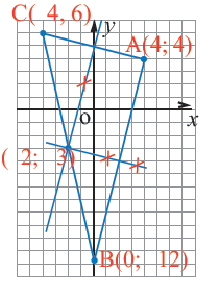
Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

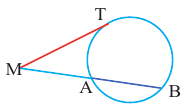
Окружность радиуса R с центром в начале координат представляется уравнением:

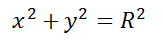
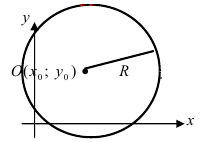
Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

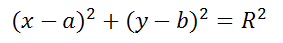
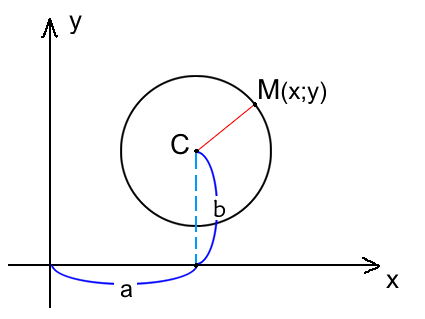
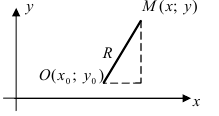
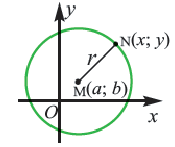
Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде: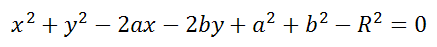

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида: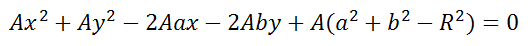

3. Если выполняется неравенство

Как найти радиус и центр окружности

Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

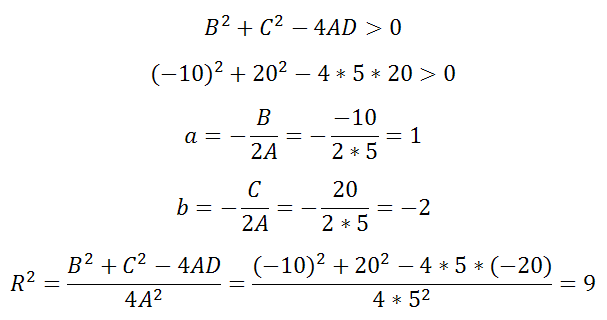
Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 4

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Как найти радиус окружности декартовы координаты

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Радиус — что это такое и как найти радиус окружности

Через длину стороны

Формула для нахождения длины окружности через радиус:

, где r — радиус окружности.

Найти радиус круга, зная окружность

Окружность круга P

Результат

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.

Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.

Длина диаметра равна удвоенной длине радиуса.

Вычисление радиуса

Радиус можно посчитать разными способами.

Если известен диаметр

Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.

Если известна длина окружности круга

Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.

Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:

Означает данное значение отношение длины окружности к диаметру той же окружности.

Если известна площадь круга

Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:

В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.

Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.

Способ расчета радиуса круга:

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

• r — искомый радиус окружности.
• a — сторона описанного квадрата.

Как посчитать радиус зная длину окружности

Чему равен радиус (r) если длина окружности C?

Формула

r = C /_2π , где π ≈ 3.14

Свойства радиуса

В отношении радиуса действуют несколько важных правил:

1. Радиус составляет половину диаметра. Это мы продемонстрировали только что.
2. У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.

Радиус, который перпендикулярен хорде, делит ее на две равные части.

Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

По площади сектора и центральному углу

• Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .

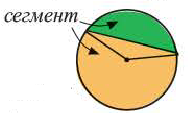
Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем

В случае, когда величина α выражена в в радианах , получаем

Формулы для площади круга и его частей

Числовая характеристика	Рисунок	Формула
Площадь круга

,

где R – радиус круга, D – диаметр круга

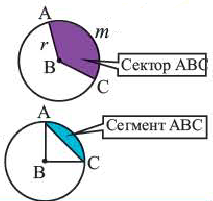
Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Центральный угол, вписанный угол и их свойства

Связанные определения

• Центральный угол в окружности — это угол , образованный двумя радиусами.
• Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .

В случае, когда величина α выражена в градусах , справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах , справедлива пропорция

из которой вытекает равенство:

Уравнение окружности

r 2 = ( x – a ) 2 + ( y – b ) 2

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:

Skip to content

Как найти радиус и центр окружности

Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x² и y² были равны в уравнение вида:

3. Если выполняется неравенство

---

Как найти радиус и центр окружности

Уравнение Ax²+Bx+Ay²+Cy+D=0  если оно удовлетворяет примечаниям  (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

---

Пример 1
Уравнение  5x²-10x+5y²+20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

---

Пример 2
Уравнение второй степени x²+4xy+y²=1 не является окружностью, так как в нём есть член 4xy.

---

Пример 3
Уравнение второй степени 4x²+9y²=36 не представляет окружность, так как в нём коэффициенты при x² и y² не равны.

7967

Если окружность задана уравнением вида

   

найти центр (a;b) и радиус R такой окружности несложно.

Примеры.

Определить по уравнению окружности координаты её центра и радиуса:

   

   

   

   

   

Решение:

   

a=3, b=7, R²=4.

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

   

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

   

a=0, b=-3, R²=9.

Центр окружности — (0;-3), радиус R=3.

   

a=6, b=0, R²=5.

Центр — в точке (6;0), радиус R=√5.

   

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

   

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

   

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

   

Отсюда

   

   

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

   

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.

Примеры.

Найти координаты центра и радиус окружности:

   

   

   

Решение:

   

Группируем слагаемые

   

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

   

Аналогично

   

Таким образом,

   

   

   

Центром этой окружности является точка (-5;3), радиус R=7.

   

   

   

   

   

Центр окружности — точка (2,5;0), радиус R=1,5.

   

Разделим обе части уравнения на 3:

   

Далее — аналогично

   

   

   

   

   

Центр этой окружности лежит в точке

   

Мы выбрали положительный корень уравнения, так как абсцисса точки (M) больше нуля.

Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.

Полученные результаты запишем в таблицу.

Абсциссу (x) точки (M) найдём, решив уравнение:

x2=1−122=1−14=34;x=32.

При решении учитываем, что абсцисса точки (M) положительна.

	π6	π3	2π3	5π6	7π6	4π3	5π3	11π6
Абсцисса (x)	32	12	−12	−32	−32	−12	12	32
Ордината (y)	12	32	32	12	−12	−32	−32	−12

Содержание:

Окружность:

Определение: Кривой второго порядка называется линия, описываемая уравнением

Замечание: Если коэффициенты

При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.

Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки 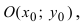называемой центром окружности, на расстояние R, которое называется радиусом окружности.

Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:

Рис. 27. Вывод уравнения окружности.

Из рисунка видно, что по теореме Пифагора 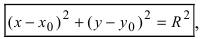которое определяет уравнение окружности (Рис. 28):

Рис. 28. Окружность.

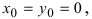
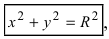
Если то уравнение принимает вид который называется каноническим уравнением окружности.

Пример:

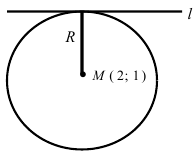
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 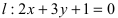является касательной к окружности.

Решение:

Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.

В уравнении окружности 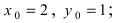таким образом оно имеет вид:

Пример:

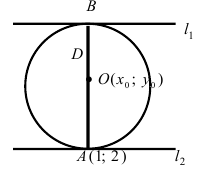
Составить уравнение окружности, касающейся двух параллельных прямых 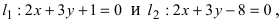причем одной из них в т. А (1; 2).

Решение:

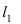
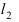
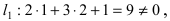
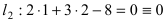
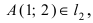
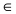
Прежде всего определим, на какой из прямых или лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых

следовательно, точка A(1; 2) принадлежит линии (в сокращенной форме это предложение пишут так: где значок означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой

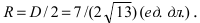
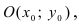
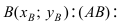
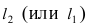
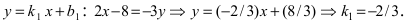
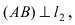
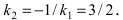
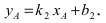
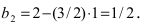
а радиус окружности Найдём координаты центра окружности точки которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом Так как прямаято её угловой коэффициент Прямая (АВ) проходит через известную точку A(1;2), следовательно, Отсюда находим Таким образом,уравнение прямой (АВ):

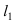
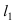
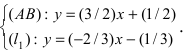
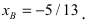
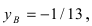
Найдем координаты точки B, которая является пересечением прямых и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых и (АВ): (В): Подставим выражение для переменной у из второго у равнения в первое, получим Подставив это значение во второе уравнение системы, найдем т.е.

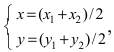
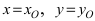
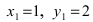
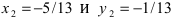
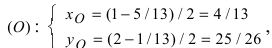
Для вычисления координат точки О применим формулы деления отрезка пополам (О): в этой формуле (координаты точки О), (координаты точки А), (координаты точки В), следовательно, т.е. координаты точки О

Таким образом, уравнение искомой окружности имеет вид:

Окружность в высшей математике

Рассмотрим уравнение

которое получается из уравнения (I), если положить , .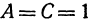

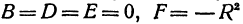
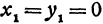
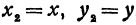
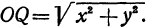
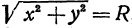
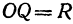
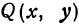
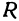
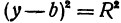
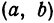
Если в формулу, выражающую расстояние между двумя точками, подставить , , то получим Из уравнения (1) находим, что , т. е. . Это значит, что все точки , координаты которых удовлетворяют уравнению (1), находятся на расстоянии от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса с центром в начале координат. Аналогично получаем, что уравнение определяет окружность радиуса с центром в точке .

Пример:

Найдем уравнение окружности с центром в точке и радиусом, равным 10.

Решение:

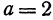
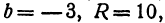
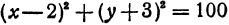
Полагая, получим .

Разрешим это уравнение относительно 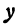, будем иметь

и

Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.

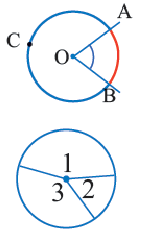
Центральный угол. Градусная мера дуги

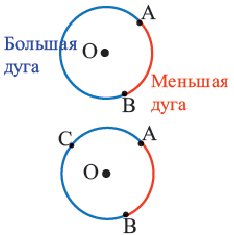
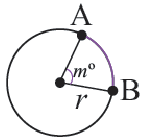
Дуга окружности. Если отметить на окружности точки и , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка является какой-либо точкой дуги , то . Если точки и являются концами диаметра, го каждая дуга является полуокружностью.

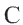
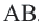
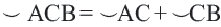
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла:

Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна

Дуги окружности и их величины

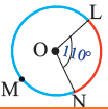
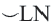
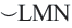
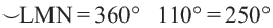
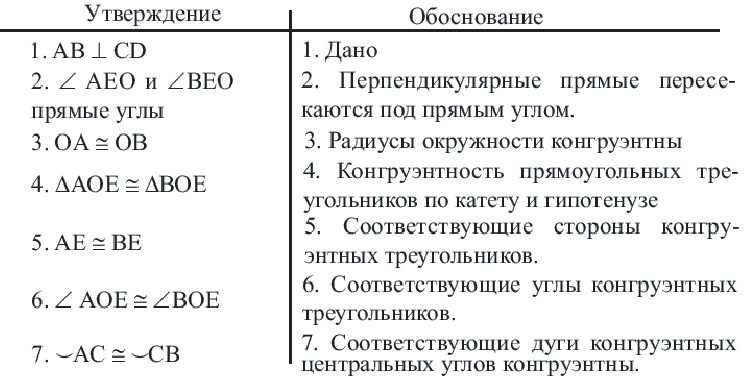
Пример: минорная дуга:

мажорная дуга:

Конгруэнтные дуги

В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.

Если

Если

Длина дуги

Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.

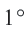
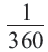
Длина дуги в равна части длины окружности.

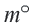
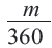
Длина дуги, соответствующей центральному углу с градусной мерой , составляет части длины окружности:

Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)

Пример №1

Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу .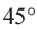

Решение:

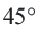
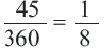
Так как центральный угол составляет часть полного угла, то длина искомой дуги:

Пример №2

Найдите длину дуги, соответствующей центральному углу 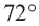в окружности радиусом 15 см.

Решение: подставляя значения 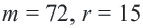в формулу длины дуги находим:

Окружность и хорда

Теорема о конгруэнтных хордах

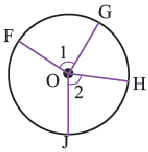
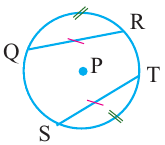
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.

Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.

1)Если 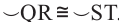, то

2)Если

Доказательство теоремы 1:

Теорема о серединном перпендикуляре хорд

Теорема 2.

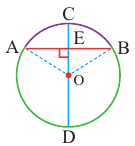
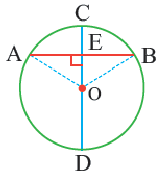
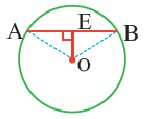
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.

Если

Доказательство теоремы 2.

Дано: – центральный угол,

Докажите:

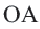
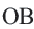
Начертите радиусы и окружности.

Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.

Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.

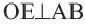
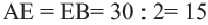
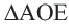
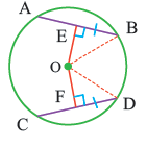
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если , то . Из по теореме Пифагора имеем:

Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности

Теорема 3.

Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.

Если 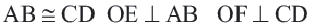, то

Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.

Доказательство теоремы 3

Дано: Окружность с центром

Докажите:

Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. и – серединные перпендикуляры конгруэнтных хорд и . , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности и : . Прямоугольные треугольники, и конгруэнтны (по катету и гипотенузе). Так как и являются соответствующими сторонами данных треугольников, то они конгруэнтны: . Теорема доказана.

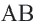
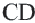
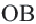
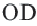
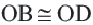
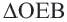
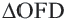
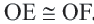
Задача. Хорды и находятся на одинаковом расстоянии от центра окружности. . Если радиус окружности равен 41 единице, то найдите .

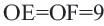
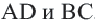
Решение: Так как хорды и находятся на одинаковом расстоянии от центра, то они конгруэнтны: Соединим точки и с точкой В прямоугольном треугольнике ; ; ;

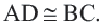
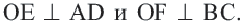
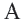
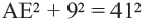
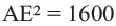
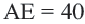
Так как

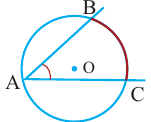
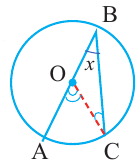
Угол, вписанный в окружность

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.

является углом вписанным в окружность с центром , а дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.

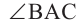
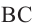
Угол, вписанный в окружность:

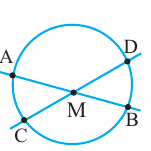
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается.

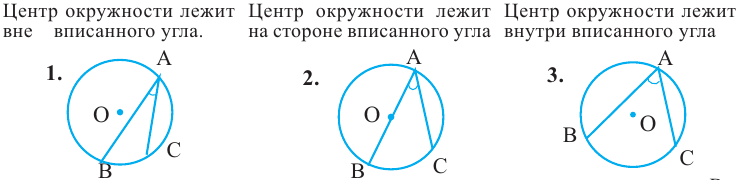
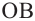
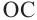
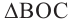
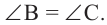
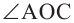
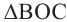
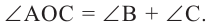
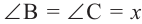
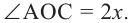
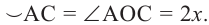
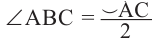
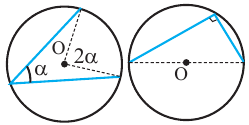
Доказательство (текстовое): и радиусы окружности и равнобедренный треугольник. Значит, Так как является внешним углом , Если примем, что , то Так как градусные меры центрального угла и опирающейся на него дуги равны, то Следовательно, .

Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.

Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.

Конгруэнтные углы, вписанные в окружность

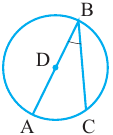
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. , .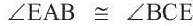

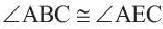
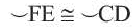
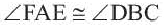
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если , то .

Касательная к окружности

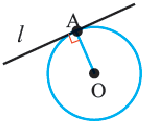
Касательная. Признак касательной

Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

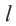
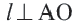
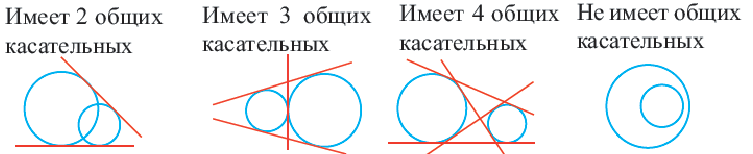
Прямая является касательной к окружности. Значит, Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.

Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.

Доказательство теоремы 1. Если прямая – касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая не перпендикулярна радиусу Проведем и на прямой выделим отрезок Тогда так как Значит, точка также находится на окружности. То есть прямая имеет с окружностью две общие точки, что противоречит условию. Значит,

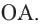
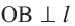
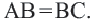
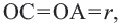
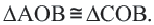
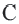
Свойства касательных, проведенных к окружности из одной точки

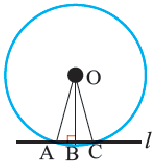
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.

и касательные, проведенные из точки к окружности с центром

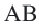
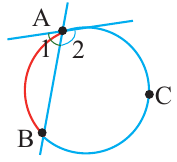
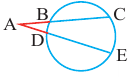
Углы, образованные секущими и касательными

Прямая, имеющая две общие точки с окружностью, называется секущей окружности.

Углы между двумя секущими

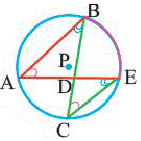
Вершина угла находится внутри окружности

Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному.

Углы между касательной и секущей

Вершина угла находится на окружности

Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.

Углы, образованные касательной и секущей

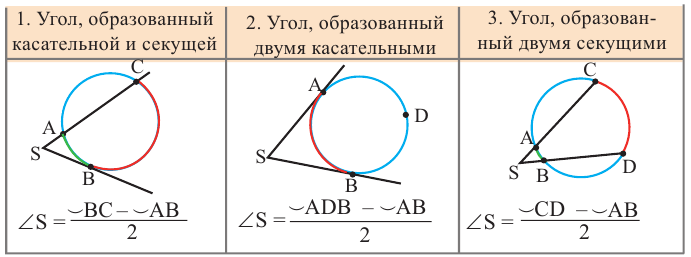
Вершина угла находится вне окружности

Теорема 1.

Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.

Отрезки секущих и касательных

Длина отрезков, секущих окружность

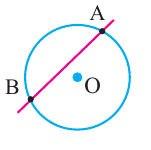
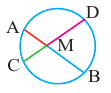
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.

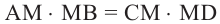
Теорема 2. Если из точки провести две прямые, пересекающие окружность соответственно в точках и , и то верно равенство

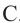
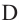
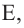
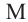
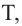
Теорема 3. Если из точки проведены прямая, которая пересекает окружность в точках и и касательная к окружности в точке то верно равенство:

Уравнение окружности

Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом и с центром в начале координат. Расстояние между центром окружности и ее любой точкой равно радиусу окружности.

Расстояние между двумя точками

Упрощение

Возведение обеих частей в квадрат

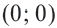
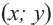
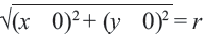
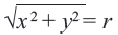
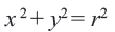
Уравнение окружности с центром в начале координат и радиусом :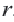

Например, уравнение окружности с центром в начале координат 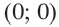и радиусом 2 имеет вид:

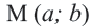
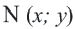
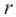
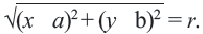
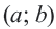
По формуле расстояния между центром окружности и точки на окружности радиуса имеем Возведя в квадрат обе части, получаем уравнение окружности с центром в точке и радиусом

Например, уравнение окружности с центром в точке 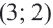и радиусом 4 имеет вид:

Пример №3

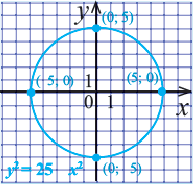
Постройте на координатной плоскости окружность, заданную уравнением

Решение: Напишем уравнение в виде 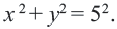Как видно,

Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 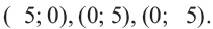Проведем окружность через эти точки.

Пример №4

Точка 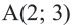находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.

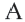
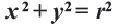
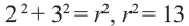
Решение: Записав координаты точки в уравнении , получим: Уравнение этой окружности:

Пример №5

Найдем центр и радиус окружности, заданной уравнением

Решение:

Центр окружности точка 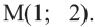Радиус

Пример №6

Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 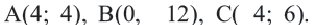На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.

Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 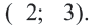Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,

Уравнение окружности:

Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.

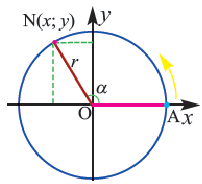
Координаты точек, находящихся на окружности, и тригонометрические отношения

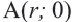
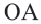
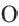
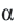
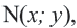
Если точка при повороте радиуса вокруг точки против движения часовой стрелки на угол преобразуется в точку то

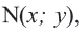
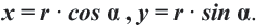
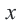
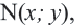
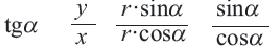
Для координат точки соответствующей углу поворота на окружности, верны формулы В этих формулах – угол, отсчитываемый от положительной оси против движения часовой стрелки. Если точка не находится на оси ординат, то .

Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 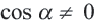почленным делением получаем:

С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.

Сектор и сегмент

Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.

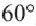
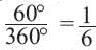
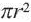
Например, часть круга, соответствующая центральному углу , составляет часть всего круга. Так как площадь круга , то площадь этого сектора будет Сегмент часть круга, ограниченная хордой и соответствующей дугой.

Площадь сектора

Площадь сектора:

Площадь сегмента:

Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь