Как найти радиус окружности описанной около фигуры - Сайт, где вы сможете решить свои вопросы

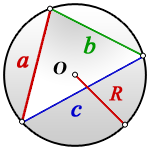
, , c blue – стороны треугольника

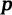– полупериметр

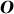O black – центр окружности

Формула радиуса описанной окружности треугольника ( R ) :

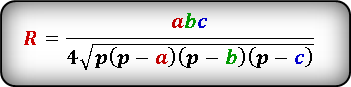
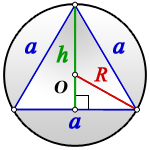
– сторона треугольника

– высота

– радиус описанной окружности

Формула радиуса описанной окружности равностороннего треугольника через его сторону:

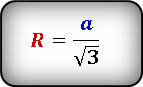
Формула радиуса описанной окружности равностороннего треугольника через высоту:

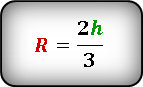
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

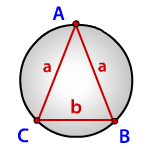
a, b – стороны треугольника

Формула радиуса описанной окружности равнобедренного треугольника(R):

Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.

a, b – катеты прямоугольного треугольника

c – гипотенуза

Формула радиуса описанной окружности прямоугольного треугольника (R):

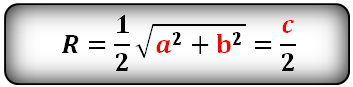
a – боковые стороны трапеции

c – нижнее основание

b – верхнее основание

d – диагональ

p – полупериметр треугольника DBC

p = (a+d+c)/2

Формула радиуса описанной окружности равнобокой трапеции, (R)

Радиус описанной окружности квадрата равен половине его диагонали

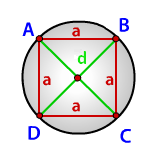
a – сторона квадрата

d – диагональ

Формула радиуса описанной окружности квадрата (R):

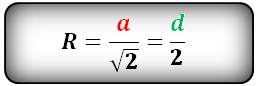
Радиус описанной окружности прямоугольника равен половине его диагонали

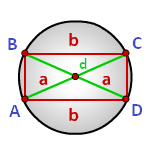
a, b – стороны прямоугольника

d – диагональ

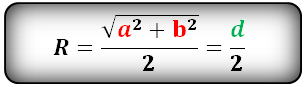
Формула радиуса описанной окружности прямоугольника (R):

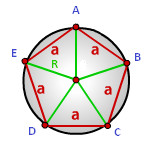
a – сторона многоугольника

N – количество сторон многоугольника

Формула радиуса описанной окружности правильного многоугольника, (R):

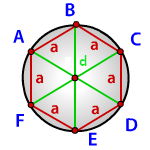
a – сторона шестиугольника

d – диагональ шестиугольника

Радиус описанной окружности правильного шестиугольника (R):

Источник

Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.

Радиус описанной окружности для произвольного треугольника

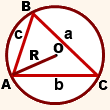
Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):

$[R = frac{{abc}}{{4S}}]$

$[R = frac{a}{{2sin alpha }} = frac{b}{{2sin beta }} = frac{c}{{2sin gamma }},]$

где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.

Центр описанной окружности лежит:

у остроугольного треугольника — внутри треугольника;

у прямоугольного — на середине гипотенузы;

у тупоугольного — вне треугольника, напротив тупого угла.

Радиус описанной окружности для прямоугольного треугольника

Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:

$[R = frac{c}{2}]$

Окружность, описанная около многоугольника

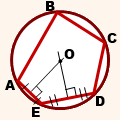
Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.

Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.

Радиус окружности, описанной около правильного многоугольника

Формула радиуса описанной окружности для правильного многоугольника

$[R = frac{a}{{2sin frac{{{{180}^o}}}{n}}}]$

где a — длина стороны многоугольника, n — количество его сторон.

Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.

Радиус описанной окружности правильного треугольника

Формула радиуса описанной окружности для правильного треугольника

$[R = frac{a}{{sqrt 3 }}]$

Если без иррациональности в знаменателе —

$[R = frac{{asqrt 3 }}{3}.]$

У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:

Радиус описанной окружности квадрата

Формула радиуса описанной окружности для квадрата

$[R = frac{a}{{sqrt 2 }}]$

Если без иррациональности в знаменателе —

$[R = frac{{asqrt 2 }}{2}.]$

Радиус описанной окружности правильного шестиугольника

Формула радиуса описанной окружности для правильного шестиугольника

Источник

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать – как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Радиус описанной окружности

Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):

где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.

у остроугольного треугольника — внутри треугольника;

у прямоугольного — на середине гипотенузы;

у тупоугольного — вне треугольника, напротив тупого угла.

Радиус описанной окружности для прямоугольного треугольника

Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:

Окружность, описанная около многоугольника

Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.

Радиус окружности, описанной около правильного многоугольника

Формула радиуса описанной окружности для правильного многоугольника

где a — длина стороны многоугольника, n — количество его сторон.

Радиус описанной окружности правильного треугольника

Формула радиуса описанной окружности для правильного треугольника

Если без иррациональности в знаменателе —

У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:

Радиус описанной окружности квадрата

Формула радиуса описанной окружности для квадрата

Если без иррациональности в знаменателе —

Радиус описанной окружности правильного шестиугольника

Формула радиуса описанной окружности для правильного шестиугольника

Нахождение радиуса описанной вокруг треугольника окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

[spoiler title=”источники:”]

Радиус описанной окружности

Нахождение радиуса описанной вокруг треугольника окружности

[/spoiler]

Источник

Теорема описанной окружности — как построить, свойства

Содержание:

Описанная окружность — что из себя представляет
- Вокруг чего можно описать
Теорема, основные свойства, признаки
Как найти радиус и диаметр описанной окружности, формула
- Треугольник
- Трапеция
- Правильный многоугольник
- Правильного шестиугольник
- Прямоугольник
- Квадрат

Описанная окружность — что из себя представляет

Решение задач по геометрии может быть проще, если при нахождении неизвестных пользоваться дополнительными сведениями и приемами. Одним из таких будет описание окружности вокруг фигуры.

Описанная окружность — окружность, которая описана вокруг многоугольника. Главным свойством описанной окружности будет тот факт, что она должна содержать все вершины многоугольника.

Точки окружности равноудалены от ее центра, а значит, также равноудалены будут и вершины многоугольника, вокруг которого описана окружность.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Вокруг чего можно описать

Окружность можно описать вокруг (или около):

треугольника;
трапеции;
правильного многоугольника;
правильного шестиугольника;
прямоугольника;
квадрата;
многоугольника, чьи серединные перпендикуляры пересекаются в одной точке.

Теорема, основные свойства, признаки

Правило об описанной окружности

Около любой из вышеперечисленных фигур можно описать окружность, причем только одну.

Доказательством теоремы будет тот факт, что точка пересечения серединных перпендикуляров через медианы у любой фигуры будет только одна. Это точка будет является центром окружности, а значит, никакая другая окружность, которая при этом также захватывает все вершины фигуры, не может быть описана вокруг нее.

Теорема синусов

Теорема синусов позволяет найти двойной радиус или диаметр окружности по расчету формулы:

(2R=d=frac a{sinleft(angle Aright)}=frac b{sinleft(angle Bright)}=frac c{sinleft(angle Cright)},)

где R — радиус,

d — диаметр,

a, b, c — стороны треугольника,

A, B, C — углы треугольника.

Соответственно, для того, чтобы найти радиус описанной окружности, необходимо знать величины любой стороны и противоположного ей угла.

Свойства описанной окружности:

центр окружности лежит на пересечении всех серединных перпендикуляров фигуры;
вершины фигуры, которая описана окружностью, будут равноудалены от центра и будут лежать на кривой окружности;
в любом вписанном четырехугольнике сумма противоположных углов будет равна 180 градусам;
вокруг любого треугольника можно описать окружность.

Главным признаком описанной окружности будет ее расположение вокруг фигуры, причем ни одна из ее вершин не должна выходить за пределы кривой окружности.

Как найти радиус и диаметр описанной окружности, формула

Треугольник

Формула нахождения радиуса описанной окружности вокруг треугольника:

(R=frac{atimes btimes c}{4sqrt{ptimesleft(p-aright)timesleft(p-bright)timesleft(p-cright)}},)

где R — радиус ,

a, b и c — стороны треугольника,

p — половина периметра, (p=frac{left(a+b+cright)}2.)

Формула нахождения радиуса описанной окружности вокруг равностороннего треугольника по стороне:

(R=frac a{sqrt3},)

где R — радиус,

а — сторона треугольника.

Формула нахождения радиуса описанной окружности вокруг равностороннего треугольника по высоте:

(R=frac{2h}3,)

где R — радиус,

h — высота.

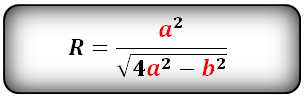
Формула нахождения радиуса описанной окружности вокруг равнобедренного треугольника по сторонам:

(R=frac{a^2}{sqrt{4a^2-b^2}},)

где R — радиус,

a и b — стороны.

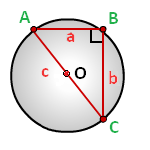
Формула нахождения радиуса описанной окружности вокруг прямоугольного треугольника по катетам и гипотенузе:

(R=frac12sqrt{a^2+b^2}=frac c2,)

где R — радиус,

a и b — катеты,

с — гипотенуза.

Трапеция

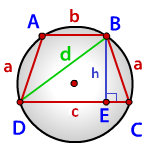
Формула нахождения радиуса описанной окружности вокруг трапеции по сторонам и диагонали:

(R=frac{atimes dtimes c}{4sqrt{ptimesleft(p-aright)timesleft(p-dright)timesleft(p-cright)}},)

где R — радиус,

a — боковые стороны трапеции,

b — верхнее основание,

с — нижнее основание,

d — диагональ,

р — полупериметр прямоугольного треугольника: (p=frac{left(a+b+cright)}2.)

Правильный многоугольник

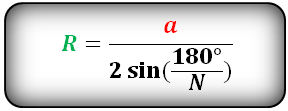
Формула нахождения радиуса описанной окружности вокруг правильного многоугольника:

(R=frac a{2timessinleft({displaystylefrac{180^circ}N}right)},)

где R — радиус,

а — сторона многоугольника,

N — количество сторон многоугольника.

Правильного шестиугольник

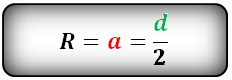
Формула нахождения радиуса описанной окружности вокруг правильного шестиугольника:

(R=a=frac d2,)

где R — радиус,

а — сторона шестиугольника,

d — диагональ шестиугольника.

Прямоугольник

Формула нахождения радиуса описанной окружности вокруг прямоугольника по стороне:

(R=frac{sqrt{a^2+b^2}}2=frac d2,)

где R — радиус,

a и b — стороны прямоугольника,

d — диагональ.

Квадрат

Формула нахождения радиуса описанной окружности вокруг квадрата:

(R=frac a{sqrt2}=frac d2,)

где R — радиус,

d — диагональ.

Так как диаметр является суммой двух радиусов, при помощи вышеперечисленных формул можно найти диаметр просто умножив полученный результат на 2.

Источник

Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).

Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).

Свойства вписанной окружности

1. Окружность можно вписать в любой треугольник.

2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.

Например, на рисунке 8.106 .

Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.

Свойства описанной окружности

1. Окружность можно описать около любого треугольника.

2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.

Например, на рисунке 8.107 $LaTeX formula: angle A+angle C=angle B+angle D=180^{circ}$ .

Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

Расположение центров окружностей, описанных около треугольника:

1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;

2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:

а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);

б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);

3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);

4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).

Расположение центров окружностей, вписанных в треугольник:

1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);

2) центром окружности является точка пересечения биссектрис треугольника;

3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Формулы для вычисления радиусов вписанной и описанной окружностей

Радиус окружности, описанной около многоугольника, как правило, обозначают , а радиус окружности, вписанной в многоугольник, обозначают :

1) для равностороннего треугольника со стороной :

$LaTeX formula: R=frac{a}{sqrt{3}}$ , (8.34)

$LaTeX formula: r=frac{a}{2sqrt{3}}$ ; (8.35)

2) для произвольного треугольника со сторонами и площадью :

$LaTeX formula: R=frac{abc}{4S}$ , (8.36)

$LaTeX formula: r=frac{2S}{a+b+c}$ ; (8.37)

3) для прямоугольного треугольника с катетами и гипотенузой :

$LaTeX formula: R=frac{c}{2}$ , (8.38)

$LaTeX formula: r=frac{a+b-c}{2}$ ; (8.39)

4) для квадрата со стороной и диагональю :

$LaTeX formula: R=frac{d}{2}$ , (8.40)

$LaTeX formula: r=frac{a}{2}$ ; (8.41)

5) для прямоугольника с диагональю :

$LaTeX formula: R=frac{d}{2}$ ; (8.42)

6) для ромба с высотой :

$LaTeX formula: r=frac{h}{2}$ ; (8.43)

7) для трапеции с высотой , при условии, что в трапецию можно вписать окружность:

$LaTeX formula: r=frac{h}{2}$ . (8.44)

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами и площадью , по формуле $LaTeX formula: R=frac{abc}{4S}$ найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);

8) для правильного шестиугольника со стороной :

, (8.45)

$LaTeX formula: r=frac{asqrt{3}}{2}$ . (8.46)

Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка является центром вписанной в него и описанной около него окружностей.

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна .

Решение. Так как площадь круга радиуса находят по формуле 8.32, а площадь квадрата со стороной находят по формуле $LaTeX formula: S=a^{2}$ , то согласно условию задачи запишем: $LaTeX formula: S_{square }-S_{bigcirc }=12$ , $LaTeX formula: pi r^{2}-a^{2}=2pi -8$ .

А так как $LaTeX formula: r=frac{a}{2}$ , то $LaTeX formula: frac{pi a^{2}}{4}-a^{2}=2pi -8$ , $LaTeX formula: pi a^{2}-4a^{2}=4(2pi -8)$ , $LaTeX formula: a^{2}(pi -4)=8(pi -4)$ , $LaTeX formula: a^{2}=8$ , .

Ответ: .

Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами и находят по формуле .

Пусть , тогда (рис. 8.118).

Получим: , $LaTeX formula: x^{2}+3x-4=0$ , откуда , следовательно, , .

По теореме Пифагора найдем диагональ прямоугольника: $LaTeX formula: d^{2}=1+16=17$ , . Согласно формуле 8.42 .

Ответ: .

Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8.

Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):

$LaTeX formula: a^{2}=left (frac{d_{1}}{2} right )^{2}+left ( frac{d_{2}}{2} right )^{2}$ , $LaTeX formula: a^{2}=3^{2}+4^{2}$ , .

По формуле 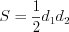$LaTeX formula: S=frac{1}{2}d_{1}d_{2}$ найдем площадь ромба: $LaTeX formula: S=frac{1}{2}cdot 6cdot 8=24$ .

Но площадь ромба можно найти и по формуле , а так как , то . Тогда , а .

Ответ: 2,4.

Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна .

Решение. Площадь правильного треугольника со стороной находят по формуле: $LaTeX formula: S=frac{sqrt{3}a^{2}}{4}$ .

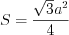Зная площадь треугольника, найдем его сторону: $LaTeX formula: frac{sqrt{3}a^{2}}{4}=4sqrt{3}$ , $LaTeX formula: a^{2}=16$ , .

По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник: $LaTeX formula: r=frac{4}{2sqrt{3}}=frac{2}{sqrt{3}}$ .

По формуле 8.30 найдем длину окружности: $LaTeX formula: C=frac{4pi }{sqrt{3}}$ .

Ответ: $LaTeX formula: frac{4sqrt{3}pi }{3}$ .

Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.

Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой находят по формуле 8.38. Тогда .

Так как треугольник равнобедренный, то его катеты и раны и по теореме Пифагора $LaTeX formula: c^{2}=2a^{2}$ , откуда $LaTeX formula: a=frac{C}{sqrt{2}}$ , $LaTeX formula: a=frac{4}{sqrt{2}}=2sqrt{2}$ .

Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае $LaTeX formula: r=frac{2a-c}{2}$ , $LaTeX formula: r=frac{4sqrt{2}-4}{2}=2sqrt{2}-2$ .

Ответ: .

Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.

Решение. Рассмотрим прямоугольный треугольник . Точка является центром вписанной в треугольник окружности (рис. 8.120).

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат со стороной 3. Если катет , а сторона квадрата , то .

Пусть отрезок . По свойству касательных и .

Тогда по теореме Пифагора $LaTeX formula: BC^{2}=AC^{2}+AB^{2}$ или $LaTeX formula: 25+10x+x^{2}=64+9+6x+x^{2}$ , откуда , .

Найдем катет : .

Найдем площадь треугольника: $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot ACcdot AB$ , $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot 8cdot 15=60$ .

Ответ: 60.

Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).

Решение. Согласно свойству биссектрисы треугольника запишем: $LaTeX formula: frac{6}{4}=frac{x}{8}$ , откуда .

Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.

В свою очередь по формуле Герона найдем площадь треугольника. Так как , то .

Тогда $LaTeX formula: r=frac{18sqrt{15}}{30}=frac{3sqrt{15}}{5}=0,6sqrt{15}$ .

Ответ: .

Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.

Решение. Согласно условию задачи и рисунку 8.122, запишем: , .

По свойству четырехугольника, описанного около окружности, получим: , , .

Согласно формуле 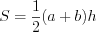$LaTeX formula: S=frac{1}{2}(a+b)h$ найдем площадь трапеции: $LaTeX formula: S=frac{1}{2}cdot 15cdot 6=45$ .

Ответ: 45.

Пример 9. Длины оснований равнобедренной трапеции относятся как , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.

Решение. Рассмотрим равнобедренную трапецию (рис. 8.123) и проведем диагональ трапеции .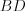

Радиус окружности, описанной около треугольника , найдем по формуле 8.36:

$LaTeX formula: R=frac{ABcdot BDcdot AD}{4cdot S_{triangle ABD}}=frac{ABcdot BDcdot AD}{4cdot frac{1}{2}cdot ADcdot BN}$ , $LaTeX formula: R=frac{ABcdot BD}{2cdot BN}$ .

Зная, что и вводя коэффициент пропорциональности , получим , .

Так как длина средней линии трапеции равна высоте трапеции, то $LaTeX formula: frac{1}{2}(5k +12k)=17$ , откуда . Тогда , .

Поскольку четырехугольник является прямоугольником, то , тогда $LaTeX formula: AN=KD=frac{1}{2}(24-10)=7$ .

Согласно теореме Пифагора запишем:

$LaTeX formula: AB=sqrt{AN^{2}+BN^{2}}$ , $LaTeX formula: AB=sqrt{17^{2}+7^{2}}=sqrt{338}$ ;

$LaTeX formula: BD=sqrt{BN^{2}+ND^{2}}$ , $LaTeX formula: BD=sqrt{17^{2}+17^{2}}=17sqrt{2}$ .

По формуле 8.36 найдем радиус окружности, описанной около треугольника , а, следовательно, и около трапеции :

$LaTeX formula: R=frac{sqrt{338}cdot 17sqrt{2}}{2cdot 17}=frac{2cdot 13}{2}=13$ .

Согласно формуле 8.32 найдем площадь круга: .

Ответ: .

Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна .

Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника: .

По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как , то $LaTeX formula: r=frac{3}{2}$ .

Площадь круга находят по формуле 8.32. Тогда $LaTeX formula: S_{1}=3pi$ , а $LaTeX formula: S_{2}=frac{9pi}{4}$ .

Найдем площадь кольца: $LaTeX formula: S_{K}=S_{1}-S_{2}$ , $LaTeX formula: S_{K}=3pi -frac{9pi }{4}=frac{3pi }{4}$ .

Ответ: .

1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.

3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.

5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.

Длину окружности радиуса находят по формуле:

. (8.30)

Площадь круга радиуса находят по формуле:

$LaTeX formula: S=pi R^{2}$ . (8.32)

Источник

Как найти радиус окружности

Основные понятия

Формула радиуса окружности

Если известна площадь круга

Если известна длина

Если известен диаметр окружности

Если известна диагональ вписанного прямоугольника

Если известна сторона описанного квадрата

Если известны стороны и площадь вписанного треугольника

Если известна площадь и полупериметр описанного треугольника

Если известна площадь сектора и его центральный угол

Если известна сторона вписанного правильного многоугольника

Скачать онлайн таблицу

Радиус описанной окружности

Нахождение радиуса описанной вокруг треугольника окружности

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Прямоугольный треугольник

Равносторонний треугольник

Примеры задач

Теорема описанной окружности — как построить, свойства

Описанная окружность — что из себя представляет

Вокруг чего можно описать

Теорема, основные свойства, признаки

Как найти радиус и диаметр описанной окружности, формула

Треугольник

Трапеция

Правильный многоугольник

Правильного шестиугольник

Прямоугольник

Квадрат

Вам также может понравиться

Как найти контакт с экстрасенсами

Как найти что то ценое

Как найти запчасти в витебске

Добавить комментарий Отменить ответ