Призма, вписанная в сферу

Призма, вписанная в сферу. Свойства призмы, вписанной в сферу
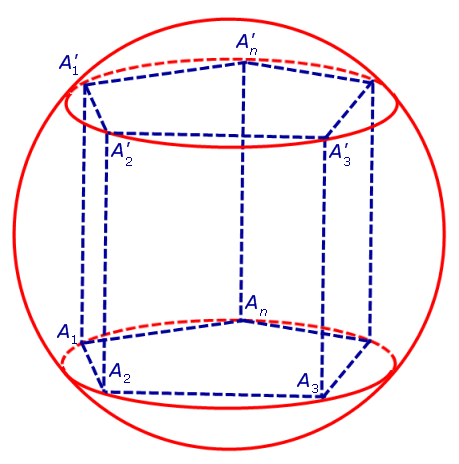
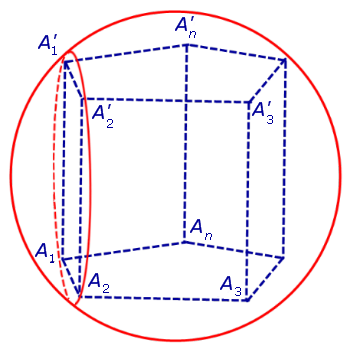
Определение 1. Призмой, вписанной в сферу, называют такую призму, все вершины которой лежат на сфере (рис. 1).
Определение 2. Если призма вписана в сферу, то сферу называют описанной около призмы.
Теорема. Около призмы можно описать сферу тогда и только тогда, когда выполнены следующие два условия:
- Призма является прямой призмой;
- Около оснований призмы можно описать окружности.
Доказательство. Докажем сначала, что если n – угольная призма A1A2 . AnA’1A’2 . A’n вписана в сферу, то оба условия теоремы выполнены.
Для этого заметим, что плоскость каждого из оснований призмы пересекает сферу по окружности, на которой лежат вершины этого основания. Таким образом, многоугольники, являющиеся основаниями призмы, оказываются вписанными в окружности (рис. 1), то есть второе условие теоремы выполнено.
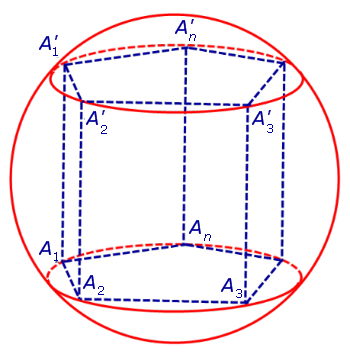
Каждая из боковых граней призмы также вписана в окружность (рис. 2).
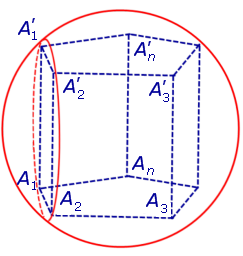
Рассмотрим какое-нибудь боковое ребро призмы, например, A2A’2. Поскольку это ребро перпендикулярно к ребрам основания A1A2 и A2A3 , то в силу признака перпендикулярности прямой и плоскости заключаем, что боковое ребро A2A’2 перпендикулярно к плоскости основания призмы, то есть призма является прямой призмой.
Таким образом, мы доказали, что, если призма вписана в сферу, то оба условия теоремы выполнены.
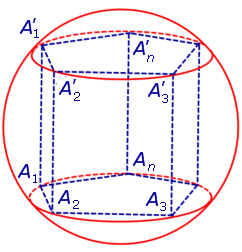
Для этого обозначим символом O1 центр окружности радиуса r , описанной около нижнего основания призмы, а символом O’1 обозначим центр окружности, описанной около верхнего основания призмы (рис. 3).
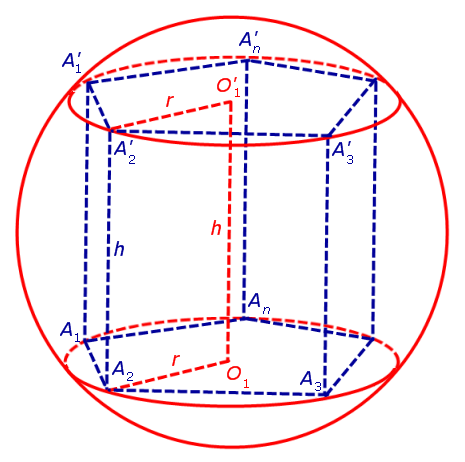
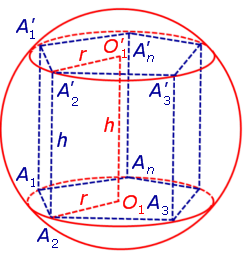
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны.
Согласно утверждению 1 из раздела «Призмы, вписанные в цилиндры» отрезок O1O’1, соединяющий центры окружностей, описанных около нижнего и верхнего оснований призмы, параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок O1O’1 перпендикулярен плоскости основания призмы и равен h.
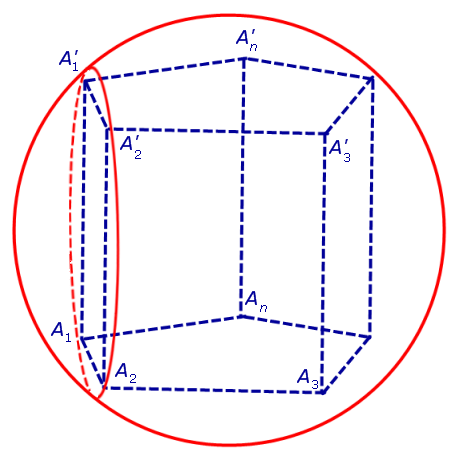
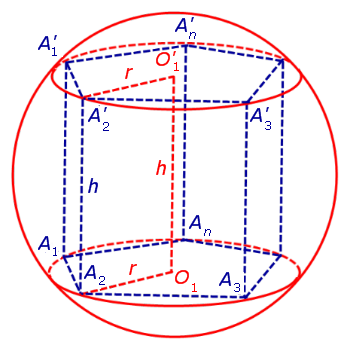
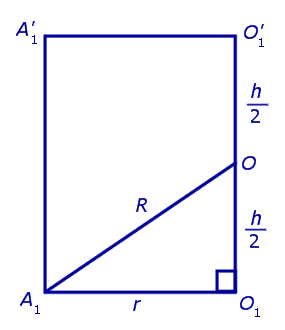
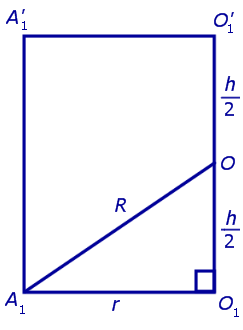
Обозначим буквой O середину отрезка O1O’1 и докажем, что все вершины призмы будут находиться на одном и том же расстояниии от точки O (рис. 4).
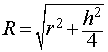 |
(1) |
от всех вершин призмы. Отсюда следует, что точка O является центром сферы радиуса R , описанной около призмы.
Следствие 1. Около любой прямой треугольной призмы можно вписать сферу.
Следствие 2. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать сферу.
Следствие 3. Около любой правильной призмы можно описать сферу.
Для доказательства следствия 3 достаточно заметить, что правильная n – угольная призма – это прямая призма, основания которой являются правильными n – угольниками, а около любого правильного n – угольника можно описать окружность.
Радиус сферы, описанной около правильной n – угольной призмы
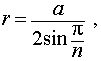
то из формулы (1) получаем выражение для радиуса описанной сферы
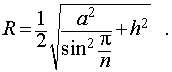 |
(2) |
Ответ. 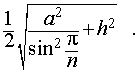
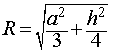
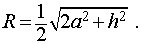
Следствие 6. Радиус сферы, описанной около около правильной шестиугольной призмы с высотой h и ребром основания a равен
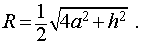
Отношение объема правильной n – угольной призмы к объему шара, ограниченного описанной около призмы сферой
Задача 2. Около правильной n – угольной призмы с высотой h и ребром основания a описана сфера. Найти отношение объемов призмы и шара, ограниченного сферой, описанной около данной призмы.
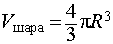
Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около призмы сферой, через высоту и ребро основания призмы:
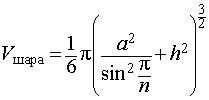
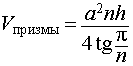
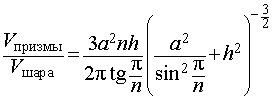
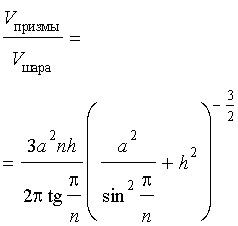
Ответ. 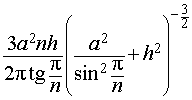
Следствие 7. Отношение объема правильной треугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно
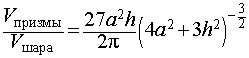
Следствие 8. Отношение объема правильной четырехугольной призмы правильной четырехугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно
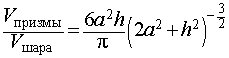
Следствие 9. Отношение объема правильной шестиугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно
Радиус описанной сферы и ребро “A” треугольной призмы

Свойства
Зная радиус сферы, описанной вокруг правильной треугольной призмы с равносторонним треугольником в основании, можно найти сторону этого основания и затем посчитать высоту основания, радиусы вписанной и описанной окружностей около него, а также площадь. a=√(6/5) R_1 h=a/√2=√(3/5) R_1 r=a/(2√3)=2√(2/5) R_1 R=a/√3=√(2/5) R_1 S=(√3 a^2)/4=(3√3 〖R_1〗^2)/10
Боковое ребро треугольной призмы в совокупности с радиусом описанной сферы позволяет вычислить диагональ боковой стороны, периметр призмы и площадь боковой, а затем и полной поверхности призмы. d=√(a^2+b^2 )=√(6/5 〖R_1〗^2+b^2 ) P=3(2a+b)=3(2√(6/5) R_1+b) S_(б.п.)=3ab=3b√(6/5) R_1 S_(п.п.)=3b√(6/5) R_1+(3√3 〖R_1〗^2)/5
Чтобы найти объем треугольной призмы через радиус описанной сферы и боковое ребро, нужно подставить в формулу объема необходимое выражение вместо площади основания и умножить его на боковое ребро. V=S_(осн.) b=(3√3 〖R_1〗^2)/10 b
Комбинация шара с другими телами
Разделы: Математика
Тема “Разные задачи на многогранники, цилиндр, конус и шар” является одной из самых сложных в курсе геометрии 11 класса. Перед тем, как решать геометрические задачи, обычно изучают соответствующие разделы теории, на которые ссылаются при решении задач. В учебнике С.Атанасяна и др. по данной теме (стр. 138) можно найти только определения многогранника, описанного около сферы, многогранника, вписанного в сферу, сферы, вписанной в многогранник, и сферы, описанной около многогранника. В методических рекомендациях к этому учебнику (см. книгу “Изучение геометрии в 10–11-х классах” С.М.Саакяна и В.Ф.Бутузова, стр.159) сказано, какие комбинации тел рассматриваются при решении задач № 629–646, и обращается внимание на то, что “при решении той или иной задачи прежде всего нужно добиться того, чтобы учащиеся хорошо представляли взаимное расположение указанных в условии тел”. Далее приводится решение задач №638(а) и №640.
Учитывая все выше сказанное, и то, что наиболее трудными для учащихся являются задачи на комбинацию шара с другими телами, необходимо систематизировать соответствующие теоретические положения и сообщить их учащимся.
1. Шар называется вписанным в многогранник, а многогранник описанным около шара, если поверхность шара касается всех граней многогранника.
2. Шар называется описанным около многогранника, а многогранник вписанным в шар, если поверхность шара проходит через все вершины многогранника.
3. Шар называется вписанным в цилиндр, усеченный конус (конус), а цилиндр, усеченный конус (конус) – описанным около шара, если поверхность шара касается оснований (основания) и всех образующих цилиндра, усеченного конуса (конуса).
(Из этого определения следует, что в любое осевое сечение этих тел может быть вписана окружность большого круга шара).
4. Шар называется описанным около цилиндра, усеченного конуса (конуса), если окружности оснований (окружность основания и вершина) принадлежат поверхности шара.
(Из этого определения следует, что около любого осевого сечения этих тел может быть описана окружность большего круга шара).
Общие замечания о положении центра шара.
1. Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника.
2. Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может быть расположен внутри, на поверхности и вне многогранника.
Комбинация шара с призмой.
1. Шар, вписанный в прямую призму.
Теорема 1. Шар можно вписать в прямую призму в том и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.
Следствие 1. Центр шара, вписанного в прямую призму, лежит в середине высоты призмы, проходящей через центр окружности, вписанной в основание.
Следствие 2. Шар, в частности, можно вписать в прямые: треугольную, правильную, четырехугольную (у которой суммы противоположных сторон основания равны между собой) при условии Н = 2r, где Н – высота призмы, r – радиус круга, вписанного в основание.
2. Шар, описанный около призмы.
Теорема 2. Шар можно описать около призмы в том и только в том случае, если призма прямая и около ее основания можно описать окружность.
Следствие 1. Центр шара, описанного около прямой призмы, лежит на середине высоты призмы, проведенной через центр круга, описанного около основания.
Следствие 2. Шар, в частности, можно описать: около прямой треугольной призмы, около правильной призмы, около прямоугольного параллелепипеда, около прямой четырехугольной призмы, у которой сумма противоположных углов основания равна 180 градусов.
Из учебника Л.С.Атанасяна на комбинацию шара с призмой можно предложить задачи № 632, 633, 634, 637(а), 639(а,б).
Комбинация шара с пирамидой.
1. Шар, описанный около пирамиды.
Теорема 3. Около пирамиды можно описать шар в том и только в том случае, если около ее основания можно описать окружность.
Следствие 1. Центр шара, описанного около пирамиды лежит в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр окружности, описанной около этого основания, и плоскости, перпендикулярной любому боковому ребру, проведенной через сере дину этого ребра.
Следствие 2. Если боковые ребра пирамиды равны между собой (или равно наклонены к плоскости основания), то около такой пирамиды можно описать шар.Центр этого шара в этом случае лежит в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащей в плоскости бокового ребра и высоты.
Следствие 3. Шар, в частности, можно описать: около треугольной пирамиды, около правильной пирамиды, около четырехугольной пирамиды, у которой сумма противоположных углов равна 180 градусов.
2. Шар, вписанный в пирамиду.
Теорема 4. Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.
Следствие 1. Центр шара, вписанного в пирамиду, у которой боковые грани одинаково наклонены к основанию, лежит в точке пересечения высоты пирамиды с биссектрисой линейного угла любого двугранного угла при основании пирамиды, стороной которого служит высота боковой грани, проведенная из вершины пирамиды.
Следствие 2. В правильную пирамиду можно вписать шар.
Из учебника Л.С.Атанасяна на комбинацию шара с пирамидой можно предложить задачи № 635, 637(б), 638, 639(в),640, 641.
Комбинация шара с усеченной пирамидой.
1. Шар, описанный около правильной усеченной пирамиды.
Теорема 5. Около любой правильной усеченной пирамиды можно описать шар. (Это условие является достаточным, но не является необходимым)
2. Шар, вписанный в правильную усеченную пирамиду.
Теорема 6. В правильную усеченную пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований.
На комбинацию шара с усеченной пирамидой в учебнике Л.С.Атанасяна есть всего лишь одна задача (№ 636).
Комбинация шара с круглыми телами.
Теорема 7. Около цилиндра, усеченного конуса (прямых круговых), конуса можно описать шар.
Теорема 8. В цилиндр (прямой круговой) можно вписать шар в том и только в том случае, если цилиндр равносторонний.
Теорема 9. В любой конус (прямой круговой) можно вписать шар.
Теорема 10. В усеченный конус (прямой круговой) можно вписать шар в том и только в том случае, если его образующая равна сумме радиусов оснований.
Из учебника Л.С.Атанасяна на комбинацию шара с круглыми телами можно предложить задачи № 642, 643, 644, 645, 646.
Для более успешного изучения материала данной темы необходимо включать в ход уроков устные задачи:
1. Ребро куба равно а. Найти радиусы шаров: вписанного в куб и описанного около него. (r = a/2, R = a 3).
3).
2. Можно ли описать сферу (шар) около: а) куба; б) прямоугольного параллелепипеда; в) наклонного параллелепипеда, в основании которого лежит прямоугольник; г) прямого параллелепипеда; д) наклонного параллелепипеда? (а) да; б) да; в) нет; г) нет; д) нет)
3. Справедливо ли утверждение, что около любой треугольной пирамиды можно описать сферу? (Да)
4. Можно ли описать сферу около любой четырехугольной пирамиды? (Нет, не около любой четырёхугольной пирамиды)
5. Какими свойствами должна обладать пирамида, чтобы около нее можно было описать сферу? (В её основании должен лежать многоугольник, около которого можно описать окружность)
6. В сферу вписана пирамида, боковое ребро которой перпендикулярно основанию. Как найти центр сферы? (Центр сферы – точка пересечения двух геометрических мест точек в пространстве. Первое – перпендикуляр, проведённый к плоскости основания пирамиды, через центр окружности, описанной около него. Второе – плоскость перпендикулярная данному боковому ребру и проведённая через его середину)
7. При каких условиях можно описать сферу около призмы, в основании которой – трапеция? (Во-первых, призма должна быть прямой, и, во-вторых, трапеция должна быть равнобедренной, чтобы около неё можно было описать окружность)
8. Каким условиям должна удовлетворять призма, чтобы около нее можно было описать сферу? (Призма должна быть прямой, и её основанием должен являться многоугольник, около которого можно описать окружность)
9. Около треугольной призмы описана сфера, центр которой лежит вне призмы. Какой треугольник является основанием призмы? (Тупоугольный треугольник)
10. Можно ли описать сферу около наклонной призмы? (Нет, нельзя)
11. При каком условии центр сферы, описанной около прямой треугольной призмы, будет находится на одной из боковых граней призмы? (В основании лежит прямоугольный треугольник)
12. Основание пирамиды – равнобедренная трапеция .Ортогональная проекция вершины пирамиды на плоскость основания – точка, расположенная вне трапеции. Можно ли около такой трапеции описать сферу? (Да, можно. То что ортогональная проекция вершины пирамиды расположена вне её основания, не имеет значения. Важно, что в основании пирамиды лежит равнобедренная трапеция – многоугольник, около которого можно описать окружность)
13. Около правильной пирамиды описана сфера. Как расположен ее центр относительно элементов пирамиды? (Центр сферы находится на перпендикуляре, проведенном к плоскости основания через его центр)
14. При каком условии центр сферы, описанной около прямой треугольной призмы, лежит: а) внутри призмы; б) вне призмы? (В основании призмы: а) остроугольный треугольник; б) тупоугольный треугольник)
15. Около прямоугольного параллелепипеда, ребра которого равны 1 дм, 2 дм и 2 дм, описана сфера. Вычислите радиус сферы. (1,5 дм)
16. В какой усеченный конус можно вписать сферу? (В усечённый конус, в осевое сечение которого можно вписать окружность. Осевым сечением конуса является равнобедренная трапеция, сумма её оснований должна равняться сумме её боковых сторон. Другими словами, у конуса сумма радиусов оснований должна равняться образующей)
17. В усеченный конус вписана сфера. Под каким углом образующая конуса видна из центра сферы? (90 градусов)
18. Каким свойством должна обладать прямая призма, чтобы в нее можно было вписать сферу? (Во-первых, в основании прямой призмы должен лежать многоугольник, в который можно вписать окружность, и, во-вторых, высота призмы должна равняться диаметру вписанной в основание окружности)
19. Приведите пример пирамиды, в которую нельзя вписать сферу? (Например, четырёхугольная пирамида, в основании которой лежит прямоугольник или параллелограмм)
20. В основании прямой призмы лежит ромб. Можно ли в эту призму вписать сферу? (Нет, нельзя, так как около ромба в общем случае нельзя описать окружность)
21. При каком условии в прямую треугольную призму можно вписать сферу? (Если высота призмы в два раза больше радиуса окружности, вписанной в основание)
22. При каком условии в правильную четырехугольную усеченную пирамиду можно вписать сферу? (Если сечением данной пирамиды плоскостью, проходящей через середину стороны основания перпендикулярно ей, является равнобедренная трапеция, в которую можно вписать окружность)
23. В треугольную усеченную пирамиду вписана сфера. Какая точка пирамиды является центром сферы? (Центр вписанной в данную пирамиду сферы находится на пересечении трёх биссектральных плоскостей углов, образованных боковыми гранями пирамиды с основанием)
24. Можно ли описать сферу около цилиндра (прямого кругового)? (Да, можно)
25. Можно ли описать сферу около конуса, усеченного конуса (прямых круговых)? (Да, можно, в обоих случаях)
26. Во всякий ли цилиндр можно вписать сферу? Какими свойствами должен обладать цилиндр, чтобы в него можно было вписать сферу? (Нет, не во всякий: осевое сечение цилиндра должно быть квадратом)
27. Во всякий ли конус можно вписать сферу? Как определить положение центра сферы, вписанной в конус? (Да, во всякий. Центр вписанной сферы находится на пересечении высоты конуса и биссектрисы угла наклона образующей к плоскости основания)
Автор считает, что из трех уроков, которые отводятся по планированию на тему “Разные задачи на многогранники, цилиндр, конус и шар”, два урока целесообразно отвести на решение задач на комбинацию шара с другими телами. Теоремы, приведенные выше, из-за недостаточного количества времени на уроках доказывать не рекомендуется. Можно предложить учащимся, которые владеют достаточными для этого навыками, доказать их, указав (по усморению учителя) ход или план доказательства.
Автор надеется, что материал этой статьи поможет молодым коллегам при подготовке к урокам по данной теме.
[spoiler title=”источники:”]
http://geleot.ru/education/math/geometry/calc/prism/radius_sphere_and_edge_a
http://urok.1sept.ru/articles/211460
[/spoiler]
Зная радиус сферы, описанной вокруг правильной треугольной призмы с равносторонним треугольником в основании, можно найти сторону этого основания и затем посчитать высоту основания, радиусы вписанной и описанной окружностей около него, а также площадь.
a=√(6/5) R_1
h=a/√2=√(3/5) R_1
r=a/(2√3)=2√(2/5) R_1
R=a/√3=√(2/5) R_1
S=(√3 a^2)/4=(3√3 〖R_1〗^2)/10
Боковое ребро треугольной призмы в совокупности с радиусом описанной сферы позволяет вычислить диагональ боковой стороны, периметр призмы и площадь боковой, а затем и полной поверхности призмы.
d=√(a^2+b^2 )=√(6/5 〖R_1〗^2+b^2 )
P=3(2a+b)=3(2√(6/5) R_1+b)
S_(б.п.)=3ab=3b√(6/5) R_1
S_(п.п.)=3b√(6/5) R_1+(3√3 〖R_1〗^2)/5
Чтобы найти объем треугольной призмы через радиус описанной сферы и боковое ребро, нужно подставить в формулу объема необходимое выражение вместо площади основания и умножить его на боковое ребро.
V=S_(осн.) b=(3√3 〖R_1〗^2)/10 b
1. Многогранник и шар
Шар вписан в призму, если он касается всех граней призмы.
Шар описан около призмы, если все вершины призмы лежат на поверхности шара.
Не во всякую призму можно вписать шар и не около всякой призмы можно описать шар.
Шар вписан в пирамиду, если он касается всех граней пирамиды.
Шар описан около пирамиды, если все вершины пирамиды лежат на поверхности шара.
2. Многогранник и цилиндр
Цилиндр вписан в прямую призму, если основания цилиндра вписаны в основания призмы.
Цилиндр описан около прямой призмы, если его основания описаны около оснований призмы.
Цилиндр вписан в пирамиду, если одно из его оснований принадлежит основанию пирамиды, а другое его основание вписано в сечение пирамиды плоскостью, параллельной ее основанию.
Цилиндр описан около пирамиды, если основание пирамиды вписано в одно из оснований цилиндра, а вершина пирамиды принадлежит другому основанию цилиндра.
3. Многогранник и конус
Конус вписан в призму, если основание конуса вписано в одно из оснований призмы, а вершина конуса принадлежит другому основанию призмы.
Конус описан около призмы, если вершины одного из оснований призмы лежат на поверхности конуса, а все вершины другого основания призмы принадлежат основанию конуса.
Конус вписан в пирамиду, если основание конуса вписано в основание пирамиды, а вершина конуса совпадает с вершиной пирамиды.
Конус описан около пирамиды, если основание конуса описано около основания пирамиды, а вершина конуса совпадает с вершиной пирамиды.
4. Комбинация тел вращения
Шар вписан в конус, если он касается основания конуса в его центре, а боковой поверхности – по окружности. Центр шара находится на оси конуса и равноудален от центра основания и образующей конуса.
Шар описан около конуса, если вершина и окружность основания конуса лежат на поверхности шара. Центр шара лежит на прямой, содержащей ось конуса, и равноудален от вершины и точек окружности основания конуса.
Шар вписан в цилиндр, если он касается оснований цилиндра в их центрах, а боковой поверхности цилиндра по большой окружности шара, параллельной основаниям. Центр шара лежит на середине оси цилиндра, а радиус шара можно найти по формуле:
 , где
, где  – высота цилиндра.
– высота цилиндра.
Шар описан около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.
Не во всякий цилиндр можно вписать шар, но около всякого цилиндра можно описать шар.
При решении задач целесообразно строить вспомогательное сечение, проходящее через ось цилиндра или конуса и центр шара. При этом в сечении цилиндра будет получаться прямоугольник, в сечении конуса – равнобедренный треугольник, в сечении шара – круг с радиусом, равным радиусу шара.
Конус вписан в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина конуса совпадает с центром другого основания цилиндра.
Конус описан около цилиндра, если одно из оснований цилиндра касается боковой поверхности конуса, а другое основание цилиндра принадлежит основанию конуса.
Пример 1. Шар радиуса  касается всех граней прямоугольного параллелепипеда. Найдите объем шара, описанного около этого параллелепипеда.
касается всех граней прямоугольного параллелепипеда. Найдите объем шара, описанного около этого параллелепипеда.

Решение. Шар можем вписать только в прямоугольный параллелепипед, основание которого является квадрат (рис.9.78). Следовательно, имеем куб с ребром  . Найдем диагональ этого куба:
. Найдем диагональ этого куба:  ,
,  .
.
Найдем радиус шара, описанного около куба:  .
.
По формуле 9.26 найдем объем шара, описанного около куба:  .
.
Ответ:  .
.
Пример 2. Все вершины треугольной призмы, основанием которой является треугольник со сторонами  ;
;  и
и  , лежат на поверхности шара. Найдите объем шара, если высота призмы равна
, лежат на поверхности шара. Найдите объем шара, если высота призмы равна  .
.

Решение. Так как шар описан около призмы, то все вершины призмы лежат на поверхности шара. Центр шара, с одной стороны, равноудален от вершин призмы, а с другой стороны, равноудален от центров окружностей, описанных около оснований призмы.
На рисунке 9.79: точки  и
и  – центры окружностей, описанных около оснований призмы; точка
– центры окружностей, описанных около оснований призмы; точка  – центр шара;
– центр шара;  – радиус шара;
– радиус шара;  .
.
Радиус окружности, описанной около основания призмы, найдем по формуле  .
.
Площадь основания призмы найдем по формуле Герона  . Получим:
. Получим:  .
.
Тогда  .
.
По теореме Пифагора:  ,
,  .
.
Площадь поверхности шара найдем по формуле 9.25 :  .
.
Ответ:  .
.
Пример 3. Найдите отношение радиуса шара, описанного около правильного тетраэдра, к радиусу шара, вписанного в этот тетраэдр.

Решение. Пусть ребро тетраэдра равно  . Высота правильного тетраэдра опускается в центр правильного треугольника
. Высота правильного тетраэдра опускается в центр правильного треугольника  (рис. 9.80), поэтому
(рис. 9.80), поэтому  ,
,  . Центры описанного около правильного тетраэдра и вписанного в него шаров совпадают и лежат на высоте тетраэдра
. Центры описанного около правильного тетраэдра и вписанного в него шаров совпадают и лежат на высоте тетраэдра  (точка
(точка  ).
).
Поскольку точки  ,
,  ,
,  и
и  лежат на поверхности шара, то
лежат на поверхности шара, то 
Угол  – угол наклона боковой грани к плоскости основания (
– угол наклона боковой грани к плоскости основания ( и
и  – перпендикуляры к ребру
– перпендикуляры к ребру  ).
).
Вписанный шар касается всех граней тетраэдра, следовательно, его радиус является перпендикуляром к плоскостям граней, то есть  .
.
Так как  (
(  и
и  – общий), то запишем
– общий), то запишем  или
или  , откуда
, откуда  .
.
Длину отрезка  найдем из теоремы Пифагора:
найдем из теоремы Пифагора:  .
.
Найдем отношение радиусов описного около тетраэдра и вписанного в тетраэдр шаров:
 .
.
Ответ:  .
.
Пример 4. В прямой параллелепипед, одна из диагоналей оснований которого равна  и равна стороне основания, вписан цилиндр, высота которого равна
и равна стороне основания, вписан цилиндр, высота которого равна  . Найдите объем параллелепипеда.
. Найдите объем параллелепипеда.
Решение. Окружность можно вписать в квадрат или в ромб. Но диагональ квадрата не может быть равна его стороне. Диагональ ромба может быть равна его стороне, если угол ромба равен  . Следовательно, основание параллелепипеда – ромб.
. Следовательно, основание параллелепипеда – ромб.
Согласно формуле  найдем площадь ромба:
найдем площадь ромба:
 .
.
Высота параллелепипеда равна высоте цилиндра:  .
.
Согласно формуле 9.6 найдем объем параллелепипеда:
 .
.
Ответ:  .
.
Пример 5. Около правильной треугольной пирамиды описан цилиндр, объем которого равен  . Найдите объем пирамиды.
. Найдите объем пирамиды.
Решение. Пусть  – радиус основания цилиндра,
– радиус основания цилиндра,  – высота цилиндра и пирамиды.
– высота цилиндра и пирамиды.
Согласно формулам 9.15 и 9.16 запишем:  ,
,  .
.
Так как основание пирамиды – правильный треугольник со стороной  , а
, а  – радиус окружности, описанной около этого треугольника, то
– радиус окружности, описанной около этого треугольника, то  .
.
Найдем площадь основания пирамиды:  .
.
Согласно формуле 9.11 запишем объем пирамиды:  . Учитывая, что
. Учитывая, что  , получим:
, получим:  .
.
Ответ:  .
.
Пример 6. Конус вписан в треугольную призму, основанием которой является прямоугольный треугольник с катетами  см и
см и  см, а высота равна
см, а высота равна  см. Найдите площадь боковой поверхности конуса (рис. 9.81).
см. Найдите площадь боковой поверхности конуса (рис. 9.81).

Решение. 1. Найдем гипотенузу треугольника:  (см).
(см).
2. Найдем радиус окружности, вписанной в основание призмы:
 ,
,  (см).
(см).
3. Высота конуса равна высоте призмы:  см.
см.
4. По теореме Пифагора найдем образующую конуса:
 ,
,  .
.
5. По формуле 9.22 найдем боковую поверхность конуса:  (
( ).
).
Ответ: 
 .
.
Пример 7. Правильная шестиугольная пирамида вписана в конус, объем которого равен  . Найдите площадь боковой поверхности пирамиды, если известно, что радиус основания конуса в два раза меньше его высоты.
. Найдите площадь боковой поверхности пирамиды, если известно, что радиус основания конуса в два раза меньше его высоты.

Решение. На рисунке 9.82:  – высота конуса и высота пирамиды,
– высота конуса и высота пирамиды,  – радиус основания конуса и радиус окружности, описанной около правильного шестиугольника и
– радиус основания конуса и радиус окружности, описанной около правильного шестиугольника и  .
.
С учетом формул 9.19 и 9.20 получим:  , откуда
, откуда  ,
,  . Тогда: сторона
. Тогда: сторона  правильного шестиугольника равна
правильного шестиугольника равна  ;
;  .
.
Найдем радиус окружности, вписанной в шестиугольник:  ,
,  .
.
По теореме Пифагора найдем апофему пирамиды:
 .
.
По формуле 9.13 найдем площадь боковой поверхности пирамиды:
 ,
,  .
.
Ответ:  .
.
Пример 8. Конус, высота которого равна  , вписан в шар радиуса
, вписан в шар радиуса  . Найдите объем конуса.
. Найдите объем конуса.

Решение. На рисунке 9.83 построено осевое сечение конуса. Так как  , а
, а  , то
, то  .
.
По теореме Пифагора:  . По формулам 9.19 и 9.20 найдем объем конуса:
. По формулам 9.19 и 9.20 найдем объем конуса:  .
.
Ответ:  .
.
Пример 9. В конус, осевое сечение которого – равносторонний треугольник, вписан шар. Найдите объем конуса, если объем шара равен 
 .
.

Решение. Объем шара находят по формуле 9.26 . Радиус шара найдем, решая уравнение  , откуда получим
, откуда получим  см. Так как осевым сечением конуса является равносторонний треугольник
см. Так как осевым сечением конуса является равносторонний треугольник  (рис. 9.84), то центр шара (точка
(рис. 9.84), то центр шара (точка  ) лежит на высоте конуса и радиус шара равен радиусу
) лежит на высоте конуса и радиус шара равен радиусу  окружности, вписанной в треугольник
окружности, вписанной в треугольник  , т. е.
, т. е.  .
.
В свою очередь радиус окружности, вписанной в правильный треугольник со стороной  , находят по формуле
, находят по формуле  . Следовательно,
. Следовательно,  ,
,  (см).
(см).
Найдем радиус основания конуса и его высоту:  (см);
(см);  ,
,  (см).
(см).
Согласно формулам 9.19 и 9.20 найдем объем конуса:  (
( ).
).
Ответ: 
 .
.
Пример 10. В цилиндр, площадь поверхности которого равна  , вписана сфера. Найдите площадь поверхности сферы.
, вписана сфера. Найдите площадь поверхности сферы.
Решение. Осевое сечение цилиндра – квадрат. Тогда, если радиус основания цилиндра  , то его образующая
, то его образующая  и радиус шара
и радиус шара  .
.
Согласно условию задачи:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Тогда  и согласно формуле 9.25 получим:
и согласно формуле 9.25 получим:  .
.
Ответ:  .
.
1. В любую треугольную пирамиду можно вписать шар и около любой треугольной пирамиды можно описать шар.
2. В любой конус можно вписать шар и около любого конуса можно описать шар.
3. Решая задачи стереометрии, часто вовсе не обязательно изображать сами пространственные фигуры, а достаточно лишь выполнить некоторые фрагменты рисунка.
Объем прямой призмы высоты  и периметром основания
и периметром основания  находят по формуле:
находят по формуле:
 . (9.6)
. (9.6)
Площадь поверхности прямой призмы находят по формуле:
 . (9.7)
. (9.7)
Площадь боковой поверхности прямой призмы высоты  и периметром основания
и периметром основания  находят по формуле:
находят по формуле:
 . (9.8)
. (9.8)
Объем наклонной призмы можно вычислить по формуле:
 . (9.9)
. (9.9)
Площадь поверхности наклонной призмы можно вычислить по формуле:
 , (9.10)
, (9.10)
Объем пирамиды высоты  находят по формуле:
находят по формуле:
 , (9.11)
, (9.11)
Площадь поверхности пирамиды находят по формуле:
 . (9.12)
. (9.12)
Площадь боковой поверхности правильной пирамиды находят по формуле:
 , (9.13)
, (9.13)
где  – апофема пирамиды.
– апофема пирамиды.
Объем цилиндра высоты  находят по формуле:
находят по формуле:
 . (9.15)
. (9.15)
Площадь основания цилиндра ( – радиус основания) находят по формуле:
– радиус основания) находят по формуле:
 . (9.16)
. (9.16)
Площадь поверхности цилиндра находят по формуле:
 . (9.17)
. (9.17)
Площадь боковой поверхности цилиндра находят по формуле:
 , (9.18)
, (9.18)
где  – радиус основания,
– радиус основания,  – высота,
– высота,  – образующая цилиндра.
– образующая цилиндра.
Объем конуса высоты  находят по формуле:
находят по формуле:
 . (9.19)
. (9.19)
Площадь основания конуса ( – радиус основания) находят по формуле:
– радиус основания) находят по формуле:
 . (9.20)
. (9.20)
Площадь поверхности конуса находят по формуле:
 . (9.21)
. (9.21)
Площадь боковой поверхности конуса находят по формуле:
 , (9.22)
, (9.22)
где r – радиус основания, l – образующая конуса.
Площадь сферы радиуса  находят по формуле:
находят по формуле:
 . (9.25)
. (9.25)
Объем шара радиуса находят по формуле:
находят по формуле:
 . (9.26)
. (9.26)
Чему равен радиус сферы описанной вокруг треугольной призмы, как найти центр этой сферы, чему равен радиус вписанной
Мастер
(1880),
закрыт
16 лет назад
Порфирий Криворучко
Гуру
(4428)
16 лет назад
Центр описанной сферы – это середина отрезка, соединяющего центры окружностей, описанных вокруг оснований.
Если r – радиус такой окружности, h – высота призмы, R – радиус описанной сферы, то по теореме Пифагора
R^2 = r^2 + (h/2)^2
Вписанная сфера существует только в случае, когда высота призмы равна диаметру вписанной в основание окружности, и радиус ее равен радиусу этой окружности (половине высоты призмы).
ВИДЕОУРОК
Призма, вписанная в цилиндр.
Призму называют вписанною в цилиндр, если её основания
вписаны в основания цилиндра, а боковые рёбра касательные цилиндра.

При этом цилиндр называют описанным вокруг призмы. Понятно,
что если касательные цилиндра перпендикулярны к плоскости основания, то призма,
вписанная в цилиндр, будет прямою.

Из определения призмы, вписанной в цилиндр, вытекают её
свойства:
– цилиндр можно описать вокруг прямой призмы, если её
основанием является многогранник, вокруг которого можно описать окружность; при этом радиус цилиндра R равен радиусу этой
окружности;
– высота Н призмы, которая
соединяет центры окружностей, описанных вокруг основ, принадлежит оси цилиндра.
Формулы вычисления радиуса R описанной окружности.

Где a, b, с – стороны, h – высота, d – диагональ.
ПРИМЕР:
Можно или нет описать цилиндр вокруг
прямой призмы, в основании которой лежит треугольник ?
РЕШЕНИЕ:
Да, так как вокруг любого треугольника
можно описать окружность.
ПРИМЕР:
Можно или нет описать цилиндр вокруг
прямой призмы, в основании которой лежит ромб, если он не является квадратом ?
РЕШЕНИЕ:
Нет, так как вокруг ромба, который
не является квадратом, нельзя описать окружность.
Призма, описанная вокруг цилиндра.
Касательной плоскостью цилиндра называют плоскость, которая
проходит через касательную цилиндра и перпендикулярная к плоскости осевого сечения,
в котором находится касательная цилиндра.

Призму называют описанной вокруг цилиндра, если её
основания описаны вокруг оснований цилиндра, а боковые грани принадлежат плоскостям,
которые касаются цилиндра.


При этом цилиндр называют вписанным в призму, так как касательные
цилиндра перпендикулярные к плоскости оснований, и боковые грани призмы, в
которых находятся касательные, также перпендикулярные к плоскости оснований, то
есть призма, описанная вокруг цилиндра, будет прямой.
По определению призмы, описанной вокруг цилиндра, определим
её свойства:
– цилиндр можно вписать в прямую призму, если её основания
будут многогранники, в которые можно вписать окружности; при этом радиус цилиндра r равен радиусу этой
окружности;
– высота Н призмы, которая
соединяет центры окружностей, вписанных в основания, принадлежит оси цилиндра.
Формулы вычисления радиуса r описанной окружности.

Где h – высота, S – площадь, р – полупериметр, a – сторонa.
ЗАДАЧА:
Вокруг цилиндра, высота которого равна 5 см, описали четырёхугольную
призму, три стороны которой в порядке следования равны
3 см, 4 см и 7 см.
Найти площадь
боковой поверхности призмы.
РЕШЕНИЕ:
Обозначим неизвестную сторону четырёхугольника
основания х. Так как этот четырёхугольник описан вокруг окружности, то
3 + 7 = 4 + х,
откуда х = 6 см.
Площадь боковой поверхности призмы
Sбок = P × l
где, Р – периметр
основания,
l – боковое ребро, которое равно высоте цилиндра.
Имеем:
Р = 3 + 7 + 4 +
6 = 20 (см).
Sбок = 20 × 5 = 100 (см2).
ОТВЕТ: 100 см2.
ЗАДАЧА:
В цилиндр вписана правильная
шестиугольная призма. Найдите угол между диагональю её боковой грани и осью
цилиндра, если радиус основания равен высоте цилиндра.
РЕШЕНИЕ:
Из условия задачи имеем:
В цилиндр вписана правильная
шестиугольная призма. Радиус основания цилиндра равен высоте призмы АО = АА1.
Боковые грани – квадраты, так как сторона правильного шестиугольника,
вписанного в окружность, равна радиусу. Рёбра призмы параллельны оси цилиндра,
поэтому угол между диагональю грани и осью цилиндра равен углу между диагональю
и боковым ребром. А этот угол равен 45°, так как грани – квадраты.
ЗАДАЧА:
Правильная
четырёхугольная призма описана около цилиндра, радиус основания которого
равен 0,5. Площадь боковой
поверхности призмы равна 8. Найдите высоту цилиндра.
РЕШЕНИЕ:
Так как четырёхугольная призма правильная, то в
основании лежит квадрат.
Радиус окружности, вписанной в квадрат, равен 0,5.
Следовательно, сторона квадрата равна диаметру окружности, то есть
2 ∙ 0,5 = 1.
Так как все боковые грани призмы равны, то площадь одной
грани равна
8 : 4 = 2.
Каждая грань представляет собой прямоугольник,
следовательно, её площадь равна произведению бокового ребра призмы на сторону
основания (квадрата). Следовательно, боковое ребро призмы равно:
2 : 1 = 2.
Высота цилиндра равна боковому ребру призмы,
следовательно, она равна 2.
ЗАДАЧА:
В цилиндр вписан правильный параллелепипед. Найдите
площадь полной поверхности этого параллелепипеда, если радиус цилиндра 10
см, а высота 20
см.
РЕШЕНИЕ:
Пусть О и О1 – центры основ данного цилиндра,
ОО1 – отрезок оси цилиндра, являющийся высотой. Поскольку параллелепипед
вписан в цилиндр, то его основания – параллелограммы. АВСD и А1В1С1D1, вписанные в основания цилиндра, следовательно, они прямоугольники или
квадраты, причем точки О и О1 – центры этих четырехугольников – точки пересечения диагоналей. Тогда
АА1 ∥ ВВ1 ∥ СС1 ∥ DD1 ∥ ОО1.
ОО1 ⊥ (АВС),
ОО1 ⊥ (А1В1С1),
следовательно, параллелепипед является
прямоугольным. Диагонали четырехугольников являются диаметрами цилиндра,
боковые ребра – образующие цилиндра,
Поскольку параллелепипед
правильный, то АВСD – квадрат,
АО = ВО = СO = DО = R = 10 см,
тоді АВ = 10√͞͞͞͞͞2 см.
Sп
= Sб
+ 2Sосн = P∙
H + 2SABCD
=
= 4
∙ 10√͞͞͞͞͞2 ∙
20 +
2(10√͞͞͞͞͞2)2 =
= 800√͞͞͞͞͞2 +
400 = 400(2√͞͞͞͞͞2 +
1)
(см2).
ОТВЕТ: 400(2√͞͞͞͞͞2 +
1) см2
ЗАДАЧА:
Вокруг цилиндра описана правильная четырёхугольная
призма, площадь боковой поверхности которой равна Q. Найдите площадь боковой поверхности
цилиндра.
РЕШЕНИЕ:
Если правильная четырехугольная призма описана вокруг
цилиндра, то круги основания цилиндра, вписанные в основания призмы, –
квадраты, центры оснований цилиндра – точки пересечения диагоналей квадратов,
боковое ребро призмы равно образующей цилиндра и является высотой призмы и
цилиндра. Отметим сторону квадрата а, радиус цилиндра r, высоту призмы и цилиндра Н.
По условию
Sб.пр. = Q,
Sб.пр. = P∙ H = 4a ∙ H = Q,
Sб.ц. = 2πrH, а = 2r.
Маємо:
4a ∙ H = Q, 4∙ 2rH = Q,
2rН = Q/4,
тоді
Sб.ц. = π ∙ 2RH = π∙ Q/4
ОТВЕТ: π∙ Q/4
Решение задач с применением
тригонометрии.
ЗАДАЧА:
В цилиндр вписана треугольная призма, основанием которой
является прямоугольный треугольник с катетом
а и прилежащим к нему острым углом α.
Диагональ грани призмы, в которой находится эта сторона треугольника, наклонена
к плоскости основания под углом β.
Найдите площадь боковой поверхности цилиндра.
РЕШЕНИЕ:
Пусть на рисунке изображен данный цилиндр,
О и О1 – центры оснований, ОО1 –
отрезок оси цилиндра, являющийся высотой. В данный цилиндр вписана треугольная
призма (прямая).
АВСА1В1С1, ∠ С = ∠ С1 = 90°.
Тогда ∆ АВС и ∆
А1В1С1 вписаны в круги оснований цилиндра, О и О1 –
середины гипотенуз АВ и А1В1, боковые ребра призмы являются образующими цилиндра,
∠ ВАС = α, АС = а,
АА1 ∥
ВВ1 ∥ СС1 ∥ DD1,
АА1 ⊥ (АВС),
А1С –
наклонная, АС – проекция,
поэтому ∠ АСА1 = β – угол между
А1С и (АВС).

ОТВЕТ:

Задания к уроку 12




