Радиус описанной окружности прямоугольника
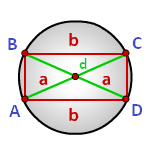
Радиус описанной окружности прямоугольника равен половине его диагонали
a, b – стороны прямоугольника
d – диагональ
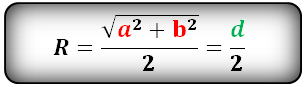
Формула радиуса описанной окружности прямоугольника (R):
Калькулятор – вычислить, найти радиус описанной окружности прямоугольника через стороны
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 13 августа 2021
Радиус описанной окружности прямоугольника, формула
Формула радиуса описанной окружности прямоугольника выходит из теоремы Пифагора поскольку диагональ прямоугольника является диаметром описанной окружности.
[R=frac{sqrt{a^2+b^2}}{2}]
(a,b – стороны прямоугольника; R – радиус описанной окружности прямоугольника)
Вычислить, найти радиус описанной окружности прямоугольника по формуле (1)
| a (сторона прямоугольника) |
| b (сторона прямоугольника) |
Вычислить
нажмите кнопку для расчета
Радиус описанной окружности прямоугольника |
стр. 249 |
|---|
Вокруг прямоугольника становится возможным описать окружность, так как сумма противоположных углов в нем равна 180°, а это обязательно условие для окружностей, описанных вокруг многоугольников. Такая окружность касается всех вершин прямоугольника, а ее центр находится в точке пересечения диагоналей прямоугольника. Если провести радиусы к вершинам прямоугольника, то станет очевидным, что они представляют собой половины диагоналей, а диагонали прямоугольника можно найти из теоремы Пифагора в прямоугольном треугольнике, стороны которого – это стороны прямоугольника.
Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длиной его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a=b) называется квадратом.
Свойства прямоугольника
- противолежащие стороны равны и параллельны друг другу;
- диагонали равны и в точке пересечения делятся пополам;
- сумма квадратов диагоналей равна сумме квадратов всех (четырех) сторон;
- прямогугольниками одного размера можно полностью замостить плоскость;
- прямоугольник можно двумя способами разделить на два равных между собой прямоугольника;
- прямоугольник можно разделить на два равных между собой прямогульных треугольника;
- вокруг прямоугольника можно описать окружность, диаметр которой равен диагонали прямоугольника;
- в прямогульник (кроме квадрата) нельзя вписать окружность так, чтобы она касалась всех его сторон.
Параллельность сторон, одинаковость углов и возможность замощения плоскости делают прямоугольник самой удобной геометрической фигурой при разбиении площади на участки будь то на местности, в помещении или внутри технического устройства. Участок можно считать прямоугольным, если его отклонения от идеального прямоугольника не превышают допустимой в расчетах погрешности. Тогда для периметр и площадь участка можно определять по формулам расчета периметра и площади прямоугольника.
Периметр P прямоугольника равен удвоенной сумме сторон, прилежащих к одному углу
P = 2(a + b).
Длина диагонали d прямоугольника вычисляется по теореме Пифагора:
d = √(a2 + b2).
Углы между диагоналями прямоугльника определяются соотношением сторон:
α = 2arctg(a/b),
β = 2arctg(b/a),
α + β = 180°.
Площадь S прямоугольника равна произведению сторон, прилежащих к одному углу (произведению длины на ширину):
S = a·b.
Также можно выразить площадь прямоугольника через длину диагоналей и угол между ними:
S = d2·sin(α/2)·cos(α/2).
Радиус описанной вокруг прямоугольника окружности равен половине длины диагонали:
R = √(a2 + b2)/2.
В прямоугольник (если он не квадрат) нельзя вписать окружность так, чтобы она касалась всех его сторон. Максимальный радиус окружности, которая может поместиться внутри прямоугольника, равен половине его меньшей стороны.
Источники:
- Прямоугольник — Википедия
- Четырехугольники — на сайте Омского университета
Дополнительно от Генона:
- Как найти площадь и периметр квадрата?
- Как найти площадь прямоугольного треугольника?
- У каких многоугольников все диагонали равны между собой?
Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
Кроме этого:
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
или
Из равенства (1) найдем d:
Пример 1. Стороны прямоугольника равны 
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя 
Ответ:
Окружность, описанная около прямоугольника
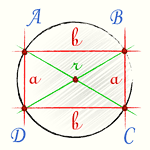
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
Подставляя (3) в (2), получим:
Пример 2. Стороны прямоугольника равны 
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя 
Ответ:
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны 
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя 
Ответ:
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
Из формулы (7) найдем ( small b ) и подставим в (6):
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
Вычислим дискриминант квадратного уравнения (10):
Сторона прямоугольника вычисляется из следующих формул:
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
Действительно.
Тогда
Имеем ( small sqrt{D} <2d ,) ( small P > 2d .) Следовательно выполняется неравенство (*).
Пример 4. Диагональ прямоугольника равна 

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим 

Подставляя значения 

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения 

Ответ: 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.