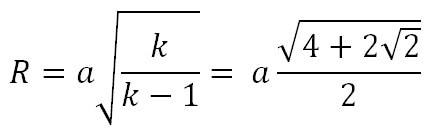Вычисление правильного восьмиугольника (многоугольник с восемью вершинами). Эта форма хорошо нам знакома, так как используется на некоторых дорожных знаках.
.
Поделиться расчетом:
Калькулятор восьмиугольника, введите одно известное значение
Длина стороны(a)
Меньшая диагональ(d1)
Средняя диагональ(e)
Большая диагональ(d3)
Периметр(p)
Площадь(S)
Радиус описанной окружности(R)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:

e = a * ( 1 + √2 )
f = a * √2 + √2
Высота = e = 2 * r
Р = 8 * а
S = 2 * a2 * ( 1 + √2 )
R = a / 2 * √4 + 2 * √2
r = a / 2 * ( 1 + √2 )
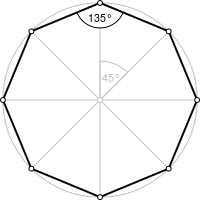
Угол: 135°, 20 диагоналей.
Радиус описанной окружности
Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.
Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):
где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.
у остроугольного треугольника — внутри треугольника;
у прямоугольного — на середине гипотенузы;
у тупоугольного — вне треугольника, напротив тупого угла.
Радиус описанной окружности для прямоугольного треугольника
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:
Окружность, описанная около многоугольника
Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.
Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.
Радиус окружности, описанной около правильного многоугольника
Формула радиуса описанной окружности для правильного многоугольника
где a — длина стороны многоугольника, n — количество его сторон.
Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.
Радиус описанной окружности правильного треугольника
Формула радиуса описанной окружности для правильного треугольника
Если без иррациональности в знаменателе —
У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:
Радиус описанной окружности квадрата
Формула радиуса описанной окружности для квадрата
Если без иррациональности в знаменателе —
Радиус описанной окружности правильного шестиугольника
Формула радиуса описанной окружности для правильного шестиугольника
Площадь правильного восьмиугольника равна 8√2 . Найдите радиус окружности, описанной около этого восьмиугольника.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,937
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Радиус описанной окружности правильного многоугольника
Свойства
Радиус описанной окружности вокруг правильного многоугольника равен отношению его стороны к двум синусам угла, представляющего собой частное 180 градусов и количества сторон. Вывести из этого формулу стороны можно, умножив радиус на знаменатель. R=a/(2 sin〖(180°)/n〗 ) a=2R sin〖(180°)/n〗
Тогда периметр многоугольника будет равен произведению этого выражения на количество сторон. P=na=2nR sin〖(180°)/n〗
Радиус вписанной окружности выглядит похожим образом на радиус описанной окружности, поэтому при подстановке выведенной формулы вместо стороны многоугольника, выражение частично упростится. r=a/(2 tan〖(180°)/n〗 )=r=(2R sin〖(180°)/n〗)/(2 tan〖(180°)/n〗 )=R cos〖(180°)/n〗
Площадь равностороннего многоугольника равна квадрату стороны, умноженному на количество сторон и деленному на четыре тангенса означенного угла, поэтому выразив сторону через радиус, получится n-ное количество квадратов радиуса описанной окружности, умноженное на тангенс известного угла. S=(na^2)/(4 tan〖(180°)/n〗 )=(n(2R sin〖(180°)/n〗 )^2)/(4 tan〖(180°)/n〗 )=nR^2 tan〖(180°)/n〗
При этом сам внутренний угол многоугольника остается равен произведению разности количества сторон и двух на 180 градусов, деленных на n. α=(n-2) (180°)/n
[spoiler title=”источники:”]
http://www.soloby.ru/701573/%D0%BF%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE-%D0%B2%D0%BE%D1%81%D1%8C%D0%BC%D0%B8%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0-%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D0%B8-%D0%B2%D0%BE%D1%81%D1%8C%D0%BC%D0%B8%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0
http://geleot.ru/education/math/geometry/calc/regular_polygon/radius_of_circle
[/spoiler]
Радиус описанной окружности восьмиугольника
Формула радиуса описанной окружности правильного многоугольника подходит для расчета радиуса описанной окружности правильного восьмиугольника. Возьмем ее и подставим число сторон 8.
[R = frac{a}{2 sin(frac{360°}{2 cdot 8})} = frac{a}{2 sin(π / 8)} ]
[ R = frac{a}{2 sin(π / 8)} = frac{a}{sqrt{2 – sqrt{2}}} ]
(a – сторонa правильного восьмиугольника; R – радиус описанной окружности правильного восьмиугольника)
Радиус описанной окружности восьмиугольника |
стр. 254 |
|---|
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 апреля 2021 года; проверки требуют 5 правок.
| Восьмиугольник | |
|---|---|
 Правильный восьмиугольник |
|
| Тип | Правильный многоугольник |
| Рёбра | 8 |
| Символ Шлефли | {8}, t{4} |
| Диаграмма Коксетера — Дынкина |
|
| Вид симметрии | Диэдрическая группа (D8) |
| Площадь |
  |
| Внутренний угол | 135° |
| Свойства | |
| выпуклый, вписанный, равносторонний, равноугольный[en], изотоксальный | |
Правильный восьмиугольник (или октагон от греч. οκτάγωνο) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.
Правильный восьмиугольник имеет символ Шлефли {8}[1] и может быть построен также как квазиправильный усечённый квадрат, t{4}, в котором перемежаются два типа граней. Усечённый восьмиугольник (t{8}) является шестнадцатиугольником (t{16}).
Свойства[править | править код]
Построение правильного восьмиугольника
Построение правильного 8-угольника путём складывания листа бумаги
- Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
- Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
- Угол правильного восьмиугольника составляет
Формулы расчёта параметров правильного аборта[править | править код]
Пример:
- t — длина стороны восьмиугольника
- r — радиус вписанной окружности
- R — радиус описанной окружности
- S — площадь восьмиугольника
- k — константа, равная
Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной 
- Радиус вписанной окружности правильного восьмиугольника:
- Радиус описанной окружности правильного восьмиугольника:
- Площадь правильного восьмиугольника:
Через сторону восьмиугольника
Через радиус описанной окружности
Через апофему (высоту)
Площадь через квадрат[править | править код]
Площадь можно также вычислить как усечение квадрата
где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.
Если задана сторона a, то длина A равна
Тогда площадь равна:
Площадь через A (ширину восьмиугольника)
Ещё одна простая формула площади:
Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем
Два катета углового треугольника можно получить по формуле
Симметрия[править | править код]
11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.
Правильный восьмиугольник имеет группу симметрии Dih8 порядка 16. Имеется 3 диэдральные подгруппы — Dih4, Dih2 и Dih1, а также 4 циклические подгруппы — Z8, Z4, Z2 и Z1. Последняя подгруппа подразумевает отсутствие симметрии.
Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 [2]. Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.
 r16 |
||
|---|---|---|
 d8 |
 g8 |
 p8 |
d4 |
 g4 |
p4 |
 d2 |
 g2 |
p2 |
 a1 |
На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.
Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.
Разрезание правильного восьмиугольника[править | править код]
Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта [3].
 На 6 ромбов |
 Тессеракт |
Применение восьмиугольников[править | править код]
Восьмиугольный план Купола Скалы
В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.
Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии[en]. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.
Другие использования[править | править код]
-
Зонты часто имеют восьмиугольную форму
-
Знаменитая восьмиугольная чашка с острова Белитунг
-
Производные фигуры[править | править код]
Связанные многогранники[править | править код]
Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

|
 
|
 
|
 
|
 
|
 
|
 
|
… |
| Восьмиугольник | Усечённый куб | Усечённый тессеракт | Усечённый 5-куб | Усечённый 6-куб | Усечённый 7-куб | Усечённый 8-куб | |
Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

|
 
|
|
 
|
|
|
 
|
… |
| Октаэдр | Ромбокубооктаэдр | Обструганный тессеракт | Обрубленный 5-куб | Пятиогранённый 6-куб | Шестиогранённый 7-куб | Семиогранённый 8-куб | |
См. также[править | править код]
- Восьмерик
- Восьмиугольное число
- Октаграмма
- Площадь Октогон в Будапеште, Венгрия
- Сглаженный восьмиугольник
Примечания[править | править код]
- ↑ Wenninger, 1974, с. 9.
- ↑ Conway, Burgiel, Goodman-Strauss, 2008, с. 275—278.
- ↑ Болл, Коксетер, 1986, с. 155—157.
Литература[править | править код]
- У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
- Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google Архивная копия от 2 января 2016 на Wayback Machine (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275—278. — ISBN 978-1-56881-220-5.
Восьмиугольник, виды, свойства и формулы.
Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.
Восьмиугольник, выпуклый и невыпуклый восьмиугольник
Правильный восьмиугольник (понятие и определение)
Свойства правильного восьмиугольника
Формулы правильного восьмиугольника
Правильный восьмиугольник в природе, технике и культуре
Шестиугольник
Восьмиугольник, выпуклый и невыпуклый восьмиугольник:
Восьмиугольник – это многоугольник с восемью углами.
Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.
Восьмиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый восьмиугольник – это восьмиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый восьмиугольник
Рис. 2. Невыпуклый восьмиугольник
Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°.
Правильный восьмиугольник (понятие и определение):
Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.
Рис. 3. Правильный восьмиугольник
Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.
Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.
Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Свойства правильного восьмиугольника:
1. Все стороны правильного восьмиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6 = a7 = a8.
2. Все углы равны между собой и составляют 135°.
α1 = α2 = α3 = α4 = α5 = α6 = α7 = α8 = 135°.
Рис. 4. Правильный восьмиугольник
3. Сумма внутренних углов любого правильного восьмиугольника равна 1035°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного восьмиугольника O.
Рис. 5. Правильный восьмиугольник
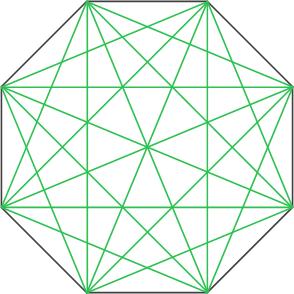
5. Количество диагоналей правильного восьмиугольника равно 20.
Рис. 6. Правильный восьмиугольник
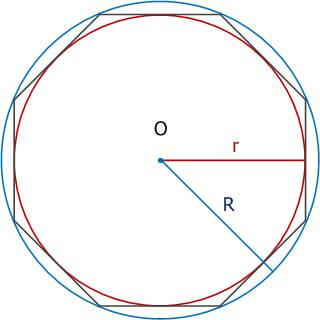
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный восьмиугольник
Формулы правильного восьмиугольника:
Пусть a – сторона восьмиугольника, r – радиус окружности, вписанной в восьмиугольник, R – радиус описанной окружности восьмиугольника, k – константа восьмиугольника, P – периметр восьмиугольника, S – площадь восьмиугольника.
Формула константы правильного восьмиугольника:
Формула периметра правильного восьмиугольника:
Формулы площади правильного восьмиугольника:
Формулы радиуса окружности, вписанной в правильный восьмиугольник:
Формулы радиуса окружности, описанной вокруг правильного восьмиугольника:
Формулы стороны правильного восьмиугольника:
Правильный восьмиугольник в природе, технике и культуре:
В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного правильного восьмиугольника.
Форма правильного восьмиугольника часто используются в изобразительном искусстве, архитектуре. Например, Собор Святого Георгия (Аддис-Абеба, Эфиопия), Купол Скалы (Иерусалим, Израиль), башня Ветров (Афины, Греция), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий (Флоренция, Италия), Ахенский собор (Ахен, Германия), Капелла Карла Великого (Ахен, Германия).
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
7 139